2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024
2. State Key Laboratory of Coastal and offshore Engineering, Dalian University of Technology, Dalian 116024, China
Level set方法是水波数值模拟中捕捉波面运动的常用方法[1-4],它通过求解Level set函数的输运方程确定交界面实时位置。然而,Level set函数在演进过程中会丧失符号距离的特征,故需要定期重构来强制恢复[5]。重构的途径有2种:一种是求解重新初始化方程,获得其稳定解[6-11];另一种是直接求解符号距离特征方程,具体方法包括快速步进法[12-16]和快速扫描法[17-21]。2类方法的不同之处在于,快速步进法是沿波前传播方向遍历网格节点,而快速扫描法是沿计算区域的坐标轴方向遍历网格节点。在快速步进重构并行研究方面,Herrmann[22]最早实现了快速步进重构的并行化,在其方案中,计算区域预先进行均匀分割,每个子区域独立进行重构,当子区域边界单元被重构后,该单元值将传递给相邻子区域上对应的虚拟单元,而相邻子区域再根据虚拟单元的值修正域内单元值。在此基础上,黄筱云等针对Level set函数值定义在网格节点的情况,提出了相互重叠内边界节点重构值传递问题的解决方案[23-24]。
上述并行方法通过均分计算区域达到平均重构开销的目的。然而,在Level set方法中,需要重构的区域位于交界面附近,重构开销与交界面的尺寸相关,而与计算区域大小无关,均分计算区域可能导致各子区域的重构计算开销差异很大。因此,本文将提出一种自适应的分区策略,新策略根据交界面位置进行划分,确保各分区内交界面的尺寸大致相等,使重构开销在线程间达到平衡,提高并行计算效率。
1 快速步进重构Level set函数ϕ符号距离特征方程为:
| $ |\nabla \phi | = 1 $ | (1) |
当采用如下迎风格式进行离散时,可得关于ϕi, j, k的二次方程:
| $ \begin{array}{l} \nabla \phi | = \left[ {\max {{\left( {D_{i, j, k}^{ - x}\phi , \; - D_{i, j, k}^{ + x}\phi , 0} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\max {\left( {D_{i, j, k}^{ - y}\phi , \; - D_{i, j, k}^{ + y}\phi , 0} \right)^2} + \\ \;\;\;\;\;\;\;\;\;{\left. {\max {{\left( {D_{i, j, k}^{ - z}\phi , \; - D_{i, j, k}^{ + z}\phi , 0} \right)}^2}} \right]^{1/2}} = 1 \end{array} $ | (2) |
式中:运算符Di, j, k-x和Di, j, k+x分别表示Level set函数空间偏导数
| $ \begin{array}{*{20}{l}} {D_{i, j, k}^{ - x}\phi = \left( {{\phi _{i, j, k}} - {\phi _{i - 1, j, k}}} \right)/\Delta h}\\ {D_{i, j, k}^{ + x}\phi = \left( {{\phi _{i + 1, j, k}} - {\phi _{i, j, k}}} \right)/\Delta h} \end{array} $ |
y和z方向上空间离散格式与之相似。该迎风格式的特点是网格节点上Level set函数的空间导数由该节点与ϕ值更小的相邻节点共同决定。因此,若这些相邻节点ϕ值已知,则该节点的值可通过求解二次方程式(2)得到。这样,ϕ值可以从交界面相邻的网格节点开始逐步向外构造,故称为快速步进重构。
快速步进重构的具体步骤如下:
1) 重构前,紧邻零等值线(面)网格节点(即内部边界节点)被标记为Alive节点,其ϕ值将采用文献[25]中的方法得到,而外侧相邻的节点定义为Close,其值通过二次方程试算得到,并根据其值放置到最小堆中,其他节点为Far节点;(在最小堆中,根结点上的ϕ值最小,任意结点上的ϕ值要大于其父结点上的值);
2) 根结点上Close节点被移出,根结点位置则被2个子结点中ϕ值较小的Close节点占据,依次,空置结点由后辈非空结点递补;
3) 被取出的Close节点将被标记成Alive,与其相邻的Far节点将被标记成Close,被添加至最小堆中,重新计算Alive新节点的相邻Close节点的ϕ值,并按照新值调整其在最小堆中的位置;
4) 当最小堆为空时,重构结束;否则,返回步骤2)。
从计算步骤来看,快速步进重构类似一个波前从等值线(面)开始,在单位法向速度作用下向两侧传播,掠过网格节点的过程。因此,快速步进重构只需在交界面周围一定带宽范围内的网格节点上执行,当波前抵达带宽边界时,即可停止重构。
2 分区并行重构按照文献[24]的方法,整个区域将沿网格线分成多个大小一致的子区域。每个子区域分配不同的线程。并行重构时,每个子区域独立执行快速步进重构。当重构的网格节点为边界节点时,其值将与之重叠的节点相比较,若小于重叠节点时,则将该值传递给重叠节点所属子区域。该相邻子区域在接收到传递值后,用该值替代重叠节点的值,并将该节点标记为Close,添加至最小堆中。同时,将域内ϕ值小于传递值的Alive节点回滚为Close,重新放回到最小堆,这个过程称为同步。
图 1描述了区域间同步的具体过程。在图 1(a)中,子区域1中节点B、C均为Alive节点,节点B的ϕ值大于节点C的ϕ值,子区域2的边界节点A为ϕ值最小的Close节点,且与子区域1中边界节点重叠;当A节点被标记成Alive后,其ϕ值将与节点C相比较,若小于节点C的值,该值将被传递相邻子区域1,如图 1(b)所示;子区域1接收到该值后,将节点C的值替换,并将节点C标记成Close,见图 1(c);然后,子区域1也将节点B的回滚成Close,见图 1(d)。

|
Download:
|
| 图 1 子区域间的同步 Fig. 1 Synchronization between sub-domains | |
当所有子区域都完成重构后,整个重构过程结束。在上述并行计算过程中,回滚操作是影响并行计算效率的关键,而回滚的次数与信息传递的次数有关。文献[24]定义了节点回滚参数Fr和信息传递参数Fc作为判断并行计算效率的指标:
| $ {{F_{\rm{r}}} = {N_{{\rm{OR}}}}/{N_{{\rm{TNN}}}}} $ | (3) |
| $ {{F_{\rm{c}}} = {N_{{\rm{OX}}}}/{N_{{\rm{TNN}}}}} $ | (4) |
式中:NOR为节点回滚操作总次数;NOX为子区域间信息传递总次数;NTNN为计算区域内重构节点总数。
3 自适应分区策略当全局重构(即计算区域内所有网格节点需要重构)时,均分计算区域可确保重构每个线程的计算开销接近。然而,因Level set方法只需局部重构,即只对交界面周围网格节点进行重构,均分策略可能会造成线程间荷载不平衡。为保证局部重构下线程荷载平衡,计算区域应根据交界面尺寸进行划分,保证每个子区域内需要重构的网格节点数目基本相同。同时,为减少信息传递,区域划分应尽量控制需要重构的内边界网格节点的数量。
新的分区策略类似k-d树的剖分方法。定义交界面为Γ,线程总数为NP,计算区域S划分过程如下:
1) 令o=1, n=Np, Γo=Γ, So=S;
2) 确定交界面Γo的坐标中值(xc, yc);
3) 比较交界面Γo与x=xc分割So所形成2个封闭边界的交点数目,定义较大者为mx;同样,确定y=yc分割So后交界面Γo与两子区域边界的交点数中的较大值my;
4) 若mx<my,Γo上x>xc的部分移到Γo,其余部分保留在Γo中,So中x>xc的网格移到So+n/2,而其他网格保留下来;否则,将交界面中y>yc的部分以及y>yc网格分别移到So+n/2和So+n/2中;
5) 若n>2,则o←o, n←n/2, Γo←Γo和o←o+n/2, n←n/2, Γo←Γo+n/2,并返回步骤2)执行递归操作。
在具体操作中,交界面的坐标中值(xc, yc)可用交界面经过网格的中心坐标的中值代替。若直线x=xc和y=yc不与网格线重合,应取最近的平行网格线代替,以保证计算区域沿网格线划分。按照该算法,椭圆边界的重构问题在4线程下区域划分如图 2(b)所示,图 2(a)则为均分区域结果。

|
Download:
|
| 图 2 计算区域自适应划分 Fig. 2 Adaptive decomposition of computational domain | |
为检验分区策略的效果,定义荷载平衡参数:
| $ {F_{\rm{b}}} = {N_{{\rm{MR}}}}/{N_{{\rm{AR}}}} - 1 $ | (5) |
式中:NMR为单一子区域节点重构次数最大值;NAR为子区域节点重构平均次数。Fb=0说明重构开销在子区域间保持平衡。
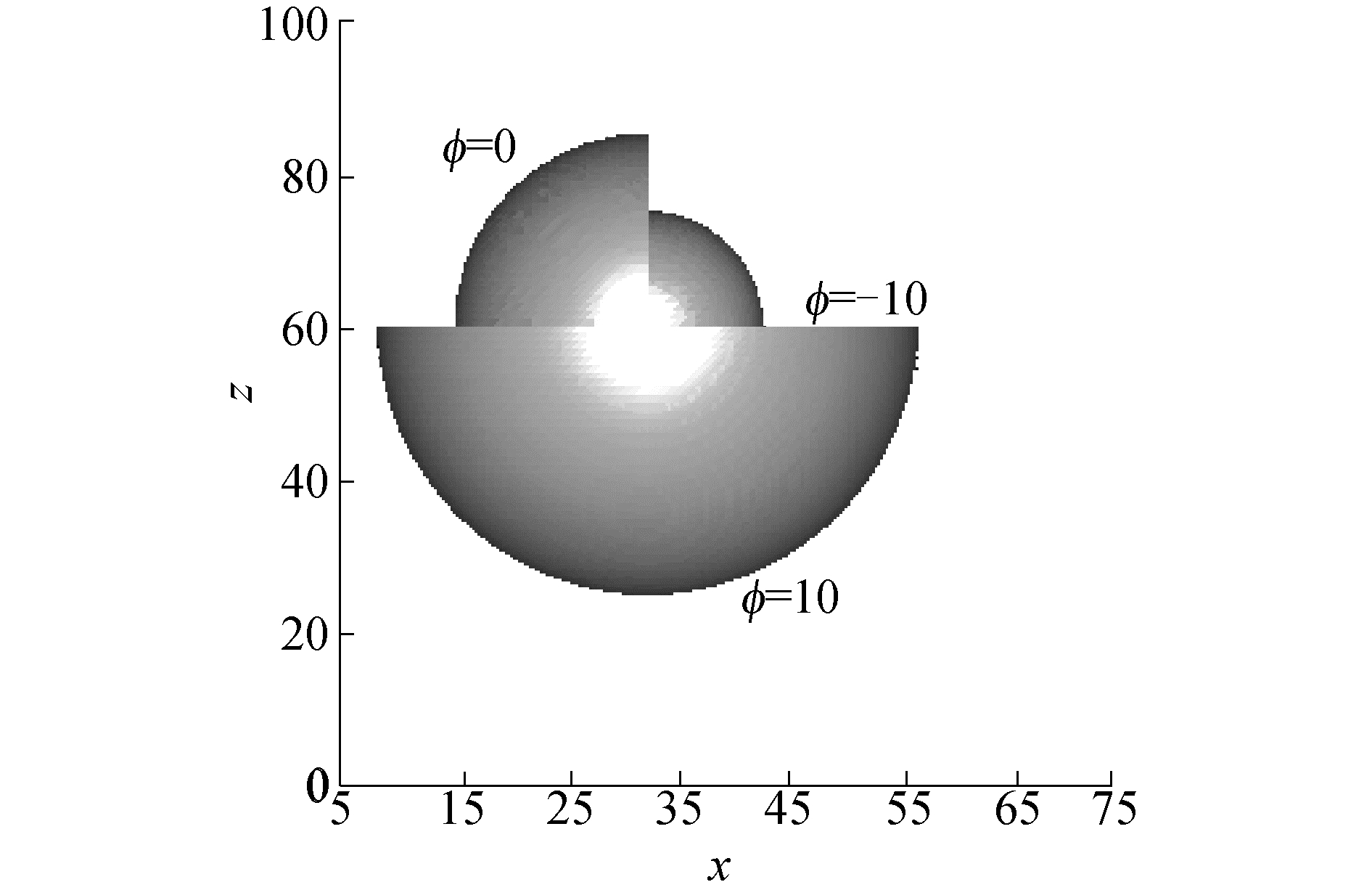
4 分区优化算例 4.1 圆球计算区域为100×100×100,圆球位于(40, 60, 60)处,球体半径为25。整个计算区域将划分成8个子区域,并选取重构的范围为ϕ∈[-12, 12]。图 3给出了重构后ϕ=-10和ϕ=10等值面结果。表 1为ϕ=10等值面所包围体积以及重构的计算误差,其中L1误差按照文献[25]计算:
|
Download:
|
| 图 3 圆球等值面重构 Fig. 3 Isosurface reconstruction of the sphere | |
| 表 1 圆球等值面f=10并行重构的计算损失和误差 Table 1 Computational loss and error of parallel reconstruction of the sphere isosurface of f=10 |
| $ {\left\| E \right\|_1} = \sum\limits_{i, j, k = 1}^N {\left| {\phi _{ijk}^{{\rm{compute}}} - \phi _{ijk}^{{\rm{actual}}}} \right|} /N $ | (6) |
式中:N为重构节点的个数。
体积采用文献[8]中的方法计算:
| $ V = \int H (\phi ){\rm{d}}\mathit{\boldsymbol{x}} $ | (7) |
式中H为Heaviside光滑函数,具体形式为:
| $ H(\phi ) = \left\{ {\begin{array}{*{20}{l}} {1, }&{\phi \le - \varepsilon }\\ {\frac{1}{2} - \frac{\phi }{{2\varepsilon }} - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }}\phi }}{\varepsilon }} \right), }&{ - \varepsilon < \phi < \varepsilon }\\ {0, }&{\varepsilon \le \phi } \end{array}} \right. $ |
其中,ε一般取为1.5Δx。
图 4给出了新旧分区策略下的加速比,可以看出,加速比随线程数的增加几乎呈线性增长,新的分区带来的加速比较均匀分区明显提高,8线程下加速比提高了1倍。

|
Download:
|
| 图 4 新旧分区策略下圆球并行重构加速比的比较 Fig. 4 Comparison of speedups between the new and old domain decomposition methods in parallel reconstruction of the sphere | |
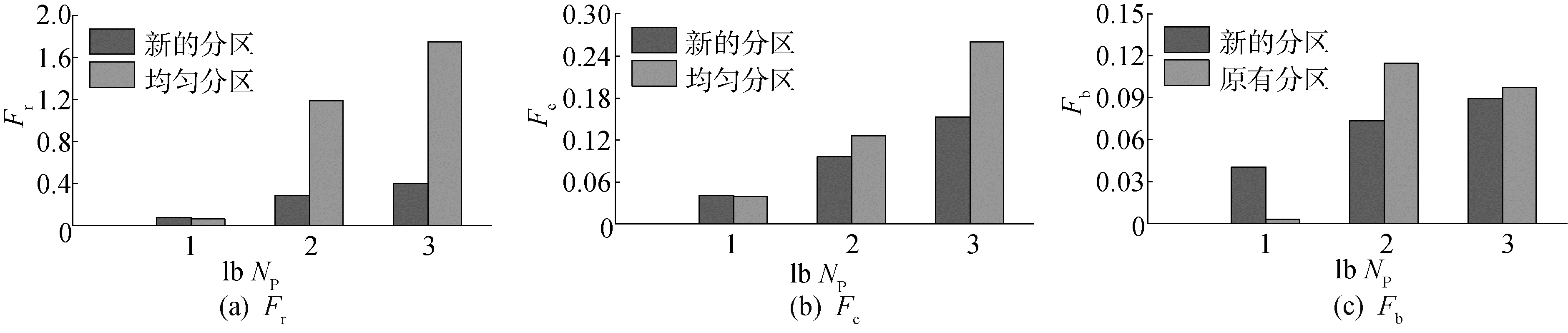
图 5给出新旧分区策略下的3个并行评估参数Fr、Fc和Fb的值。容易看出,随着分区数量的增加,均匀分区会导致子区域间信息传递次数和节点回滚次数明显增加;而新分区策略可有效降低信息传递次数,使节点回滚次数大幅减少,线程间荷载更趋于平衡。

|
Download:
|
| 图 5 新旧分区策略下圆球并行重构评估参数的对比 Fig. 5 Comparison of the assess parameters between the new and old domain decomposition methods in parallel reconstruction of the sphere | |
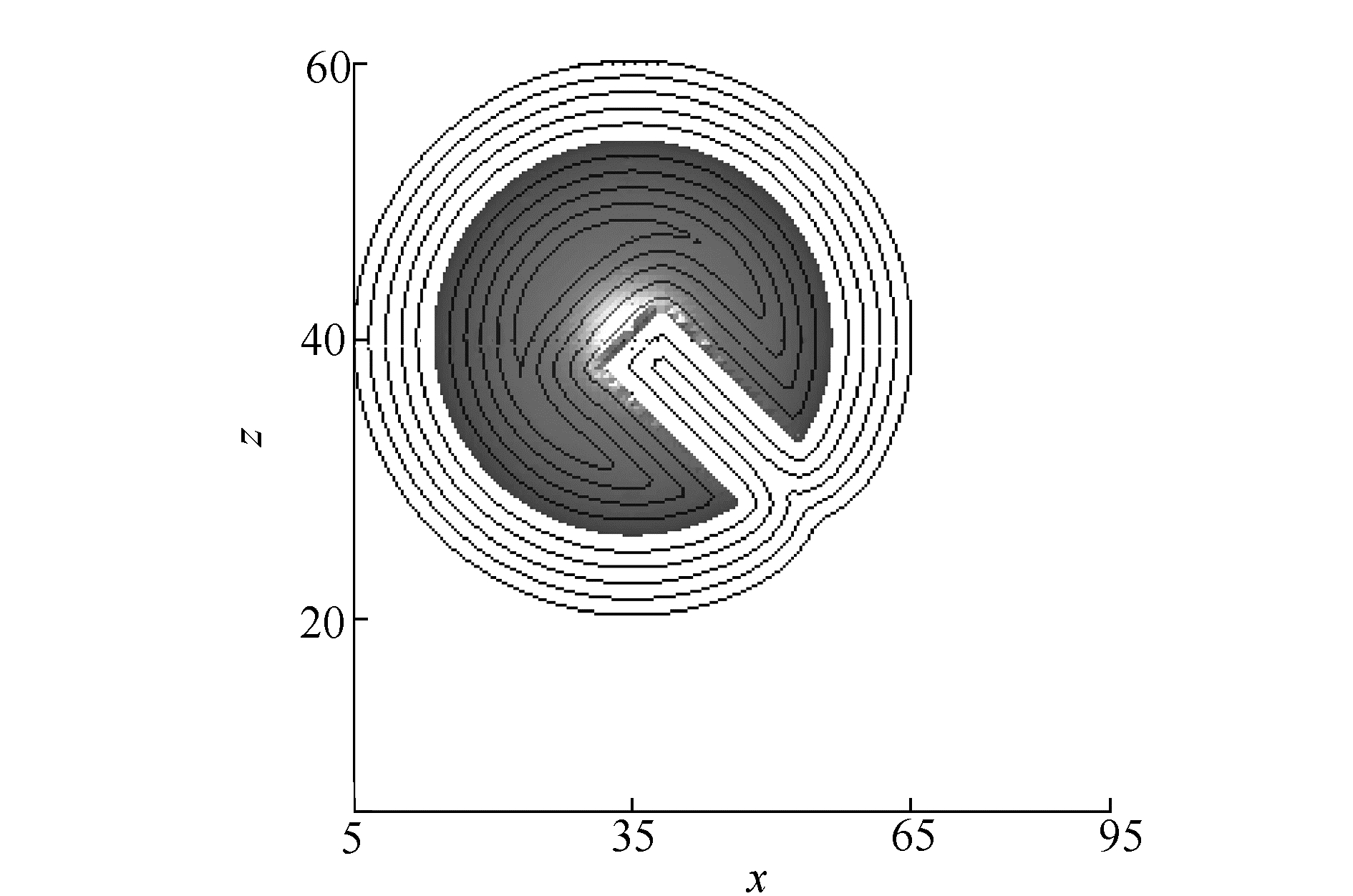
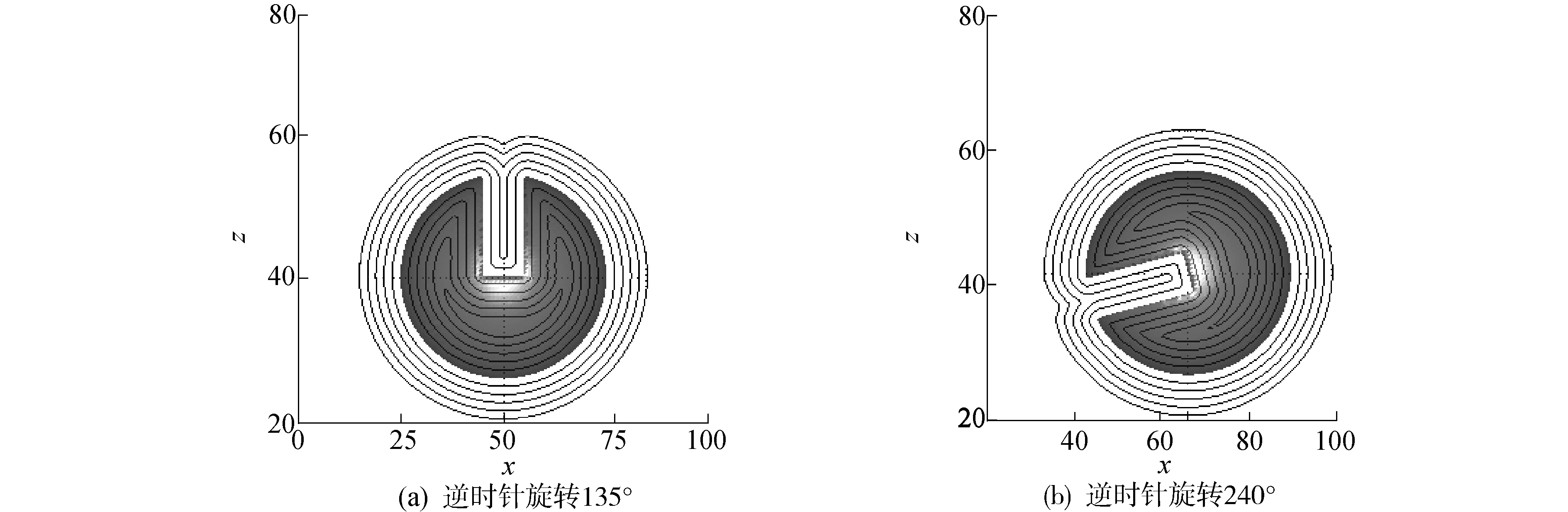
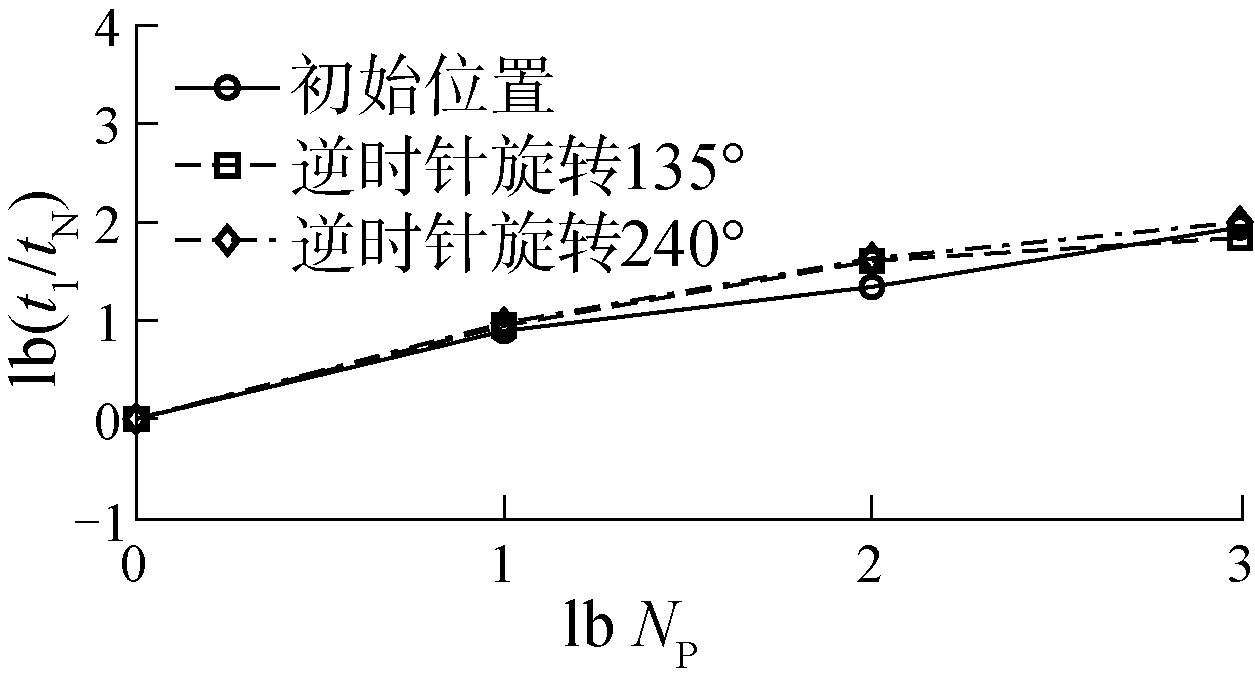
半径为25的Zalesak球放置在100×100×100的计算区域中,球心位置同样为(40, 60, 60)。该球的缺口宽度为10,深度为25,与x轴夹角呈-45°。重构过程中,整个计算区域将划分成8个子区域,重构的范围仍取ϕ∈[-12, 12]。图 6给出了Zalesak球内外两侧ϕ值构造结果,其中,实线表示平面y为60与ϕ=-10、-8、-6、-4、-2、2、4、6、8、10重构等值面的交线。表 2给出了ϕ=5等值面所包围体积以及重构的计算误差。图 7比较了新分区策略与均分策略下的加速比,可以看出,新分区策略较原有策略在计算效率方面能得到明显的提升。8线程下,新分区获得的加速为旧分区的2倍,其主要原因是8线程下均匀分区造成节点回滚次数是新分区的4倍左右(见图 8(a))。从图 8也可以看出,均匀分区下的Fc和Fb值均大于新分区的情况。图 9为Zalesak圆球绕轴x=50,y=50逆时针旋转135°和240°后重构的等值面结果。而图 10比较了Zalesak球在初始位置以及逆时针旋转135°和240°后采用新分区并行算法获得的加速比,可见Zalesak球在计算区域内位置几乎不影响新分区算法的加速比。
|
Download:
|
| 图 6 Zalesak球重构等值面 Fig. 6 Zalesak sphere′s reconstructed isosurfaces | |
| 表 2 Zalesak球等值面f=5并行重构的计算损失和误差 Table 2 Computational loss and error of parallel reconstruction of the Zalesak′s sphere isosurface of f=5 |

|
Download:
|
| 图 7 新旧分区策略下Zalesak球并行重构加速比的比较 Fig. 7 Comparison of speedups between the new and old domain decomposition methods in parallel reconstruction of the Zalesak′s sphere | |
|
Download:
|
| 图 8 新旧分区策略下Zalesak球并行重构评估参数的对比 Fig. 8 Comparison of the assess parameters between the new and old domain decomposition methods in parallel reconstruction of the Zalesak′s sphere | |
|
Download:
|
| 图 9 Zalesak球逆时针旋转135°和240°后的重构结果 Fig. 9 Isosurfaces reconstrcution results of the Zalesak sphere after counterclockwise rotation of 135°和240° | |
|
Download:
|
| 图 10 Zalesak球不同位置下的并行重构加速比 Fig. 10 Parallel reconstruction speedups of Zalesak′s sphere at different location | |
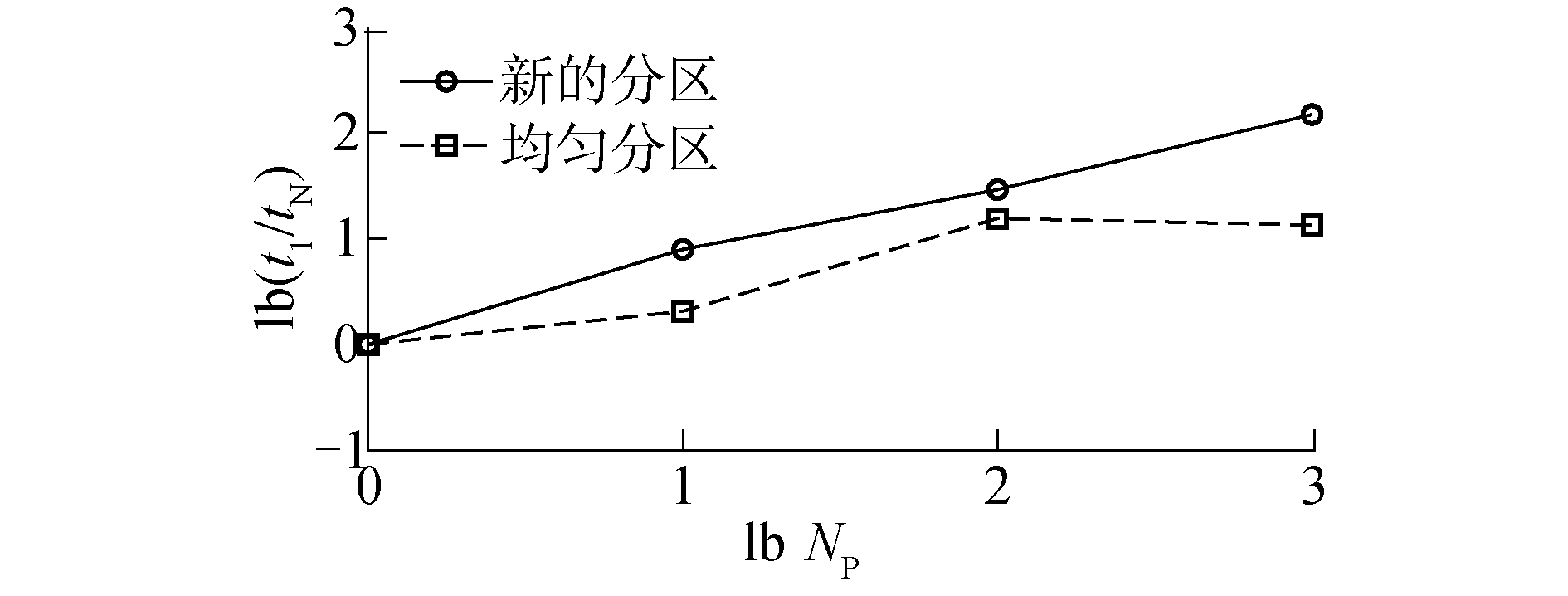
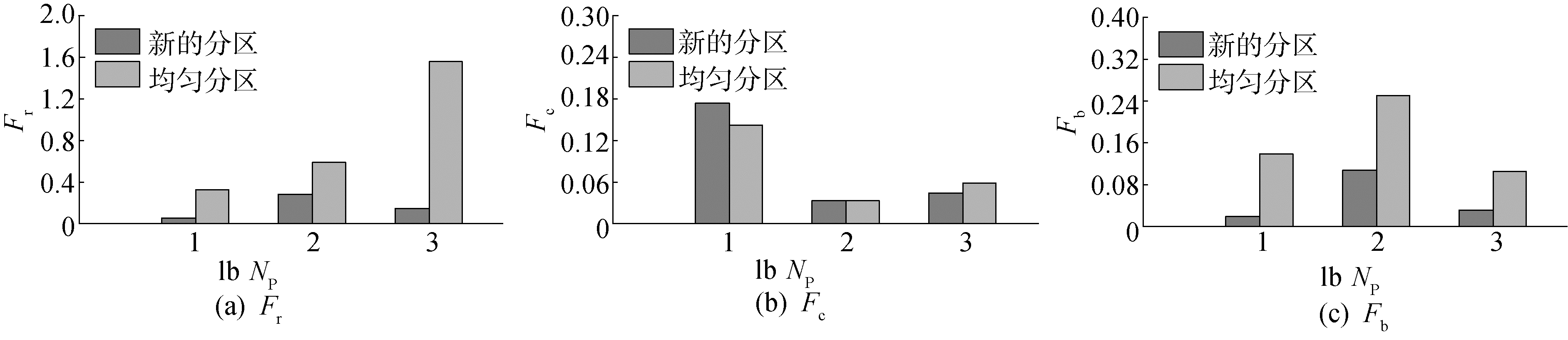
哑铃由两球体和一圆柱体构成,球体的中心分别位于(40, 60, 60)和(70, 30, 40)处,半径均为20, 圆柱的断面半径为10,其轴线与两球体中心连线重合。整个计算区域大小同样为100×100×100。并行模型根据哑铃表面的位置将整个计算区域划分成8个子区域。局部重构的范围限制在ϕ∈[-12, 12]。在图 11中,实线分别表示不同视角下各平面y=45(正视)、x=55(侧视)、z=50(俯视)与ϕ=-10, -8, -6, -4, -2, 2, 4, 6, 8, 10重构等值面的交线。表 3给出了ϕ=5等值面所包围体积以及重构的计算误差。从图 12可以看出,新分区策略在不同线程数下获得的加速比均高于均分策略。图 13则给出了新旧分区下的并行评估参数的值,8线程下旧分区策略的节点回滚参数值远高于新分区的情况,这导致8线程下均分策略的加速比不到新分区策略的一半。

|
Download:
|
| 图 11 哑铃重构等值面 Fig. 11 Dumbbell′s reconstructed isosurfaces | |
| 表 3 哑铃等值面f=5并行重构的计算损失和误差 Table 3 Computational loss and error of the parallel isosurface reconstruction of the dumbbell isosurface of f=5 |
|
Download:
|
| 图 12 新旧分区策略下哑铃并行重构加速比的比较 Fig. 12 Comparison of speedups between the new and old domain decomposition methods in parallel reconstruction of the dumbbell | |
|
Download:
|
| 图 13 新旧分区策略下哑铃并行评估参数的对比 Fig. 13 Comparison of parallel assess parameters between the new and old domain decomposition strategies methods in parallel reconstruction of the dumbbell | |
1) 基于区域分解的并行重构模型能够有效节省计算时间。
2) 自适应分区策略能够保证子区域计算荷载平衡,并有效减少子区域间信息传递次数和节点回滚次数。
3) 与均分计算区域的并行模型相比,采用自适应分区策略的并行模型能获得更高的加速比。
| [1] |
HUANG Xiaoyun, LI Shaowu. A two-dimensional numerical wave flume based on SA-MPLS method[J]. Acta oceanologica sinica, 2012, 31(3): 18-30. DOI:10.1007/s13131-012-0203-2 (  0) 0)
|
| [2] |
LI Shaowu, ZHUANG Qian, HUANG Xiaoyun, et al. 3D simulation of flow with free surface based on adaptive octree mesh system[J]. Transactions of Tianjin University, 2015, 21(1): 32-40. DOI:10.1007/s12209-015-2314-2 (  0) 0)
|
| [3] |
CUBOS-RAMÍREZ J M, RAMÍREZ-CRUZ J, SALINAS-VÁZQUEZ M, et al. Efficient two-phase mass-conserving level set method for simulation of incompressible turbulent free surface flows with large density ratio[J]. Computers & fluids, 2016, 136: 212-227. (  0) 0)
|
| [4] |
MCSHERRY R J, CHUA K V, STOESSER T. Large eddy simulation of free-surface flows[J]. Journal of hydrodynamics, series B, 2017, 29(1): 1-12. DOI:10.1016/S1001-6058(16)60712-6 (  0) 0)
|
| [5] |
CHOPP D L. Computing minimal surfaces via level set curvature flow[J]. Journal of computational physics, 1993, 106(1): 77-91. (  0) 0)
|
| [6] |
SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of computational physics, 1994, 114(1): 146-159. (  0) 0)
|
| [7] |
RUSSO G, SMEREKA P. A remark on computing distance functions[J]. Journal of computational physics, 2000, 163(1): 51-67. (  0) 0)
|
| [8] |
ENRIGHT D, FEDKIW R, FERZIGER J, et al. A hybrid particle level set method for improved interface capturing[J]. Journal of computational physics, 2002, 183(1): 83-116. (  0) 0)
|
| [9] |
HARTMANN D, MEINKE M, SCHRÖDER W. Differential equation based constrained reinitialization for level set methods[J]. Journal of computational physics, 2008, 227(14): 6821-6845. DOI:10.1016/j.jcp.2008.03.040 (  0) 0)
|
| [10] |
SALIH A, GHOSH MOULIC S. A mass conservation scheme for level set method applied to multiphase incompressible flows[J]. International journal for computational methods in engineering science and mechanics, 2013, 14(4): 271-289. DOI:10.1080/15502287.2012.711991 (  0) 0)
|
| [11] |
SABELNIKOV V, OVSYANNIKOV A Y, GOROKHOVSKI M. Modified level set equation and its numerical assessment[J]. Journal of computational physics, 2014, 278: 1-30. DOI:10.1016/j.jcp.2014.08.018 (  0) 0)
|
| [12] |
TSITSIKLIS J N. Efficient algorithms for globally optimal trajectories[J]. IEEE transactions on automatic control, 1995, 40(9): 1528-1538. DOI:10.1109/9.412624 (  0) 0)
|
| [13] |
SETHIAN J A. Fast marching methods[J]. SIAM review, 1999, 41(2): 199-235. DOI:10.1137/S0036144598347059 (  0) 0)
|
| [14] |
CHOPP D L. Some improvements of the fast marching method[J]. SIAM journal on scientific computing, 2001, 23(1): 230-244. DOI:10.1137/S106482750037617X (  0) 0)
|
| [15] |
ENRIGHT D, LOSASSO F, FEDKIW R. A fast and accurate semi-Lagrangian particle level set method[J]. Computers & structures, 2005, 83(6/7): 479-490. (  0) 0)
|
| [16] |
HASSOUNA M S, FARAG A A. MultiStencils fast marching methods:a highly accurate solution to the Eikonal equation on Cartesian domains[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(9): 1563-1574. DOI:10.1109/TPAMI.2007.1154 (  0) 0)
|
| [17] |
TSAI Y H R, CHENG L T, OSHER S, et al. Fast sweeping algorithms for a class of Hamilton-Jacobi equations[J]. SIAM journal on numerical analysis, 2003, 41(2): 673-694. (  0) 0)
|
| [18] |
ZHAO Hongkai. Parallel implementations of the fast sweeping method[J]. Journal of computational mathematics, 2007, 25(4): 421-429. (  0) 0)
|
| [19] |
QIAN Jianliang, ZHANG Yongtao, ZHAO Hongkai. Fast sweeping methods for Eikonal equations on triangular meshes[J]. SIAM journal on numerical analysis, 2007, 45(1): 83-107. (  0) 0)
|
| [20] |
LI Fengyan, SHU Chiwang, ZHANG Yongtao, et al. A second order discontinuous Galerkin fast sweeping method for Eikonal equations[J]. Journal of computational physics, 2008, 227(17): 8191-8208. DOI:10.1016/j.jcp.2008.05.018 (  0) 0)
|
| [21] |
DETRIXHE M, GIBOU F, MIN C. A parallel fast sweeping method for the Eikonal equation[J]. Journal of computational physics, 2013, 237: 46-55. DOI:10.1016/j.jcp.2012.11.042 (  0) 0)
|
| [22] |
HERRMANN M. A domain decomposition parallelization of the fast marching method annual research briefs[R]. Stanford, CA: Center for Turbulence Research, 2003: 253-261.
(  0) 0)
|
| [23] |
黄筱云, 董国海, 赵利平, 等. Level set函数重新初始化的并行快速步进法[J]. 哈尔滨工程大学学报, 2016, 37(5): 666-671, 689. HUANG Xiaoyun, DONG Guohai, ZHAO Liping, et al. A parallelized fast marching method for reinitialization of level set function[J]. Journal of Harbin Engineering University, 2016, 37(5): 666-671, 689. (  0) 0)
|
| [24] |
黄筱云, 董国海, 常佳夫, 等. Level set函数快速步进重构并行算法的改进[J]. 哈尔滨工程大学学报, 2017, 38(6): 836-842. HUANG Xiaoyun, DONG Guohai, CHANG Jiafu, et al. Improvement of parallel fast marching method for reconstruction of level set function[J]. Journal of Harbin Engineering University, 2017, 38(6): 836-842. (  0) 0)
|
| [25] |
LOSASSO F, FEDKIW R, OSHER S. Spatially adaptive techniques for level set methods and incompressible flow[J]. Computers & fluids, 2006, 35(10): 995-1010. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


