在火炮设计、引信控制、弹丸空气动力学的研究过程中,弹体飞行姿态参数的准确测量对加快武器研究进度和武器的智能化意义重大[1-2]。国内外MEMS陀螺传感器的漂移,抗高过载的能力等参数,还达不到旋转弹体姿态高精度测量的要求[3]。由于地磁测量技术具有可靠性高、无累积误差、抗冲击能力强、成本低廉等优点[4],随着地磁场理论的不断完善,为提高国内火炮弹药的打击精度,国内外学者对地磁场理论进行了深入研究,在导航、测姿领域取得了极大的发展[5-6]。
针对飞机用地磁导航系统,Goldenberg[7]开展了关于地磁场图的测速定位方法研究,该方法必须在知道该地地磁场图的条件下才能正常使用。而对于旋转弹体,根据陀螺稳定原理,弹体在空气中具有追随稳定性[8-9],可以认为旋转弹丸的速度矢量始终保持在射击平面内,从而保证弹体的偏航角在短时间内稳定不变。Harkins等[10]在不知道当地地磁场强度的大小基础上提出了一种非正交磁传感器交叉比值的旋转弹体姿态测试方法,但其特征点的选取容易引入误差,导致最终的姿态角解算误差较大。
已有的以地球磁场作为测量基准的姿态测试方法为避免使用地磁场强度作为先决条件,多采用单点特征比值来解算,不具有统计特征。本文针对旋转弹体,为提高姿态测量精度,提出了一种利用三正交磁传感器安装方式的积分比值姿态测试方法,利用多点的统计特征比值来代替单点特征比值,建立弹体俯仰角与磁传感器输出信号积分比值的数学关系,最终通过半实物实验对积分比值法的姿态角解算精度进行验证。
1 姿态解算算法本文将三正交比值法[11-12]推广到3个正交安装的磁传感器的积分比值计算,在不增加传感器个数的同时,提高测试数据利用率。避免使用单点特征值,利用测试数据的统计特征,增强姿态角解算算法的抗干扰能力,从而提高姿态角解算精度。
1.1 磁传感器安装定义o-xbybzb为弹体坐标系,弹体沿xb轴正方向飞行,并沿轴旋转。O-NED为地理坐标系,如图 1所示,其中γ表示旋转弹体横滚角,ψ表示弹体的磁偏航角,θ表示弹体俯仰角。

|
Download:
|
| 图 1 弹上磁传感器示意 Fig. 1 Magnetic sensors installation on projectile | |
磁传感器Msx、Msy和Msz敏感方向分别沿弹体坐标系的3轴正方向安装,其中Msx安装在弹体轴向,与Msy和Msz两两正交。根据载体坐标系与导航坐标系之间的转换规律,得到磁传感器的输出:
| $\left\{ \begin{align} & {{M}_{x}}=|B|(\cos I\cos \psi \cos \theta -\sin I\sin \theta ) \\ & {{M}_{y}}=|B|\cos I(\cos \psi \sin \theta \sin \gamma -\cos (\omega \gamma )\sin \psi )+ \\ &\;\;\;\;\;\;\;\;\;\;|B|\sin I\cos \theta \sin (\omega \gamma ) \\ & {{M}_{z}}=|B|\cos I(\cos \psi \sin \theta \cos \gamma +\sin (\omega \gamma )\sin \psi )+ \\ &\;\;\;\;\;\;\;\;\;\;|B|\sin I\cos \theta \cos (\omega \gamma ) \\ \end{align} \right. $ | (1) |
式中:ψ=D+Ψ;D表示磁偏角;Ψ表示真实偏航角;I表示地磁倾角。
式(1)所得到的三轴传感器输出,3个方程相互不独立,无法直接解算得到全部的姿态角。但是由于旋转弹体的射程基本上都在几十公里以内,弹道高度一般都低于10 km。以南京地区地磁场为例,在弹丸射程范围内,地磁场强度变化率为-3.5×10-7%,磁倾角和磁偏角变化率均小于0.3%;在弹道高度内,地磁场强度变化率为1.1×10-7%,磁倾角和磁偏角变化率均小于0.02°。因此,在常规炮弹的射程范围内,可将当地磁倾角I和磁偏角D认为定值。
1.2 三正交比值法文献[11]研究了一种基于3个正交安装的磁传感器极值比的姿态角解算方法,通过测得的x轴与y、z两轴单个周期输出的单点峰值比来解算姿态角,图 2给出在磁偏航角ψ=30°和地磁倾角I=48°时,俯仰角为θ=30°情况下x、y、z三轴传感器的仿真曲线,从图中可以看到在一个旋转周期内极值点A、B、C、D处三正交磁传感器比值随θ不同而变化。
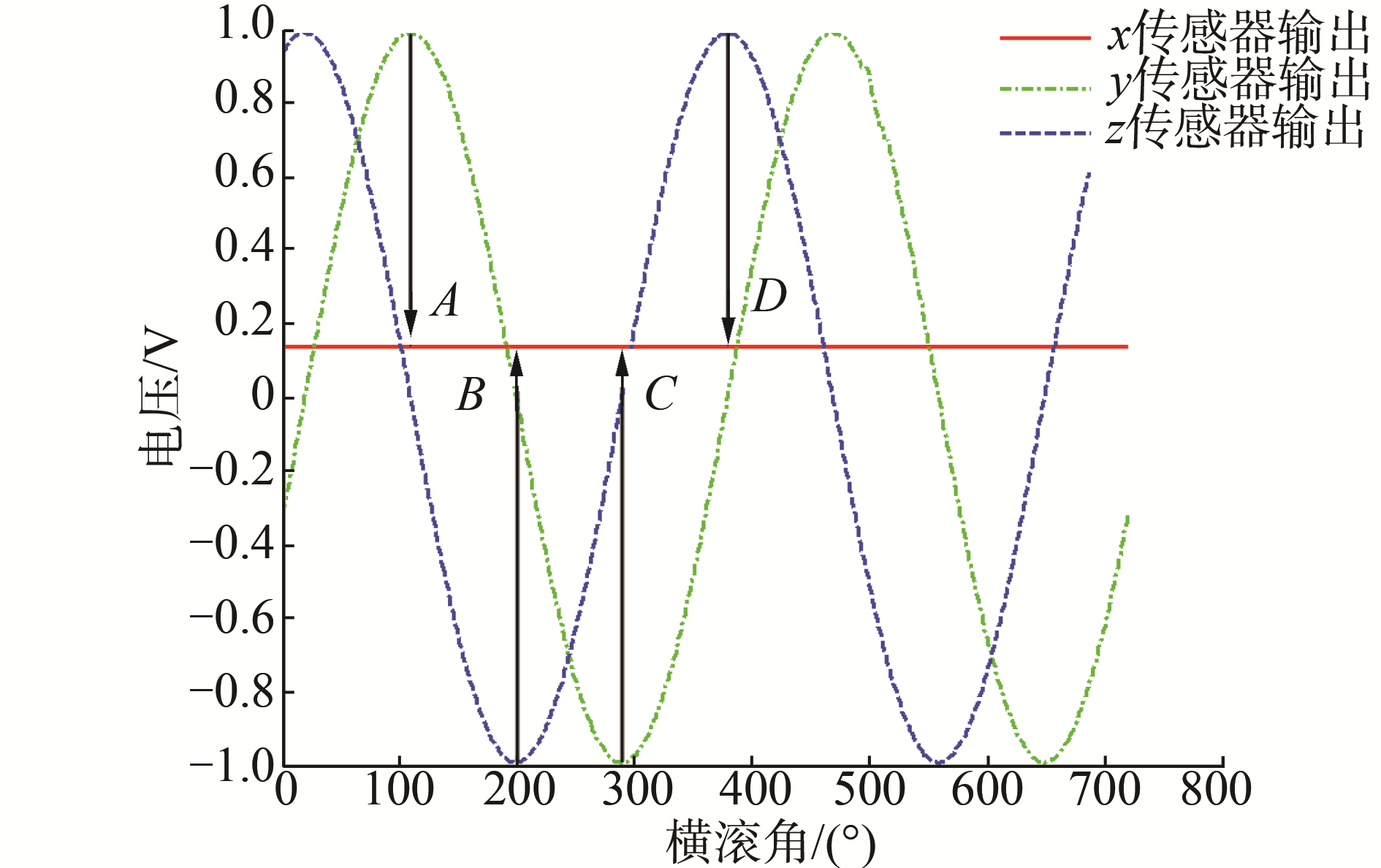
|
Download:
|
| 图 2 x、y、z三轴磁传感器输出 Fig. 2 x, y, z axis magnetic sensor′s output | |
当三轴磁传感器的检测值My、Mz取得极大值或极小值时,求解得到My、Mz取极值时的横滚角值,然后代入到My和Mz,最终得到Mx与My、Mz取得极值时的比值。
在实际解算过程中,传感器输出端不可避免地会有较大噪声干扰,如果只用单点的极值的测量值来计算极值比,必然将引入噪声干扰,噪声越大,姿态角误差就越大。因此,三正交比值法在信噪比较差的情况下姿态角解算误差会比较大,必须先对数据进行滤波降噪才能进行后续解算,这样严重影响数据处理速度。
1.3 积分比值法为增强姿态角解算算法的抗噪声干扰能力,提高姿态角解算精度,本文在三正交比值法的基础上提出积分比值姿态解算算法。
为方便进行讨论,根据旋转弹体特征,提出以下2个假设:1)磁偏航角ψ在飞行过程中不变;2)在弹体半个旋转周期内,俯仰角和横滚角速率近似不变[13]。
为方便运算,对式(1)中的My、Mz进行三角变换:
| $\left\{ \begin{array}{*{35}{l}} {{M}_{y}}=|B|\cos I\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\cdot \sin (\omega \gamma +\alpha ) \\ {{M}_{z}}=|B|\cos I\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\cdot \sin \left( \omega \gamma +\alpha -\frac{\pi }{2} \right) \\ \end{array} \right. $ | (2) |
式中:
| $\begin{align} & A=\cos \psi \sin \theta +\tan I\cos \theta \\ & \alpha =\arctan (-\sin \psi /A) \\ \end{align} $ |
由式(1)、式(2)可以得,在磁倾角I和磁偏航角ψ不变的情况下,弹体旋转一周,Mx的大小、My和Mz的曲线幅值$|B|\cos I\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }$只与俯仰角θ有关。可将Mx与My、Mz进行比值运算,消除当地地磁强度大小的影响,避免地磁强度测量引入的误差。
图 3给出在磁偏航角ψ=30°和地磁倾角I=48°时,俯仰角为θ=0°情况下xs、y两轴传感器的仿真曲线。从图中可以看到一个旋转周期内y轴传感器输出曲线的上下积分面大小与x轴输出随着θ不同而变化。为增强所测数据的利用率,提高姿态角解算精度,对My、Mz进行积分运算,得到上/下半周期的积分面积Supy/Sdowny和Supz/Sdownz。首先计算零点时的横滚角值,即My=0,则:
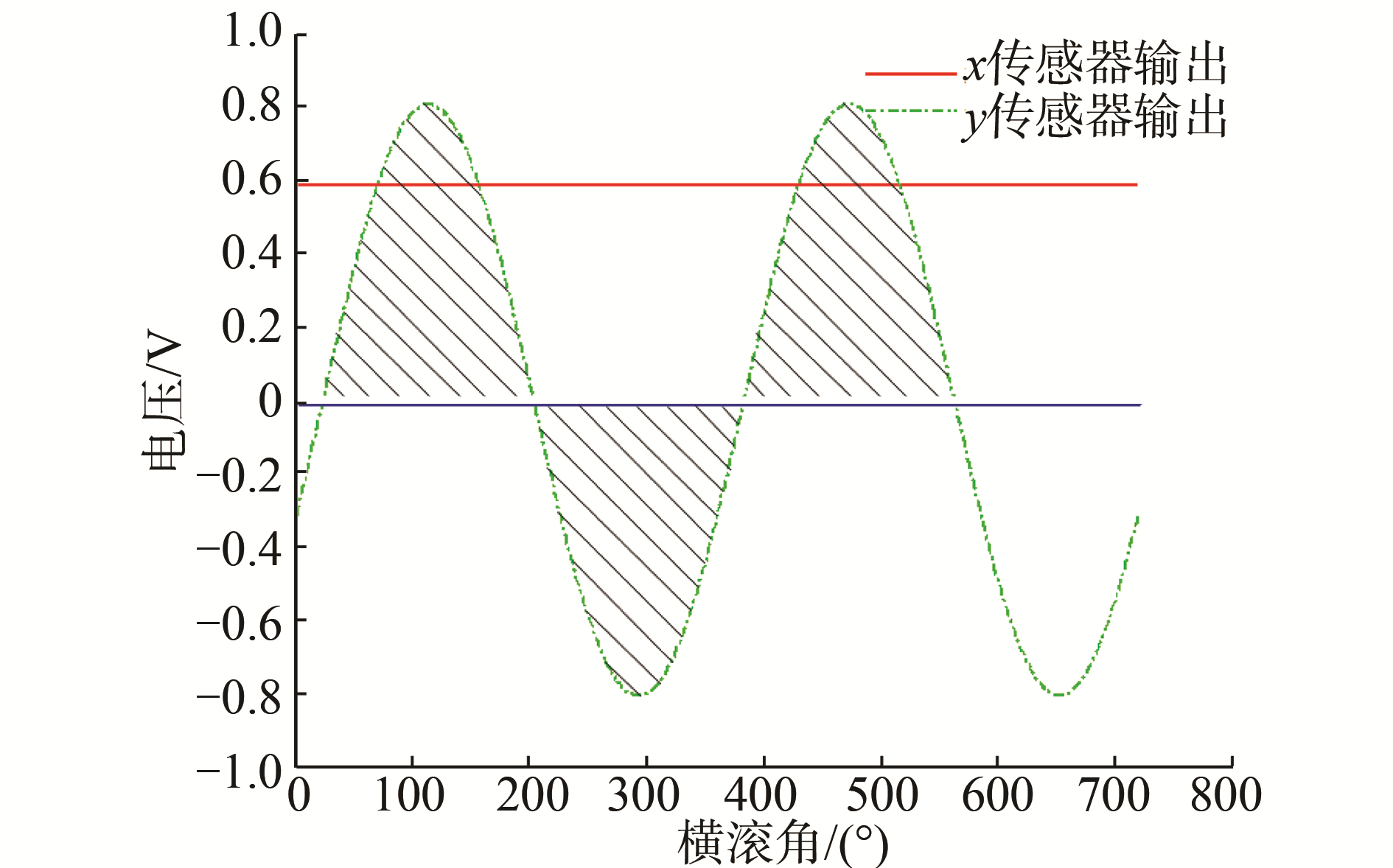
|
Download:
|
| 图 3 俯仰角为0°时x、y轴的传感器输出 Fig. 3 x, y axis sensor output when the pitch angle is 0° | |
| $|B|\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\cdot \sin (\gamma +\alpha )=0 $ | (3) |
求解得到:
| $\left\{ \begin{array}{*{35}{l}} {{\gamma }_{1}}=-\alpha =\arctan (\sin \psi /A) \\ {{\gamma }_{2}}=\pi -\alpha =\pi +\arctan (\sin \psi /A) \\ {{\gamma }_{3}}=2\pi -\alpha =2\pi +\arctan (\sin \psi /A) \\ \end{array} \right. $ | (4) |
对My进行积分运算,得到:
| $\left\{ \begin{array}{*{35}{l}} {{S}_{\text{upy}}}=|B|\cos I\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\int_{{{\gamma }_{1}}}^{{{\gamma }_{2}}}{\sin }\left( {{\omega }_{1}}\gamma +\alpha \right)\text{d}\gamma \\ {{S}_{\text{downy}}}=|B|\cos I\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\int_{{{\gamma }_{2}}}^{{{\gamma }_{3}}}{\sin }\left( {{\omega }_{2}}\gamma +\alpha \right)\text{d}\gamma \\ \end{array} \right. $ | (5) |
式中ω1=π/Δt1;ω2=π/Δt2;Δt1和Δt2分别表示上、下半周期所用时间。
在俯仰角不变时,Mx在一个旋转周期内为恒定值。可以利用Mx与My积分的比值,消除当地磁场强度在计算过程中的影响:
| $\left\{ \begin{align} & {{R}_{\text{ uppy }}}=\frac{\cos \psi \cos \theta -\tan I\sin \theta }{\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\int_{{{\gamma }_{1}}}^{{{\gamma }_{2}}}{\sin }\left( {{\omega }_{1}}\gamma +\alpha \right)\text{d}\gamma } \\ & {{R}_{\text{ dowany }}}=\frac{\cos \psi \cos \theta -\tan I\sin \theta }{\sqrt{{{A}^{2}}+{{\sin }^{2}}\psi }\int_{{{\gamma }_{2}}}^{3}{\sin }\left( {{\omega }_{2}}\gamma +\alpha \right)\text{d}\gamma } \\ \end{align} \right. $ | (6) |
同理可得Mx与Mz积分的比值。
由于旋转弹体的转速会在飞行过程中缓慢减小,为消除转速在积分比值中的影响,将式(6)中的转速提取出来并求解积分得到:
| $\left\{ \begin{array}{l} {W_{{\rm{ dowany }}}} = \frac{{{R_{{\rm{ dowany }}}}}}{{{\omega _2}}} = - \frac{{\cos \psi \cos \theta - \tan I\sin \theta }}{{2\sqrt {{A^2} + {{\sin }^2}\psi } }}\\ {W_{{\rm{down}}xy}} = \frac{{{R_{{\rm{down}}xy}}}}{{{\omega _2}}} = - \frac{{\cos \psi \cos \theta - \tan I\sin \theta }}{{2\sqrt {{A^2} + {{\sin }^2}\psi } }} \end{array} \right. $ | (7) |
ψ和I值一定的情况下,Wupxy、Wdownxy只与θ有关。在25°≤ψ≤35°,I=48°时,积分比值Wupxy和Wdownxy曲线如图 4所示,上、下半周期的积分比值与弹体俯仰角θ一一对应。解算过程中,可以先计算出每半个周期内Mx与My、Mz积分的比值,并除以每半个周期内的横滚角转速,得到积分比值upxy、Wdownxy和Wupxz、Wdownxz,查表求解俯仰角值。然后,利用解算出的各半周期的俯仰角θ和已知的偏航角ψ由式(4)可以求解出My=0、Mz=0时刻的横滚角γ。

|
Download:
|
| 图 4 25°≤ψ≤35°,I=48°时,积分比值曲线 Fig. 4 Integral ratio curves when 25°≤ψ≤35°, I=48° | |
在实际解算过程中,由于磁传感器输出无平移项、无趋势项,积分比值法解算出的积分误差影响不大,利用积分得到的统计特征值能够有效地减小随机噪声干扰的影响,因此积分比值法在信噪比较差的情况下,姿态角解算误差依然很小[14-15]。
为提高数据处理速度,只对数据进行简单叠加来计算上/下积分面积,可见产生积分误差的原因与选取的积分点数量有关。半个周期内分别均匀选取18和180个点进行计算,与计算得到的积分比值理论值相比会产生一定的积分误差,在俯仰角θ∈[0°, 90°]范围内,造成的俯仰角误差如图 5所示,从图中可以看出均匀选取180个点计算积分造成的俯仰角误差可以控制在±0.005°以内,造成的积分误差很小。
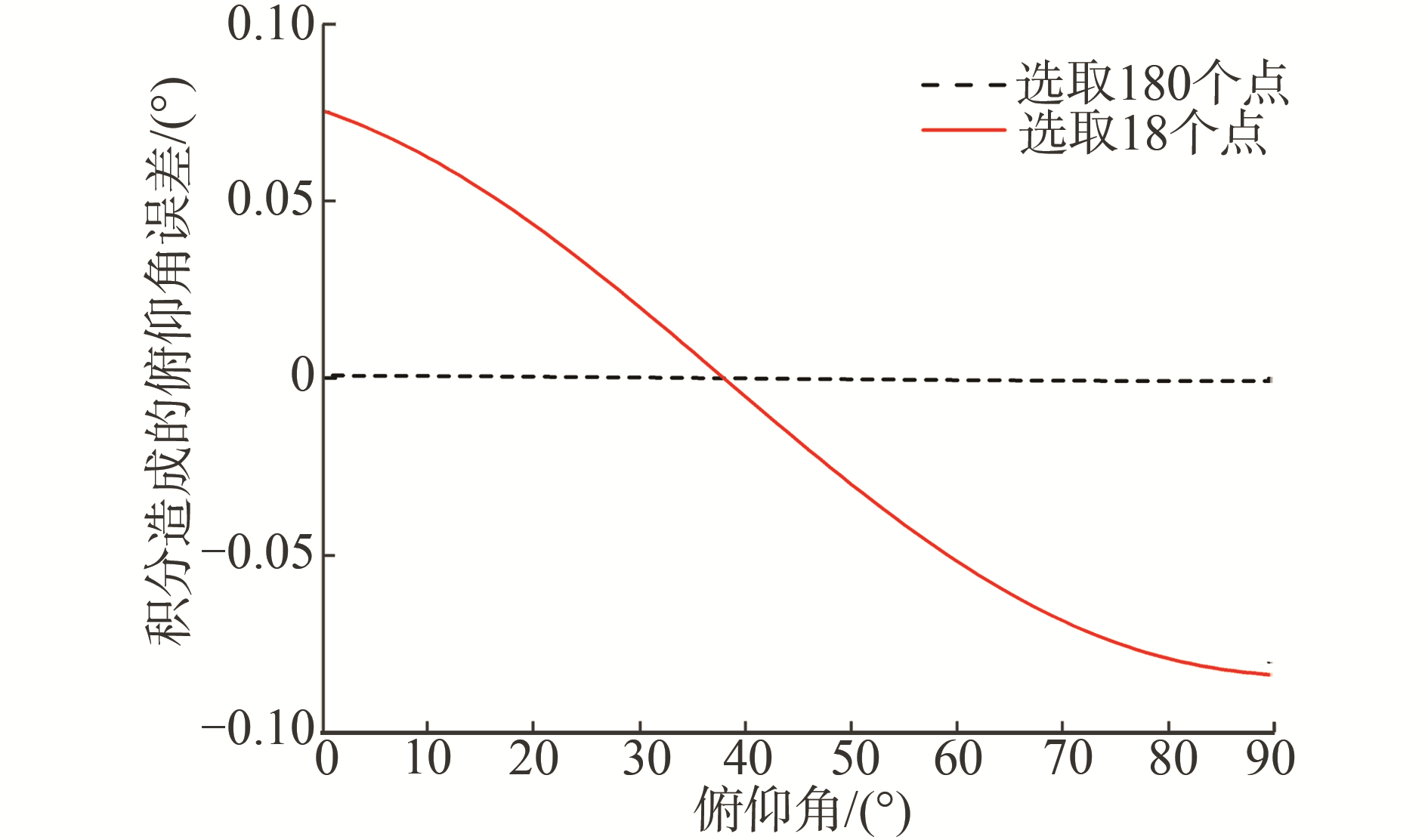
|
Download:
|
| 图 5 积分引入的俯仰角误差 Fig. 5 Pitch angle error introduced by integral | |
积分比值法的前提条件是磁偏航角ψ不变,但在弹体飞行过程中磁偏航角ψ会发生微小的变化,那么通过事先做好的Wupxy和Wdownxy与θ的标定曲线查表获得的俯仰角就会出现误差。设θ∈[0°, 90°]范围,ψ在[27°, 33°]范围内变化,假设ψ不变引起的理论俯仰角查表误差如图 6所示,其中俯仰角的查表误差在±1.5°以内。
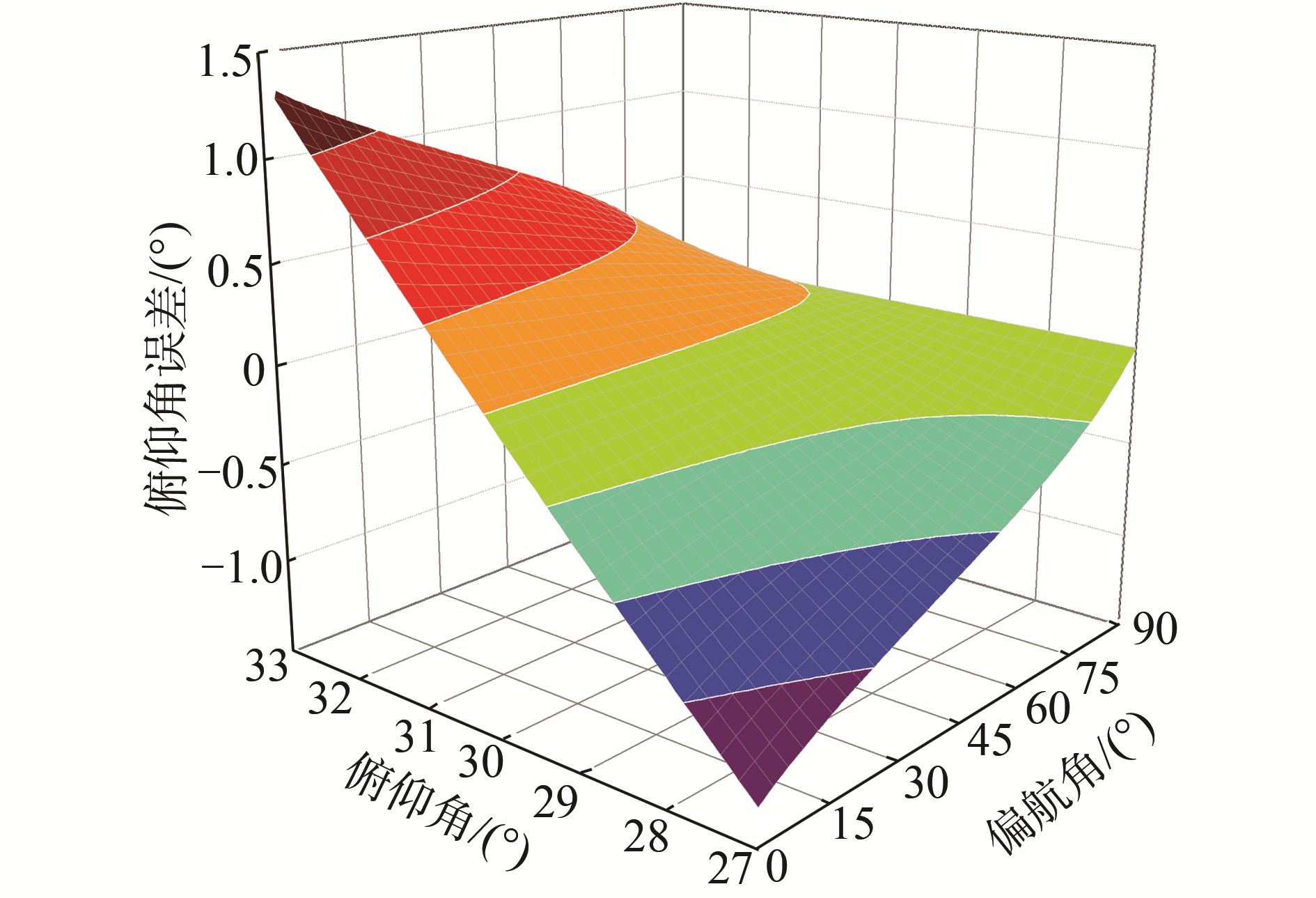
|
Download:
|
| 图 6 偏航角造成的俯仰角误差 Fig. 6 Pitch angle error introduced by yaw angle | |
为削弱偏航角不变的假设造成的俯仰角误差,利用磁传感器的输出和一次解算得到的俯仰角和横滚角估计值,对磁偏航角进行修正,修正公式为:
| $\tan \psi = \frac{{{M_z}\sin \gamma - {M_y}\cos \gamma }}{{{M_x}\cos \theta + {M_y}\sin \gamma \sin \theta + {M_z}\cos \gamma \sin \theta }} $ | (8) |
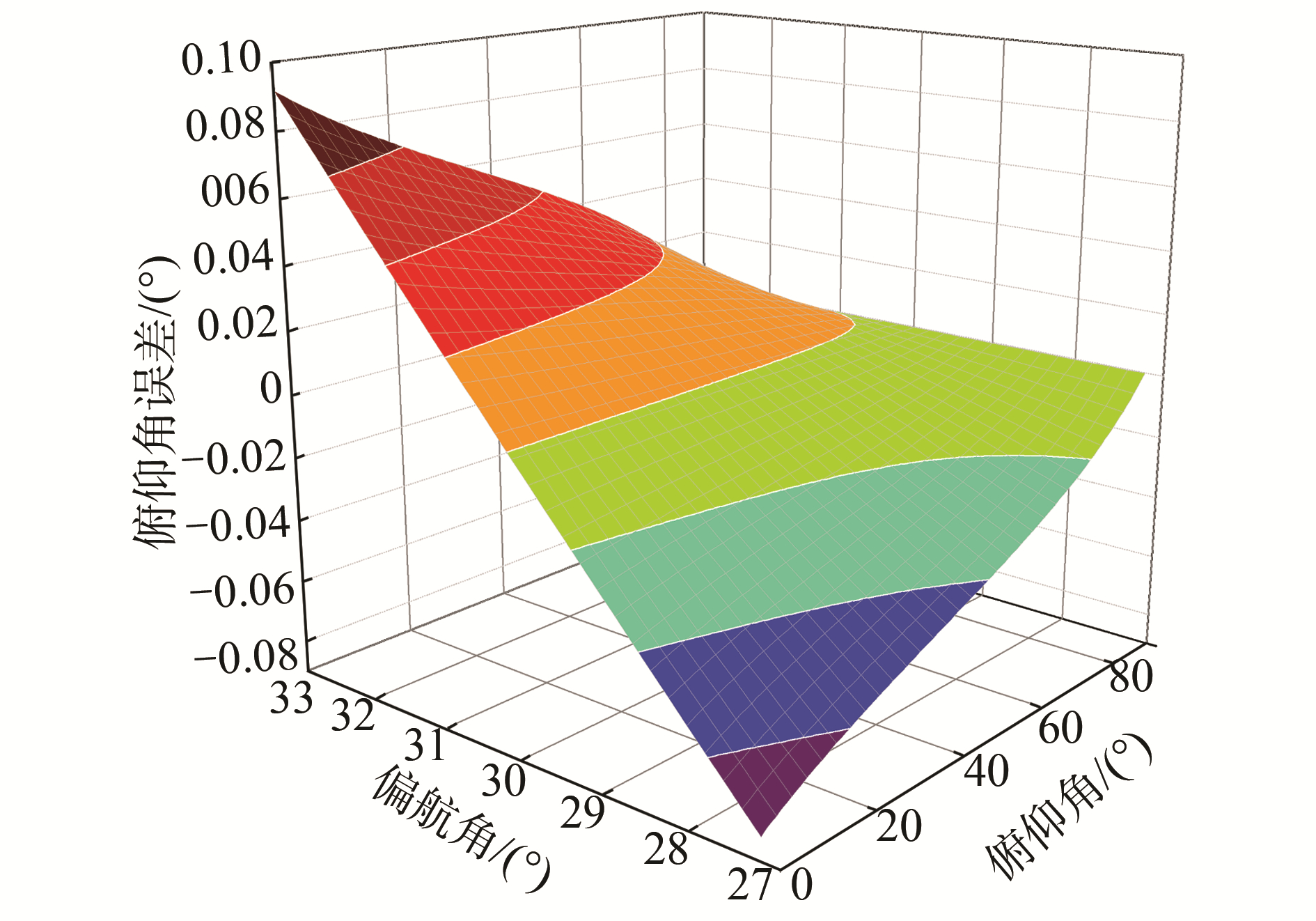
利用修正后的磁偏航角,对俯仰角和横滚角进行二次查表和解算,得到修正后的偏航角变化造成的俯仰角误差如图 7所示,二次解算误差能够保持在±0.1°以内。
|
Download:
|
| 图 7 偏航角修正后的俯仰角误差 Fig. 7 Pitch angle error after the yaw angle corrections | |
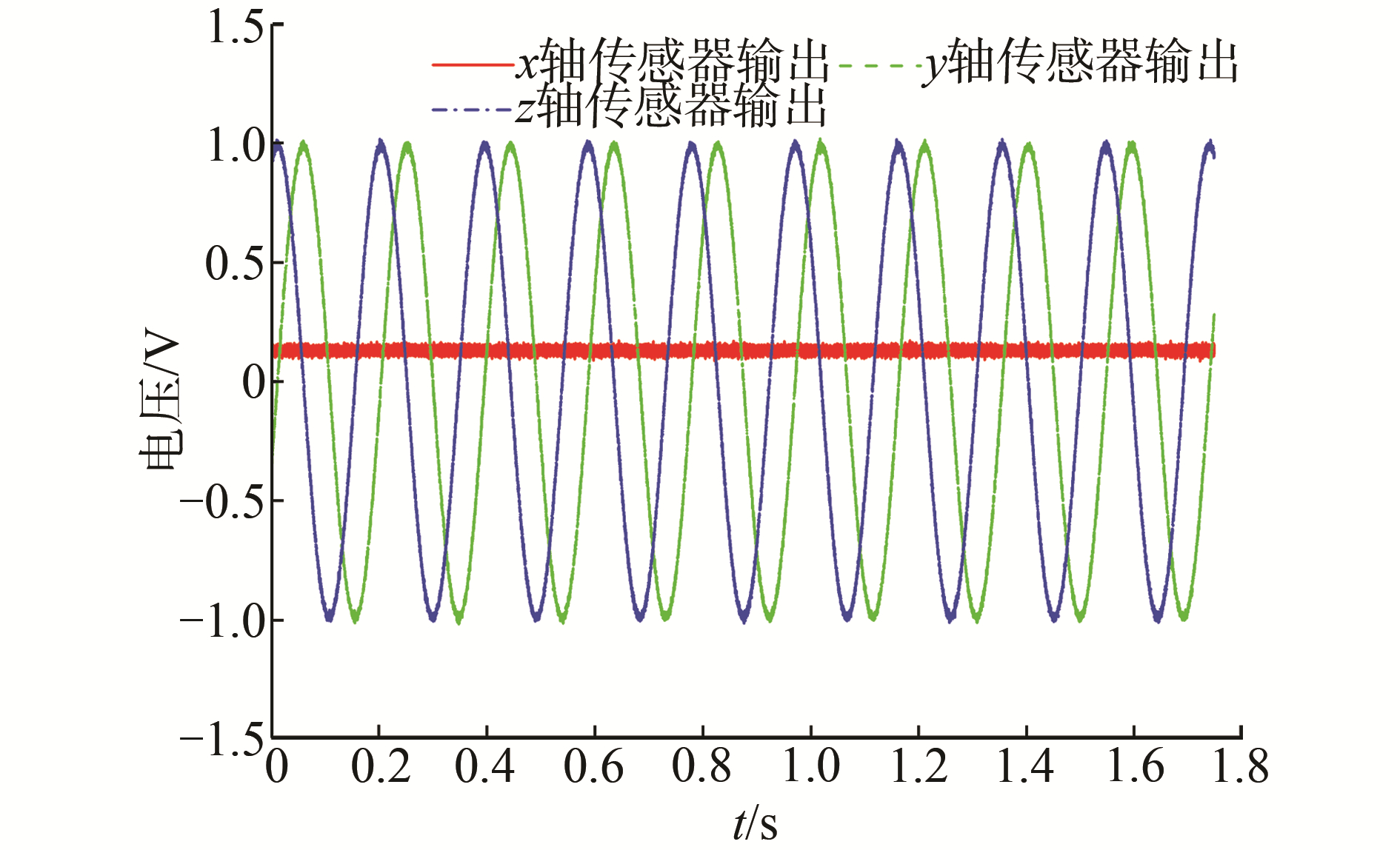
为验证积分比值法的姿态角解算精度和抗噪声干扰的能力,对积分比值法和三正交比值法进行数值仿真对比分析。假设地磁倾角I=48°,设定偏航角为30°,俯仰角为30°,横滚角速率ω=5 r/s,在磁传感器输出端叠加均值为0、标准差为10-2 G的随机白噪声,磁传感器理论输出曲线如图 8所示。利用两种算法分别解算姿态角,得到的姿态角解算误差分别如图 9和图 10所示。
|
Download:
|
| 图 8 磁传感器理论输出曲线 Fig. 8 Magnetic sensor theoretical output curve | |
|
Download:
|
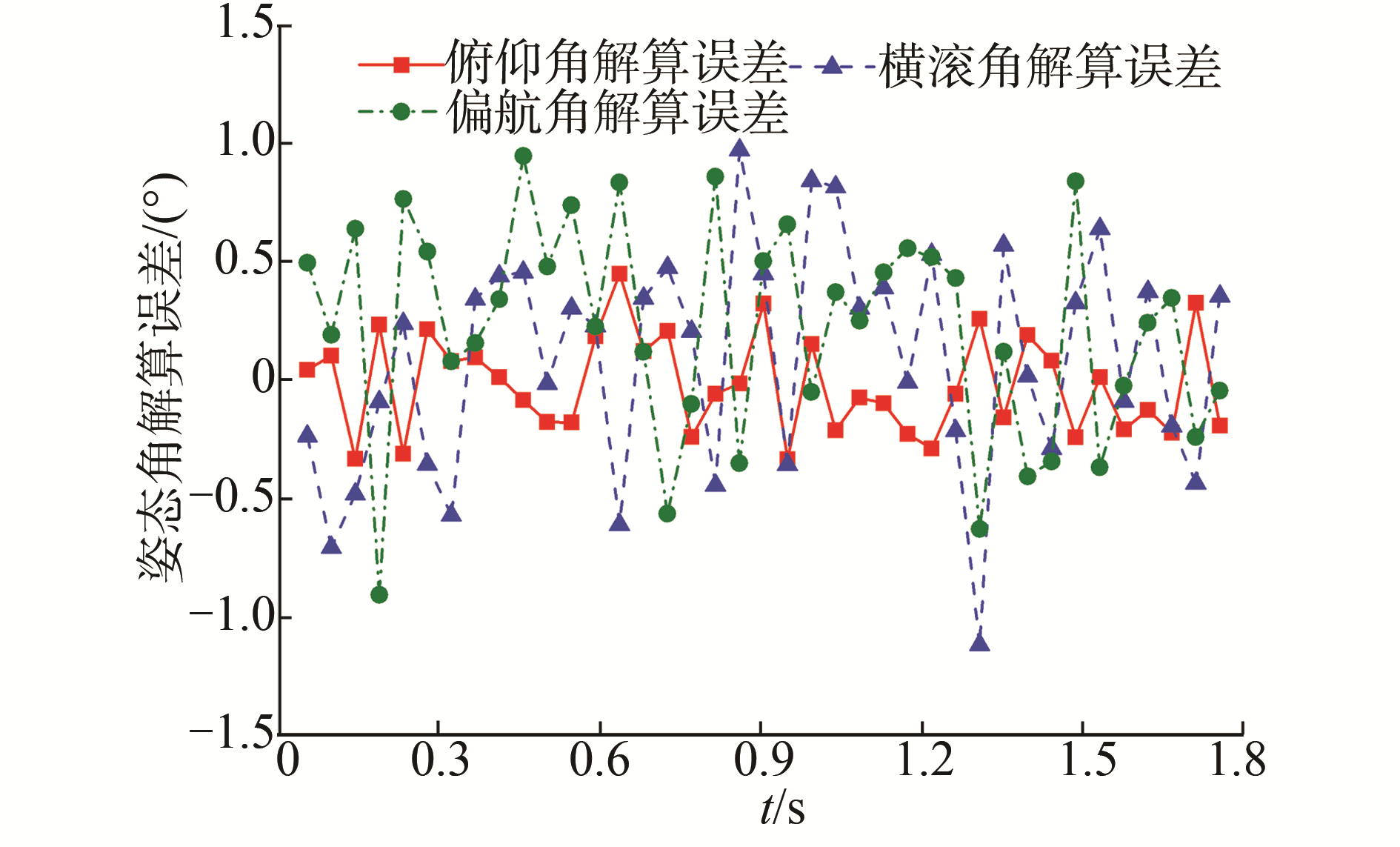
| 图 9 三正交比值法姿态角解算误差 Fig. 9 The attitude error of three orthogonal ratio method | |

|
Download:
|
| 图 10 积分比值法姿态角解算误差 Fig. 10 The attitude error of integral ratio method | |
图 9和图 10给出了2种解算方法的姿态角误差仿真结果,在低信噪比情况下,三正交比值法的姿态角解算误差在±1.5°以内,而积分比值法仿真解算误差在±0.3°以内,可见积分比值法在噪声干扰较大情况下的姿态解算精度要优于三正交比值法。
3 半实物实验验证根据以上理论分析和仿真对比研究,利用Honeywell公司生产的磁传感器HMC1021/1022设计了姿态测试硬件电路,并制作了半实物装置机械外壳。利用三轴无磁转台模拟弹丸的实际运动状态,对积分比值法进行半实物实验验证,半实物装置安装在三轴无磁手动转台上的实物如图 11所示。

|
Download:
|
| 图 11 半实物实验装置 Fig. 11 Semi-physical experiment device | |
首先做出偏航角为30°时,南京地区xy、xz轴积分比值标定曲线,如图 12所示。

|
Download:
|
| 图 12 积分比值标定曲线S Fig. 12 Integral ratio calibration curve | |
由于实际测量时传感器的灵敏度误差等因素,从图 12可以看出实际的标定曲线与理论曲线在斜率上有所不同,实验过程中现场标定xy、xz积分比值曲线,不影响姿态解算结果。
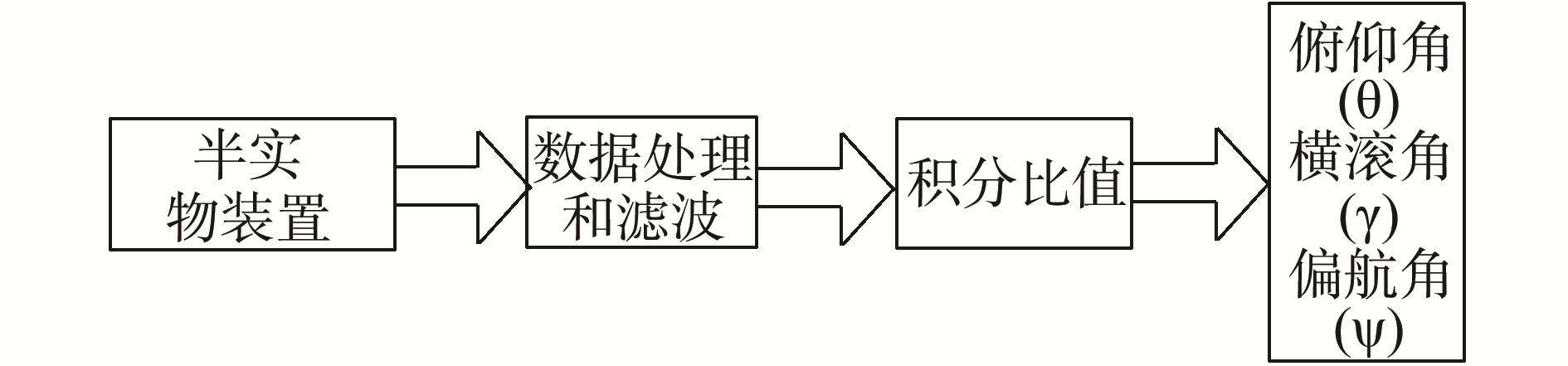
图 13给出了实验装置的系统框图,调节转台使偏航角为30°,俯仰角设为30°,转动横滚轴,利用半实物装置采集姿态运动时的三轴地磁传感器输出数据,得到滤波后的实验曲线如图 14所示,利用积分比值法解算姿态角,得到的姿态角解算误差如图 15。
|
Download:
|
| 图 13 实验系统框图 Fig. 13 The system block diagram of the experimental setup | |

|
Download:
|
| 图 14 半实物实验曲线 Fig. 14 Semi-physical experimental curve | |
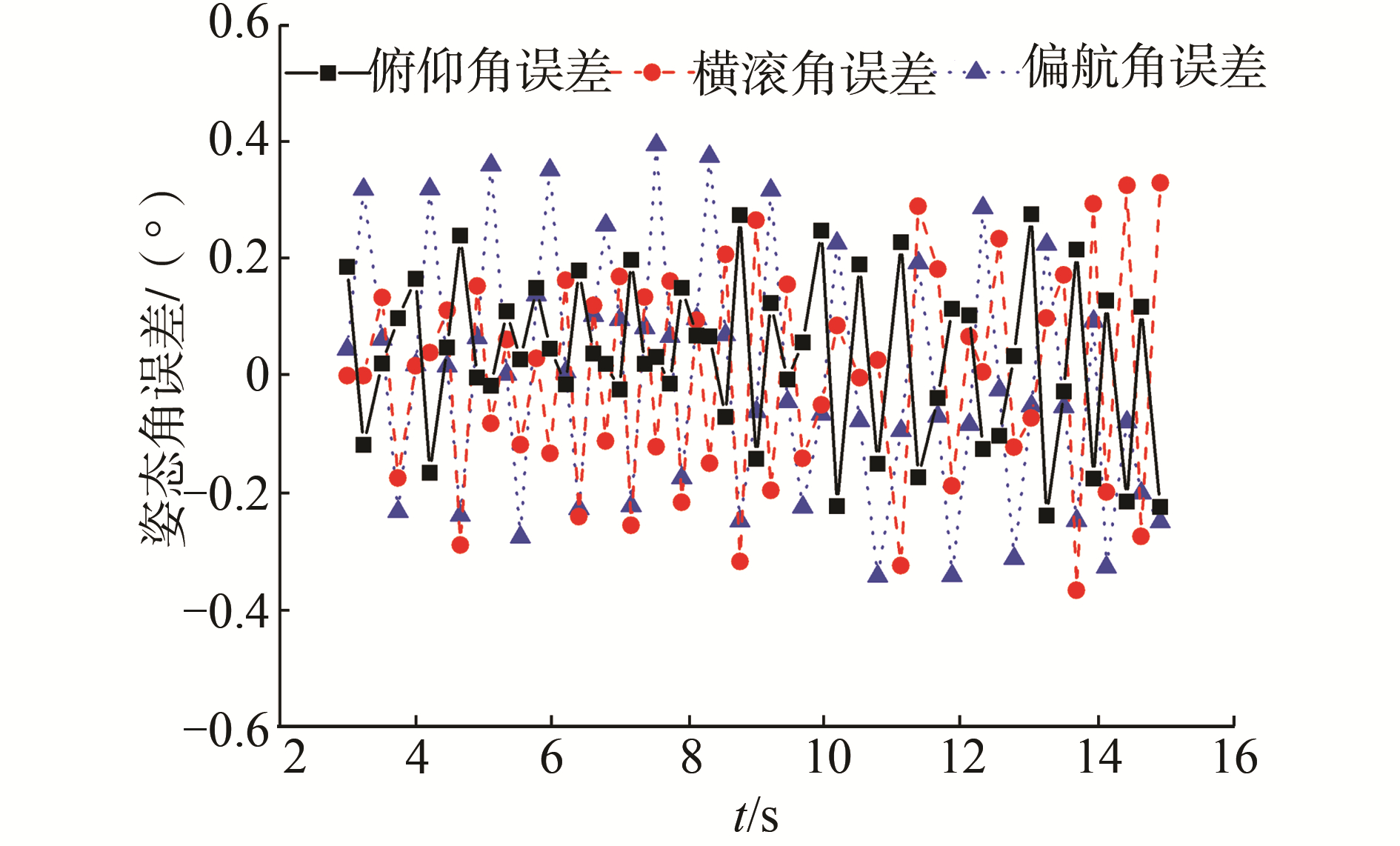
|
Download:
|
| 图 15 半实物实验的姿态角误差 Fig. 15 Attitude errors of semi-physical experimental | |
从实验结果可以看出,利用本文提出的积分比值法,在三轴无磁手动转台转速控制较差的情况下,俯仰角、横滚角和偏航角解算误差在±0.6°以内,解算精度较高。
4 结论1) 本文在三正交比值法的基础上提出了利用三正交磁传感器的积分比值姿态测试方法,通过数值仿真和半实物实验,验证了积分比值算法的姿态角解算误差在±0.6°以内。与三正交比值法相比,积分比值算法具有数据利用率高、姿态解算精度高、鲁棒性强等特点。
2) 本文所提出的积分比值算法,为进一步提高弹上地磁姿态测试精度提供了理论依据,对国内常规弹药打击精度技术的突破性研究具有一定的借鉴意义。
| [1] |
AGARWAL V, ARYA H, BHAKTAVATSALA S. Design and development of a real-time DSP and FPGA-based integrated GPS-INS system for compact and low power applications[J]. IEEE transactions on aerospace and electronic systems, 2009, 45(2): 443-454. DOI:10.1109/TAES.2009.5089533 (  0) 0)
|
| [2] |
XU Miaomiao, BU Xiongzhu, YU Jing, et al. Spinning projectile's attitude measurement with LW infrared radiation under sea-sky background[J]. Infrared physics & technology, 2018, 90: 214-220. (  0) 0)
|
| [3] |
CHEN Xiyuan, TANG Chuanye. Improved class of angular rate-based coning algorithms[J]. IEEE transactions on aerospace and electronic systems, 2016, 52(5): 2220-2229. DOI:10.1109/TAES.2016.150450 (  0) 0)
|
| [4] |
赵国荣, 黄婧丽, 苏艳琴, 等. 基于滚动时域估计的飞行器姿态估计及三轴磁强计在线校正[J]. 物理学报, 2015, 64(21): 210502. ZHAO Guorong, HUANG Jingli, SU Yanqin, et al. Attitude estimation and three-axis magnetometer on-line calibration based on moving horizon estimation[J]. Acta physica sinica, 2015, 64(21): 210502. DOI:10.7498/aps.64.210502 (  0) 0)
|
| [5] |
王仕成, 吕志峰, 张金生, 等. 基于半实物仿真的地磁导航等值线匹配算法评估[J]. 北京航空航天大学学报, 2015, 41(2): 187-192. WANG Shicheng, LYU Zhifeng, ZHANG Jinsheng, et al. Evaluation of ICCP algorithm for geomagnetic navigation based on hardware-in-the-loop simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 187-192. DOI:10.3969/j.issn.1005-4561.2015.02.044 (  0) 0)
|
| [6] |
张涛, 郑建华, 高东. 一种利用磁强计和星敏感器的自主导航方法[J]. 宇航学报, 2017, 38(2): 152-158. ZHANG Tao, ZHENG Jianhua, GAO Dong. A method of autonomous navigation using the magnetometer and star sensor[J]. Journal of astronautics, 2017, 38(2): 152-158. DOI:10.3873/j.issn.1000-1328.2017.02.006 (  0) 0)
|
| [7] |
GOLDENBERG F. Geomagnetic navigation beyond the magnetic compass[C]//Proceedings of 2006 IEEE/ION Position, Location, and Navigation Symposium. Coronado, CA, USA, 2006: 684-694.
(  0) 0)
|
| [8] |
刘周, 谢立军, 杨云军, 等. 弹丸旋转空气动力效应非定常数值模拟[J]. 航空学报, 2016, 37(5): 1401-1410. LIU Zhou, XIE Lijun, YANG Yunjun, et al. Unsteady numerical simulation of aerodynamic effect of a spinning projectile[J]. Acta aeronautica et astronautica sinica, 2016, 37(5): 1401-1410. (  0) 0)
|
| [9] |
马杰, 陈志华, 姜孝海. 高速旋转条件下的弹丸气动特性研究[J]. 弹道学报, 2015, 27(2): 1-6. MA Jie, CHEN Zhihua, JIANG Xiaohai. Aerodynamic characteristics of a projectile with high spinning speeds[J]. Journal of ballistics, 2015, 27(2): 1-6. DOI:10.3969/j.issn.1004-499X.2015.02.001 (  0) 0)
|
| [10] |
HEPNER D J, HARKINS T E. Determining inertial orientation of a spinning body with body-fixed sensors[C]//Proceedings of SPIE 4025, Acquisition, Tracking, and Pointing XIV. Orlando, FL, USA, 2000: 68-78.
(  0) 0)
|
| [11] |
向超, 卜雄洙, 李玎. 基于三正交磁传感器的新型旋转弹体定姿方法[J]. 中国惯性技术学报, 2011, 19(4): 443-446,451. XIANG Chao, BU Xiongzhu, LI Ding. New spinning projectile's attitude measurement based on three pairwise-orthogonal magnetic sensors[J]. Journal of Chinese inertial technology, 2011, 19(4): 443-446,451. (  0) 0)
|
| [12] |
XIANG Chao, BU Xiongzhu, YANG Bo. Three different attitude measurements of spinning projectile based on magnetic sensors[J]. Measurement, 2014, 47: 331-340. DOI:10.1016/j.measurement.2013.09.002 (  0) 0)
|
| [13] |
YU Jing, BU Xiongzhu, XIANG Chao, et al. Spinning projectile's attitude measurement using intersection ratio of magnetic sensors[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2017, 231(5): 866-876. DOI:10.1177/0954410016644628 (  0) 0)
|
| [14] |
SONG Lan, PETERS D K, HUANG Weimin, et al. Parallel communication mechanisms in solving integral equations for electromagnetic scattering based on the method of moments[C]//Proceedings of the 18th International Conference on Algorithms and Architectures for Parallel Processing. Guangzhou, China, 2018: 498-507.
(  0) 0)
|
| [15] |
TOMCZYK K. New algorithm for determining the dynamic error for the integral-square criterion[J]. Journal of physics:conference series, 2018, 1065(8): 082001. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


