随着陆地上不可再生资源的加速消耗,愈显海洋开发的重要性和迫切性[1]。海洋开发需要先进的技术和装备,AUVMS作为水下作业的重要装备之一,在海洋开发中发挥着重要的作用[2-3]。
水下作业中,水下机器人(autonomous under- water vehicle, AUV)一般处于艇体动力悬停状态,其机械手作业将影响艇体姿态、位置。并且由于机械手展臂较长,艇体及手关节的微小偏差都将严重影响机械手的末端精度,因此水下机械手末端精度是AUVMS研究的重点内容之一[4-5]。
水下机械手末端精度表示为末端目标点与实际点之间的位置偏差。在末端精度测量中,需实时测量出机械手末端实际点的位置坐标或位姿坐标。目前,可用于实时测量末端坐标的测量方式主要有:激光测量方式、球杆仪和视觉系统测量等。基于激光测量方式的测量仪器有激光干涉仪[6]、激光追踪仪[7]等,此类方式陆上测量精度高、测量范围大,但激光本身对环境要求较高,水中颗粒物、杂质等会引起激光散射和折射,散折射的激光会导致测量结果不精确,因此激光方式不适宜于本文工作环境。球杆仪[8]测量精度较高,但由于自身长度较小,导致其测量范围有限,不适用于本文机械手的作业范围末端位姿测量。视觉测量系统[9-10](包括单目、双目视觉)效率高、测量简单;但基于水下视觉的坐标测量精度达不到5 mm量级以内[11-12],不满足末端精度小于5 mm要求。同时,不同测量方法的原理和装置不同,其原理性误差分析未有标准方法可循。因此,本文研究AUVMS的水下机械手末端精度测量方法以及该测量方法对应的原理性误差分析方法。
针对上述问题,本文提出2种AUVMS机械手末端精度测量方法,以适应不同测量需求。一种方法是为检测机械手末端运动是否到达某一规定的范围内,本文提出一种基于水下视觉的AUVMS机械手末端精度测量方法;另一种是针对末端精度具体数值的测量问题,本文提出了一种接触式水下机械手末端精度测量方法。并且针对接触式机械手末端精度测量方法的原理性误差问题,本文提出基于数值迭代方式的原理性误差分析方法;该误差分析方法可供与本文测量原理相近的测量方法进行原理性误差分析时参考。为验证本文末端精度测量方法测量效果,在AUVMS艇体固定和动力悬停状态下,进行了机械手末端精度测量的水池实验验证。
1 AUVMS结构与精度要求AUVMS样机如图 1所示,由AUV(艇体)和机械手组成[13-14];外形为椭圆流线型,尺寸为2.0 m×0.6 m×0.6 m,空重约205.0 kg;共有2个水平主推进器、2个侧向推进器及4个垂直推进器;配置深度、速度、姿态角度等传感器和视觉系统。

|
Download:
|
| 图 1 AUVMS实验样机 Fig. 1 AUVMS experimental prototype | |
实验样机搭载的机械手精度需满足指标为:1) AUVMS艇体水下动力悬停时,机械手动态末端精度在±150 mm以内;2) AUVMS艇体固定时,机械手静态末端精度具体数值在±5 mm以内。
2 AUVMS末端精度测量方法 2.1 末端精度范围测量方法针对技术指标“AUVMS艇体水下动力悬停时,机械手动态末端精度在±150 mm以内”,本节研究其测量方法。
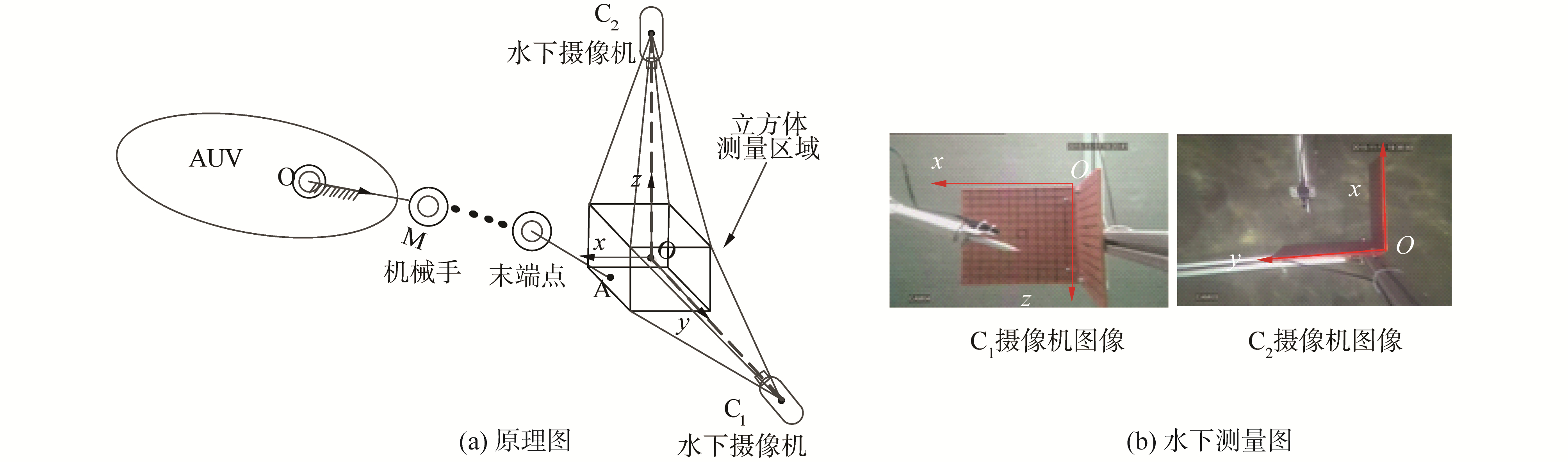
水下动力悬停时,艇体处于微动状态,将直接影响机械手末端精度。机械手末端精度难以通过激光等方式进行测量。进一步分析技术指标,只需测量出系统机械手末端是否在某一个范围。因此,本文首先提出一种水下视觉末端精度范围测量方法,该方法采用水下视觉进行机械手的非接触式末端精度范围测量。其原理及水下测量如图 2所示。
|
Download:
|
| 图 2 水下视觉方法原理 Fig. 2 Schematic diagram of underwater stereo vision | |
在图 2(a)中,设定机械手末端目标点为立方体区域中心(立方体边长为a),当AUVMS艇体动力悬停时,如若机械手末端长期处于区域内,即表明动态末端精度范围在±a/2 mm以内。而图 2(b)中,2块正方形测量板,相互垂直安装,组成立方体区域;摄像机C1、C2以左视图和俯视图方向安装,C1、C2视线交点O为立方体区域中心。
根据技术指标要求,设计正方形板边长a为300 mm,当机械手末端进入、长时间处于正方体内,即认定为满足该项技术指标要求。结合图 2,本文方法检测过程如下:
1) AUVMS动力悬停状态下,控制机械手末端运动向目标点(立方体区域中心O)运动;
2) 通过摄像机C1观察,机械手末端如果处于图 3(b)中xOz平面内,则x、z方向满足机械手末端精度范围在±150 mm以内;反之,则不满足;
|
Download:
|
| 图 3 精度测量方法原理 Fig. 3 Schematic diagram of precision measurement method | |
3) 通过摄像机C2观察,机械手末端如果处于图 3(b)中xOy平面内,则x、y方向满足机械手末端精度范围在±150 mm以内;反之,则不满足。
基于C1、C2的图像,即可测量机械手末端点在x、y、z方向精度范围是否在±150 mm内。同时,由于本文末端精度范围测量方法只为验证机械手末端精度是否在立方体区域内。
2.2 接触式末端精度测量方法针对技术指标“AUVMS艇体固定时,机械手静态末端精度具体数值在±5 mm以内”,本节研究其测量方法。需测量得出机械手末端静态精度具体数值,本文提出一种接触式水下机械手末端精度测量方法。
1) 方法测量原理。
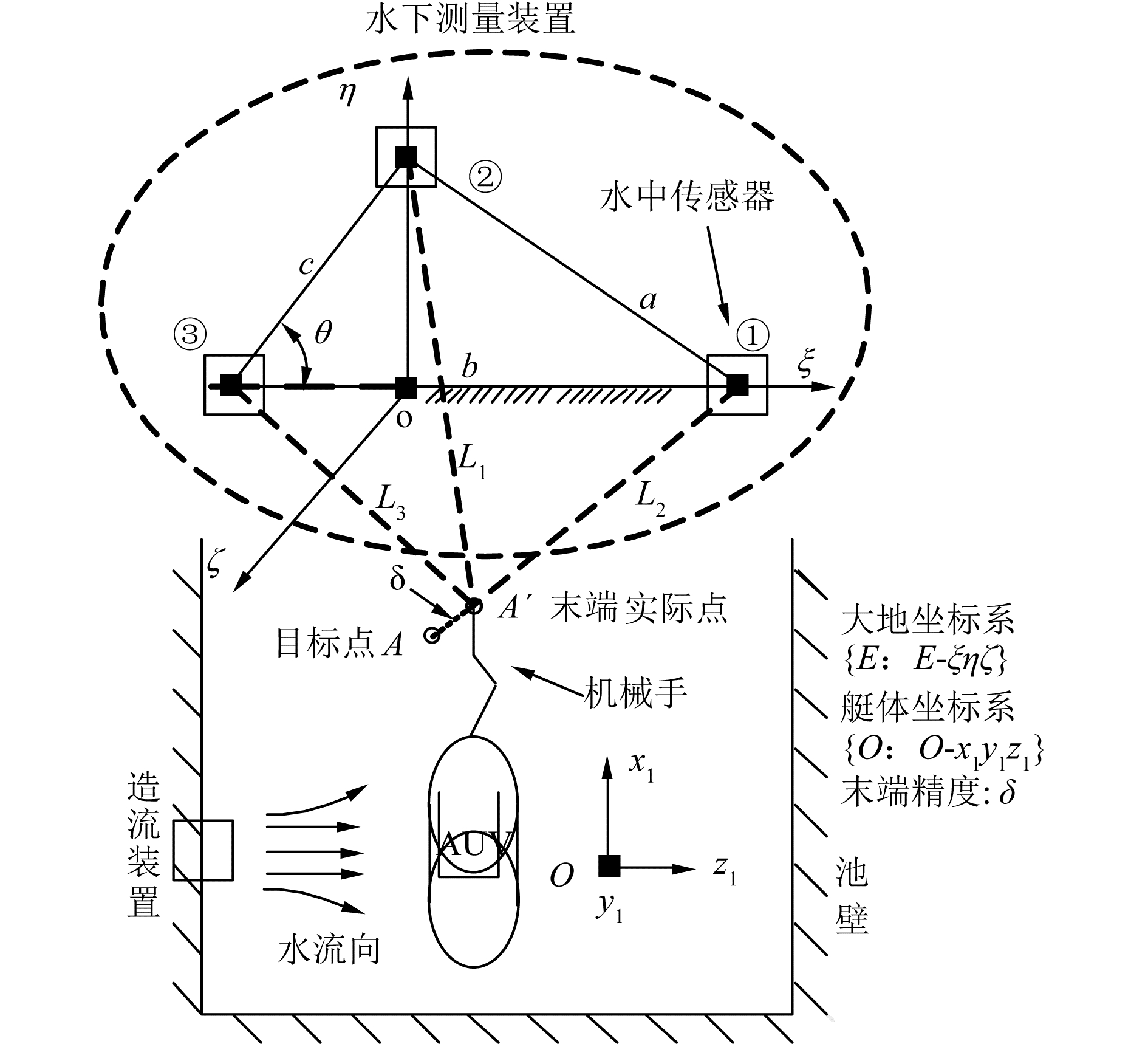
本文方法原理如图 3所示。图 3中水下环境为三维环境,传感器为接触式拉伸传感器,分别安装于①、②、③点,位于大地坐标系{E},但不在同一直线上,相互距离为a、b、c;图示中,末端精度δ表示为目标点与实际点的偏离程度。
结合图 3说明本文方法基本原理。在图 3中,存在2个坐标系:大地坐标系{E:E-ξηζ}和艇体坐标系{O:O-x1y1z1}。其中,目标点在艇体坐标系{O}中,实际点在大地坐标系{E}下;因此需将目标点与实际点转换到同一坐标系下,才能得出末端精度δ。测量过程中,首先大地坐标系{E}下,测量传感器到机械手末端距离L1、L2、L3,通过L1、L2、L3推算末端实际点坐标。其次,通过空间坐标转换将目标点从坐标系{O}转换到{E}中。最后,大地坐标系{E}下,比较实际点与目标点偏差程度,即末端精度δ。因此,本文方法主要涉及2个问题:1)大地坐标系{E}中实际点坐标测量;2)艇体坐标系{O}中目标点转换到大地坐标系{E}下。
2) 大地坐标系中实际点坐标测量。
阐述大地坐标系{E}中实际点坐标测量过程。大地坐标系{E}下,测得传感器到机械手末端的距离L1、L2、L3,结合传感器之间相对距离值a、b、c,得到实际点A′坐标方程式:
| $ \left\{ {\begin{array}{*{20}{l}} {x_b^2 + y_b^2 + {{\left( {{z_b} - a \cdot \cos \theta } \right)}^2} = L_1^2} \\ {x_b^2 + {{\left( {{y_b} - a \cdot \sin \theta } \right)}^2} + z_b^2 = L_2^2} \\ {x_b^2 + y_b^2 + {{\left( {{z_b} - a \cdot \cos \theta + b} \right)}^2} = L_3^2} \end{array}} \right. $ | (1) |
式中:θ为传感器安装位置夹角。经式(1)解算,可得实际点A′(xb, yb, zb)坐标所示:
| $ \left\{ {\begin{array}{*{20}{c}} {{x_b} = \pm \sqrt {L_1^2 - y_b^2 - {{\left( {{z_b} - a \cdot \cos \theta } \right)}^2}} } \\ {{y_b} = \left( {L_1^2 - L_2^2 + {a^2} - 2 \cdot {{(a \cdot \cos \theta )}^2} + } \right.} \\ {2a \cdot {z_b} \cdot \cos \theta )/2a \cdot \sin \theta } \\ {{z_b} = \left( {L_3^2 - L_1^2 - {b^2} + 2a \cdot b \cdot \cos \theta } \right)/2b} \end{array}} \right. $ | (2) |
3) 艇体坐标系中目标点坐标转换。
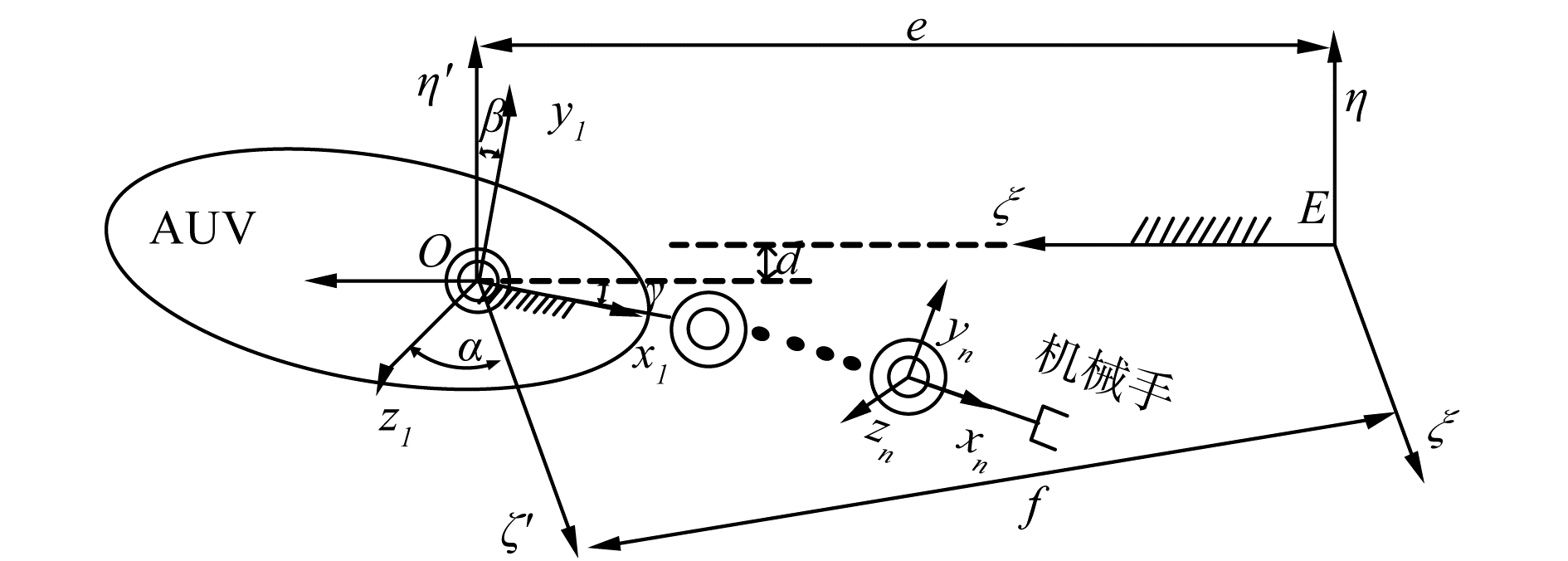
艇体坐标系{O}中目标点转换到大地坐标系{E}中。艇体坐标系{O}与大地坐标系{E}的原点不重合、各坐标轴不平行,导致坐标系之间不能直接转换。为此,本文构建一个媒介坐标系{O:O-ξ′η′ζ′},将艇体坐标系{O}中目标点转换到{C}中,再通过{C}转换到大地坐标系{E}下。
媒介坐标系{C}如图 4所示,{C}原点与{O}原点重合,{C}各坐标轴与{E}各坐标轴平行。
|
Download:
|
| 图 4 坐标系{C}与{O}、{E}位置关系 Fig. 4 The position relation diagram of coordinate system {C} and {O}, {E} | |
目标点坐标转换的过程和原理如下:
① 目标点位置转换到媒介坐标系{C}。
定义OP为坐标系{O},CP为坐标系{C};OCP为{C}与{O}之间的旋转矩阵,如图 4所示。根据坐标系旋转变换得出{C}与{O}之间的旋转矩阵为:
| $ _o^c{\bf{P}} = \left[ {\begin{array}{*{20}{c}} {c{\rm{ \mathsf{ α} }} c{\rm{ \mathsf{ β} }} }&{c{\rm{ \mathsf{ α} }} s{\rm{ \mathsf{ β} }} s\gamma - s{\rm{ \mathsf{ α} }} c\gamma }&{c{\rm{ \mathsf{ α} }} s{\rm{ \mathsf{ β} }} c\gamma + s{\rm{ \mathsf{ α} }} s\gamma } \\ {s{\rm{ \mathsf{ α} }} c{\rm{ \mathsf{ β} }} }&{s{\rm{ \mathsf{ α} }} s{\rm{ \mathsf{ β} }} s\gamma + c{\rm{ \mathsf{ α} }} c\gamma }&{s{\rm{ \mathsf{ α} }} s{\rm{ \mathsf{ β} }} c\gamma - c{\rm{ \mathsf{ α} }} s\gamma } \\ { - s{\rm{ \mathsf{ β} }} }&{c{\rm{ \mathsf{ β} }} s\gamma }&{c{\rm{ \mathsf{ β} }}c\gamma } \end{array}} \right] $ | (3) |
式中sα=sin α,cα=cos α,其余相同。
根据式(3)可得{C}与{O}关系如下:
| $ ^c\mathit{\boldsymbol{P}}{ = ^o}\mathit{\boldsymbol{P}} \cdot _o^c\mathit{\boldsymbol{P}} $ | (4) |
通过式(4)可将艇体坐标系{O}中目标点转换到媒介坐标系{C}下。
② 媒介坐标系{C}转换到大地坐标系{E}。
定义EP为坐标系{E},CEP为{C}与{O}之间的平移矩阵。由于{C}与{E}坐标轴平行,根据坐标系平移变换方法,得出{C}与{E}的平移矩阵为:
| $_C^E\mathit{\boldsymbol{P}} = {\left[ {\begin{array}{*{20}{c}} d&e&f \end{array}} \right]^{\text{T}}} $ | (5) |
根据式(5)可得{C}与{E}的坐标系关系:
| $^\mathit{\boldsymbol{E}}\mathit{\boldsymbol{P}}{ = ^C}\mathit{\boldsymbol{P}} + _C^E\mathit{\boldsymbol{P}} $ | (6) |
通过式(6)将目标点转换到大地坐标系{E}。基于上述1)、2)过程,得到转换后的目标点转换坐标AZ (ξ, η, ζ)为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} \xi \\ \eta \\ \zeta \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\rm{c}}\alpha {\rm{c}}\beta \quad \;\;\;{\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma - {\rm{s}}\alpha {\rm{c}}\gamma \;\;\;\quad \;{\rm{c}}\alpha {\rm{s}}\beta {\rm{c}}\gamma + {\rm{s}}\alpha {\rm{s}}\gamma }\\ {{\rm{s}}\alpha {\rm{c}}\beta \quad {\rm{s}}\alpha {\rm{s}}\beta {\rm{s}}\gamma + {\rm{c}}\alpha {\rm{c}}\gamma \;\quad \;\;\;\;\;\;\;{\rm{s}}\alpha {\rm{s}}\beta {\rm{c}}\gamma - {\rm{c}}\alpha {\rm{s}}\gamma }\\ { - {\rm{s}}\beta \quad \;\;\;\;\;\;\;\;\;{\rm{c}}\beta {\rm{s}}\gamma \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{c}}\beta {\rm{c}}\gamma } \end{array}} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}}\\ {{z_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} d\\ e\\ f \end{array}} \right] \end{array} $ | (7) |
式中α、β、γ、d、e、f为坐标转换参数。
式(7)转换参数为未知量,求解过程如下:
① 坐标系{O}中,选取机械手关节上的O、P、Q,此三点坐标值通过接触式传感器测量得出;
② 坐标系{E}中,通过实际点测量过程,测量得到O、P、Q的坐标值,表示为O′、P′、Q′;
③ 将O、P、Q点作为目标点,O′、P′、Q′作为目标点转换点,分别代入式(7)左右端,联立可得α、β、γ、d、e、f。
4) 方法测量步骤。
基于上述分析,归纳本文方法测量步骤如下:
① 艇体坐标系{O}中,给定目标点坐标A(x1, y1, z1),控制机械手向目标点运动,稳定后的机械手末端在大地坐标系{E}中实际点为A′;
② 通过实际点坐标测量,得到实际点A′的坐标值A′(xb, yb, zb);
③ 将艇体坐标系{O}中目标点A,通过媒介坐标系{C}转换,得到大地坐标系{E}中目标点转换坐标AZ(ξ, η, ζ);
④ 大地坐标系{E}中,通过实际点A′、目标点转换坐标AZ,得出末端精度δ:
| $ \delta = \left| { \pm \sqrt {{{\left( {{x_b} - \xi } \right)}^2} + {{\left( {{y_b} - \eta } \right)}^2} + {{\left( {{z_b} - \zeta } \right)}^2}} } \right| $ | (8) |
由于测量方法原理不完善或测量元件误差等影响,将导致测量方法中存在原理性误差;而方法原理不同,其误差分析未有标准可循。因此,本节分析测量方法中误差因素,并提出基于数值迭代方式的原理性误差分析方法,得出原理性误差范围。
基于本文精度测量方法原理和步骤分析,原理性误差主要来自于传感器测量误差和传感器安装误差。进一步分析,传感器测量误差、传感器安装误差主要影响到步骤②和③;分别表现为实际点的坐标测量误差和目标点的坐标转换误差。接下来,从坐标测量误差和坐标转换误差角度,分析本文原理性误差范围。
2.3.1 坐标测量误差分析坐标测量误差来源于实际点坐标测量阶段(②)。根据测量方法原理进行分析,其影响因素主要为2部分,各部分误差数值如下。
1) 受传感器测量精度影响,传感器测量值L1、L2、L3中存在测量误差,具体数值为±0.001%·L(传感器测量精度与测量长度L为正比例关系);
2) 由于a、b、c的数值通过接触式拉伸传感器测量得出,受传感器测量精度影响,a、b、c中存在测量误差,其误差分别为±0.001%·a、±0.001%·b、±0.001%·c。
包含误差因素L1、L2、L3和a、b、c表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{L_{{\rm{e}}\;1}} = {L_1} \pm 0.001\% \cdot {L_1}, }&{{a_{\rm{e}}} = a \pm 0.001\% \cdot a}\\ {{L_{{\rm{e}}\;2}} = {L_2} \pm 0.001\% \cdot {L_2}, }&{{b_{\rm{e}}} = b \pm 0.001\% \cdot b}\\ {{L_{{\rm{e}}\;3}} = {L_3} \pm 0.001\% \cdot {L_3}, }&{{c_{\rm{e}}} = c \pm 0.001\% \cdot c} \end{array}} \right. $ | (9) |
式中:Le1、Le2、Le3和ae、be、ce为包含了误差因素的相关测量参数;后文带有下标“e”为包含误差因素的相关参数。
将式(6)代入式(2),得出包含误差因素的实际点坐标Ae′(xbe, ybe, zbe):
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{be}}}} = \pm \sqrt {L_{{\rm{e}}1}^2 - y_{{\rm{be}}}^2 - {{\left( {{z_{{\rm{be}}}} - {a_{\rm{e}}} \cdot \cos {\theta _{\rm{e}}}} \right)}^2}} }\\ {{y_{{\rm{be}}}} = \frac{{L_{{\rm{e}}1}^2 - L_{{\rm{e}}2}^2 + a_{\rm{e}}^2 - 2 \cdot {{\left( {{a_{\rm{e}}} \cdot \cos {\theta _{\rm{e}}}} \right)}^2} + 2{a_{\rm{e}}} \cdot {z_{{\rm{be}}}} \cdot \cos {\theta _{\rm{e}}}}}{{2{a_{\rm{e}}} \cdot \sin {\theta _{\rm{e}}}}}}\\ {{z_{{\rm{be}}}} = \frac{{L_{{{\rm{e}}3}}^2 - L_{{\rm{e}}1}^2 - b_{\rm{e}}^2 + 2{a_{\rm{e}}} \cdot {b_{\rm{e}}} \cdot \cos {\theta _{\rm{e}}}}}{{2{b_{\rm{e}}}}}} \end{array}} \right. $ | (10) |
| $ cos\ {\theta _{\rm{e}}} = \left( {a_{\rm{e}}^2 + b_{\rm{e}}^2 - c_{\rm{e}}^2} \right)/2{a_{\rm{e}}}{b_{\rm{e}}} $ | (11) |
包含误差因素的实际点坐标Ae′(xbe, ybe, zbe)与未考虑误差的实际点坐标A′(xb, yb, zb)的差值,即为实际点坐标测量误差表达式δC,为:
| $ {\delta _{\rm{C}}} = \left| { \pm \sqrt {{{\left( {{x_{{\rm{be}}}} - {x_{\rm{b}}}} \right)}^2} + {{\left( {{y_{{\rm{be}}}} - {y_{\rm{b}}}} \right)}^2} + {{\left( {{z_{{\rm{be}}}} - {z_{\rm{b}}}} \right)}^2}} } \right| $ | (12) |
接下来,分析坐标测量误差的具体数值范围。坐标测量误差主要受传感器测量误差影响,其与测量长度L1、L2、L3相关;但进一步分析,坐标测量误差与L1、L2、L3的相关性呈现非线性关系;即并不是机械手末端可达空间(机械手末端运动空间)最边缘点误差最大;且机械手可达空间内,坐标测量误差为一个存在最大值的误差范围。针对此问题,本文提出基于数值迭代方式的原理性误差分析方法。其过程如下:
1) 在艇体坐标系{O:O-x1y1z1},x1、y1、z1 3个方向,每个方向各自间隔1 mm取点,机械手可达空间内共取50 000个坐标点;
2) 将上述坐标点A′,代入式(1)得到坐标点对应的L1、L2、L3参数值;
3) 将L1、L2、L3代入式(9~11),得到坐标点A′对应的包含了误差因素的坐标Ae′;
4) 将A′和Ae′代入式(12),可得当前坐标点的坐标测量误差δC;
5) 重复迭代50 000次上述2)~4)过程,得到50 000个坐标点测量误差组成区间,即为机械手可达空间内精确的坐标测量误差范围。
坐标测量误差数值范围如图 5所示。

|
Download:
|
| 图 5 坐标测量误数值范围 Fig. 5 The numerical range of coordinate measurement error | |
图 5中,实际点最大坐标测量误差δC max为0.325 mm,误差数值范围为0~0.325 mm。
2.3.2 坐标转换误差分析坐标转换误差产生原因及其影响因素。坐标转换误差来源于目标点坐标系转换阶段(③);其影响因素主要分为以下2部分:
1) 转换参数求解过程,O′、P′、Q′坐标值通过空间坐标测量方法测量,其包含坐标测量误差;
2) 转换参数求解过程,受传感器测量精度影响,O、P、Q坐标值中存在传感器测量误差。
分析O′、P′、Q′和O、P、Q坐标值中包含的误差数值。如下所示:
1) 大地坐标系{E}中,O′、P′、Q′坐标值中坐标测量误差为0~0.325 mm(2.3.1节推导得出);
2) 艇体坐标系{O}中,O、P、Q的坐标值中传感器测量误差为±0.001%·L。
接下来,与2.3.1节类似,基于误差影响因素,得出坐标转换误差表达式。具体思路如下:
1) 包含了误差因素的O、P、Q和O′、P′、Q′坐标值表示为Oe、Pe、Qe和Oe′、Pe′、Qe′;
2) 将Oe、Pe、Qe和Oe′、Pe′、Qe′代入式(4)左右端,联立求解得出包含误差影响因素的坐标转换参数αe、βe、γe、de、ee、fe;
3) 基于此组坐标转换参数αe、βe、γe、de、ee、fe数值,将目标点A转换到大地坐标系{E}下,得到包含误差影响因素的转换值AZe(ξe, ηe, ζe);
4) AZe(ξe, ηe, ζe)与AZ(ξ, η, ζ)的差值,即为坐标转换误差δZ:
| $ {\delta _z} = \left| { \pm \sqrt {{{\left( {{\xi _e} - \xi } \right)}^2} + {{\left( {{\eta _e} - \eta } \right)}^2} + {{\left( {{\zeta _e} - \zeta } \right)}^2}} } \right| $ | (13) |
基于上述坐标转换误差表达式(13),与2.3.1节同理,通过数值迭代方式,得到具体的坐标转换误差数值范围。坐标转换误差分析时,在测量误差范围0~0.325 mm内部,以相同间隔取10 000组误差进行迭代,得到坐标转换误差δZ误差范围,如图 6所示。其目标点最大坐标转换误差为1.055 mm,误差数值范围为0.088~1.055 mm。

|
Download:
|
| 图 6 坐标转换误差数值范围 Fig. 6 The numerical range of coordinate conversion error | |
基于上述2.3.1~2.3.2节推导,坐标测量误差范围为0~0.325 mm,坐标系转换误差范围为0.088~1.055 mm。基于上文分析,二者叠加即为本文末端精度测量方法的原理性误差,其具体数值范围0.088~1.380 mm。同时,本文基于数值迭代的原理性误差分析方法与具体的测量结构无关,该误差分析方法可为与本文测量原理相近的测量装置进行原理性误差分析时参考。
3 精度测量水池实验验证 3.1 末端精度范围测量方法实验为验证本文提出的水下视觉末端精度范围测量方法的有效性,本小节进行AUVMS艇体水下动力悬停状态的机械手末端精度范围测量实验。
水池实验如图 7所示,水池可自主造流,造流装置和流速如文献[15]所示。实验中,以边长300 mm的立方体区域中心为目标点;水下动力悬停时,控制机械手向目标点运动,600 s实验时间内,基于视觉观察机械手末端是否稳定于立方体内部。

|
Download:
|
| 图 7 水下视觉末端精度范围测量实验 Fig. 7 Experimental diagram of the end precision range measurement based on underwater vision | |
在实验时间0~600 s内,AUVMS动力悬停状态下,从视觉图像中观察机械手末端长期处于立方体内部(边长300 mm);即为机械手末端能够稳定在目标点的±150 mm范围内。实验表明,本文方法能准确测量水下机械手末端精度范围,验证本文方法有效性;并且末端精度范围满足课题第1项技术指标要求。
3.2 接触式末端精度测量方法实验接下来,AUVMS艇体固定和艇体动力悬停状态下,进行末端静态精度和动态精度测量实验;结合原理性误差范围,验证机械手末端精度是否满足课题技术指标要求。
3.2.1 静态末端精度测量实验首先,AUVMS艇体固定状态下,进行静态末端精度测量实验,实验环境与3.1节一致。实验中,在机械手可达空间随机选取4个目标点,对4个目标点分别重复测量10次,得到40次静态末端精度测量数值;测量实验图和实验结果如图 8所示。

|
Download:
|
| 图 8 静态末端精度测量实验 Fig. 8 The static end precision measurement experiment | |
图 8所示的实验结果分布于1.206~3.307 mm内,最大值为3.307 mm。结合原理性误差(0.088~1.380 mm)进行分析,最终得出40次机械手静态末端精度集中于1.294~4.687 mm,最大值为4.687 mm。
实验结果表明,本文方法能够实时、有效测量得到机械手末端精度,验证本文方法有效性。同时,末端精度数值满足课题第2项技术指标要求。
3.2.2 动态末端精度测量实验为进一步验证接触式机械手末端精度测量方法的有效性,在AUVMS艇体水下动力悬停状态下,进行机械手动态末端精度测量实验验证。
实验水流环境与3.1节一致。在机械手可达空间内随机选取10个目标点,进行机械手末端精度测量;测量结果如图 9所示。将10个目标点的动态末端精度实验结果进行归纳,如表 1所示。

|
Download:
|
| 图 9 动态末端精度测量结果 Fig. 9 Dynamic end precision measurement results | |
| 表 1 10组目标点的动态末端精度测量结果 Table 1 Dynamic end precision measurement results for 10 sets of target points |
分析表 1,在AUVMS艇体水下动力悬停状态下,10组测量实验得到的机械手末端最大动态末端精度为136.83 mm;考虑本文精度测量方法的原理性误差为1.380 mm(0.088~1.380 mm),最终得出本文机械手动态末端精度最大为138.21 mm;其精度数值在±150 mm以内,满足课题指标要求。
上述实验结果表明:本文接触式机械手末端精度测量方法能够准确的测量AUVMS搭载的水下机械手末端精度,进一步验证本文方法的有效性。
4 结论1) 为检测AUVMS机械手末端运动是否到达某一规定的范围内,提出了一种水下视觉末端精度范围测量方法。水池实验结果表明:本文方法能够准确的测量AUVMS机械手末端精度范围,验证了本文方法的有效性。
2) 为检测AUVMS机械手末端精度的具体数值,提出了一种接触式水下机械手末端精度测量方法;在AUVMS艇体固定和艇体动力悬停状态下。水池实验结果表明:本文方法能够实时、有效测量机械手作业范围内部不同目标点的末端精度,验证了本文方法的有效性。
3) 本文提出基于数值迭代方式的原理性误差分析思路,得出本文方法原理性误差为0.088~1.380 mm。本文原理性误差分析思路与测量装置结构无关,该思路可为与本文测量原理相近的测量方法进行误差分析时参考。
| [1] |
徐玉如, 李彭超. 水下机器人发展趋势[J]. 自然杂志, 2011, 33(3): 125-132. XU Yuru, LI Pengchao. Developing tendency of unmanned underwater vehicles[J]. Chinese journal of nature, 2011, 33(3): 125-132. (  0) 0)
|
| [2] |
SIMETTI E, CASALINO G, TORELLI S, et al. Floating underwater manipulation:developed control methodology and experimental validation within the TRIDENT project[J]. Journal of field robotics, 2014, 31(3): 364-385. DOI:10.1002/rob.2014.31.issue-3 (  0) 0)
|
| [3] |
MARANI G, CHOI S K, YUH J. Underwater autonomous manipulation for intervention missions AUVs[J]. Ocean engineering, 2009, 36(1): 15-23. DOI:10.1016/j.oceaneng.2008.08.007 (  0) 0)
|
| [4] |
YANG Chao, WANG Yujia, YAO Feng. Driving performance of underwater long-arm hydraulic manipulator system for small autonomous underwater vehicle and its positioning accuracy[J]. International journal of advanced robotic systems, 2017, 14(6): 1-18. (  0) 0)
|
| [5] |
LYNCH B, ELLERY A. Efficient control of an AUV-manipulator system:an application for the exploration of Europa[J]. IEEE journal of oceanic engineering, 2014, 39(3): 552-570. DOI:10.1109/JOE.2013.2271390 (  0) 0)
|
| [6] |
丁雅斌, 梅江平, 张文昌, 等. 基于单目视觉的并联机器人末端位姿检测[J]. 机械工程学报, 2014, 50(21): 174-179. DING Yabin, MEI Jiangping, ZHANG Wenchang, et al. Position and orientation measurement of parallel robot based on monocular vision[J]. Journal of mechanical engineering, 2014, 50(21): 174-179. (  0) 0)
|
| [7] |
王一, 刘常杰, 任永杰, 等. 工业坐标测量机器人定位误差补偿技术[J]. 机械工程学报, 2011, 47(15): 31-36. WANG Yi, LIU Changjie, REN Yongjie, et al. Compensation for positioning error of industrial coordinate measurement robot[J]. Journal of mechanical engineering, 2011, 47(15): 31-36. (  0) 0)
|
| [8] |
孙天慧, 田文杰, 王辉, 等. 基于球杆仪的三坐标并联动力头运动学标定方法[J]. 机械工程学报, 2012, 48(5): 22-27. SUN Tianhui, TIAN Wenjie, WANG Hui, et al. Kinematic calibration of 3-DOF spindle head using double-ball bar[J]. Journal of mechanical engineering, 2012, 48(5): 22-27. (  0) 0)
|
| [9] |
解则晓, 辛少辉, 李绪勇, 等. 基于单目视觉的机器人标定方法[J]. 机械工程学报, 2011, 47(5): 35-39. XIE Zexiao, XIN Shaohui, LI Xuyong, et al. Method of robot calibration based on monocular vision[J]. Journal of mechanical engineering, 2011, 47(5): 35-39. (  0) 0)
|
| [10] |
刘常杰, 马爽, 郭寅, 等. 高精度柔性坐标测量系统及其校准技术研究[J]. 光学学报, 2013, 33(10): 120-126. LIU Changjie, MA Shuang, GUO Yin, et al. Study on calibration technology of high-precision flexible coordinate measurement system[J]. Acta optica sinica, 2013, 33(10): 120-126. (  0) 0)
|
| [11] |
李煊, 张铭钧. 水下双目视觉系统中的目标分割和目标定位[J]. 华中科技大学学报(自然科学版), 2017, 45(12): 53-59. LI Xuan, ZHANG Mingjun. Target segmentation and target positioning of underwater binocular vision system[J]. Journal of Huazhong University of Science & Technology (natural science edition), 2017, 45(12): 53-59. (  0) 0)
|
| [12] |
ZHANG Mingjun, LI Shupeng, LI Xuan. Research on technologies of underwater feature extraction and target location based on binocular vision[C]//Proceedings of the 27th Chinese Control and Decision Conference (CCDC). Qingdao, China: IEEE, 2015: 15341469.
(  0) 0)
|
| [13] |
杨超, 郭佳, 张铭钧. 基于RBF神经网络的作业型AUV自适应终端滑模控制方法及实验研究[J]. 机器人, 2018, 40(3): 336-345. YANG Chao, GUO Jia, ZHANG Mingjun. Adaptive terminal sliding mode control method based on RBF neural network for operational AUV and its experimental research[J]. Robot, 2018, 40(3): 336-345. (  0) 0)
|
| [14] |
杨超, 张铭钧, 秦洪德, 等. 水下机器人-机械手姿态调节系统研究[J]. 哈尔滨工程大学学报, 2018, 39(2): 377-383. YANG Chao, ZHANG Mingjun, QIN Hongde, et al. Attitude control system for autonomous underwater vehicle-manipulator system[J]. Journal of Harbin Engineering University, 2018, 39(2): 377-383. (  0) 0)
|
| [15] |
LIU Weixin, WANG Yujia, LIU Xing, et al. Weak thruster fault detection for AUV based on stochastic resonance and wavelet reconstruction[J]. Journal of central south university, 2016, 23(11): 2883-2895. DOI:10.1007/s11771-016-3352-1 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


