涡旋压缩机是一种新型高效的容积式压缩机,具有结构紧凑、微振低噪、运转平稳和可靠性高等诸多优点[1-2],已在制冷、空调、增压泵和涡旋空压机等领域得到广泛应用[3-7]。
由涡旋型线构造的涡旋齿是涡旋压缩机的主要结构,而涡旋型线是设计和研究的基础。目前构造涡旋齿的型线可分为2大类:等截面型线和变截面型线,对于等截面型线,因其涡旋齿承受的气体力波动较小,设计加工也较为方便而得到了普遍的应用,但是却不能充分利用毛坯材料,同时若要增加等截面的压缩比就必须增加涡旋齿的圈数,这样会导致轴向泄漏线长度增加和整机尺寸过大。对于变截面型线,通常是由组合型线构成的,如基圆渐开线—高次曲线—圆弧的组合型线和基圆渐开线—高次曲线—基圆渐开线的组合型线,可以通过较少的圈数就可以实现大的压缩比,并可减少泄漏线的长度使整机效率提高。因此变截面的研究成为了一个热点,MURRAY对变截面涡旋压缩机的结构进行了描述并对其性能的优势作了分析[8],SHAFFER等[9]采用控制容积法建立了变截面涡旋几何模型。彭斌等[10]建立了变截面涡旋压缩机的数学模型并进行了试验验证。王立存等[11]运用泛函,对变壁厚涡旋型线理论及形状优化做了研究。LIU等[12-13]建立了变壁厚涡旋压缩机的几何模型并运用有限元法对其进行了优化。邬再新等[14]建立了渐开线—高次曲线组合型线的几何模型并对其进行了有限元分析,刘涛等[15]通过Matlab遗传算法工具箱对组合型线进行了优化,但这些文献主要集中在型线和几何模型上,而对变截面涡旋压缩机齿厚变化规律的研究还很鲜见。
本文利用微分几何中的Frenet标架,提出一种涡旋型线,即由不同基圆半径的圆渐开线组合而成的组合型线,并且建立了变截面涡旋压缩机的齿厚计算模型,定量化研究了变截面涡旋压缩机的齿厚变化规律,从而实现从经验设计到定量化设计的过渡,为涡旋齿的柔性化设计奠定理论基础。
1 变截面涡旋齿的建立 1.1 涡旋型线的微分几何关系图 1是任意涡旋型线的微分几何关系示意图。图中M为型线切点,φ为型线切向角参数,a是基圆半径,α是单位切向量,β是单位法向量,Rn是切点处的法向分量,称为展弦,Rt是与Rn垂直的切向分量,称为任意渐开线基圆半径,且满足:

|
Download:
|
| 图 1 型线的微分几何关系示意 Fig. 1 Schematic diagram of differential geometry relation for scroll profile | |
| ${\mathit{\boldsymbol{R}}_t}(\varphi ) = \frac{{{\rm{d}}{\mathit{\boldsymbol{R}}_{\rm{n}}}(\varphi )}}{{{\rm{d}}\varphi }} $ | (1) |
在平面直角坐标系中,曲线r=r(s)可以表示为
| $\mathit{\boldsymbol{r}} = \mathit{\boldsymbol{r}}(s) = (x(s), y(s)) $ | (2) |
式中s是弧长参数。
由微分几何理论,记型线在切点的切线与x轴正向的夹角为φ=φ(s),则在切点处的单位切向量和单位法向量分别为:
| $\mathit{\boldsymbol{\alpha }}(s) = \left( {{x^\prime }(s), {y^\prime }(s)} \right) = (\cos \varphi (s), \sin \varphi (s)) $ | (3) |
| $\mathit{\boldsymbol{\beta }}(s) = \left( { - {y^\prime }(s), {x^\prime }(s)} \right) = ( - \sin \varphi (s), \cos \varphi (s)) $ | (4) |
由于α(s)是单位向量场,故有α(s)⊥α′(s),所以α′(s)与β(s)存在:
| ${\mathit{\boldsymbol{\alpha }}^\prime }(s) = {\kappa _r}\mathit{\boldsymbol{\beta }}(s) $ | (5) |
式中κr是平面曲线的相对曲率。
对式(3)求导,可得:
| ${\mathit{\boldsymbol{\alpha }}^\prime }(s) = {\varphi ^\prime }(s)( - \sin \varphi (s), \cos \varphi (s)) = {\varphi ^\prime }(s)\mathit{\boldsymbol{\beta }}(s) $ | (6) |
结合式(5)与式(6),得到:
| ${\kappa _r} = {\varphi ^\prime }(s) $ | (7) |
由平面曲线的基本公式知,型线在切点处的曲率半径为:
| $\rho (\varphi ) = \frac{1}{{{\kappa _r}}} = \frac{{{\rm{d}}s}}{{{\rm{d}}\varphi }} $ | (8) |
综合式(2)~(5),得到平面曲线的Frenet标架{r(s); α(s), β(s)}沿曲线运动的公式为:
| $\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}^\prime }(s) = \mathit{\boldsymbol{\alpha }}(s)}\\ {{\mathit{\boldsymbol{\alpha }}^\prime }(s) = {\mathit{\boldsymbol{\kappa }}_r}\mathit{\boldsymbol{\beta }}(s)}\\ {{\mathit{\boldsymbol{\beta }}^\prime }(s) = - {\mathit{\boldsymbol{\kappa }}_r}\mathit{\boldsymbol{\alpha }}(s)} \end{array}} \right. $ | (9) |
利用Frenet标架的运动公式,由初值(x(φ0), y(φ0))和式(8),可以唯一确定涡旋型线母线方程为:
| $\left\{ {\begin{array}{*{20}{l}} {x(\varphi ) = x\left( {{\varphi _0}} \right) + \int_{{\varphi _0}}^\varphi \rho (\varphi )\cos \varphi (s){\rm{d}}\varphi }\\ {y(\varphi ) = y\left( {{\varphi _0}} \right) + \int_{{\varphi _0}}^\varphi \rho (\varphi )\sin \varphi (s){\rm{d}}\varphi } \end{array}} \right. $ | (10) |
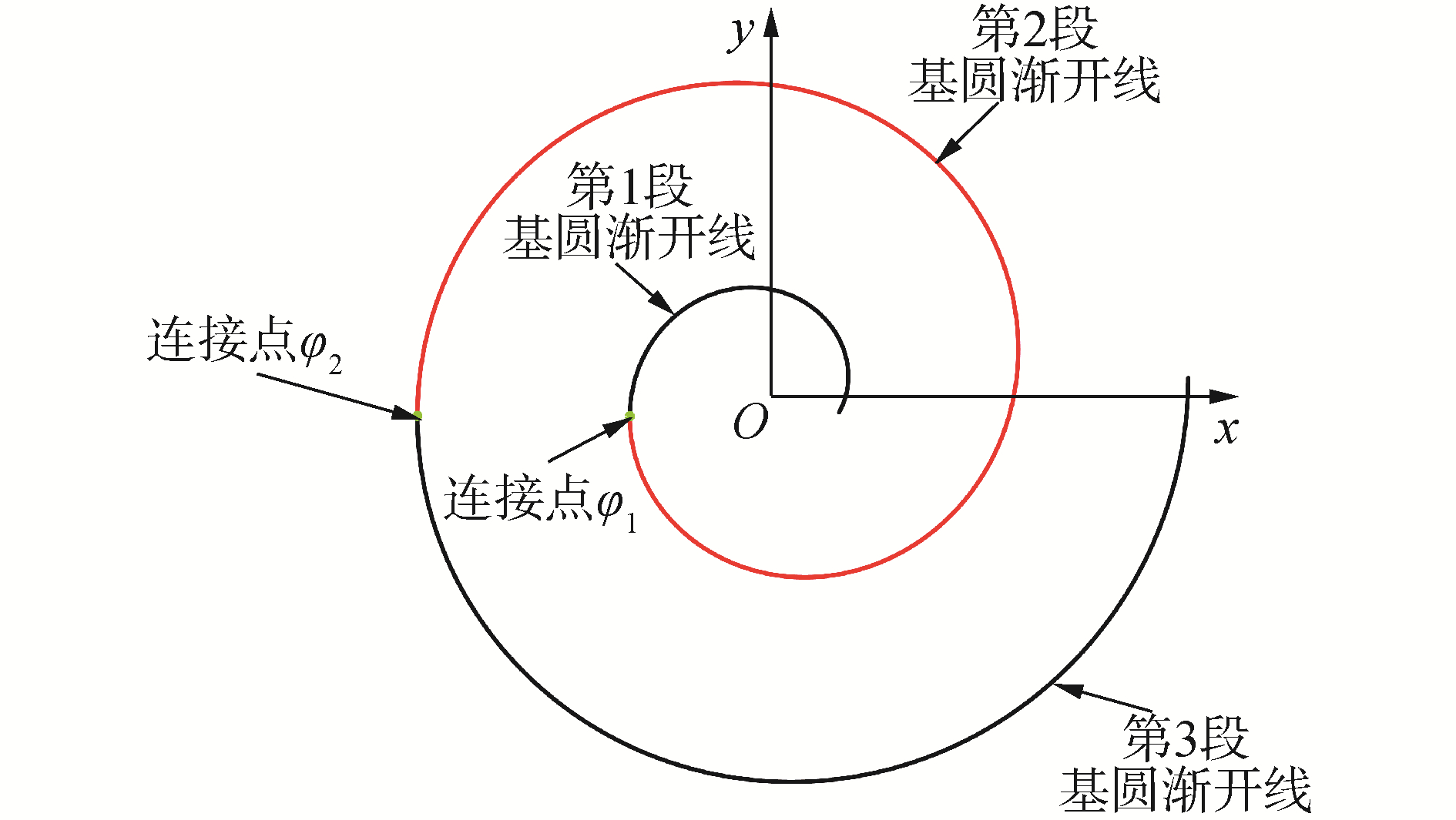
如图 2所示,组合型线的母线均选用基圆渐开线,但首末两段渐开线的基圆半径相同,而中间段渐开线的基圆半径与首末两段渐开线的基圆半径不同。根据式(10),组合型线各段的母线方程可表示为:
|
Download:
|
| 图 2 组合型线的母线 Fig. 2 Generating line of the combination profile | |
第1段基圆渐开线母线方程为:
| $\left\{ {\begin{array}{*{20}{l}} {{x_1} = {x_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {{\rho _1}} (\varphi )\cos \varphi {\rm{d}}\varphi }\\ {{y_1} = {y_0}\left( {{\varphi _0}} \right) + \int_0^\varphi {{\rho _1}} (\varphi )\sin \varphi {\rm{d}}\varphi } \end{array}, \varphi \in \left[ {0, {\varphi _1}} \right)} \right. $ | (11) |
第2段基圆渐开线母线方程为:
| $\left\{ {\begin{array}{*{20}{l}} {{x_2} = {x_1}\left( {{\varphi _1}} \right) + \int_{{\varphi _1}}^\varphi {{\rho _2}} (\varphi )\cos \varphi {\rm{d}}\varphi }\\ {{y_2} = {y_1}\left( {{\varphi _1}} \right) + \int_{{\varphi _1}}^\varphi {{\rho _2}} (\varphi )\sin \varphi {\rm{d}}\varphi } \end{array}, \varphi \in \left[ {{\varphi _1}, {\varphi _2}} \right)} \right. $ | (12) |
第3段基圆渐开线母线方程为:
| $\left\{ {\begin{array}{*{20}{l}} {{x_3} = {x_2}\left( {{\varphi _2}} \right) + \int_{{\varphi _2}}^\varphi {{\rho _3}} (\varphi )\cos \varphi {\rm{d}}\varphi }\\ {{y_3} = {y_2}\left( {{\varphi _2}} \right) + \int_{{\varphi _2}}^\varphi {{\rho _3}} (\varphi )\sin \varphi {\rm{d}}\varphi } \end{array}, \varphi \in \left[ {{\varphi _2}, 6\pi } \right)} \right. $ | (13) |
在连接点φ1和φ2处,为满足型线的连续性和光滑性条件,则曲率半径函数可表征为:
| $\left\{ {\begin{array}{*{20}{l}} {{\rho _1}(\varphi ) = \int_0^\varphi {{a_1}} {\rm{d}}\varphi }\\ {{\rho _2}(\varphi ) = {\rho _1}\left( {{\varphi _1}} \right) + \int_{{\varphi _1}}^\varphi {{a_2}} {\rm{d}}\varphi }\\ {{\rho _3}(\varphi ) = {\rho _2}\left( {{\varphi _2}} \right) + \int_{{\varphi _2}}^\varphi {{a_1}} {\rm{d}}\varphi } \end{array}} \right. $ | (14) |
式中:a1是首末2段基圆渐开线的基圆半径;a2是中间段基圆渐开线的基圆半径。为计算方便,取初值x0(φ0)=a1,y0(φ0)=0。
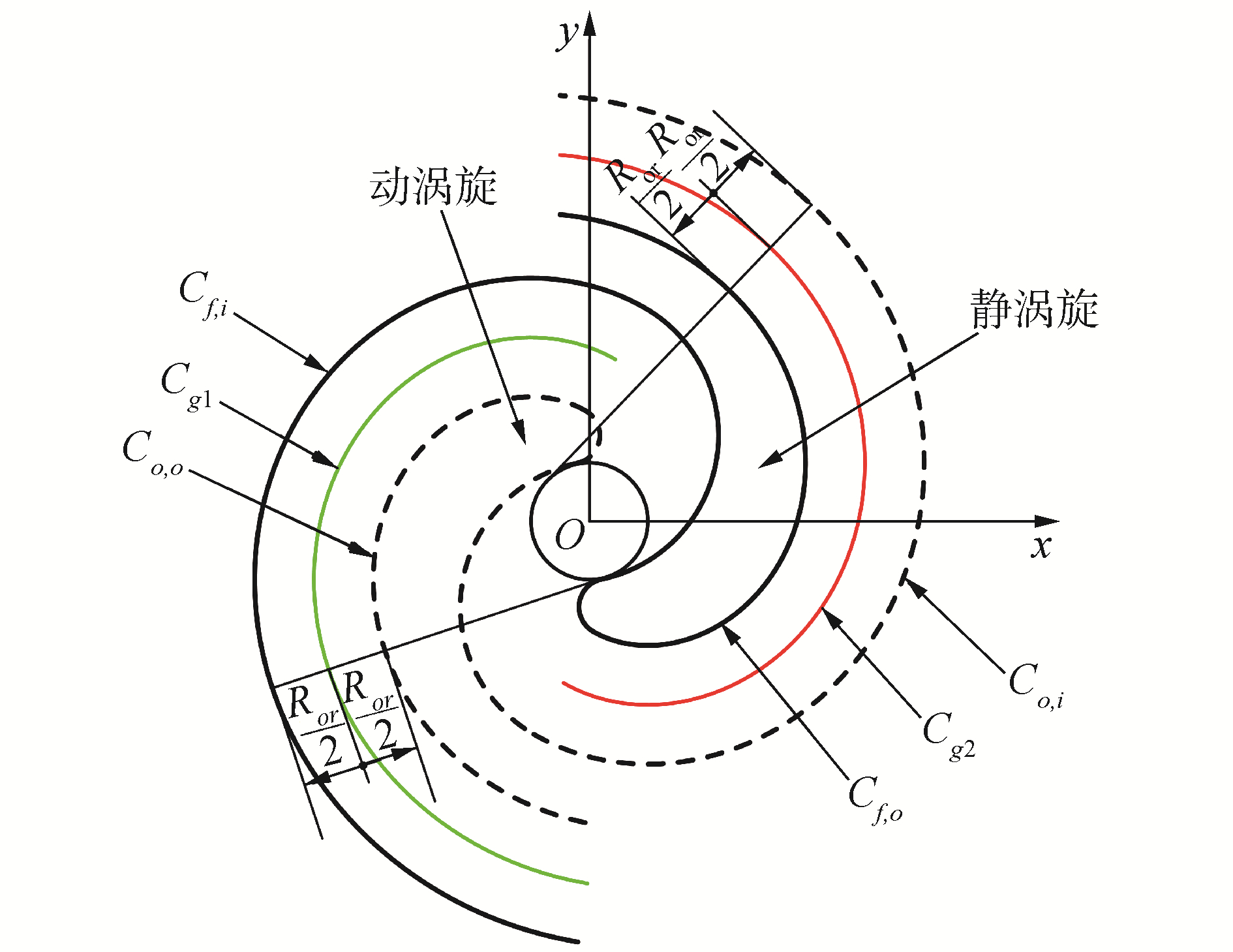
1.3 涡旋齿内外壁型线的生成在图 3中,涡旋齿的内外壁型线由对应的母线生成[16],以Cg1为母线,以其内法向等距线Co, o构成动涡旋的外壁型线,外法向等距线Cf, i构成静涡旋的内壁型线,再以母线Cg1的中心对称曲线Cg2作为另外的一条母线,以其内法向等距线Cf, o构成静涡旋的外壁型线,外法向等距线Co, i构成动涡旋内壁型线。由同一条母线生成的内外法向等距线是一对共轭型线,即Cf, i和Co, o是一对共轭型线,Cf, o和Co, i是另一对共轭型线。
|
Download:
|
| 图 3 涡旋齿型线 Fig. 3 Scroll profiles of scroll teeth | |
则涡旋压缩机静涡旋的型线方程可表示为:
| $\begin{array}{l} {C_{f, i}} = \left[ {{R_{\rm{n}}}(\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right] + \exp ({\rm{j}}\varphi ) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{R_{\rm{t}}}(\varphi )\exp \left[ {{\rm{j}}\left( {\varphi \frac{\pi }{2}} \right)} \right] \end{array} $ | (15) |
| $\begin{array}{l} {C_{f, o}} = \left[ {{R_n}(\varphi ) - \frac{{{R_{{\rm{or}}}}}}{2}} \right]\exp [{\rm{j}}(\varphi + \pi )] + \\ \;\;\;\;\;\;\;\;\;\;\;\;{R_{\rm{t}}}(\varphi )\exp \left[ {{\rm{j}}\left( {\varphi + \frac{\pi }{2} + \pi } \right)} \right] \end{array} $ | (16) |
同理,涡旋压缩机动涡旋的型线方程可表示为:
| $\begin{array}{l} {C_{o, i}} = \left[ {{R_{\rm{n}}}(\varphi ) + \frac{{{R_{{\rm{or}}}}}}{2}} \right]\exp [{\rm{j}}(\varphi + \pi )] + \\ \;\;\;\;\;\;\;\;\;\;\;\;{R_{\rm{t}}}(\varphi )\exp \left[ {{\rm{j}}\left( {\varphi + \frac{\pi }{2} + \pi } \right)} \right] \end{array} $ | (17) |
| $\begin{array}{l} {C_{o, o}} = \left[ {{R_{\rm{n}}}(\varphi ) - \frac{{{R_{{\rm{or}}}}}}{2}} \right] + \exp ({\rm{j}}\varphi ) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{R_{\rm{t}}}(\varphi )\exp \left[ {{\rm{j}}\left( {\varphi \frac{\pi }{2}} \right)} \right] \end{array} $ | (18) |
式中Ror为回转半径。
综上理论分析,建立了由3条基圆渐开线组合而成的变截面涡旋齿的几何模型,如图 4所示。图中虚线部分是由一条基圆渐开线构成的等截面涡旋齿,可以看出,任意等截面的涡旋齿可以用较少圈数的变截面涡旋齿来代替,以减少泄漏量,提高效率。

|
Download:
|
| 图 4 变截面涡旋齿 Fig. 4 Variable cross-section scroll tooth | |
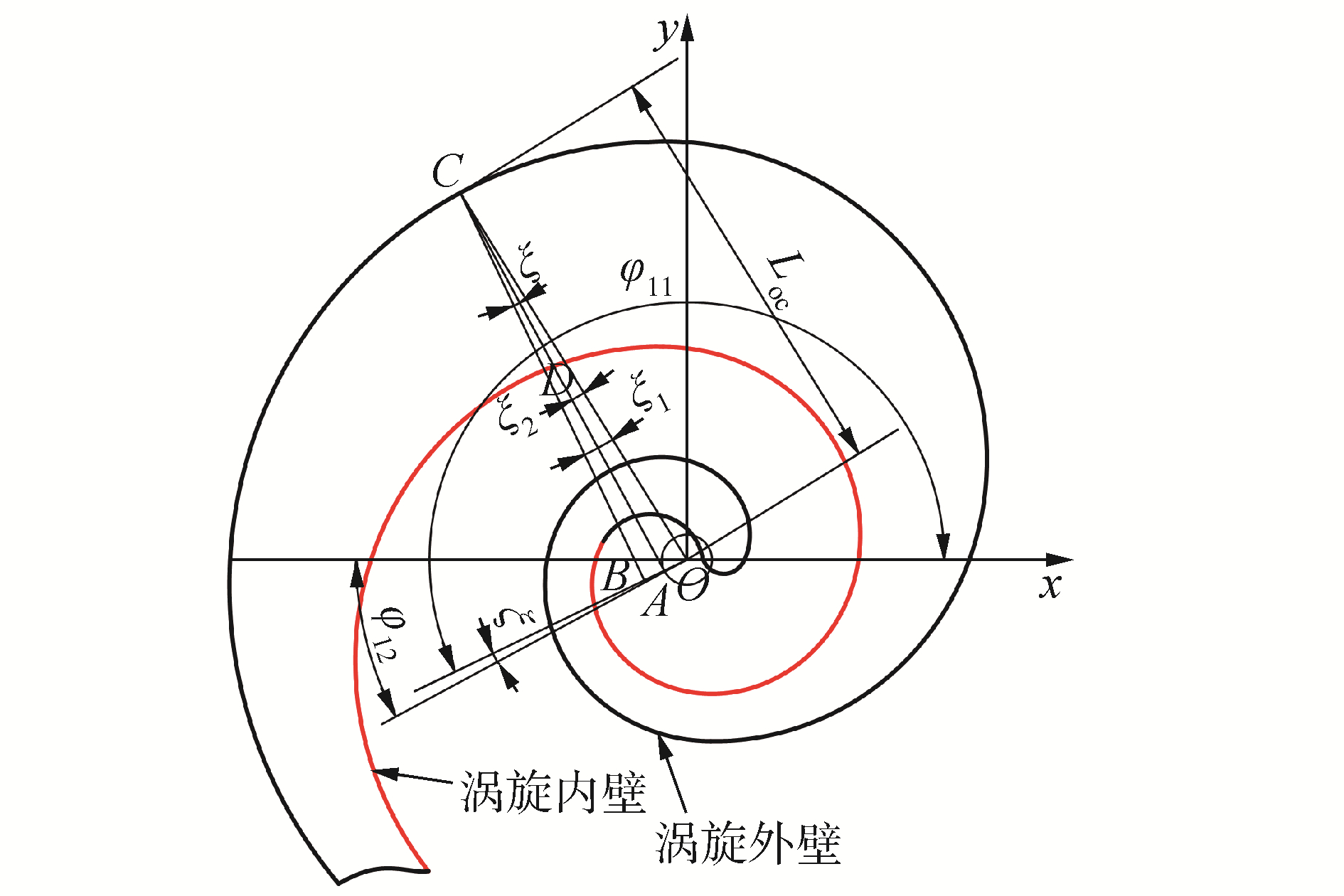
如图 5所示,φ11为外壁型线在点C处的切向角,φ12为内壁型线在点D处的切向角,根据涡旋型线的生成原理并结合图中的几何关系,可得φ11与φ12满足以下关系:
|
Download:
|
| 图 5 涡旋齿厚计算模型 Fig. 5 The calculation model of scroll tooth thickness | |
| ${\varphi _{12}} = {\varphi _{11}} - \pi + \zeta $ | (19) |
设C点的坐标为C(x0, y0),则OC之间的距离由下式计算可得到:
| ${L_{oc}} = \sqrt {x_o^2\left( {{\varphi _{11}}} \right) + y_o^2\left( {{\varphi _{11}}} \right)} $ | (20) |
OB的长度为外壁型线的基圆半径,OA的长度为内壁型线的基圆半径,可分别由Rt(φ11)和Rt(φ12)计算得出。
综合以上的分析并由图中的几何关系,得变截面涡旋齿的齿厚计算公式为:
| $t = {L_{CD}} = {L_{AC}} - {L_{AD}} = {L_{oC}}\cos {\zeta _2} - \left[ {{R_{\rm{n}}}\left( {{\varphi _{12}}} \right) + \frac{{{R_{{\rm{or}}}}}}{2}} \right] $ | (21) |
式中:
| $\left\{ {\begin{array}{*{20}{l}} {\sin {\zeta _1} = \frac{{{L_{OB}}}}{{{L_{OC}}}} = \frac{{{R_{\rm{t}}}\left( {{\varphi _{11}}} \right)}}{{{L_{OC}}}}}\\ {\sin {\zeta _2} = \frac{{{L_{OA}}}}{{{L_{OC}}}} = \frac{{{R_{\rm{t}}}\left( {{\varphi _{12}}} \right)}}{{{L_{OC}}}}}\\ {\zeta = {\zeta _1} - {\zeta _2}} \end{array}} \right. $ |
在第2段基圆半径a2=4.069 mm,回转半径Ror=2.6 mm,连接点φ1=2π,φ2=4π的条件下,仅改变基圆半径a1,得到了齿厚的变化规律曲线图,如图 6所示,由图可得,齿厚的变化是按照等齿厚—变齿厚—等齿厚的变化规律进行的,并且随着基圆半径a1的增大,首末2段等齿厚部分的齿厚在增大,而最大齿厚反而在减小。与此同时,若两基圆半径a2和a1的差值越大,则中间段变齿厚部分的齿厚变化幅度也会越大。

|
Download:
|
| 图 6 基圆半径a1变化下的齿厚曲线 Fig. 6 Tooth thickness curves under the change of the radius of base circle a1 | |
在第1段基圆半径a1=2.069 mm,回转半径Ror=2.6 mm,连接点φ1=2π,φ2=4π的条件下,只改变基圆半径a2,得到其齿厚的变化曲线图,如图 7所示。由图可知,其变化规律同样是按照等齿厚—变齿厚—等齿厚的变化规律进行的,但由于基圆半径a1是保持不变的,故首末两段等齿厚部分的齿厚保持不变。随着基圆半径a2的增大,中间段变齿厚部分的齿厚也在相应的变大,并且变化的幅度比较大。

|
Download:
|
| 图 7 基圆半径a2变化下的齿厚曲线 Fig. 7 Tooth thickness curves under the change of the radius of base circle a2 | |
在基圆半径a1=2.069 mm,a2=3.069 mm,连接点φ1=2π,φ2=4π的条件下,只改变回转半径Ror,得到其齿厚的变化规律曲线如图 8所示,由图可知,齿厚的变化规律也是按等齿厚—变齿厚—等齿厚的变化规律进行的,并且随着Ror的增大,首末两段等齿厚部分的齿厚和中间段变齿厚部分的齿厚均在减小。

|
Download:
|
| 图 8 回转半径Ror变化下的齿厚曲线 Fig. 8 Tooth thickness curves under the change of the radius of rotation Ror | |
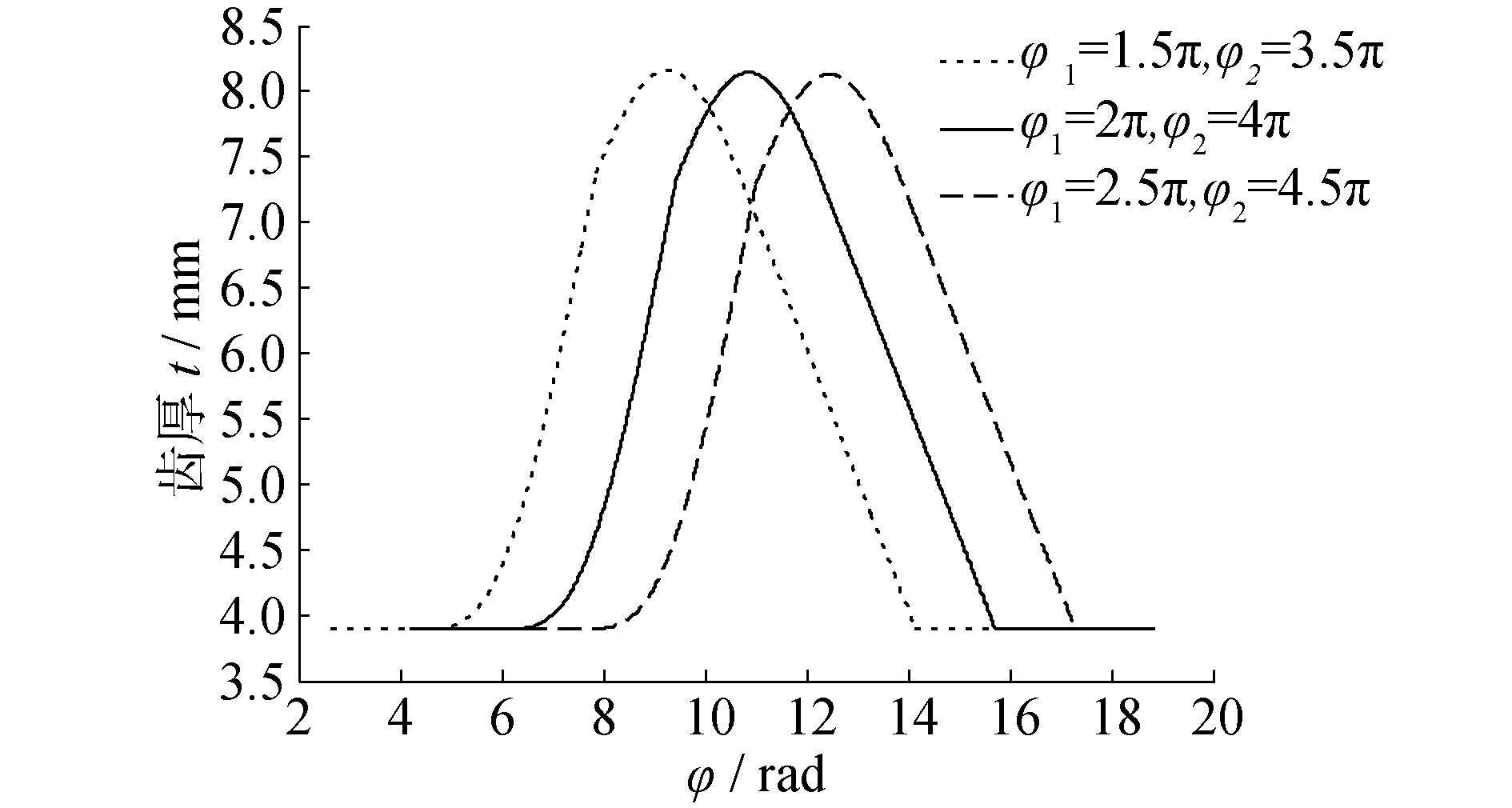
在基圆半径a1=2.069 mm,a2=3.069,回转半径Ror=2.6 mm的条件下,仅改变连接点φ1和φ2时,其齿厚的变化规律如图 9所示,由图可以看出,连接点φ1和φ2的变化,对整个变截面涡旋齿齿厚大小的影响很小,即随着φ1和φ2的增大,涡旋齿的齿厚大小基本保持不变,但涡旋齿等齿厚部分和变齿厚部分的起始位置会向后推移。图 10是当连接点分别为φ1=1.5π、φ2=3.5π,φ1=2π、φ2=4π和φ1=2.5π、φ2=4.5π时,所得到的变截面涡旋齿,可以看出变齿厚的起始位置在逐渐往后移动。
|
Download:
|
| 图 9 连接点φ1和φ2变化下的齿厚曲线 Fig. 9 Tooth thickness curves under the change of the connection points φ1 and φ2 | |

|
Download:
|
| 图 10 不同连接点对涡旋齿的影响 Fig. 10 The effect of different connection points on the scroll teeth | |
1) 利用Frenet标架的运动公式,唯一确定了涡旋型线的母线方程。并且在构造组合型线时,选用了不同基圆半径的基圆渐开线,既充分利用了圆渐开线容易加工且具有良好工作性能的优势,同时又克服了使用单一的圆渐开线而使压缩比减小和涡旋盘尺寸过大的缺点。
2) 建立的变截面涡旋齿的齿厚计算模型简洁直观,且具有一定的通用性,该模型能够准确描述涡旋齿的变化规律,可以将其灵活运用到其他类型的组合型线中。
3) 涡旋齿的齿厚受型线参数的影响,它们之间存在着精确、定量的关系,利用这种定量关系,能够很好地帮助工程设计人员设计变截面涡旋型线。
| [1] |
刘振全. 涡旋式流体机械与涡旋压缩机[M]. 北京: 机械工业出版社, 2009: 1-11.
(  0) 0)
|
| [2] |
程哲铭, 欧阳新萍, 雷蓉. 涡旋式压缩机涡旋型线的研究综述与前景[J]. 流体机械, 2015, 43(1): 51-56. CHENG Zheming, OUYANG Xinping, LEI Rong. Overview and prospect of the research on profile of scroll compressor[J]. Fluid machinery, 2015, 43(1): 51-56. DOI:10.3969/j.issn.1005-0329.2015.01.011 (  0) 0)
|
| [3] |
LU Yiji, ROSKILLY A P, JIANG Long, et al. Analysis of a 1 kW organic Rankine cycle using a scroll expander for engine coolant and exhaust heat recovery[J]. Frontiers in energy, 2017, 11(4): 527-534. DOI:10.1007/s11708-017-0516-0 (  0) 0)
|
| [4] |
IVLEV V I, MISYURIN S Y. Calculated and experimental characteristics of a scroll machine operating in the air motor mode[J]. Doklady physics, 2017, 62(1): 42-45. DOI:10.1134/S1028335817010116 (  0) 0)
|
| [5] |
CHA D A, KWON O K, OH M D. An experimental study on semiconductor process chiller using the digital scroll compressor[J]. Journal of mechanical science and technology, 2014, 28(8): 3345-3352. DOI:10.1007/s12206-014-0745-7 (  0) 0)
|
| [6] |
唐景春, 李晨凯, 叶斌, 等. 采用涡旋压缩机的电动汽车空调准双级压缩热泵性能实验研究[J]. 制冷学报, 2018, 39(1): 34-39. TANG Jingchun, LI Chenkai, YE Bin, et al. Experimental study on performance of heat pump cycle of quasi two-stage compression for electric vehicle air-conditioning with scroll compressor[J]. Journal of refrigeration, 2018, 39(1): 34-39. DOI:10.3969/j.issn.0253-4339.2018.01.034 (  0) 0)
|
| [7] |
IVLEV V I, BOZROV V M, VORONOV V A. Testing a scroll machine in pneumatic motor-expander modes[J]. Journal of machinery manufacture and reliability, 2015, 44(2): 120-124. DOI:10.3103/S1052618815020053 (  0) 0)
|
| [8] |
MURRAY C J. Variable wall thickness boosts scroll compressor's performance[J]. Design news, 1997, 53(5): 116-117. (  0) 0)
|
| [9] |
SHAFFER B R, GROLL E A. Variable wall thickness scroll geometry modeling with use of a control volume approach[J]. International journal of refrigeration, 2013, 36(7): 1809-1820. DOI:10.1016/j.ijrefrig.2013.08.003 (  0) 0)
|
| [10] |
彭斌, 孙迎. 变截面涡旋压缩机数学模型及试验研究[J]. 机械工程学报, 2015, 51(14): 185-191. PENG Bin, SUN Ying. Investigation of mathematical modeling and experiment for variable thickness scroll compressor[J]. Chinese journal of mechanical engineering, 2015, 51(14): 185-191. (  0) 0)
|
| [11] |
王立存, 陈进, 张贤明, 等. 基于泛函的制冷涡旋压缩机变壁厚涡旋型线理论及形状优化[J]. 中国机械工程, 2010, 21(16): 1898-1901. WANG Licun, CHEN Jin, ZHANG Xianming, et al. Study on geometry theory of variable wall thickness scroll profiles and shape optimization based on functional theory[J]. China mechanical engineering, 2010, 21(16): 1898-1901. (  0) 0)
|
| [12] |
LIU Yangguang, TANG Y, CHANG Yuchoung, et al. Optimum design of scroll profiles created from involute of circle with variable radii by using finite element analysis[J]. Mechanism and machine theory, 2012, 55: 1-17. DOI:10.1016/j.mechmachtheory.2012.04.002 (  0) 0)
|
| [13] |
LIU Yangguang, HUNG C, CHANG Yuchoung. Study on involute of circle with variable radii in a scroll compressor[J]. Mechanism and machine theory, 2010, 45(11): 1520-1536. DOI:10.1016/j.mechmachtheory.2010.07.001 (  0) 0)
|
| [14] |
邬再新, 杜文武, 刘涛, 等. 渐开线-高次曲线组合型线涡旋压缩机的设计及有限元分析[J]. 压缩机技术, 2011(2): 5-9. WU Zaixin, DU Wenwu, LIU Tao, et al. Design of involute-higher curve combined profile for scroll compressor and finite element analysis[J]. Compressor technology, 2011(2): 5-9. DOI:10.3969/j.issn.1006-2971.2011.02.002 (  0) 0)
|
| [15] |
刘涛, 吴虎. 基于MATLAB遗传算法工具箱的组合涡旋型线优化[J]. 流体机械, 2010, 38(7): 24-26, 84. LIU Tao, WU Hu. Optimization of hybrid scroll wraps based on MATLAB genetic algorithm toolbox[J]. Fluid machinery, 2010, 38(7): 24-26, 84. DOI:10.3969/j.issn.1005-0329.2010.07.006 (  0) 0)
|
| [16] |
刘涛, 邬再新, 刘振全. 法向等距线法生成涡旋压缩机型线的研究[J]. 机械工程学报, 2004, 40(6): 55-58. LIU Tao, WU Zaixin, LIU Zhenquan. Study on generating profile with nomal-equidistant-curve method for scroll compressor[J]. Chinese journal of mechanical engineering, 2004, 40(6): 55-58. DOI:10.3321/j.issn:0577-6686.2004.06.011 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


