微电子技术和无线电技术的快速发展使得低功耗和小型的无线设备、传感、数据传输、驱动和医用植入物等越来越普及,电池作为最常用的电源存在使用寿命短,更换成本高以及能量密度低的缺陷[1-5]。鉴于这一问题,各国研究者致力于从周围环境中收集能量(包括热能、风能、太阳能以及振动能等)并转换成电能。其中,振动能普遍存在于环境中且不依赖与气候条件,振动能量收集器能够将机械振动转化为长时间不间断的电力。振动能量常见收集方式有电磁[6]、静电[7]和压电[8-11]。其中基于压电转换的机制以其结构紧凑,转换效率高及易于微集成化等优势应用前景广阔。
为了最大限度地提高输出功率,对压电振动能量收集器的几何形状和材料等研究成果颇多。在同一条件下,相比其他结构形式,悬臂梁存在大应力、应变和变形特点,产生最高的同体积电功率,因此大多数压电能量收集器采用悬臂梁结构[10-13]。然而,悬臂梁的几何形状将大大影响其能量收集能力,ACˇG eponis等[3]改进了带不规则截面的梯形悬臂梁,输出电压密度提高了9.9%,功率密度提高了3倍以上。Sameh等[14]得出,与矩形光束相比,梯形悬臂梁在单位面积上产生的能量更大,因为应变的分布是均匀的。Jessy等[15]发现悬臂梁式压电梁的功率输出受其负载分布不均的限制,利用梯形截面悬臂梁结构,在整个梁中张力均布,每单位体积的输出功率增加了30%。Muthalif等[16]用能量法确定任意形状梁的固有频率,得出能量收集最佳结构形状为三角形梁,虽然其产生的平均应变是矩形梁的2倍,产生电压也最高,但是固有频率为矩形梁的3倍,对低频能量收集不利。Hosseini等[17]发现增加悬臂梁梯形基的比值,可使具有均匀厚度的梯形V形悬臂梁达到最大共振频率和最高灵敏度。Chen等[18]得出梯形和三角形悬臂梁可以改善梁表面的应变分布,产生的电压比矩形的更大。Ayed等[19]通过Galerkin方法获得梁尖端位移、产生电压和收获功率的解,并得出对于特定的电阻值,二次形状梁产生的能量是矩形梁的2倍之多。Matova等[20]发现仅在长悬臂梁结构中,锥形可增加梁中的平均应力,从而增加压电材料的电荷变化。以上只是对单一悬臂梁在固定环境激励频率下的发电性能做了研究,当环境频率发生变化时,发电性能将大幅降低的缺陷方面未做改进。
压电悬臂梁在其固有频率处转换效率最高,一旦激振频率偏离装置的固有频率,装置的发电幅值就会急剧下降以至无法供给电子元器件。压电能量收集装置工作环境的振动源频率主要分布在5~250 Hz[4],一般低于压电悬臂梁的固有频率,最简单的方法是在悬臂梁的自由端附加质量调整其系统谐振频率[8, 10, 21]。环境中振动频率是变化或完全随机的,严重制约了振动能量收集装置的发电性能。拓宽能量收集装置的频带宽度,使其有效响应环境中激振源的频率,是有效改进压电能量收集器的发电功率的重要途径。Shaofan等[11]通过在固支梁的两侧安装不同大小的附加质量块使频带变宽;Huan等[13]通过研究串联、并联方式,整合多个压电双晶片形成不同的纵横比的宽带系统;Shahruz等[21]设计了由21个悬臂梁组成的压电集能器,实现了宽频集能。以上研究者都是利用矩形悬臂梁组成压电悬臂梁阵列,并没有对发电能力较好的梯形和三角形等变形截面悬臂梁做阵列方面的研究。
本文利用梯形截面悬臂梁比矩形截面悬臂梁可以提供额外能量,比三角形截面悬臂梁易于安装附加质量的特点,通过在双晶压电悬臂梁上附加质量,从而使单个梯形压电悬臂梁能量收集器的共振频率变小,发电功率最大化。
1 单悬臂梁压电振子模型 1.1 单悬臂梁数学模型单悬臂梁压电振子的结构主要由基梁、压电片和质量块组成,金属基梁的上下表面都贴有压电陶瓷,一端固定于基座中,质量块固定在梁的自由端,如图 1所示。在振动平面内建立坐标系,假设悬臂梁为对称结构,梁的长度方向为x轴,梁宽度方向为z轴,纵向为y轴,梁在外部激励的作用下产生加速度为ü(t)的振动,且在t时刻产生的纵向位移为y(x, t),则可以表示为[21]:

|
Download:
|
| 图 1 悬臂梁压电振子示意 Fig. 1 Schematic of piezoelectric vibrator of cantilever beam | |
| $y(x, t) = \phi (x)q(t) $ | (1) |
对所有x∈[0, l],且t≥0,ϕ(x)是形状函数,q(t)是广义坐标函数。
考虑到悬臂梁的形状对固有频率的影响,设悬臂梁的长度为l,高度为h,固定端的宽度为w0,末端宽度为w1,函数w(x)可以表示梁在长x处的宽度。当w0=w1表示为矩形结构,当w0≠w1为梯形结构梁,当w1=0时,为等腰三角形梁:
| $w(x) = {w_0} + \frac{{{w_1} - {w_0}}}{l}x $ | (2) |
形状函数ϕ(x)按其一阶振型可表示为:
| $\begin{array}{l} \phi (x) = \sin \left( {\lambda (\alpha )\frac{x}{l}} \right) - \frac{{\sin (\lambda (\alpha )) + \sinh (\lambda (\alpha ))}}{{\cos (\lambda (\alpha )) + \cosh (\lambda (\alpha ))}}\\ \left[ {\cos \left( {\lambda (\alpha )\frac{x}{l}} \right) - \cosh \left( {\lambda (\alpha )\frac{x}{l}} \right)} \right] - \sinh \left( {\lambda (\alpha )\frac{x}{l}} \right) \end{array} $ | (3) |
频率参数λ(α)取决于悬臂梁自由端的质量块与悬臂梁的质量比:
| $\alpha = {m_0}/\left( {{m_b} + 2{m_p}} \right) $ | (4) |
式中:m0表示悬臂梁自由端附加质量;mb表示悬臂弹性基梁的质量;mp表示一个压电片的质量。
利用泰勒级数方法将以下函数$\sin \left({\lambda (\alpha)\frac{x}{l}} \right)$、$\sinh \left({\lambda (\alpha)\frac{x}{l}} \right)$、$\cos \left({\lambda (\alpha)\frac{x}{l}} \right)$和$\cosh \left({\lambda (\alpha)\frac{x}{l}} \right)$展开[19],取前2项代入式(3),可得:
| $\phi (x) = a(\alpha ){\left( {\frac{x}{l}} \right)^2} - b(\alpha ){\left( {\frac{x}{l}} \right)^3} $ | (5) |
其中:
| $\left\{ {\begin{array}{*{20}{l}} {a(\alpha ) = \frac{{\sin (\lambda (\alpha )) + \sinh (\lambda (\alpha ))}}{{\cos (\lambda (\alpha )) + \cosh (\lambda (\alpha ))}}{\lambda ^2}(\alpha )}\\ {b(\alpha ) = \frac{1}{3}{\lambda ^3}(\alpha )} \end{array}} \right. $ | (69) |
λ(α)的取值大小由α的值决定,根据文献[22]将其对应数值进行函数拟合:
| $\lambda \left( \alpha \right) = \frac{{0.000807{\alpha ^4} + 0.24{a^3} + 32.63{\alpha ^2} + 177.2\alpha + 91}}{{{\alpha ^3} + 48.15{\alpha ^2} + 143.8\alpha + 48.45}} $ | (7) |
a(α)和b(α)可以通过计算得到,当α≥0时,在[0, l]上很容易证明式(3)和式(5)的数值结果很相近。
在单悬臂梁压电振子的研究过程中,系统广义质量m、广义弯曲刚度k以及广义有效载荷p(t)[21]分别计算为:
| $m = \int_0^l \rho hw(x){\phi ^2}(x){\rm{d}}x + {m_0}{\phi ^2}(x) $ | (8) |
| $k = \int_0^l E \frac{{w(x){h^3}}}{{12}}{\left( {\frac{{{d^2}\phi (x)}}{{d{x^2}}}} \right)^2}{\rm{d}}x $ | (9) |
| $p(t) = - \left( {\int_0^l \rho w(x)h{\rm{d}}x + {m_0}\phi (l)} \right)\ddot u(t) $ | (10) |
式中:ρ为单悬臂梁密度;E为单悬臂梁杨氏模量。
将式(2)、式(5)分别代入式(8)~(10)可以得到广义质量、弯曲刚度和有效载荷的表达式,略。对于所有t≥0,设:
| $\left\{ {\begin{array}{*{20}{l}} {{a_1} = {a^2}(\alpha )/30 - 2a(\alpha )b(\alpha )/42 + {b^2}(\alpha )/56}\\ {{a_2} = {a^2}(\alpha )/6 - 2a(\alpha )b(\alpha )/7 + {b^2}(\alpha )/8}\\ {{a_3} = {{[a(\alpha ) - b(\alpha )]}^2}}\\ {{a_4} = 2{a^2}(\alpha ) - 4a(\alpha )b(\alpha ) + 3{b^2}(\alpha )}\\ {{a_5} = 2{a^2}(\alpha ) - 8a(\alpha )b(\alpha ) + 9{b^2}(\alpha )}\\ {{a_6} = a(\alpha ) - b(\alpha )}\\ {{a_7} = a(\alpha ) - b(\alpha )}\\ {{a_7} = a(\alpha )/12 - b(\alpha )}\\ {{a_8} = a(\alpha )/4 - b(\alpha )/5} \end{array}} \right. $ | (11) |
利用广义质量、弯曲刚度和有效载荷的计算结果和式(11)可以得到单悬臂梁广义系统的二阶常微分方程:
| $\begin{array}{l} \left[ {\rho hl\left( {{a_1}{w_0} + {a_2}{w_1}} \right) + {m_0}a_3^2} \right]\ddot q(t) + c\dot q(t) + \\ \left[ {E{h^3}\left( {{a_4}{w_0} + {a_5}{w_1}} \right)/\left( {12{l^3}} \right)} \right]q(t) = \\ \quad - \left[ {{m_0}{a_6} + \rho hl\left( {{a_7}{w_0} + {a_8}{w_1}} \right)} \right]\ddot u(t) \end{array} $ | (12) |
式中:初始条件为q(0)=0,$\dot q$(0)=0;系统阻尼系数c为一个正实数。
式(12)建立的是均质悬臂梁模型,为了建立准确的压电悬臂梁振动频率模型,需要将压电振子各个材料的参数等效代入,设压电晶片的宽度和长度与悬臂基梁保持一致,双压电晶片悬臂梁的等效材料参数有等效厚度$\tilde h$,等效密度$\tilde \rho$以及等效弹性模量$\tilde E$[23]:
| $\tilde h = 2{h_p} + {h_b} $ | (13) |
式中:hp表示压电陶瓷片的厚度;hb表示悬臂基梁的厚度。等效密度$\tilde \rho$为:
| $\tilde \rho = \frac{{{V_p}{\rho _p} + {V_b}{\rho _b}}}{{{V_p} + {V_b}}} = \frac{{2{h_p}{\rho _p} + {h_b}{\rho _b}}}{{2{h_p} + {h_b}}} $ | (14) |
式中:Vp表示双压电陶瓷片的体积;Vb表示悬臂基梁的体积;ρp表示压电陶瓷片的密度;ρb表示悬臂基梁的密度。等效弹性模量$\tilde E$为:
| $\tilde E = \frac{{\sum {{E_i}} {h_i}}}{{\sum {{h_i}} }} = \frac{{2{h_p}{E_p} + {h_b}{E_b}}}{{2{h_p} + {h_b}}}\ $ | (15) |
式中:Ep表示压电陶瓷片的弹性模量;Eb表示悬臂基梁的弹性模量。
利用系统方程(12)得到q(t),代入方程(1),可以得到阻尼悬臂梁的横向位移值。由已知条件很容易验证,式(5)中以x为自变量的ϕ(x)在[0, l]单调递增,由此当x取值为l时ϕ(x)最大,因此,悬臂梁末端位移取得最大值|y(l, t)|。通过应用拉普拉斯变换式(1),得到:
| $y(x, s) = \phi (x)q(s) $ | (16) |
可以通过梁在外部激励下产生的加速度ü(t)来定义悬臂梁末端的横向位移,传递函数如下:
| ${G_{{\rm{end}}}}(s) = y(l, s)/\ddot u(s) $ | (17) |
式中,ü(s)是ü(t)通过拉普拉斯变换所得。利用式(5)、(12)和(16)代入式(17)可得:
| $\begin{array}{l} {G_{{\rm{end}}}}(s) = \frac{{\phi (l)q(s)}}{{\ddot u(s)}} = \\ - \frac{{{a_6}\left[ {{a_6}{m_0} + \left( {{a_7}{w_0} + {a_8}{w_1}} \right)\rho hl} \right]}}{{m{s^2} + cs + k}} \end{array} $ | (18) |
悬臂梁系统的固有频率可以表示为:
| ${\omega _{\rm{r}}} = {\omega _n}{\left( {1 - 2{\xi ^2}} \right)^{\frac{1}{2}}} $ | (19) |
式中系统无阻尼自然频率ωn以及系统阻尼比ξ表示为:
| ${\omega _n} = {(k/m)^{\frac{1}{2}}}, \xi = \frac{c}{2}{(mk)^{ - \frac{1}{2}}}\ $ | (20) |
当0 < ξ≪1时,可以忽略阻尼的影响,ωr≈ωn,此时系统的振幅最大,利用无穷大范数的定义可得振幅|Gend(jω)|的最大值‖Gend‖∞≈a6p/(2ξk)。系统的振动频率和振动幅值是压电振子设计的主要参数:
| ${\omega _{\rm{r}}} = {\left( {\frac{{{w_0}{a_4} + {w_1}{a_5}}}{{{w_0}{a_1} + {w_1}{a_2} + 0.5{a_3}\alpha \left( {{w_0} + {w_1}} \right)}}} \right)^{\frac{1}{2}}}{\left( {\frac{E}{\rho }} \right)^{\frac{1}{2}}}\left( {\frac{{\sqrt 3 h}}{{6{l^2}}}} \right) $ | (21) |
| $\begin{array}{*{20}{c}} {{{\left\| {{G_{{\rm{end}}}}} \right\|}_\infty } = }\\ {{a_6}\left( {\frac{{\alpha {a_6}\left( {{w_0} + {w_1}} \right) + 2\left( {{a_7}{w_0} + {a_8}{w_1}} \right)}}{{{a_4}{w_0} + {a_5}{w_1}}}} \right)\left( {\frac{\rho }{{\xi E}}} \right)\left( {\frac{{3{l^4}}}{{{h^2}}}} \right)} \end{array} $ | (22) |
本文的设计基于梯形面悬臂梁的发电性能优于矩形面悬臂梁的结论[17-20, 23],考虑到便于安装附加质量来调节固有频率,故选用梯形面悬臂梁。设计悬臂梁压电振子过程中,主要考虑发电能力,所以金属弹性梁选用磷青铜,其密度为8 920 kg/m3,弹性模量为106 GPa,阻尼系数c=0.01,压电陶瓷选用PZT-5H,其密度为7 500 kg/m3,弹性模量为61 GPa,其压电应变常数为d31=-2.74×10-10 C/N,d33=5.93×10-10 C/N;梁的长度为l=70 mm,压电片的厚度hp=0.2 mm,弹性基梁的厚度hb=0.1 mm,弹性基梁的两端的宽度为w0=7 mm,w1=4 mm,附加在悬臂梁上的质块质量为6 g。由以上参数可以计算出质量比α的值为4,依据式(7)可以得到,λ= 0.917,则有频率ωr=79.74 rad/s=12.7 Hz,‖Gend‖∞= 8.111 ×10-3 s2。利用式(6)以及式(7)~(20)得:
| ${G_{{\rm{end}}}}(s) = - \frac{{0.001154}}{{0.00419{s^2} + 0.01s + 9.85309}} $ | (23) |
由此可得其传递函数的频率特性曲线图,如图 2所示。

|
Download:
|
| 图 2 梯形悬臂梁系统的频率特性曲线 Fig. 2 Frequency characteristic curve of trapezoidal cantilever beam system | |
从图中明显可以看到存在一个波峰,而振动波峰对应的横坐标为自然频率。只有当激励频率等于固有频率时,振动最为剧烈,出现明显波峰;当激励频率沿其固有频率增大或者减小时,振动幅值剧烈下降,如图出现高斜率波形。
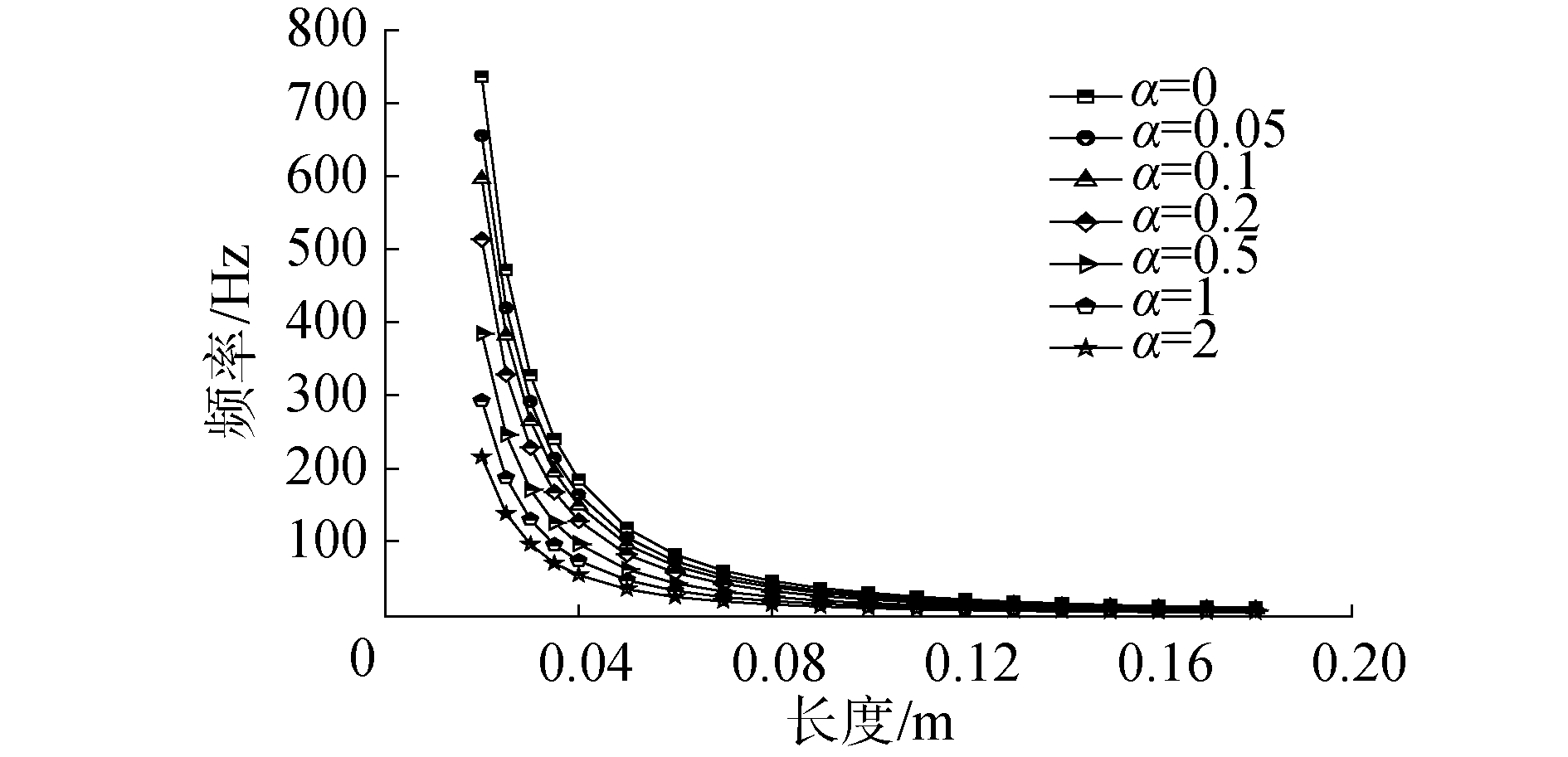
悬臂梁的自然频率的影响因素很多,考虑到实际应运中的加工和成本问题,依据参考文献选择较优的宽度和厚度参数(压电片和弹性基梁的厚度为0.2 mm和0.1 mm,梯形梁的基础宽度为7 mm,梯形边斜率一致保持不变,研究在不同质量比α下,长度与悬臂梁频率的关系。图 3显示了当悬臂梁的长度在20~200 mm上,质量比α值分别为0、0.05、0.1、0.2、0.5、1和2时的变化趋势,在悬臂梁等长情况下,附加质量与悬臂梁的总质量比越大时系统频率越低,梁的长度值变大时系统固有频率明显降低;当悬臂梁的长度小于15 mm时,随着长度减小,频率呈现直线增长。故悬臂梁的长度需要根据环境激励频率来选取。
|
Download:
|
| 图 3 悬臂梁长度对固有频率的影响 Fig. 3 Influence of the length of the cantilever beam on the natural frequency | |
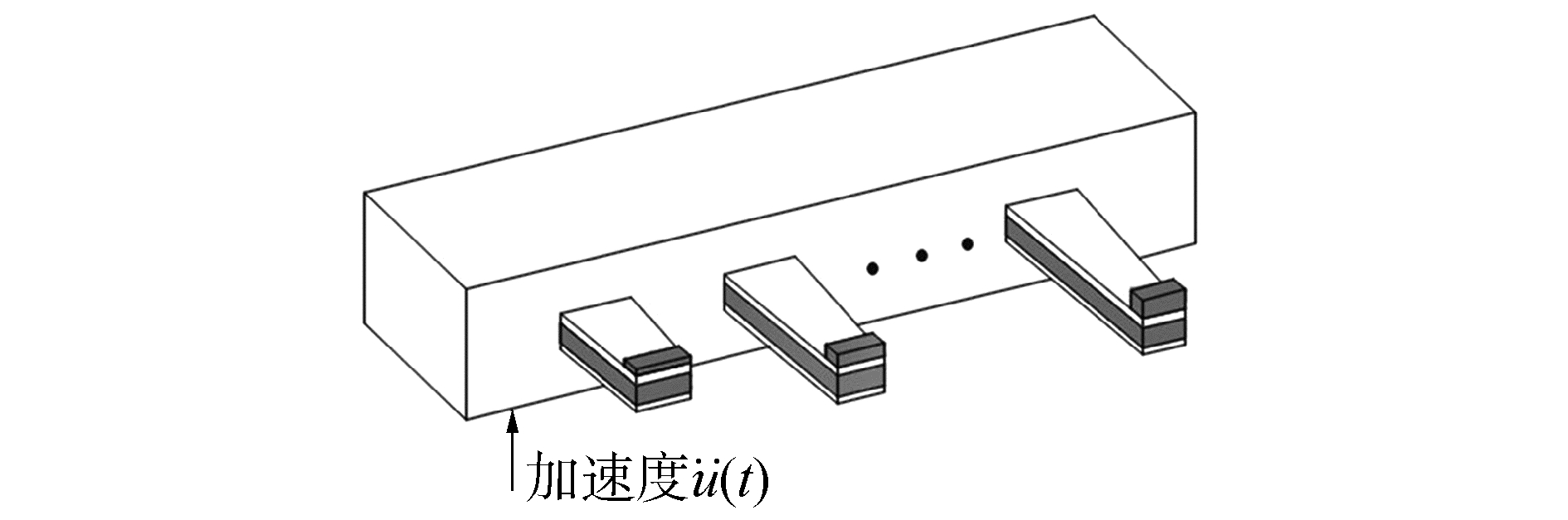
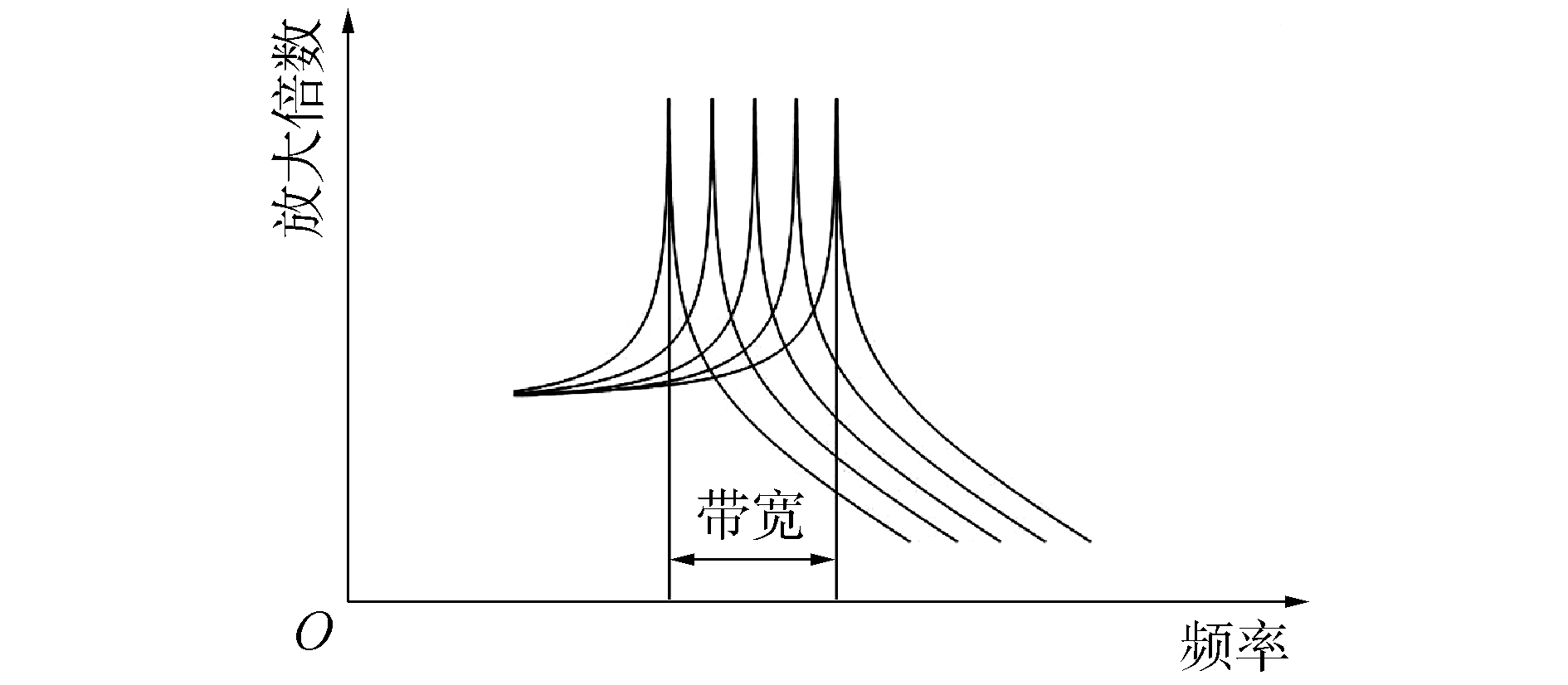
单悬臂梁对频率很敏感,当环境振动频率与其固有频率相同时,压电发电效果明显,当环境振动频率偏离其固有频率时,压电发电效果明显下降。故而考虑到利用多个固有频率相近且连续的单悬臂梁压电振子组成一个压电悬臂梁阵列,这样可以有效拓宽工作带宽,使得压电振子阵列在一定频率带宽内产生谐振,从而提高能量收集器的输出功率,复合悬臂梁结构如图 4所示。设计复合型多悬臂梁压电振子的主要条件有:多个悬臂梁的固有频率有微小差别,可以由连续的频率序列构成一个频率宽带;各个梁的频率响应幅值应该相等[20]。如图 5为满足上述2个条件的频率响应示意图,每个峰值点横坐标代表每个梁的固有频率,系统机构的频带为峰值的宽度。
|
Download:
|
| 图 4 能量收集系统结构示意 Fig. 4 Schematic of piezoelectric energy harvesting system | |
|
Download:
|
| 图 5 多悬臂梁压电振子频响示意 Fig. 5 Frequency response of multiple piezoelectric vibrators | |
复合悬臂梁压电振子设计过程中的重要参数是频率和振幅,其取决于梁的维度尺寸、材料以及附加质量。研究结构参数过程中,选择保持基础宽度7 mm和厚度参数(压电片和弹性基梁的厚度为0.2 mm和0.1 mm不变,仅仅通过改变长度参数来分析。在式(22)中,令无穷范数‖Gend‖∞为r,且r>0,可得:
| ${l^4} = \frac{{r\xi \left( {{a_4}{w_0} + {a_5}{w_1}} \right)}}{{3{a_6}\left( {\alpha {a_6}\left( {{w_0} + {w_1}} \right) + 2\left( {{a_7}{w_0} + {a_8}{w_1}} \right)} \right)}}\frac{E}{\rho }{h^2} $ | (24) |
将式(24)代入(21)式可得:
| ${\omega _{\rm{r}}} = {\left( {\frac{{3{a_6}\left( {\alpha {a_6}\left( {{w_0} + {w_1}} \right) + 2\left( {{a_7}{w_0} + {a_8}{w_1}} \right)} \right)}}{{2\left( {{w_0}{a_1} + {w_1}{a_2}} \right) + \alpha {a_3}\left( {{w_0} + {w_1}} \right)}}} \right)^{\frac{1}{2}}}{\left( {\frac{1}{{r\xi }}} \right)^{\frac{1}{2}}} $ | (25) |
式中:
| ${F_\omega }(\alpha ) = {\left( {\frac{{3{a_6}\left( {\alpha {a_6}\left( {{w_0} + {w_1}} \right) + 2\left( {{a_7}{w_0} + {a_8}{w_1}} \right)} \right)}}{{2\left( {{w_0}{a_1} + {w_1}{a_2}} \right) + \alpha {a_3}\left( {{w_0} + {w_1}} \right)}}} \right)^{\frac{1}{2}}} $ | (26) |
| ${F_E}(\alpha ) = {\left( {\frac{{{a_4}{w_0} + {a_5}{w_1}}}{{3{a_6}\left( {\alpha {a_6}\left( {{w_0} + {w_1}} \right) + 2\left( {{a_7}{w_0} + {a_8}{w_1}} \right)} \right)}}} \right)^{\frac{1}{4}}} $ | (27) |
可以看出Fw(α)和FE(α)的值随着α的增大而减小,是单调减函数。由此可以得出:
| ${\omega _{\min }} = 1.5{\left( {\frac{1}{{r\xi }}} \right)^{\frac{1}{2}}} < {\omega _r} \le 2.1943{\left( {\frac{1}{{r\xi }}} \right)^{\frac{1}{2}}} = {\omega _{\max }}\ $ | (28) |
利用α和λ(α)的值,计算梯形上下底边定长情况下的参数结果如表 1所示。
| 表 1 α对应下Fw(α)和FE(α)的值 Table 1 Values of Fw(α) and FE(α) corresponding to α |
由式(28)可以看出多悬臂梁压电振子系统的最大与最小固有频率比是1.463,即多悬臂梁压电振子系统的工作频率范围是一个有限值,不能无限制的加宽工作频带。
2.2 多悬臂梁设计实例 2.2.1 不同质量比的多悬臂梁系统设计复合梁压电振子时,选用的材料同上。其中,压电片的厚度hp=0.2 mm,弹性基梁的厚度hb=0.5 mm,等效厚度为0.9 mm。其他的结构尺寸如表 2所示。
| 表 2 多悬臂梁压电振子结构参数 Table 2 Structural parameters of multiple piezoelectric vibrators |
表 2中给出了10个梁的参数,当梁长度为62 mm时,梁的频率为130.25 Hz;当梁的长度为57.4 mm时,其频率为103.26 Hz。复合悬臂梁阵列结构的设计中,悬臂梁末端的附加质量可以大大降低悬臂梁的固有频率,还可以使机构的体积变小,附加质量由梁的三维结构和悬臂梁自由端附加质量与悬臂梁的质量比决定,通过调整梁的长度和附加质量,使梁的固有频率间隔为3 Hz,则其系统的频带宽度为27 Hz,即103~130 Hz(648.8~818.4 rad/s)。
多梯形悬臂梁系统的指对数频率特性曲线如图 6所示,在频率区间[648.8 rad/s, 818.4 rad/s],各个梁所对应的伯德图的峰值相等,小于多悬臂梁压电振子系统的最大与最小固有频率比的极限值。当α取值变化时,通过选择合理参数,可以使各个峰值相等,能最大限度地提高系统的发电性能。与文献[21]中指对数频率特性曲线图的变化趋势一致,并且放大倍数更高,每个悬臂梁的固有频率间隔为3 Hz,可以在频带内更高效的收集能量,明显得出此多悬臂梁系统设计合理。

|
Download:
|
| 图 6 多悬臂梁(10个)指对数频率特性曲线 Fig. 6 Logarithmic frequency characteristic curve of multi cantilever beams (the number is 10) | |
下面的例子是选取悬臂梁自由端附加质量与悬臂梁总质量比α为0.5时的参数,选用的材料同上。压电片的厚度hp=0.2 mm,弹性基梁的厚度hb=0.5 mm。其他的结构尺寸如表 3所示。
| 表 3 多悬臂梁压电振子结构参数 Table 3 Structural parameters of multiple piezoelectric vibrators |
表 3中给出了12个悬臂梯形梁的维度参数,当梁长度为66.8 mm时,梁的频率为66 Hz;当梁的长度为53.1 mm时,其频率为99 Hz。复合悬臂梁阵列结构设计中,通过调整梁的长度和附加质量,使梁的固有频率间隔为3 Hz,则其系统的频带宽度为33 Hz,即66~99 Hz(415.6~622.2 rad/s)。每个梁的自然频率相接近,当环境振动频率变化时,均有悬臂梁产生谐振,故而有效的拓宽了工作频率范围。
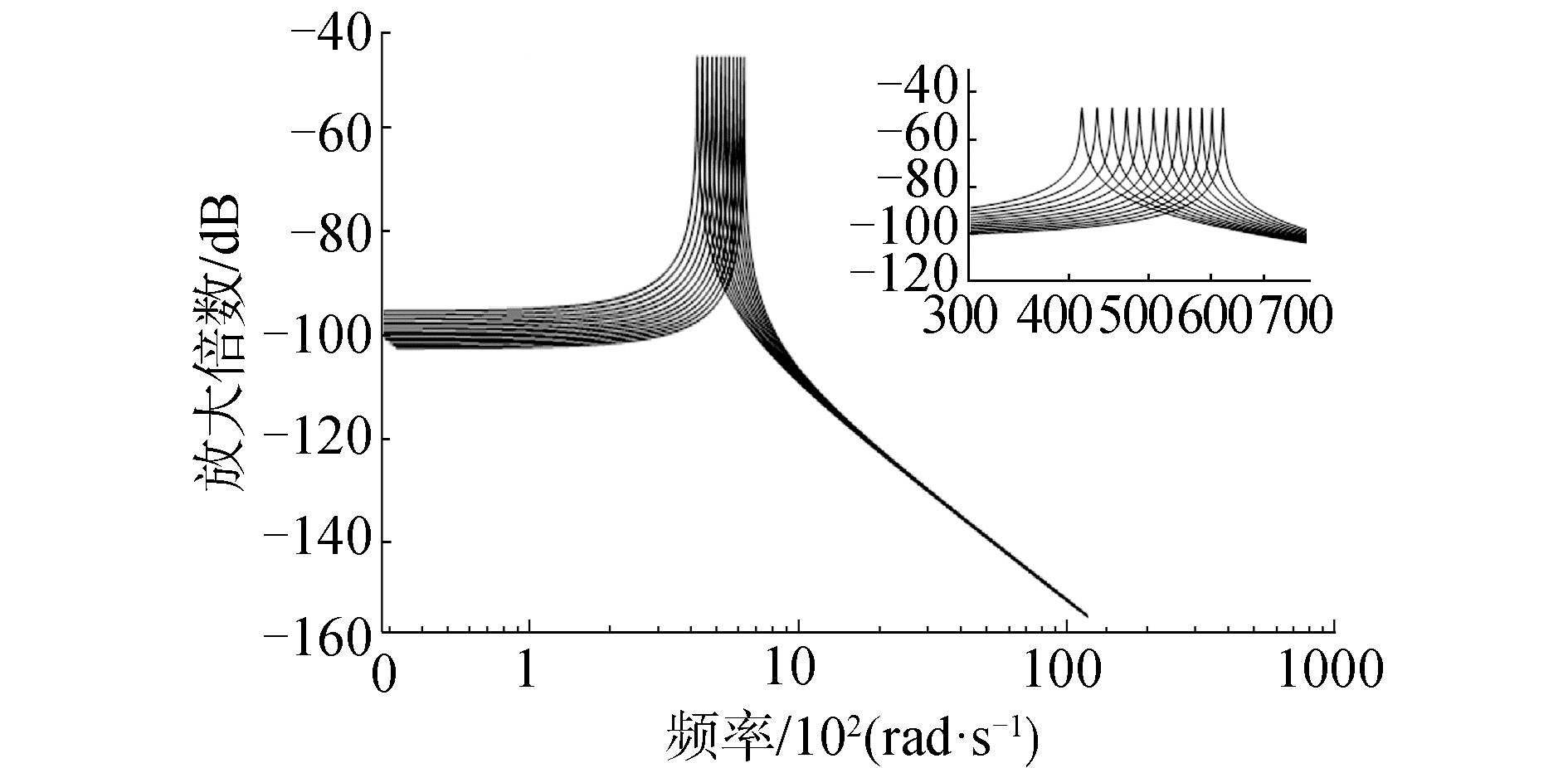
如图 7可以看出12个梯形悬臂梁压电振子在其固有频率处的放大倍数相同,即悬臂梁末端位移随频率变化规律是一致的,与文献[21]中图 10的变化趋势相同。当每个悬臂梁处于谐振状态时,其自由端的振幅相同,符合设计初衷。
|
Download:
|
| 图 7 多悬臂梁(12个)指对数频率特性曲线 Fig. 7 Logarithmic frequency characteristic curve of multi cantilever beams (the number is 12) | |
这2组多悬臂梁压电能量收集器的设计可以达到环境中激振频率变化时收集能量的要求,所收集的能量是多个梁收集能量的叠加,保证了在频带宽度内任何频率下均可收集到高的电能,设计合理。
3 结论1) 为了研究复合梯形悬臂梁系统的频率响应,建立了描述梯形悬臂梁质量系统横向振动的数学模型,推导出一个将梯形悬臂梁三维尺寸和附加质量相联系的传递函数,通过传递函数可以将梯形悬臂梁末端位移与振动源施加的加速度联系起来。
2) 在单梯形悬臂梁质量系统模型的基础上分析推导出了2种不同质量比模式下多梯形悬臂梁复合压电能量收集系统的模型。
3) 通过合理选择梯形悬臂梁的三维尺寸及末端附加质量,可以得到等放大倍数、等频率间隙的宽频带能量收集系统,当激励频率在复合能量收集器的频带宽度内随机变化时,均可以高效率的收集能量。
| [1] |
刘少刚, 程千驹, 赵丹, 等. 分段线性压电能量收集器机电耦合建模[J]. 哈尔滨工程大学学报, 2016, 37(11): 1573-1579. LIU Shaogang, CHENG Qianju, ZHAO Dan, et al. Electromechanical coupling modeling research on the piecewise-linear piezoelectric energy harvester[J]. Journal of Harbin Engineering University, 2016, 37(11): 1573-1579. (  0) 0)
|
| [2] |
袁江波, 谢涛, 单小彪, 等. 复合型悬臂梁压电振子振动模型及发电试验研究[J]. 机械工程学报, 2010, 46(9): 87-92. YUAN Jiangbo, XIE Tao, SHAN Xiaobiao, et al. Vibrated model and experiments of multiple piezoelectric cantilevers in energy harvesting[J]. Journal of mechanical engineering, 2010, 46(9): 87-92. (  0) 0)
|
| [3] |
EPONIS A, MAŽEIKA D, BAKANAUSKAS V. Trapezoidal cantilevers with irregular cross-sections for energy harvesting systems[J]. Applied sciences, 2017, 7(2): 134. DOI:10.3390/app7020134 (  0) 0)
|
| [4] |
王海, 邱皖群, 周璇, 等. 多质量块宽频压电能量收集器[J]. 压电与声光, 2015, 37(6): 1003-1008. WANG Hai, QIU Wanqun, ZHOU Xuan, et al. A multiple mass broadband piezoelectric energy harvesting device[J]. Piezoelectrics & acoustooptics, 2015, 37(6): 1003-1008. (  0) 0)
|
| [5] |
刘少刚, 程千驹, 赵丹, 等. 一种宽频压电能量收集装置的建模与实验研究[J]. 振动与冲击, 2016, 35(24): 27-32. LIU Shaogang, CHENG Qianju, ZHAO Dan, et al. Modeling and experiment of a piezoelectric energy harvester with wide operation bandwidth[J]. Journal of vibration and shock, 2016, 35(24): 27-32. (  0) 0)
|
| [6] |
LENG Yonggang, TAN Dan, LIU Jinjun, et al. Magnetic force analysis and performance of a tri-stable piezoelectric energy harvester under random excitation[J]. Journal of sound and vibration, 2017, 406: 146-160. DOI:10.1016/j.jsv.2017.06.020 (  0) 0)
|
| [7] |
PHU LE C, HALVORSEN E, SØRÅSEN O, et al. Wideband excitation of an electrostatic vibration energy harvester with power-extracting end-stops[J]. Smart materials and structures, 2013, 22(7): 075020. DOI:10.1088/0964-1726/22/7/075020 (  0) 0)
|
| [8] |
LI Pengwei, LIU Ying, WANG Yanfen, et al. Low-frequency and wideband vibration energy harvester with flexible frame and interdigital structure[J]. AIP advances, 2015, 5(4): 047151. DOI:10.1063/1.4919711 (  0) 0)
|
| [9] |
展永政, 王光庆. 双自由度压电振动能量采集器的力-电输出特性分析[J]. 振动工程学报, 2014, 27(6): 871-877. ZHAN Yongzheng, WANG Guangqing. Force-electrical output characteristic analysis of piezoelectric vibration energy harvester with two degrees of freedom[J]. Journal of vibration engineering, 2014, 27(6): 871-877. DOI:10.3969/j.issn.1004-4523.2014.06.010 (  0) 0)
|
| [10] |
DHAKAR L, LIU Huicong, TAY F E H, et al. A new energy harvester design for high power output at low frequencies[J]. Sensors and actuators A:physical, 2013, 199: 344-352. DOI:10.1016/j.sna.2013.06.009 (  0) 0)
|
| [11] |
QI Shaofan, SHUTTLEWORTH R, OLUTUNDE OYADIJI S, et al. Design of a multiresonant beam for broadband piezoelectric energy harvesting[J]. Smart materials and structures, 2010, 19(9): 094009. DOI:10.1088/0964-1726/19/9/094009 (  0) 0)
|
| [12] |
ESMAEILI A, SOUSA J M M. Power density ratio optimization of bimorph piezocomposite energy harvesters using a multidisciplinary design feasible method[J]. Composite structures, 2017, 165: 171-179. DOI:10.1016/j.compstruct.2017.01.031 (  0) 0)
|
| [13] |
XUE Huan, HU Yuantai, WANG Qingming. Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2008, 55(9): 2104-2108. DOI:10.1109/TUFFC.903 (  0) 0)
|
| [14] |
AYED S B, NAJAR F, ABDELKEFI A. Shape improvement for piezoelectric energy harvesting applications[C]//Proceedings of the 3rd International Conference on Signals, Circuits and Systems. Medenine, Tunisia, 2010: 1-6.
(  0) 0)
|
| [15] |
BAKER J, ROUNDY S, WRIGHT P. Alternative geometries for increasing power density in vibration energy scavenging for wireless sensor networks[C]//Proceedings of the 3rd International Energy Conversion Engineering Conference. San Francisco, California, 2005: 5617.
(  0) 0)
|
| [16] |
MUTHALIF A G A, DIYANA NORDIN N H. Optimal piezoelectric beam shape for single and broadband vibration energy harvesting:modeling, simulation and experimental results[J]. Mechanical systems and signal processing, 2015, 54-55: 417-426. DOI:10.1016/j.ymssp.2014.07.014 (  0) 0)
|
| [17] |
HOSSEINI R, HAMEDI M. An investigation into resonant frequency of trapezoidal V-shaped cantilever piezoelectric energy harvester[J]. Microsystem technologies, 2016, 22(5): 1127-1134. DOI:10.1007/s00542-015-2583-7 (  0) 0)
|
| [18] |
CHEN Z S, YANG Y M, DENG G Q. Analytical and experimental study on vibration energy harvesting behaviors of piezoelectric cantilevers with different geometries[C]//Proceedings of International Conference on Sustainable Power Generation and Supply. Nanjing, China, 2009: 1-6.
(  0) 0)
|
| [19] |
AYED S B, ABDELKEFI A, NAJAR F, et al. Design and performance of variable-shaped piezoelectric energy harvesters[J]. Journal of intelligent material systems and structures, 2014, 25(2): 174-186. DOI:10.1177/1045389X13489365 (  0) 0)
|
| [20] |
MATOVA S P, RENAUD M, JAMBUNATHAN M, et al. Effect of length/width ratio of tapered beams on the performance of piezoelectric energy harvesters[J]. Smart materials and structures, 2013, 22(7): 075015. DOI:10.1088/0964-1726/22/7/075015 (  0) 0)
|
| [21] |
SHAHRUZ S M. Design of mechanical band-pass filters with large frequency bands for energy scavenging[J]. Mechatronics, 2006, 16(9): 523-531. DOI:10.1016/j.mechatronics.2006.04.003 (  0) 0)
|
| [22] |
KARNOVSKY I A, LEBED O I. Free vibrations of beams and frames[M]. New York: McGraw-Hill, 2004: 186-189.
(  0) 0)
|
| [23] |
SCHACHTELE J, GOLL E, MURALT P, et al. Admittance matrix of a trapezoidal piezoelectric heterogeneous bimorph[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2012, 59(12): 2765-2776. DOI:10.1109/TUFFC.2012.2518 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


