2. 伍伦贡大学, 机械、材料、机电一体化和生物医学工程系, 新南威尔士 2522
2. School of Mechanical, Materials, Mechatronics and Biomedical Engineering, University of Wollongong, New South Wales 2522, Australia
热裂纹是液态金属凝固(尤其是后期)过程中容易产生的缺陷。此时由于液态金属中固相体积分数较多,且已连接成网络,液态金属无法补缩,因此当晶粒冷却收缩时,很容易被拉开而形成热裂纹[1-6]。不过,残存于晶粒之间的液膜,由于表面张力(确切地说是其分力)的作用,可以在一定程度上抵抗这种收缩,从而在一定程度上避免或缓解了热裂纹的产生。关于这方面的研究(尤其定量研究)尚不多见,只是在文献[7-8]中略有指出:当晶粒收缩时,晶粒边界间距变大,此时液膜表面由平面变为曲面,曲率半径由原来的无穷大变为有限值。曲率半径的大小和晶粒边界间距有一定关系,一般随着间距的变大而变小,并且存在一个合适的间距,此时曲率半径达到最小,为间距的一半,液膜的抗拉强度也达到最大。
本文对这一结论重新进行了研究,从液膜质量守恒这一条件出发,定量地得到了液膜曲率半径与晶粒边界间距之间的解析关系,研究发现,液膜最小曲率半径并不是晶粒边界间距的一半,而是比这个值稍大些,这与传统观点不一致。
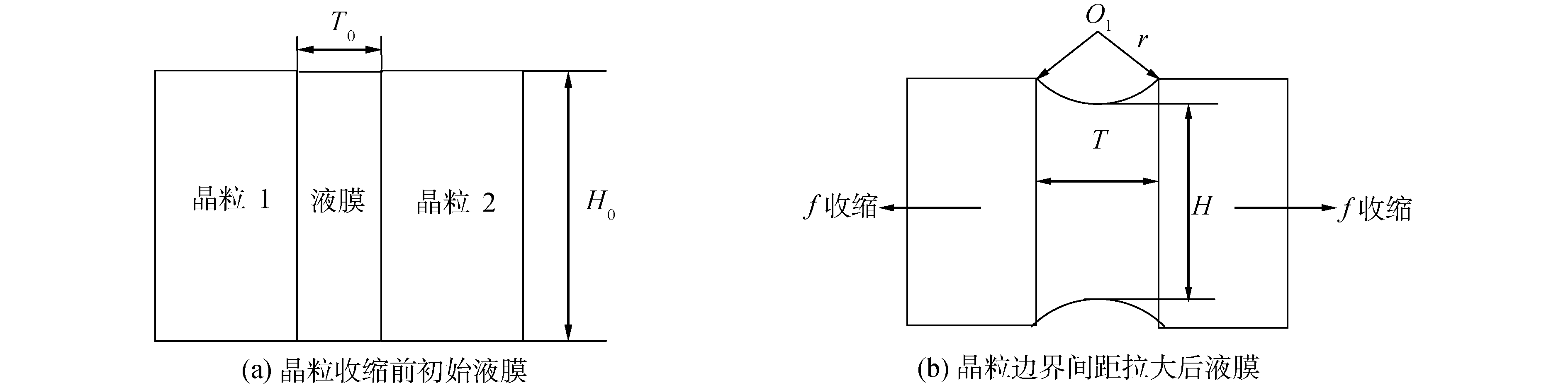
1 液膜抗拉能力的计算 1.1 弯曲液面的附加压力图 1(a)为初始间距为T0的2个晶粒(以二维为例),中间通过液膜连接在一起,当晶粒尚未收缩时,液膜的自由表面为平面,表面张力为σ,方向为水平。此时液膜曲率半径为无穷大。在凝固后期,晶粒因冷却而产生收缩,晶粒边界间距被拉大至T,如图 1(b),由于没有液态金属补充,液膜的自由表面也由平面变为了圆弧面(线),曲率半径为有限值r。
|
Download:
|
| 图 1 液膜曲率半径与晶粒边界间距的关系 Fig. 1 Relationship between the radius of curvature of liquid film and grain spacing | |
液体自身是不能承受拉力的,因此抵抗收缩,主要靠液膜的表面张力。如图 2(a),在弯曲表面$\overset\frown{AC}$上任取一段微分圆弧$\overset\frown{mn}$,根据热力学理论可知[7],其端点m、n各受到表面张力σ的作用,方向与该点处表面相切。由于微分圆弧有一定长度,因此2个端点处的表面张力并不共线,而是具有一定的夹角,将这2个力合成后,会得到一个指向圆弧曲率中心的力,大小为ΔP=σ/r[7],这个力称为附加压力,如图 2(b)。由于这段圆弧是任意取的,因此弯曲表面$\overset\frown{AC}$处处存在这一附加压力,方向均指向曲率中心O1。

|
Download:
|
| 图 2 液膜抗裂拉力的形成 Fig. 2 Formation of tensile strength of liquid film | |
当晶粒冷却收缩时,液膜的表面会对晶粒收缩有一个抵抗作用,这个抵抗力是由附加压力的水平分力提供的,如图 2(c)。为了求出这个力,首先应求出作用于$\overset\frown{mn}$上的总附加压力:
| ${\rm{d}}f = \Delta P{\rm{d}}s $ | (1) |
式中:ds为微分圆弧$\overset\frown{mn}$的长度,大小为ds=rdθ;ΔP为附加压力σ/r。
总附加压力df的水平分力为:
| ${\rm{d}}{f_x} = {\rm{d}}f\sin \theta $ | (2) |
将相关量代入式(2)得:
| ${\rm{d}}{f_x} = \frac{\sigma }{r}\sin \theta r{\rm{d}}\theta $ | (3) |
对右半段圆弧$\overset\frown{BC}$积分,就得到与右侧收缩拉力相抗
衡的总水平分力Fx:
| $\begin{array}{l} {F_x} = \int\limits_B^c {\rm{d}} {f_x} = \int\limits_0^{{\theta _1}} {\frac{\sigma }{r}} \sin \theta r{\rm{d}}\theta = \\ - \sigma \cos \left. \theta \right|_{{\theta _1}}^0 = \sigma \left( { - 1 + \cos {\theta _1}} \right) \end{array} $ | (4) |
式(4)积分的结果为负号,说明其方向指向x轴负向,和右侧的收缩拉力方向相反。
左侧半圆弧$\overset\frown{AB}$的处理与此类似,只是与Fx方向相反,指向x轴正向,它与左侧的收缩拉力相抗衡。
还可以将Fx换算成抗拉强度,大小为:
| ${\sigma _x} = {F_x}/\Delta y $ | (5) |
式中Δy为圆弧$\overset\frown{mn}$在y方向上的投影, 如图 2(b)。可通过积分求得:
| $\Delta y = \int\limits_B^c {\rm{d}} y $ | (6) |
式中:dy为任意位置处微分圆弧$\overset\frown{mn}$的y向投影分量nq,大小为nq=dy=dssinθ;
将dy代入式(6)得到Δy:
| $\Delta y = \left| {\int\limits_{{\theta _1}}^0 r \sin \theta {\rm{d}}\theta } \right| = | - r\cos \theta |_{{\theta _1}}^0| = r\left( {1 - \cos {\theta _1}} \right) $ | (7) |
将式(7)代入式(5)得到抗拉应力:
| ${\sigma _x} = - (\sigma /r) $ | (8) |
同理,负号表示此应力方向为-x轴方向。可见,其绝对值与附加压力一样,与文献[7]中的结论一致,但二者的性质、作用却大不一样。
由于液膜对收缩力的抵抗取决于表面张力和曲率半径,当表面张力一定的时候,抗收缩应力主要取决于曲率半径,而曲率半径和晶粒边界间距T有关,因此还要考虑二者的关系。
2 液膜曲率半径与晶粒间隙的关系 2.1 质量守恒当晶粒之间的液膜因晶粒收缩而被拉开的时候,形状变为曲边四边形,如图 3中的ACFE。由于没有液体及时补充,因此四边形的面积和最初的面积一样保持不变(质量守恒)。

|
Download:
|
| 图 3 液膜的解析分析 Fig. 3 Analytical analysis of liquid film | |
建立图 3(a)所示的直角坐标系,由几何关系可知上下2个圆弧的曲率中心坐标分别为:${O_1}\left({0, r + \frac{H}{2}} \right)$, ${O_2}\left({0, - r - \frac{H}{2}} \right)$,据此可分别写出圆O1、O2的方程:
| ${x^2} + {\left[ {y - \left( {r + \frac{H}{2}} \right)} \right]^2} = {r^2} $ | (9) |
| ${x^2} + {\left[ {y - \left( { - r - \frac{H}{2}} \right)} \right]^2} = {r^2} $ | (10) |
考虑到圆弧$\overset\frown{EF}$位于圆O1下部,而$\overset\frown{AC}$位于圆O2上部,因此这两段弧的解析方程分别为:
| ${y_1} = \left( {r + \frac{H}{2}} \right) - \sqrt {{r^2} - {x^2}} $ | (11) |
| ${y_2} = - \left( {r + \frac{H}{2}} \right) + \sqrt {{r^2} - {x^2}} $ | (12) |
这样,曲边四边形ACEF的面积为:
| $S = \int_{ - \frac{T}{2}}^{\frac{T}{2}} {\left( {{y_1} - {y_2}} \right)} {\rm{d}}x $ | (13) |
进一步处理得:
| $S = \int_\limits{ - \frac{T}{2}}^{\frac{T}{2}} {\left[ {2\left( {r + \frac{H}{2}} \right) - 2\sqrt {{r^2} - {x^2}} } \right]} {\rm{d}}x $ | (14) |
积分后:
| $S = 2\left( {r + \frac{H}{2}} \right)T - 2\left[ {\frac{T}{2}\sqrt {{r^2} - \frac{{{T^2}}}{4}} + {r^2}\arcsin \left( {\frac{T}{{2r}}} \right)} \right] $ | (15) |
式(15)包含了T和H,但二者并不是孤立的,根据图 3(b)的几何关系有:
| $\overline {{O_1}{K^2}} + \overline {K{C^2}} = \overline {{O_1}{C^2}} $ |
即:
| ${(r - \Delta H)^2} + {\left( {\frac{T}{2}} \right)^2} = {r^2} $ | (16) |
式中:$\Delta H = \overline {KB} = \frac{{{H_0} - H}}{2}$,代入式(16)后展开得:
| $\frac{H}{2} = \frac{{{H_0}}}{2} - r + \sqrt {{r^2} - {{\left( {\frac{T}{2}} \right)}^2}} $ |
将该式再代入式(15)并整理得:
| $S = T{H_0} + T\sqrt {{r^2} - \frac{{{T^2}}}{4}} - 2{r^2}\arcsin \left( {\frac{T}{{2r}}} \right)\ $ | (17) |
由于液膜没有液体补充,因此质量是守恒,二维情况下相当于面积不变,因此S应等于液膜最初的面积S0=T0H0,即:
| $T{H_0} + T\sqrt {{r^2} - \frac{{{T^2}}}{4}} - 2{r^2}\arcsin \left( {\frac{T}{{2r}}} \right) = {T_0}{H_0} $ | (18) |
式(18)表达了晶粒实时间距T与曲率半径r的关系。由于该式比较复杂,无法直观判断T与r的关系,因此利用Matlab软件采用数值方法,在液膜初始尺寸H0一定的情况下,计算了不同的初始间距(T0)下的T和r的曲线关系(虽然不是真实值,但不影响问题的讨论), 如图 4(a)所示。

|
Download:
|
| 图 4 晶粒边界间距与曲率半径的关系 Fig. 4 The relationship between grain spacing and radius of curvature | |
从图中可以看,在H0一定的情况,随着晶粒边界间距的扩大,每一个T0都有一个T~r关系,总的趋势是,随着T的增大,r径逐渐变小,并存在极值,即存在一个间距T(以下记作Tmin),对应着最小的曲率半径rmin。
将每一个T0及其所对应的rmin, 作图,如图 4(b),可看出,随着T0的增大,相应rmin呈增大趋势,即大的初始间距对应较大的最小曲率半径rmin。
2.3 曲率半径与晶粒尺寸的关系另外还考察了在晶粒边界间距T0不变的情况下,取不同晶粒尺寸(H0为3.01、3.02、3.03、3.04、3.05 mm)对Tmin和rmin的影响。计算表明,不同的H0,T和r之间的变化趋势基本一致,5条T~r曲线重合,如图 5(a)所示,并且与rmin相对应的Tmin都约等于1.25,而rmin则略有不同,这是因为H0不同的原因(参见式(20)),如图 5(b)所示。

|
Download:
|
| 图 5 晶粒尺寸与曲率半径的关系 Fig. 5 The relationship between grain size and radius of curvature | |
以上通过数值方法定性地得到了液膜几何尺寸与最小曲率半径之间的关系,下面精确求解rmin。观察图 4(a)曲线的趋势可知,对于一组确定的(T0, H0),存在一个Tmin,使得$\partial r/\partial T = 0$,因此可根据这一条件精确求得rmin。对式(18)采用复合函数求导法则对T求偏导:
| $\begin{array}{l} {H_0} + \sqrt {{r^2} - \frac{{{T^2}}}{4}} + T\frac{{2r\frac{{\partial r}}{{\partial T}} - \frac{T}{2}}}{{2\sqrt {{r^2} - \frac{{{T^2}}}{4}} }} - \left( {\frac{{\partial r}}{{\partial T}}} \right) \cdot \\ 4{\mathop{\rm rarcsin}\nolimits} \left( {\frac{T}{{2r}}} \right) - \frac{{\frac{1}{{2r}} - \frac{T}{{2\sqrt r }}\frac{{\partial r}}{{\partial T}}}}{{\sqrt {1 - {{\left( {\frac{T}{{2r}}} \right)}^2}} }}2{r^2} = 0 \end{array} $ | (19) |
令式中的$\partial r/\partial T = 0$,整理得到:
| ${H_0}\sqrt {{r^2} - \frac{{{T^2}}}{4}} - \frac{{{T^2}}}{2} = 0 $ |
解此方程:
| ${r_{\min }} = \sqrt {\frac{{{T^2}}}{4} + \frac{{{T^4}}}{{4H_0^2}}} $ | (20) |
式(20)为在某一初始(T0, H0)情况下, 最小曲率半径rmin和T之间的关系。将这一结果与文献[7-8]中的结论进行了比较,发现二者并不相同。在文献[7-8]中的rmin=T/2,此时液膜曲面变为图 6所示的虚线半圆;而本文的结果为${r_{\min }} = \sqrt {\frac{{{T^2}}}{4} + \frac{{{T^4}}}{{4H_0^2}}} $,即为图中的实线圆弧。

|
Download:
|
| 图 6 传统最小曲率半径与本文最小曲率半径比较示意 Fig. 6 A comparison between the traditional and currently calculated minimum radius of curvature | |
很明显, ${r_{\min }} = \sqrt {\frac{{{T^2}}}{4} + \frac{{{T^4}}}{{4H_0^2}}} > \sqrt {\frac{{{T^2}}}{4}} = \frac{T}{2}$,即本文的rmin要比文献[7-8]中的rmin稍大。传统理论中的rmin没有考虑晶粒的尺寸H0(可看成本文中H0→∞的特例),而本文考虑了这一点,因此更合理些,原因为:1)从数学角度讲,如果rmin=T/2,则式(19)中分母$\sqrt {{r^2} - \frac{{{T^2}}}{4}} $这一项为零,因而无意义;2)实际晶粒总是有大小的,H0不能按无穷大处理, 而本文考虑了这一点,这也解释了2.3节中,为什么在T相同的情况下, rmin还有所不同的原因;传统理论中因为rmin只与T有关,即rmin=T/2,因此rmin均相同;3)rmin=T/2只是一种理想情况,实际无法达到。因为虽然当rmin=T/2时,液膜抗拉强度达到理论的最大值,但此时也是液膜即将破裂的临界点,此时凝固条件稍有波动,液膜就会被拉破,所以实际上rmin很难达到T/2,而本文的结论,可以很好地避开上述问题,更加合理。
3 结论1) 本文得到的液膜最小曲率半径与传统理论不同,传统的最小曲率半径未涉及晶粒尺寸,而本文则考虑了这一点。
2) 分析表明,晶粒尺寸对最小曲率半径有影响,进而影响液膜抗拉能力,这一结果更接近实际情况,可为实际的凝固工艺的制定提供有意义的参考。
| [1] |
陈德平, 许健, 杨刚, 等. 不同浇注方式下铸造风机主轴的热裂模拟及工艺优化[J]. 金属铸锻焊技术, 2011, 40(7): 54-56, 62. CHEN Deping, XU Jian, YANG Gang. Simulation of hot tearing of fan main shaft casting under different pouring methods and its process optimization[J]. Casting·forging·welding, 2011, 40(7): 54-56, 62. (  0) 0)
|
| [2] |
谢正茂, 阎顺祥, 赵小军, 等. NT缸体铸造裂纹产生原因分析[J]. 热加工工艺, 2017, 46(5): 243-247. XIE Zhengmao, YAN Shunxiang, ZHAO Xiaojun, et al. Analysis on causes of casting cracks in NT cylinder block[J]. Hot working technology, 2017, 46(5): 243-247. (  0) 0)
|
| [3] |
虞强, 彭家锋, 刘国江. 铸造起重机吊具横梁裂纹原因及改造措施[J]. 机电工程技术, 2017, 46(8): 203-205. YU Qiang, PENG Jiafeng, LIU Guojiang. The reasons and measures of casting crane beam crack[J]. Mechanical & electrical engineering technology, 2017, 46(8): 203-205. DOI:10.3969/j.issn.1009-9492.2017.08.060 (  0) 0)
|
| [4] |
宋平, 常伟, 苑英伟, 等. 5083铝合金大规格扁锭铸造热裂纹缺陷的研究[J]. 有色金属加工, 2016, 45(5): 22-25. SONG Ping, CHANG Wei, YUAN Yingwei, et al. Study of hot cracking in casting of large-size 5083 aluminum alloy ingot[J]. Nonferrous metals processing, 2016, 45(5): 22-25. DOI:10.3969/j.issn.1671-6795.2016.05.005 (  0) 0)
|
| [5] |
石照夏, 董建新, 张麦仓. 汽车增压器涡轮用铸造高温合金热裂研究进展[J]. 材料工程, 2012, 40(6): 91-96. SHI Zhaoxia, DONG Jianxin, ZHANG Maicang. Development of hot tearing on cast superalloys used for auto turbocharger turbine wheel[J]. Journal of materials engineering, 2012, 40(6): 91-96. DOI:10.3969/j.issn.1001-4381.2012.06.020 (  0) 0)
|
| [6] |
XU Rongfu, ZHENG Hongliang, LUO Jie, et al. Role of tensile forces in hot tearing formation of cast Al-Si alloy[J]. Transactions of nonferrous metals society of China, 2014, 24(7): 2203-2207. DOI:10.1016/S1003-6326(14)63333-1 (  0) 0)
|
| [7] |
祖方遒, 袁晓光, 梁维中. 铸件成形原理[M]. 北京: 机械工业出版社, 2013: 28-29.
(  0) 0)
|
| [8] |
刘文君, 蒋斌, 杨青山. 双辊铸造热裂形成及工艺控制[J]. 材料导报A:综述篇, 2011, 25(9): 126-130. LIU Wenjun, JIANG Bin, YANG Qingshan. Hot tearing formation and control in twin-roll casting[J]. Materials review, 2011, 25(9): 126-130. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


