自然循环过程在工业锅炉,制冷系统以及先进核电厂中得到了广泛的应用和重视。自然循环不需要主泵提供动力,具有简化能动设备,提高系统可靠性和安全性等优点。同时,自然循环驱动力较低,流动和传热的耦合更加复杂,容易出现流动不稳定性及传热恶化。自然循环流动沸腾不稳定性的研究对热力系统的设计和运行具有重要意义。
在两相流动沸腾中,因通道尺寸、回路布置以及运行参数的不同可能会发生多种流动不稳定性。在常规通道中已经有了许多关于流动不稳定性的研究,如Boure等[1]、Kakac等[2]对流动沸腾通道中常见的不稳定性的特征和机理进行了总结。杨瑞昌等[3]在自然循环回路中发现了高频的声波型脉动和低频的密度波脉动,并观察到了两相流体和单相流体交替通过实验段出口的现象。文献[4-6]对低压自然循环反应堆中比较容易出现的密度波不稳定性、闪蒸不稳定性和喷泉不稳定性进行了实验和理论研究。Yu等[7]在小通道中对密度波不稳定性、压力降型脉动和流量漂移现象的机理进行了解释。
关于逆流的研究主要集中在小尺寸通道内,当小尺寸通道内气泡形成特定的流型时,部分液体会沿着与流动方向相反的方向返回通道入口,即发生了逆流[8-10]。在常规通道中仅有少量关于逆流的研究。郭予飞等[11]在流动脉动的最小值处记录到了负流量,Jain等[12]、Wang等[13]在常规通道实验研究中提到了逆流的发生,Jain等[12]使用反接的皮托管验证了逆流的存在。Steinke等[14]基于小通道内发现的逆流现象指出,对于并联布置的常规通道,在特定的压降、热流密度和质量流速工况组合中也可能会发生逆流。文献[1-14]没有给出常规通道下逆流的具体特征及其机理。本文利用内径为14 mm的圆形不锈钢常规加热通道,并在低压自然循环实验中综合考虑入口流量、水温和压力等参数的变化,验证逆流的存在,通过对比实验热流密度和Zhao关系式、Umekawa关系式的临界热流密度预测值,分析逆流发生的机理。
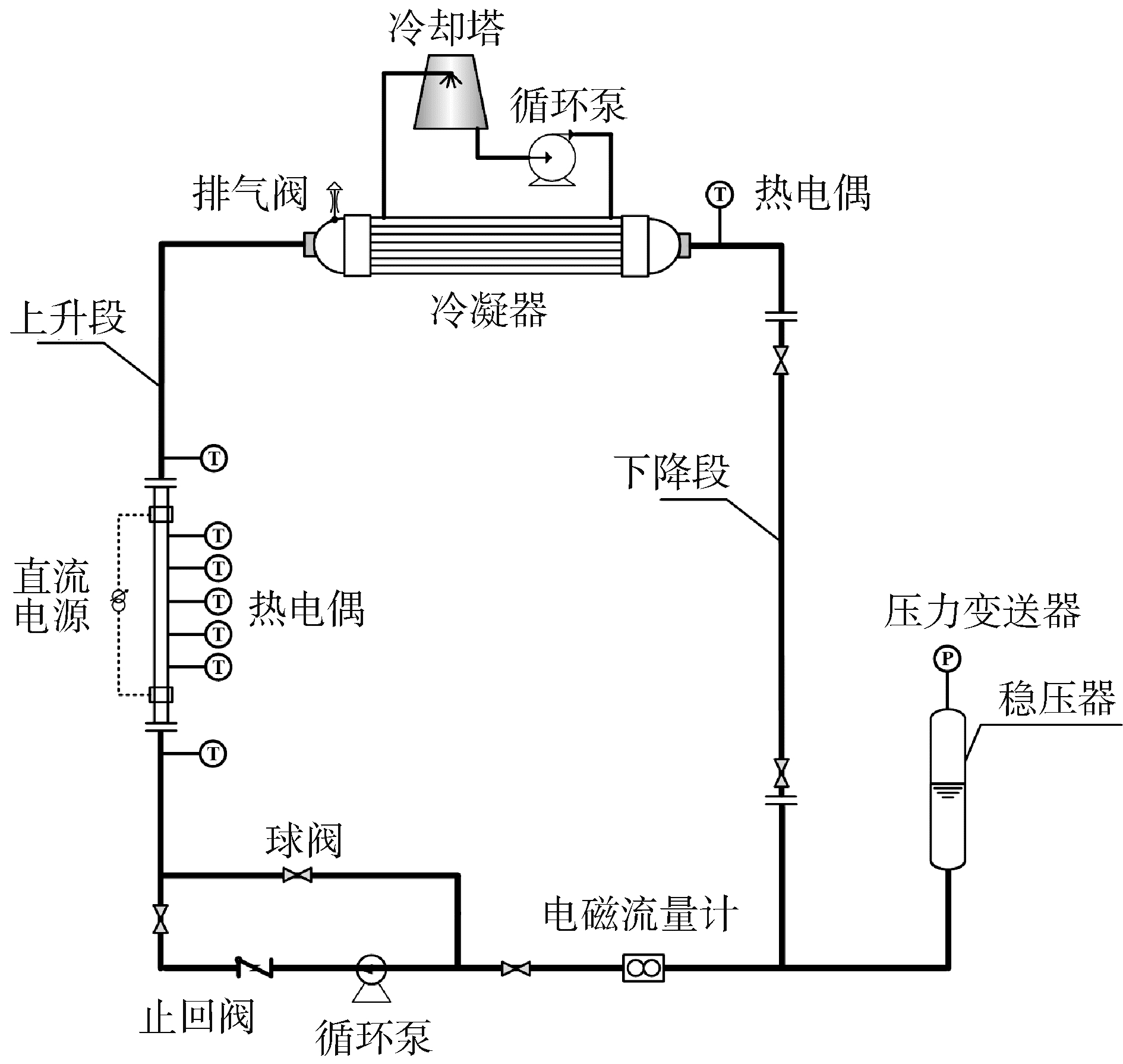
1 流动沸腾不稳定性实验研究 1.1 自然循环实验装置实验装置包含2个回路:自然循环主回路和冷凝回路。自然循环主回路由电加热实验段、上升段、冷凝器、下降段、相关的连接管段和测量仪表组成;冷凝回路为冷凝器的二次侧提供冷却水,为自然循环主回路提供热阱,冷却水流量可以调节。以去离子水为工质,图 1所示为实验台的示意图。不锈钢实验段通过直流电进行均匀加热,在实验回路的顶部设置一个管壳式冷凝器为热流体提供冷却。系统压力由一个氮气稳压器提供,稳压器容积较大,其内径约为0.3 m,高度约为1.4 m。氮气空间为整个系统提供了较大的可压缩容积。实验段和上升段的内径分别为14、40 mm,长度分别为1.6、3.0 m,下降段总长5.0 m。
|
Download:
|
| 图 1 自然循环实验台 Fig. 1 Natural circulation experimental facility | |
实验段为一个不锈钢圆管通道,其水力直径为14 mm,根据文献[15-17]给出的分类准则,该通道应被归入常规通道。实验段示意如图 2所示,图中Tw为壁面温度。实验段通过安装在上下法兰之间的聚四氟乙烯绝缘垫片与实验台的其他部分进行绝缘。在实验段的外壁面上粘贴有21根直径为0.3 mm的N型热电偶,实验段的下半部分热电偶布置间距为10 cm,上半部分布置间距为5 cm,在靠近实验段出口的部分布置更多的热电偶能获得更详细的两相段壁温分布。使用直流电给实验段加热,电流通过霍尔电流传感器进行转换后由一块Agilent万用表测量,同时测量了实验段2个接电端子之间的电压。实验段的入口和出口水温通过两根铠装热电偶测量。整个实验段外部覆盖了保温层以减小向环境的散热。

|
Download:
|
| 图 2 实验段示意 Fig. 2 Test section | |
本文主要进行了低压(P < 0.5 MPa)高入口过冷度(ΔTsub>30 ℃)下的自然循环实验。实验中的最大热流密度可达到450 kW/m2。通过对稳压器内加注氮气来调节系统压力,由于系统压力相对较低,稳压器内会发生一定程度的压力波动。实验中通过调节冷凝回路的冷凝水流量来调节冷凝器出口和实验段入口温度。在冷凝器出口和实验段入口各有一根铠装热电偶用以测量流体温度。首先使用循环泵驱动流体流动并在实验段内进行加热,待冷、热段建立一定的温度差之后关闭并隔离循环泵,进入自然循环。在实验段入口温度达到预设值并保持稳定不变之后记录数据。逐步增加加热功率以获得同一压力同一入口过冷度下从单相到两相的不同工况。
1.4 数据处理实验中通过焊接在加热段外壁面的热电偶测量壁温,由于实验段壁厚较小(1 mm),忽略实验段的热容可以通过稳态导热方程推算实验段内壁温。
在单相流动状态下,可以根据进、出口温度和流量推算实验段的热平衡效率:
| $ \varphi = \frac{{W{C_{\rm{p}}}\left( {{T_{{\rm{out}}}} - {T_{{\rm{in}}}}} \right)}}{{UI}} $ | (1) |
式中:W为质量流速;Cp为定压比热;Tin和Tout分别为进、出口水温;U和I分别为电压和电流。
实验段内壁面的热流密度为:
| $ q = \frac{{\varphi UI}}{{{\rm{ \mathsf{ π} }}DL}} $ | (2) |
式中:D为实验段内径;L为实验段加热长度。
稳态导热方程:
| $ \frac{{{{\rm{d}}^2}T}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}T}}{{{\rm{d}}r}} + \frac{{{q_V}}}{\lambda } = 0 $ | (3) |
边界条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {r = {R_{\rm{o}}}}\\ {T = {T_{\rm{o}}}}\\ { - \frac{{{\rm{d}}T}}{{{\rm{d}}r}} = 0} \end{array}} \right. $ | (4) |
求解得到实验段内壁温为:
| $ {T_{\rm{i}}} = {T_{\rm{o}}} - \left( {\frac{{{q_{\rm{V}}}}}{{4\lambda }}\left( {R_{\rm{i}}^2 - R_{\rm{o}}^2} \right) + \frac{{{q_{\rm{V}}}}}{{2\lambda }}R_{\rm{o}}^2\ln \left( {\frac{{{R_{\rm{o}}}}}{{{R_{\rm{i}}}}}} \right)} \right) $ | (5) |
式中:r为距实验段中轴线的距离;qV为体积释热率;λ为导热系数;Ri和Ro分别为实验段内、外壁面距实验段中轴线的距离;Ti和To分别为实验段内、外表面的温度。
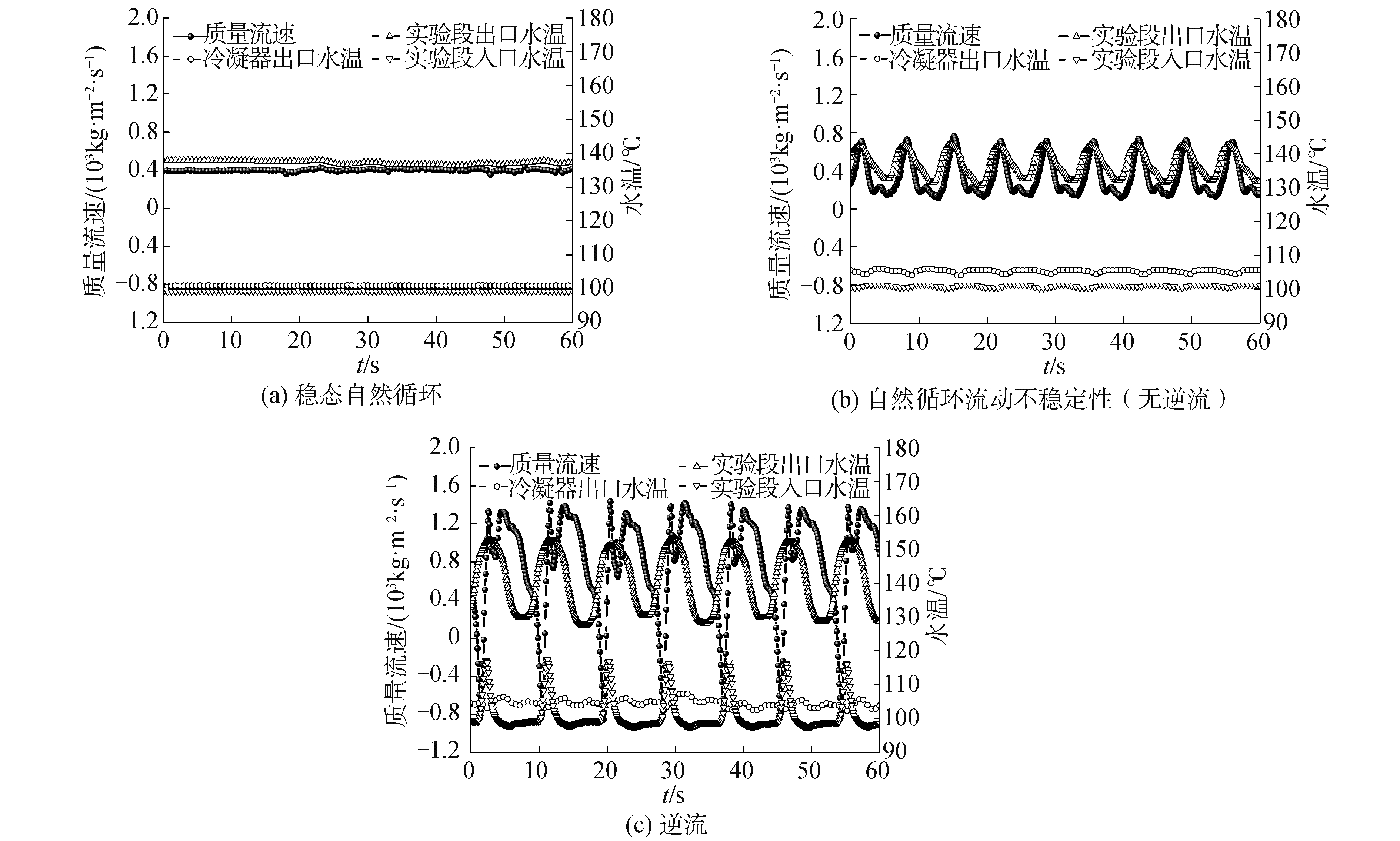
2 实验结果与讨论 2.1 逆流的基本特征 2.1.1 入口流量和温度固定系统压力(P=0.4 MPa)与实验段入口温度(ΔTsub=40 ℃),逐步增加加热功率,可以得到不同热流密度下的自然循环工况。本文主要获得了3种自然循环工况:稳定流动、流动不稳定性(无逆流)和逆流。在低热流密度(q=154 kW/m2)下自然循环是稳定的,流量及实验段进出口水温都能保持稳定,如图 3(a)所示;当热流密度达到一定值(q=194 kW/m2)后发生流动不稳定性,此时实验段入口流量发生较大幅度的波动,如图 3(b)所示;随着热流密度的进一步增加(q=331 kW/m2),流量剧烈波动,安装在实验段上游的流量计在流量波动的波谷处测量到负流量,如图 3(c)所示。
|
Download:
|
| 图 3 不同热流密度下的自然循环流动 Fig. 3 Natural circulation flow under different heat fluxes | |
由于向环境外的散热,实验段入口温度一般比冷凝器出口温度低。在检测到负流量的这种工况下,实验段入口温度也发生了波动,温度呈现脉冲式的波动,在波峰处超过了实验段上游冷凝器出口处的温度。结合入口流量和温度信号,可以得出在高热流密度下,当流量发生波动时,在低流量周期内,实验段入口附近被加热后的流体沿与主流相反的方向流出了实验段入口,上游的流量计和热电偶分别检测到负流量和温度脉冲,即实验段内发生了逆流。
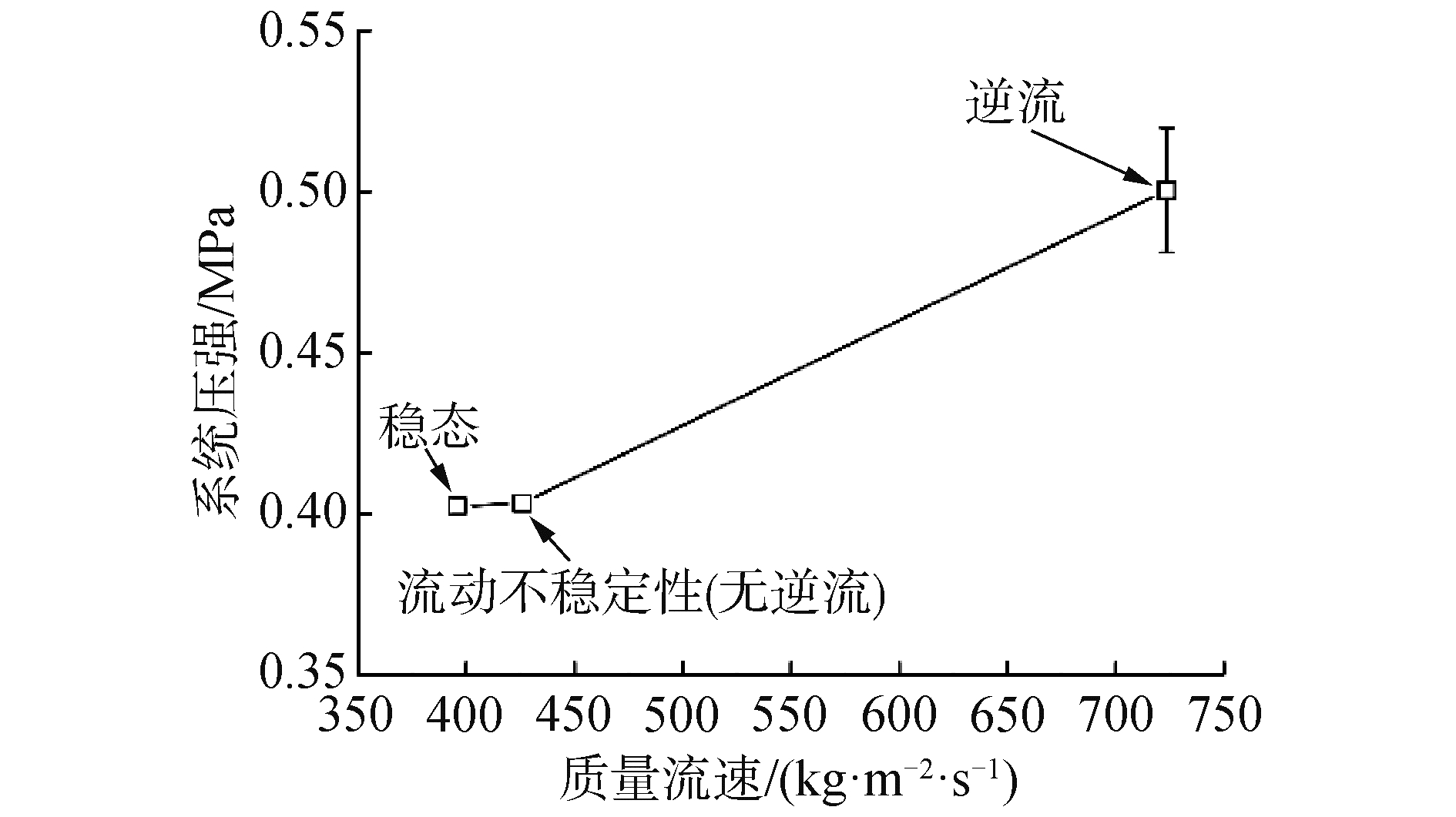
2.1.2 系统压强图 4所示为前面所述3种工况下稳压器内压强变化。在未发生逆流的工况下,系统压强能维持稳定,实验段内发生逆流后,部分流体反向流出实验段入口,涌入上游的稳压器中,造成稳压器内压强波动。回路中的可压缩容积(稳压器)使系统成为低刚性的系统,稳压器的存在为压强波动提供了缓冲空间。发生逆流时的剧烈流量波动实质上为加热的实验段与上游稳压器之间相互作用的结果。在高热流密度下,实验段内的剧烈汽化导致局部压强升高,当实验段内压强超过上游驱动力时,流体被推出实验段入口,涌入稳压器内;当稳压器内积聚较大的压力后,实验段上游的驱动力增加,驱动过冷流体涌出稳压器并迅速通过实验段,产生如图 3(c)所示的剧烈流量波动。这流动不稳定性(无逆流)和逆流的产生同时受到加热段内气泡行为和回路可压缩容积的影响,这两种不稳定性为复合型流动不稳定性。
|
Download:
|
| 图 4 不同质量流速下的系统压力 Fig. 4 System pressure under different mass fluxes | |
对于实验段出口为泡状流或环状流等流型的工况,因为出口一直为饱和液体和饱和气体的混合物,出口温度应该保持在当地压强对应的饱和温度上。在本文所遇到的工况中,发生流动不稳定性后实验段出口温度发生了波动,如图 3(b)和图 3(c)所示。两相流动沸腾下实验段出口水温波动表明,实验段出口存在单相过冷液体和气液两相混合物的交替通过,这是由于实验段上游能量的积蓄和释放过程过于剧烈导致的。当实验段上游积蓄了较大的势能之后,在能量释放的过程中,大量过冷流体迅速通过加热实验段,在到达实验段出口之前不能被加热至饱和状态,此时的水温低于当地饱和压强对应的饱和温度;在低流量蓄压过程中,实验段出口为饱和气液混合物或饱和气体,此时的出口温度为当地压强对应的饱和温度。由于单相过冷流体和气液两相混合物交替通过实验段出口,因此产生了如图 3所示的出口水温波动。
2.2.2 间歇干涸在本文流量波动的波谷附近,尤其是发生逆流的工况中,通过实验段的流量非常低,实验段内没有足够的流体补充进去,因此可能在靠近实验段出口位置处发生了间歇干涸型沸腾临界。许多学者在流动不稳定性或者流量脉动条件下进行了临界热流密度(critical heat flux, CHF)的研究,Umekawa等[18]基于加热壁面导热的集中参数模型推导了一个适用于大振幅流量波动下预测CHF的关系式,文献[19-21]提出了预测脉动流条件下CHF的经验关系式。文献[18]关系式和文献[21]关系式为:
| $ {q_{{\rm{CHF}}}} = h{\theta _{{\rm{CHF}}}}/\left[ {1 - \exp \left( { - 0.5\tau /{\tau _{\rm{W}}}} \right)} \right] $ | (6) |
| $ F = {F_{p, \lim }} + \left( {1 - {F_{p, \lim }}} \right)\exp \left( { - 2\left( {\frac{{\Delta G}}{{{G_{{\rm{AVE}}}}}}} \right)\left( {\frac{{{t_{{\rm{tr}}}}}}{\tau }} \right)} \right) $ | (7) |
其中,文献[18]关系式适用于:0<ΔG/G < 10.2和2<τ < 6 s下的工况,文献[21]关系式适用于:0<ΔG/G < 3和1.04<τ < 10.6 s下的工况。
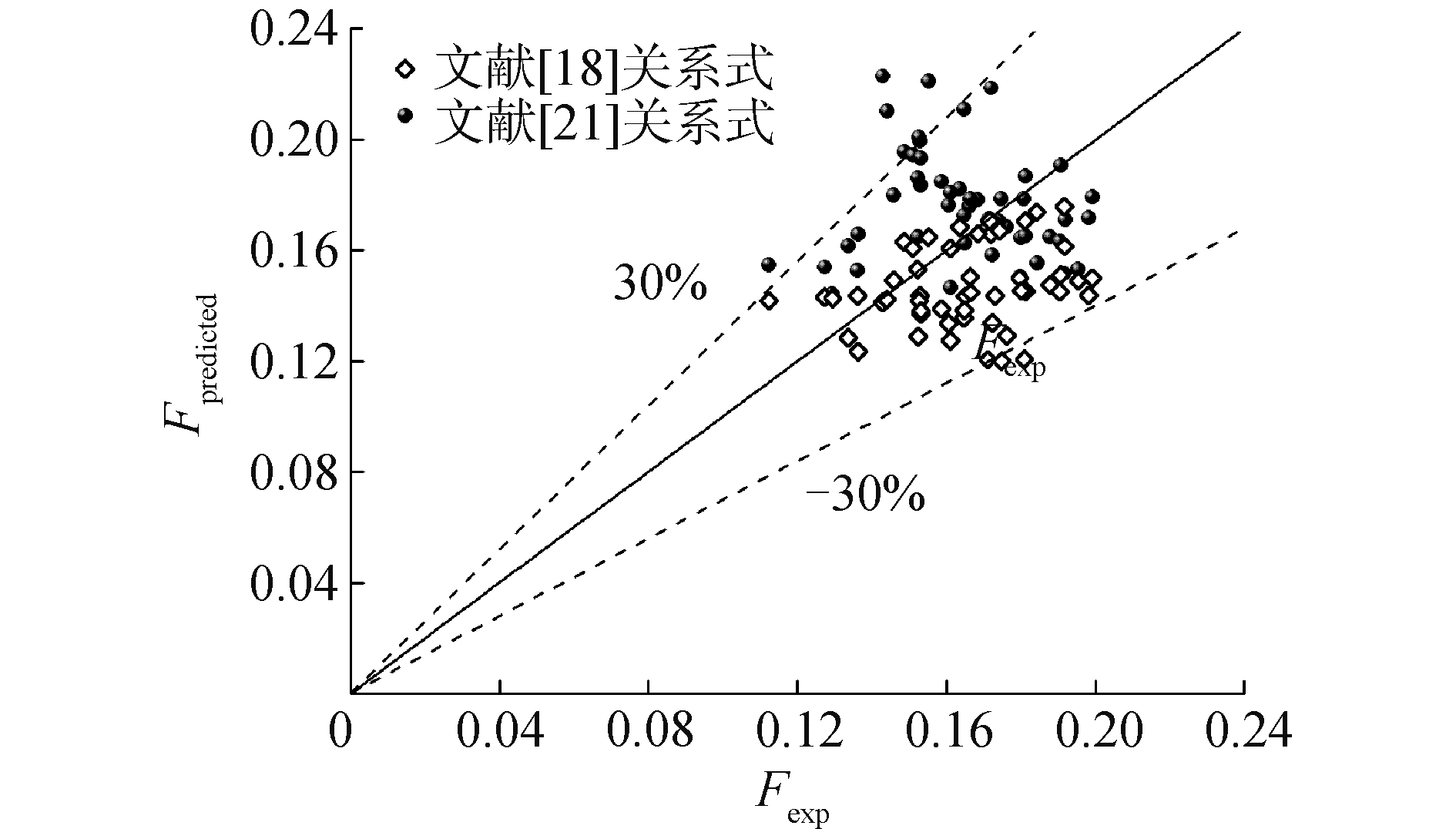
文献[18]和文献[21]关系式的适用范围与本文中的工况范围(2<ΔG/G < 6, 6 s<τ < 10 s)更为接近,为了验证实验段出口处是否发生了间歇干涸,本文将逆流工况下的实验热流密度值Fexp与上述2个关系式给出的CHF计算值Fpredicted进行了对比,如图 5所示。其中,平均流量GAVE对应的稳态CHF值来自2006 CHF lookup-table[22],无量纲流量脉动振幅和间歇干涸型临界热流密度因子定义为:
|
Download:
|
| 图 5 实验热流密度与CHF预测值 Fig. 5 Experimental heat flux and predicted CHF | |
| $ \frac{{\Delta G}}{{{G_{{\rm{AVE}}}}}} = \frac{{{G_{{\rm{max}}}} - {G_{{\rm{min}}}}}}{{{G_{{\rm{AVE}}}}}} $ | (8) |
| $ F = \frac{{{q_{{\rm{CHF}}}}}}{{{q_{{\rm{CHF}}, {\rm{AVE}}}}}} $ | (9) |
实验热流密度与上述2个经验关系式的预测值吻合较好,说明发生逆流时实验段内发生了间歇干涸。本文中涉及的工况下流量波动振幅较大(2<ΔG/G < 6),因此在相对较低的热流密度下实验段内也达到了间歇干涸型临界热流密度,即流动不稳定性导致了间歇干涸型沸腾临界的提前发生。
间歇干涸的发生解释了常规通道中逆流的产生。发生流动不稳定后,在流量波动的波谷附近,由于实验段内没有足够的流体补充发生了间歇干涸, 发生间歇干涸的地方剧烈汽化,产生局部超压,剧烈的汽化推动上游的气液界面沿与主流相反的方向移动,将上游的流体推出实验段,这部分已经被加热过的流体涌入上游的稳压器内,导致实验段入口负流量,入口温度脉冲,同时上游稳压器内发生较大的压力上升和波动。
逆流的发生与自然循环工况和实验回路的结构有密切关系。自然循环工况下,实验段上游驱动力不足,当实验段内发生间歇干涸时局部压力可以超过上游压力;另一方面,实验段内产生的高压蒸汽需要通过一个长3 m的上升段才能在顶部的冷凝器中得到冷却,实验段的高压无法及时被排出。同时,实验段上游的可压缩容积为逆流的发生提供了条件,稳压器可以吸收逆流产生的高压。
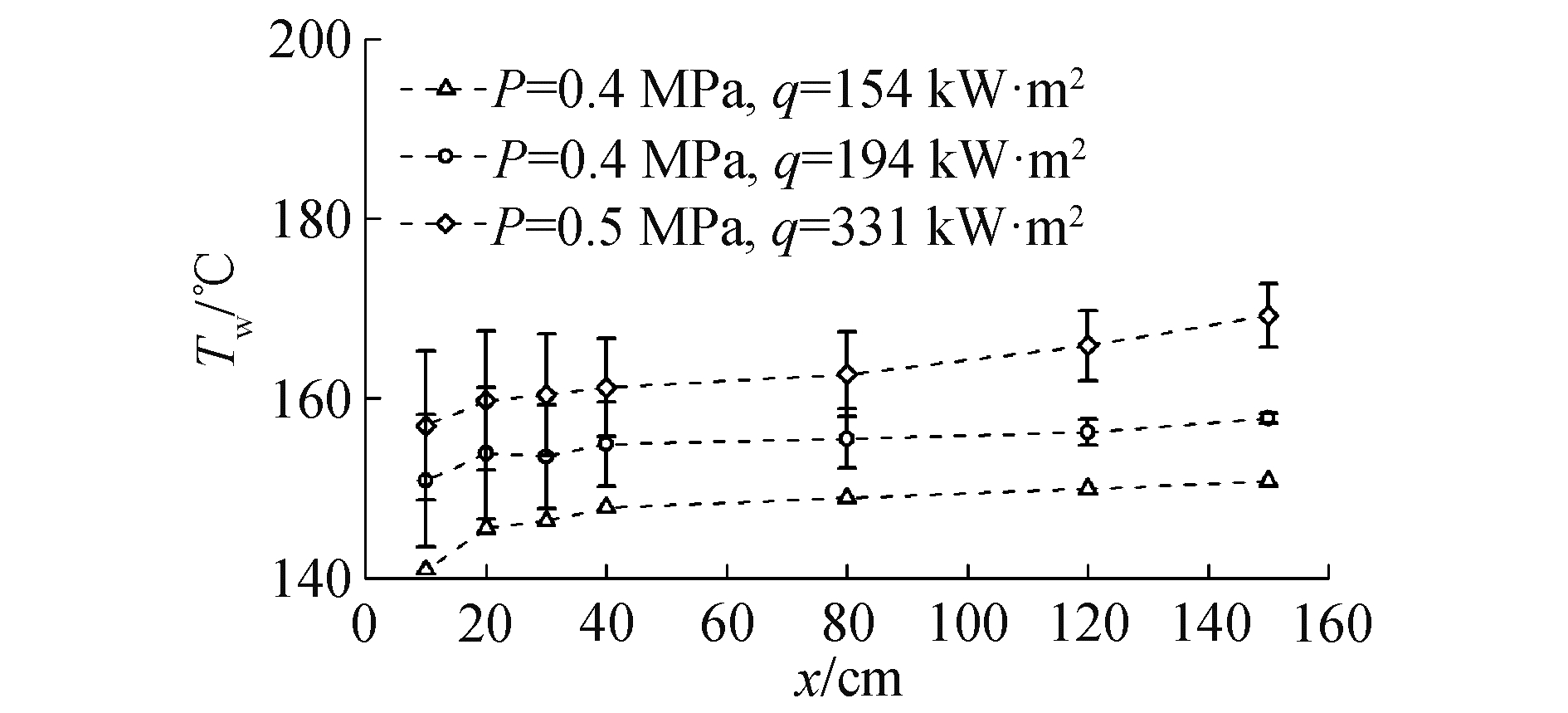
2.2.3 壁温分布实验段壁温分布如图 6所示,实验段入口温度ΔTsub为40 ℃。稳态自然循环下壁温也是稳定的,越靠近实验段出口的壁温越高。发生流动不稳定性后,实验段壁温发生波动,波动振幅越靠近出口越小,在接近出口处的壁温近似是稳定的。然而,发生逆流时,壁温波动幅度沿实验段并没有出现明显的降低,靠近实验段出口处的壁温依然发生了较大幅度的波动。这3种工况下靠近实验段出口处的壁温波动差异主要来自实验段出口处流型和换热机理的差异。未发生逆流时,在一个流量波动周期内,实验段出口的加热壁面始终与液相流体或液膜之间存在对流换热,加热段内产生的热量通过覆盖在内壁面的饱和液体或液膜带走,换热系数变化较小,因此壁温波动幅度也很小;发生逆流后,由于一个流量波动周期内会出现零流量甚至逆流,实验段内剧烈汽化时,局部段内气相压力升高,推动上下游流体朝2个方向移动。这就导致了该段内没有液体能够补充进来,加热壁面的液膜厚度逐渐减小,实验段出口出现间歇干涸。此时加热段的热量靠单相饱和蒸汽带走,换热系数较低,加热壁面得不到充足的冷却而导致壁温大幅升高。当高流量到来时,实验段被液相流体冷却,对流换热系数较大,壁温因而大幅下降,从而出现较大幅度的壁温波动。
|
Download:
|
| 图 6 加热壁面壁温度分布 Fig. 6 Heating surface temperature profile | |
综合出口水温的波动、壁温分布和间歇干涸的发生可以得到,在无逆流的流动不稳定性中实验段内为单相过冷液体和两相混合物的交替通过;发生逆流后,实验段内还存在单相过冷液体、两相混合物和单相蒸汽的交替通过,即发生逆流后实验段内加热壁面存在周期性干涸和再润湿的过程。
3 结论1) 在低压自然循环工况下的流动沸腾实验研究中,随着热流密度的增加发现了3个流动沸腾模式:稳定流动、流动不稳定性(无逆流)和逆流。
2) 逆流存在以下特征:加热段入口负流量、入口水温发生脉动和稳压器内压力大幅波动,以上3点也证实了逆流的发生。
3) 流动不稳定性导致了间歇干涸型沸腾临界的发生,逆流是由于间歇干涸的发生导致的。
4) 未发生逆流的流动不稳定中,单相液体和两相混合物交替通过实验段;发生逆流时,单相液体、两相混合物和单相蒸汽交替通过实验段。
| [1] |
BOURE J A, BERGLES A E, TONG L S. Review of two-phase flow instability[J]. Nuclear engineering and design, 1973, 25(2): 165-192. DOI:10.1016/0029-5493(73)90043-5 (  0) 0)
|
| [2] |
KAKAC S, BON B. A review of two-phase flow dynamic instabilities in tube boiling systems[J]. International journal of heat and mass transfer, 2008, 51(3/4): 399-433. (  0) 0)
|
| [3] |
杨瑞昌, 王彦武, 王飞, 等. 自然循环过冷沸腾流动不稳定性的实验研究[J]. 核动力工程, 2005, 26(4): 317-322. YANG Ruichang, WANG Yanwu, WANG Fei, et al. Experimental study of flow instability in a natural circulation system with sub-cooled boiling[J]. Nuclear power engineering, 2005, 26(4): 317-322. DOI:10.3969/j.issn.0258-0926.2005.04.003 (  0) 0)
|
| [4] |
SHI Shanbin, HIBIKI T, ISHII M. Startup instability in natural circulation driven nuclear reactors[J]. Progress in nuclear energy, 2016, 90: 140-150. DOI:10.1016/j.pnucene.2016.03.016 (  0) 0)
|
| [5] |
SHI Shanbin, ISHII M. Modeling of flashing-induced flow instabilities for a natural circulation driven novel modular reactor[J]. Annals of nuclear energy, 2017, 101: 215-225. DOI:10.1016/j.anucene.2016.11.005 (  0) 0)
|
| [6] |
SHI Shanbin, SCHLEGEL J P, BROOKS C S, et al. Experimental investigation of natural circulation instability in a BWR-type small modular reactor[J]. Progress in nuclear energy, 2015, 85: 96-107. DOI:10.1016/j.pnucene.2015.06.014 (  0) 0)
|
| [7] |
YU Zhiting, YUAN Hongsheng, CHEN Chong, et al. Two-phase flow instabilities of forced circulation at low pressure in a rectangular mini-channel[J]. International journal of heat and mass transfer, 2016, 98: 438-447. DOI:10.1016/j.ijheatmasstransfer.2016.03.047 (  0) 0)
|
| [8] |
KUANG Y W, WANG W, MIAO J Y, et al. Flow boiling of ammonia and flow instabilities in mini-channels[J]. Applied thermal engineering, 2017, 113: 831-842. DOI:10.1016/j.applthermaleng.2016.11.093 (  0) 0)
|
| [9] |
KUANG Yiwu, WANG Wen, MIAO Jianyin, et al. Theoretical analysis and modeling of flow instability in a mini-channel evaporator[J]. International journal of heat and mass transfer, 2017, 104: 149-162. DOI:10.1016/j.ijheatmasstransfer.2016.08.042 (  0) 0)
|
| [10] |
WANG Guodong, CHENG Ping. An experimental study of flow boiling instability in a single microchannel[J]. International communications in heat and mass transfer, 2008, 35(10): 1229-1234. DOI:10.1016/j.icheatmasstransfer.2008.07.019 (  0) 0)
|
| [11] |
郭予飞, 苏光辉, 喻真烷, 等. 低压低含汽率工况下两相自然循环流动不稳定的实验研究[J]. 核科学与工程, 1999, 19(2): 137-141. GUO Yufei, SU Guanghui, YU Zhenwan, et al. Experimental study on two-phase natural circulation flow instability under low pressure and low steam quality[J]. Chinese journal of nuclear science and engineering, 1999, 19(2): 137-141. (  0) 0)
|
| [12] |
JAIN K C, PETRICK M, MILLER D, et al. Self-sustained hydrodynamic oscillations in a natural-circulation boiling water loop[J]. Nuclear engineering and design, 1966, 4(3): 233-252. DOI:10.1016/0029-5493(66)90049-5 (  0) 0)
|
| [13] |
WANG Q, CHEN X J, KAKAÇ S, et al. An experimental investigation of density-wave-type oscillations in a convective boiling upflow system[J]. International journal of heat and fluid flow, 1994, 15(3): 241-246. DOI:10.1016/0142-727X(94)90044-2 (  0) 0)
|
| [14] |
STEINKE M E, KANDLIKAR S G. Flow boiling and pressure drop in parallel flow microchannels[C]//Proceedings of the ASME 1st International Conference on Microchannels and Minichannels. Rochester, New York, USA, 2003.
(  0) 0)
|
| [15] |
KEW P A, CORNWELL K. Correlations for the prediction of boiling heat transfer in small-diameter channels[J]. Applied thermal engineering, 1997, 17(8): 705-715. (  0) 0)
|
| [16] |
KANDLIKAR S G, GRANDE W J. Evolution of microchannel flow passages thermohydraulic performance and fabrication technology[J]. Heat transfer engineering, 2003, 24(1): 3-17. DOI:10.1080/01457630304040 (  0) 0)
|
| [17] |
CHENG P, WU H Y. Mesoscale and microscale phase-change heat transfer[J]. Advances in heat transfer, 2006, 39: 461-563. DOI:10.1016/S0065-2717(06)39005-3 (  0) 0)
|
| [18] |
UMEKAWA H, OZAWA M, MITSUNAGA T, et al. Scaling parameter of CHF under oscillatory flow conditions[J]. Heat transfer-asian research, 1999, 28(6): 541-550. DOI:10.1002/(SICI)1523-1496(1999)28:6<541::AID-HTJ10>3.0.CO;2-E (  0) 0)
|
| [19] |
KIM Y I, BAEK W P, CHANG S H. Critical heat flux under flow oscillation of water at low-pressure, low-flow conditions[J]. Nuclear engineering and design, 1999, 193(1/2): 131-143. (  0) 0)
|
| [20] |
OKAWA T, GOTO T, MINAMITANI J, et al. Liquid film dryout in a boiling channel under flow oscillation conditions[J]. International journal of heat and mass transfer, 2009, 52(15/16): 3665-3675. (  0) 0)
|
| [21] |
ZHAO D W, SU G H, LIANG Z H, et al. Experimental research on transient critical heat flux in vertical tube under oscillatory flow condition[J]. International journal of multiphase flow, 2011, 37(9): 1235-1244. DOI:10.1016/j.ijmultiphaseflow.2011.06.012 (  0) 0)
|
| [22] |
GROENEVELD D C, SHAN J Q, VASIĆ A Z, et al. The 2006 CHF look-up table[J]. Nuclear engineering and design, 2007, 237(15/16/17): 1909-1922. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


