2. 德州农工大学 海洋工程系, 美国德克萨斯州卡城 77843;
3. 上海船舶运输研究所 航运技术与安全国家重点实验室, 上海 200135
2. Department of Ocean Engineering, Texas A & M University, College Station 77843, USA;
3. State Key Laboratory of Navigation and Safety Technology, Shanghai Ship and Shipping Research Institute, Shanghai 200135, China
船舶喷水推进系统推力预报是喷水推进系统动力性能的一项重要内容。其预报方法主要有3种:试验统计法、模型试验法和计算流体力学(computation fluid dynamic, CFD)方法。20世纪90年代国外开展了大量针对船舶与喷水推进系统相互作用和喷水推进流道的试验研究[1-2]。ITTC推荐船舶喷水推进系统推力的采用动量通量法和直接测量方法之后,基于粘流CFD的船舶喷水推进数值模拟开始快速发展。Watson[3]针对喷水通道进行研究仅限于流通本身,未考虑到船舶影响。Kimball[4]对喷水推进系统进行了试验和数值方面的综合研究;Takai[5]基于CFDSHIP_IOWA粘流软件对带有喷水推进系统的船舶进行了多目标优化;Eslamdoost[6]利用商业软件SHIPFLOW的势流计算模块XPAN和叠模计算模块XBOUND对喷水推进船体相互作用问题进行了分析,研究了喷水推进负推力减额等问题。刘承江等[7]对喷水推进推力计算的CFD方法、喷水推进-船体相互作用[8]、进水流通参数化计方法[9]问题进行了大量研究;龚杰等[10]采用虚拟盘法和重叠网格法对旋转叶轮进行数值模拟,对比研究了2种模型对喷水推进船舶内外流场的影响;胡健[11]对影响喷水推进器水动力性能的因素进行了研究。
现有对船舶喷水推进系统推力计算的数值方法主要集中在采用粘流CFD软件,通过动量流量法进行计算,该方法虽能够达到比较好的效果并且能捕捉流场细节,但其不适用于船舶初期设计阶段的对喷水推进推力快速计算的需求,且粘流CFD的计算效率仍有待提高。本文基于边界层理论研究控制体进流面的边界层速度、压力分布,实现喷水推进推力的快速迭代求解,通过与相同模型的粘流CFD结果对比分析研究本方法的适用性。
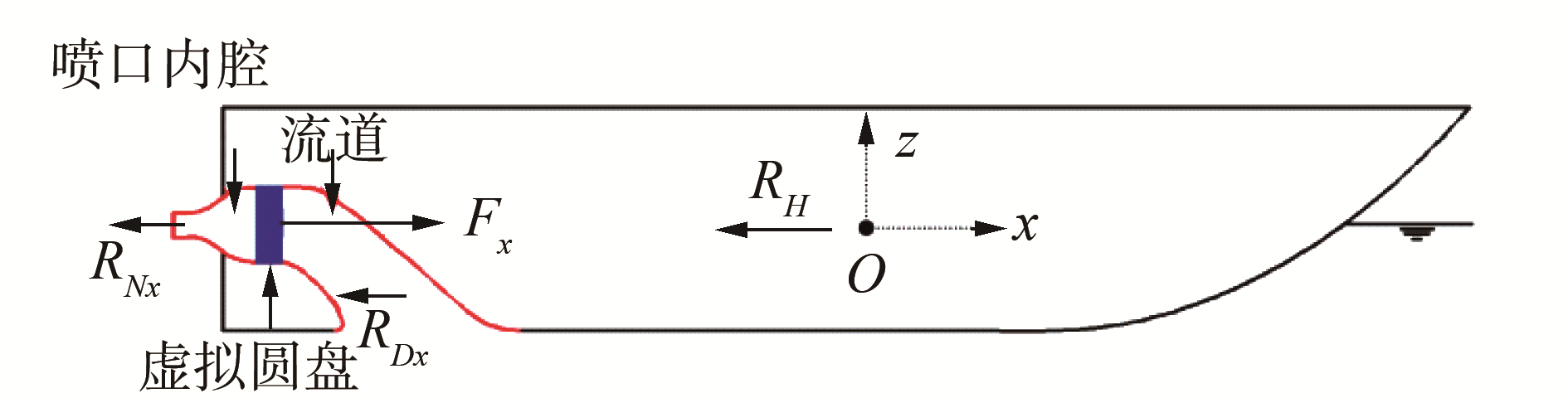
1 喷水推进系统数学模型 1.1 船舶受力平衡方程喷水推进系统和船体模型由船体表面与喷水推进内部流道两部分组成。在本文将旋转叶片及整流定子假设为一个虚拟圆盘(图 1所示),在虚拟盘前后发生压力跃变[6],以此建立喷水推进推力计算模型。
|
Download:
|
| 图 1 喷水推进船舶受力 Fig. 1 Force balance diagram of waterjet propelled ship | |
对于整体模型,考虑船体纵向所受合力为:
| $ {R_{P,x}} = {R_H} + {R_{D,x}} + {R_{N,x}} $ | (1) |
式中:RH为除流道外船体阻力;RD,x为虚拟圆盘前方的喷水流道纵向受力;RN,x为虚拟圆盘后方与喷口之间的喷口内腔纵向受力。
假设虚拟盘前后压力分别为P1和P2,盘面积为叶片位置流道截面积A,则船体和流道所受合力与喷水推进系统产生的推力平衡为:
| $ {R_{P,x}} = {F_x} = \left( {{P_1} - {P_2}} \right)A = \Delta pA $ | (2) |
假设喷口内腔面积为S,则喷口内腔纵向受力:
| $ {R_{N,x}} = \iint\limits_S {\sigma {n_x}{\text{d}}s} = \iint\limits_S {p{n_x}{\text{d}}s} + \iint\limits_S {\tau {n_x}{\text{d}}s} $ | (3) |
喷水推进流道内的实际流动可以认为是2种不同条件下的流体状态的叠加。假设流道喷口内腔内流体初始状态是在没有叶片加速作用时的实际流速,再通过对该流体施加恒定的压力,使其与有旋转叶片加速时的流速一致。因此,通过减去流道内的常数压力跃变,喷口内腔的速度场仍然保持与现实中相同,从而喷口内腔处的压力由一个没有旋转叶片时的定常压力Pd和有旋转叶片时盘面处决定的压力差Δp组成:
| $ \iint\limits_S {p{n_x}{\text{d}}s} = \iint\limits_S {{p_{\text{d}}}{n_x}{\text{d}}s} + \iint\limits_S {\Delta p{n_x}{\text{d}}s} $ | (4) |
对于喷口内腔:
| $ \iint\limits_S {\Delta p{n_x}{\text{d}}s} = \Delta p\left( {A - {A_{{\text{out}}}}} \right) $ | (5) |
式中:Aout为喷口处截面积,联立式(1)~(5)后得:
| $ \Delta p{A_{{\text{out}}}} = {R_H} + {R_{D,x}} + \left( {\iint\limits_S {{p_{\text{d}}}{n_x}{\text{d}}s} + \iint\limits_S {\tau {n_x}{\text{d}}s}} \right) $ | (6) |
式(7)即为整个系统中除了盘面处压力差之外的其他力之和:
| $ {R_{Td}} = {R_H} + {R_{D,x}} + \left( {\iint\limits_S {{p_{\text{d}}}{n_x}{\text{d}}s} + \iint\limits_S {\tau {n_x}{\text{d}}s}} \right) $ | (7) |
最终得到盘面处压力差的表达式为
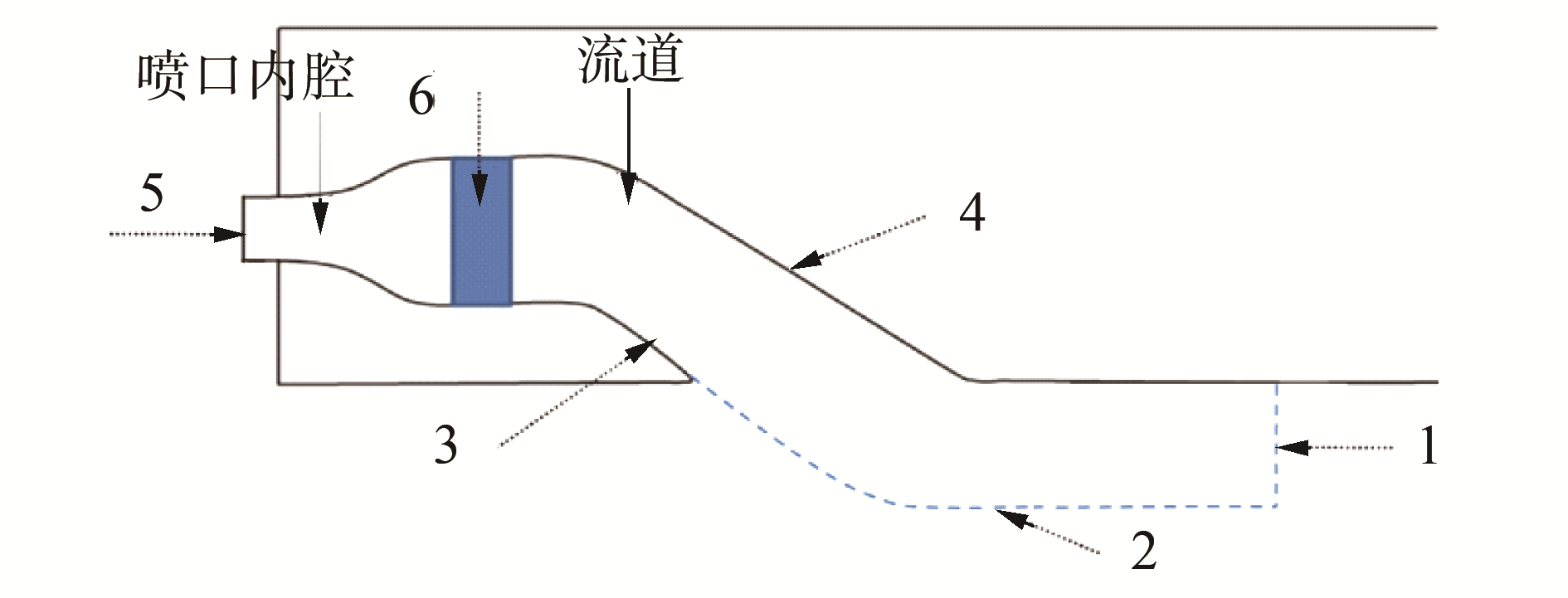
第23届和24届ITTC会议对船舶喷水推进系统的控制体水动力模型进行了定义和说明[12-13],如图 2所示,进流面1、虚拟控制体在流体内部的边界面2、流道内壁面3、流道内壁面4和喷口5组成了封闭的虚拟控制体模型。圆盘6为虚拟盘体,在此处流体压力发生跃变增压Δp。边界面1的位置一般取在距进流口前端一个流道直径的距离[9]。
|
Download:
|
| 图 2 喷水推进流道控制体图 Fig. 2 Virtual control volume of waterjet intake duct | |
对于进流面1的中心和喷口5的中心有:
| $ \begin{array}{*{20}{c}} {\left( {{{\bar p}_1} + \rho g{{\bar h}_1} + (1/2)\rho \bar u_1^2} \right) + \Delta p = {{\bar p}_5} + \rho g{{\bar h}_5} + }\\ {(1/2)\rho \bar u_5^2} \end{array} $ | (8) |
化简得到喷口速度和航速的比值(喷速比)k:
| $ \begin{array}{l} k = \frac{{{{\bar u}_5}}}{{{u_0}}} = \\ \;\;\;\;\sqrt {\frac{{\left( {{{\bar p}_1} - {{\bar p}_5}} \right)}}{{(1/2)\rho u_0^2}} + \frac{{\Delta p}}{{(1/2)\rho u_0^2}} + \frac{{2g\left( {{{\bar h}_1} - {{\bar h}_5}} \right)}}{{u_0^2}} + \frac{{\bar u_1^2}}{{u_0^2}}} \end{array} $ | (9) |
式中:u0为船舶航速,u1和u5、p1和p5、h1和h5分别为进流面和喷口出流面在对应面上的平均速度、平均压力和距基线平均高度。
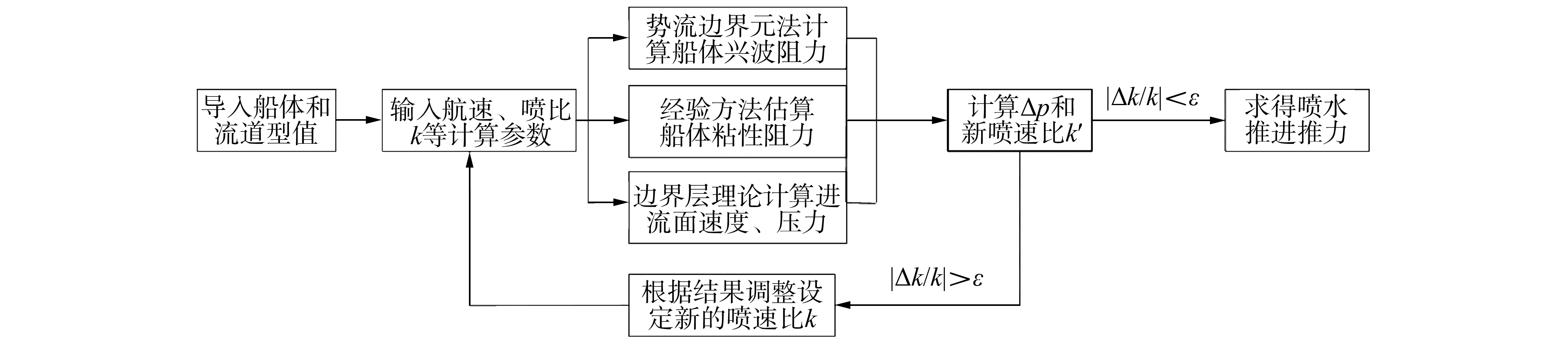
喷水推进推力迭代计算流程如图 3所示,速度比k作为初始值输入,通过计算压差Δp和相关参数后可以由式(9)得到新的速度比k′,根据是否满足收敛标准进行下一步计算。根据喷水推进总推力为:
|
Download:
|
| 图 3 喷水推进推力迭代计算流程 Fig. 3 Iterative process of waterjet thrust | |
| $ {T_g} = N\rho {\bar u_5}{A_5}\left( {{{\bar u}_5} - \alpha {u_0}} \right) $ | (10) |
式中:N为喷水推进装置数量,A5为喷口截面积,α为进流面边界层影响系数。当速度比计算收敛后,即可计算喷水推进总推力Tg。喷水推进净推力Tnet=(1-tj)Tg,其中tj为动量推力减额系数。当喷口完全暴露在空气或完全浸没在水中喷射时,动量推力减额系数tj可忽略[7, 14]。
2 迭代计算模块数值求解方法 2.1 兴波阻力数值求解方法基于势流理论的边界方法,在船舶水动数值计算方面得到广泛应用[15-17]。基于势流理论的基本假设,流体是无旋无粘的不可压缩理想流体。不考虑非定常扰动,则流场中总速度势Φ(x, y, z)=-u0x+φ(x, y, z),-u0x表示均匀来流产生的速度势,φ为船舶匀速向前运动引起的定常扰动势。非定常扰动势由以下边界条件方程组式(11)求解得到,而后通过伯努利方程对船体表面延纵向压力积分获得船舶兴波阻力分为3种情况:
1)
| $ \frac{{\partial \varphi }}{{\partial \mathit{\boldsymbol{n}}}} = \left\{ {\begin{array}{*{20}{l}} {{u_0}{n_x},}&{喷口之外}\\ {k{u_0}{n_x},}&{喷口处} \end{array}} \right. $ |
2) 自由液面z=0处,
3) 无穷远方处,φ→0
| $ {\varphi _{xx}} - 2{\varphi _x}/\Delta x = - \frac{8}{{{u_0}}}\left( {2h\left( {{x_T} - {y_T}} \right)/\Delta x + \frac{{2h}}{{2x}}\left( {{x_T} - y} \right)} \right) $ | (11) |
式中:n=(nx, ny, nz)是船体表面上的外法向量;k是速度比;在方艉条件中,h是方艉边缘的高度;xT和yT分别是方艉纵向和横向坐标;Δx是方艉后方自由液面的一小段距离,其值可取为纵向面元长度的一半。
2.2 粘性阻力求解方法船体摩擦阻力部分采用1957ITTC摩擦阻力系数公式换算得到摩擦阻力:
| $ {R_f} = \frac{1}{2}\rho u_0^2S\left( {\Delta {C_f} + \frac{{0.075}}{{{{\left( {\lg {R_{\rm{e}}} - 2} \right)}^2}}}} \right) $ | (12) |
式中:Re=u0Lwl/ν,u0为船舶航速;Lwl为水线长;ν为水的运动粘度;S为船体湿表面积。粗糙度补贴系数ΔCf=0.4×10-3。
船体粘压阻力采用巴普米尔近似公式得[18]:
| $ {R_{{\rm{pv}}}} = 0.045\rho u_0^2{A_{\rm{m}}}{\left( {{A_{\rm{m}}}/2{L_r}} \right)^{1/4}} $ | (13) |
式中:Am为船舯横剖面面积;Lr为船体去流段长度,应满足Lr≥4.08
控制体进流面边界层速度、压力通过边界层理论进行计算。边界层理论速度分布公式为:
| $ u = \left\{ {\begin{array}{*{20}{l}} {{u_0}{{\left( {\frac{y}{\delta }} \right)}^{1/n}},\quad y \le \delta }\\ {{u_0},\quad y > \delta } \end{array}} \right. $ | (14) |
式中:y为距船物面的垂直距离; u为该处的速度;u0为船舶航速;指数n在模型尺度计算时取7,实船计算取9[12];δ为边界层厚度与进流面相同纵向位置的船体边界层厚度,可采用平板流动边界层公式δ=0.37x(u0x/υ)-1/5计算。
喷水推进控制体进流横截面一般采用半椭圆形表示:
| $ {(x/(W/2))^2} + {\left( {y/{Y_0}} \right)^2} = 1 $ | (15) |
式中:W为进流面宽度;Y0为进流面有效进流厚度;Y0的具体计算式见文献[19]。
边界层影响系数α的计算公式:
| $ \alpha = \int\limits_{{A_1}} {{u^2}{\rm{d}}A} /\left( {{u_0}\int\limits_{{A_1}} {u{\rm{d}}A} } \right) $ | (16) |
当Y0和δ的关系确定之后,即可计算进流面平均速度u1。对于船模,当Y0≤δ时,
| $ {\bar u_1} = \left\{ {\begin{array}{*{20}{c}} {\frac{{4{u_0}}}{{\rm{ \mathsf{ π} }}}{{\left( {\frac{{{Y_0}}}{\delta }} \right)}^{1/7}}\int_0^1 {{t^{1/7}}} {{\left( {1 - {t^2}} \right)}^{1/2}}{\rm{d}}t,\quad {Y_0} \le \delta }\\ {\frac{{4{u_0}}}{{\rm{ \mathsf{ π} }}}\left[ {{{\left( {\frac{{{Y_0}}}{\delta }} \right)}^{1/7}}\int_0^{\frac{\delta }{{{Y_0}}}} {{t^{1/7}}} {{\left( {1 - {t^2}} \right)}^{1/2}}{\rm{d}}t + } \right.}\\ {\left. {\int_{\frac{\delta }{{{V_0}}}}^1 {{{\left( {1 - {t^2}} \right)}^{1/2}}} {\rm{d}}t} \right],\quad {Y_0} > \delta } \end{array}} \right. $ | (17) |
进流面平均压力由p1=pdynamic+pstatic确定,其中pdynamic为平均动压,pstatic为平均静压。
3 三体船喷水推进推力数值计算 3.1 三体船模型修改和阻力修正本文以某型方艉喷水推进三体船船模为研究对象(图 4),开展本文喷水推进推力数值计算方法研究。三体船模型在船舶主体艉部安装三套喷水推进装置。三体船船模型长4.0 m,型宽0.87 m,吃水0.12 m, 排水量64.8 kg。

|
Download:
|
| 图 4 带喷水推进装置三体船物理模型 Fig. 4 Ship model of trimaran with waterjet devices | |
采用边界元法计算面元影响系数过程中,为避免由三体船流道及喷口物面与自由面相互穿透引起的数值异常,在不修改喷水推进流道物理模型的情况下,对三体船主体进行适当加长处理,以使兴波数值计算正常,同时还需要对加长船体所增加的阻力数值采用适当方法进行修正。
修正后的总阻力为:
| $ {R_t} = R_t^\prime + \Delta {R_t} $ | (18) |
式中:R′t为加长后三体船总阻力,ΔRt=ΔRf+ΔRpv+ΔRw为总阻力修正值。
根据阻力的组成成分分别对加长处理后三体船的摩擦阻力、粘压阻力和兴波阻力进行修正:
1) 摩擦阻力修正ΔRf=Rf-R′f。采用1957ITTC摩擦阻力公式对加长前后三体船摩擦阻力进行修正:
| $ \Delta {R_f} = 0.5\rho u_0^2\left( {S{C_f} - {S^\prime }C_f^\prime } \right) $ | (19) |
式中:S和Cf分别为未加长三体船模型的湿表面积和摩擦阻力系数;S′和C′f分别为加长三体船模型的湿表面积和摩擦阻力系数。
2) 粘压阻力修正ΔRpv=Rpv-R′pv。采用粘压阻力近似公式得到加长前后三体船粘压阻力修正值:
| $ \Delta {R_{pv}} = 0.045\rho u_0^2{A_m}\left[ {{{\left( {{A_m}/2L_r^\prime } \right)}^{1/4}} - {{\left( {{A_m}/2{L_r}} \right)}^{1/4}}} \right] $ | (20) |
式中:Lr和L′r为三体船模型加长前后的去流段长度。
3) 兴波阻力修正ΔRw=Rw-R′w。根据波浪能量理论,单位波长的船体兴波波能等于兴波阻力在2倍波长上所做的功,可以得到Fr与船舶兴波阻力系数关系为:
| $ {C_w} \propto \left( {A + B\cos \frac{{2{\rm{ \mathsf{ π} }}mL}}{\lambda }} \right)F{r^4} $ | (21) |
式中:A、B和m为常数,λ为兴波波长。在船体修正加长占船长比例较小时,假设加长前后船体兴波变化较小,则
为研究合适的主船体加长长度及验证阻力修正方法的适用性,选用初始模型不带喷水推进流道的三体船裸船体模型,对主船体以艉封板为横剖面纵向向后分别延长1.25%Lpp、2.50%Lpp和3.75%Lpp,计算3个方案三体船在Fr为0.30~0.60下的总阻力。
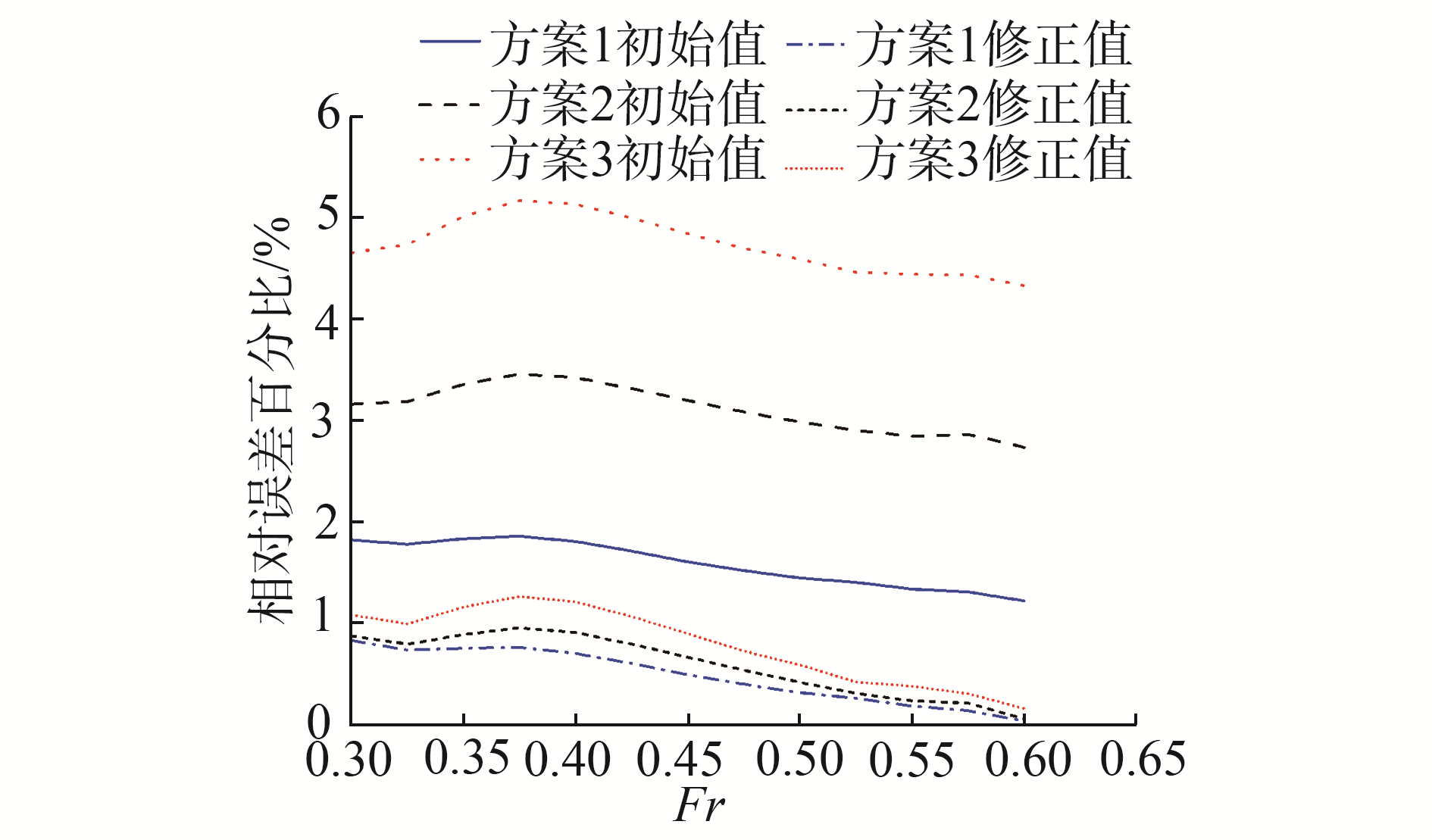
总阻力修正前后与初始裸船体阻力的相对误差如图 5所示。修正后总阻力的相对误差随Fr的提高而变小,3种方案的误差结果均较小,在1%左右,该结果表明本文采用的阻力修正方法能够有效对部分加长的船体总阻力进行修正。由于方案1的船体增加长度过小,船体艉封板与喷水推进喷口仍有部分穿透无法进行数值计算, 最终船体的加长方案选择方案2主船体增长2.5% Lpp,并采用上述修正方法对总阻力修正。
|
Download:
|
| 图 5 各加长方案阻力相对误差分布 Fig. 5 The relative error of each lengthening scheme | |
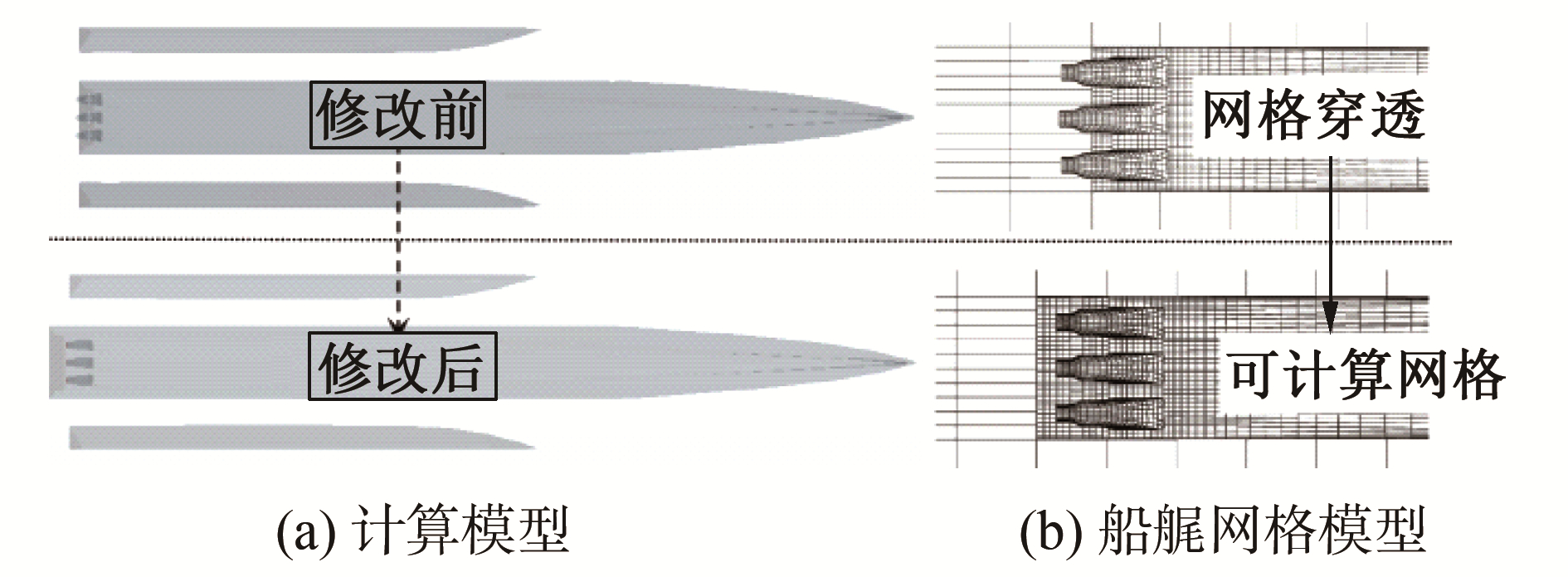
图 6为带喷水推进流道三体船加长前后的计算模型和网格对比。由于船体对称性,对一半船体和自由液面进行网格划分,修改后的船体表面共划分1 150个面元并在船艉流道处进行加密处理,自由液面共划分1 434个面元(图 7),共计算Fr为0.30~0.60航速范围内均布的13个工况。
|
Download:
|
| 图 6 计算模型和船艉网格修正前后对比 Fig. 6 Geometry and mesh of the original and modified model in wave-making resistance calculation | |

|
Download:
|
| 图 7 三体船修改模型自由面网格和船体湿表面网格 Fig. 7 Mesh of free surface and wetted hull | |
粘流CFD对比研究中三体船模型为带有喷水推进流道、转子、定子和喷口的完整模型(图 4),其中转子为4叶片,定子为5叶片。
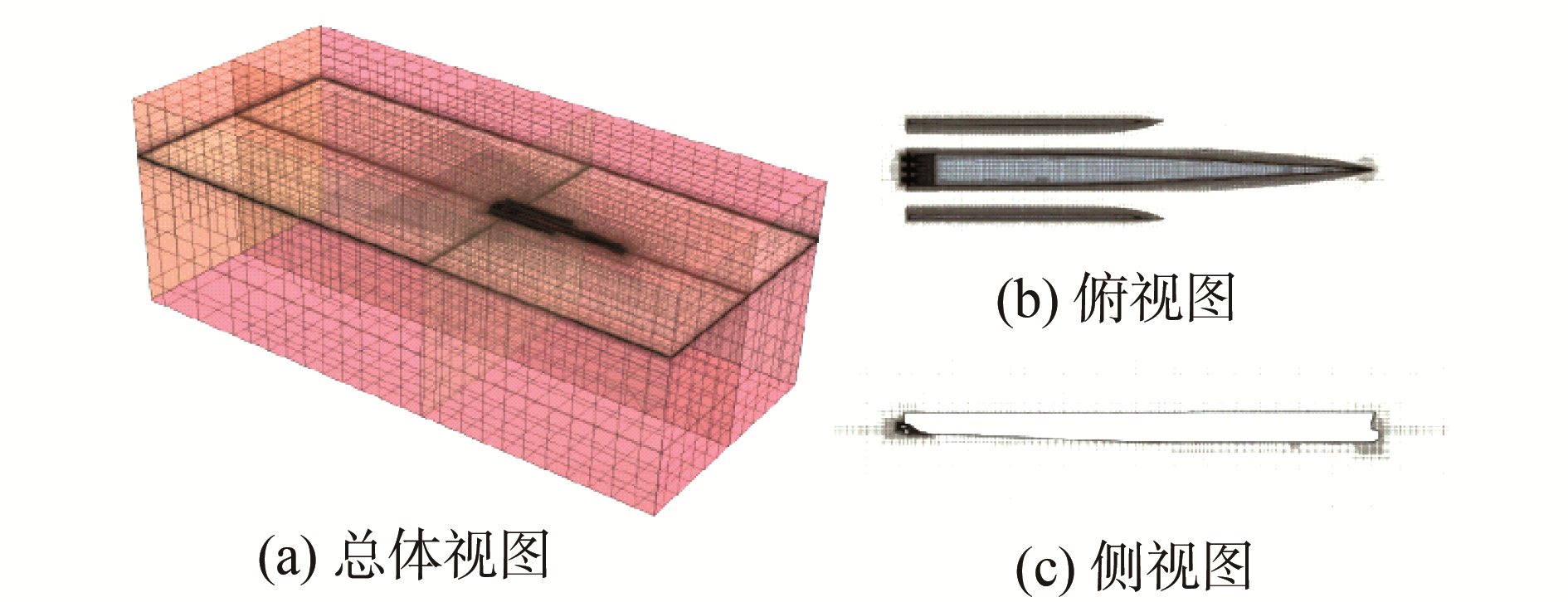
船长为Lpp, 计算域入口距船艏1Lpp,出口距船艉2.5Lpp,侧边界距船中1Lpp,上边界距船中0.5Lpp,下边界距船中1.5Lpp。船体边界层网格厚度为2 cm共8层,增长因子1.414,船体表面网格Y+值均小于100。体网格采用棱柱层和切割体网格形成的混合网格,如图 8所示,网格划分方式和密度经过相关网格无关性研究,得到最终的网格数量为320万。取Fr为0.30、0.45、0.60共计3个航速点开展船模自航数值模拟。
|
Download:
|
| 图 8 粘流CFD对比模型网格划分图 Fig. 8 Mesh of the RANS CFD comparison model | |
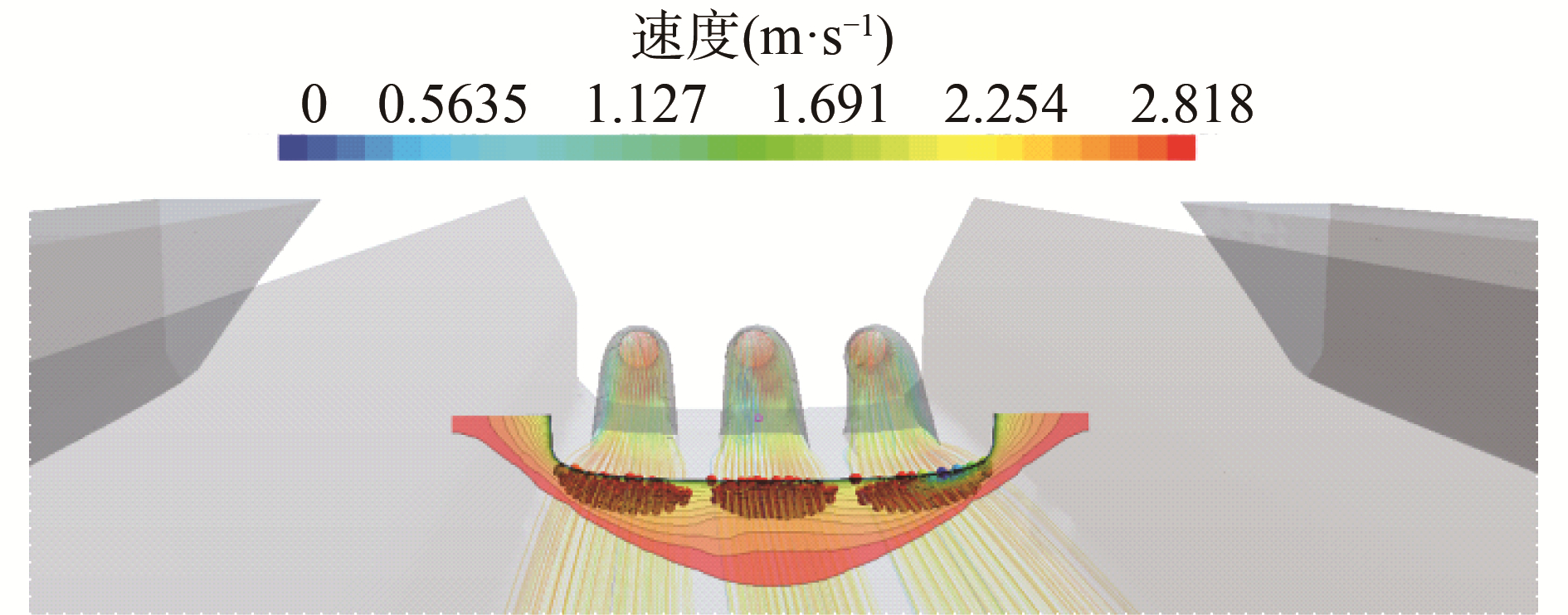
图 9为粘流CFD计算中三体船3个喷水推进装置控制体进流面处船体边界层分布、进流面范围和控制体流线分布。船体边界层厚度在船底部中间处和船体两侧达到最大,在船体两侧舭部最小。进流面的范围和船体表面曲率相关,喷水推进中间流道因处于船平底处使得进流面呈常规半椭圆形状,左右两侧的流道因靠近船舭部曲面曲率变化较大处,进流面分布呈倾斜的半椭圆形状。
|
Download:
|
| 图 9 粘流CFD计算控制体进流面(Fr=0.45) Fig. 9 The capture area in RANS CFD model (Fr=0.45) | |
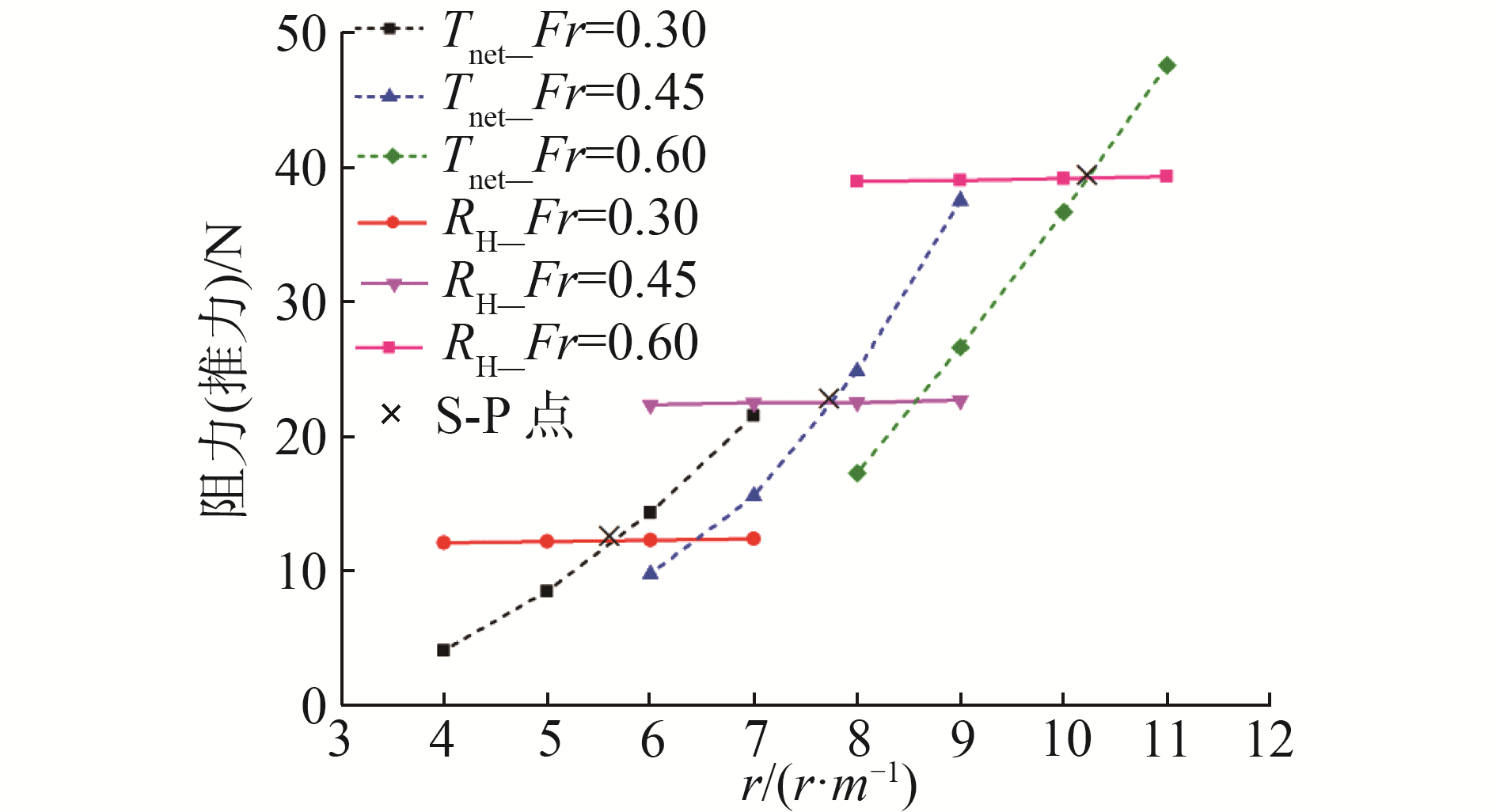
将本文采用的紊流边界层进流面范围计算结果与粘流CFD计算结果对比(图 10)。粘流结果显示,进流面宽度W和高度Y0均随航速增加而减小,本文计算进流面高度变化趋势与粘流结果相似,进流面高度Y0较粘流结果大35%左右。进流面宽度W在Fr为0.60时两者大小接近相等。图 11为粘流CFD计算的3个航速下船模Tnet(r)和RH(r)曲线,得到对应船模自航点(S-P点)。采用本文迭代收敛的喷速比与粘流CFD计算的喷速比随Fr变化对比如图 12所示,k在Fr为0.30~0.60变化不大,整体呈下降趋势,计算值均布在1.6左右。Fr为0.30、0.45、0.60 3个航速点k值分别为:1.673、1.563和1.556,与粘流结果计算相比两者喷速比k差值百分比约2%。

|
Download:
|
| 图 10 不同航速下流道进流面范围及进流速度比 Fig. 10 The capture area and inlet velocity ratio for different speeds | |
|
Download:
|
| 图 11 喷水推进三体船粘流CFD自航点获取曲线 Fig. 11 Self-propulsion curves and points in RANS CFD | |
|
Download:
|
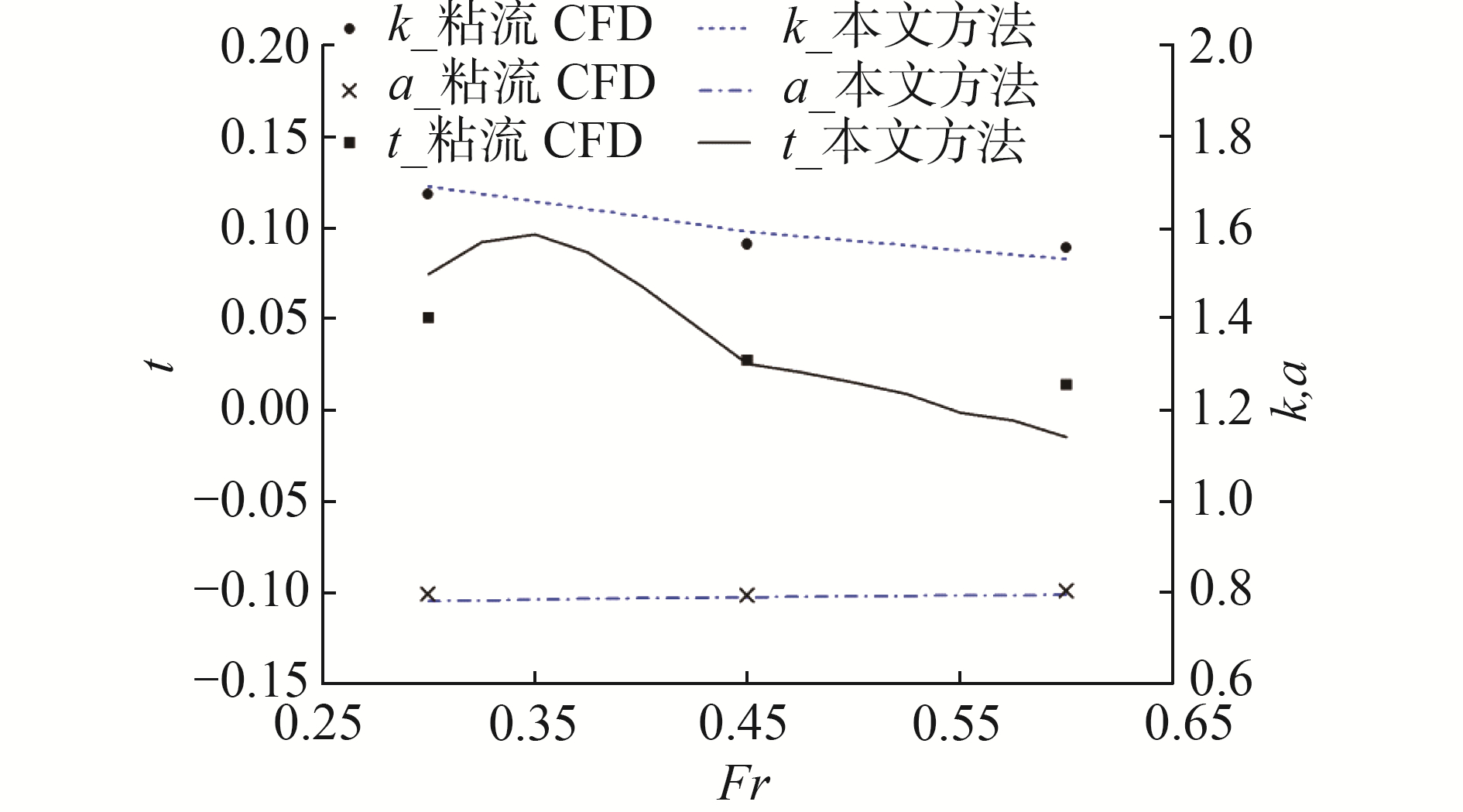
| 图 12 边界层影响系数、喷速比和推力减额分数分布 Fig. 12 Comparison of influence coefficient α, velocity ratio k and thrust deduction fraction t | |
进流面速度u/u0分布决定了边界层影响系数α大小(本文α取3个流道的均值)。在Fr为0.30~0.60,本文方法计算的α为0.782~0.795,并随Fr逐渐递增(图 12),与粘流方法的α比较最大误差为2%。
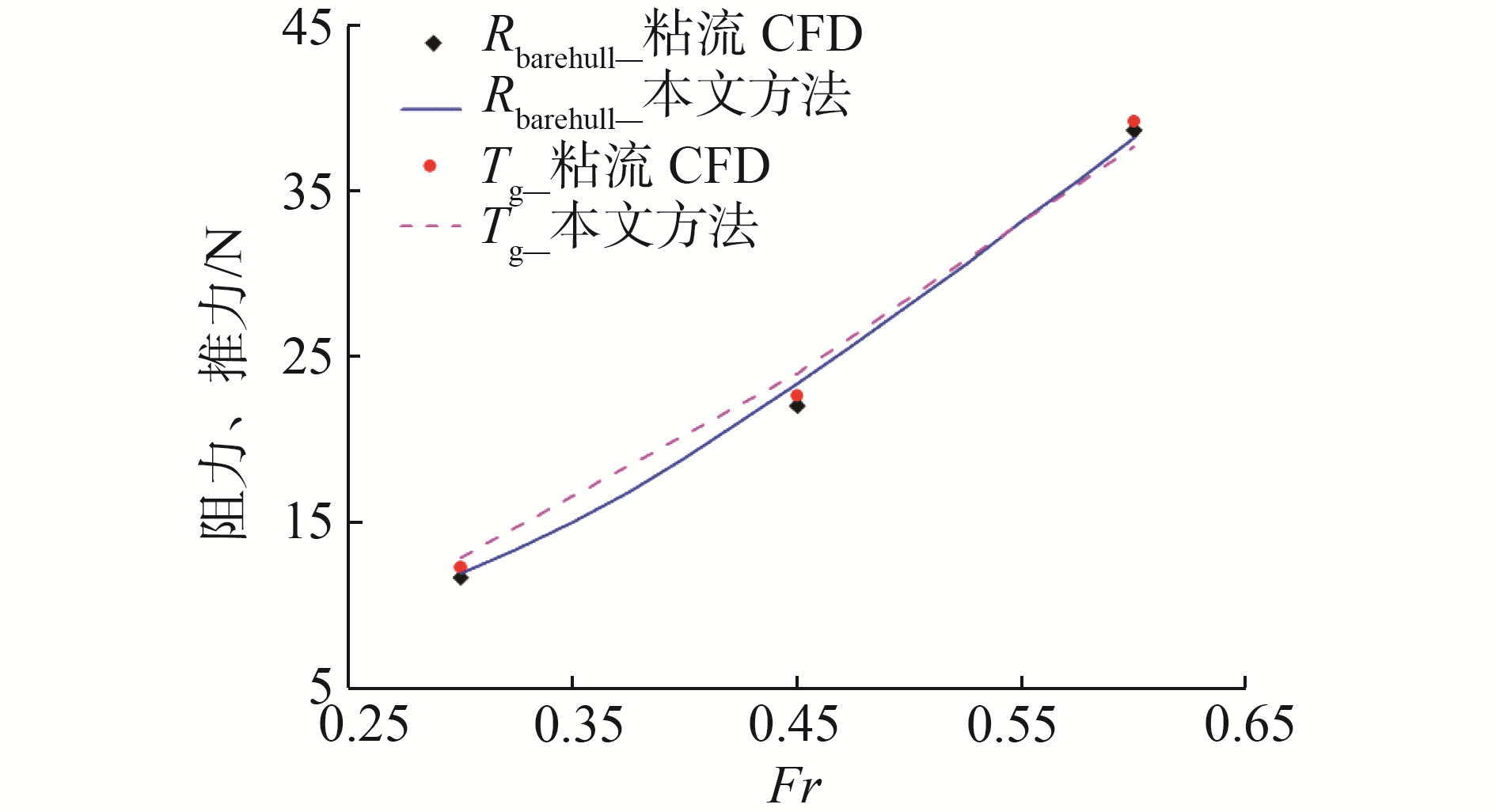
三体船喷水推进推力和裸船阻力随Fr分布如图 13所示。计算的裸船阻力和喷水推进推力在Fr < 0.45时大于粘流结果,在Fr=0.60时小于粘流计算结果。两者裸船阻力数值计算结果总体差距小于3%,推力数值差值百分比小于5%。通过式
|
Download:
|
| 图 13 三体船阻力和喷水推进推力 Fig. 13 Barehull resistance and waterjet thrust | |
| $ t = 1 - \frac{{{R_{{\rm{barefull }}}}}}{{{T_g}}} = 1 - \frac{{{R_{{\rm{barehull }}}}}}{{Nk\rho u_0^2{A_5}(k - \alpha )}} $ | (22) |
式(22)通过计算船模喷水推进系统推力减额(图 12)。在0.35<Fr < 0.60范围内推力减额逐渐减小,在Fr=0.60时出现负推力减额分数为-0.02。
4 结论1) 船体加长2.5%Lpp时,该修正方法能够有效预报未加长船体总阻力。
2) 喷水推进流道的获流面采用半椭圆形能够有效预报获流面的物理参数。在Fr为0.3~0.6,本文方法预报的三体船裸船阻力和喷水推进推力与粘流方法的相对误差分别小于3%和5%,该方法能够快速有效预报三体船喷水推进推力和减额等关键性能。
本文喷水推进推力性能计算的预报方法针对三体船开展了研究,后续将拓展至更多船型进行方法适用性及其应用研究。
| [1] |
VAN TERWISGA T. The effect of waterjet-hull interaction on thrust and propulsive efficiency[C]//Proceedings of 1st International Conference on Fast Sea Transportation Conference. Trondheim, Norway, 1991: 1149-1167.
(  0) 0)
|
| [2] |
ALEXANDER K V, COOP H, VAN TERWISGA T. Waterjet-hull interaction:recent experimental results[J]. SNAME transactions, 1993, 102: 275-335. (  0) 0)
|
| [3] |
WATSON S J P. The use of CFD in sensitivity studies of inlet design[C]//RINA International Conference on Waterjet Propulsion, Latest Developments. Amsterdam, 1998. Paper No.8.
(  0) 0)
|
| [4] |
KIMBALL R W. Experimental investigations and numerical modeling of a mixed flow marine waterjet[D]. Cambridge: Massachusetts Institute of Technology, 2001.
(  0) 0)
|
| [5] |
TAKAI T. Simulation based design for high speed sea lift with waterjets by high fidelity urans approach[D]. Iowa City: University of Iowa, 2010.
(  0) 0)
|
| [6] |
ESLAMDOOST A. The hydrodynamics of waterjet/hull interaction[D]. Gothenburg: Chalmers University of Technology, 2014.
(  0) 0)
|
| [7] |
刘承江, 王永生, 张志宏, 等. 喷水推进器推力的CFD计算方法研究[J]. 计算力学学报, 2008, 25(6): 927-931. LIU Chengjiang, WANG Yongsheng, ZHANG Zhihong, et al. Research on computational methods of waterjet thrust using CFD[J]. Chinese journal of computational mechanics, 2008, 25(6): 927-931. (  0) 0)
|
| [8] |
刘承江, 王永生, 古成中. 船-泵相互作用对喷水推进器推进性能的影响[J]. 上海交通大学学报, 2016, 50(1): 91-97. LIU Chengjiang, WANG Yongsheng, GU Chengzhong. Influence of hull-waterjet interaction on propulsion performances of waterjet[J]. Journal of Shanghai JiaoTong University, 2016, 50(1): 91-97. DOI:10.3969/J.ISSN.1671-9964.2016.01.016 (  0) 0)
|
| [9] |
丁江明, 王永生. 喷水推进器进水流道参数化设计方法[J]. 哈尔滨工程大学学报, 2011, 32(4): 423-427. DING Jiangming, WANG YongSheng. Research on the parametric design of an inlet duct found in a marine waterjet[J]. Journal of Harbin Engineering University, 2011, 32(4): 423-427. DOI:10.3969/j.issn.1006-7043.2011.04.005 (  0) 0)
|
| [10] |
龚杰, 郭春雨, 张海鹏. 喷水推进船模旋转叶轮流场的数值分析[J]. 上海交通大学学报, 2017, 51(3): 326-331. GONG Jie, GUO Chunyu, ZHANG Haipeng. Numerical analysis of impeller flow field of waterjet self-propelled ship model[J]. Journal of Shanghai Jiao Tong University, 2017, 51(3): 326-331. (  0) 0)
|
| [11] |
胡健, 黄胜, 马骋, 等. 影响喷水推进器水动力性能的若干因素[J]. 哈尔滨工程大学学报, 2008, 29(1): 11-15, 44. HU Jian, HUANG Sheng, MA Cheng, et al. Factors influencing the hydrodynamics of waterjet propellers[J]. Journal of Harbin Engineering University, 2008, 29(1): 11-15, 44. DOI:10.3969/j.issn.1006-7043.2008.01.003 (  0) 0)
|
| [12] |
ITTC. The specialist committee on validation of waterjet test procedures[C]//Proceedings of the 23rd ITTC. Venice, Italy, 2002: 387-415.
(  0) 0)
|
| [13] |
ITTC. The specialist committee on validation of waterjet test procedures: Final report and recommendations to the 24th ITTC. Proceedings of the 24th ITTC, Edinburgh, UK, 2005, VolumeⅡ, 471-508.
(  0) 0)
|
| [14] |
ESLAMDOOST A, LARSSON L, BENSOW R. Net and gross thrust in waterjet propulsion[J]. Journal of ship research, 2016, 60(2): 1-14. (  0) 0)
|
| [15] |
ZHANG Lei, ZHANG Jianing, ZHANG haojian, et al. Numerical research on the added mass of trimaran from transition state to semi-planing state based on the boundary element method[C]//Proceedings of the ISOPE2017, San Francisco, USA, 2017;984-989.
(  0) 0)
|
| [16] |
RONALD W., YEUNG, LU Wang. Radiation and exciting forces of axisymmetric structures with a moonpool in waves[J]. Journal of marine science and application, 2018(3): 297-311. (  0) 0)
|
| [17] |
MUHAMMAD Z R, TEMARE P, TAN M. Hydrodynamic coefficients for a 3-d uniform flexible barge using weakly compressible smoothed particle hydrodynamics[J]. Journal of marine science and application, 2018(3): 330-340. (  0) 0)
|
| [18] |
侯远杭, 黄胜, 梁霄. PSO训练的弹性RBFNN在船型优化中的应用研究[J]. 哈尔滨工程大学学报, 2017, 38(2): 175-180. HOU Yuanhang, HUANG Sheng, LIANG Xiao. Ship hull optimization based on PSO training FRBF neural network[J]. Journal of Harbin Engineering University, 2017, 38(2): 175-180. (  0) 0)
|
| [19] |
刘志林, 于瑞亭, 等. 喷水推进船舶边界层影响系数的计算方法研究[J]. 船舶力学, 2012, 16(10): 1115-1121. LIU Zhilin, YU Ruiting, et al. Study of a method for calculating boundary layer influence coefficients of ship and boat propelled by water-jet[J]. Journal of ship mechanics, 2012, 16(10): 1115-1121. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


