2. 中船动力研究院有限公司 上海 200120
2. China Shipbuilding Power Engineering Institute Co., Ltd., Shanghai 200120, China
当前降低内燃机氮氧化物排放的措施主要包括前处理,如燃油乳化、进气加湿等[1-2];缸内净化,如低温燃烧、喷射优化、废气再循环、米勒循环等[3-5];后处理,如SCR、NOx吸附等[6]。使用建模仿真的分析方法为探索降低氮氧化物排放提供了有效的途径,如柴油机的试验[7],同时生产设计需求又促使排放预测模型及求解方法等基础内容的发展。Zeldovich[8]提出一氧化氮的生成机理并得到了广泛的认可。Lavoie等[9]认为在内燃机燃烧计算中OH及N2O对NO生成的影响也需要考虑,并一直作为预测内燃机中NO生成的机理。NO生成预测的难点是燃烧产物化学反应平衡的计算。在化学平衡求解方面,Gordon等[10]及Reynolds[11]推导化学平衡计算程序和STANJAN程序。Pope[12]提出的吉布斯函数连续方法及CEQ计算程序以解决部分情况下STANJAN和NASA程序不收敛的问题。在柴油机燃烧产物计算方面,Rakopoulos等[13]使用Newton-Raphson(N-R)迭代法计算了基于11种物质架构模型的柴油机燃烧产物并给出了计算程序。周松等[14-15]提出了23种物质架构模型计算内燃机燃烧产物并进行了化学平衡计算分析。Anetor等[16]对Zeldovich机理及求解方法进行了的数学分析。这些计算模型和计算方法在全世界范围内产生了极大的影响并促进了内燃机优化及排放优化的研究,并使用多种技巧解决函数最优值及矩阵奇异的问题[17]。但是计算过程十分复杂,计算精度不高。当前,人工智能的研究热潮促进了优化算法的发展。粒子群优化算法结构简单、容易实现,并且可以避免求解过程中矩阵奇异的优势。本文使用文献[13-15]使用的12种柴油机燃烧产物架构预测柴油机内NO的生成过程。为了使该问题能够使用智能优化算法求解,进行了3方面的修改:1)求解时将燃烧产物化学平衡方程组的求解问题转换为无约束最小化的优化问题;2)根据燃烧产物化学平衡的特征,在基本粒子群算法的基础上增加了搜索过程中的扰动以增加全局搜索能力;3)粒子初值由随机自由分布修改为在给定初值附近分布以增加搜索的针对性。通过3个方面的修改,扰动粒子群算法在求解内燃机NO生成模型中表现出良好的性能。
1 STANJAN算法STANJAN算法使用最小化Gibbs自由焓的方法计算物质化学反应平衡时的浓度。在STANJAN算法中假设系统包含s种物质,所有物质由a种元素构成。一个物质j分子中具有原子i的个数为nij,物质j在相m中的摩尔分数为xj,相m中的所有物质的物质的量为Nm,则根据原子守恒和摩尔分数的定义有:
| $\sum\limits_{j = 1}^s {{n_{ij}}} {\bar N_j}{x_j} = {P_i}, \quad i = 1, 2, \cdots , a $ | (1) |
| $\sum\limits_{j = 1}^s {{x_j}} = 1 $ | (2) |
式中:j为m相中物, m=1, 2, …, p。
建立系统的Gibbs总能量,使用拉格朗日乘子法:
| ${x_j} = \exp \left( { - {{\tilde g}_j} + \sum\limits_{i = 1}^s {{\lambda _i}} {n_{ij}}} \right), \quad j = 1, 2, \cdots , s $ | (3) |
式中:${\tilde g_j}$为纯物质j的比Gibbs自由焓与RT的比值;λi为拉格朗日乘子,也称为元素势(element potential)。式(1)~(3)构成了使用最小化Gibbs自由焓方法时需要求解的方程组。该方程组为关于xj、λi和Nm的s+a+p个方程。根据式(3)可以将s个xj使用a个λi表示,于是方程组中的方程减少为关于λi和Nm的a+p个方程。再通过式(1)和式(2)的对偶问题及其求解策略并针对亏秩矩阵、无下降方向等问题的“矩阵调节”、“峰顶插值”和“阻尼防抖”等多种技巧,方程组可解。
2 扰动粒子群算法 2.1 优化目标考虑具有多个输入变量X和多个输出变量Y的方程组,其一般形式均可表示为:
| $F(X) = Y $ | (4) |
根据式(4)很容易构造出式(5),
| $\bar F(X) = F(X) - Y $ | (5) |
并且容易得到:
结论1 式(4)有解的充分必要条件是式(5)的函数值等于零。
将式(5)取二范数,可得到式(6)所示的关系。
| $\tilde F = {\left\| {\bar F} \right\|_2} = \sqrt {{{\left( {{{\bar f}_1}} \right)}^2} + l + {{\left( {{{\bar f}_n}} \right)}^2}} \ge 0 $ | (6) |
结论2 式(5)等于零的充分必要条件是函数(6)取到最小值。
根据上述结论,可得到式(7)所示关系,
| $\min \tilde F \Leftrightarrow \bar F(X) = 0 \Leftrightarrow F(X) = Y $ | (7) |
即可得到推论:式(4)有解的充分必要条件是式(6)取到最小值。
根据式(7)的推理,可以容易的将求解式(4)的问题转化为函数最小化的问题。
2.2 粒子群算法粒子群算法根据模拟鸟群觅食的过程提出, 算法以其简洁的计算方法和较好的收敛效果得到了广泛的应用和认可。算法的基本过程为:1)初始化鸟群位置和飞行方向;2)根据距离食物最近的鸟的位置和自身距离食物最近时的位置更新飞行方向;3)更新距离食物最近的鸟的位置和自身距离食物最近时的位置。重复迭代过程2)和3)即可求出最优解。粒子飞行速度与位置的更新方程为:
| $\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_{k + 1}} = \mathit{\boldsymbol{\omega }}{\mathit{\boldsymbol{v}}_k} + {\varphi _1}{r_1}\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_p}} \right) + {\varphi _2}{r_2}\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_g}} \right)}\\ {{\mathit{\boldsymbol{x}}_{k + 1}} = {\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (8) |
式中:v代表粒子速度;x代表粒子位置;xp代表粒子经历过的最好位置;xg代表所有粒子中的最好位置;ω、φ1、φ2为调整因子。
2.3 扰动粒子群算法根据内燃机燃烧的实际问题,燃油在完全燃烧或者不完全燃烧时氮气、水蒸气、二氧化碳、一氧化碳等物质的摩尔分数较大,可达到10-1的量级;其他物质的摩尔分数很小,从10-3到10-10, 甚至更低。在仅考虑大摩尔分数的燃烧产物的情况下,计算燃油燃烧得到的燃烧产物摩尔分数与考虑多种物质化学平衡得到的燃烧产物摩尔分数差距,数值上通常小于0.1。因此,可以认为其最优值在大物质0.1范围内。假设根据大物质的摩尔分数为x0*,粒子则在x0*范围内随机分布:
| ${x_0} = x_0^* + 0.2\left( {{N_{{\rm{rnd}}}} - 0.5} \right) $ | (9) |
式中:Nrnd为0~1的随机数。
为了增强局部搜索,在粒子往最优值移动的过程中,随机在任意分量上增加一个扰动,如式(10)所示。如果扰动更优则接受否则拒绝:
| ${x_i} = {x_i} + 2a\left( {{N_{{\rm{rnd}}}} - 0.5} \right){x_i} $ | (10) |
为了研究算法的性能,取柴油的分子式为C12H26,燃烧产物架构为12种物质架构,即H、O、N、H2、OH、CO、NO、O2、H2O、CO2、N2及Ar,分别计算了温度为2 200 K,压强为1 700 MPa,油气当量比为0.88和1.11时的燃烧产物平衡浓度,并与Newton-Raphson(N-R)下降法、STANJAN算法、基本PSO算法进行了对比。算例1、2在Matlab的结果如表 1和表 2所示。所有算法的停止条件均为:1)函数值达到目标精度10-10;2)迭代过程数值下降十分慢或者不再下降;3)达到最大迭代次数400次。满足其中一个条件,则停止。由于N-R迭代法一直作为一种较好的方法推荐用于求解非线性方程组,但是作者在计算中发现基本的N-R迭代在本算例中无法收敛。因此,采用了N-R下降法。STANJAN方法的值使用Colorado大学提供的计算化学平衡浓度的程序实现。
| 表 1 算例1中燃烧产物平衡时的摩尔分数 Table 1 The mole fractions of combustion products at chemical equilibrium in case 1 |
| 表 2 算例2中燃烧产物平衡时的摩尔分数 Table 2 The mole fractions of combustion products at chemical equilibrium in case 2 |
从表 1和表 2中可知,STANJAN算法和扰动PSO算法计算的结果较为接近,有效位的第1位的值完全一样。N-R下降法与这2个算法计算的结果在计算结果的数量级上基本一致,但是有效位的值基本不一致。差别最大的是基本粒子群算法计算的结果相差较大。从表 2中可知,扰动PSO算法与N-R下降法有9种物质在数量级上一致。扰动PSO算法与STANJAN算法有8种物质在数量级上一致。N-R下降法与STANJAN算法有6种物质在数量级上一致。基本粒子群算法的结果与扰动粒子群算法、N-R下降法及STANJAN算法在数量级上有比较大的不一致。
表 1和表 2的结果只能对各算法的性能进行模糊的评估。为了对算法的性能进行量化分析,使用2个指标对算法性能实施量化:1)根据式(6)计算各算法的结果达到的优化目标值;2)根据多维空间中点的距离的概念量化各算法的结果在空间中的分布情况。考虑到燃烧产物中物质的摩尔分数的量级相差比较大,由于大数吃小数的关系,多维空间中的欧式距离修改为:
| $\rho (a, b) = \sqrt {{{\left( {\ln {a_1}/{b_1}} \right)}^2} + \cdots + {{\left( {\ln {a_n}/{b_n}} \right)}^2}} $ | (11) |
根据式(6)和(11)得出各算法的性能值如表 3和表 4所示。从表 3中可知,扰动PSO给出的计算结果的目标优化值最低,达到0。其次为基本粒子群算法,最后分别为N-R下降法和STANJAN算法。从计算结果的最终分布位置可知,扰动PSO算法的计算结果与STANJAN算法的计算结果距离最近,其值达到0.04。N-R下降法的计算结果到扰动PSO算法的计算结果和STANJAN算法的计算结果的距离基本一样,分别为1.83和1.84。这说明这3个算法的计算结果在空间上可近似看成短底等腰三角形分布。基本粒子群算法的计算结果与其他算法的计算结果都比较远,其值大于91.52,而其优化目标值却与N-R下降法和STANJAN算法相当。这说明基本粒子群算法陷入局部最优值。根据以上分析可知,表 1中扰动粒子群和STANJAN算法具有较好的性能,其计算结果具有较大的可信度。其次为N-R下降法。
| 表 3 算例1中算法性能对比 Table 3 The comparasion of algorithms in case 1 |
| 表 4 算例2中算法性能对比 Table 4 The comparasion of algorithms in case 2 |
根据表 4中的分析数据可知,扰动粒子群算法给出的计算结果达到的目标优化值最低,达到0.00。其次为基本粒子群算法,最后分别为STANJAN算法和N-R下降法。从计算结果的最终分布位置可知,扰动PSO算法的计算结果与N-R下降法的计算结果距离最近,其值达到2.09。扰动PSO算法的计算结果与STANJAN算法的计算结果距离稍远,其值为4.44。而N-R下降法的计算结果与STANJAN算法的计算结果距离为5.23。这说明这3个算法的计算结果在空间上可近似看成等边三角形分布。基本粒子群算法的计算结果与其他算法的计算结果都比较远,其值大于143.20,而其优化目标值却比N-R下降法和STANJAN算法小。这说明基本粒子群算法陷入局部最优值。根据以上分析可知,表 2中扰动粒子群和N-R下降法具有较好的性能,其计算结果具有较大的可信度。其次为STANJAN算法。
根据表 3和表 4中的数据分析结果可知,扰动PSO在这两次算例中均具有较好的表现;STANJAN算法和N-R下降法性能相当;基本粒子群算法具有较好的寻优能力但是极易陷入局部最优值。
图 1中给出的是算例1及算例2中各算法的迭代收敛过程。从中可以观察到,基本粒子群算法和N-R下降法停止时均未达到最大迭代次数,也未达到预设精度,这说明这2个算法停止时是由于下降速度太低而停止。基本粒子群算法中的所有粒子均陷入局部最优值无法逃离出来而N-R下降法则是由于下降路线陷入平坦区域无法继续下降。扰动粒子群算法的停止原因为迭代达到预设精度。基本粒子群算法和扰动粒子群算法的迭代次数明显高于N-R下降法,这主要是由算法的特性决定。粒子群算法迭代搜索下降路线而N-R下降法根据方程泰勒展开式确定下降步长。另外,N-R下降法中的迭代次数为接受的下降步长次数,未包括拒绝的下降步长迭代次数。

|
Download:
|
| 图 1 Newton-Raphson(N-R)下降法、基本粒子群算法、扰动粒子群算法的收敛过程 Fig. 1 The convergence of Newton-Raphson (N-R) downhill method, basic PSO, and perturbed PSO | |
为了验证本方法的有效性,使用本文提出的方法预测了一台大功率船用二冲程柴油机在一个工作循环内NO的生成过程。并将此预测结果与使用AVL Boost软件的计算值进行了对比,结果如图 2所示。从图 2中可以看出使用本文提出的方法与使用AVL Boost得到的计算值及变化趋势基本一致。大功率船用二冲程柴油机的建模方法及优化方法可参考文献[18-19]。在计算过程中,Boost软件中得出的NO生成速率的峰值为0.122 3 kg/s,本文得出的峰值为0.113 7 kg/s,约低于Boost计算值的7.03%。Boost软件中得出的NO生成量为2.268 6 kg,本文得出的峰值为2.231 0 kg/s,约低于Boost计算值的1.65%。Boost计算的NO排放浓度为415.5 mg/kg,本文计算的NO排放浓度为408.6 mg/kg,约低于Boost计算值的1.65%。
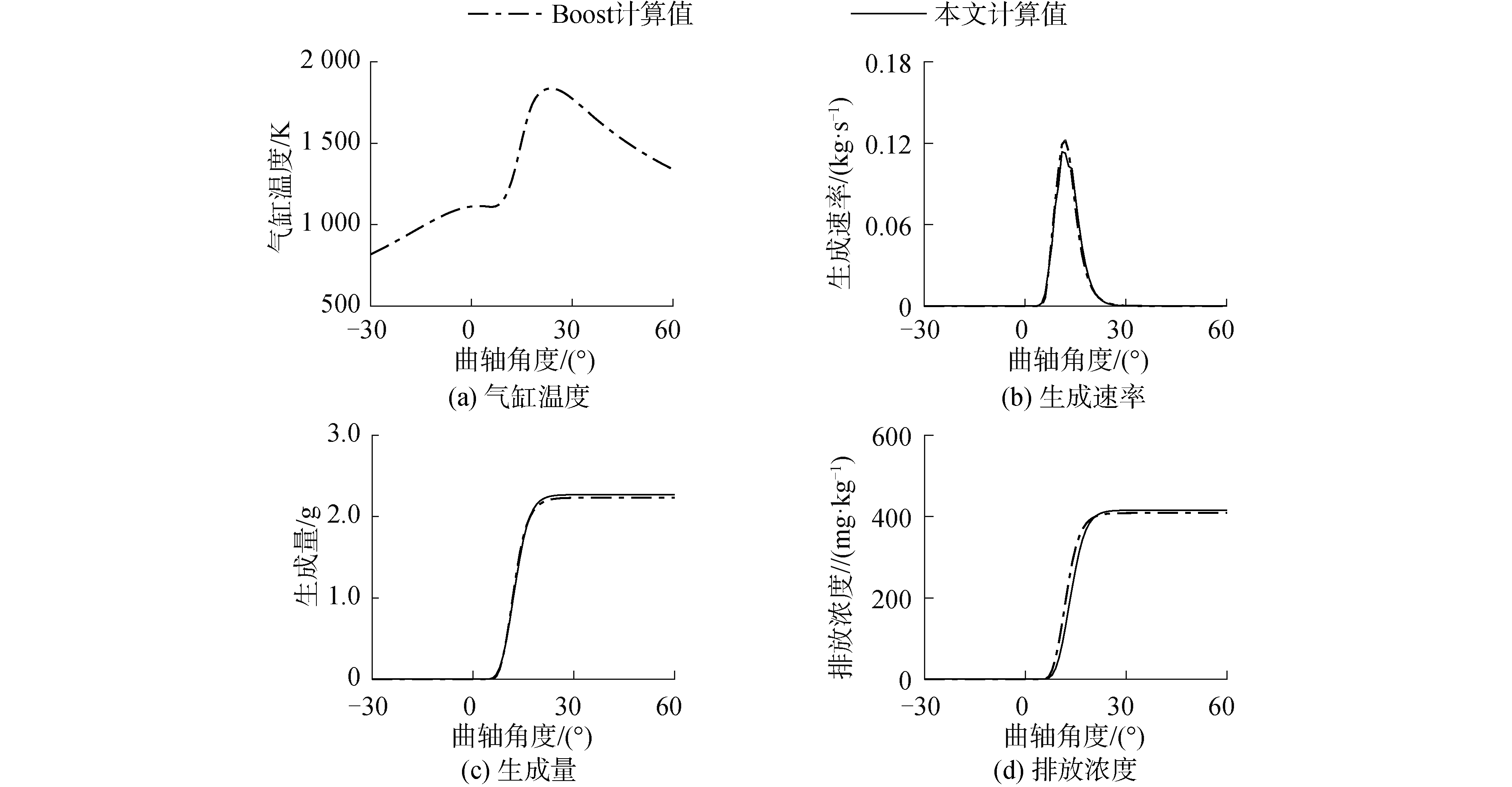
|
Download:
|
| 图 2 缸内一氧化氮生成预测 Fig. 2 The prediction of nitric oxide in cylinder | |
1) 扰动粒子群算法可以准确的计算出燃烧产物的平衡浓度。扰动粒子群算法实现简单,与迭代法相比具有更强的寻优能力,与基本粒子群算法相比具有更强的全局寻优能力,能够有效的避免陷入局部最优值。
2) STANJAN算法寻优过程采用的是最速下降法和N-R迭代法,其寻优能力与N-R迭代法相当。STANJAN算法增加了许多保证算法收敛的技术,算法稳定性比单纯使用N-R迭代法要好。
3) 使用最小化Gibbs自由焓的方法和使用平衡常数法求解化学反应平衡浓度的结果基本一致。在燃烧反应中考虑的物质种类较多时,使用最小化Gibbs自由焓可以得到更小的方程组,求解过程相对平衡常数法更为简单。
| [1] |
WEI Mingrui, THANH SA N, TURKSON R F, et al. Water injection for higher engine performance and lower emissions[J]. Journal of the energy institute, 2017, 90(2): 285-299. DOI:10.1016/j.joei.2015.12.003 (  0) 0)
|
| [2] |
VELLAIYAN S, AMIRTHAGADESWARAN K S. The role of water-in-diesel emulsion and its additives on diesel engine performance and emission levels:a retrospective review[J]. Alexandria engineering journal, 2016, 55(3): 2463-2472. DOI:10.1016/j.aej.2016.07.021 (  0) 0)
|
| [3] |
THANGARAJA J, KANNAN C. Effect of exhaust gas recirculation on advanced diesel combustion and alternate fuels-a review[J]. Applied energy, 2016, 180: 169-184. DOI:10.1016/j.apenergy.2016.07.096 (  0) 0)
|
| [4] |
MOHAN B, YANG Wenming, CHOU S K. Fuel injection strategies for performance improvement and emissions reduction in compression ignition engines-a review[J]. Renewable and sustainable energy reviews, 2013, 28: 664-676. DOI:10.1016/j.rser.2013.08.051 (  0) 0)
|
| [5] |
AGARWAL A K, SINGH A P, MAURYA R K. Evolution, challenges and path forward for low temperature combustion engines[J]. Progress in energy and combustion science, 2017, 61: 1-56. DOI:10.1016/j.pecs.2017.02.001 (  0) 0)
|
| [6] |
GURUSAMY P, GANDHI U, MANGALANATHAN U, et al. Measurement of diesel exhaust fluid concentration in urea-SCR after-treatment system[J]. International journal of precision engineering and manufacturing, 2017, 18(8): 1085-1092. DOI:10.1007/s12541-017-0127-z (  0) 0)
|
| [7] |
牛晓晓, 王银燕, 王正祥, 等. 柴油机性能及排放预测高效试验设计应用研究[J]. 应用科技, 2018, 45(05): 95-101. NIU Xiaoxiao, WANG Yinyan, WANG Zhengxiang, et al. Application of high-efficiency experimental design method for predicting the performance and emission of diesel engine[J]. Applied science and technology, 2018, 45(05): 95-101. (  0) 0)
|
| [8] |
ZELDOVICH J. The oxidation of nitrogen in combustion and explosions[J]. Acta physicochim, 1946, 21(4): 577-628. (  0) 0)
|
| [9] |
LAVOIE G A, HEYWOOD J B, KECK J C. Experimental and theoretical study of nitric oxide formation in internal combustion engines[J]. Combustion science and technology, 1970, 1(4): 313-326. DOI:10.1080/00102206908952211 (  0) 0)
|
| [10] |
GORDON S, MCBRIDE B J. Computer program for calculation of complex chemical equilibrium compositions, rocket performance, incident and reflected shocks, and chapman-jouguet detonations[R]. Washington, D.C.: National Aeronautics and Space Administration, 1976.
(  0) 0)
|
| [11] |
REYNOLDS W C. The element potential method for chemical equilibrium analysis: implementation in the interactive program STANJAN[R]. California: Stanford University, Department of Mechanical Engineering, 1986.
(  0) 0)
|
| [12] |
POPE S B. Gibbs function continuation for the stable computation of chemical equilibrium[J]. Combustion and flame, 2004, 139(3): 222-226. DOI:10.1016/j.combustflame.2004.07.008 (  0) 0)
|
| [13] |
RAKOPOULOS C D, HOUNTALAS D T, TZANOS E I, et al. A fast algorithm for calculating the composition of diesel combustion products using 11 species chemical equilibrium scheme[J]. Advances in engineering software, 1994, 19(2): 109-119. DOI:10.1016/0965-9978(94)90064-7 (  0) 0)
|
| [14] |
周松, 马强, 李晓波. 内燃机一氧化氮生成机理及计算研究[J]. 哈尔滨工程大学学报, 1997, 18(4): 25-30. ZHOU Song, MA Qiang, LI Xiaobo. The study of formation mechanism and calculation of nitric oxide in internal combustion engine[J]. Journal of Harbin Engineering University, 1997, 18(4): 25-30. (  0) 0)
|
| [15] |
周松, 马强, 熊承刚. 内燃机燃烧产物平衡浓度及化学反应平衡常数的计算[J]. 哈尔滨工程大学学报, 1997, 18(5): 85-89. ZHOU Song, MA Qiang, XIONG Chengang. Calculation of equilibrium concentration of combustion products and equilibrium constant of chemical reactions in internal combustion engine[J]. Journal of Harbin Engineering University, 1997, 18(5): 85-89. (  0) 0)
|
| [16] |
ANETOR L, ODETUNDE C, OSAKUE E E. Computational analysis of the extended Zeldovich mechanism[J]. Arabian journal for science and engineering, 2014, 39(11): 8287-8305. DOI:10.1007/s13369-014-1398-7 (  0) 0)
|
| [17] |
ONUH EI, INAMBAO FL. An evaluation of neat biodiesel/diesel performance, emission pattern of NOx and CO in compression ignition engine[J]. International journal of global warming, 2018, 14: 21-39. (  0) 0)
|
| [18] |
TANG Yuanyuan, ZHANG Jundong, GAN Huibing, et al. Development of a real-time two-stroke marine diesel engine model with in-cylinder pressure prediction capability[J]. Applied energy, 2017, 194: 55-70. DOI:10.1016/j.apenergy.2017.03.015 (  0) 0)
|
| [19] |
唐元元, 张均东, 贾宝柱, 等. 气缸体对船舶柴油机模型精度的影响[J]. 哈尔滨工程大学学报, 2017, 38(12): 1836-1843. TANG Yuanyuan, ZHANG Jundong, JIA Baozhu, et al. The effect of cylinder body on the accuracy of marine diesel engine model[J]. Journal of Harbin Engineering University, 2017, 38(12): 1836-1843. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


