2. 北京交通大学 土木建筑工程学院, 北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
近年,我国的高速铁路建设取得了巨大的发展,为保证线路的平顺性和稳定性,高速铁路线路中桥梁所占的比例急剧增加,“以桥代路”的修建方式导致一条线路中可能存在长达几十公里的高架桥。这使得地震发生时列车在桥上运行的概率越来越大,一旦发生意外,后果不堪设想。因此,地震作用下车桥耦合振动问题受到越来越多的学者重视[1-5]。
研究地震作用下车桥耦合振动,尤其是长大桥梁在地震和列车作用下的动力问题,地震动的空间变异性是不可忽视的一个因素。它通常包含3个方面:行波效应、不相干效应和局部场地效应[6]。针对行波效应对车桥耦合系统地震响应的影响,Xia等[7]、Zhang等[8]、林玉森等[9]进行了研究;针对不相干效应,杜宪亭等[5]基于谱理论的无/有条件模拟技术,研究了其对地震作用下车桥耦合系统动力响应的影响。但是,局部场地效应方面,尤其是关于地形条件对耦合体系地震响应的影响的研究,却并不多见。乔宏等[10]依据粘弹性边界理论,建立了考虑局部地形条件的三维场地模型,研究了地震纵波(P波)和剪切波中的SH波垂直入射条件下地形对车桥耦合系统地震响应的影响。但是,其研究并未考虑SV波入射的情况,也没有考虑地震动斜入射的影响。当震源深度较浅时,地震波并不是垂直于土体地表入射的[11],并且地震动的斜入射引起的地面运动非一致变化会对场地的地震反应有较大影响[12]。因此,在研究地形条件对车桥耦合系统地震响应的影响时,考虑地震动的斜入射情况十分必要。
本文借助粘弹性边界,通过有限元建模,建立了考虑地震SV波入射角度的桥址处场地模型,通过在粘弹性边界上施加等效荷载来模拟地震波传播过程,从而获得作用于桥梁各支撑位置的地震时程。基于Matlab编程,将上述地震作用以位移时程的形式施加于车桥耦合系统,研究局部地形条件和地震波入射角度对车桥耦合系统地震响应的影响。
1 局部场地中地震动斜入射的实现 1.1 局部场地的有限元建模有限元方法是模拟地震波在土体中传播的有效方法之一[13],使用该方法的一个必要步骤就是从无限尺寸的土体中切取出有限尺寸的区域进行建模。为了保证模拟的真实性,切取出来的有限区域须具有与原无限土体相同的性质,而这就需要在计算区域上引入合适的人工边界条件,以达到模拟波动透射的过程。杜修力等[14]提出的改进粘弹性人工边界,除具有以上性质之外,还具有计算精度高、应用方便等优点,因此,本文参考该人工边界进行建模。
在有限元建模的过程中,桥梁所在场地可以采用实体单元建模,其周围的粘弹性人工边界则可以采用弹簧阻尼单元来模拟。
1.2 外源输入的等效边界力法地震波的斜入射问题可以看成一种外源波动问题。为了实现地震波的传播过程,可在人工边界上施加随时间变化的等效荷载[15],等效荷载的法向力和切向力的计算式分别为:
| $\begin{aligned} \boldsymbol{F}_{N}=& A\left[C_{\mathrm{N}} \dot{\boldsymbol{u}}_{\mathrm{N}}(x, y, z, t)+K_{\mathrm{N}} \boldsymbol{u}_{\mathrm{N}}(x, y, z, t)+\right.\\ &\left.\boldsymbol{\sigma}_{0}(x, y, z, t)\right] \end{aligned} $ | (1) |
| $\begin{aligned} \boldsymbol{F}_{\mathrm{T}}=& A\left[C_{\mathrm{T}} \dot{\boldsymbol{u}}_{\mathrm{T}}(x, y, z, t)+K_{\mathrm{T}} \boldsymbol{u}_{\mathrm{T}}(x, y, z, t)+\right.\\ &\left.\boldsymbol{\tau}_{0}(x, y, z, t)\right] \end{aligned} $ | (2) |
式中:x、y、z表示人工边界节点的坐标;uN(x, y, z, t)和uT(x, y, z, t)分别为节点(x, y, z)在t时刻的法向和切向位移; σ0(x, y, z, t)和τ0(x, y, z, t)分别为节点(x, y, z)处由自由场波动产生的法向和切向应力; A为边界节点所代表的面积; KN、KT、CN和CT分别为边界节点在法向和切向上构造粘弹性人工边界时附加的弹簧、阻尼系数。
假设平面SV波以角度θ1从左下方向有限域传播,并在地表产生反射,形成反射角为θ1的反射平面SV波和反射角为θ2的反射平面P波,如图 1所示。依据波动理论和弹性力学的相关知识,可确定式(1)和式(2)中的位移项和应力项[16],从而可以得到作用于各个人工边界上的等效荷载,将其施加于桥梁场地有限元模型并进行时程分析,即可实现地震波在土体中的传播过程。

|
Download:
|
| 图 1 平面SV波斜入射 Fig. 1 Oblique incidence of plane SV wave | |
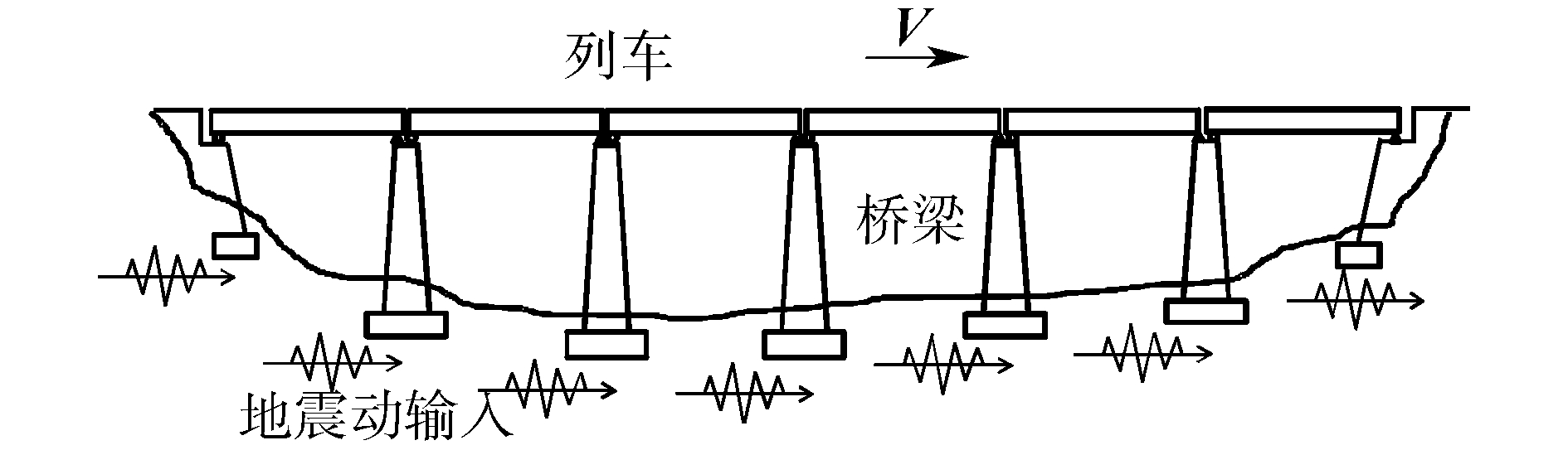
如图 2所示为地震作用下车桥耦合动力分析模型,它由承受地震作用的桥梁子系统和车辆子系统组成。
|
Download:
|
| 图 2 地震作用下车桥系统示意 Fig. 2 Train-bridge system subjected to seismic load | |
在建立地震作用下车桥系统运动方程时,引入如下假定:
1) 每节车都由车体、转向架、轮对所组成,各组成部件之间通过弹簧、阻尼器相联;2)不同车体之间相互独立,且不考虑车辆沿着桥梁纵向的振动;3)列车通过桥梁时速度保持不变;4)地震动直接作用于桥梁结构,对车辆子系统的影响则通过轮轨关系实现;5)分析时不考虑轨道结构自身的弹性变形,假设轨道结构和桥梁之间不存在相对位移。
这样,在绝对坐标系下车辆子系统和桥梁子系统的运动方程分别为:
| $\boldsymbol{M}_{\mathrm{V}} \ddot{\boldsymbol{u}}_{\mathrm{V}}+\boldsymbol{C}_{\mathrm{V}} \dot{\boldsymbol{u}}_{\mathrm{V}}+\boldsymbol{K}_{\mathrm{V}} \boldsymbol{u}_{\mathrm{V}}=\boldsymbol{F}_{\mathrm{V}, \mathrm{B}} $ | (3) |
| $\left[\begin{array}{cc}{\boldsymbol{M}_{\mathrm{ss}}} & {\boldsymbol{M}_{\mathrm{sb}}} \\ {\boldsymbol{M}_{\mathrm{bs}}} & {\boldsymbol{M}_{\mathrm{bb}}}\end{array}\right]\left[\begin{array}{c}{\ddot{\boldsymbol{u}}_{\mathrm{s}}} \\ {\ddot{\boldsymbol{u}}_{\mathrm{b}}}\end{array}\right]+\left[\begin{array}{cc}{\boldsymbol{C}_{\mathrm{ss}}} & {\boldsymbol{C}_{\mathrm{sb}}} \\ {\boldsymbol{C}_{\mathrm{bs}}} & {\boldsymbol{C}_{\mathrm{bb}}}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{\dot u}_{\mathrm{s}}} \\ {\boldsymbol{\dot u}_{\mathrm{b}}}\end{array}\right]+\\ \;\;\;\;\;\;\;\; \left[\begin{array}{ll}{\boldsymbol{K}_{\mathrm{ss}}} & {\boldsymbol{K}_{\mathrm{sb}}} \\ {\boldsymbol{K}_{\mathrm{bs}}} & {\boldsymbol{K}_{\mathrm{bb}}}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{u}_{\mathrm{s}}} \\ {\boldsymbol{u}_{\mathrm{b}}}\end{array}\right]=\left[\begin{array}{c}{\boldsymbol{F}_{\mathrm{B}, \mathrm{V}}} \\ {\bf{0}}\end{array}\right] $ | (4) |
式中:M、C、K分别为质量、阻尼和刚度矩阵; 下标B和V分别代表桥梁子系统和车辆子系统; u、$\mathit{\boldsymbol{\dot u}}$和ü分别代表位移、速度和加速度向量; ub,即桥梁位移向量,又可以分解为us和ub, 它们分别代表桥梁上部结构和支撑处的位移;Mss、Msb、Mbs、Mbb分别为桥梁上部自由度质量矩阵、支撑处自由度质量矩阵及支撑节点对上部结构节点的质量贡献矩阵。
基于式(4),可以得到桥梁子系统上部结构的运动方程:
| $\begin{aligned} \boldsymbol{M}_{\mathrm{ss}} \ddot{\boldsymbol{u}}_{\mathrm{s}}+\boldsymbol{C}_{\mathrm{s}} \dot{\boldsymbol{u}}_{\mathrm{s}}+\boldsymbol{K}_{\mathrm{ss}} \boldsymbol{u}_{\mathrm{s}}=&-\boldsymbol{K}_{\mathrm{bb}} \boldsymbol{u}_{\mathrm{b}}-\boldsymbol{C}_{\mathrm{sb}} \dot{\boldsymbol{u}}_{\mathrm{b}}-\\ \boldsymbol{M}_{\mathrm{b}} \ddot{\boldsymbol{u}}_{\mathrm{b}}+\boldsymbol{F}_{\mathrm{B}, \mathrm{V}} \end{aligned} $ | (5) |
分析时,采用集中质量矩阵,则Msb=0;根据文献[17],式(5)中等号${\mathit{\boldsymbol{C}}_{{\rm{sb}}}}{\mathit{\boldsymbol{\dot u}}_{\rm{b}}}$可以不考虑。忽略${\mathit{\boldsymbol{C}}_{{\rm{sb}}}}{\mathit{\boldsymbol{\dot u}}_{\rm{b}}}$和${{\mathit{\boldsymbol{M}}}_{{\rm{sb}}}}{\mathit{\boldsymbol{\ddot u}}_{\rm{b}}}$,并引入振型分解法对式(5)进行处理[18],可得:
| $\begin{array}{l} {{\ddot q}_i} + 2{\xi _i}{\omega _i}{{\dot q}_i} + \omega _i^2{q_i} = \varphi _i^{\rm{T}}{\mathit{\boldsymbol{M}}_{{\rm{ss}}}}\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{\omega }}_i^2{u_{\rm{b}}}} \right) + \mathit{\boldsymbol{\varphi }}_i^{\rm{T}}{\mathit{\boldsymbol{F}}_{{\rm{B}}, {\rm{V}}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, \cdots , {N_{{\rm{num}}}} \end{array} $ | (6) |
式中:φi为第i阶振型向量;qi为第i阶广义振型坐标;ωi为第i阶圆频率; Nnum为分析中所使用的桥梁模态总数; 影响矩阵R为:
| $\boldsymbol{R}=-\boldsymbol{K}_{\mathrm{ss}}^{-1} \boldsymbol{K}_{\mathrm{sb}} $ | (7) |
式(3)和式(6)即地震作用下车辆子系统和桥梁子系统的运动方程,基于Matlab编制计算程序,通过迭代求解可得到车桥系统的地震响应。
3 地震动斜入射下车桥系统地震响应 3.1 分析流程基于上述地震动斜入射实现方法及地震作用下车桥耦合动力分析模型,可以得到考虑地形条件及地震动斜入射的车桥耦合动力分析的基本步骤为:
1) 根据桥梁所处的场地地形条件,建立场地的有限元分析模型,并在模型中添加粘弹性人工边界。
2) 当入射地震波为SV波时,通过式(1)、式(2)计算作用在人工边界上的等效荷载;若入射地震波不是SV波,则需根据地震波类型选取对应的等效荷载计算公式[18]。
3) 将步骤2)得到的等效荷载施加于步骤1)中所建立的有限元模型中的人工边界处,通过时程分析,即可获得考虑地形条件影响的桥梁各支撑处的地震动时程。
4) 将步骤3)中获得的地震动时程作为输入,基于Matlab程序进行迭代计算,最终获得考虑地形条件和地震动斜入射的车桥系统的地震响应。
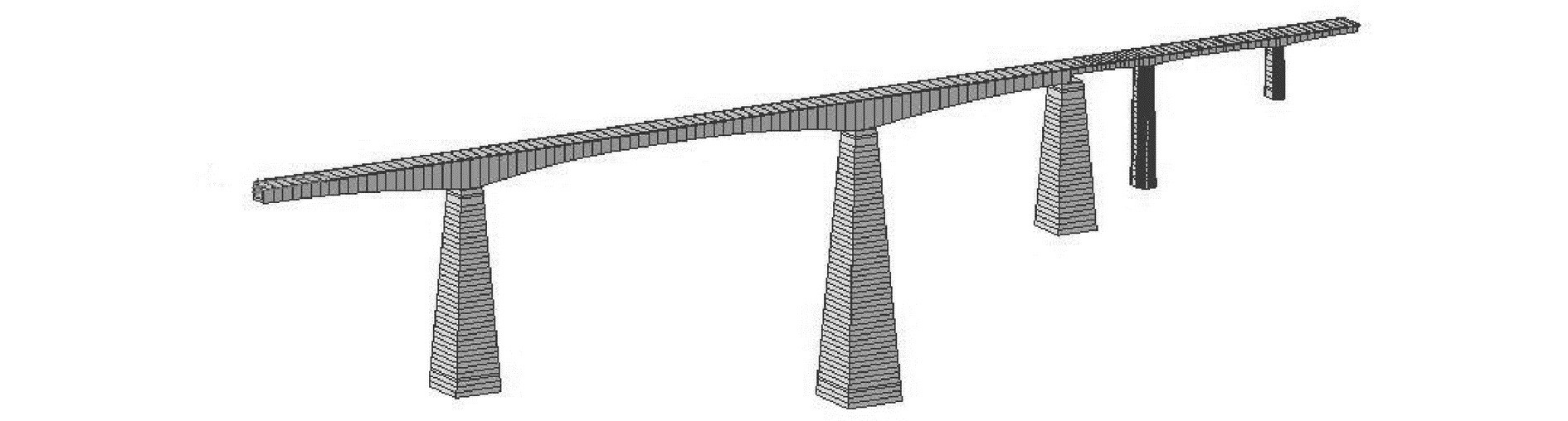
3.2 桥梁和列车参数选取一座实际桥梁进行分析。该桥梁位于一座V形山谷中,如图 3所示。桥梁全长为466 m,由一座(88+168+88) m的预应力混凝土刚构桥和一座(33+56+33) m的预应力混凝土连续梁桥组成。沿着桥梁的纵向,将桥墩分别编号为1#~5#,其对应的桥墩高度分别为77、103、56、46和20 m。两边的桥台则编号为A和B。墩梁之间的连接条件除图中标注的以外,均为滑动支座。

|
Download:
|
| 图 3 桥梁示意 Fig. 3 Diagram of the bridge | |
采用梁单元建立桥梁有限元模型,如图 4所示。建模时设置桥梁墩底固结,墩顶和对应主梁节点之间通过设置主从节点连接。
|
Download:
|
| 图 4 桥梁有限元模型 Fig. 4 Finite element model of the bridge | |
取桥梁结构的前80阶振型进行地震作用下车桥耦合分析,基于Matlab编制计算程序,且在计算过程中,各阶模态的阻尼比均取为0.025。
车辆模型选择ICE3高速列车,假设共有8节,依据文献[1]建立其运动方程。
轮轨关系采用竖向密贴,横向线性蠕滑的接触关系假定[19],并在计算中采用德国低干扰谱作为轨道不平顺激励。
3.3 场地参数及输入地震动假设其所在场地的土体为均质土体,土体弹性模量为5 GPa,密度为2 610 kg/m3,泊松比为0.26。计算得到场地土体的剪切波速为871 m/s,依据文献[20],分析时可暂不考虑桩土相互作用对系统动力响应的影响。选取某实际地震波作为地震激励,其位移时程及对应的位移频谱如图 5所示。依据图 5(b),确定建模时的单元尺寸为4 m[21]。综合考虑桥梁总长、山谷深度以及计算规模,最终确定模型的总尺寸为624 m×160 m×120 m,如图 6所示。依据文献[14],可计算出粘弹性边界的参数。以前、后侧边界为例,其粘弹性边界的参数为KN=5.66×107 N/m3,CN=4.39×106 N·s/m3,KT=1.83×107 N/m3,CT=2.5×106 N·s/m3。采用ANSYS建模,模型中,土体采用Solid45单元模拟,粘弹性人工边界则采用Combin14单元实现。

|
Download:
|
| 图 5 地震动特性 Fig. 5 Characteristics of seismic ground motion | |

|
Download:
|
| 图 6 桥址处场地模型 Fig. 6 FE model of the local topography | |
假设该地震波为平面SV波,则根据式(1)、式(2)即可求得作用于场地有限元模型上的等效荷载,从而得到考虑地形条件和地震波入射角度影响的地震动输入。场地有限元模型作为图 1中的有限域,将入射波平面与竖直平面的夹角θ1,定义为地震波入射角。如表 1所示为是否考虑地形条件情况下、地震波以不同角度入射时,桥台A和支撑2#处的竖向地震动峰值。从表中可以看出,考虑地形条件影响后,竖向地震动峰值明显放大;不同入射角情况下,各支撑处的地震动峰值随入射角的变化规律不同。
| 表 1 考虑/不考虑地形、不同入射角条件下地震动峰值位移 Table 1 Peak values of vertical ground motion under different conditions |
根据式(3)和式(6),编制分析程序,最终可以获得考虑地形条件和地震动入射角度影响的车桥耦合系统地震响应。
在计算中,分别考虑无地震、有地震但不考虑地形、有地震且考虑地形3种情况,分析车桥系统的动力响应。在不考虑地形影响的模型中,类比文献[10],把模型的上表面取为自由水平面。
假设平面SV波分别以0°、15°和30°入射,研究地震波入射角度对车桥系统动力响应的影响。计算中均假设列车上桥时刚好发生地震。
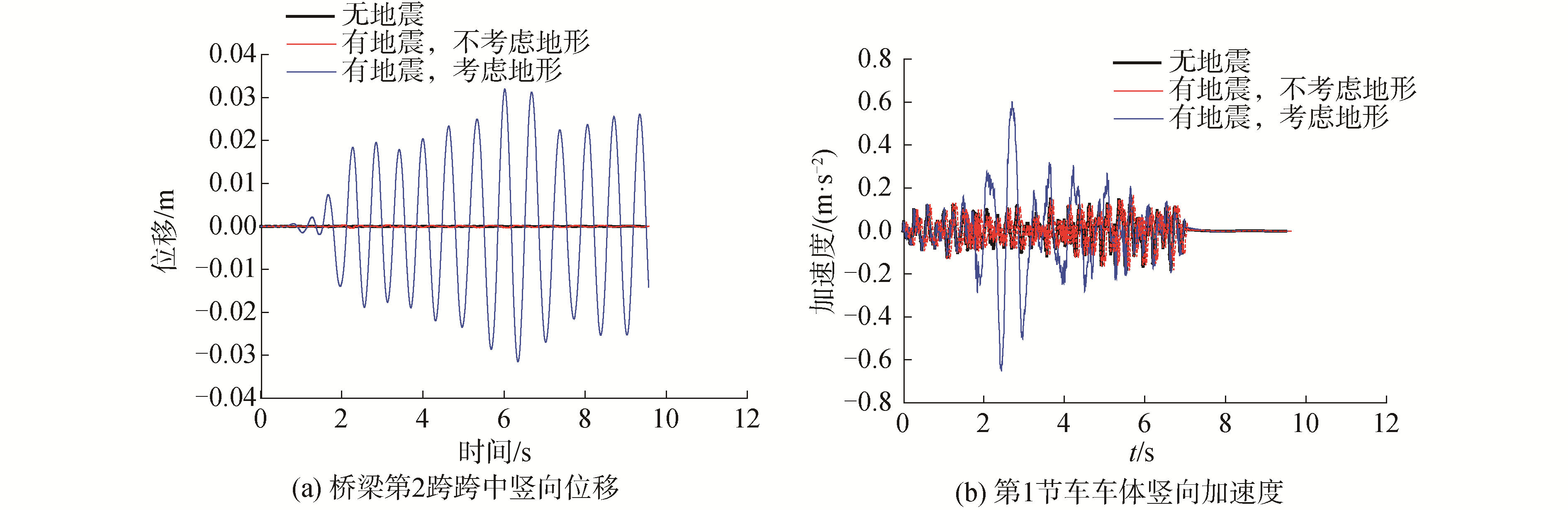
假设车速为250 km/h,如图 7所示为3种不同情况下桥梁第2跨跨中竖向位移时程和列车第1节车车体竖向加速度时程。其中,“有地震”指的是平面SV波垂直入射的情况(即入射角为0)。
|
Download:
|
| 图 7 不同条件下车桥系统竖向响应时程 Fig. 7 Vertical response of the train-bridge system under various conditions | |
从图 7可以看出,无地震条件下和有地震但不考虑地形条件下车桥系统的动力响应基本相同。这是因为地震作用下车桥耦合分析中只考虑横桥向和竖向的地震动输入,而根据波动理论,SV垂直入射且土体模型的上表面为自由水平面时,其产生的横桥向和竖向的地面运动均为0。从图 7还可以看出,考虑了地形条件之后,桥梁子系统和车辆子系统的地震响应均有所增加,车辆子系统的动力响应放大了3.6倍,桥梁子系统则更多,说明了在进行地震作用下车桥系统动力分析时考虑地形条件的必要性。
如图 8所示为车速为250 km/h时,平面SV波分别以0°、15°、30°入射时桥梁最大跨的跨中竖向位移时程和第1节列车车体竖向加速度时程。

|
Download:
|
| 图 8 不同入射角度下车桥系统竖向响应时程 Fig. 8 Vertical response of the train-bridge coupled system with different incident angles | |
从图 8可以看出,不同地震波入射角度情况下,车桥系统动力响应峰值出现的时间有一定差异,这是因为地震波以不同角度入射时,到达地表的时间不同。另外,地震波以不同角度入射时,车桥系统地震响应的峰值也不相同:在所研究的入射角度范围内,当地震波以30°入射时,系统的动力响应最大;以15°入射时,系统的动力响应最小。
如图 9所示为不同入射角度条件下桥梁第2跨跨中竖向位移峰值和第1节列车车体竖向加速度峰值随车速的变化。

|
Download:
|
| 图 9 不同入射角度下车桥系统的竖向响应随车速的变化 Fig. 9 Maximum vertical train-bridge response as a function of the train speed for different incident angles | |
从图 9中可以看出,相同车速情况下,桥梁跨中位移最大值和车体加速度最大值随入射角的变化规律相同,即在本文研究的3种情况中,在入射角为30°时达到最大值,在入射角为15°时为最小值。
如图 10所示为不同入射角度条件下列车8节车的轮重减载率和脱轨系数最大值随车速的变化。

|
Download:
|
| 图 10 不同入射角度下行车安全指标随车速的变化 Fig. 10 Maximum running safety indexes of train as a function of the train speed for different incident angles | |
从图 10中可以看出,相同车速条件下,轮重减载率和脱轨系数随入射角度的变化规律与图 9中桥梁竖向位移及车体竖向加速度的变化规律基本相同。不同入射角度下,轮重减载率随车速的变化规律不同,但脱轨系数随车速的变化规律基本一致,即随着车速的增加,脱轨系数增大。
4 结论1) SV波入射情况下,地形条件对车桥系统的地震响应有重要影响。考虑地形条件影响后,车桥系统的地震响应明显增大,因此,在进行地震作用下车桥耦合动力分析时,应充分考虑桥梁所处的场地条件的影响。
2) 地震波入射角度对车桥系统的地震响应有重要影响,不同的入射角度会导致响应峰值及峰值出现时间的不同。
本文研究的几种情况中,地震波30°入射时车桥系统动力响应最大,说明了在对列车进行安全性分析时仅仅考虑地震波垂直入射的情况是不够的,应综合考虑各个角度以找出最不利情况,而这则需要对更多的入射角度进行分析及验证。关于SV波入射条件下的最不利入射角度,将在后续研究中给出。
| [1] |
XIA H, DE ROECK G, GOICOLEA J M. Bridge vibration and controls: new research[M]. New York: Nova Science Publishers Inc., 2011.
(  0) 0)
|
| [2] |
LI Yongle, ZHU Siyu, CAI C S, et al. Dynamic response of railway vehicles running on long-span cable-stayed bridge under uniform seismic excitations[J]. International journal of structural stability and dynamics, 2016, 16(5): 1550005. DOI:10.1142/S0219455415500054 (  0) 0)
|
| [3] |
张楠, 夏禾, DE ROECK G. 多点激励作用下车-桥-地震耦合系统分析[J]. 哈尔滨工程大学学报, 2011, 32(1): 26-32. ZHANG Nan, XIA He, DE ROECK G. Analysis of a vehicle-bridge-earthquake interactive system under multi-support excitations[J]. Journal of Harbin Engineering University, 2011, 32(1): 26-32. DOI:10.3969/j.issn.1006-7043.2011.01.006 (  0) 0)
|
| [4] |
雷虎军, 李小珍. 非一致地震激励下列车-轨道-桥梁耦合振动模型[J]. 西南交通大学学报, 2013, 48(5): 803-809. LEI Hujun, LI Xiaozhen. Dynamic model for train-track-bridge coupling system subjected to non-uniform seismic excitation[J]. Journal of Southwest Jiaotong University, 2013, 48(5): 803-809. DOI:10.3969/j.issn.0258-2724.2013.05.004 (  0) 0)
|
| [5] |
杜宪亭, 夏禾. 地震空间变异性对车桥系统响应的影响分析[J]. 工程力学, 2012, 29(9): 106-111. DU Xianting, XIA He. Influence of spatial variation of seismic ground motion on dynamic response of train-bridge system[J]. Engineering mechanics, 2012, 29(9): 106-111. (  0) 0)
|
| [6] |
DER KIUREGHIAN A, NEUENHOFER A. Response spectrum method for multi-support seismic excitations[J]. Earthquake engineering & structural dynamics, 1992, 21(8): 713-740. (  0) 0)
|
| [7] |
XIA He, HAN Yan, ZHANG Nan, et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations[J]. Earthquake engineering & structural dynamics, 2006, 35(12): 1563-1579. (  0) 0)
|
| [8] |
ZHANG Zhichao, ZHANG Yahui, LIN Jiahao, et al. Random vibration of a train traversing a bridge subjected to traveling seismic waves[J]. Engineering structures, 2011, 33(12): 3546-3558. DOI:10.1016/j.engstruct.2011.07.018 (  0) 0)
|
| [9] |
林玉森.地震作用下高速铁路桥上列车走行性研究[D].成都: 西南交通大学, 2007. LIN Yusen. Study on train runnabilities during earthquake on high-speed railway bridge[D]. Chengdu: Southwest Jiaotong University, 2007. (  0) 0)
|
| [10] |
乔宏, 夏禾, 杜宪亭, 等. 考虑地形条件影响的车桥耦合系统地震响应分析[J]. 振动与冲击, 2015, 34(17): 69-76. QIAO Hong, XIA He, DU Xianting, et al. Seismic response analysis of a train-bridge coupled system considering topographic effects[J]. Journal of vibration and shock, 2015, 34(17): 69-76. (  0) 0)
|
| [11] |
TAKAHIRO S. Estimation of earthquake motion incident angle at rock site[C]//Proceeding of the 12th World Conference Earthquake Engineering. New Zealand, 2000.
(  0) 0)
|
| [12] |
尤红兵, 赵凤新, 荣棉水. 地震波斜入射时水平层状场地的非线性地震反应[J]. 岩土工程学报, 2009, 31(2): 234-240. YOU Hongbing, ZHAO Fengxin, RONG Mianshui. Nonlinear seismic response of horizontal layered site due to inclined wave[J]. Chinese journal of geotechnical engineering, 2009, 31(2): 234-240. DOI:10.3321/j.issn:1000-4548.2009.02.014 (  0) 0)
|
| [13] |
刘毅, 李雄彦, 薛素铎. 地震动斜入射对桩-土-网壳结构地震响应影响[J]. 振动工程学报, 2015, 28(1): 139-147. LIU Yi, LI Xiongyan, XUE Suduo. The effect of oblique incidence of seismic wave on seismic response of pile-soil-latticed shell[J]. Journal of vibration engineering, 2015, 28(1): 139-147. (  0) 0)
|
| [14] |
杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49-56. DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in FEA for near-field wave problem[J]. Chinese journal of theoretical and applied mechanics, 2006, 38(1): 49-56. (  0) 0)
|
| [15] |
赵建锋, 杜修力, 韩强, 等. 外源波动问题数值模拟的一种实现方式[J]. 工程力学, 2007, 24(4): 52-58. ZHAO Jianfeng, DU Xiuli, HAN Qiang, et al. An approach to numerical simulation for external source wave motion[J]. Engineering mechanics, 2007, 24(4): 52-58. DOI:10.3969/j.issn.1000-4750.2007.04.010 (  0) 0)
|
| [16] |
周晨光.高土石坝地震波动输入机制研究[D].大连: 大连理工大学, 2009. ZHOU Chenguang. Research on the mechanism of seismic wave input about high rockfill dam[D]. Dalian: Dalian University of Technology, 2009. (  0) 0)
|
| [17] |
WILSON E L. Three-dimensional static and dynamic analysis of structures: a physical approach with emphasis on earthquake engineering[M]. California: Computers and Structures Inc., 2002.
(  0) 0)
|
| [18] |
TSAI H C. Modal superposition method for dynamic analysis of structures excited by prescribed support displacements[J]. Computers & structures, 1998, 66(5): 675-683. (  0) 0)
|
| [19] |
ZHANG N, XIA H, GUO W W, et al. A vehicle-bridge linear interaction model and its validation[J]. International journal of structural stability and dynamics, 2010, 10(2): 335-361. DOI:10.1142/S0219455410003464 (  0) 0)
|
| [20] |
QIAO Hong, XIA He, DU Xianting. Dynamic analysis of an integrated train-bridge-foundation-soil system by the substructure method[J]. International journal of structural stability and dynamics, 2018, 18(5): 1850069. DOI:10.1142/S0219455418500694 (  0) 0)
|
| [21] |
LYSMER J, KUHLEMEYER R L. Finite Dynamic model for infinite media[J]. Journal of the engineering mechanics division, 1969, 95(4): 859-878. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


