随着国家利益向远海方向拓展,船舶或大型海洋工程设备在海上航行、作业频繁,发生事故的风险也随之增大。现阶段对于在海上发生故障的船舶或大型海洋工程设备,若船员级(包括临时聘请专家上船)维修难以满足需要,则需将其运至岸基维修,但无论是拖轮拖带还是半潜船运输,运输过程中都具有较大的风险,而且运输费用昂贵,经济性差。为了在故障发生地实现对故障船舶或大型海洋工程设备的及时维修,文献[1-2]提出了自航式半潜维修船概念设计,该船是基于集成创新理念设计的集高技术与多功能于一体的新船型,可将故障船舶或大型海洋工程设备浮装至维修甲板上开展维修作业,从而实现维修工作由岸基拓展至远海。采用半潜维修船实现对故障船舶或大型海洋工程设备的现场维修,在一定程度上可降低其上岸维修的时间、费用和风险,提高运输或生产作业效率。
在船舶安全理论方面,文献[3-5]分别从船舶完整稳性的发展、船舶稳性与安全、船舶动稳性方面进行了回顾与总结。文献[6]介绍了提高船舶完整稳性与安全的可操作方法,如设计灵便的船舶安全决策支持系统[7]。针对半潜船,文献[8]探讨了半潜船处于静水和波浪中的初稳性高度理论限值计算公式,在此基础上,文献[9]探究了半潜船初稳性高度限值的影响因素及其作用机理。在船舶压载方面,文献[10]提出了船舶减摇的压载系统优化控制策略,随后应用此策略并引入专家系统设计了多功能船舶监控与数据采集系统[11];文献[12]建立了起重船舶压载水调配优化模型,实现了压载舱压载水总调配量最小的目标。本文综合有关半潜船理论、压载系统优化方法、船舶安全理论的相关研究,针对半潜维修船携带维修设备较重,致使难以安全托举故障船舶或大型海洋工程设备出水的情况,以最大化安全性为目标,研究船舶上浮工况多功能浮力舱配置及船舶压载优化问题。
1 多功能浮力舱配置及压载优化模型 1.1 多功能浮力舱配置问题描述对于损害严重、维修任务量大的船舶或大型海洋工程设备,半潜维修船在执行维修任务时需携带较多的维修设备以满足对其进行海上的基地级维修需要。为了维修的便利性,半潜维修船往往通过浮装作业将大型海洋工程设备承托于维修甲板上使其脱离水面。在半潜维修船托举故障设备上浮的过程中,若维修设备过重,可能导致船舶举力不足,难以托举故障设备出水,或托举故障设备后安全性达不到要求。因此在半潜维修船浮装故障设备之前,可在舷侧配置一定数量的多功能浮力舱,为托举故障设备出水提供充足的支持力,并增加船舶整体的安全性。该舱为可移动式水密箱体,能够安装在船舶两舷侧,并使其上表面与甲板面平齐,临时增加甲板面积与压载舱,此外该舱还可兼做维修等功能舱室,远海维修任务结束后即可将其放置在维修甲板上。在解决多功能浮力舱配置数量问题之前,作出如下几点假设:1)配置同一类型的多功能浮力舱,将其简化为长方体,各参数已知;2)多功能浮力舱与船体形成牢固的整体;3)假设维修设备的重量与维修舱大小有关;4)作业水域满足规范中半潜船潜浮作业的要求[8]。
1.2 参数与变量半潜维修船的船宽、型深和维修作业吃水分别为B、D、TM。为便于描述半潜维修船压载舱、维修舱等舱室以及配置的多功能浮力舱的信息,建立船舶坐标系,以艉垂线与基平面的交点为坐标原点o,基平面与中线面的交线为x轴,指向船艏为正;艉垂线为z轴,向上为正;过坐标原点且垂直于xoz面的直线为y轴,指向右舷为正。
记B为N个压载舱的集合,第n个压载舱Bn的最大压载量为WnB,满舱压载水的重心坐标为[xnB, ynB, znB];M为R个维修舱的集合,第r个舱室Mr装载维修设备的重量为WrM,重心坐标为[xrM, yrM, zrM];F为配置的K个多功能浮力舱的集合,第k个浮力舱Fk的长宽高分别为a、b、h,最大压载量为WkF,满舱压载水的重心坐标为[xkF, ykF, zkF],配置的浮力舱总数K为设计变量。为准确表述涉及到的变量,作出如下定义:
定义1 将压载舱或浮力舱的压载重量与压载舱或浮力舱的最大压载量的比值记为压载系数。
定义2 将维修舱内维修设备的重量与维修舱内以压载水计量的满舱重量的比值记为维修设备重量系数。
根据以上定义,压载舱的压载系数θnB、浮力舱的压载系数θkF为设计变量,第r个维修舱装载维修设备的重量WrM取以压载水计量其满舱重量的μ(维修设备重量系数)倍。
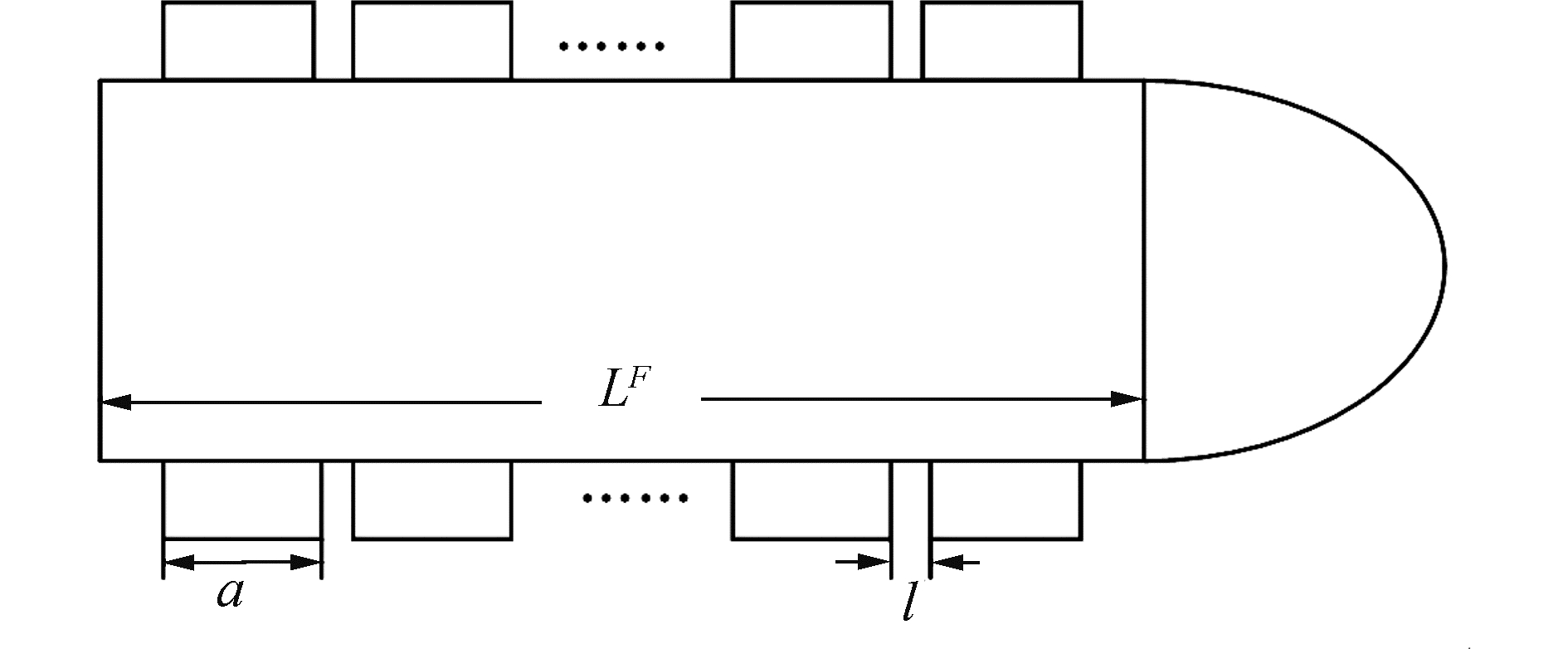
多功能浮力舱按照船体两舷成对配置、单舷居中排列的原则布置,图 1为多功能浮力舱布置的示意图,其中LF为可布置浮力舱的船舷长度,l为浮力舱之间的安全距离。当多功能浮力舱数量确定后,各舱的重心坐标等信息即可确定。
|
Download:
|
| 图 1 多功能浮力舱布置原则 Fig. 1 Layout principle of multi-functional buoyancy tanks | |
由于船舶从浮装吃水上浮至维修作业吃水的过程中,船舶与故障船舶或设备整体所受浮力不断减小,故上浮至维修作业吃水TM时,整体所受浮力最小,因此主要研究维修作业吃水下的浮力舱配置问题(当且仅当D-h < TM < D时)。规范要求一般半潜船应在规定的风、浪外界环境条件下进行半潜作业[8],如基本无浪的平静水域,或蒲氏风级及有义波高限制下的水域。此时船舶受风、浪影响倾斜角度较小,故采用初稳性值GM作为衡量船舶上浮工况安全性的目标函数:
| $ {\rm{GM}} = {\rm{KB}} + {\rm{BM}} - {\rm{KG}} - \delta {\rm{G}}{{\rm{M}}_{\rm{f}}} $ | (1) |
式中:GM为经自由液面修正后的初稳性值;KB为浮心高度;BM为横稳心半径;KG为重心高度;δGMf为自由液面对初稳性高度的修正值。
由于布置了多功能浮力舱,船舶整体所受浮力改变,在相同吃水条件下KB、BM按下式计算:
| $ {\rm{KB}} = \left( {{\Delta ^0}Z_B^0 + \delta {W_F}\delta {z_F}} \right)/\left( {{\Delta ^0} + \delta {W_F}} \right) $ | (2) |
| $ {\rm{BM}} = \left( {{\rm{B}}{{\rm{M}}^0}{\Delta ^0} + \rho I_T^F} \right)/\left( {{\Delta ^0} + \delta {W_F}} \right) $ | (3) |
式中:Δ0为原排水量;ZB0为原浮心的z坐标值;δWF为布置浮力舱增加的排水量;δzF为浮力舱的浮心高度;BM0为原横稳心半径;ρ为海水密度;ITF为浮力舱水线面面积对纵向中心轴的横向惯性矩分别为:
| $ \delta {W_F} = K\rho ab\left( {h - D + {T_{\rm{M}}}} \right) $ | (4) |
| $ \delta {x_F} = \left( {{T_{\rm{M}}} + D - h} \right)/2 $ | (5) |
| $ I_T^F = Ka\left[ {{{\left( {B/2 + b} \right)}^3} - {{\left( {B/2} \right)}^3}} \right]/3 $ | (6) |
布置多功能浮力舱后船体的重心高度及自由液面对初稳性高度的修正值:
| $ \begin{array}{*{20}{c}} {{\rm{KG}} = \left[ {M_z^0 + M_z^M + M_z^C + \sum\limits_{n = 1}^N {W_B^n\theta _B^n\left( {\left( {z_B^n - z_{B'}^n} \right)\theta _B^n + } \right.} } \right.}\\ {\left. {\left. {z_{B'}^n} \right) + \sum\limits_{k = 1}^K {\left( {W_F^k\theta _F^k\left( {\left( {z_F^k - z_{F'}^k} \right)\theta _F^k + z_{F'}^k} \right) + \tau W_F^kz_F^k} \right)} } \right] \times }\\ {{{\left[ {{W^0} + {W_M} + {W_C} + \sum\limits_{n = 1}^N {W_B^n\theta _B^n} + \sum\limits_{k = 1}^K {\left( {W_F^n\theta _F^n + \tau W_F^k} \right)} } \right]}^{ - 1}}} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {\delta {\rm{G}}{{\rm{M}}_f} = \rho \left[ {\sum\limits_{n = 1}^N {\left\lceil {\theta _B^n\left( {1 - \theta _B^n} \right)} \right\rceil i_B^n} + \sum\limits_{k = 1}^K {⌈\theta _F^k\left( {1 - } \right.} } \right.}\\ {\left. {\left. {\theta _F^k} \right)⌉i_F^k} \right] \times {{\left( {{\Delta ^0} + \delta {W_F}} \right)}^{ - 1}}} \end{array} $ | (8) |
式中:Mz0、MzM、MzC分别为空船、维修设备、故障船舶或设备的z向力矩;zB′n、zF′k为压载舱、浮力舱底部的z坐标值;W0、WM、WC分别为空船、维修设备、故障船舶或设备的重量;τ为浮力舱自重系数;iBn、iFk为压载舱、浮力舱的自由液面面积对其倾斜轴线的横向惯性矩;
半潜维修船上浮工况多功能浮力舱配置及压载优化模型如下:
| $ \max {\rm{GM}} $ | (9) |
s.t.
| $ Ka/2 + \left( {K/2 - 1} \right)l \le {L^F} $ | (10) |
| $ {\rm{GM}} \ge \underline {{\rm{GM}}} $ | (11) |
| $ \underline {{T_{\rm{R}}}} \le {T_{\rm{R}}} \le \overline {{T_{\rm{R}}}} $ | (12) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^n} + \sum\limits_{k = 1}^K {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)} + }\\ {{W_M} + {W_C} \ge {\rm{WB}} + \delta {W_F}} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^ny_B^n} + \sum\limits_{k = 1}^K {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)y_F^k} + }\\ {M_y^M + M_y^C + M_y^0 = 0} \end{array} $ | (14) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^nx_B^n} + \sum\limits_{k = 1}^K {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)x_F^k} + M_x^M + }\\ {M_x^C + M_x^0 = \left( {{\Delta ^0} + \delta {W_F}} \right){X_B}} \end{array} $ | (15) |
| $ \theta _B^n \in \left[ {0,1} \right],n = 1,2, \cdots ,N $ | (16) |
| $ \theta _F^k \in \left[ {0,1} \right],k = 1,2, \cdots ,K $ | (17) |
| $ K = 2t,\forall t \in {{\bf{Z}}^ + } $ | (18) |
式中:GM为初稳性高度最小限值;TR为船舶横摇固有周期,
半潜维修船上浮工况多功能浮力舱配置及压载优化模型中,目标函数为复杂的非线性函数,较难进行线性化处理,直接使用线性优化方法求解难以实现。为简化求解方法,将式(9)~(18)的模型分解为2阶段求解。
第1阶段:
| $ \max \left\{ {{\rm{GM}}\left( {{K^ * }} \right)} \right\} $ | (19) |
s.t.
| $ {K^ * }a/2 + \left( {{K^ * }/2 - 1} \right)l \le {L^F} $ | (20) |
| $ {\rm{GM}}\left( {{K^ * }} \right) \ge \underline {{\rm{GM}}} $ | (21) |
| $ \underline {{T_{\rm{R}}}} \le {T_{\rm{R}}} \le \overline {{T_{\rm{R}}}} $ | (22) |
| $ {K^ * } = 2t,\forall t \in {{\bf{Z}}^ + } $ | (23) |
第2阶段:
| $ \max {\rm{GM}}\left( {{K^ * }} \right) $ | (24) |
s.t.
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^n} + \sum\limits_{k = 1}^{{K^ * }} {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)} + }\\ {{W_M} + {W_C} \ge {\rm{WB}} + \delta {W_F}} \end{array} $ | (25) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^ny_B^n} + \sum\limits_{k = 1}^{{K^ * }} {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)y_F^k} + }\\ {M_y^M + M_y^C + M_y^0 = 0} \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N {W_B^n\theta _B^nx_B^n} + \sum\limits_{k = 1}^{{K^ * }} {\left( {W_F^k\theta _F^k + \tau W_F^k} \right)x_F^k} + M_x^M + }\\ {M_x^C + M_x^0 = \left( {{\Delta ^0} + \delta {W_F}} \right){X_B}} \end{array} $ | (27) |
| $ \theta _B^n \in \left[ {0,1} \right],n = 1,2, \cdots ,N $ | (28) |
| $ \theta _F^k \in \left[ {0,1} \right],k = 1,2, \cdots ,{K^ * } $ | (29) |
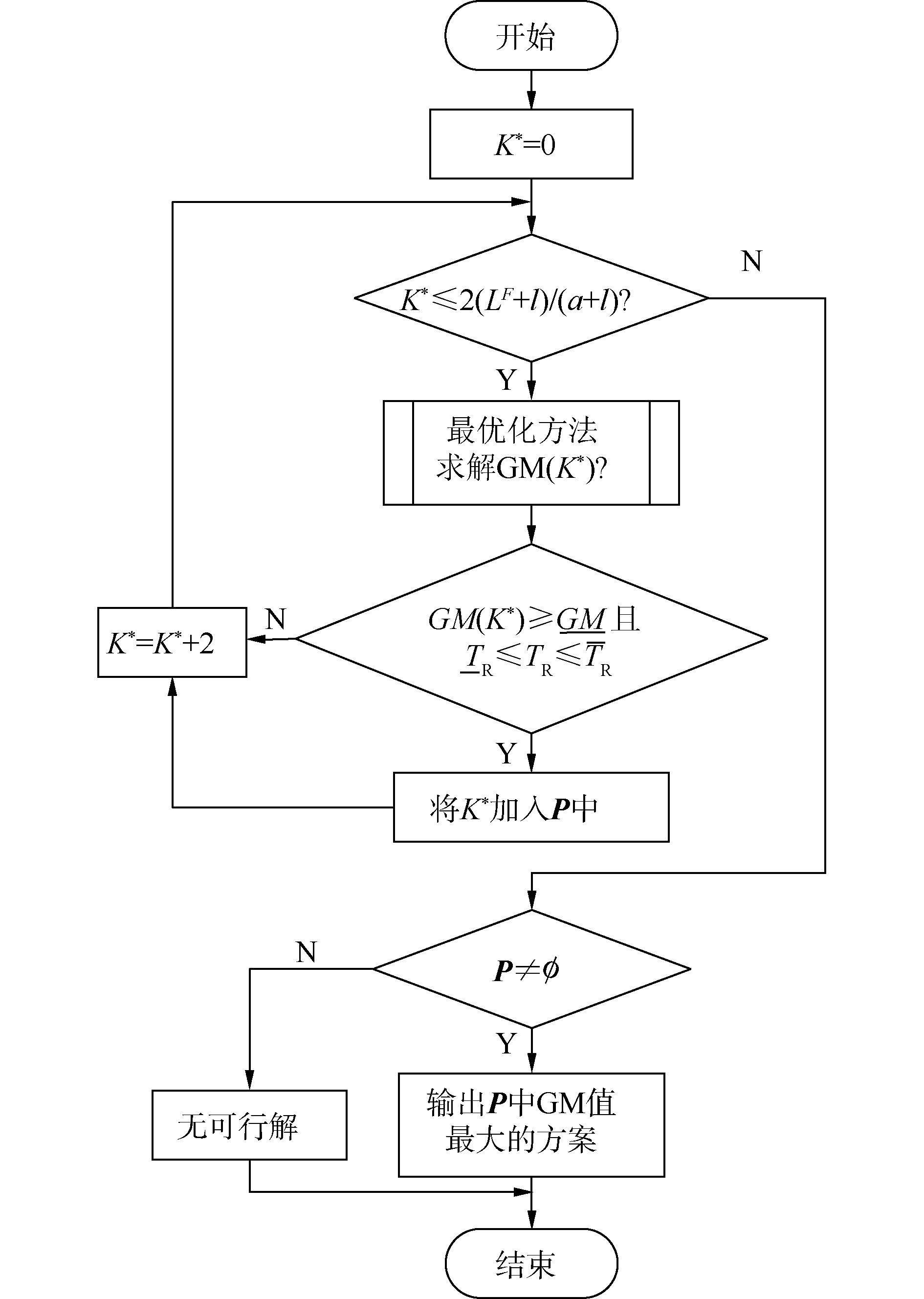
第1阶段为式(19)~(23),首先根据式(20)、(23)确定浮力舱配置数量,并根据多功能浮力舱的布置原则确定其布置位置,进而得到在船舶坐标系中的位置坐标等数据;其次将这些数据传递至第2阶段,第2阶段为式(24)~(29),是在确定的多功能浮力舱配置数量下求解对应的压载优化方案,并将目标函数GM值返回第1阶段,判断是否满足式(21)、(22),若满足则将该多功能浮力舱配置方案加入可行解集P中,不满足则删去该方案;最后通过式(19)选择可行解集P中GM值最大的方案作为最优方案。由于可布置多功能浮力舱的船舷长度有限,可采用枚举法确定第一阶段的多功能浮力舱配置数量,第2阶段可采用一般非线性最优化方法搜索全局最优解(例如,可以采用Lingo中提供的Global求解器进行求解)。该两阶段方法的求解流程见图 2。
|
Download:
|
| 图 2 2阶段方法求解流程 Fig. 2 Solution flow chart of two-stage method | |
参考一型船长228 m、船宽43 m、型深13 m的半潜船体,其中压载舱78个、维修舱7个。采取由下而上、从后至前、先中间后左右舷的编号方式对压载舱进行顺序编号,压载舱的各项参数已知。假设半潜维修船执行某次远海维修任务时携带的维修设备较重,在托举某故障大型海洋工程设备出水时存在一定的安全风险,因此考虑配置多功能浮力舱辅助船舶安全托举故障设备。维修作业吃水TM=10.3 m,该吃水下排水量为82 206 t,浮心坐标为(112.79, 0, 5.45)。可布置多功能浮力舱的船舷长度LF取140 m,l取2 m,维修设备重量系数μ取1.1,横摇周期取14~16 s。该故障大型海洋工程设备重30 000 t,重心高度27 m。当故障设备重心与浮心在一条铅垂线上时,求解多功能浮力舱配置及压载优化模型得到最优方案为配置8个多功能浮力舱,初稳性高度GM值为7.20 m,横摇周期为14.87 s。
该方案对应的压载计划为:θB1~θB9、θB13、θB20~θB38、θB40~θB76、θF2~θF4、θF6~θF8为0%;θB10~θB12、θB14~θB19为100%;θB39为40.4%;θB77为0.03%;θB78为0.35%;θF1为4.82%;θF2为4.78%。
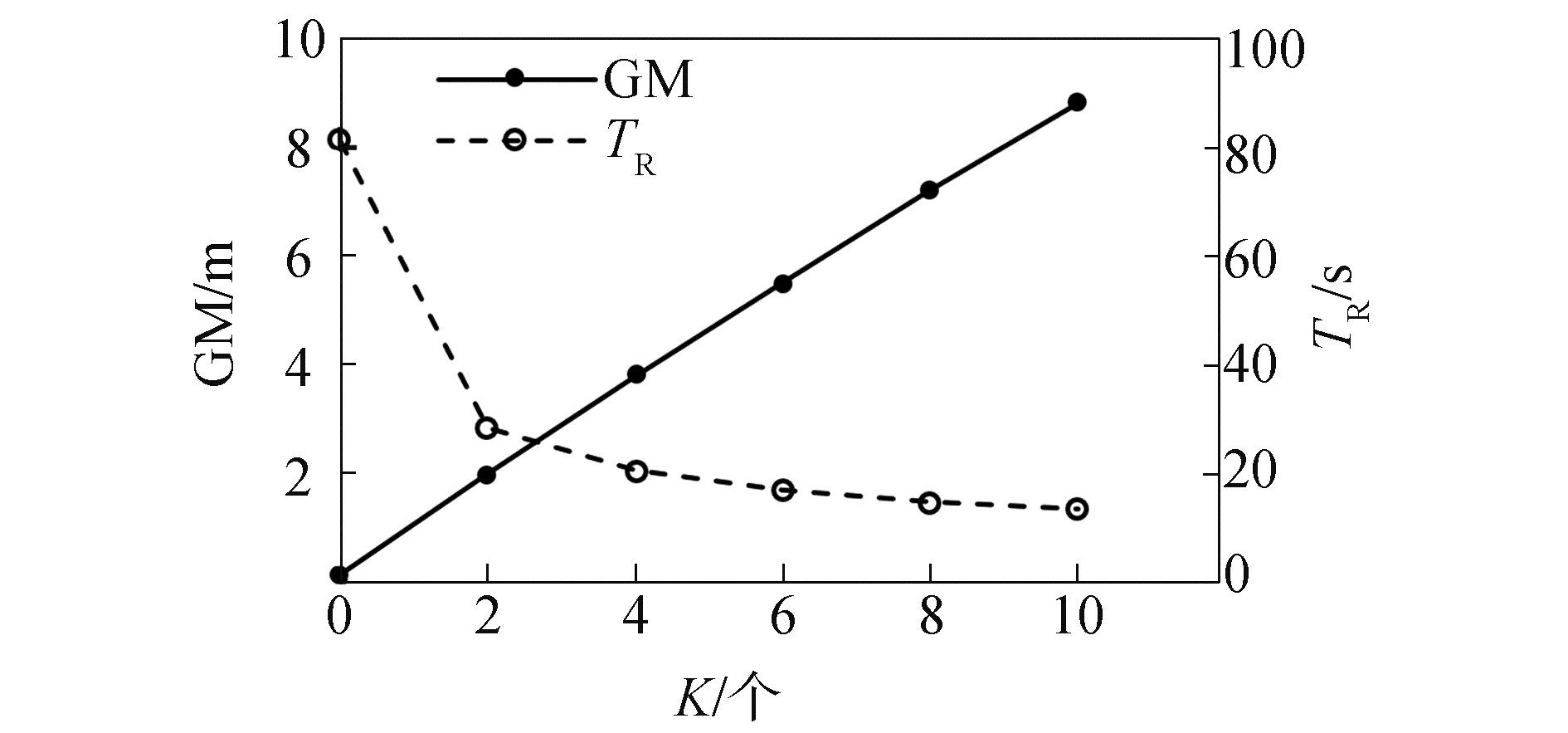
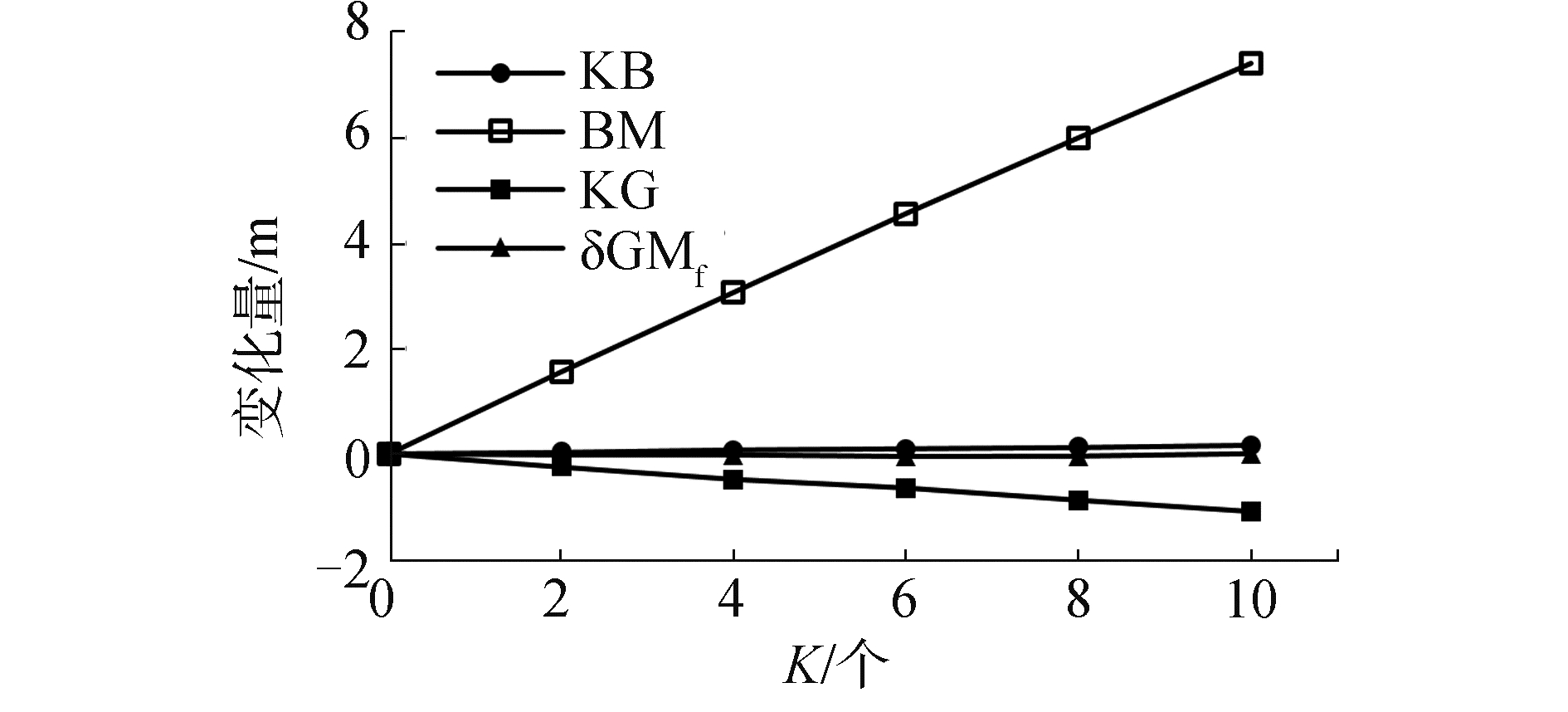
在求解最优方案的过程中,发现随着多功能浮力舱配置数量的增多,初稳性高度大幅度提升,对应的横摇周期呈下降趋势,见图 3。为深入探究多功能浮力舱配置数量对初稳性高度的影响,根据式(1),将初稳性高度分成4个量分别探讨,见图 4。该图是以未配置多功能浮力舱(即K=0)的GM值为基准的比较结果,可以看出随着多功能浮力舱配置数量的增多,KB存在小幅度的增加,KG呈现略大程度的减低,δGMf在小范围内波动,但BM呈现大幅度增加的趋势,其程度远远超过以上3个量的变化幅度。因此BM的增大是GM随着多功能浮力舱配置数量增多而提高的主要原因。根据式(3)可知,由于配置多功能浮力舱,增大了水线面面积,且浮力舱距纵向中心轴线较远,其水线面面积对纵向中心轴的横向惯性矩较大,故配置多功能浮力舱是BM增大的主要原因。由此可见,增加多功能浮力舱的配置数量,对提高初稳性高度具有显著的效果。
|
Download:
|
| 图 3 多功能浮力舱配置方案与初稳性关系 Fig. 3 Relation between equipment plan of multi-functional buoyancy tanks and initial metacentric height | |
|
Download:
|
| 图 4 K对初稳性各量的影响 Fig. 4 Effects on each part of initial metacentric height by K | |
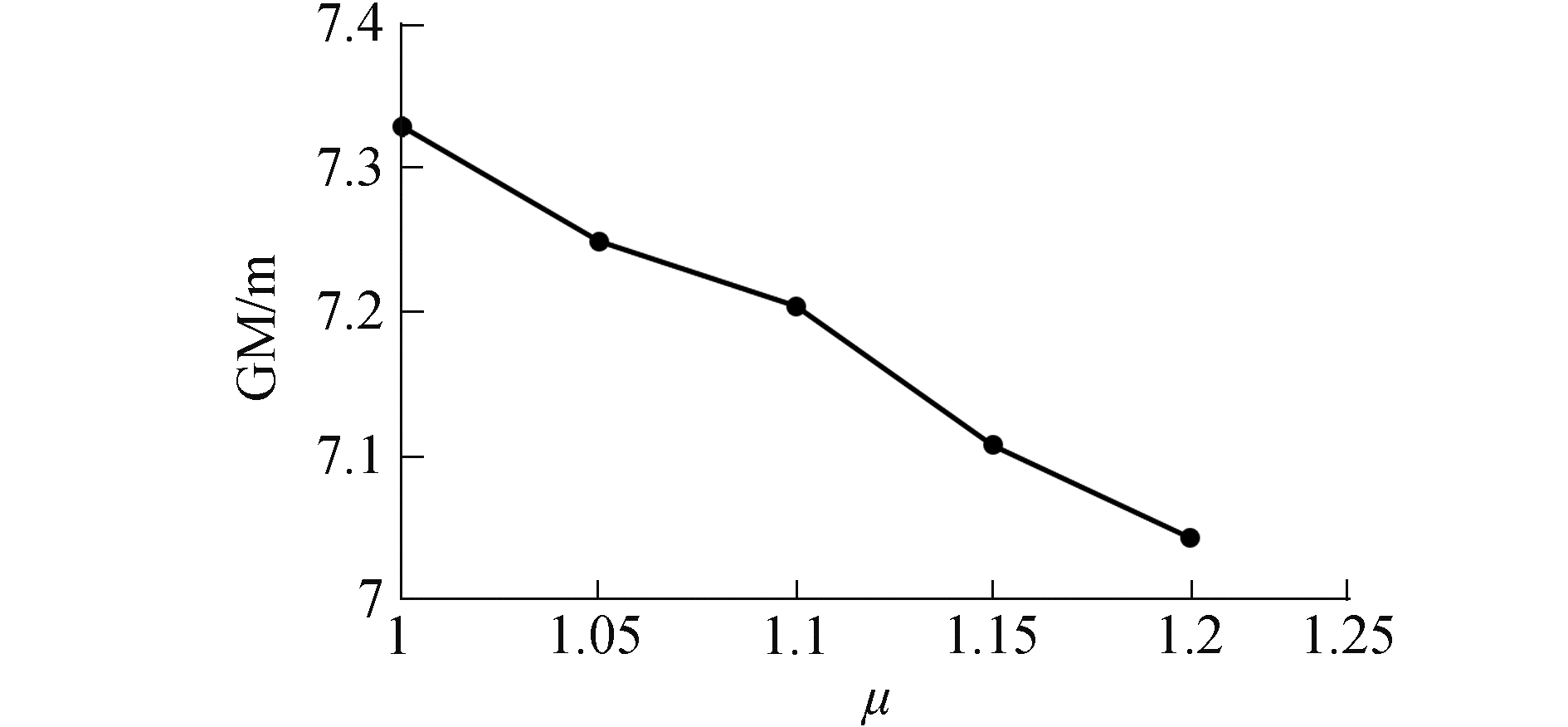
由于航次的维修任务不同,所需携带的维修设备也不尽相同,即维修设备重量系数的取值不同。为探究维修设备重量系数μ对初稳性高度的影响,对于最优方案,即配置8个多功能浮力舱的方案,在μ允许的变化范围内,采用变参数分析法对μ进行敏感性分析,结果见图 5、6。
|
Download:
|
| 图 5 μ敏感性分析 Fig. 5 Sensitivity analysis of μ | |
|
Download:
|
| 图 6 μ对初稳性各量的影响 Fig. 6 Effects on each part of initial metacentric height by μ | |
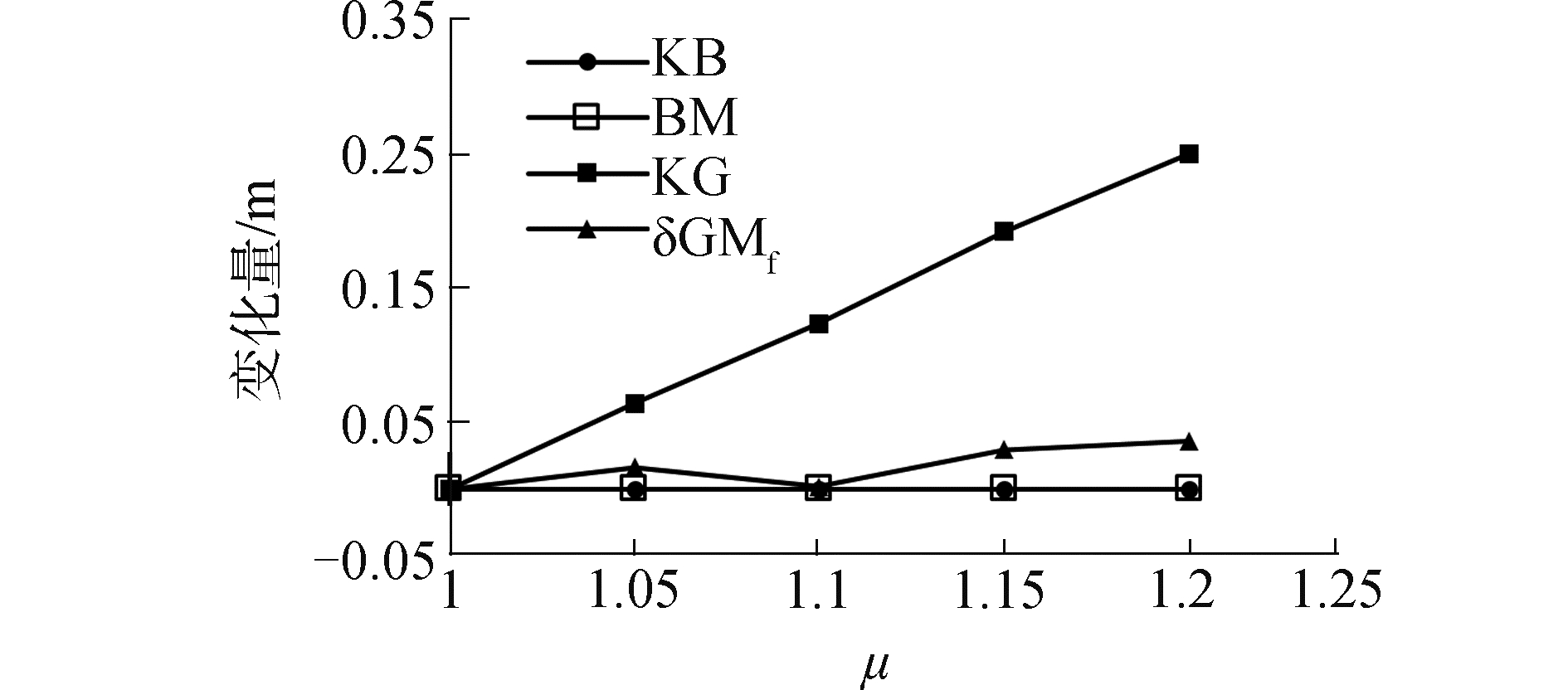
由图 5可以看出,随着维修设备重量系数μ的增加,初稳性高度值呈下降趋势。为深入探究μ对初稳性高度的影响,根据式(1),将初稳性高度分成4个量分别探讨,见图 6。该图是以μ=1时的GM值为基准的比较结果,可以看出在保证船体正浮的情况下,KB、BM不随μ的变化而变化,δGMf小范围内波动,KG的变化最为明显,随着μ的增加而增加。因此KG增加是GM随μ的增加而降低的主要原因。通过比较μ各值下的最优压载方案发现,随着μ的增加,可调压载水量减少,其降低船舶重心的能力减弱,是导致船舶重心升高的主要原因。
半潜维修船在浮装大型故障设备时,故障设备放置位置不同会导致整体重心、船舶浮心等的相对位置变化,需要不同的压载方案进行调整,对稳性会产生一定的影响。对于最优方案,即当浮力舱配置数量为8个时,船舶整体的浮心坐标为(112.11, 0.00, 5.57),分别对故障设备放置位置在x、y方向上作敏感性分析。
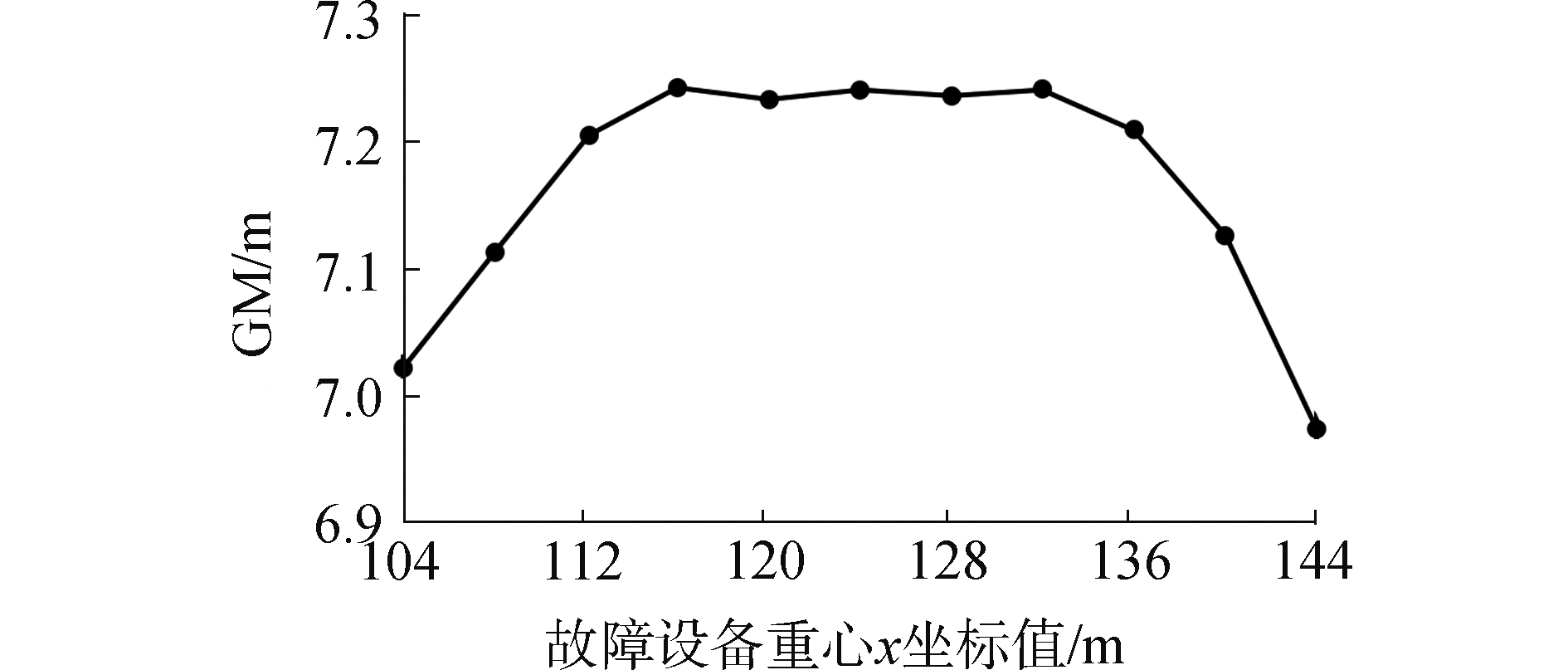
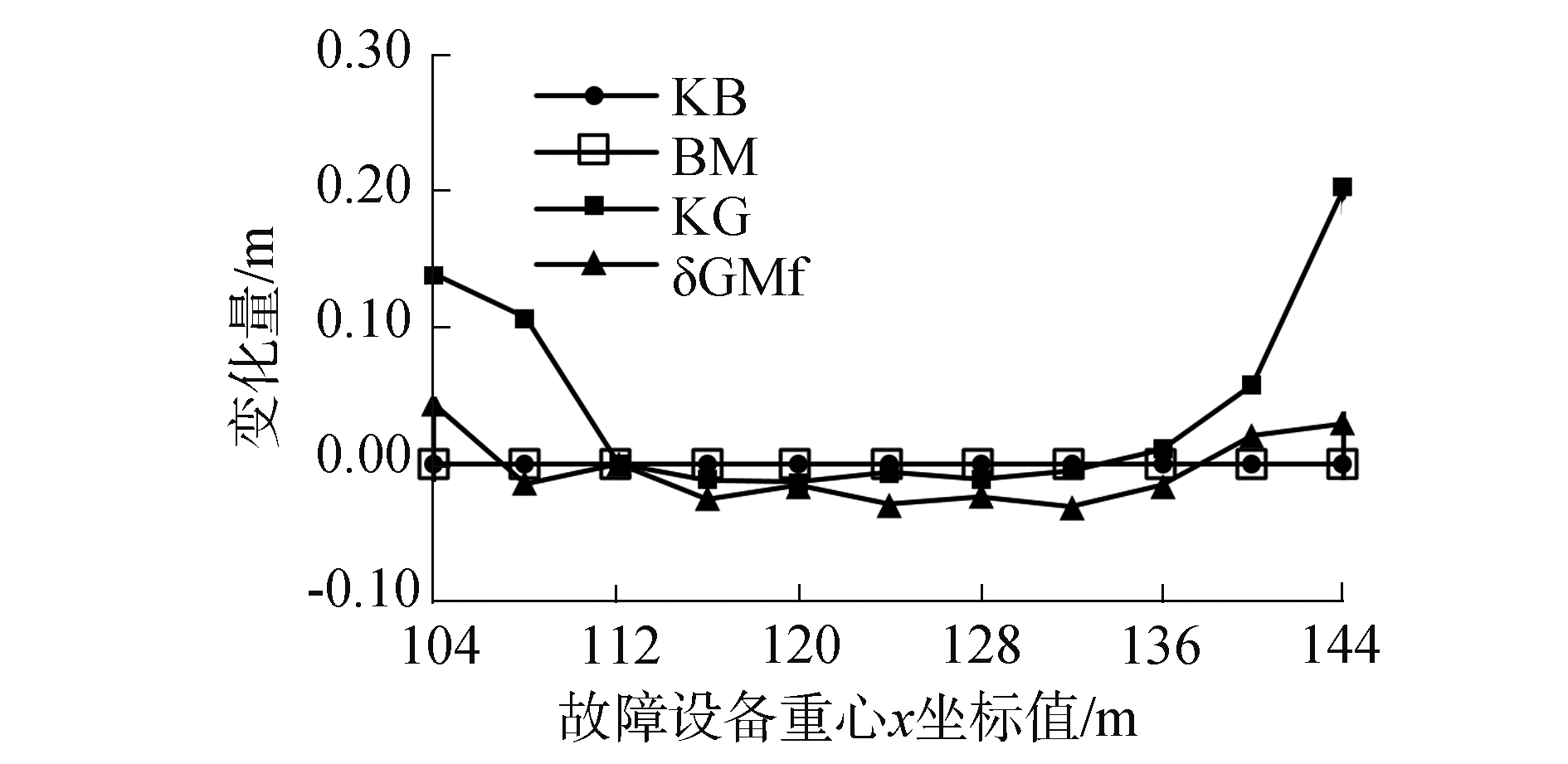
图 7是基于故障设备重心y坐标值为0时的计算结果,从图中可以看出随着故障船舶或设备重心x坐标值的增大,初稳性高度GM值总体呈现先增大、继而趋于平稳、后减小的趋势,在x∈[116, 132]的区域内GM值趋于平稳,且维持在较高水平,说明故障设备重心的x坐标值在该区域内时对GM值的影响较小,半潜维修船在浮装故障设备时将故障设备重心x坐标值控制在该区域内对初稳性有利。为了深入探究该区域出现的原因,采用与分析μ相同的方法得到图 8。该图是以最优方案的GM值为基准比较的结果,可以看出在保证船体正浮的情况下,KB、BM不随x的变化而变化,δGMf小范围内波动,KG的变化最为明显,随着x的增大呈现先减小、继而趋于平稳、后增加的趋势。因此KG变化是GM随x的变化而变化的主要原因。通过分析不同x值下的压载方案发现,当x取104 m或144 m时,更多的压载水用于保证船体正浮,压载水降低船舶重心的能力减弱,是导致船舶重心升高的主要原因。
|
Download:
|
| 图 7 故障设备重心x坐标值敏感性分析 Fig. 7 Sensitivity analysis of broken-down equipment′s coordinate value x | |
|
Download:
|
| 图 8 故障设备重心x坐标值对初稳性各量的影响 Fig. 8 Effects on each part of initial metacentric height by broken-down equipment′s coordinate value x | |
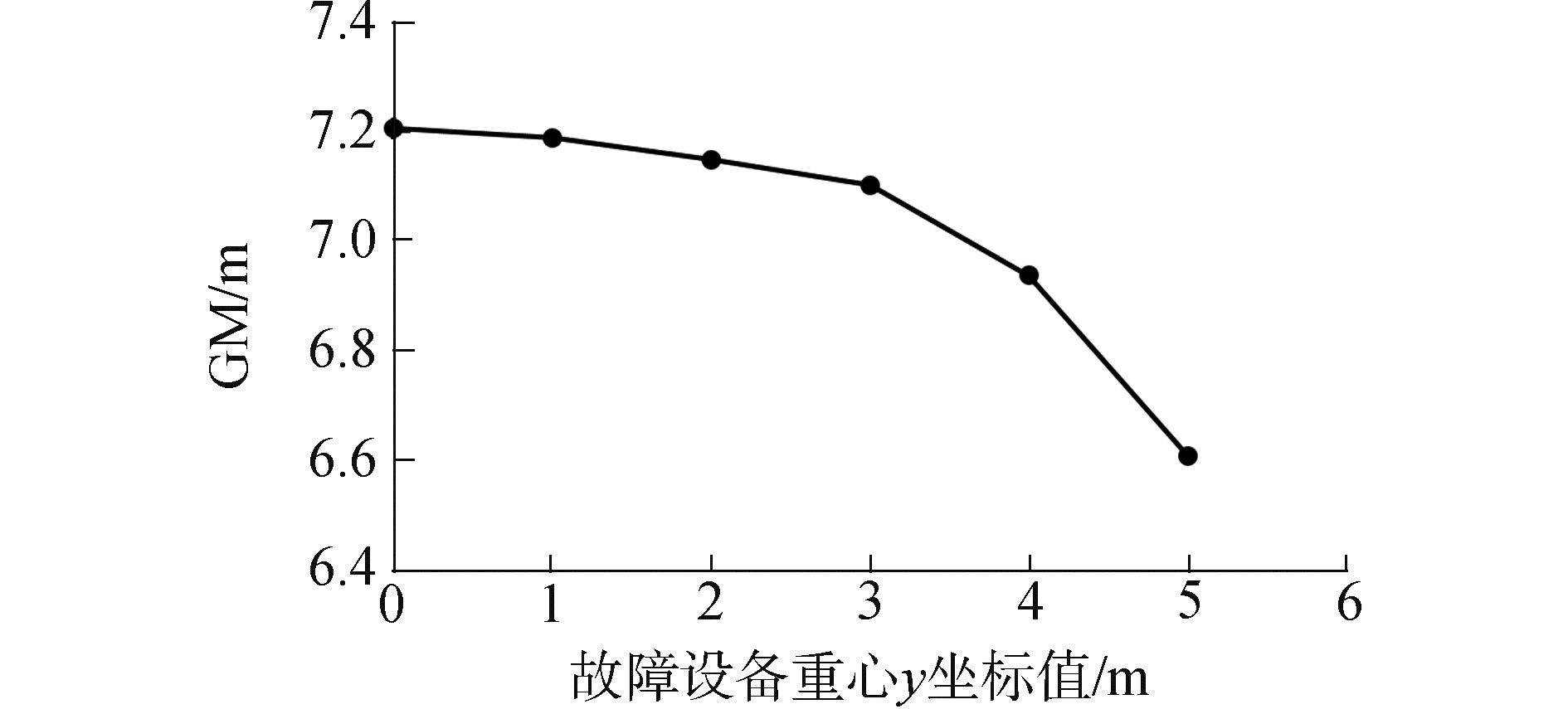
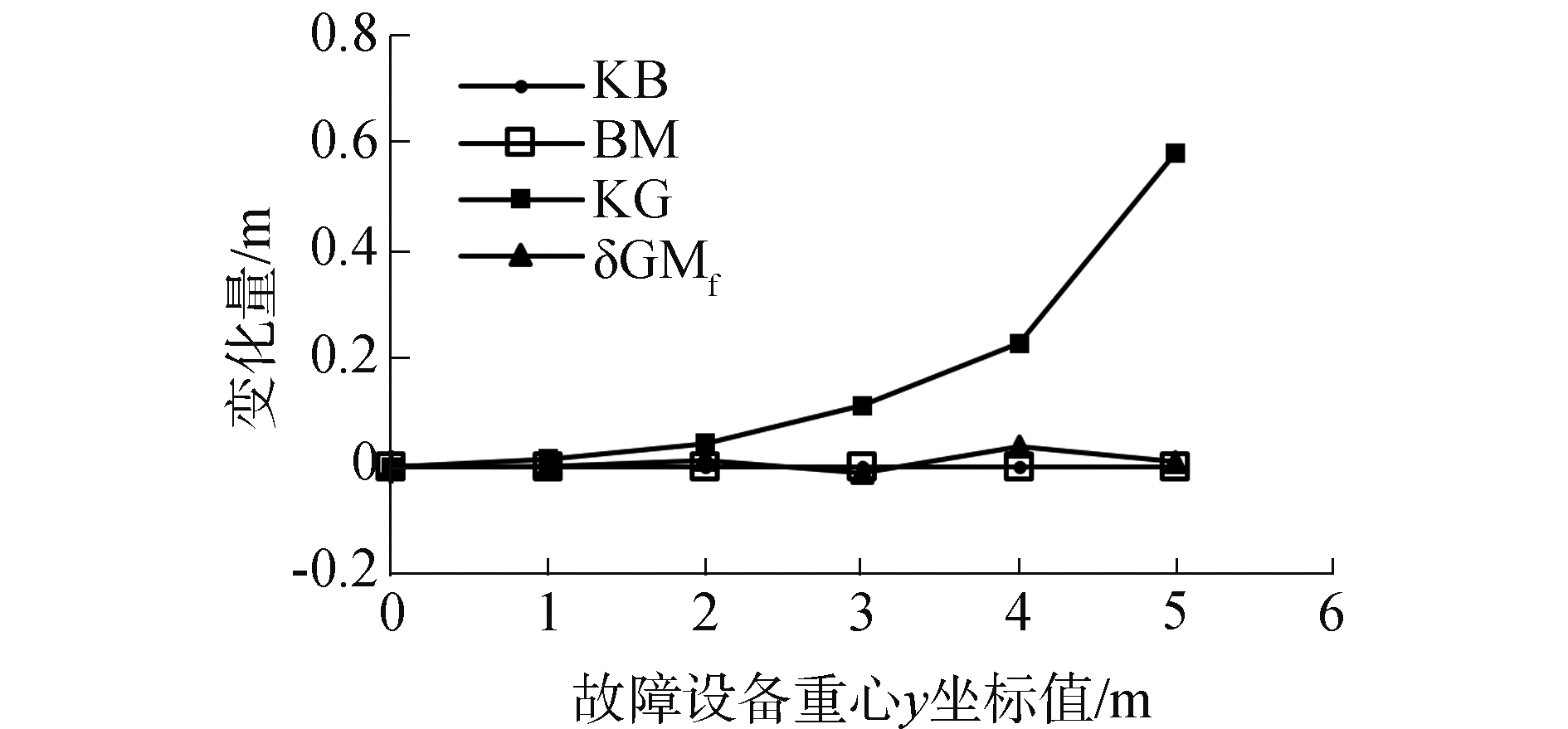
图 9为基于故障设备重心x坐标值为112.11 m,即与船舶整体浮心x坐标值相等时的计算结果,由于船舶是左右对称的,向左舷或右舷移动计算结果基本相同,故只讨论向右舷移动的情况。从图中可以看出初稳性高度值随着故障船舶或设备重心y坐标值的增大而降低,即故障设备越偏离维修甲板y向的中心,初稳性高度值越小,因此故障设备放置应使其重心尽可能接近y=0的位置。为深入探究y坐标值对初稳性高度的影响,采用与分析μ相同的方法得到图 10。该图是以y=0时的GM值为基准比较的结果,可以看出在保证船体正浮的情况下,KB、BM不随y的变化而变化,δGMf小范围内波动,KG的变化最为明显,随着y的增加而增加。因此KG增加是GM随y的增加而降低的主要原因。通过分析不同y值下的压载方案发现,随着y的增加,更多的压载水用于保证船体正浮(特别地,当故障设备移动到y=6 m处时,压载水已难以保证船体正浮),压载水降低船舶重心的能力减弱,是导致船舶重心升高的主要原因。
|
Download:
|
| 图 9 故障设备重心y坐标值敏感性分析 Fig. 9 Sensitivity analysis of broken-down equipment′s coordinate value y | |
|
Download:
|
| 图 10 故障设备重心y坐标值对初稳性各量的影响 Fig. 10 Effects on each part of initial metacentric height by broken-down equipment′s coordinate value y | |
1) 计算结果表明建立的半潜维修船上浮工况多功能浮力舱配置及压载优化模型能为决策者提供安全可靠的浮力舱配置方案及相应的船舶压载方案。
2) 在维修作业吃水处,按照设定的原则配置多功能浮力舱,可有效增加水线面面积,对提高船舶初稳性高度具有较大的作用。
3) 通过变参数分析法,探究了维修设备重量系数、故障船舶或设备放置位置对初稳性高度的影响规律:在保证维修能力的前提下,降低维修设备重量对维修作业吃水下的船舶初稳性有利;存在一个优化放置区域,当故障船舶或设备的重心位于该区域时船舶初稳性较大,超出该区域初稳性会降低。
该方法为解决半潜维修船携带维修设备浮装故障船舶或大型海洋工程设备至维修作业吃水的安全问题提供了一种途径,可为半潜维修船具体维修任务中上浮作业提供指导。此外,若携带的维修设备较轻,半潜维修船在浮装故障船舶或大型海洋工程设备时,也可能导致压载能力不足,难以安全下潜至浮装吃水。由于下潜作业过程可能遇到的问题较上浮作业有较大差异,因此将在后续文章中介绍。
| [1] |
谢新连, 桑惠云, 张扬. 一种舰船远海维修保障新方案[J]. 舰船科学技术, 2013, 35(12): 50-54. XIE Xinlian, SANG Huiyun, ZHANG Yang. A novel scheme for ship repair support at sea[J]. Ship science and technology, 2013, 35(12): 50-54. DOI:10.3404/j.issn.1672-7649.2013.12.011 (  0) 0)
|
| [2] |
桑惠云, 谢新连, 马梦知. 自航式半潜维修船的需求分析与概念设计[J]. 中国航海, 2014, 37(4): 79-83. SANG Huiyun, XIE Xinlian, MA Mengzhi. Conceptual design of self-propelled semi-submergible repair ship and its requirement analysis[J]. Navigation of China, 2014, 37(4): 79-83. DOI:10.3969/j.issn.1000-4653.2014.04.017 (  0) 0)
|
| [3] |
FRANCESCUTTO A. Intact stability criteria of ships-past, present and future[J]. Ocean engineering, 2016, 120: 312-317. DOI:10.1016/j.oceaneng.2016.02.030 (  0) 0)
|
| [4] |
BACKALOV I, BULIAN G, CICHOWICZ J, et al. Ship stability, dynamics and safety:status and perspectives from a review of recent STAB conferences and ISSW events[J]. Ocean engineering, 2016, 116: 312-349. DOI:10.1016/j.oceaneng.2016.02.016 (  0) 0)
|
| [5] |
NEVES M A S. Dynamic stability of ships in regular and irregular seas-an overview[J]. Ocean engineering, 2016, 120: 362-370. DOI:10.1016/j.oceaneng.2016.02.010 (  0) 0)
|
| [6] |
BACKALOV I, BULIAN G, ROSÉN A, et al. Improvement of ship stability and safety in intact condition through operational measures:challenges and opportunities[J]. Ocean engineering, 2016, 120: 353-361. DOI:10.1016/j.oceaneng.2016.02.011 (  0) 0)
|
| [7] |
BACKALOV I. Impact of contemporary ship stability regulations on safety of shallow-draught inland container vessels[J]. Safety science, 2015, 72: 105-115. DOI:10.1016/j.ssci.2014.09.001 (  0) 0)
|
| [8] |
谢新连, 李晓君, 苏晨, 等. 关于半潜船初稳性高度限值的探讨[J]. 大连海事大学学报, 2014, 40(3): 37-41. XIE Xinlian, LI Xiaojun, SU Chen, et al. Discussion about the metacentric height limit of a loaded semi-submersible vessel[J]. Journal of Dalian Maritime University, 2014, 40(3): 37-41. DOI:10.3969/j.issn.1006-7736.2014.03.008 (  0) 0)
|
| [9] |
李晓君, 谢新连, 赵家保. 影响半潜船初稳性高度限值因素及其作用机理[J]. 哈尔滨工程大学学报, 2015, 36(1): 109-112, 118. LI Xiaojun, XIE Xinlian, ZHAO Jiabao. The influencing factors of semi-submersible vessel's metacentric height limits and mechanism of action[J]. Journal of Harbin Engineering University, 2015, 36(1): 109-112, 118. (  0) 0)
|
| [10] |
BARA C, CORNOIU M, POPESCU D. An optimal control strategy of ballast systems used in ship stabilization[C]//Proceedings of the 20th Mediterranean Conference on Control & Automation. Barcelona, Spain, 2012: 878-883.
(  0) 0)
|
| [11] |
BARA C, POPESCU D, FILIP F G. SCADA system for ship stabilization designed using an expert system[J]. IFAC proceedings volumes, 2013, 46(24): 1-6. DOI:10.3182/20130911-3-BR-3021.00014 (  0) 0)
|
| [12] |
刘志杰, 刘晓宇, 熊伟, 等. 起重船舶压载水调配优化模型[J]. 交通运输工程学报, 2017, 17(2): 83-89. LIU Zhijie, LIU Xiaoyu, XIONG Wei, et al. Optimization model of ballast water allocation for crane ship[J]. Journal of traffic and transportation engineering, 2017, 17(2): 83-89. DOI:10.3969/j.issn.1671-1637.2017.02.009 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


