2. 河北环境工程学院 信息工程系, 河北 秦皇岛 066102;
3. 上海工程技术大学 数理与统计学院, 上海 201620
2. Department of Information Engineering, Hebei University of Environmental Engineering, Qinhuangdao 066102, China;
3. School of Mathematics, Physicals and Statistics, Shanghai University of Engineering Science, Shanghai 201620, China
在分子建模、基因蛋白质交互网络、社交网络等领域,通常用图来表示其中的复杂模型。随着图的重要性日益凸显,高效的图数据管理成为当前数据库领域研究的重点问题之一。
子图同构查询是图数据查询中的基础问题。给定数据图G和查询图Q,子图同构[1-5]是在G中找到所有与Q有相同结构的子图。子图同构查询广泛应用于蛋白质相互作用分析、图分类、电子电路计算机辅助设计、化学复合搜索和无线感知网络等领域。虽然子图同构理论上属于NP-hard[6]问题,但已有很多方法可以在较为合理的时间内返回子图同构的查询结果。
现有的子图同构算法[7-19]通常采用“过滤—验证”策略,主要是通过构建图索引,以较小的代价快速对数据图进行剪枝来搜索与查询图同构的子图。依据其适用的对象可以分为两类:
1) 针对小图的图数据库进行子图同构查询,主要算法包括FG-Index[11]、gIndex[12]、Graph-Grep[13]、gCode[14]、C-Tree[15]。当数据图为一个大图时,这类方法效率低下甚至失效;
2) 针对一个大图进行子图同构查询,主要算法包括VF2[16]、QuickSI[9]、GraphQL[17]、SPath[3]、TurboIso[18]和TurboIsoBoosted[19]等。文献[18]已经验证,TurboIso算法能够应用于大图,且算法性能优于VF2、QuickSI、GraphQL和Spath算法。
TurboIsoBoosted[19]算法是在TurboIso算法的基础上的优化和改进,它利用数据图中顶点之间的关系为数据图构建索引。然后利用索引在这2个超图上进行顶点过滤,最后对得到的候选集合进行子图同构验证。通过在Yeast、Human和Wordnet数据集上分别执行TurboIso和TurboIsoBoosted算法可知,与不构建超图的子图同构算法(TurboIso)相比,应用超图的子图同构算法(TurboIsoBoosted)把平均迭代次数从900、2 914和3 914次减少到551、112和900次。超图索引具有较强的剪枝效果,可以有效减少候选顶点的个数从而提高子图同构查询的效率。
TurboIsoBoosted算法在进行子图同构查询时采用为数据图构建索引的方法,是目前查询性能最好的算法。但是,TurboIsoBoosted算法在索引构建方面仍然存在一些不足:1)查找等价顶点时存在冗余计算导致算法效率低;2)索引构建时中间结果数据量大导致算法空间占用大、扩展性差。针对这些问题,本文在深入分析了顶点邻居的存储结构后,根据语法等价的顶点的不同类别用不同方式表示等价顶点的邻居集合,设计了基于2次排序查找等价顶点的索引构建算法(adapted graph based on T-SSEsearch, AGTS)来降低索引构建的空间占用量,提升索引构建的效率和扩展性。
1 子图同构相关概念子图同构查询既适用于有向图,也适用于无向图。为了方便论述,在本文中只讨论顶点带标签的无向图,将顶点带有标签的无向图简称图。
定义1(图[19]):图G是一个四元组G={V, E, Σ, L}。其中,V是顶点的非空集合,E⊆V×V是边的集合,Σ是顶点标签的集合,L是标签分配函数,对∀v∈V都有L(v)表示顶点v标签,其中,L(v)∈Σ。
定义2(子图同构[19]):给定数据图G={V, E, Σ, L}和查询图Q={VQ, EQ, ΣQ, LQ},子图同构是一个双射函数f: VQ→V,同时满足如下2个条件:1)∀u∈VQ,LQ(u)=L(f(u));2)∀(ui, uj)∈EQ,(f(ui), f(uj))∈E。
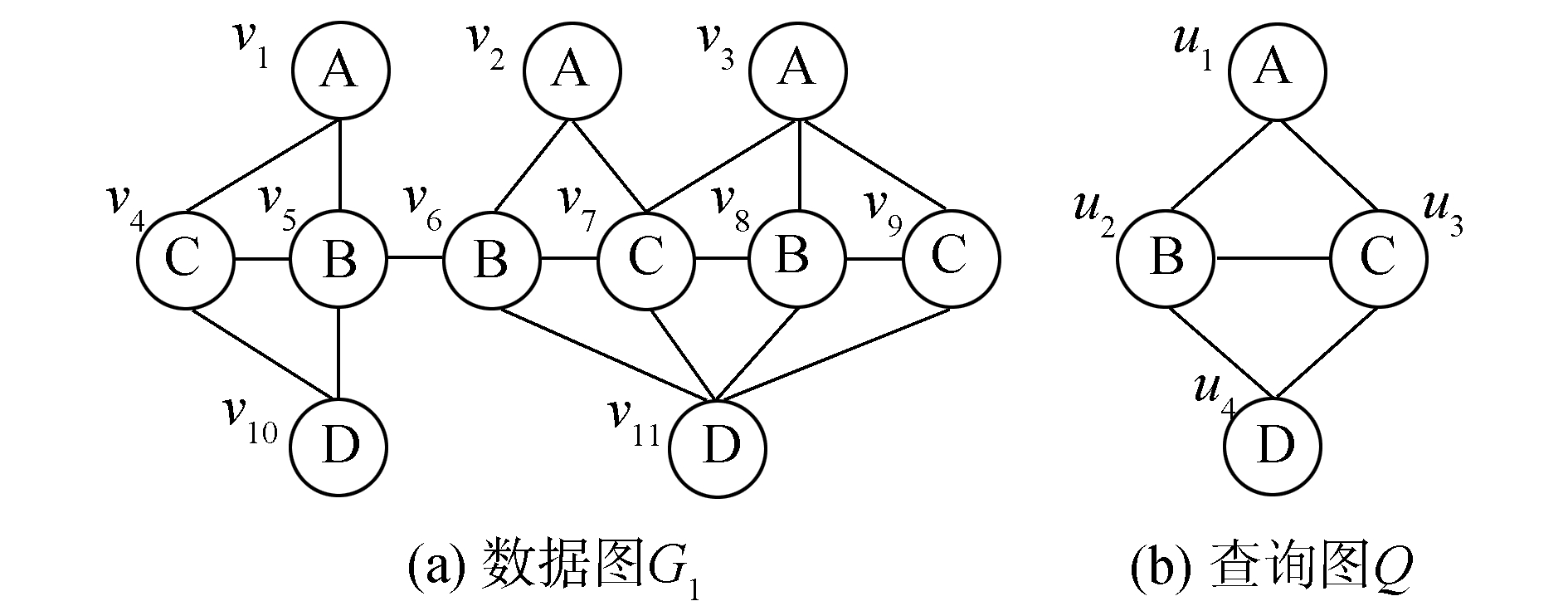
例1,给定如图 1所示的数据图G1和查询图Q,其中G1中的子图(v1, v5, v4, v10)、(v2, v6, v7, v11)、(v3, v8, v7, v11)和(v3, v8, v9, v11)均与查询图Q同构。
|
Download:
|
| 图 1 数据图G1和查询图Q Fig. 1 Data graph G1 and query graph Q | |
定义3(语法包含[19]):给定数据图G和其中的一对顶点vi和vj,如果L(vi)=L(vj)并且Adj(vj)-{vi}⊆Adj(vi)-{vj},其中Adj(vi)和Adj(vj)分别是vi和vj的邻居集合,则称vi语法包含vj,记为vi>vj。语法包含简称包含,用SC表示。
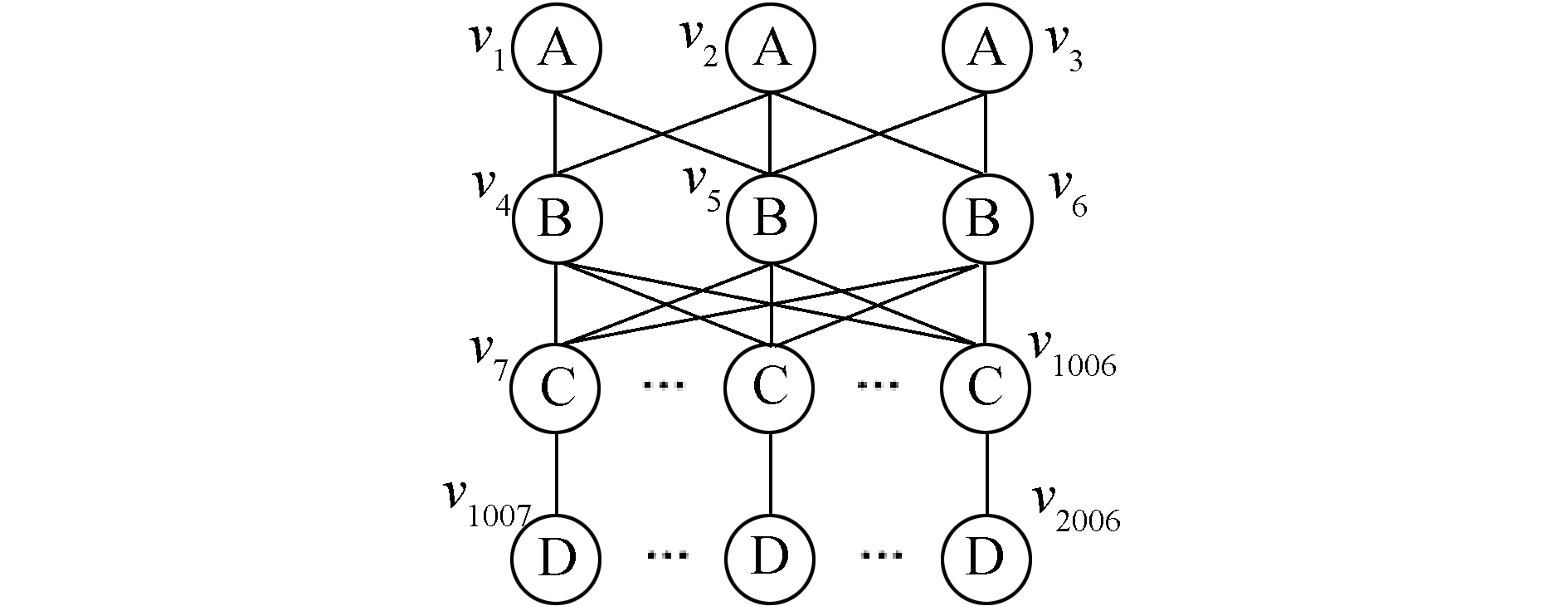
例2,在图 2所示的数据图G2中,顶点v1、v2和v3具有相同的标签,即L(v1)=L(v2)=L(v3)=A,它们的邻居集合分别是:Adj(v1)={v4, v5},Adj(v2)={v4, v5, v6}和Adj(v3)={v5, v6}。因为Adj(v1)-{v2}⊆Adj(v2)-{v1},所以可知v2语法包含v1,即v2>v1,同理,v2>v3。
|
Download:
|
| 图 2 数据图G2 Fig. 2 Data graph G2 | |
定义4(语法等价[19]):给定数据图G和其中的一对顶点vi和vj,如果L(vi)=L(vj)并且Adj(vj)-{vi}=Adj(vi)-{vj},则称vi语法等价于vj,记为vi≃vj。语法等价简称等价,用SE表示。vi≃vj也称vi和vj是语法等价顶点,简称等价顶点。
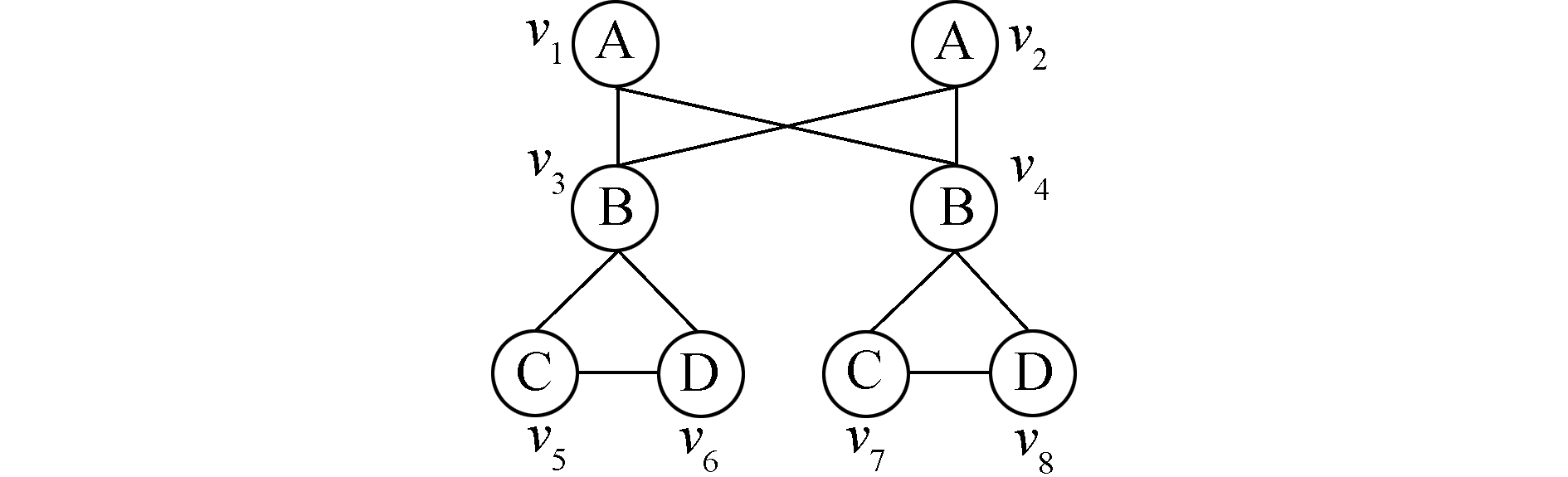
例3,在图 3所示的数据图G3中,顶点v1和v2有相同的标签,即L(v1)=L(v2),它们的邻居集合分别是:Adj(v1)={v3, v4},Adj(v2)={v3, v4},因为Adj(v1)-{v2}=Adj(v2)-{v1},所以v1≃v2。
|
Download:
|
| 图 3 数据图G3 Fig. 3 Data graph G3 | |
根据语法等价关系,可以对数据图进行语法等价类的划分。如图 3所示的G3中的顶点,只有v1≃v2,因此,图G3的等价类可以划分为7个:{v1, v2}、{v3}、{v4}、{v5}、{v6}、{v7}和{v8}。
2 高效的数据图索引构建方法 2.1 问题分析TurboIsoBoosted算法中数据图索引构建的关键步骤是查找等价顶点。TurboIsoBoosted按照顶点序号升序分步查找每个顶点的等价顶点:1)在当前顶点的一步可达邻居中遍历查找两两互连的等价顶点;2)在两步可达的邻居中遍历查找互不相连的等价顶点。这样可以准确地找出所有的等价顶点,但过程中存在重复计算的问题,严重影响了SE超图的构建效率。
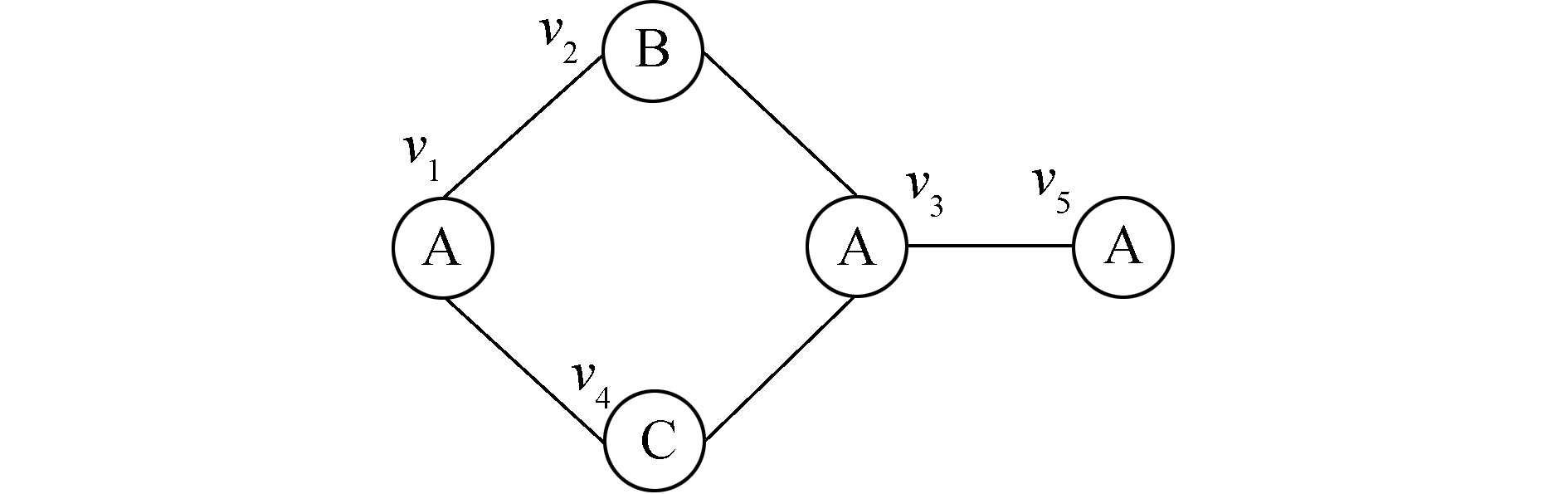
在图 4所示的数据图G4中,以查找顶点v1的等价顶点为例说明TurboIsoBoosted算法查找等价顶点的过程。首先遍历其一步可达的邻居集合,发现不存在与之等价的顶点,因为其中没有顶点标签为A;然后遍历其2步可达的邻居集合,在通过路径v1v2v3验证顶点v3时,因为v3和v1的标签相同但邻居不同,所以v3和v1不是等价顶点,v3不会被标记为已访问顶点,而通过路径v1v4v3时又会再次对v3进行验证,因此存在顶点的重复计算。
|
Download:
|
| 图 4 数据图G4 Fig. 4 Data graph G4 | |
此外,TurboIsoBoosted算法索引构建的空间代价较高,因为在执行过程中需要维护2个倒排表,分别存储顶点与其一步可达和两步可达的邻居映射关系。当数据规模变大时,超图构建算法的效率会变差且扩展性较差,因此,需要对超图构建的算法进行优化和改进。
2.2 基本思想为了减少顶点的重复计算,对等价顶点的查找过程进行深入研究后发现:两两互连的等价顶点,其邻居集合中包含对方顶点;两两互不相连的等价顶点的邻居集合中不包含对方顶点。而在两两互连的等价顶点邻居中加入顶点自身后,可以使得其邻居集合完全相等;在两两互不相连的等价顶点的邻居中去掉顶点自身,也可以得到完全相等的邻居集合。因此,本文提出将顶点自身加入到其邻居集合中,形成新的邻居链表的表示,以此来查找两两互连的等价顶点,然后在新的邻居链表中去掉顶点自身来查找两两互不相连的等价顶点。
由此提出基于2次排序查找等价顶点的数据图索引的构建方法(AGTS)来减少顶点的重复计算,从而提高索引构建效率。AGTS算法构建数据图索引的主要过程是:
1) 利用顶点的邻居集合对顶点进行第1排序,查找两两互连的等价顶点;将未访问顶点的邻居链表中去掉顶点自身,并按照其邻居进行第2次排序,查找两两互不相连的等价顶点,将两次查找结果取并得到所有的等价顶点;
2) 根据等价顶点划分等价类,将同一个等价类中的顶点形成一个超顶点,然后按照原图中边的关系连接超顶点,得到语法等价超图,即SE超图;
3) 在SE超图中,按照其中超顶点之间的包含关系形成对应的有向边,得到语法包含超图即SC超图。
2.3 算法描述算法1用于构建数据图的索引,数据图G中顶点的邻居集合采用包含顶点自身的邻居链表来表示。SE超图和SC超图与原数据图G具有相同的标签集合(第1行)。首先,将顶点按标签分组,建立标签与顶点的倒排表(第2行);然后将每组中的所有顶点存入数组SA,对组中的顶点进行第1次排序,查找其中两两互连的等价顶点,将等价类中的等价顶点压缩成一个超顶点(第3行)。在第1次排序后,将组中未被访问顶点的邻居链表中去掉顶点自身,并重新加入到数组SA中;对组中的顶点进行第2次排序,查找剩余顶点间互不相连的等价关系,将等价类中的等价顶点压缩成一个超顶点(第4行)。这样就找到了数据图中所有的等价顶点并形成了超顶点。然后为超顶点加边:若2个超顶点中所包含的原数据图中的顶点之间有边,则在这2个超顶点之间加入一条无向边(第5行),将所有的超顶点间边找到就形成了SE超图。最后在SE超图上查找超顶点的包含关系,在有包含关系的超顶点间加上一条由包含超顶点指向被包含超顶点的有向边(第6行),当找到超顶点间所有的有向边并对其进行传递约减最终形成SC超图(第7行)。
构建数据图索引的算法AGTS的具体描述如算法1所示。
算法1 AGTS
输入:数据图G
输出:SE超图和SC超图
Begin
Σsh←Σ
对顶点v∈V按标签分组
T-SSEsearch(SA, 1)
T-SSEsearch (SA, 2)
在超顶点Vsh中形成边Ese
for each edge (v, v′)∈E do
if v∈h, v′∈h′ and h≠h′ then Ese← Ese∪{(h, h′)}
按照超顶点的包含关系添加有向边形成Esc
transitivereduction(Vsh, Esc)
return SE超图和SC超图
End
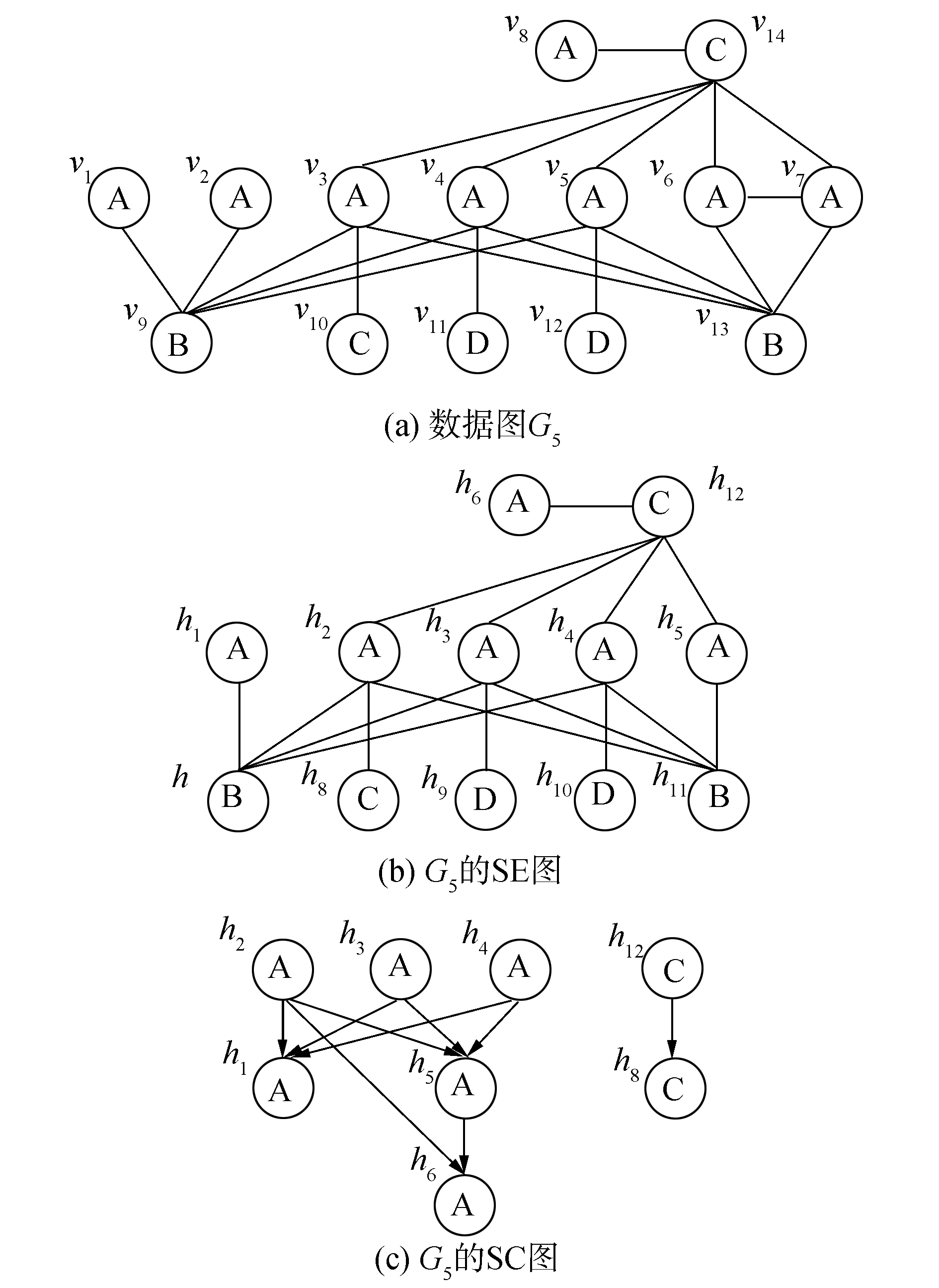
例如,在图 5(a)的图G5中,由于v1≃v2,v6≃v7,则G5的SE超图如图 5(b)所示。在图 5(b)中查找超顶点之间的包含关系,并进行传递约减最终得到的SC图如图 5(c)所示,其中省略了单个顶点。
|
Download:
|
| 图 5 数据图G5及其SE超图和SC超图 Fig. 5 Data graph G5 and its hypergraphs SE and SC | |
其中查找等价顶点的算法T-SSEsearch是一个递归的查找过程。Repartition函数是对图中的顶点按照等价关系进行快速排序,排序方式采取的是三数取中法。通过Repartition函数可以获得分界点的位置,包括:分界点temp、左右边界ltemp和rtemp(第2行)。若eqv未被访问,则创建一个与eqv标签相同的超顶点h,将eqv放入超顶点h中,并将eqv标记为已访问(第3~4行)。参数flag表示排序的次数,Clique依据flag的值和等价顶点个数来判断:若flag为1,在Repartition函数中直接比较邻居集合找到两两互连的等价顶点,则Clique为1;若flag为2,在Repartition函数中将邻居链表中的顶点自身去掉再比较的邻居集合,若等价顶点有多个,则找到的是两两互不相连的等价顶点,那么Clique为2;若当前等价顶点只有枢轴顶点一个,则Clique为0,即没有与之等价的顶点。将找到的所有等价顶点放入超顶点h中(第5~14行)。在temp左右两边递归调用T-SSEsearch算法以找到同标签的其他等价顶点(第15~17行)。具体描述如算法2所示。
算法2 T-SSEsearch
输入:顶点的数组SA[vfirst, v1, …, vlast], flag
输出:超顶点Vsh
Begin
while first < last do
Repartition(first, last, flag)
if eqv is not visited then
add eqv to Vsh, mark eqv as visited
if flag=1 then
h.Clique ← 1
for each i∈[first, ltemp]∪[rtemp, last] do
add SA[i] to Vsh
if flag=2 then
if ltemp-first + last-rtemp >=2 then
h.Clique ← 2
else h.Clique ← 0
for each i∈[first, ltemp]∪[rtemp, last] do
add SA [i] to Vsh
first←ltemp
T-SSEsearch (SA[vfirst, …, vlast], flag)
last ← temp-1
End
例如,在如图 5(a)所示的数据图G5中,标签为A的顶点的邻居集合的不同表示如表 1所示,其中第2列用来查找两两互连的等价顶点,第3列用来查找两两互不相连的等价顶点。
对数据图G5中标签为A的顶点使用T-SSEsearch算法查找等价顶点的主要过程:1)顶点按照序号升序排列,即{v1, v2, v3, v4, v5, v6, v7, v8},它们的邻居集合存储如表 1第2列所示,经过第1次排序后得到的顶点顺序为{v1, v3, v2, v5, v8, v6, v7, v4},通过比较得到v6和v7是互连的等价顶点;2)对剩余顶点仍按照序号升序排列,即{v1, v2, v3, v4, v5, v8},它们的邻居集合存储如表 1第3列所示,经过第2次排序后得到的顶点顺序为{v1, v2, v4, v8, v5, v3},通过比较得到v1和v2是互不相连的等价顶点。剩余顶点没有与其他顶点存在等价关系,单个顶点即为一个等价类,即数据图G5中标签为A的顶点共有6个等价类:{v1, v2}、{v3}、{v4}、{v5}、{v6, v7}和{v8},因此,对应形成如图 5(b)所示的6个超顶点h1~h6。
| 表 1 数据图G5中标签为A的顶点的两类邻居链表表示 Table 1 Representations of two adjacent lists of vertices labelled with A in G5 |
根据文献[24]可知,TurboIsoBoosted算法计算等价顶点的时间复杂度为O(|V|×N×d),其中d是图G中顶点的最大度,N是顶点中|2-step-SL(v)|的最大值,2-step-SL(v)表示图G中一步可达或是两步可达且标签与v相同的邻居顶点的集合。
而本文提出的AGTS算法在同一标签组中判断每一对顶点的等价性时需要依次对u和v的邻居顶点进行比较判断。由于本文中的无向图均采用邻接链表进行存储,而且分组后的顶点按序号升序存储,所以判断顶点u和v是否等价的时间复杂度为O(du+dv)。排序是采用三数取中的快速排序方法,当比较代价为O(1)时,排序的复杂度为O(|V|log|V|),而AGTS算法需要比较任一顶点的所有邻居,所以比较代价为Σv∈VO(dv)=O(|E|),那么2次排序查找等价顶点的时间复杂度为O(|V|log|V|×avg(du))=O(|E|log|V|)。
因此,AGTS算法在查找等价顶点的时间复杂度是O(|E|log|V|)。显然,AGTS算法在时间上要比TurboIsoBoosted算法构建图索引时高效。
2.4.2 空间复杂度TurboIsoBoosted算法在查找等价顶点过程中需要判断顶点一步可达和2步可达的邻居,所以在算法执行过程中要记录下顶点与其一步可达和2步可达的邻居之间的映射关系。由于无向图的邻接表中直接相连的两条边需要存储2次,所以存储一步可达的邻居映射关系需要的空间为2|E|;用2-step(v)表示与图中顶点v 2步可达的邻居集合,则存储2步可达的邻居映射关系最多需要的空间为|V|×|N|,其中|N|表示2-step(v)集合中的最大值;那么算法在查找等价顶点时的空间复杂度为O(2|E|+|V|×|N|)。
而本文提出的AGTS算法只需要比较顶点间直接相连的邻居,即只需存储顶点与其一步可达的邻居的映射关系,因此,AGTS算法的空间复杂度为O(2|E|)=O(|E|)。
由此可见,AGTS算法将查找等价顶点的空间需求降为线性,使得图索引构建算法在空间复杂度上得到了极大地优化。
3 基于实际数据集的实验比较 3.1 实验环境实验所用机器的基本配置为Intel Core i5-2 410 M主频为2.3 GHz的CPU,4 GB的内存和500 GB的硬盘,操作系统为64位的Windows 7。实验运行环境为Microsoft Visual Studio 2010,编程语言为Visual C++。
3.2 数据集本文使用5个具有不同特征的真实图数据集来测试算法性能,分别是:Yeast、Human、Wordnet、Youtube和Email,数据集的统计信息如表 2所示。Yeast是一个稀疏图,其中的顶点标签种类多;Human是一个稠密图,表示的是蛋白质交互网络图,其中的每个顶点的度都很大,因此查询顶点对应的候选顶点集合也很大;Wordnet是一个规模较大的稀疏图,但其标签种类只有5种;Youtube是一个顶点的标签只有1种的社交网络图;Email是一个无标签的图,为了便于实验,从130个标签中为其中的每个顶点随机地分配标签。实验中的查询图是从数据图中随机挑选的连通子图,每个查询图包含1~10条边。
| 表 2 数据集统计信息 Table 2 Statistical information of data sets |
由于TurboIsoBoosted算法是目前最优的通过顶点等价的定义对数据图构建超图索引的算法。因此,实验主要将本文提出的超图构建算法AGTS与TurboIsoBoosted算法中超图构建部分进行实验对比。2种算法最终得到的SE超图和SC超图是相同的,所以实验的评价指标包括:1)超图索引的构建时间;2)构建超图时内存使用情况。
3.3.1 超图索引的构建时间超图索引构建时间的快慢对子图同构算法的执行效率有显著的影响。表 3展示了这2个算法在5个数据集上构建超图索引所需要的平均时间的对比。其中,directSEsearch代表TurboIsoBoosted算法中超图构建部分。前4个数据集给出的是构建SE超图和SC超图的时间之和,Email数据集只给出SE超图的平均构建时间,因为Email数据集中超顶点间的SC关系比较多,导致构建SC超图所需要的时间比较长,为了方便对比,在Email数据集上略去了SC超图的构建时间。
| 表 3 超图构建的平均时间 Table 3 Average time of hypergraph adaptation |
由表 3可知,AGTS算法比TurboIsoBoosted算法的超图构建算法高效。且随着数据图规模的增大,AGTS算法的高效性尤其明显,在Wordnet数据集上,AGTS算法比TurboIsoBoosted算法的构建索引部分快了将近2个数量级。在查找等价顶点的过程中,TurboIsoBoosted是依次遍历图中顶点的一步与两步可达邻居集合;而AGTS算法根据等价顶点类别的不同分别查找,减少了顶点的查找和验证次数。
3.3.2 内存占用情况算法执行过程中内存占用越少,说明算法的空间复杂度越低,也就是说当数据规模增大时,不会对内存的占用产生巨大的影响,因而算法的扩展性也不会受到影响。
表 4展示了这2个算法在5个数据集上构建超图过程中计算机内存的占用情况对比。从表中可知,AGTS算法的内存占有量要小于TurboIsoBoosted算法,AGTS算法的内存占有量比TurboIsoBoosted算法的内存占有量减少了约45%~71.43%。这是因为TurboIsoBoosted算法需要2个倒排表来存储顶点与1步可达和2步可达邻居的映射关系,且在等价顶点的查找过程中需要频繁访问和维护这2个倒排表,使内存消耗增大。而AGTS算法只需要维护一个倒排表来存储顶点与其1步可达邻居的映射关系,减少了内存的占有量。由此可见,AGTS算法的空间复杂度最低,并且有良好的扩展性。
| 表 4 超图构建过程中内存占用情况 Table 4 Memory occupancy in hypergraph adaptation |
1) 通过对等价顶点的研究,提出了应用两种不同的邻居链表来表示顶点的邻居信息的思想,以此提出了通过两次排序查找等价顶点的图索引构建算法AGTS,解决了现有子图同构算法在对数据图构建索引的预处理中存在效率低扩展性差的问题。
2) 从空间和时间复杂度方面说明了AGTS算法的优越性,并在5个数据集上进行实验,实验结果说明,与现有方法相比,AGTS算法提高了超图构建的时间效率,降低了超图构建时占用的内存空间,提高了超图构建算法的扩展性。
下一步还将就基于该索引的子图同构算法进行进一步研究。
| [1] |
BONNICI V, GIUGNO R, PULVIRENTI A, et al. A subgraph isomorphism algorithm and its application to biochemical data[J]. BMC bioinformatics, 2013, 14(S7): S13. (  0) 0)
|
| [2] |
KIM J, SHIN H, HAN W A, et al. Taming subgraph isomorphism for RDF query processing[J]. Proceedings of the VLDB endowment, 2015, 8(11): 1238-1249. DOI:10.14778/2809974 (  0) 0)
|
| [3] |
ZHAO Peixiang, HAN Jiawei. On graph query optimization in large networks[J]. Proceedings of the VLDB endowment, 2010, 3(1/2): 340-351. (  0) 0)
|
| [4] |
BONNICI V, GIUGNO R. On the variable ordering in subgraph isomorphism algorithms[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2017, 14(1): 193-203. (  0) 0)
|
| [5] |
余靖, 韩玉. URSI:高效的子图同构查询算法[J]. 燕山大学学报, 2016, 40(6): 517-523. YU Jing, HAN Yu. URSI:High efficient query algorithm on subgraph isomorphism[J]. Journal of Yanshan University, 2016, 40(6): 517-523. DOI:10.3969/j.issn.1007-791X.2016.06.007 (  0) 0)
|
| [6] |
SHAMIR R, TSUR D. Faster subtree isomorphism[C]//Proceedings of the 5th Israeli Symposium on Theory of Computing and Systems. Ramat-Gan, Israel, 1997: 126-131.
(  0) 0)
|
| [7] |
SAMSI S, GADEPALLY V, HURLEY M, et al. Static graph challenge: subgraph isomorphism[C]//Proceedings of the IEEE High Performance Extreme Computing Conference. Waltham, MA, USA, 2017: 1-6.
(  0) 0)
|
| [8] |
REN Xuguang, WANG Junhu. Multi-query optimization for subgraph isomorphism search[J]. Proceedings of the VLDB endowment, 2016, 10(3): 121-132. DOI:10.14778/3021924 (  0) 0)
|
| [9] |
ZHAO Peixiang, YU J X, YU P S. Graph indexing: Tree + delta < =graph[C]//Proceedings of the 33rd International Conference on Very Large Data Bases. Vienna, Austria, 2007: 938-949.
(  0) 0)
|
| [10] |
LEE J, HAN W S, KASPEROVICS R, et al. An in-depth comparison of subgraph isomorphism algorithms in graph databases[J]. Proceedings of the VLDB endowment, 2012, 6(2): 133-144. DOI:10.14778/2535568 (  0) 0)
|
| [11] |
CHENG J, KE Yiping, NG W, et al. FG-index: towards verification-free query processing on graph databases[C]//Proceedings of 2007 ACM SIGMOD International Conference on Management of Data. Beijing, China, 2007: 857-872.
(  0) 0)
|
| [12] |
YAN Xifeng, YU P S, HAN Jiawei. Graph indexing based on discriminative frequent structure analysis[J]. ACM transactions on database systems, 2005, 30(4): 960-993. DOI:10.1145/1114244 (  0) 0)
|
| [13] |
SHASHA D, WANG J T L, GIUGNO R. Algorithmics and applications of tree and graph searching[C]//Proceedings of the 21st ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems. Madison, Wisconsin, USA, 2002: 39-52.
(  0) 0)
|
| [14] |
ZOU Lei, CHEN Lei, YU J X, et al. A novel spectral coding in a large graph database[C]//Proceedings of the 11th International Conference on Extending Database Technology: Advances in Database Technology. Nantes, France, 2008: 181-192.
(  0) 0)
|
| [15] |
HU Huahai, SINGH A K. Closure-tree: an index structure for graph queries[C]//Proceedings of the 22nd International Conference on Data Engineering. Atlanta, GA, USA, 2006: 38.
(  0) 0)
|
| [16] |
CORDELLA L P, FOGGIA P, SANSONE C, et al. A (sub)graph isomorphism algorithm for matching large graphs[J]. IEEE transactions on pattern analysis and machine intelligence, 2004, 26(10): 1367-1372. DOI:10.1109/TPAMI.2004.75 (  0) 0)
|
| [17] |
HE Huahai, SINGH A K. Graphs-at-a-time: query language and access methods for graph databases[C]//Proceedings of 2008 ACM SIGMOD International Conference on Management of Data. Vancouver, Canada, 2008: 405-418.
(  0) 0)
|
| [18] |
HAN W S, LEE J, LEE J H. Turboiso: towards ultrafast and robust subgraph isomorphism search in large graph databases[C]//Proceedings of 2013 ACM SIGMOD International Conference on Management of Data. New York, USA, 2013: 337-348.
(  0) 0)
|
| [19] |
REN Xuguang, WANG Junhu. Exploiting vertex relationships in speeding up subgraph isomorphism over large graphs[J]. Proceedings of the VLDB endowment, 2015, 8(5): 617-628. DOI:10.14778/2735479 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


