2. 海军工程大学 舰船与海洋学院, 湖北 武汉 430033
2. College of Naval Architecture and Ocean Engineering, Naval University of Engineering, Wuhan 430033, China
小水线面双体船(small water-plane area twin hull,SWATH)具有形状细长、面积较小的水线面和深置于水中、排水体积较大的下体。与排水量相当的常规单体船相比,其在大风浪中的运动响应、运动加速度和失速较小,自然运动周期较长,具有较好的稳定性和优良的耐波性[1-4]。
学者针对小水线面双体船的耐波性进行了大量研究,多数研究是在频域内采用二维切片法[5-8]。开展耐波性计算时,一般分别求解小水线面双体船船体、粘性和稳定鳍的水动力系数及波浪干扰力。耐波性频域方法适合于解决船舶周期性的稳态运动问题,无法处理大幅运动、甲板上浪、艏部出水等非线性和瞬态问题,而在时域内可以更好地求解上述问题。但针对小水线面双体船的耐波性的时域研究并不多见。Hong[9]、Aurthur[10]、Fang[11]、Liang[12]等在切片法基础上,建立了时域内的小水线面双体船耐波性计算方法,但时域内每一时间步的船体水动力系数均是基于频域中水动力系数的稳态结果。这种由频域切片法拓展而来的时域方法没有考虑水动力的记忆效应,因此存在理论上的缺陷。
在时域内求解船舶耐波性时,需要求解表示记忆效应的时延函数,求解方法可以分为直接法和间接法。直接法是指在时域内直接建立初边值问题,基于脉冲响应函数法,将扰动速度势分为瞬时效应和记忆效应分别求解,进而得到时延函数等水动力系数[13]。间接法是指频时域转换法,将在频域求解得到的水动力系数变换至时域,得到时延函数[14]。唐恺[13]的相关研究表明,与直接法相比,频时域转换法更为便捷,且在中低速下的计算结果与直接计算法非常接近。Kim[15]、洪亮[16]、Jiang[17]等采用此种方法研究了波浪中船体与液舱晃荡耦合运动的时域模拟。
本文以三维移动脉动源格林函数为内核,将频域内的水动力系数转换至时域求解时延函数,并计入2片体之间的水动力干扰、粘性和稳定鳍的影响,建立了小水线面双体船耐波性时域线性计算方法。比较了在平动坐标系和随动坐标系下求解船体运动方程对运动计算结果的影响,并与频域计算结果和试验结果进行了对比。
1 常规船舶耐波性时域计算方法 1.1 坐标系在研究船舶耐波性问题时,一般引入如图 1所示的三维空间直角坐标系,分别为:空间固定坐标系O0X0Y0Z0、空间平动坐标系Oxyz和空间随动坐标系O′x′y′z′。空间平动坐标系Oxyz位于船体的平衡位置上,以船体航速U随船平移。其原点O为船体重心在未受扰动的静水面上的投影点,平面Oxy与未受扰动时的静水面重合。空间随动坐标系O′x′y′z′与船体固联,随船一起作摇荡运动。在t=0时刻,空间随动坐标系O′x′y′z′与空间平动坐标系Oxyz重合。空间随动坐标系在空间平动坐标系Oxyz中的位置表示了船体的六自由度运动(η1, η2, η3, η4, η5, η6)。

|
Download:
|
| 图 1 耐波性研究坐标系 Fig. 1 Coordinate systems of seakeeping investigation | |
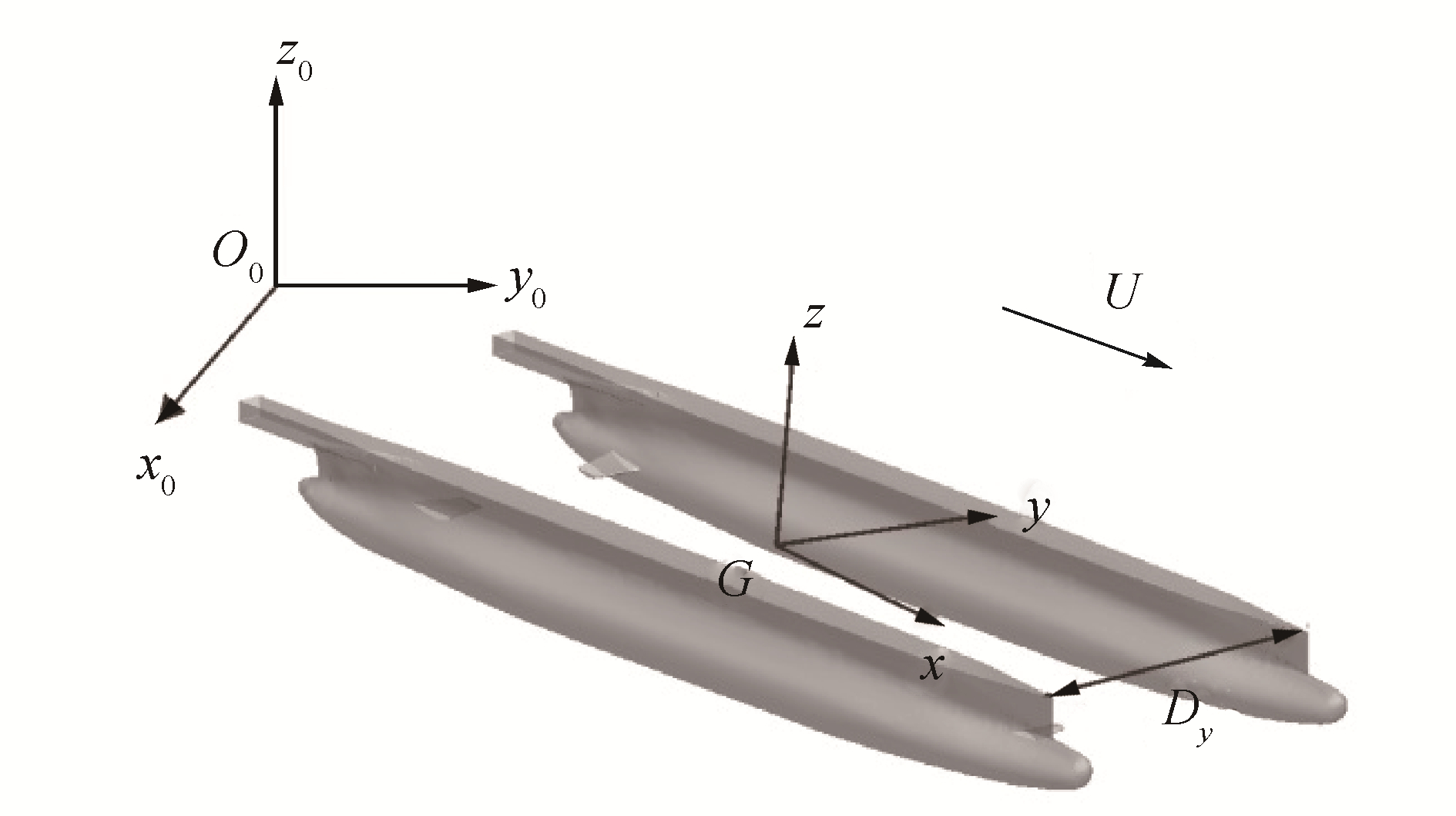
Bailey[18]为了研究船舶在波浪中的操纵性问题,提出了船舶耐波性和操纵性的统一数学模型,建立如图 2所示的2个坐标系:空间固定坐标系O0X0Y0Z0和重心随动坐标系Gxyz。船体在重心随动坐标系下的六自由度运动速度可以表示为(u, v, w, p, q, r)。
|
Download:
|
| 图 2 重心随动坐标系 Fig. 2 Body-fixed coordinate system | |
船体在重心随动坐标系下的运动速度与在平动坐标系下的速度存在转换关系。
1.2 常规船舶船体运动方程在耐波性平动坐标系Oxyz下,根据Cummins[19]和Ogilvie[20]的相关推导,时域内的船体运动方程为:
| $ \begin{array}{*{20}{c}} {\sum\limits_{j = 1}^6 {\left\{ {\left[ {{\mathit{\boldsymbol{M}}_{ij}} + {\mathit{\boldsymbol{A}}_{ij}}\left( \infty \right)} \right]{{\mathit{\boldsymbol{\ddot \eta }}}_j} + {\mathit{\boldsymbol{B}}_{ij}}\left( \infty \right){{\mathit{\boldsymbol{\dot \eta }}}_j} + } \right.} }\\ {\left. {{\mathit{\boldsymbol{C}}_{ij}}{\mathit{\boldsymbol{\eta }}_j} + \int_0^t {{\mathit{\boldsymbol{K}}_{ij}}\left( \tau \right){{\mathit{\boldsymbol{\dot \eta }}}_j}\left( {t - \tau } \right){\rm{d}}\tau } } \right\} = {\mathit{\boldsymbol{F}}_i}} \end{array} $ | (1) |
式中:Mij为广义质量,Aij(∞)为频率无穷大时的附加质量,Bij(∞)为频率无穷大时的阻尼系数,Cij为静水力系数。Kij为辐射力时延函数,Fi为船体受到的波浪力:
| $ {\mathit{\boldsymbol{F}}_i}\left( t \right) = \int_{ - \infty }^t {{h_i}\left( \tau \right)\zeta \left( {t - \tau } \right){\rm{d}}\tau } $ | (2) |
式中:hi(τ)为波浪力脉冲响应函数,ζ为入射波波面高度。
| $ {h_i}\left( t \right) = {\mathop{\rm Re}\nolimits} \left\{ {\frac{1}{{\rm{ \mathsf{ π} }}}\int_0^\infty {{\mathit{\boldsymbol{F}}_i}\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega } } \right\} $ | (3) |
Fi(ω)为频域内船体运动频率为ω时受到的波浪力。
在重心随动坐标系Gxyz下的时域船体运动方程为[20]:
| $ \begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{\bar M}} + \mathit{\boldsymbol{\bar M}}_A^\infty } \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot u}}}\\ {\mathit{\boldsymbol{\dot v}}}\\ {\mathit{\boldsymbol{\dot w}}}\\ {\mathit{\boldsymbol{\dot p}}}\\ {\mathit{\boldsymbol{\dot q}}}\\ {\mathit{\boldsymbol{\dot r}}} \end{array}} \right] + \left( {{{\mathit{\boldsymbol{\bar N}}}^\infty } + {{\mathit{\boldsymbol{\bar C}}}_{RB}}} \right)\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{p}}\\ \mathit{\boldsymbol{q}}\\ \mathit{\boldsymbol{r}} \end{array}} \right] + }\\ {\mathit{\boldsymbol{\bar g}}\left[ {\begin{array}{*{20}{c}} {\int_0^t {\left( {u - {z_g}q} \right){\rm{d}}t} }\\ {\int_0^t {\left( {v + {z_g}p + U\psi } \right){\rm{d}}t} }\\ {\int_0^t {\left( {w - U\theta } \right){\rm{d}}t} }\\ \varphi \\ \theta \\ \psi \end{array}} \right] + \int\limits_0^t {\left\{ {\mathit{\boldsymbol{\bar K}}\left( \tau \right)\left[ {\begin{array}{*{20}{c}} {u\left( {t - \tau } \right)}\\ {v\left( {t - \tau } \right)}\\ {w\left( {t - \tau } \right)}\\ {p\left( {t - \tau } \right)}\\ {q\left( {t - \tau } \right)}\\ {r\left( {t - \tau } \right)} \end{array}} \right]{\rm{d}}\tau } \right\}} = \mathit{\boldsymbol{\bar F}}} \end{array} $ | (4) |
式中:
定义J和L分别为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_{ij}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ 0&1&0&{{z_g}}&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{L}}_{ij}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&{ - 1}&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{array}} \right]} \end{array} $ | (5) |
则
在平动坐标系下,辐射力时延函数Kij(t)可由频域内的附加质量Aij或阻尼系数Bij来求解,具体表达式为:
| $ {\mathit{\boldsymbol{K}}_{ij}}\left( t \right) = - \frac{2}{{\rm{ \mathsf{ π} }}}\int_0^\infty {\left[ {{\mathit{\boldsymbol{A}}_{ij}}\left( \omega \right) - {\mathit{\boldsymbol{A}}_{ij}}\left( \infty \right)} \right]\omega \sin \left( {\omega t} \right){\rm{d}}\omega } $ | (6) |
| $ {\mathit{\boldsymbol{K}}_{ij}}\left( t \right) = \frac{2}{{\rm{ \mathsf{ π} }}}\int_0^\infty {\left[ {{\mathit{\boldsymbol{B}}_{ij}}\left( \omega \right) - {\mathit{\boldsymbol{B}}_{ij}}\left( \infty \right)} \right]\cos \left( {\omega t} \right){\rm{d}}\omega } $ | (7) |
在式(6)和式(7)中,积分上限为无穷大。但一般数值求解时延函数Kij时,是在有限频率进行积分计算。为了减小数值误差,采用Lee[13]提出的方法来消除截断频率Ω的影响。
假设Bij*(ω)=Bij(ω)-Bij(∞),则
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}_{ij}^ * \left( \omega \right) = \int_0^\infty {{\mathit{\boldsymbol{K}}_{ij}}\left( t \right)\cos \left( {\omega t} \right){\rm{d}}t} = \left[ {{\mathit{\boldsymbol{K}}_{ij}}\left( t \right)\frac{{\sin \left( {\omega t} \right)}}{\omega }} \right]_0^\infty + }\\ {\left[ {{{\mathit{\boldsymbol{K'}}}_{ij}}\left( t \right)\frac{{\cos \left( {\omega t} \right)}}{{{\omega ^2}}}} \right]_0^\infty - \int_0^\infty {{{\mathit{\boldsymbol{K''}}}_{ij}}\left( t \right)\frac{{\cos \omega t}}{{{\omega ^2}}}{\rm{d}}t} = }\\ { - {{\mathit{\boldsymbol{K'}}}_{ij}}\left( 0 \right)\frac{1}{{{\omega ^2}}} + \mathit{\boldsymbol{O}}\left( {{\omega ^{ - 3}}} \right)} \end{array} $ | (8) |
假设截断频率Ω足够大,则时延函数Kij可以表示为:
| $ {\mathit{\boldsymbol{K}}_{ij}}\left( t \right) = \frac{2}{{\rm{ \mathsf{ π} }}}\int_0^\mathit{\Omega } {\mathit{\boldsymbol{B}}_{ij}^ * \left( \omega \right)\cos \left( {\omega t} \right){\rm{d}}\omega } + {\mathit{\boldsymbol{\varepsilon }}_{ij}}\left( t \right) $ | (9) |
式中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varepsilon }}_{ij}}\left( t \right) \equiv \frac{2}{{\rm{ \mathsf{ π} }}}\int_\mathit{\Omega }^\infty {\mathit{\boldsymbol{B}}_{ij}^ * \left( \omega \right)\cos \left( {\omega t} \right){\rm{d}}\omega } \approx }\\ { - \frac{2}{{\rm{ \mathsf{ π} }}}{{\mathit{\boldsymbol{K'}}}_{ij}}\left( 0 \right)\int_\mathit{\Omega }^\infty {\frac{{\cos \left( {\omega t} \right)}}{{{\omega ^2}}}{\rm{d}}\omega } = }\\ { - \frac{2}{{\rm{ \mathsf{ π} }}}{{\mathit{\boldsymbol{K'}}}_{ij}}\left( 0 \right)\frac{{\cos \left( {\mathit{\Omega }t} \right) + \mathit{\Omega }t \cdot {{\rm{S}}_i}\left( {\mathit{\Omega }t} \right)}}{\mathit{\Omega }}} \end{array} $ | (10) |
| $ {{\rm{S}}_i}\left( z \right) = - \int_z^\infty {\frac{{\sin t}}{t}{\rm{d}}t} $ | (11) |
三维移动脉动源格林函数的物理含义为一边移动一边脉动的点源产生的速度势,能准确表征船体移动和摇荡运动之间的兴波干扰,理论上能够严格描述有航速船舶摇荡运动产生的速度势[22]。本文频域内的附加质量Aij和阻尼系数Bij均基于三维移动脉动源格林函数求解。
在重心随动坐标系Gxyz下的辐射力时延函数
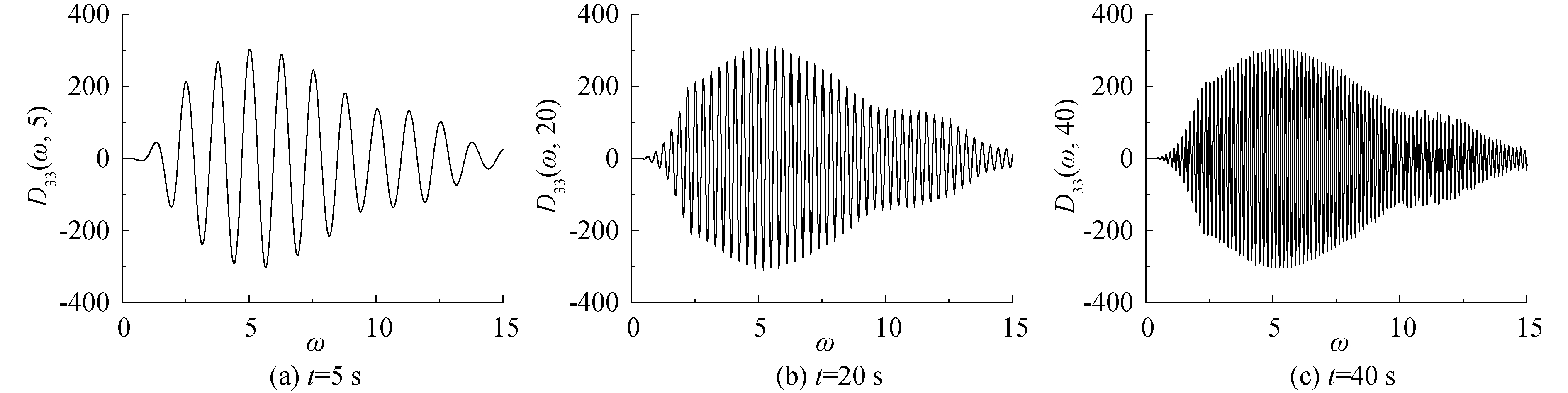
观察式(3)、(6)、(7),积分函数中存在sin(ωt)项和cos(ωt)项。采用式(7)来求解时延函数Kij,设被积函数为[Bij(ω)-Bij(∞)]cos(ωt)为Dij(ω, t)。以Wigley Ⅲ船的阻尼B33为例,被积函数D33(ω, t)在不同时刻的函数图像如图 3所示。由图可知,被积函数呈现出振荡特点,且随着时间增加,振荡加剧。
|
Download:
|
| 图 3 不同时刻的被积函数D33(ω, t)变化曲线 Fig. 3 Typical images of integrand D33(ω, t) | |
由于在频域计算时一般只取有限个数的计算频率,且被积函数存在高频振荡的特性,若直接采用梯形法等一般积分方法进行数值处理,则会存在较大的数值误差。因此本文采用如下方法进行处理:
1) 对在频域求解得到的阻尼系数B进行拟合;
2) 在拟合得到的阻尼系数B的基础上进行加密处理,得到B1, B2, …, Bn;
3) 在阻尼系数BiBi+1之间进行线性插值,即Bi(ω)=aiω+bi。其中:
| $ {\omega _i} < \omega < {\omega _{i + 1}},{a_i} = \frac{{{B_{i + 1}} - {B_i}}}{{{\omega _{i + 1}} - {\omega _i}}},{b_i} = \frac{{{B_i}{\omega _{i + 1}} - {B_{i + 1}}{\omega _i}}}{{{\omega _{i + 1}} - {\omega _i}}} $ | (12) |
4) BiBi+1之间的积分可直接采用解析形式积分,从而提高计算精度和效率。时延函数Kij(t)可表示为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{ij}}\left( t \right) = \sum\limits_{i = 1}^{n - 1} {\frac{2}{{\rm{ \mathsf{ π} }}}\int_{{\omega _i}}^{{\omega _{i + 1}}} {\left[ {{a_i}\omega + {b_i} - {B_{ij}}\left( \infty \right)} \right]\cos \left( {\omega t} \right){\rm{d}}\omega } } = }\\ {\sum\limits_{i = 1}^{n - 1} {\frac{2}{{\rm{ \mathsf{ π} }}}\left[ {{a_i}\left( {\omega \frac{{\sin \omega t}}{t} + \frac{{\cos \omega t}}{{{t^2}}}} \right) + \left( {{b_i} - {\mathit{\boldsymbol{B}}_{ij}}\left( \infty \right)} \right)\frac{{\sin \omega t}}{t}} \right]_{{\omega _i}}^{{\omega _{i + 1}}}} } \end{array} $ | (13) |
时延函数
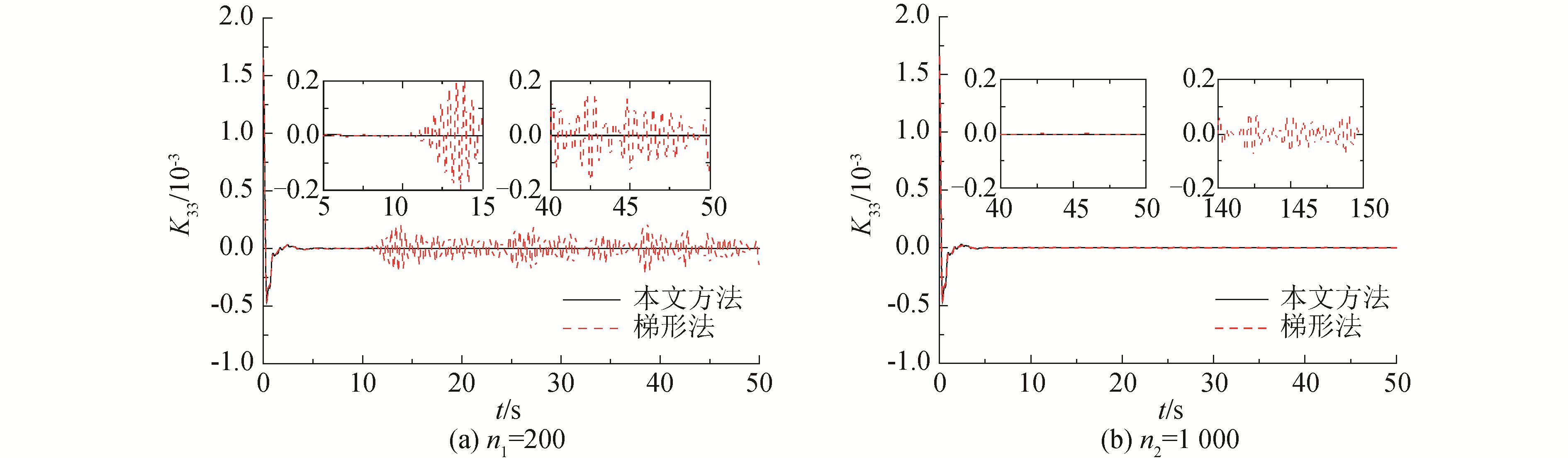
取阻尼系数加密时的个数为n1=200和n2=1 000,分别采用上述积分方法和梯形积分法对时延函数进行计算。由图 4可知,在n1=200时,采用本文积分方法求得的数值较为稳定,而采用梯形积分法的结果在t>10 s时开始出现振荡。当n2=1 000时,两种积分方法在t < 50 s时都可以得到收敛的结果。随着时间的增加,采用梯形积分法的结果又出现振荡。表明通过增加加密个数,可以减缓梯形法结果的振荡。但随着时间t的增大,积分函数的振荡加剧,采用梯形法求得的时延函数又会出现振荡。而使用本文积分方法可以采用解析形式求解,计算结果更稳定准确。
|
Download:
|
| 图 4 积分方法对时延函数的影响 Fig. 4 Effect of integral method on retard function | |
针对时延函数、船体运动响应等开展数值验证,与已发表的文献结果和试验结果进行对比,计算对象为Wigley Ⅲ和S60船模,其主要参数如表 1所示。
| 表 1 船模主要参数 Table 1 Main parameters of hull models |
为了便于描述和比较运动结果,对垂荡响应幅值Za和纵摇响应幅值θa进行无因次化处理。无因次化公式如表 2所示。其中,ζa为入射波波幅,k为波数,g为重力加速度。k=2π/λ,λ为入射波波长。
| 表 2 运动结果无因次化定义 Table 2 Definition of the non-dimensional ship responses |
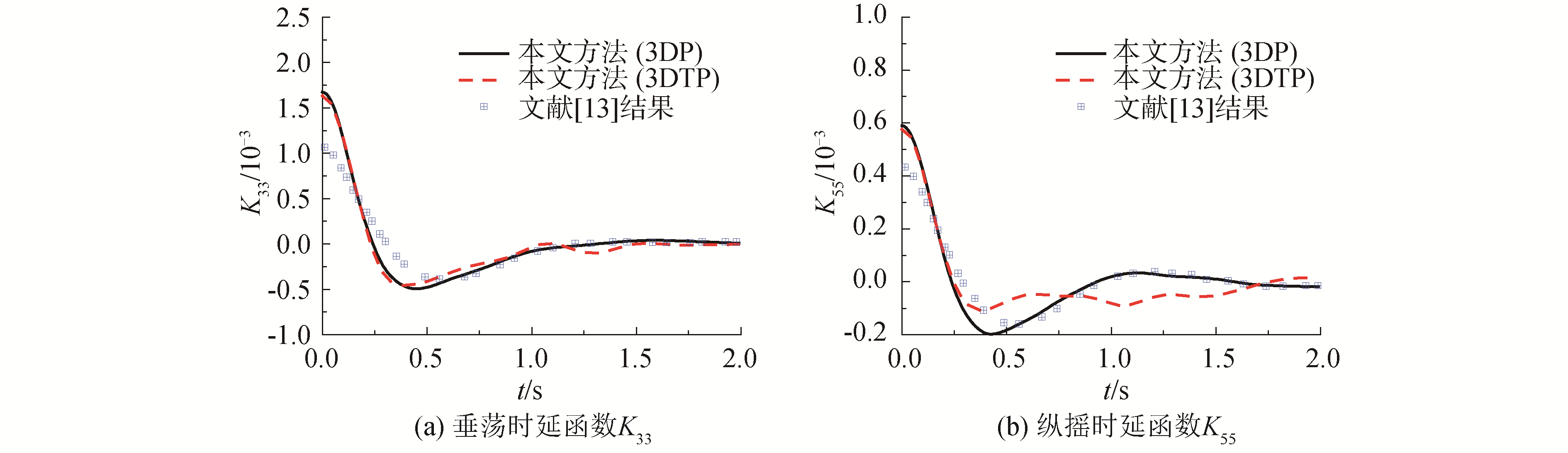
图 5和图 6对比了不同航速下的时延函数计算结果。图中3DP表示基于三维脉动源格林函数(three dimensional pulsating source green function,3DP),3DTP表示基于三维移动脉动源格林函数(three dimensional translating-pulsating source green function,3DTP)。
|
Download:
|
| 图 5 Fn=0.2时的Wigley Ⅲ船模时延函数对比 Fig. 5 Comparison of retard function of Wigley Ⅲ at Fn=0.2 | |
|
Download:
|
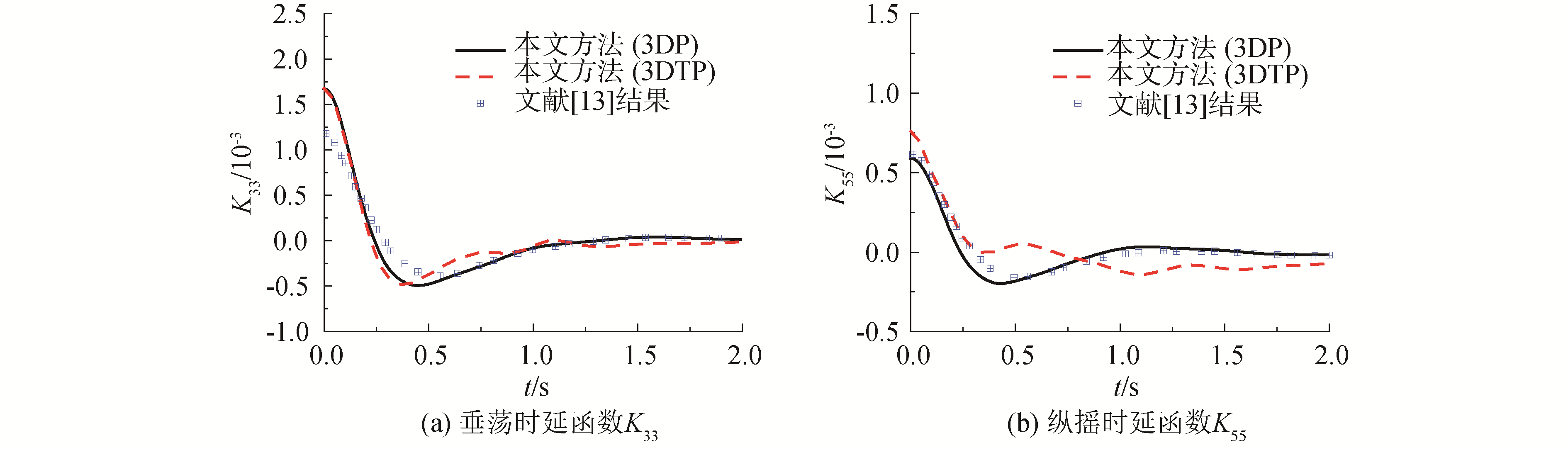
| 图 6 Fn=0.3时的Wigley Ⅲ船模时延函数对比 Fig. 6 Comparison of retard function of Wigley Ⅲ at Fn=0.3 | |
由图 6可知,本文基于3DP的时延函数计算结果与同样基于3DP的唐恺[13]的计算结果在t>0.5 s时吻合较好。在t < 0.5 s时两者之间存在差异,可能是由于截断频率Ω不同造成的。基于3DP与基于3DTP的时延函数相比,垂荡时延函数差别较小,而纵摇时延函数差别较大,这主要是由于两类格林函数求得的水动力系数不同造成的。鉴于3DTP的理论推导更严格和完善,直接计入了航速效应,因此基于3DTP的结果更为合理。
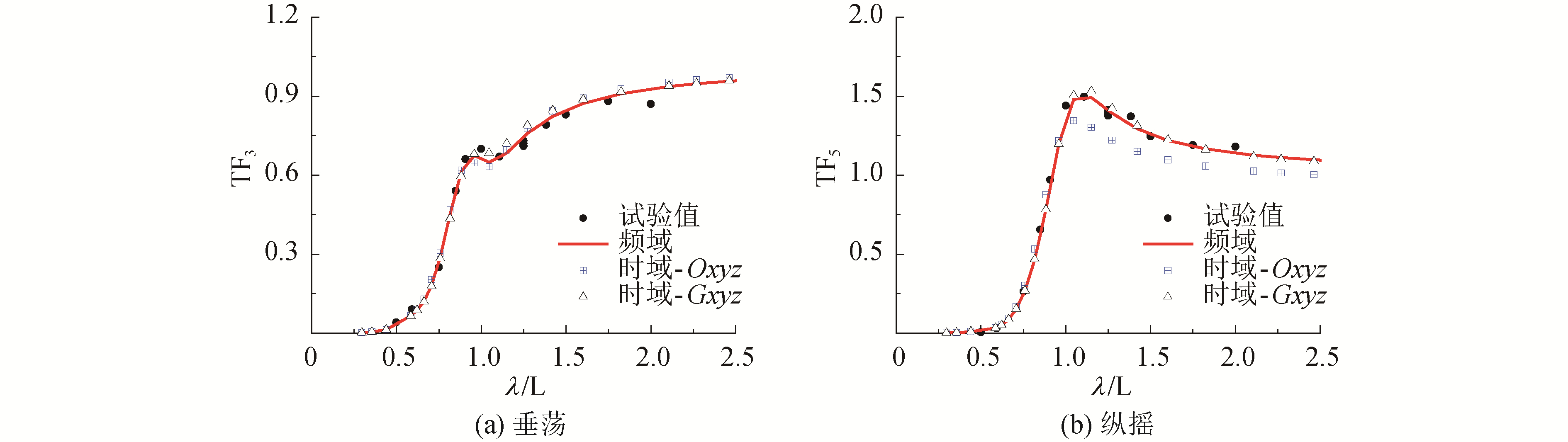
图 7和图 8给出了不同航速下Wigley Ⅲ船模的纵向运动传递函数。图中频域计算结果基于3DTP,时域-Oxyz表示在耐波性平动坐标系下的计算结果,时域-Gxyz表示在重心随动坐标系下的计算结果,试验结果来自荷兰代尔夫特大学的试验报告[23]。由图可知,基于3DTP的运动传递函数频域计算结果与试验结果吻合良好,表明三维移动脉动格林函数在处理有航速船舶的耐波性问题时可以取得较好的结果。
|
Download:
|
| 图 7 Fn=0.2时的Wigley Ⅲ船模运动传递函数对比 Fig. 7 Comparison of the transfer function of Wigley Ⅲ at Fn=0.2 | |
|
Download:
|
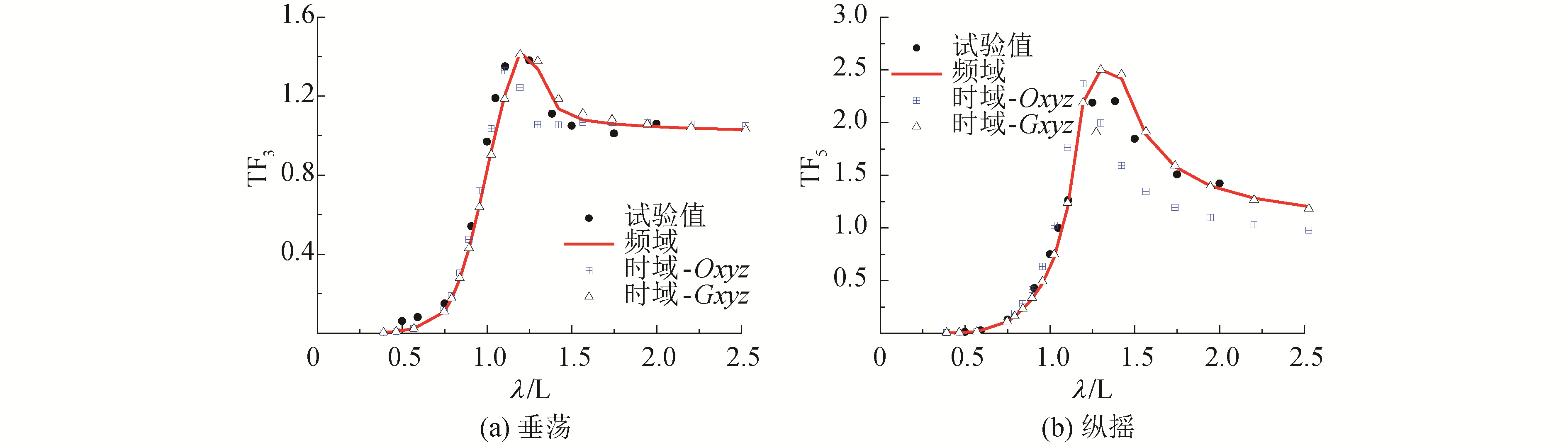
| 图 8 Fn=0.3时的Wigley Ⅲ船模运动传递函数对比 Fig. 8 Comparison of the transfer function of Wigley Ⅲ at Fn=0.3 | |
对比频域计算结果与耐波性平动坐标系Oxyz下的时域计算结果可以发现,时域内求得的运动传递函数与频域结果存在偏差,特别是纵摇传递函数的偏差较大。在Fn=0.2时,时域内求得的垂荡传递函数与频域结果吻合良好,而在Fn=0.3时,两者在共振区附近有较大误差。随着航速增加,时域内求得的垂荡传递函数和纵摇传递函数与频域结果的偏差逐渐增大。
对比频域计算结果与重心随动坐标系Gxyz下的时域计算结果可以发现,两者在各航速下均吻合较好。表明应用频时域转换法在时域内求解船体运动时,为提高计算结果精度,应在重心随动坐标系下进行。
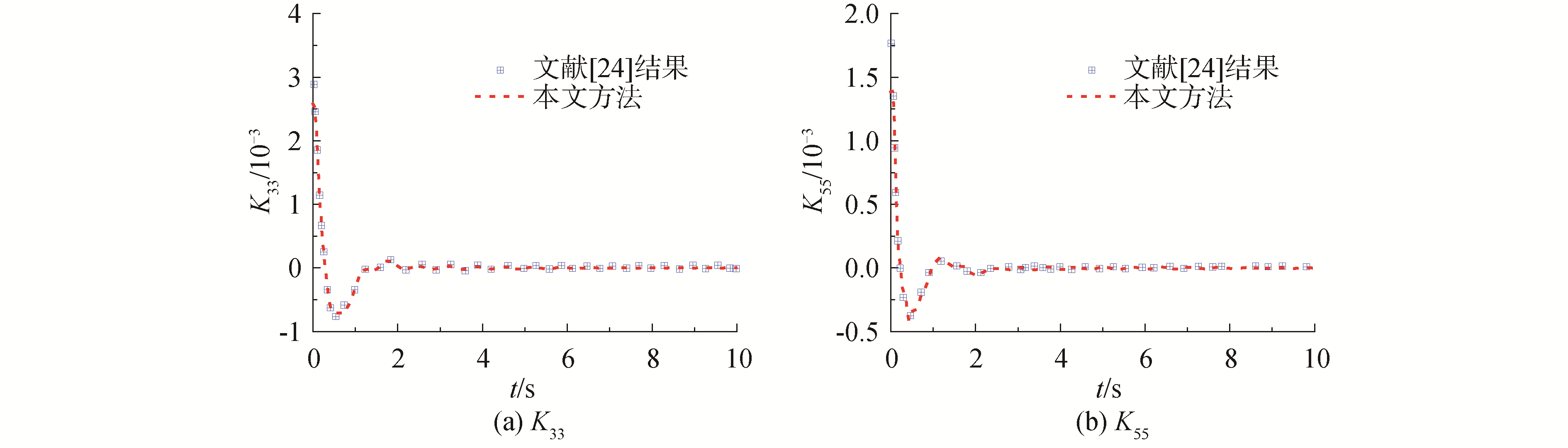
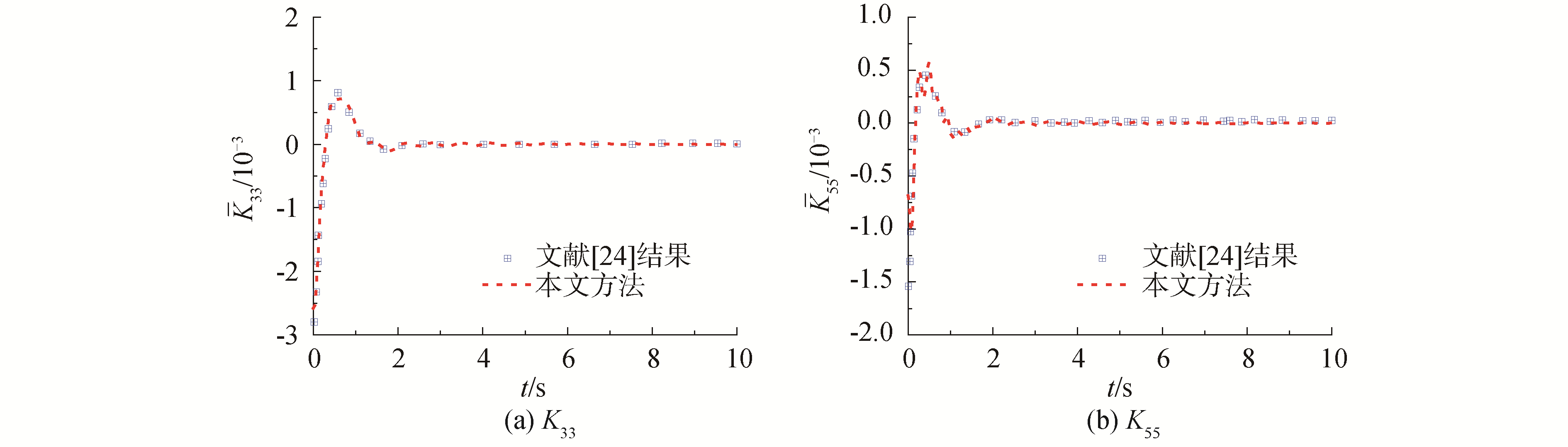
图 9和图 10分别给出了S60船模在耐波性平动坐标系下和在重心随动坐标系下的时延函数,图中同时给出了Ballard[24]的计算结果。由图中可知,本文的时延函数计算结果与Ballard的计算结果吻合良好,验证了本文数值处理方法的正确性。时延函数在初始时刻的数值较大,随着时间增加,数值趋于零,表明记忆效应逐渐减弱。
|
Download:
|
| 图 9 S60耐波性平动坐标系下的时延函数Kij Fig. 9 Comparison of the retard function Kij of S60 at Oxyz | |
|
Download:
|
|
图 10 S60重心随动坐标系下的时延函数 |
|
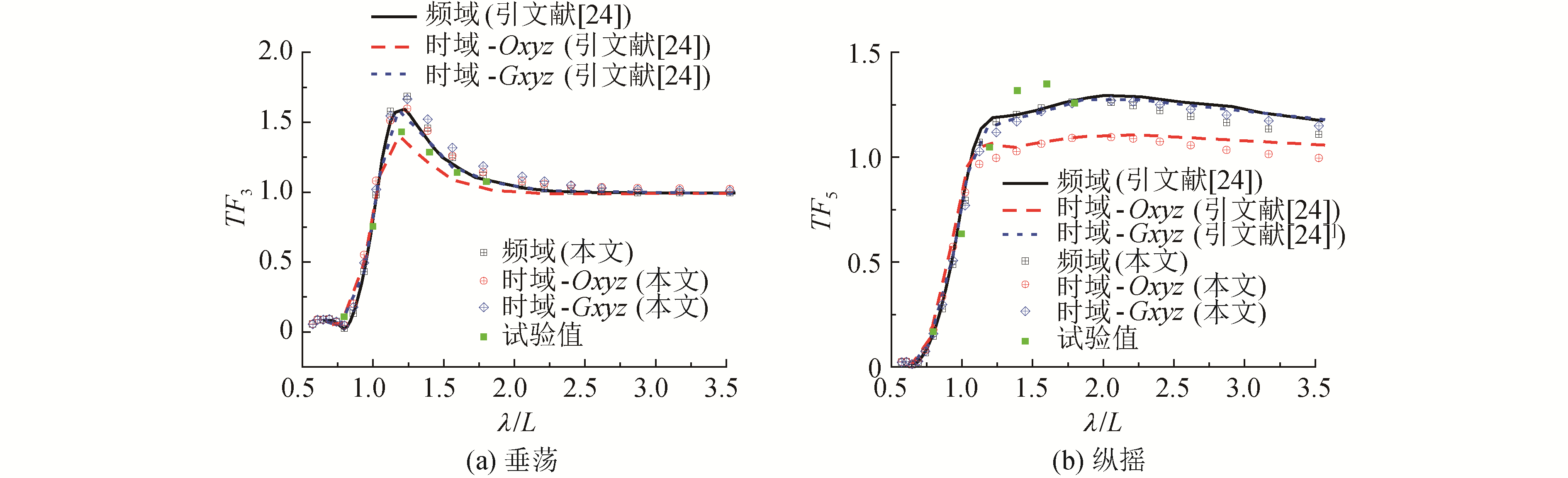
图 11给出了S60船模在Fn=0.2时的垂荡传递函数和纵摇传递函数,图中Ballard的频域计算结果基于三维脉动源格林函数。由图可知,由于S60的航速(Fn=0.2)在中低速范围内,基于三维移动脉动源格林函数的频域计算结果与基于三维脉动源格林函数的频域计算结果差别不大,2者吻合良好。与试验值相比,两者在短波区域的数值计算结果较为准确,而共振区附近计算的垂荡传递函数偏大。
|
Download:
|
| 图 11 S60运动传递函数对比(Fn=0.2) Fig. 11 Comparison of the transfer functions of S60 at Fn=0.2 | |
对比在耐波性平动坐标系下求得的时域结果,本文的垂荡传递函数计算结果与Ballard的计算结果存在一定差别。本文求得的垂荡传递函数时域结果与频域结果差别较小,而Ballard求得的垂荡传递函数在共振区附近与频域结果存在较大差异。而两者的纵摇传递函数吻合较好,在λ/L>1时,与频域结果相比均存在一定的偏移。
对比在重心随动坐标系下求得的时域结果,本文求得的垂荡传递函数和纵摇传递函数与频域结果存在微小的偏差,而Ballard的运动传递函数时域结果与频域结果几乎完全吻合,可能是由数值处理上的误差造成的。两者的运动计算结果均表明,应在重心随动坐标系下求解船体运动方程。
Ballard[24]对于在平动坐标系和重心随动坐标系下求解船体运动方程得到不同结果的原因进行了分析,主要是由于平动坐标系下的纵摇-纵摇附加质量A55在频率接近0时趋近于无穷大,由A55求得的时延函数K55(t)不准确,造成时域内的运动计算结果与频域结果存在偏差。而在重心随动坐标系下的水动力系数MA55在频率接近0时并没有趋近于无穷大,由MA55求得的时延函数
以上通过针对Wigley Ⅲ和S60两型船模,在耐波性平动坐标系和重心随动坐标系下对辐射力时延函数和运动传递函数进行计算,验证了针对常规单体船的耐波性时域计算方法。由于在重心随动坐标系下求解船体运动方程可以得到与频域中相同的运动传递函数,因此后文均在重心随动坐标系下求解时域船体运动方程,开展耐波性理论计算。
2 SWATH耐波性时域计算方法 2.1 粘性和稳定鳍的影响与常规单体船不同,SWATH的耐波性计算必须计入粘性和稳定鳍的影响[5]。粘性的影响主要体现在阻尼系数Bij(v)、静水力系数Cij(v)和波浪干扰力Fi(v),稳定鳍的影响主要体现在附加质量Aij(f)、阻尼系数Bij(f)、静水力系数Cij(f)和波浪干扰力Fi(f)。由于缺少合理可靠的理论模型,上述系数的求解计算一般多采用学者Lee提出的半理论半经验公式[5, 25]。在耐波性平动坐标系下,两者的影响对船体的作用力可以分别表示为:
| $ \mathit{\boldsymbol{F}}{v_i} = \mathit{\boldsymbol{B}}_{ij}^{\left( v \right)}{{\dot \eta }_j} + \mathit{\boldsymbol{C}}_{ij}^{\left( v \right)}{\eta _j} + \mathit{\boldsymbol{F}}_i^{\left( v \right)} $ | (14) |
| $ \mathit{\boldsymbol{F}}{f_i} = \mathit{\boldsymbol{A}}_{ij}^{\left( f \right)}{{\ddot \eta }_j} + \mathit{\boldsymbol{B}}_{ij}^{\left( f \right)}{{\dot \eta }_j} + \mathit{\boldsymbol{C}}_{ij}^{\left( f \right)}{\eta _j} + \mathit{\boldsymbol{F}}_i^{\left( f \right)} $ | (15) |
根据
在时域内求解SWATH船体运动时,需时时计入粘性和稳定鳍的影响,因此将在重心随动坐标系下的常规船舶时域运动方程式(4)改写为:
| $ \begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{\bar M}} + \mathit{\boldsymbol{\bar M}}_A^\infty } \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot u}}}\\ {\mathit{\boldsymbol{\dot v}}}\\ {\mathit{\boldsymbol{\dot w}}}\\ {\mathit{\boldsymbol{\dot p}}}\\ {\mathit{\boldsymbol{\dot q}}}\\ {\mathit{\boldsymbol{\dot r}}} \end{array}} \right] + \left( {{{\mathit{\boldsymbol{\bar N}}}^\infty } + {{\mathit{\boldsymbol{\bar C}}}_{RB}}} \right)\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{p}}\\ \mathit{\boldsymbol{q}}\\ \mathit{\boldsymbol{r}} \end{array}} \right] + \mathit{\boldsymbol{\bar g}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_1}}\\ {{\mathit{\boldsymbol{\eta }}_2}}\\ {{\mathit{\boldsymbol{\eta }}_3}}\\ {{\mathit{\boldsymbol{\eta }}_4}}\\ {{\mathit{\boldsymbol{\eta }}_5}}\\ {{\mathit{\boldsymbol{\eta }}_6}} \end{array}} \right] + }\\ {\int_0^t {\left\{ {\mathit{\boldsymbol{\bar K}}\left( \tau \right)\left[ {\begin{array}{*{20}{c}} {u\left( {t - \tau } \right)}\\ {v\left( {t - \tau } \right)}\\ {w\left( {t - \tau } \right)}\\ {p\left( {t - \tau } \right)}\\ {q\left( {t - \tau } \right)}\\ {r\left( {t - \tau } \right)} \end{array}} \right]d\tau } \right\}} = \mathit{\boldsymbol{\bar F}}h + \mathit{\boldsymbol{\bar F}}v + \mathit{\boldsymbol{\bar F}}f} \end{array} $ | (16) |
式中:
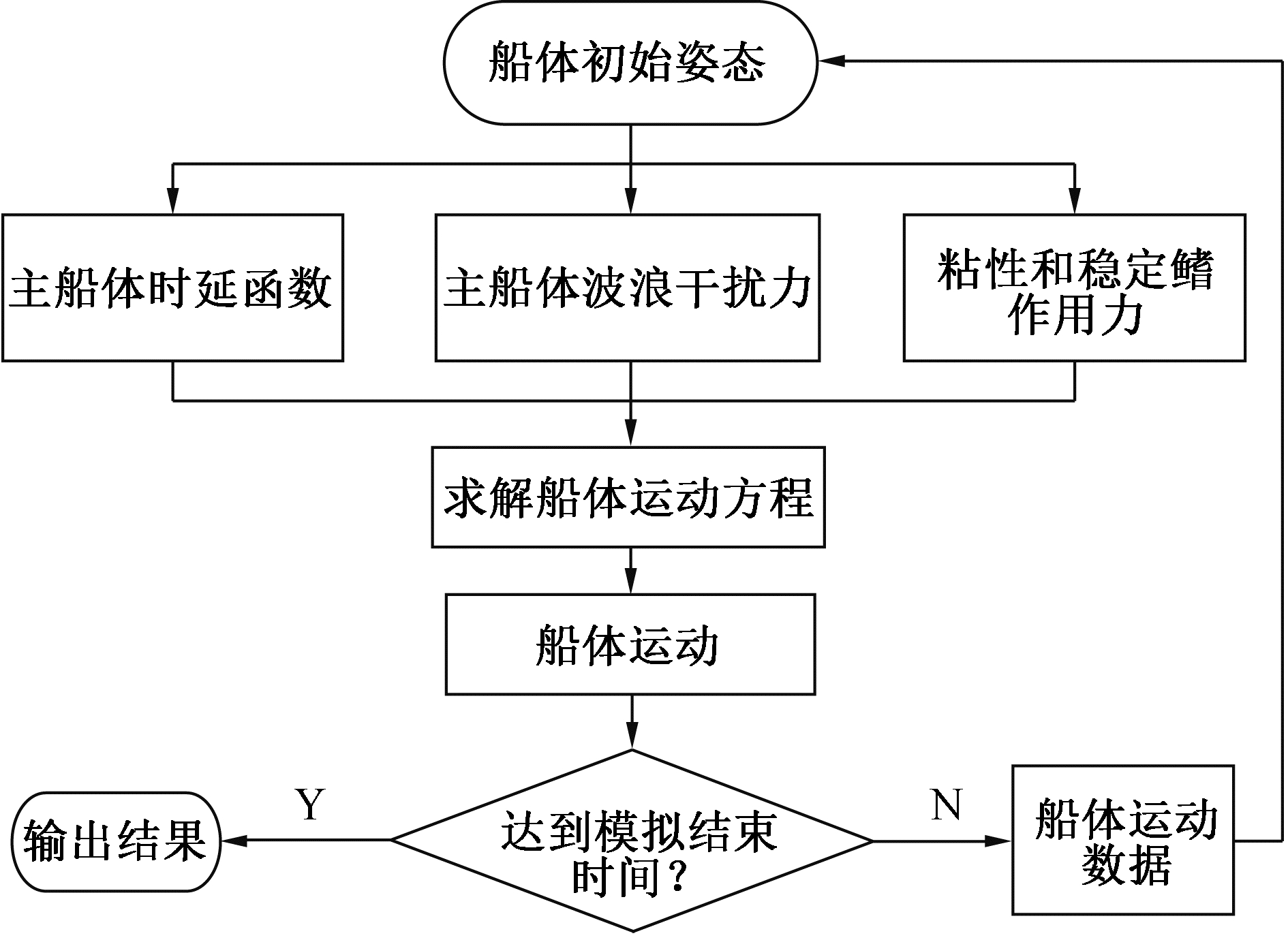
时域内的小水线面双体船船体运动数值求解流程如图 12所示。
|
Download:
|
| 图 12 时域SWATH船体运动数值求解流程 Fig. 12 Process of numerical computation in time domain | |
开展数值计算的小水线面双体船模型为SWATH 6A[5],其主要参数如表 3所示。
| 表 3 SWATH 6 A模型主要参数 Table 3 Main parameters of SWATH 6 A |
图 13给出了基于三维移动脉动源格林函数求解水动力系数时SWATH 6 A模型表面的面元划分和模型的横剖图。通过侧视图可以看出,SWATH 6 A具有垂直且连续的小水线面支柱。

|
Download:
|
| 图 13 SWATH 6 A模型面元划分与横剖图 Fig. 13 Panels distribution and body plans for SWATH 6 A | |
SWATH 6 A艏艉安装有稳定鳍,表 4给出了稳定鳍的主要参数,其中纵向位置以船中为参考,-表示为船艏方向。
| 表 4 稳定鳍主要参数 Table 4 General properties of stabilizing fins |
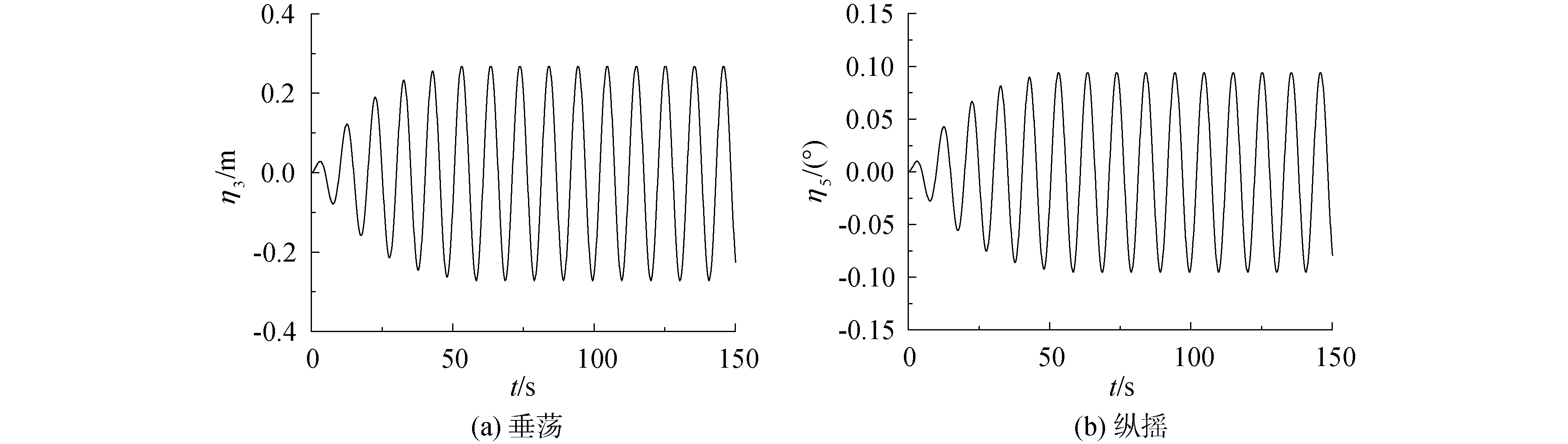
图 14和图 15给出了SWATH 6 A在不同航速下共振区附近的运动响应时历曲线。可见船体运动从静止状态逐渐增大,之后保持稳定的简谐运动。
|
Download:
|
| 图 14 SWATH 6 A的垂荡和纵摇响应时历曲线(λ/L=2.27, Fn=0) Fig. 14 Time history of heave and pitch of SWATH 6 A at λ/L=2.27, Fn=0 | |

|
Download:
|
| 图 15 SWATH 6 A的垂荡和纵摇响应时历曲线(λ/L=5.58, Fn=0.538) Fig. 15 Time history of heave and pitch of SWATH 6 A at λ/L=5.58, Fn=0.538 | |
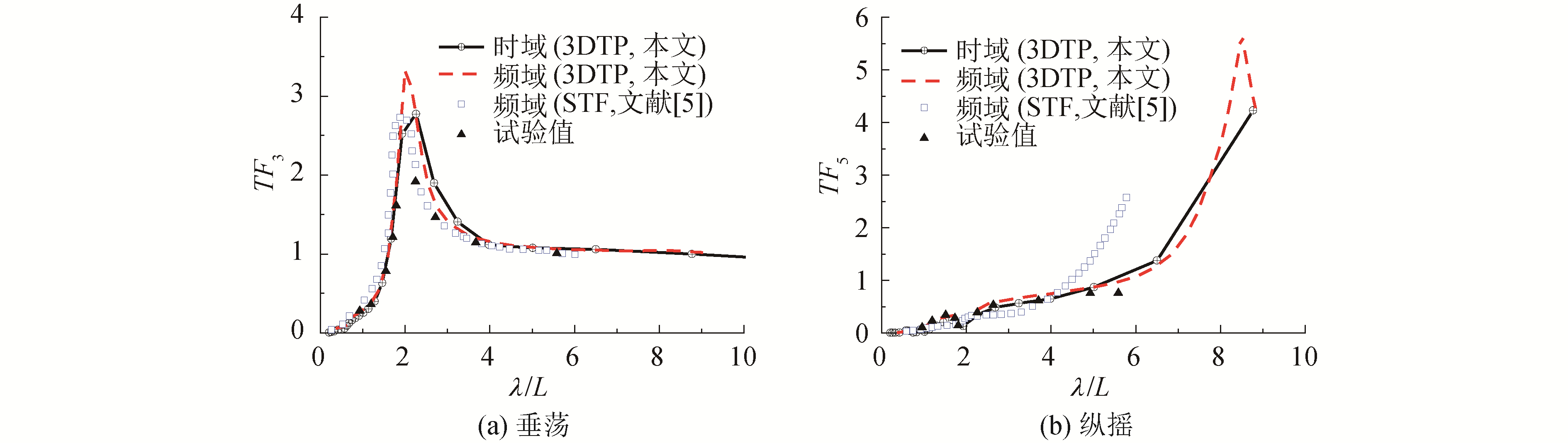
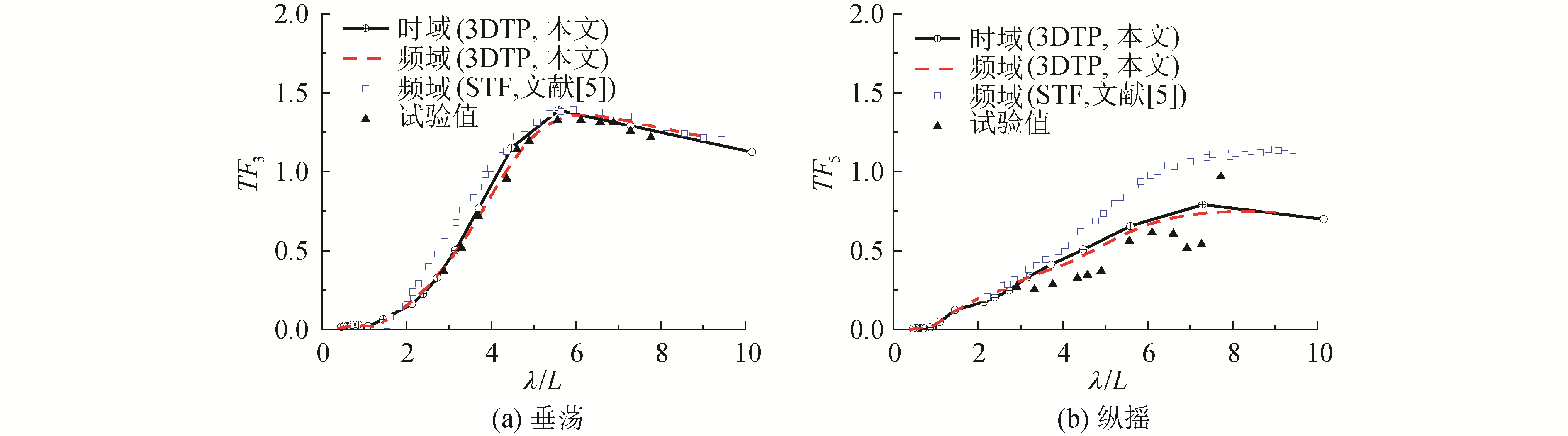
图 16和图 17对比了SWATH 6 A在顶浪规则波中,以不同航速航行时的运动传递函数时域结果、频域结果和试验结果,图中STF表示采用二维切片法计算,试验结果来自文献[5]。由图可知,对垂荡运动传递函数,基于3DTP的结果与切片法结果、试验结果吻合良好。对纵摇传递函数,基于3DTP的结果优于切片法结果,与试验值更接近。基于3DTP的时域计算结果和频域计算结果稍有差别,其原因应该属于数值处理上的误差,比如时延函数计算,截断频率选取以及无穷大时的附加质量和阻尼系数计算等。
|
Download:
|
| 图 16 SWATH 6 A顶浪规则波中的垂荡和纵摇传递函数(Fn=0) Fig. 16 Comparison of heave and pitch of SWATH 6 A at Fn=0, head wave | |
|
Download:
|
| 图 17 SWATH 6 A顶浪规则波中的垂荡和纵摇传递函数(Fn=0.538) Fig. 17 Comparison of heave and pitch of SWATH 6 A at Fn=0.538, head wave | |
1) 以三维移动脉动源格林函数为内核,将频域内的水动力系数转换至时域求解时延函数,建立了常规船舶的耐波性时域线性计算方法,比较了在平动坐标系和随动坐标系下求解船体运动对运动计算结果的影响。在此基础上,计入两片体间的水动力干扰、粘性和稳定鳍的影响,建立了小水线面双体船耐波性时域线性计算方法。求解时延函数高效快速,结果更准确。
2) 在重心随动坐标系下求解船体运动方程,能够得到更准确的运动计算结果。
3) 建立的SWATH耐波性时域计算方法可靠,计算结果与频域计算结果和试验结果吻合良好,可为后期进一步开展时域非线性计算方法研究提供支撑。
| [1] |
QIAN Peng, YI Hong, LI Yinghui. Numerical and experimental studies on hydrodynamic performance of a small-waterplane-area-twin-hull (SWATH) vehicle with inclined struts[J]. Ocean engineering, 2015, 96: 181-191. DOI:10.1016/j.oceaneng.2014.12.039 (  0) 0)
|
| [2] |
BRIZZOLARA S, VERNENGO G. Automatic optimization computational method for unconventional S.W.A.T.H. ships resistance[J]. International journal of mathematical models and methods in applied sciences, 2011, 5(5): 882-889. (  0) 0)
|
| [3] |
BOUSCASSE B, BROGLIA R, STERN F. Experimental investigation of a fast catamaran in head waves[J]. Ocean engineering, 2013, 72: 318-330. DOI:10.1016/j.oceaneng.2013.07.012 (  0) 0)
|
| [4] |
孙小帅, 姚朝帮, 熊鹰, 等. 基于移动脉动源格林函数的小水线面双体船耐波性频域计算[J]. 上海交通大学学报, 2018, 52(6): 698-707. SUN Xiaoshuai, YAO Chaobang, XIONG Ying, et al. Frequency domain computation study on the seakeeping performance of Small-Waterplane-Area Twin Hull based on the translating-pulsating source Green Function[J]. Journal of Shanghai Jiao Tong University, 2018, 52(6): 698-707. (  0) 0)
|
| [5] |
LEE C M. Theoretical prediction of motion of small-waterplane-area, twin-hull (SWATH) ships in waves[R]. DTNSRDC Report, SPD-76-0046, 1976.
(  0) 0)
|
| [6] |
HONG Y S. Improvements in the prediction of heave and pitch motions for SWATH ships[R]. DTNSRDC Departmental report SDR0928-02, Bethesda, 1980.
(  0) 0)
|
| [7] |
MCCREIGHT K K, STAHL R. Vertical plane motions of SWATH ships in regular waves[R]. DTNSRDC Report, SPD-1076-01, 1983.
(  0) 0)
|
| [8] |
毛筱菲. 小水线面双体船在波浪中的运动响应预报[J]. 船海工程, 2006(4): 13-15. MAO Xiaofei. Numerical study of the motion response prediction of SWATH ship in waves[J]. Ship & ocean engineering, 2006(4): 13-15. (  0) 0)
|
| [9] |
HONG Y S. The effect of strut shape on swath ship motion[R]. DTNSRDC Report, SPD-85/048, 1985.
(  0) 0)
|
| [10] |
ARTHUR E K. Time domain simulation of SWATH ship motions[D]. UK: University of Glasgow, 1988.
(  0) 0)
|
| [11] |
FANG M C, CHIOU S C. SWATH ship motion simulation based on a self-tuning fuzzy control[J]. Journal of ship research, 2000, 44(2): 108-119. (  0) 0)
|
| [12] |
LIANG Lihua, WANG Baohua, ZHANG Songtao, et al. Stabilizer fin effect on SWATH ship motions and disturbance observer based control design[C]//Proceeds of 2013 IEEE International Conference on Mechatronics and Automation. Takamatsu, Japan, 2013.
(  0) 0)
|
| [13] |
唐恺, 朱仁传, 缪国平, 等. 时域分析波浪中浮体运动的时延函数计算[J]. 上海交通大学学报, 2013, 47(2): 300-306. TANG Kai, ZHU Renchuan, MIAO Guoping, et al. Calculation of retard function for time-domain analyzing floating body in waves[J]. Journal of Shanghai Jiao Tong University, 2013, 47(2): 300-306. (  0) 0)
|
| [14] |
CHAKRABARTI S K. Numerical models in fluid-structure interaction[M]. Cambridge, MA: MIT Press, 2005: 211-251.
(  0) 0)
|
| [15] |
KIM Y, NAM B W, KIM D W, et al. Study on coupling effects of ship motion and sloshing[J]. Ocean engineering, 2007, 34(16): 2176-2187. DOI:10.1016/j.oceaneng.2007.03.008 (  0) 0)
|
| [16] |
洪亮, 朱仁传, 缪国平, 等. 波浪中船体与液舱晃荡耦合运动的时域数值计算[J]. 哈尔滨工程大学学报, 2012, 33(5): 635-641, 647. HONG Liang, ZHU Renchuan, MIAO Guoping, et al. Numerical calculation of ship motions coupled with tank sloshing in time domain based on potential flow theory[J]. Journal of Harbin Engineering University, 2012, 33(5): 635-641, 647. DOI:10.3969/j.issn.1006-7043.201109044 (  0) 0)
|
| [17] |
JIANG Shengchao, TENG Bin, BAI Wei, et al. Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action[J]. Ocean engineering, 2015, 108: 140-154. DOI:10.1016/j.oceaneng.2015.07.044 (  0) 0)
|
| [18] |
BAILEY P A, PRICE W G, TEMAREL P. A unified mathematical model describing the maneuvering of a ship travelling in a seaway[J]. Trans RINA, 1998, 140: 131-149. (  0) 0)
|
| [19] |
CUMMINS W E. The impulse response function and ship motions[R]. Washington DC: David Taylor Model Basin, 1962.
(  0) 0)
|
| [20] |
OGILVIE T F. Recent progress toward the understanding and prediction of ship motions[C]//Proceedings of the 5th Symposium on Naval Hydrodynamics. Bergen, Norway, 1964: 3-80.
(  0) 0)
|
| [21] |
SKEJIC R. Maneuvering and seakeeping of a single ship and of two ships in interaction[D]. Norway: Norwegian University of Science and Technology, 2008.
(  0) 0)
|
| [22] |
YAO Chaobang, DONG Wencai. Study on fast integration method for Bessho form translating-pulsating source Green's function distributing on a panel[J]. Ocean engineering, 2014, 89: 10-20. DOI:10.1016/j.oceaneng.2014.06.016 (  0) 0)
|
| [23] |
JOURNÉE J M J. Experiments and calculations on 4 Wigley hull forms in head waves[R]. Ship Hydromechanics Laboratory, Delft University of Technology, 0909, 1992.
(  0) 0)
|
| [24] |
BALLARD E J, HUDSON D A, PRICE W G, et al. Time domain simulation of symmetric ship motions in waves[J]. International journal of maritime engineering, 2003, 145. DOI:10.3940/rina.ijme.2003.a2.22031 (  0) 0)
|
| [25] |
SUN X S, YAO C B, YE Q. Numerical investigation on seakeeping performance of SWATH with three dimensional translating-pulsating source green function[J]. Engineering analysis with boundary elements, 2016, 73: 215-225. DOI:10.1016/j.enganabound.2016.10.005 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


