2. 海军工程大学 动力工程学院, 湖北 武汉 430033;
3. 92728部队, 上海 200436
2. College of Marine Power Engineering, Naval University of Engineering, Wuhan 430033, China;
3. Unit 92728, People's Liberation Army, Shanghai 200436, China
对于螺旋桨推进船螺旋桨的抽吸加速了船艉的水流,使得船体的阻力增加,船体阻力增额即为推力减额,螺旋桨推进的推力减额为正。喷水推进推力减额的定义与螺旋桨推进有着显著的差别。喷水推进自航试验时推进器推力很难直接测量,常采用动量流量法来确定,因此喷水推进器的推力减额包括船体自航时阻力增额和喷水推进推力计算方法引起的动量减额。国外相关研究表明喷水推进器的推力减额在-6%~20%变化,在中高航速时推力减额可能为负值[1]。
Coop通过模型和实尺度测量、经验公式和理论分析等方法研究了船泵相互作用。他认为船泵相互作用的主要因素包含:推进器产生的升力和力矩,艉流动量损失和进水口处滑行面的损失。文中指出在滑行艇驼峰航速附近负推力减额可达-8%[2]。Van等[3-4]认为中高航速时进水流道受到较大的抬升力,造成自航时船体的纵倾角降低,进而推力减额出现负值。Van在第24届ITTC喷水推进专家委员会上系统回顾总结了前期有关喷水推进器的研究和ITTC相关规程。考虑到直接测量推力方法有困难,报告主要讨论了动量通量的方法。推力减额被分解为两部分:一部分代表裸船拖曳阻力与净推力之间的关系,即阻力增额;一部分代表总推力与净推力的关系,即动量减额[5]。Cusanelli通过船模试验评估了JHSS船采用螺旋桨推进、轴流泵推进和混流泵推进三种方案。和螺旋桨推进相比,喷水推进自航船模姿态与裸船拖曳船模姿态差别更大[6]。文献[7]中的试验和计算表明,喷水推进船自航时船体的纵倾角是增加的。Kandasamy[8]计算了傅氏数在0.4~0.7之间的推力减额(推力减额在0.16~0.08之间)。喷水推进导致船体纵倾角和升沉发生变化,进而船体阻力增加。Arash[9]采用数值计算的方法系统地研究了某喷水推进快艇的推力减额,其船模自航计算姿态依据试验数据给定。孙存楼[10]研究了某喷水推进双体船负推力减额的机理,分析了流场及航态的变化,认为低速时的抽吸作用导致了较大的正推力减额,中高航速时摩擦阻力的降低是出现负推力减额的主要原因。但文献[10]将低速时压阻力增加定性地归结为抽吸作用,而未作进一步定量分析;采用流量边界条件来代替泵的作用,未能分析动量减额分数的影响。国内关于喷水推进自航试验的研究尚在起步阶段。郭春雨[11]综述了ITTC规程下喷水推进三体船自航试验的研究进展,认为试验条件基本成熟,国内开展船体-喷水推进泵自航试验迫在眉睫。蔡佑林[12]介绍了动量通量法试验技术发展现状,提出我国发展相关技术的建议。
本文通过数值计算预报了某喷水推进三体船推力减额,并与实验值进行了比较。将推力减额分解为阻力增额和动量减额,将阻力增额影响因素分为局部作用和全局作用,将动量减额分为进口阻力和出口阻力,解释了喷水推进推力减额低航速时较大,高航速时为负值这一变化规律。
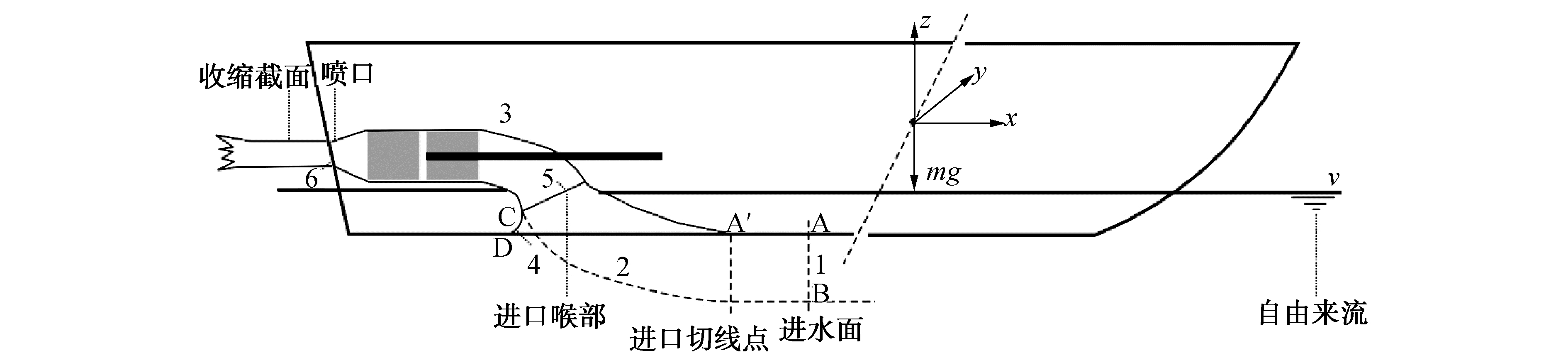
1 喷水推进基本理论 1.1 喷水推进船推力减额喷水推进自航试验时测量推力有2种方法:直接测量推力法和动量通量法。直接测量推力法装置复杂,成本较高,较少得到采用[3]。动量通量法测量喷水推进器的流量及流场,然后根据动量定理来间接得到推进器的推力,这种方法获得了船池的广泛采用。图 1为喷水推进器流场控制体[13]。图中x方向为指向船艏的方向。喷水推进控制体在x方向的动量控制方程为:
| $ \iint\limits_{{{A}_{1}}+{{A}_{6}}}{\rho {{\mathit{\boldsymbol{u}}}_{\text{x}}}\left( {{\mathit{\boldsymbol{u}}}_{\text{k}}}{{\mathit{\boldsymbol{n}}}_{\text{k}}} \right)\text{d}A=\iint\limits_{{{A}_{1}}+{{A}_{2}}+{{A}_{3}}+{{A}_{6}}}{{{\sigma }_{x}}\text{d}A+\iiint{\rho {{F}_{\text{P}x}}\text{d}\mathit{V}}}} $ | (1) |
|
Download:
|
| 图 1 喷水推进器流场控制体 Fig. 1 Control volume of waterjet propulsor | |
式中:ρ为水密度;ux为x方向速度分量;uk为表面k上流体的速度矢量;nk为表面k法向矢量;σx为表面力;FPx为泵体积力。方程左边为控制体在x方向上的动量变化,即自航试验时得到的总推力Tg。方程右边第1项为作用于面1、面2、面3、面6上的压力和切应力。方程右边第2项为泵的体积力。面1~面6的定义参考文献[13]。
自航试验时,总推力Tg表示为:
| $ {{T}_{\text{g}}}=\frac{\rho Q_{\text{J}}^{2}}{{{A}_{6}}}\cos {{\theta }_{6}}-\rho {{Q}_{\text{J}}}{{c}_{\text{m1}}}{{U}_{0}} $ | (2) |
式中:QJ为推进器的体积流量;A6为喷口截面积;θ6为射流与水平方向的夹角;cm1为截面1的进流动量系数;U0为航速。
喷水推进器的实际推力(净推力Tnet)包括物理边界A3和A4泵体上的受力:
| $ {{T}_{\text{net}}}=\iint\limits_{{{A}_{3}}+{{A}_{4}}}{{{\sigma }_{x}}\text{d}A+\iiint{\rho {{F}_{\mathit{P}x}}\text{d}\mathit{V}}} $ | (3) |
式(1)和式(3)的主要差别在于是否考虑面1、面2、面4、面6上的压力。总推力Tg和净推力Tnet的差别用动量减额分数tj表示:
| $ {{T}_{\text{net}}}={{T}_{\text{g}}}\left( 1-{{t}_{\text{j}}} \right) $ | (4) |
喷水推进器在船后工作引起船体阻力的变化称为阻力增额。采用阻力增额分数来表示净推力Tnet和裸船体阻力RBH、自航强制力Ra之间的关系:
| $ {{R}_{\text{BH}}}-{{R}_{\text{a}}}={{T}_{\text{net}}}\left( 1-{{t}_{\text{r}}} \right) $ | (5) |
喷水推进推力减额与动量减额分数tj、阻力增额分数tr的关系:
| $ \left( 1-t \right)=\left( 1-{{t}_{\text{r}}} \right)\left( 1-{{t}_{\text{j}}} \right) $ | (6) |
喷水推进船阻力增额主要体现在4个方面:
1) 船体几何的变化:喷水推进器流道及喷口的安装使得船底及艉板几何面积减小,影响了船体的静压阻力及摩擦阻力;
2) 推进器的抽吸作用:喷水推进器的抽吸破坏了船底的边界层,同时又在流道唇部后方形成新的边界层,船底的流场发生变化,主要影响动压阻力及摩擦阻力;
3) 喷水推进器在船后喷射水流,影响了艉板后的兴波及流场;
4) 喷水推进器的安装及工作使得船体姿态发生了变化,进而影响了船体的阻力。
为便于分析,将前3点归结为局部作用,将船体姿态的变化归结为全局作用。
1.2 自航试验相似条件自航试验需要确定船体、推进器实尺度与模型尺度的相似条件。目前常用的有等推力系数法和等流量系数法。本文中的试验采用等推力系数法。等推力系数法认为模型与实尺度推进器推力系数相等,推力减额无尺度效应。等推力系数法自航强制力Ra由下式确定:
| $ {{R}_{\text{a}}}={{R}_{\text{m}}}-\frac{{{R}_{\text{s}}}}{{{\text{ }\!\!\lambda\!\!\text{ }}^{3}}} $ | (7) |
式中:Rm为船模阻力;Rs为实船阻力;λ为船模缩尺比。
2 计算结果及分析 2.1 船模几何及阻力预报本文研究对象为某三体船模,船模水线长度5.23 m,采用双泵推进。船模阻力及自航试验在挪威的MARINTEK船池开展。三体船模几何如图 2所示。

|
Download:
|
| 图 2 三体船几何示意 Fig. 2 Geometry of trimaran model | |
采用VOF方法来追踪自由液面,湍流模型采用SST k-ω模型。考虑到船体对称性,计算时取船体的一侧进行计算。计算区域入口边界取船艏向前延伸1倍船长处,出口边界取船艉向后延伸3倍船长处,侧边界及下方边界均取1.5倍船长,上方边界取水线上方1倍船长。网格模型采用切割体网格和棱柱层网格,对水线面,船艉处进行了网格加密,以捕捉兴波及艉板浸湿情况[14]。船模裸船阻力计算网格节点总数为202万,船模表面yplus在100左右。
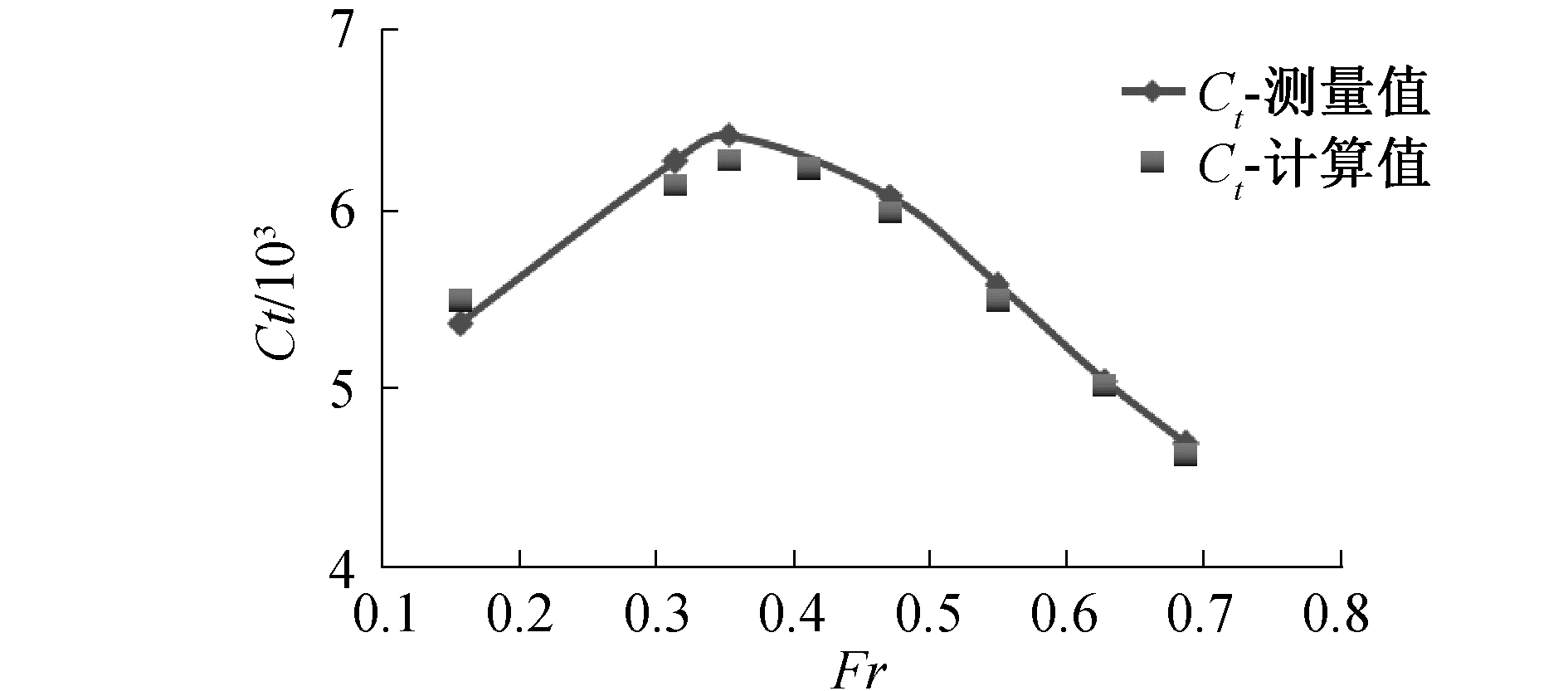
根据船体的受力及力矩平衡得到船体的纵倾角及升沉。三体船裸船拖曳阻力系数数值计算值与实验测量值对比见图 3,在计算航速范围内,船模阻力数值计算值与船模试验测量值误差不超过3%。
|
Download:
|
| 图 3 阻力系数计算值与测量值对比 Fig. 3 Comparison of the computed and measured resistance coefficient | |
由于喷水推进自航试验的主要目的是研究船泵相互作用,而非泵的水力性能,因此在数值计算时可采用体积力方法来代替泵叶轮及导叶的作用以降低计算量。由于泵的射流经过导叶的整流后旋转分量较小,因此本文的体积力法忽略了旋转分量的影响。保留泵的轮毂、外壳、轴,去掉叶轮及导叶几何,在此区域沿轴线施加一维均匀分布的动量源项代替叶轮及导叶的作用。调整动量源项的大小使得推进器推力加上强制力可以克服自航时船模的阻力,最终得到船模自航时的姿态、阻力、推力减额及推进器的流量等参数。在计算过程中对船模沿推进器轴线施加一个外力,其值等于泵的推力以考虑推力对船模姿态的影响。
为比较体积力法和实际泵模拟对计算结果的影响,分别采用体积力法和实泵模拟计算实尺度喷水推进自航工况。实泵模拟和体积力法计算结果见表 1。表中R0、T0、Q0分别为实泵模拟方法的阻力、推力及流量。采用体积力法计算得到的船体阻力、推进器流量、推力与实泵模拟差别较小。流道的压力分布除流道出口端略有差别,其他部分压力分布基本一致。2种方法得到的船体压力分布差别更小,故体积力法可用于研究喷水推进船推力减额。
| 表 1 两种方法自航计算结果 Table 1 Computation with two different methods |
为确保船模自航计算结果准确,本文针对Fr=0.687这一航速进行了网格无关性分析,按照1.3的比例对所有方向的网格进行加密,得到190万、290万、604万节点数的三套网格。三套网格的计算结果见表 2。表中纵倾角以艏倾为正,升沉以向上为正方向。可看到中等加密网格与细网格预报的阻力、纵倾角、升沉、流量等值差别不大。为平衡计算量和计算精度,选择290万节点的网格进行其他航速的计算和分析。
| 表 2 不同网格数目计算结果 Table 2 Computation with different grid sizes |
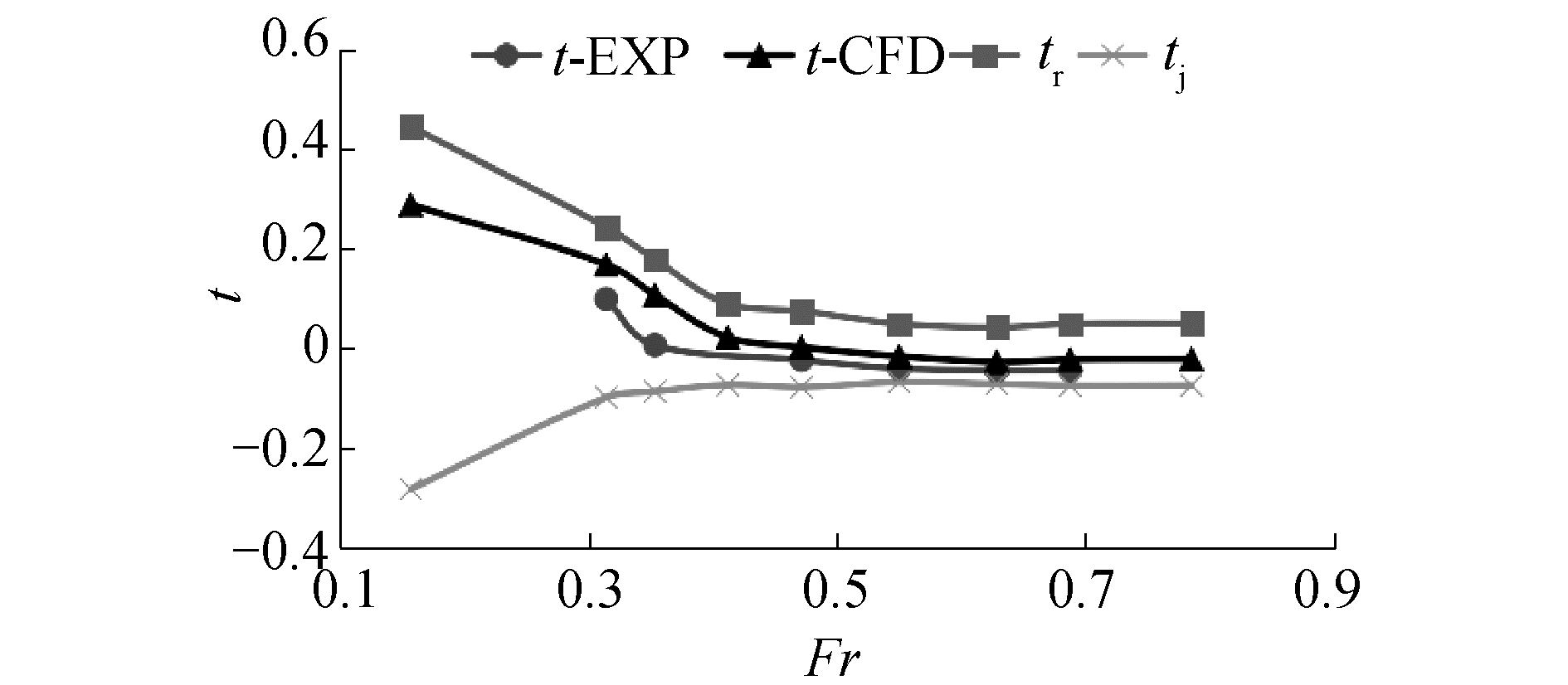
表 3对比了流量、推力减额计算值与试验测量值,流量数值计算值与实验测量值差别在3%以内。表中,EXP为试验值,CFD为计算值。图 4为推力减额的计算值与实验测量值对比。在较高航速时推力减额计算值与测量值吻合较好,而低航速时有一定偏差。当航速Fr>0.471时,推力减额为负。Fr=0.157时,阻力增额tr达到了0.447,随着航速的提高,阻力增额减小。动量减额一直为负,说明动量通量法预报总推力Tg小于净推力Tnet,这是本船模在中高航速下推力减额为负的原因。
| 表 3 流量及推力减额计算值和测量值对比 Table 3 Comparison of the computed and measured data |
|
Download:
|
| 图 4 推力减额计算值与实验值对比 Fig. 4 Comparison of the computed and measured thrust deduction fraction | |
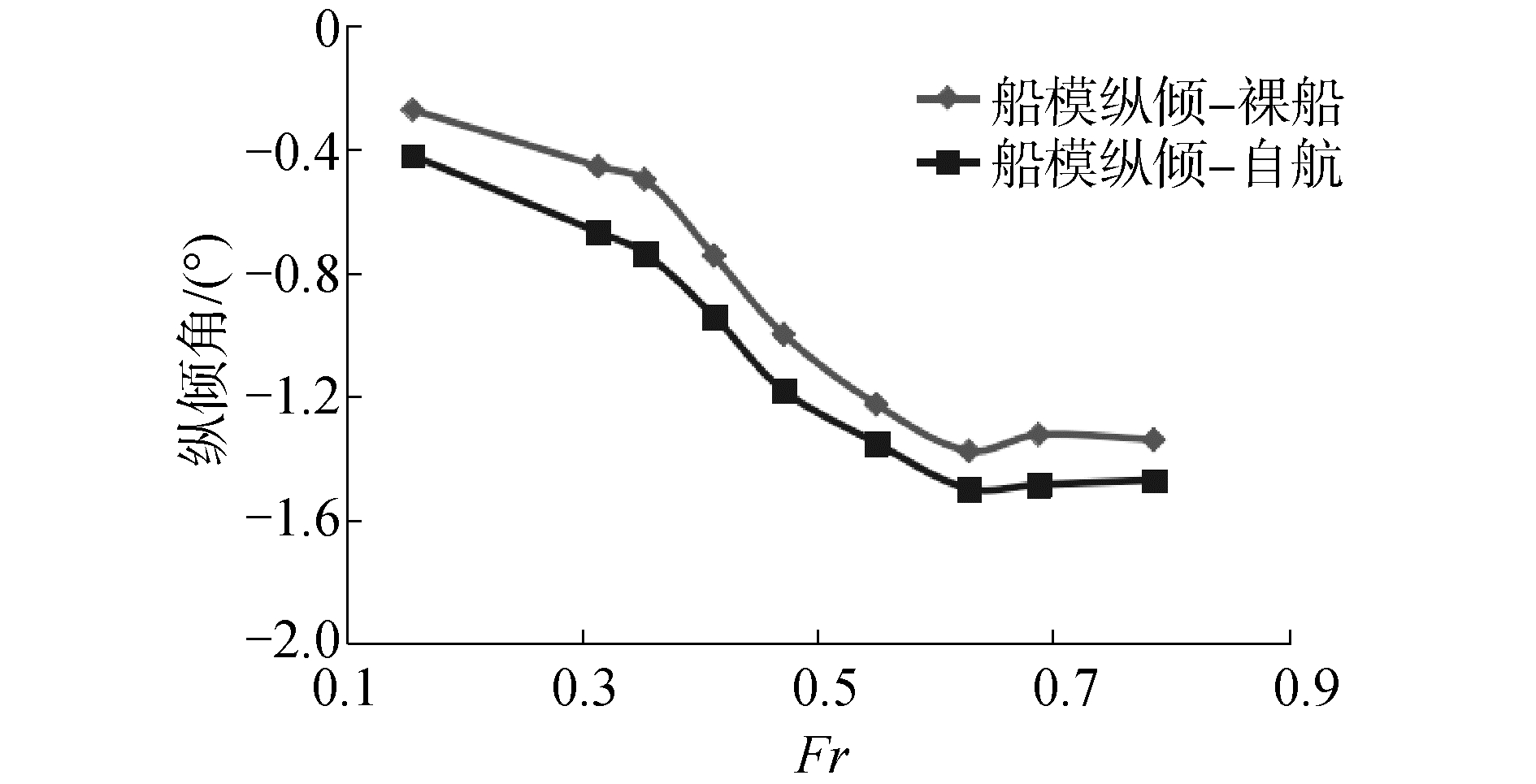
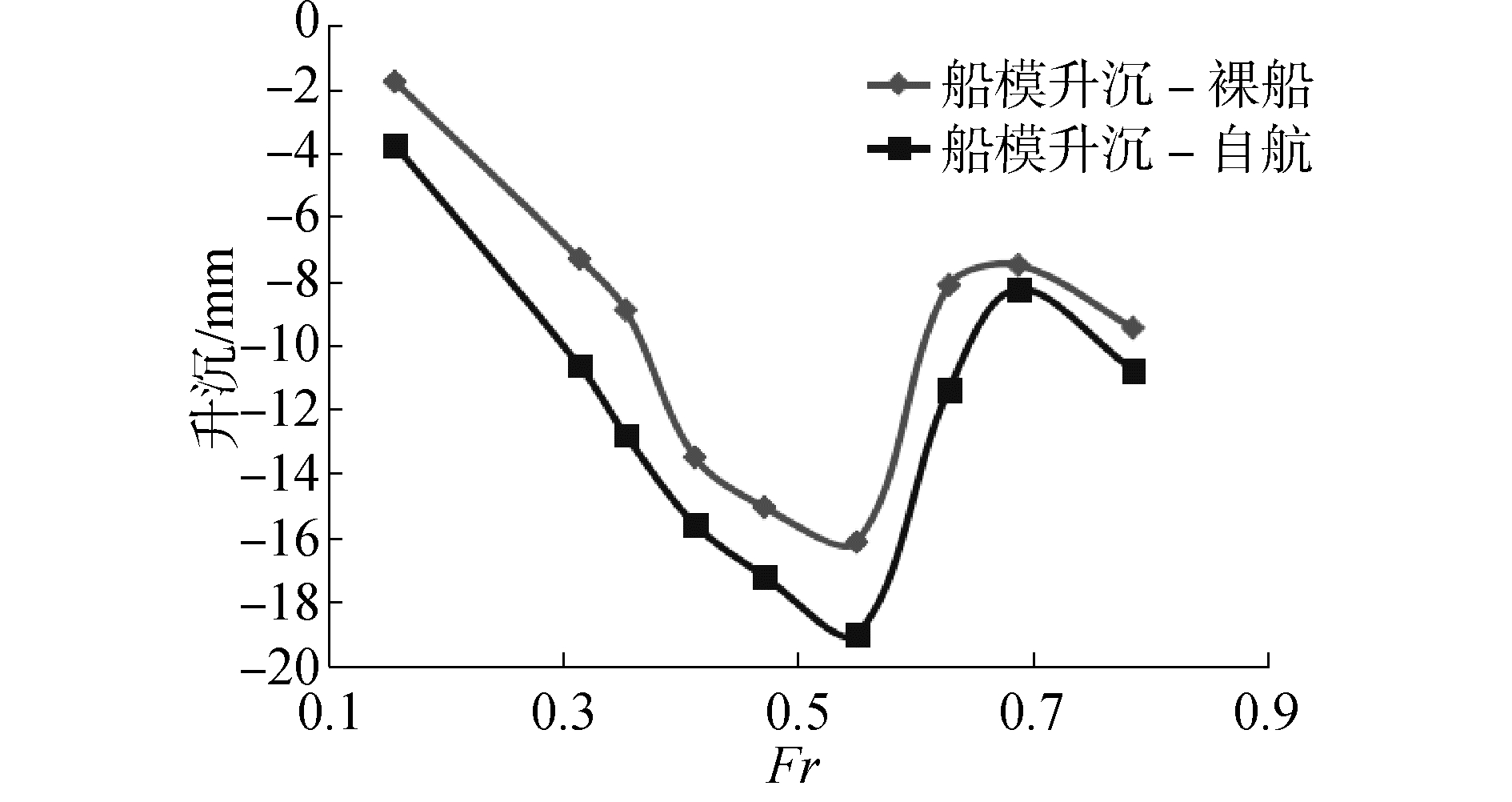
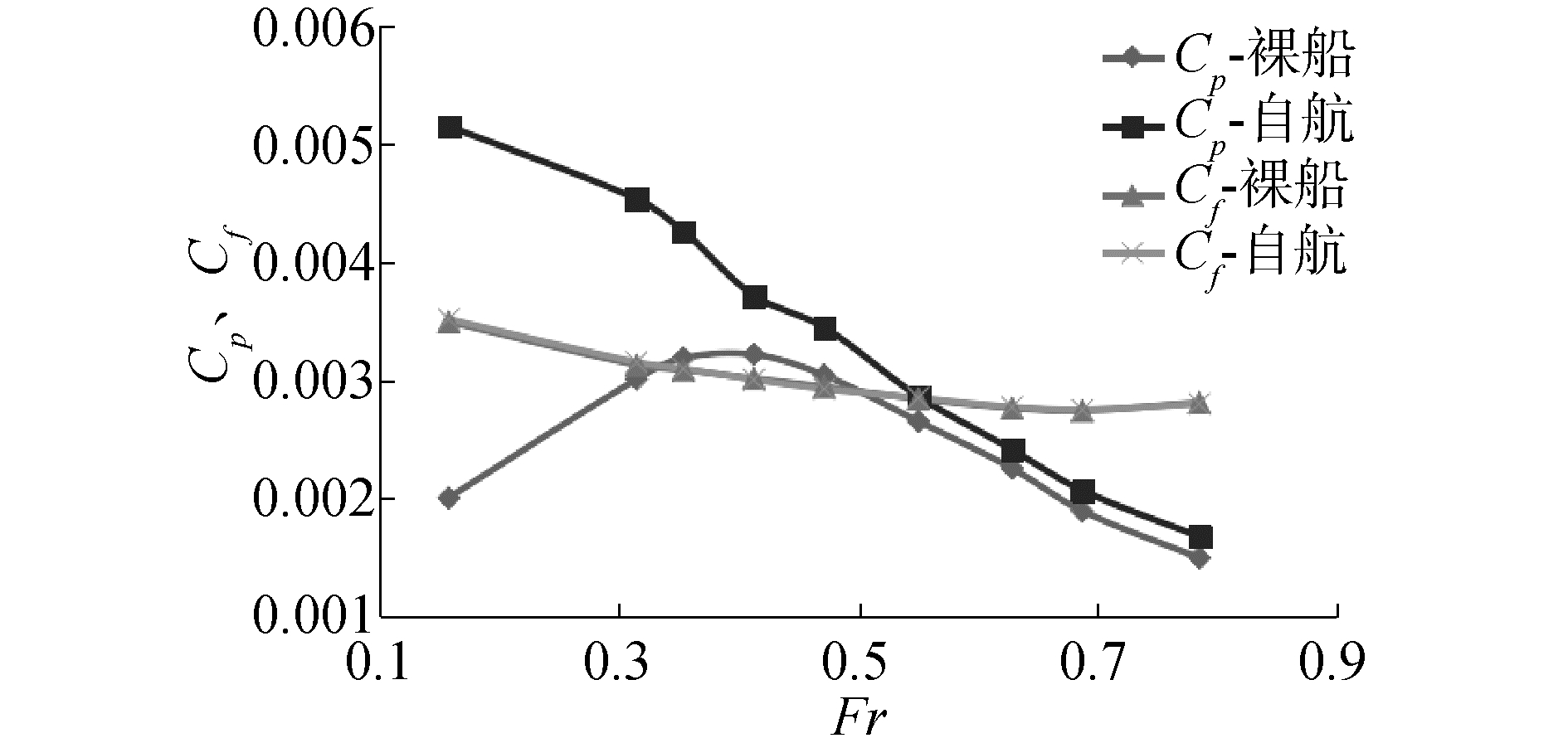
为研究喷水推进推力减额的变化规律,首先研究喷水推进时船体阻力的变化情况,即阻力增额的变化规律。图 5和图 6分别为裸船体与自航船体纵倾角,升沉计算值。自航时船体的纵倾角增加,船体下沉,吃水增加。图 7为裸船体和自航船体计算得到的摩擦阻力、压阻力的变化情况。自航时摩擦阻力变化较小,而压阻力增加。在较低航速时自航船体压阻力系数增额较大,较高航速时自航船体压阻力系数增额较小。
|
Download:
|
| 图 5 裸船和自航船体的纵倾角 Fig. 5 Trim angle of bare hull and self-propelled hull | |
|
Download:
|
| 图 6 裸船和自航船体的升沉 Fig. 6 Sinkage of bare hull and self-propelled hull | |
|
Download:
|
| 图 7 裸船和自航船体的阻力成分 Fig. 7 Resistance components of bare hull and self-propelled hull | |
为进一步分析自航时船体阻力的变化,将阻力增额的影响因素分解为全局作用(船体姿态变化造成的影响)和局部作用(推进器安装及抽吸的影响)。保持自航时船体的姿态与裸船体姿态相同,此状态称之为自航过渡状态。自航过渡状态与裸船阻力的差值即为局部作用的影响,自航状态与自航过渡状态船体阻力的差值即为全局作用的影响。
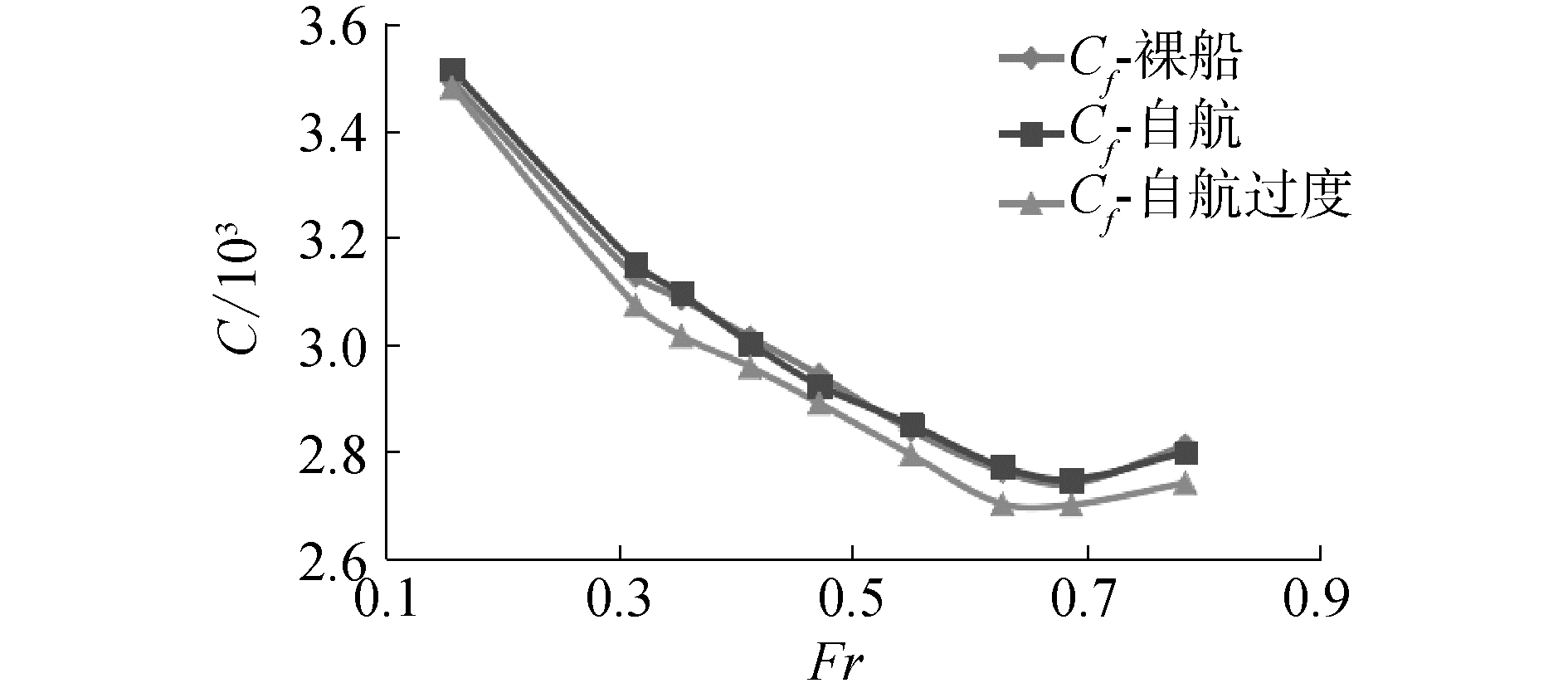
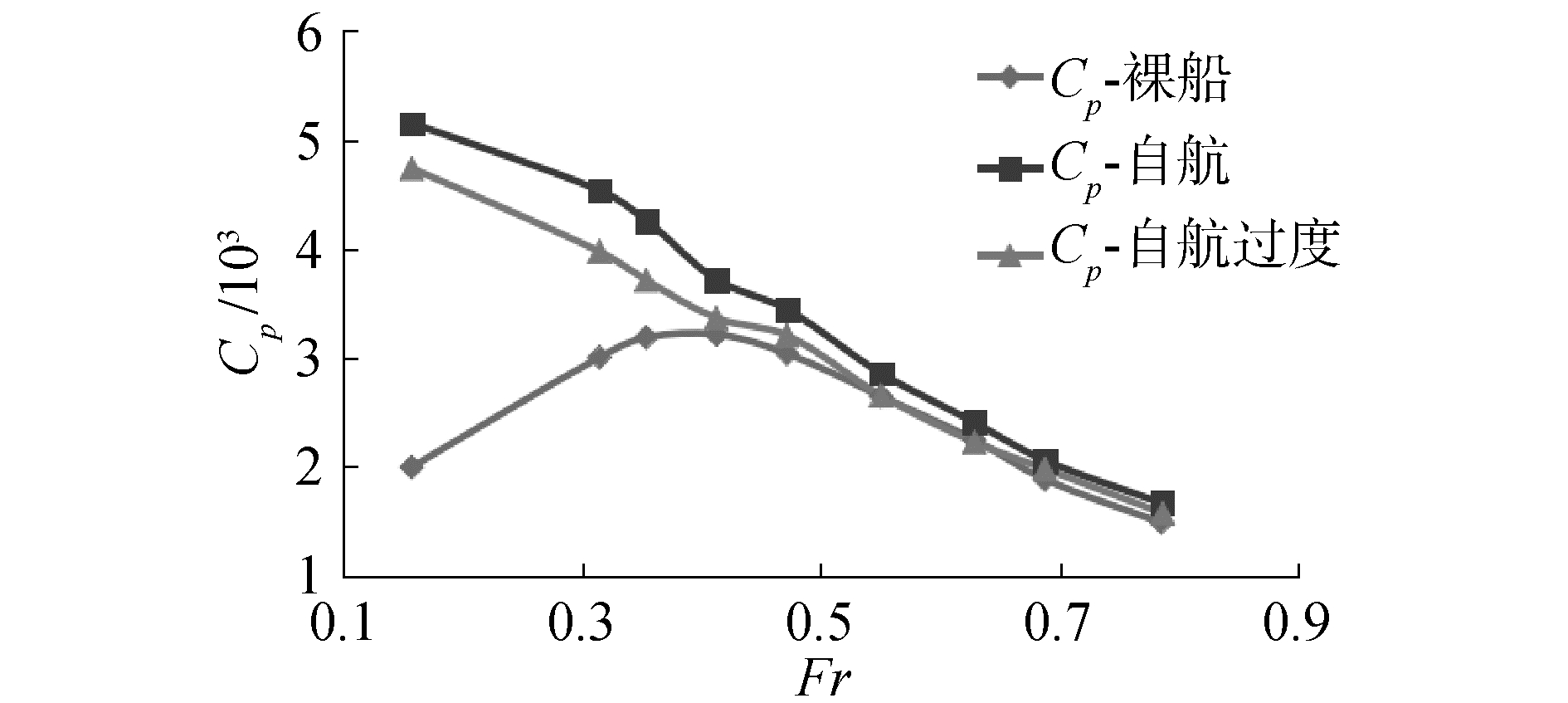
图 8为3种状态下船体摩擦阻力系数。自航船体和裸船体摩擦阻力差别较小。流道安装导致船体湿表面积减小,推进器抽吸破坏了船艉的边界层,因此自航过渡状态的摩擦阻力较小。自航时船体倾角增大,吃水增加,湿表面积增加,故自航状态相对于过渡状态摩擦阻力增加。图 9为3种状态下船体压阻力系数。低航速时自航过渡状态船体压阻力系数相对于裸船增加较多,即局部作用较为明显,而高航速时主要为全局作用,即船体姿态的变化影响较大。
|
Download:
|
| 图 8 3种状态下船体摩擦阻力系数 Fig. 8 Friction resistance coefficient of three conditions | |
|
Download:
|
| 图 9 3种状态下船体压阻力系数 Fig. 9 Pressure resistance coefficient of three conditions | |
以Fr=0.157为例,分析喷水推进低速时阻力增额较大的原因。由于高速方艉船艉板是否浸湿对阻力性能有重大影响[5],本文将艉板的受力单独列出。列出静压阻力的变化主要是为了分析船体几何变化对阻力的影响。列出动压阻力变化主要是为了分析推进器的抽吸作用对阻力的影响。表 4为Fr=0.157时3种状态下船体的阻力成分。由于片体阻力较小且基本不受局部作用的影响,故表中未列出。表中负号表示推力,正号为阻力。表中船体为去除尾板后的船体部分。
| 表 4 Fr=0.157时阻力成分 Table 4 Resistance components at Fr=0.157 |
从表 4可以看到,在Fr=0.157航速下局部作用(喷水推进器的安装和工作,SPBH-BH)导致阻力增大了6.1 N,全局作用(船模倾角和吃水的变化SP-SPBH)导致船模阻力增加了1.1 N。从阻力成分的变化来看,静压阻力是阻力变化的主要因素(+4.9 N),其次是动压阻力(+2.2 N),摩擦阻力几乎没有变化。
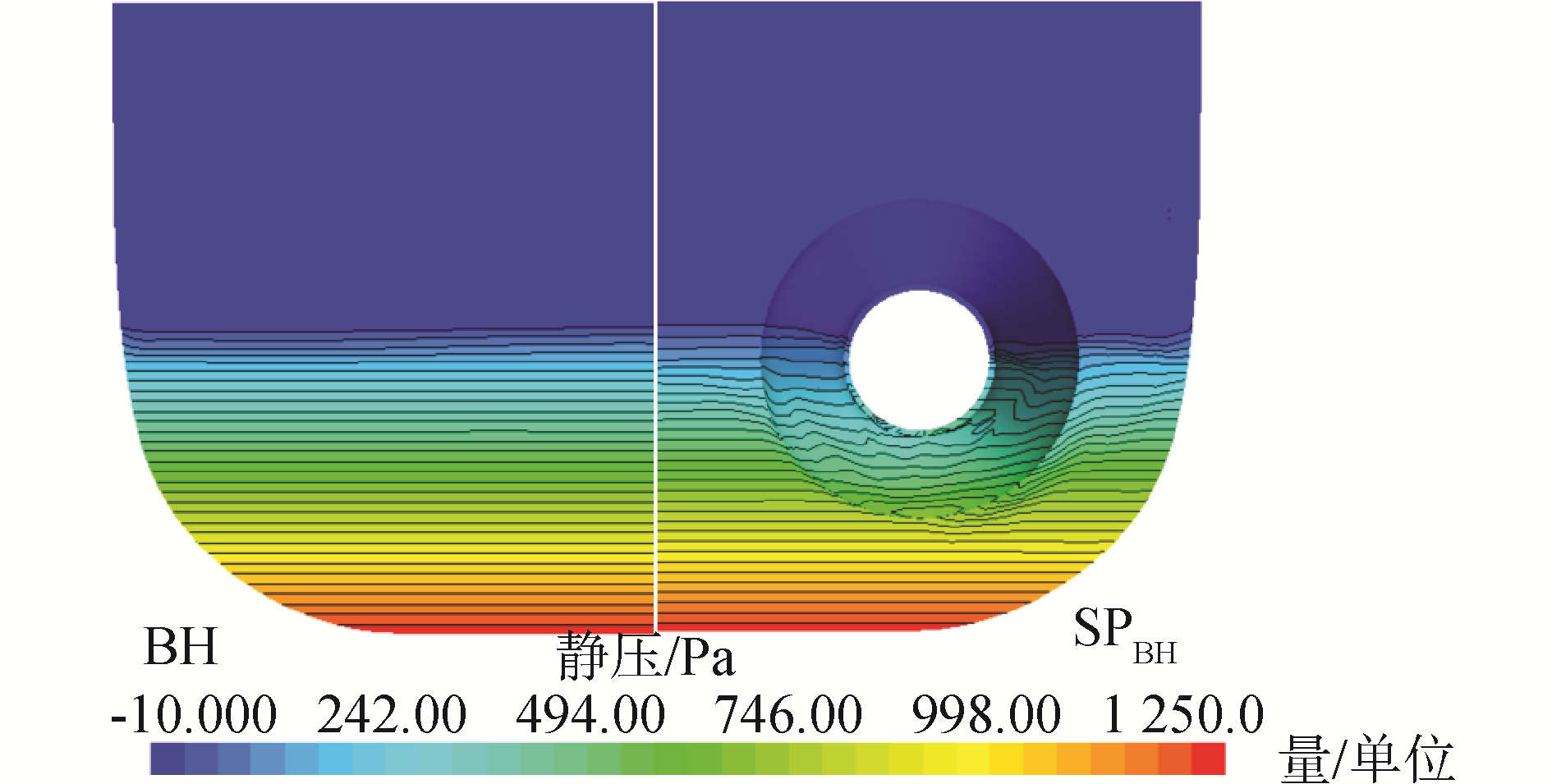
局部作用下静压阻力增加了4.5 N(即自航过渡状态的静压阻力与裸船静压阻力差值),主要原因是进水流道及喷口的安装使得船体几何面积减小,而此部分船体几何所受静压力指向船艏方向。艉板表面静压力分布见图 10。静压阻力值与船体的姿态和船体几何有关,与航速没有直接关系。低航速时总阻力较小,静压阻力差值占的比重大,故低航速时阻力增额尤为明显。高航速时总阻力较大,静压阻力差值占总阻力的比重较小,故阻力增额系数较小。
|
Download:
|
| 图 10 主体艉板静压力分布 Fig. 10 Static pressure contour on main transom | |
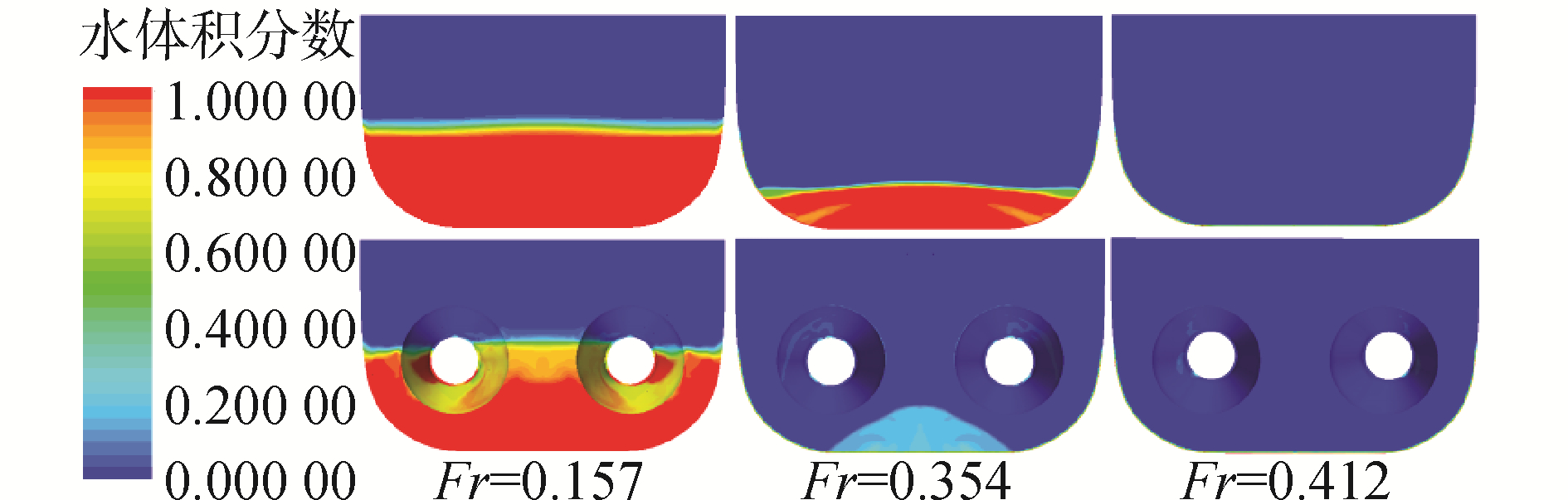
图 11为不同航速下裸船和自航船体艉板水气分布。当0.354 < Fr < 0.412时,裸船的艉板由湿变干,此时裸船的阻力系数达到最大值。安装喷水推进器后,推进器的射流降低了船艉的波高。Fr>0.354时,自航船艉板几乎全部是干的,推进器在水面以上喷射,此时裸船和自航船艉板几何的差别不再影响船体艉板的受力。
|
Download:
|
| 图 11 裸船和自航时船尾板的水气分布 Fig. 11 Water distribution at transom of bare hull and self-propelled hull | |
表 5为Fr=0.412时3种状态下船体的阻力成分。在Fr=0.412航速下局部作用(喷水推进器的安装和工作,SPBH-BH)导致阻力增大了1.5 N,全局作用(船模倾角和吃水的变化SP-SPBH)导致船模阻力增加了6.0 N。航速较高时,射流在水面上,局部作用较小,全局作用是影响阻力增额的主要因素。
| 表 5 Fr=0.412时阻力成分 Table 5 Resistance components at Fr=0.412 |
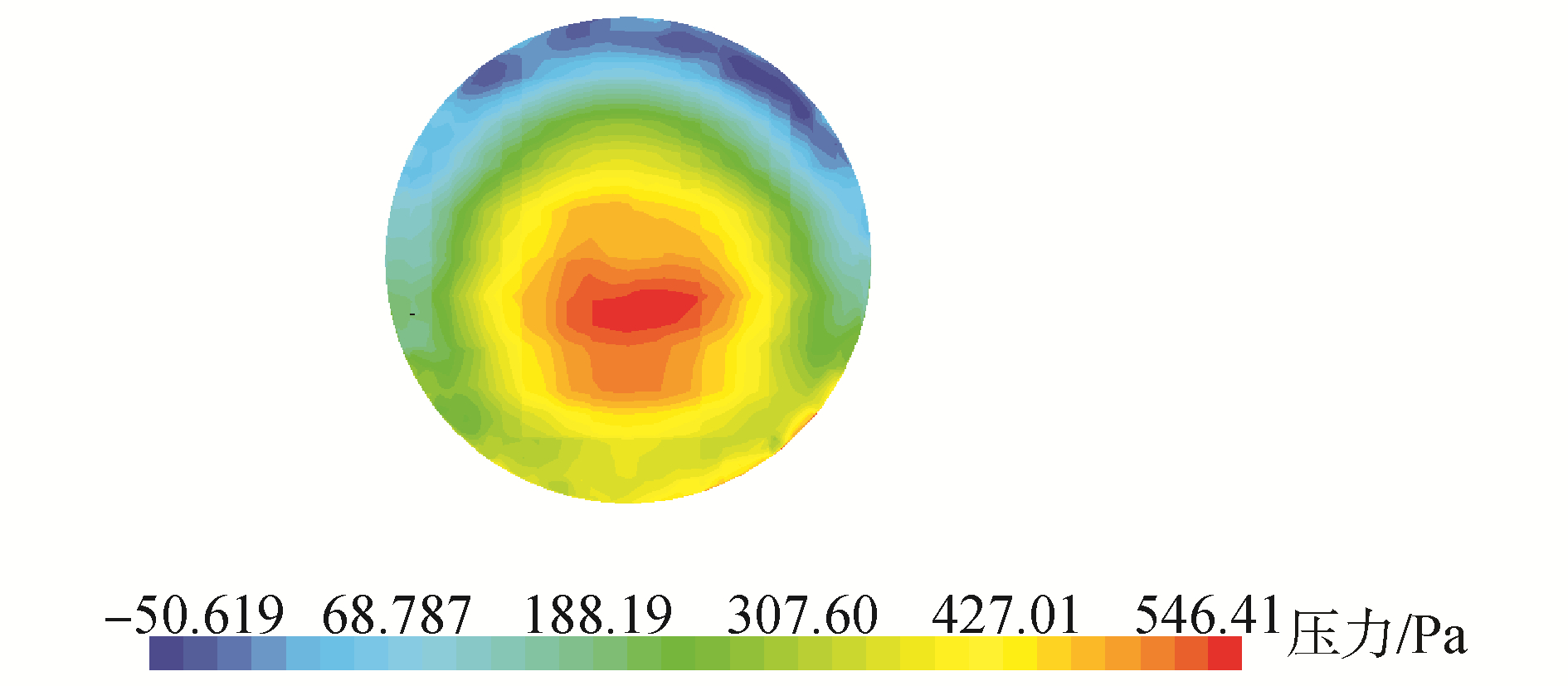
喷水推进的动量减额是由喷水推进推力计算方法引起的。喷水推进自航试验采用动量通量法计算推力,但是忽略了进流时面1,面2、面4及喷口出流面6上的压力分布,因此引入动量减额来代表这一差异。图 12为Fr=0.157时喷口出流面上的压力分布。此时喷口浸没在水中,受静压影响明显,压力最低点出现在最上方,压力最高点出现在圆心下方处。在此航速下若忽略喷口静压分布,采用动量通量法计算的总推力Tg与净推力Tnet差别较大,即动量减额分数的绝对值较大。
|
Download:
|
| 图 12 Fr=0.157时喷口压力分布 Fig. 12 Pressure contour at nozzle exit at Fr=0.157 | |
将图 1中面1、面2、面4上压力沿轴向积分为进口阻力Rin,将喷口出流面6上压力沿轴向积分为出口阻力Rout。有关进口阻力和出口阻力的定义可参考文献[5]。
| $ {{T}_{\text{g}}}-{{T}_{\text{net}}}=-\iint\limits_{{{A}_{1}}+{{A}_{2}}+{{A}_{4}}}{{{\sigma }_{\text{x}}}\text{d}A+}\iint\limits_{{{A}_{6}}}{{{\sigma }_{\text{x}}}\text{d}A={{R}_{\text{in}}}+{{R}_{\text{out}}}} $ | (8) |
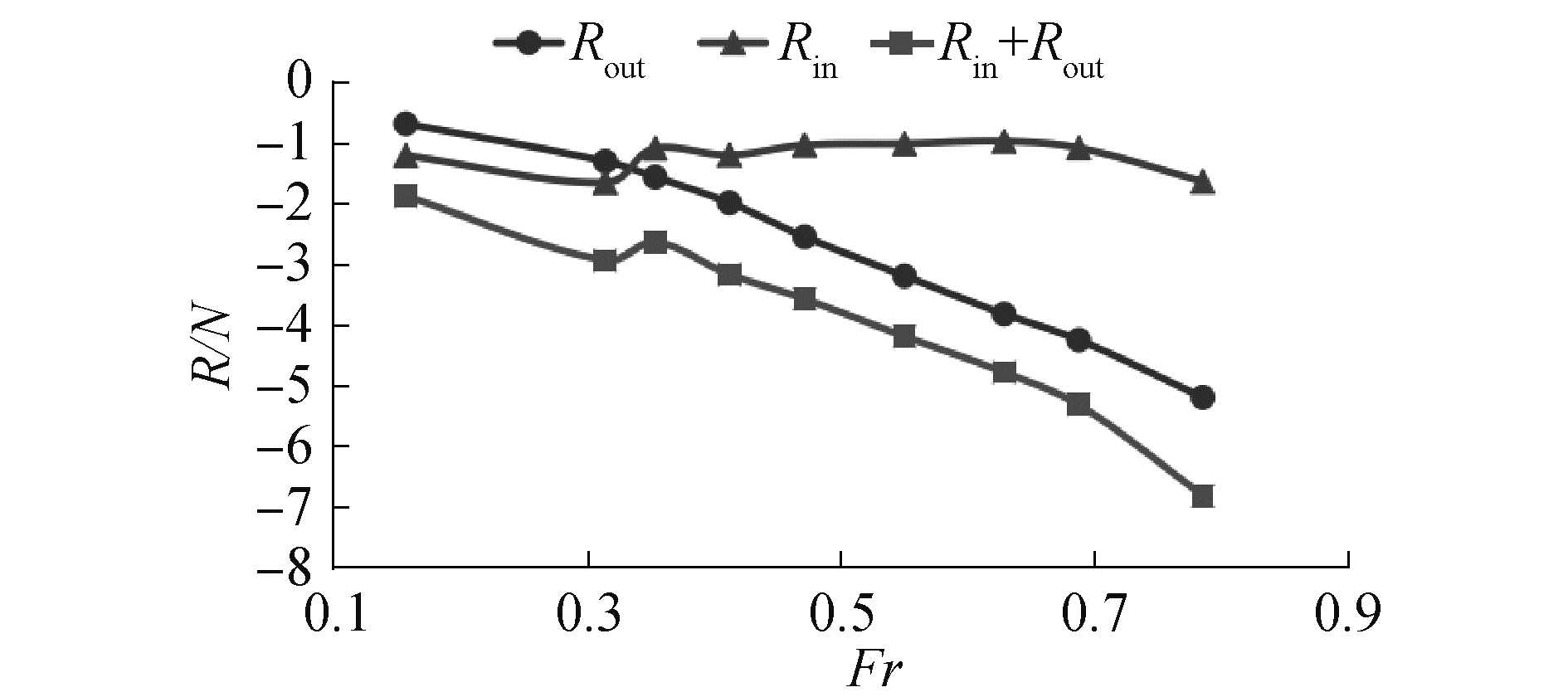
图 13为进口阻力和出口阻力随航速变化示意图。出口阻力主要受流量及是否水中喷射影响,在计算的航速范围内呈单调变化的趋势,在较高航速时占主要成分。进口阻力受航速、流量、航态、伴流等因素的影响,不随航速单调变化。进口阻力在Fr=0.314和Fr=0.354航速时出现拐点,此时对应艉板由湿变干的临界航速。
|
Download:
|
| 图 13 进口阻力和出口阻力 Fig. 13 Intake drag and exit drag | |
1) 喷水推进在较低航速时推力减额较大,随着航速的提高,推力减额不断减小。当Fr>0.471时,推力减额为负且基本不随航速变化。
2) 对于本船模而言,负动量减额导致了高航速时的负推力减额。船模自航试验时采用动量通量法计算推力Tg,此推力比推进器实际推力Tnet小,即动量减额为负。
3) 传统观点认为低航速时较大的推力减额是喷水推进器的抽吸导致的。而本文研究表明下静压阻力的变化是主要原因。低速时喷口在水下喷射,同时喷水推进器流道及喷口的安装使船体及尾板几何面积有较大减小,静压阻力增大。
4) 高航速时喷水推进器在水面以上喷射,船体姿态的变化是阻力增额的主要原因。
5) 出口阻力随航速增加而增大,在较高航速时是导致总推力Tg与净推力Tnet差别的主要原因。
| [1] |
VAN T T. The effect of waterjet-hull interaction on thrust and propulsive efficiency[C]//Proceedings of the International Conference on Fast Sea Transportation, FAST' 91. Trondheim, Norway, 1991: 1149-1167.
(  0) 0)
|
| [2] |
COOP H G. Investigation of hull-waterjet interaction effects[D]. University of Canterbury, 1995.
(  0) 0)
|
| [3] |
VAN T T. Waterjet-hull interaction[D]. Delft: Delft University of Technology, 1996.
(  0) 0)
|
| [4] |
ALEXANDER K, COOP H, VAN T T. Waterjet-hull interaction:recent experimental results[J]. SNAME transactions, 1994, 102: 87-105. (  0) 0)
|
| [5] |
VAN T T. Report of the specialist committee on validation of waterjet test procedures to the 24th ITTC[C]//The 24th International Towing Tank Conference. Edinburgh, UK: ITTC, 2005.
(  0) 0)
|
| [6] |
CUSANELLI D S, CARPENTERER S A. Axial waterjet(AxWJ) model 5662: Hull resistance and model-scale powering with LDV nozzle design[R]. West Bethesda: NSWC, 2007.
(  0) 0)
|
| [7] |
PAUL R. Waterjet Self-propulsion model test for application to a high-speed sealift ship[R]. American: California State University, 2007.
(  0) 0)
|
| [8] |
KANDASAMY M, GEORGIEV S, GEORGIEV E, et al. Numerical and experimental evaluation of waterjet propelled Delft catamarans[C]//Proceedings of the 11th International Conference on Fast Sea Transportation. Honolulu, Hawaii, USA, 2011: 847-850.
(  0) 0)
|
| [9] |
ESLAMDOOST A. The hydrodynamics of waterjet/hull interaction[D]. Gothenburg, Sweden: Department of Shipping and Marine Technology, Chalmers University of Technology, 2014.
(  0) 0)
|
| [10] |
孙存楼, 王永生, 徐文珊. 喷水推进船负推力减额机理研究[J]. 水动力学研究与进展, 2011, 26(2): 177-185. SUN Cunlou, WANG Yongsheng, XU Wenshan. Mechanism of negative thrust deduction factor of waterjet hull[J]. Chinese journal of hydrodynamics, 2011, 26(2): 177-185. DOI:10.3969/j.issn.1000-4874.2011.02.006 (  0) 0)
|
| [11] |
郭春雨, 龚杰, 李茂华, 等. ITTC规程下喷水推进三体船自航试验研究进展[J]. 船海工程, 2014, 43(6): 15-18, 24. GUO Chunyu, GONG Jie, LI Maohua, et al. Development of propulsion test for trimaran with waterjets following the ITTC procedure[J]. Ship & ocean engineering, 2014, 43(6): 15-18, 24. DOI:10.3963/j.issn.1671-7953.2014.06.014 (  0) 0)
|
| [12] |
蔡佑林, 沈兴荣, 孙群. 喷水推进船航速预报的动量通量试验技术发展现状[J]. 中国造船, 2015, 56(2): 131-141. CAI Youlin, SHEN Xingrong, SUN Qun. Developing status of water-jet ship velocity prediction based on momentum flux test technology[J]. Shipbuilding of China, 2015, 56(2): 131-141. DOI:10.3969/j.issn.1000-4882.2015.02.016 (  0) 0)
|
| [13] |
DYNE G, KRUPPA C, LAMBERTI B, et al. The specialist committee on validation of waterjet test procedures final report and recommendation to the 21st ITTC[C]//21st ITTC. Trondheim Norway, 1996.
(  0) 0)
|
| [14] |
易文彬, 王永生, 彭云龙, 等. 考虑航行姿态的船模阻力及流场数值预报[J]. 海军工程大学学报, 2016, 28(5): 26-30. YI Wenbin, WANG Yongsheng, PENG Yunlong, et al. Resistance and flow field prediction of ship model with consideration of voyage attitude[J]. Journal of Naval University of Engineering, 2016, 28(5): 26-30. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


