2. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001
2. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
高光谱图像由于具有较高的空间分辨率和光谱分辨率,在遥感图像应用领域优于其他光谱,在民用和军事上都有大量的应用,如大气环境监测、植被保护和战场目标发现等。近年来,一种不需要任何先验信息的异常目标检测问题的研究成为高光谱图像处理的热点问题,该问题的解决类似于一种盲信号处理问题的解决过程。Reed等[1]提出经典的RX异常检测算法,解决高光谱图像异常检测问题。以该方法为基础,提出了许多改进算法,用于高光谱图像异常检测问题的解决。如Molero等[2]提出的快速RX异常目标检测算法,通过在RX算法中引入多核节点聚类,加速RX算法检测速度。RX算法基于似然比检测算子完成检测过程,是一种建立在线性基础上的方法,但是高光谱图像在整个获取和后续处理中,整个图像的波段间是一种非线性的关系,因此RX算法具有一定的局限性;Kwon等[3]将非线性引入RX算法,提出Kernel RX算法,基于核函数的方法,对于高光谱图像波段间的非线性问题进行处理,改善了经典RX算法的检测性能;Khazai等[4]假设高光谱图像背景数据符合球形协方差矩阵,对Kernel RX检测算子进行修正,得到了较好的异常检测结果;Zhou等[5]提出了一种聚类Kernel RX算法,该算法先对背景像元进行聚类,然后利用快速特征分解算法产生异常检测算子,进行异常目标检测。基于Kernel RX检测算子的方法检测性能明显优于RX异常检测算子,但是该类算法也存在算法复杂度增加和检测时间长的不足。近年来,稀疏表示被引入到异常目标检测中,取得了比较好的异常目标检测结果。Chen等[6]在高光谱图像目标检测中引入稀疏表示解决方法,该算法基于低维子空间中的高光谱图像像元可以表示为稀疏线性训练样本的组合,对目标检测效果较好;Yuan等[7]在高光谱异常目标检测中引入稀疏表示,提出了稀疏差异指数的概念并给出了公式,把它应用于异常目标检测,得到了较好的异常检测结果;Li等[8-9]利用背景联合稀疏表示提出了一个新的异常目标检测模型,算法估计正交背景互补子空间,在局部区域内自适应地选择更多的代表性背景,从而提高了稀疏表示算法的异常目标检测精度; Zhao等[10-11]对高光谱图像的稀疏特性进行了分析,提出了一种基于稀疏评分估计框架的异常检测算法,检测效率较高。基于稀疏表示的异常检测算法,突破了传统广义概率似然估计和非线性核函数等方法的局限性,提高了异常目标检测精度和鲁棒性,但是利用稀疏表示方法在提高检测性能和降低虚警率方面需要进一步优化和改进。
基于以上分析,利用高光谱图像的空间特性和光谱特性,联合稀疏表示方法和RX异常检测方法的优点,对经典的RX异常检测方法进行改进,提出了基于空间预处理和双边滤波的稀疏RX(spatial prepro- cessing and bilateral filtering, SPBF-RX)高光谱图像异常目标检测算法。该算法基于2类高光谱图像(真实的和合成的),利用空间预处理方法和双边滤波,使得待处理的高光谱图像在空间特性和光谱特性上得到改善,然后利用稀疏差异指数对高光谱图像进行处理,进行异常目标检测,得到处理后的图像数据,最后将得到的这些图像数据作为RX异常检测器的输入,得到异常目标检测结果。
1 空间预处理预处理的主要目的是对高光谱图像进行必要的光谱维和空间维处理,采用光谱维和空间维结合[12]的方法对高光谱图像进行变换,提高异常目标检测能力。假设Y是一个具有混合像元的高光谱图像数据,其波段为L,数据模型矩阵形式为:
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{AE}} + \mathit{\boldsymbol{n}} $ | (1) |
式中:Y为L×P维的光谱特征矩阵;列向量A=[a1 a2 … ap]为P个端元向量;E=[e1 e2 … ep]T为每一列端元向量占有的丰度值向量;A和E都是未知量;n为一个L维的噪声。
定义ζ(i, j)为一个标量权重为:
| $ \zeta \left( {i,j} \right) = \sum\limits_{r = i - d}^{i + d} {\sum\limits_{s = j - d}^{j + d} {\beta \left( {r - i,s - j} \right) \cdot \gamma \left( {r - i,s - j} \right)} } $ | (2) |
式中:
| $ \gamma \left( {r - i,s - j} \right) = \gamma \left( {\mathit{\boldsymbol{Y}}\left( {r,s} \right)\mathit{\boldsymbol{Y}}\left( {i,j} \right)} \right) $ | (3) |
式中:γ是中心像元Y(i, j)和相邻像元Y(r, s)之间的相似度计算,i, j, r, s∈RL×P;d是空间处理窗口的半径,在实际计算中,处理的空间区域是以Y(i, j)为中心像元,尺寸为l×l大小的正方形,且l取奇数,因此,d=(l-1)/2。ζ(i, j)的值是通过β加权γ得到的,β是一个标量值,在l×l限定的空间区域内,可以任意设定β值从而使γ值加权得到ζ(i, j)。
η(i, j)每一个像元的空间衍生加权因子:
| $ \eta \left( {i,j} \right) = {\left( {1 + \sqrt {\zeta \left( {i,j} \right)} } \right)^2} $ | (4) |
式中η(i, j)≥1。
由此得到:
| $ \mathit{\boldsymbol{Y' = }}\frac{1}{{\eta \left( {i,j} \right)}}\left( {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{\bar T}}} \right) + \mathit{\boldsymbol{\bar T}} $ | (5) |
式中:
双边滤波是在高斯滤波器基础上,由Tomasi等[13]进行改进得到的一种非线性的滤波算法。对于空间预处理后的有L个波段的高光谱数据向量Y′,给定滤波窗口R,对高光谱图像的双边滤波器定义为[14]:
| $ {g^i}\left( {x,y} \right) = \frac{{\sum\limits_m^n {\left[ {{\omega ^i}\left( {x,y,m,n} \right){{Y'}^i}\left( {m,n} \right)} \right]} }}{{\sum\limits_m^n {{\omega ^i}\left( {x,y,m,n} \right)} }} $ | (6) |
i=1, 2, …, L;m, n∈R。Y′i(m, n)是高光谱数据Y′第i个波段图像坐标为(m, n)中的一个像元,(m, n)代表双边滤波器窗口
同时,定义域核为:
| $ {f^i}\left( {x,y,m,n} \right) = \exp \left( { - \frac{{{{\left( {x - m} \right)}^2} + {{\left( {y - n} \right)}^2}}}{{2\sigma _f^2}}} \right) $ | (7) |
值域核为式(8):
| $ {h^i}\left( {x,y,m,n} \right) = \exp \left( { - \frac{{{{\left\| {{{\mathit{\boldsymbol{Y'}}}^i}\left( {x,y} \right) - {{\mathit{\boldsymbol{Y'}}}^i}\left( {m,n} \right)} \right\|}^2}}}{{2\sigma _h^2}}} \right) $ | (8) |
得到权重系数ωi(x, y, m, n)为:
| $ \begin{array}{*{20}{c}} {{\omega ^i}\left( {x,y,m,n} \right) = {f^i}\left( {x,y,m,n} \right) \cdot {h^i}\left( {x,y,m,n} \right) = }\\ {\exp \left( { - \frac{{{{\left( {x - m} \right)}^2} + {{\left( {y - n} \right)}^2}}}{{2\sigma _f^2}}} \right) \cdot }\\ {\exp \left( { - \frac{{{{\left\| {{{\mathit{\boldsymbol{Y'}}}^i}\left( {x,y} \right) - {{\mathit{\boldsymbol{Y'}}}^i}\left( {m,n} \right)} \right\|}^2}}}{{2\sigma _n^2}}} \right) = }\\ {\exp \left( { - \frac{{{{\left( {x - m} \right)}^2} + {{\left( {y - n} \right)}^2}}}{{2\sigma _f^2}} - } \right.}\\ {\left. {\frac{{{{\left\| {{{\mathit{\boldsymbol{Y'}}}^i}\left( {x,y} \right) - {{\mathit{\boldsymbol{Y'}}}^i}\left( {m,n} \right)} \right\|}^2}}}{{2\sigma _h^2}}} \right)} \end{array} $ | (9) |
式中:ωi(x, y, m, n)同时考虑了空间域与值域的差别,定义域核fi(x, y, m, n)为高斯滤波器,是一个空间邻近度因子,由像元之间的空间距离决定;hi(x, y, m, n)是像元幅度邻近度因子,由像元之间的反射强度之差决定,参数σf和σh分别控制着反射强度因子和空间临近度因子的衰减程度。
3 基于稀疏RX的高光谱异常检测方法 3.1 稀疏表示及差异指数高光谱图像数据Y′在稀疏表示的情况下,利用字典学习方法,将图像数据表示为一个训练样本的线性组合,即由背景子字典Db和目标子字典Dt构成,Y′处于一个由背景和目标共同张成的空间里:
| $ \begin{array}{*{20}{c}} {Y' \approx \alpha _1^bd_1^b + \alpha _2^bd_2^b + \cdots + \alpha _{{N_b}}^bd_{{N_b}}^b + \alpha _1^td_1^t + }\\ {\alpha _2^td_2^t + \cdots + \alpha _{{N_t}}^td_{{N_t}}^t = }\\ {\underbrace {\left[ {d_1^bd_2^b \cdots d_{{N_b}}^b} \right]}_{{\mathit{\boldsymbol{D}}_b}}\underbrace {{{\left[ {\alpha _1^b\alpha _2^b \cdots \alpha _{{N_b}}^b} \right]}^{\rm{T}}}}_{{\mathit{\boldsymbol{\alpha }}_b}} + }\\ {\underbrace {\left[ {d_1^td_2^t \cdots d_{{N_b}}^t} \right]}_{{\mathit{\boldsymbol{D}}_t}}\underbrace {{{\left[ {\alpha _1^t\alpha _2^t \cdots \alpha _{{N_b}}^t} \right]}^{\rm{T}}}}_{{\mathit{\boldsymbol{\alpha }}_t}} = }\\ {{\mathit{\boldsymbol{D}}_b}{\mathit{\boldsymbol{\alpha }}_b} + {\mathit{\boldsymbol{D}}_t}{\mathit{\boldsymbol{\alpha }}_t} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_b}}&{{\mathit{\boldsymbol{D}}_t}} \end{array}} \right]}_\mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{c}} {{\alpha _b}}\\ {{\alpha _t}} \end{array}} \right] = \mathit{\boldsymbol{D\alpha }}} \end{array} $ | (10) |
式中:字典D是由背景子字典Db和目标子字典Dt构成的L×(Nb+Nt)的矩阵;α是对应的未知稀疏系数权向量。稀疏系数权向量α=αb+αt,αb为背景系数权向量,αt为目标系数权向量。若Y是一个背景像元,则αb是稀疏的,αt是一个零向量;若Y是一个目标像元,则αb是一个零向量,而αt是稀疏的。
因此,根据像元Y的稀疏表示其系数向量α的非零系数位置,就可以判别该像元是背景还是目标[6]。求解高光谱像元Y的稀疏表示的系数向量α就是求解最优化问题:
| $ \mathit{\boldsymbol{\alpha }} = \arg \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}{\rm{subject}}\;{\rm{to}}\;\mathit{\boldsymbol{D\alpha }} = \mathit{\boldsymbol{X}} $ | (11) |
由于向量α稀疏的特性,可以用求解l1范数的最小值问题来解决该最优化问题。
由于高光谱图像数据分布的稀疏性,对其进行处理得到需要的异常目标,可以从稀疏编码等角度进行分析,通过研究采用稀疏差异指数[4, 7]进行图像重构,再进行异常检测。该指数由光谱稀疏指数和空间稀疏指数构成。光谱稀疏指数为:
| $ {\rm{SD}}{{\rm{I}}_{{\rm{Spectral}}}} = \frac{{\sum\limits_{i = 1}^N {\left\| {\mathit{\boldsymbol{\alpha }}_i^ * - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\alpha }}_i^ * /N} } \right\|_2^2} }}{N} $ | (12) |
式中:α*为权向量; N是权向量α*的维数。
SDISpatialj为第j个波段的空间稀疏差异指数:
| $ {\rm{SDI}}_{{\rm{Spatial}}}^j = \frac{{\sum\limits_{i = 1}^N {\left\| {\mathit{\boldsymbol{\theta }}_i^ * - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\theta }}_i^ * /N} } \right\|_2^2} }}{N} $ | (13) |
式中:θ*是第j个波段的协同表示的权向量;N是其维数,即为第j个波段中局部背景字典原子个数。
因此,空间协同稀疏差异指数表示为:
| $ {\rm{SD}}{{\rm{I}}_{{\rm{Spatial}}}} = \frac{1}{\mathit{\Psi }}\sum\limits_{j = 1}^\mathit{\Psi } {{\rm{SDI}}_{{\rm{Spatial}}}^j} $ | (14) |
式中Ψ为波段总数。将式(12)和式(14)获得的光谱的稀疏差异指数和空间的稀疏差异指进行协同稀疏,得到一个新的光谱和空间协同稀疏加权的差异指数:

|
(15) |
式中:τ为加权系数; SDInew同时反映了光谱相关性和空间相关性。根据每个像元的SDInew值设定阈值,进行异常目标检测。
3.2 RX异常目标检测器RX异常目标检测器[15]中,将具有L个波段的高光谱图像数据表示为一个L维列向量y(n),设YB为包含M个像元的L×M背景矩阵:
| $ {\mathit{\boldsymbol{Y}}_B} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_1}}&{{\mathit{\boldsymbol{y}}_2}}& \cdots &{{\mathit{\boldsymbol{y}}_M}} \end{array}} \right] $ | (16) |
假设背景噪声向量为n,目标光谱向量为s,背景均值为μb,异常目标均值为μs,背景协方差为Cb。从而有H0成立时a=0,服从多维高斯分布N(μb, Cb);H1成立时a>0,服从多维高斯分布N(μs, Cb)。则RX算法区分目标的二值假设定义为:
| $ \left\{ \begin{array}{l} {{\rm{H}}_0}:\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{n}},\;\;\;目标不存在\\ {{\rm{H}}_1}:\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\alpha s}} + \mathit{\boldsymbol{n}},\;\;\;目标存在 \end{array} \right. $ | (17) |
设r为观测数据,RX算子的判决表达式为:
| $ \begin{array}{*{20}{c}} {{R_x}\left( \mathit{\boldsymbol{r}} \right) = {{\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)}^{\rm{T}}}{{\left( {\frac{M}{{M + 1}}{{\hat C}_b} + \frac{1}{{M + 1}}\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right){{\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)}^{\rm{T}}}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)\begin{array}{*{20}{c}} {{H_1}}\\ > \\ < \\ {{H_0}} \end{array}\eta } \end{array} $ | (18) |
式中:M为像元数,而对于实际数据来说,可以近似认为M→∞,故式(18)可以简化为:
| $ {R_x}\left( \mathit{\boldsymbol{r}} \right) = {\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)^{\rm{T}}}\hat C_b^{ - 1}\left( {\mathit{\boldsymbol{r}} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)\begin{array}{*{20}{c}} {{{\rm{H}}_1}}\\ > \\ < \\ {{{\rm{H}}_0}} \end{array}\eta $ | (19) |
式(19)为RX算子的一般形式,
| $ {{\mathit{\boldsymbol{\hat \mu }}}_b} = \frac{1}{M}\sum\limits_{i = 1}^M {{\mathit{\boldsymbol{x}}_i}} $ | (20) |
| $ {{\mathit{\boldsymbol{\hat C}}}_b} = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {{\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\hat \mu }}}_b}} \right)}^{\rm{T}}}} $ | (21) |
原始高光谱图像经过空间预处理和双边滤波得到一个异常目标, 相比于背景信息突出的高光谱图像,然后利用稀疏差异指数重构高光谱图像数据矢量,再用RX异常检测器进行异常目标检测,得到最终的异常目标检测结果,该算法的实现步骤如下:
1) 利用获取到的真实的高光谱图像和合成的高光谱图像,作为仿真图像数据Y;
2) 对仿真图像数据Y利用空间预处理方法进行处理;
3) 再利用双边滤波对处理后的高光谱图像Y′进行滤波处理,得到新的高光谱图像Y″;
4) 对高光谱图像Y″利用稀疏分解方法计算稀疏差异指数,并重构成新的高光谱图像数据向量;
5) 利用RX异常检测器进行异常目标检测,并以灰度图像的形式输出;
6) 为了得到清晰的检测结果,将灰度图像以一定的阈值转化为二值图像。
4 仿真分析 4.1 真实高光谱图像数据采用仿真的方法对提出的算法(SPBF-RX)进行分析和验证。仿真采用的是圣地亚哥海军机场的一部分遥感图像,该图像是异常目标检测算法常用的仿真图像,具有较好的可类比性。原图像是空间大小为400×400像元,空间分辨率3.5 m,去除由于水蒸气、噪声等干扰严重的波段,剩余波段为126个。从中截取含有38个异常目标、空间尺寸大小为100×100像元的区域进行仿真检测,如图 1所示。

|
Download:
|
| 图 1 仿真用的高光谱图像 Fig. 1 The hyperspectral imagery as simulation | |
首先,对图 1(a)所列的高光谱图像进行空间预处理,空间预处理方法中参数的选择,主要涉及处理时空间尺寸的大小,采用文献[16]所示的方法,空间尺寸选择7×7像元,结果如图 2所示,这是空间预处理后的第15波段的高光谱图像。通过空间预处理,图像目标点更有利于检测和识别。

|
Download:
|
| 图 2 空间预处理后的第15波段数据 Fig. 2 The 15th bands data of spatial preprocessing | |
空间预处理之后的图像进行双边滤波,双边滤波具有保持图像边缘信息,去除图像噪声干扰的作用,是一种充分利用高光谱图像空间信息和灰度特性的非线性滤波方法。得到的结果如图 3所示。高光谱图像经过双边滤波处理之后,目标信息和背景信息区分度更大,有利于后续高光谱图像异常目标检测精确度的提高。

|
Download:
|
| 图 3 双边滤波后的第15波段数据 Fig. 3 The 15th bands data of bilateral filtering | |
对处理后的高光谱图像计算稀疏差异指数,进而得到一个由稀疏差异指数重构的图像数据向量,最后通过RX异常检测器得到检测结果,如图 4所示,在相同条件下,仿真了SU-RX算法[17],KRX(Kernel RX)算法[3]和RX算法[1]。实验中获取的总像元数是400,从图 4中能得到,本文提出的SPBF-RX算法检测精确度最高,优于其他几类线性RX算法或者非线性KRX算法,说明本算法采用的处理策略是合适的,通过空间预处理和双边滤波,从光谱特性和空间特性层面使原始高光谱图像数据得到修正,处理后的图像更易于后续目标检测。

|
Download:
|
| 图 4 真实图像4种算法的异常检测结果 Fig. 4 Anomaly detection results of four algorithms for true imagery | |
高光谱图像异常目标检测评价指标中,在获取的总像元中,含有的目标像元数、虚警像元数和能检测到的异常目标数目,是3个重要的性能指标。同上,设定检测到的总的像元数目为400,通过仿真实验,在38个异常目标中,SPBF-RX算法能检测到36个、SU-RX算法能检测到34个、KRX算法能检测到34个、RX算法能检测到23个,从异常目标检测和数目角度,SPBF算法检测性能最好,RX算法检测性能最差;从400个总像元中,目标所占像元数和虚警所占像元数角度对比,SPBF算法目标数为257个、虚警数为143个,SU-RX算法目标数为223个、虚警数为177个,KRX算法目标数为199个、虚警数为201个,RX算法目标数为159个、虚警数为241个。由此,又一次验证SPBF-RX算法检测性能最优,虚警率低。
因为高光谱图像像元总数随着目标图像的不同会发生变化,由此需要在不同像元总数的情况下,对算法性能的有效性和鲁棒性进行比较分析,根据实际情况选取总的像元数在0~300,检测指标为总像元中目标所占数目和虚警所占数目,如图 5和图 6所示,能够得到几种算法的检测规律。通过分析可以得到,SPBF-RX算法具有高的目标检测率和低的虚警检测率,特别是随着总像元数目的增加,SPBF-RX检测性能越来越好,具有稳定的鲁棒性。

|
Download:
|
| 图 5 4种算法检测的目标占总像元数目的比较 Fig. 5 Comparison of the pixel number of detected targets from four algorithm | |

|
Download:
|
| 图 6 4种算法检测的虚警占总像元数目的比较 Fig. 6 Comparison of the pixel number of false detection from four algorithm | |
从上述的定性指标和定量指标的检测规律来看,SPBF-RX算法相比于SU-RX算法、KRX算法和RX算法来说,算法的检测效果远远优于其他算法,说明通过对高光谱图像进行空间预处理和双边滤波,图像得到一定程度的改善,即异常目标相对于背景分布来说,更加突出和有利于检测。
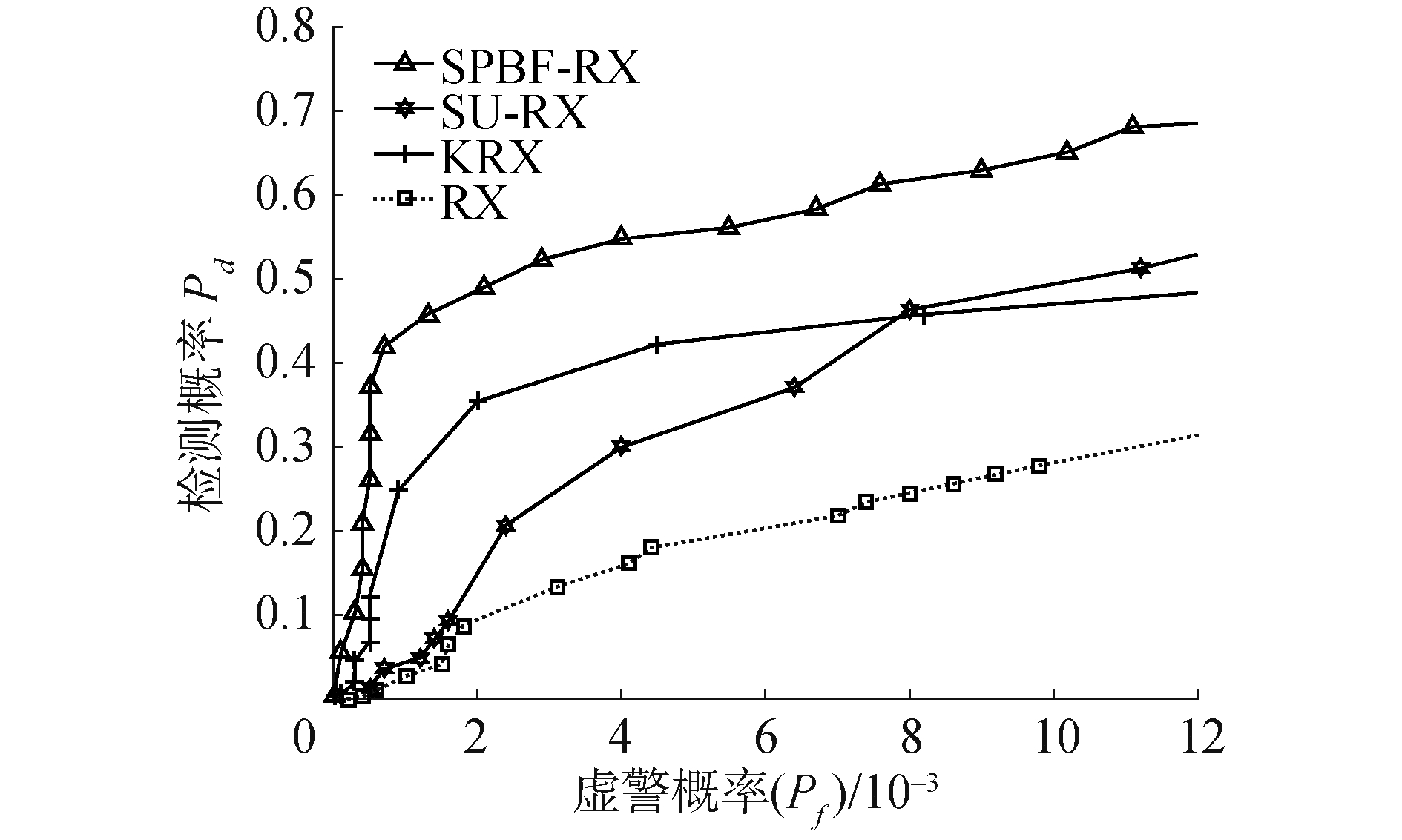
ROC是高光谱图像异常目标检测中常用的一种重要性能分析指标,ROC用于描述检测概率Pd与虚警概率Pf之间的变化关系[18]。将检测概率(Pd)定义为检测到的真实目标像元数目Nhit与地面真实目标像元数目Ntarget的比值;虚警概率(Pf)定义为检测到的虚警像元数目Nmiss同整幅图像像元数目总和Ntotal的比值。利用ROC指标对SPBF-RX算法、SU-RX算法、KRX算法和RX算法的检测性能进行分析,从图 9中能够发现,SPBF-RX算法检测性能具有极强的鲁棒性,检测性能优于其他几类算法,这与前文各项指标对SPBF-RX算法的分析是一致的。
|
Download:
|
| 图 7 4种异常检测算法的ROC比较 Fig. 7 ROC comparison of four anomaly detection algorithms | |

|
Download:
|
| 图 9 合成图像4种算法的异常检测结果 Fig. 9 Anomaly detection results of four algorithms for synthetic imagery | |
综上所述,利用真实的高光谱图像对提出的异常目标检测算法进行验证,SPBF-RX算法改进了传统RX算法的检测性能,降低了虚警率。
4.2 合成的高光谱图像高光谱图像属于大数量数据,因此提出的算法要满足处理大数据的要求。上文采用的真实高光谱图像,空间大小为100×100像元,波段为126个,这样的图像数据量大小不足以说明算法处理大数据量的能力。为了验证算法对于大数据量的处理性能,利用真实的AVIRIS图像合成一个新的背景复杂的高光谱图像,用于异常目标检测算法分析,合成的高光谱图像波段数为189个,空间尺寸为200×200像元。根据Chang等[19-20]所述的图像合成过程能得到,背景如果没有附加噪声则含有的目标点为25个,这些点以整个图像的中心为排列中心, 按照5×5矩阵的形式排列,图 8所示的为加入噪声之后的图像,可识别的点为21个[21-22]。

|
Download:
|
| 图 8 AVIRIS合成的异常目标检测图像 Fig. 8 Synthetic imagery of anomaly targets detection by AVIRIS | |
对该合成图像利用SPBF-RX、SU-RX、KRX和RX算法进行仿真得到如下结论,SPBF-RX算法在复杂背景大数据量的情况下,能够检测到15个异常目标;SU-RX算法对于该合成图像只能检测到4个异常目标;经典的KRX算法能检测到5个异常目标;RX算法能检测到14个异常目标。因此,能够得到,对于该合成图像来说,SPBF-RX算法能够很好地处理复杂大数量的图像数据;RX检测算法也能得到较好检测结果;但是KRX算法和SU-RX对于该合成图像的检测效果都不好,都存在检测精度不高的问题。综上,本文提出的SPBF-RX算法对于高光谱图像来说,具有鲁棒性强、检测精度高、虚警率低的特点。
5 结论1) 异常目标和背景信息稀疏表示模型的构建,并在此基础上与经典的RX异常检测器结合,提高传统RX异常检测器的检测性能;
2) 有效利用高光谱图像的空间和光谱特性,对高光谱图像进行空间预处理和双边滤波,使得高光谱图像目标特性相对比背景特性更加突出;
3) 稀疏差异指数中的高光谱图像空间特性和光谱特性的协同处理机制,使得稀疏差异指数可以很好地区分出异常目标信息和背景信息,从而提高异常检测的精度。
本文提出的SPBF-RX算法,利用2组实际和合成的高光谱图像进行仿真,得到的仿真结果与SU-RX算法、KRX算法、RX算法得到的结果进行比较,SPBF-RX在检测精度、虚警率和鲁棒性等方面都明显优于其他几种算法。因此,SPBF-RX算法是有效的和合理的,但是该算法也存在算法结构复杂,算法计算时间长等不足,需要在后续的工作中改进和完善。
| [1] |
REED I S, YU X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution[J]. IEEE transactions on acoustics, speech, and signal processing, 1990, 38(10): 1760-1770. DOI:10.1109/29.60107 (  0) 0)
|
| [2] |
MOLERO J M, PAZ A, GARZÓN E M, et al. Fast anomaly detection in hyperspectral images with RX method on heterogeneous Clusters[J]. The journal of supercomputing, 2011, 58(3): 411-419. DOI:10.1007/s11227-011-0598-0 (  0) 0)
|
| [3] |
KWON H, NASRABAD N M. Kernel RX-algorithm:a nonlinear anomaly detector for hyperspectral imagery[J]. IEEE transactions on geoscience and remote sensing, 2005, 43(2): 388-397. DOI:10.1109/TGRS.2004.841487 (  0) 0)
|
| [4] |
KHAZAI S, MOJARADI B. A modified kernel-RX algorithm for anomaly detection in hyperspectral images[J]. Arabian journal of geosciences, 2015, 8(3): 1487-1495. DOI:10.1007/s12517-013-1218-5 (  0) 0)
|
| [5] |
ZHOU Jin, KWAN C, AYHAN B, et al. A novel cluster kernel RX algorithm for anomaly and change detection using hyperspectral images[J]. IEEE transactions on geoscience and remote sensing, 2016, 54(11): 6497-6504. DOI:10.1109/TGRS.2016.2585495 (  0) 0)
|
| [6] |
CHEN Yi, NASRABADI N M, TRAN T D. Sparse representation for target detection in hyperspectral imagery[J]. IEEE journal of selected topics in signal processing, 2011, 5(3): 629-640. DOI:10.1109/JSTSP.2011.2113170 (  0) 0)
|
| [7] |
YUAN Zongze, SUN Hao, JI Kefeng, et al. Local sparsity divergence for hyperspectral anomaly detection[J]. IEEE geoscience and remote sensing letters, 2014, 11(10): 1697-1701. DOI:10.1109/LGRS.2014.2306209 (  0) 0)
|
| [8] |
LI Jiayi, ZHANG Hongyan, ZHANG Liangpei, et al. Hyperspectral anomaly detection by the use of background joint sparse representation[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2015, 8(6): 2523-2533. DOI:10.1109/JSTARS.2015.2437073 (  0) 0)
|
| [9] |
YUAN Yuan, ZHENG Xiangtao, LU Xiaoqiang. Discovering diverse subset for unsupervised hyperspectral band selection[J]. IEEE transactions on image processing, 2017, 26(1): 51-64. (  0) 0)
|
| [10] |
ZHAO Rui, DU Bo, ZHANG Liangpei. Hyperspectral anomaly detection via a sparsity score estimation framework[J]. IEEE transactions on geoscience and remote sensing, 2017, 55(6): 3208-3222. DOI:10.1109/TGRS.2017.2664658 (  0) 0)
|
| [11] |
ZHAO Rui, DU Bo, ZHANG Liangpei, et al. A robust background regression based score estimation algorithm for hyperspectral anomaly detection[J]. ISPRS journal of photogrammetry and remote sensing, 2016, 122: 126-144. DOI:10.1016/j.isprsjprs.2016.10.006 (  0) 0)
|
| [12] |
ZORTEA M, PLAZA A. Spatial preprocessing for endmember extraction[J]. IEEE transactions on geoscience and remote sensing, 2009, 47(8): 2679-2693. DOI:10.1109/TGRS.2009.2014945 (  0) 0)
|
| [13] |
TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]//Proceedings of the Sixth International Conference on Computer Vision. Bombay, India, India, 1998: 839-846.
(  0) 0)
|
| [14] |
廖建尚, 王立国, 郝思媛. 基于双边滤波和空间邻域信息的高光谱图像分类方法[J]. 农业机械学报, 2017, 48(8): 140-146, 211. LIAO Jianshang, WANG Liguo, HAO Siyuan. Hyperspectral image classification method combined with bilateral filtering and pixel neighborhood information[J]. Transactions of the Chinese society for agricultural machinery, 2017, 48(8): 140-146, 211. (  0) 0)
|
| [15] |
XU Yang, WU Zebin, LI Jun, et al. Anomaly detection in hyperspectral images based on low-rank and sparse representation[J]. IEEE transactions on geoscience and remote sensing, 2016, 54(4): 1990-2000. DOI:10.1109/TGRS.2015.2493201 (  0) 0)
|
| [16] |
ACITON, DIANI M, CORSINI G. On the CFAR property of the RX algorithm in the presence of signal-dependent noise in hyperspectral images[J]. IEEE transactions on geoscience and remote sensing, 2013, 51(6): 3475-3491. DOI:10.1109/TGRS.2012.2221128 (  0) 0)
|
| [17] |
成宝芝, 赵春晖, 张丽丽, 等. 联合空间预处理与谱聚类的协同稀疏高光谱异常检测[J]. 光学学报, 2017, 37(4): 0428001. CHENG Baozhi, ZHAO Chunhui, ZHANG Lili, et al. Joint spatial preprocessing and spectral clustering based collaborative sparsity anomaly detection for hyperspectral images[J]. Acta optica sinica, 2017, 37(4): 0428001. (  0) 0)
|
| [18] |
谷延锋, 刘颖, 贾友华, 等. 基于光谱解译的高光谱图像奇异检测算法[J]. 红外与毫米波学报, 2006, 25(6): 473-477. GU Yanfeng, LIU Ying, JIA Youhua, et al. Anomaly detection algorithm of hyperspectral images based on spectral analyses[J]. Journal of infrared and millimeter waves, 2006, 25(6): 473-477. DOI:10.3321/j.issn:1001-9014.2006.06.018 (  0) 0)
|
| [19] |
GAO Gui. A parzen-window-kernel-based CFAR algorithm for ship detection in SAR images[J]. IEEE geoscience and remote sensing letters, 2011, 8(3): 557-561. DOI:10.1109/LGRS.2010.2090492 (  0) 0)
|
| [20] |
CHANG C I, JIAO Xiaoli, WU Chaocheng, et al. Component analysis-based unsupervised linear spectral mixture analysis for hyperspectral imagery[J]. IEEE transactions on geoscience and remote sensing, 2011, 49(11): 4123-4137. DOI:10.1109/TGRS.2011.2142419 (  0) 0)
|
| [21] |
ZHANG Hongyan, ZHAI Han, ZHANG Liangpei, et al. Spectral-spatial sparse subspace clustering for hyperspectral remote sensing images[J]. IEEE transactions on geoscience and remote sensing, 2016, 54(6): 3672-3684. DOI:10.1109/TGRS.2016.2524557 (  0) 0)
|
| [22] |
DU Bo, ZHAO Rui, ZHANG Liangpei, et al. A spectral-spatial based local summation anomaly detection method for hyperspectral images[J]. Signal processing, 2016, 124: 115-131. DOI:10.1016/j.sigpro.2015.09.037 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


