2. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
潜水器是人类从事海洋开发的重要装备之一,随着海洋开发步伐的加快,提高航速、安全性和设计效率,降低艇体重量等日益受到关注和重视。然而,潜水器的设计过程涉及的学科众多,且需要进行大量的协调和反复修改。传统潜水器设计基于串行模式进行,缺乏有效的解耦及协调手段,存在计算花费大、设计周期长、最优解难以获得等不足。多学科设计优化在航空领域应用[1],其在复杂系统的设计过程中集成了各学科知识,充分考虑了学科间的耦合关系,以有效的设计/搜索策略为基础,同时针对复杂系统的整个设计过程,基于具有分布式特性的计算机网络系统,进行有效的组织、管理,并将学科之间的相互作用所产生的协同效应进行有效利用,最终目标是获得设计对象的整体最优解[2]。
多学科设计优化适用于复杂系统设计的优化求解,已在众多领域进行了成功应用。在潜水器设计领域将其应用多学科设计优化得到很多应用。文献[3-5]应用到AUV设计; 文献[6-7]应用到鱼雷设计;应用到载人潜水器设计;文献[12]应用到深海空间站设计;文献[13]应用到微小型水下航行器设计等。以上研究对于提高潜水器的总体性能、促进其技术进步等起到了重要的作用。准确的学科分析模型是实现潜水器多学科设计优化的关键工作之一,对于其性能的提升起着至关重要的作用。然而,以上研究的学科建模大多基于公式,尽管这种方法计算花费低、建模难度小,但计算精度低。随着技术的发展,近似模型、参数化建模等方法已引入到学科建模中。然而,近似模型的样本点数量与其拟合精度很难平衡,而直接将参数化分析应用于学科建模将导致整个求解过程变得十分复杂。在这种情况下,利用近似模型和参数化分析的优点,建立基于参数化分析和近似模型的分析模型,可有效提高潜水器性能与设计效率。
本研究针对一型潜水器[5]的主体结构设计,设计了基于参数化的无人水下航行器外形阻力、耐压壳体结构分析流程,并建立了近似模型,进一步基于上述近似模型建立了无人潜水器主体结构优化模型,进行了优化的求解,选取了其中的方案进行了对比。
1 外形阻力分析模型 1.1 阻力求解方法利用RANS法求解外形阻力,其在时均化的N-S方程中,以某种模型的方式将瞬态脉动量体现出来,雷诺时均化后的不可压连续性方程和RANS方程:
| $ \partial \left( {{{\bar u}_i}} \right)/\partial {x_i} = 0 $ | (1) |
| $ \begin{array}{l} \partial \left( {{\rho _i}{{\bar u}_i}} \right)/\partial t + {\rho _j}{{\bar u}_j}({\partial _i}{{\bar u}_i}/\partial {x_j}) = \\ \rho {{\bar F}_i} - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} - \rho \overline {u_i^\prime } \overline {u_j^\prime } } \right) \end{array} $ | (2) |
式中:ui、uj为速度分量时均值,m/s;p为压强时均值,Pa;RiN=(λ0+Δλi)PN-IN为流体密度,kg/m3;KNM{viM;ciM}={PN;RiN}为动力粘性系数,m2/s;
由于
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} $ | (3) |
| $ \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \omega {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\mathit{\Gamma }_\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right){\rm{ + }}{G_\omega } - {Y_\omega } + {D_\omega } $ | (4) |
式中:Gk和Gw为由于平均速度梯度引起的湍流动能;Yk和Yw为关于k和w的湍流耗散项。
1.2 基于STAR-CCM+的外形阻力分析利用STAR-CCM+进行阻力计算,通过设计参数的设置,可实现几何模型的参数化。潜水器外形见图 1。

|
Download:
|
| 图 1 潜水器外形 Fig. 1 Exterior map of submersible | |
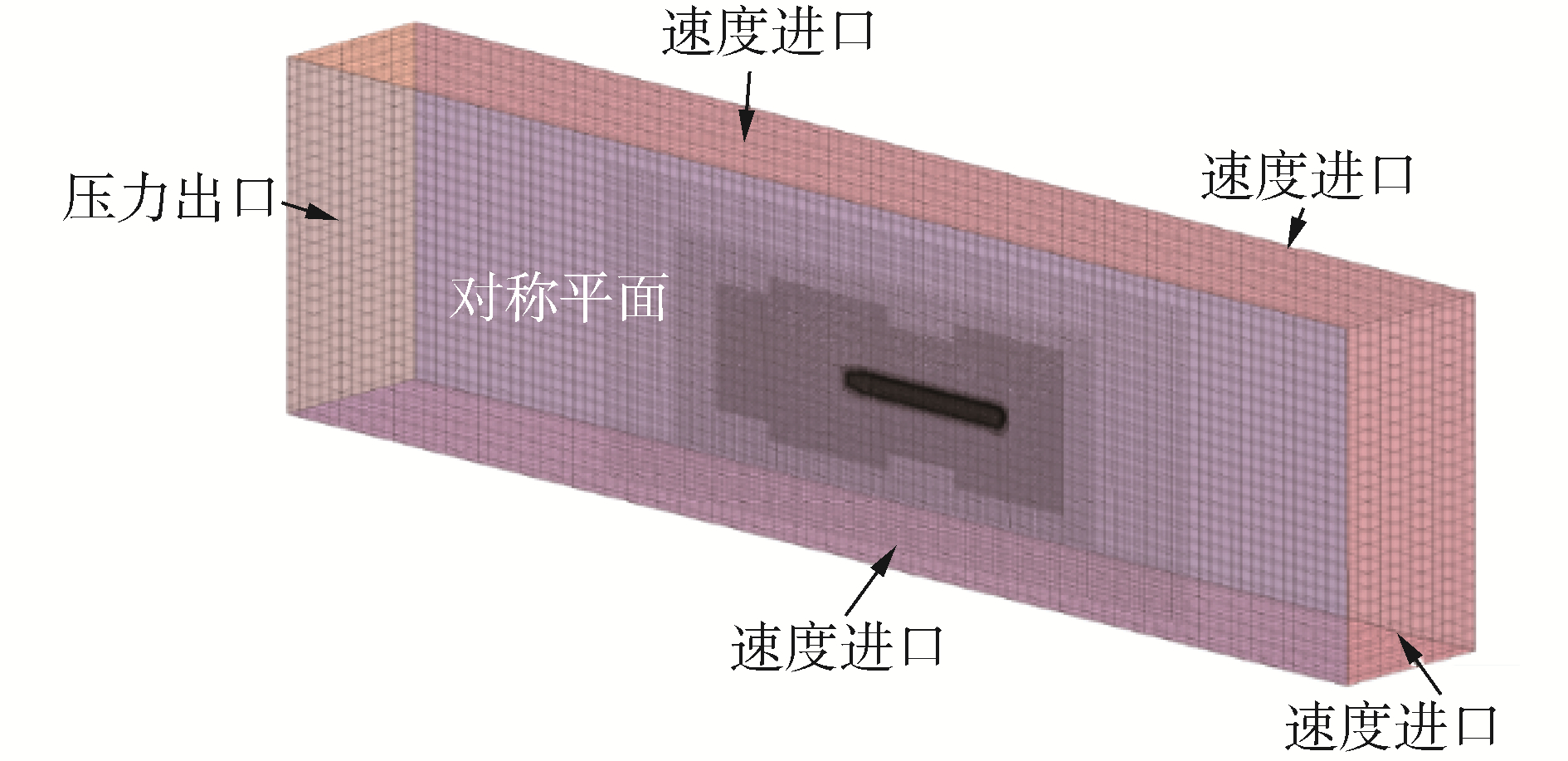
图 1中,主要参数包括总长度x1、半球形封头半径x2、圆柱壳体长度x3和艉部长度x4。外形为对称模型,以中纵剖面为界计算一半模型在水中运动的阻力[15]。将原点设置于模型的艉部,即艉部断电为原点,计算区域为长方体,尺度为前后均为20 m,上、下、侧面均为5 m,各层的网格均为加密网格,模型设置为水平,采用SSTρi湍流模型,强度0.01,粘度比10。模型设置如图 2。
|
Download:
|
| 图 2 计算域网格与边界条件设置 Fig. 2 Calculation area network grid and boundary conditions | |
计算模型水深400 m、速度30 m/s条件下的航行阻力为6 873.02 N,则整体阻力为13 746.04 N。同文献[4]对比两者相比误差为5.2%,说明计算结果具有一定准确性。
1.3 外形阻力参数化分析流程利用STAR-CCM+软件Java宏录制的功能,对Java宏文件进行二次编译。在STAR-CCM+软件中完成所有设置后开始录制宏文件,记录修改需求参数的命令。为便于修改,需要进行外形的参数、计算的时间步长(隐式定长的除外)、内部迭代的次数、计算所需时间等的记录。概括而言,主要包括模型尺度和计算时长的修改、计算结果的输出等。Java宏文件准备完毕后通过*.bat批处理文件直接运行Java宏文件,系统直接调用cmd.exe并运行批处理文件中的各个命令[16]。参数化的无人潜水器主体结构外形分析流程见图 3。

|
Download:
|
| 图 3 外形参数化分析流程 Fig. 3 Parametric analysis process of shape | |
通过编写*.bat文件调用STAR-CCM+,将前面所述的初始设置以*.sim格式保留在文件中,为了方便Isight软件对于程序进行读取和编辑,Java宏文件进行外形参数设置的保留。分析过程所设计的控制参数、计算结果等借助于Isight软件进行后处理[17],将计算所生成的结果文件存放于相应的工作目录下。得到81组样本点列于下表。
| 表 1 外形阻力样本点 Table 1 Sample points of shape resistance |
采用Abaqus有限元软件进行耐压结构的分析,包括最大应力σmax和极限载荷Pcr的求解。屈曲分析包括线性和非线性2部分,线性分析首先进行,随后采用弧长法(需要考虑和引入初挠度),即Riks法进行非线性的分析,在此部分中非线性的影响还需要考虑材料和几何,计算得到的极限载荷在载荷比例因子变化曲线中的位置处于最高处,采用Riks法与Newton-Raphson法结合求解非线性屈曲问题。具体过程为[18]:
| $ \Delta {{\rm{ \mathsf{ λ} }}_i} = \Delta {{\rm{ \mathsf{ λ} }}_0}, \Delta u_i^N = \Delta {{\rm{ \mathsf{ λ} }}_0}v_0^N $ | (1) |
对于第i增量步(i=1, 2, 3, …):
1)内部结点应力为:
| $ {I^N} = \int_V {{\beta ^N}} :\sigma {\rm{d}}V;{K^{NM}} = \partial {I^N}/\partial {u^M} $ | (2) |
2)检查平衡方程:
| $ R_i^N = \left( {{{\rm{ \mathsf{ λ} }}_0} + \Delta {{\rm{ \mathsf{ λ} }}_i}} \right){P^N} - {I^N} $ | (3) |
若各项值非常小,说明结果收敛,如果不收敛,则需求解方程
| $ {K^{NM}}\{ v_i^M;c_i^M\} = \{ {P^N};R_i^N\} $ | (4) |
2个方向的分量是PN、RN,2个方向的位移分量是viN、ciN。
3)将矢量(
| $ \left\{ {\left( {0; - {\rho _i}} \right) + {\rm{ }}\left( {\tilde c_i^N;{\rho _i}} \right) + \mu \left( {\tilde v_i^N;1} \right)} \right\}:\left( {\tilde v_0^N;1} \right) = 0 $ | (5) |
式中
4)下一次迭代:
| $ \left\{ \begin{array}{l} \Delta u_{i + 1}^N = \Delta u_i^N + c_i^N + \mu v_i^N\\ \Delta {{\rm{ \mathsf{ λ} }}_{i + 1}} = \Delta {{\rm{ \mathsf{ λ} }}_i} + \mu ;i = i + 1 \end{array} \right. $ | (6) |
下一次迭代则返回式(1)时,式(2)中需要做出额外修正,此时Abaqus软件会在这个阶段后,令voN=viN。
2.2 耐压壳结构有限元分析耐压壳体选用圆柱和球壳组合形式,采用Abaqus中的的Shell壳单元建立模型,宽度、高度、艇长方向分别为X轴、Y轴、Z轴,上述3个坐标轴方向依次设置为向左为正、向上为正、艇长,具体如图 4。

|
Download:
|
| 图 4 有限元模型与坐标系方向 Fig. 4 Finite element model and coordinate direction | |
假设潜水器在深水中处于静水压力为均匀的条件下,其所承受的载荷是关于3个平面是对称的,只需对关键节点处的线位移进行约束,而不需使用角位移约束,边界条件施加情况见下表。采用25 mm×25 mm的网格尺寸,网格划分见图 5。

|
Download:
|
| 图 5 耐压壳整体网格划分及环肋网格划分 Fig. 5 Block grid division of pressure resistant shell and ring ribbed grid division | |
| 表 2 耐压壳结构边界条件施加 Table 2 Application of boundary conditions for pressure resistant shell structures |
耐压壳体参数化分析流程与图 3所的外形参数分析流程类似,具体不同在于:1)设计变量为耐压壳体主体及环肋的尺寸及相应的控制参数;2)Abaqus的脚本编程基于Python语言,建模、属性设置、载荷与边界条件设置、网格划分、分析和后处理操作等基于Python语言。
为实现耐压壳的参数化建模,利用Abaqus软件进行耐压壳的参数化建模,需要对于模型的相关参数在Python文件中进行修改。这就需要借助Abaqus进程外的批处理*.bat文件来完成这个过程,最终实现Abaqus有限元分析软件能在的后台完成分析。需要首先进行耐压壳单元最大应力和模态特征值的计算,然后计算载荷因子曲线,经过后处理得到耐压壳的极限载荷。计算得到81组样本点值见表 3。
| 表 3 耐压壳体样本点 Table 3 Sample points of pressure shell |
响应面模型(response surface method,RSM)基本原理是通过变量和响应之间所存在多项式关系,对于两者通过简单函数关系进行表达,具有透明性高、简单、高效的特点。响应面模型按照阶数可分为一阶~四阶。其中,二阶响应面模型可表达为:
| $ \hat y\left( x \right) = {a_0} + \sum\limits_{i = 1}^n {{b_i}{x_i}} + \sum\limits_{i = 1}^n {{c_{ii}}x_i^2} + \sum\limits_{ \le i \ne j \le n}^n {{d_{ij}}{x_i}{x_j}} $ | (7) |
式中:ŷ(x)为响应面近似值;xi为设计变量;n为设计变量个数;a0、bi、cii、dij为待定系数。
响应面模型的拟合精度的预测可借助复相关系数R2进行预测,R2的取值范围为[0, 1],R2越接近1则近似模型拟合精度越高。R2可得到:
| $ {R^2} = 1 - \left( {\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} /\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} } \right) $ | (8) |
式中:yi为第i个样本对应的状态变量的响应值;ŷi为第i个样本对应的状态变量的近似值;
采用二阶响应面模型对于表 1的样本点进行拟合,得到R2为0.989 71,满足工程需要。抽取其中10个预测值与计算值进行对比,见图 6。

|
Download:
|
| 图 6 Rx预测值与计算值对比 Fig. 6 Comparison of forecast and calculated values for Rx | |
图 6中,10个预测值与计算值均非常接近。最终得到的结果如表 4。
| 表 4 外形响应面模型系数表 Table 4 Shape response model coefficient table |
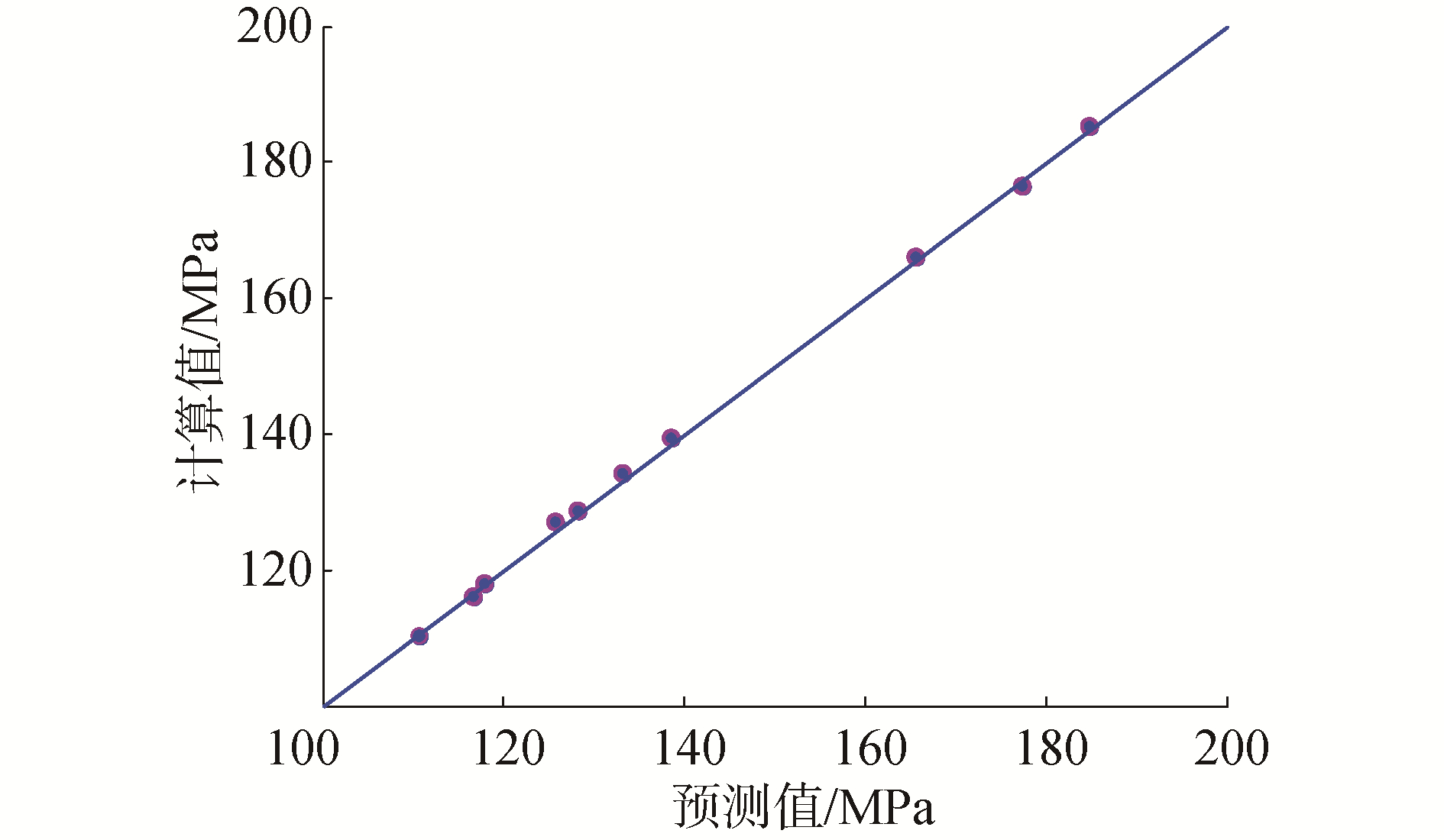
采用二阶响应面模型对于表 3的样本点进行拟合,σmax和Pcr的R2分别为0.999 32、0.983 51,满足工程需要。抽取σmax和Pcr的10个预测值与计算值进行对比,见图 7、图 8。
|
Download:
|
| 图 7 σmax预测值与计算值对比 Fig. 7 Comparison of forecast and calculated values for σmax | |

|
Download:
|
| 图 8 Pcr预测值与计算值对比 Fig. 8 Comparison of forecast and calculated values for Pcr | |
图 7,图 8中预测值和计算值均非常接近。得到的二次多项式系数如表 5。
| 表 5 耐压壳体响应面模型系数表 Table 5 Model coefficient table of RSM for pressure shell |
多目标优化的目标是得到Pareto最优解集,即Pareto前沿。非支配排序遗传算法(NSGA)是遗传算法针对多目标优化的变形形式,第2代非支配排序遗传算法(NSGA-Ⅱ)是NSGA的改进形式[19],NSGA-Ⅱ通过不仅引入了精英策略,其还将拥挤距离引入其中,这样就保留了进化过程中的优良种群,使Pareto解集的解呈均匀分布和种群多样的分布状态。第2代非支配排序遗传算法的求解步骤为:
1)初始种群的赋予的同时,进行排序种群的排序,此代种群为P0,其是随机产生的,初始种群进行选择、交叉与变异,进一步产生新种群,即Q0种群,令t=0;
2)构造新种群,对于Rt进行非劣排序,得到非劣前端F1,F2,…;
3)按拥挤比较操作pn对所有Fi进行排序,将最优秀的N个个体组成种群Pt+1;
4)对种群Pt+1执行选择、交叉和变异,进一步得到种群Qt+1;
5)若满足优化条件,则计算程序终止,若不满足,则令t=t+1,并返回至2)重新执行。
4.2 优化模型确定外形阻力Rx、极限载荷Pcr、质量M、排水体积Δ为无人潜水器主体结构优化的目标函数。其中,Rx、Pcr通过将表 4、表 5的近似模型系数代入式(7)得到,质量M、排水体积Δ通过以下得到:
| $ \left\{ \begin{array}{l} M = {M_f}({x_2}, {x_3}, {x_4}, {\rho _f}, {t_f}) + {M_N}({y_1}, \cdots {y_5}, {\rho _N})\\ \Delta = {\Delta _f}({x_2}, {x_3}, {x_4}, {t_f}) + {\Delta _N}({y_1}, \cdots {y_5}, {\rho _N}) \end{array} \right. $ | (9) |
式中:ρ为密度;下标f为非耐压结构;N为耐压结构。以外形阻力Rx最小、排水体积最大、极限载荷Pcr最大、质量M最小为目标。建立主体结构多学科优化模型:
| $ \left\{ \begin{array}{l} {\rm{max}}:\{ V;{P_{cr}}\} \\ {\rm{min}}:\{ M;{R_x}\} \\ {\rm{s}}{\rm{.t}}:\{ {\sigma _{{\rm{max}}}} \le \left[ \sigma \right]\\ DV:\begin{array}{*{20}{c}} {{x_2}, {x_3}, {x_4};}\\ {{y_1}, {y_2}, {y_3}, {y_4}, {y_5}} \end{array} \end{array} \right. $ | (10) |
式中[σ]为耐压壳体材料许用应力,MPa。其通过式(11)求出。
| $ \left[ \sigma \right] = 0.85{\sigma _s} $ | (11) |
式中σs为壳体材料屈服极限,MPa。
5 优化求解采用NSGA-II进行式(11)优化的求解,种群数量100、进化代数50、交叉0.9、交叉分布指数10、变异分布指数20。得到的Pareto解集见图 9。

|
Download:
|
| 图 9 Pareto解集 Fig. 9 Pareto solution | |
| 表 6 初始方案与优化方案对比 Table 6 Initial programme and optimization options |
表 6中,与初始方案相比,优化1、优化2在各个优化目标上均取得了优化的效果,但两者在优化目标的优化程度上有所不同。优化方案1对阻力与重量的优化效果更为明显,Rx、M分别降低5.75%、8.59%;优化方案2的Pcr提高104.87%,Δ提高2.13%。
6 结论1)通过针对STAR-CCM+和Abaqus进行的二次开发实现了外形阻力、耐压壳体的参数化分析,可避免设计过程中频繁的模型修改,实现了设计效率的提高;
2)采用二阶响应面拟合得到分析模型具有极高的精度,进一步将分析模型模型引入到主体结构优化模型,在满足了工程需要的同时,降低了计算成本、提高了设计效率;
3)基于NSGA-II对于优化模型进行优化求解得到了Pareto解集,选取其中的2个方案与初始方案进行对比,结果表明:2个优化方案均实现了优化,且各自在不同性能的提升方面效果明显。
| [1] |
唐正茂, 解德, 马士虎. 船舶概念设计阶段多学科和多目标优化研究[J]. 船舶力学, 2010, 14(8): 879-886. TANG Zhengmao, XIE De, MA Shihu. Application of multidisciplinary design optimization and multi-objective problem in conceptual design of ship[J]. Journal of ship mechanics, 2010, 14(8): 879-886. DOI:10.3969/j.issn.1007-7294.2010.08.008 (  0) 0)
|
| [2] |
王振国, 陈小前, 罗文彩, 等. 飞行器多学科设计优化理论与应用研究[M]. 北京: 国防工业出版社, 2006. WANG Zhenguo, CHEN Xiaoqian, LUO Wencai, et al. Research on the theory and application of multidisciplinary design optimization of flight vehicles[M]. Beijing: National Defense Industry Press, 2006. (  0) 0)
|
| [3] |
BELEGUNDU A D, HALBERG E, YUKISH M A, et al. Attribute-based multidisciplinary optimization of undersea vehicles[C]//Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization. Long Beach, CA, 2000. http://www.researchgate.net/publication/269224423_Attribute-based_multidisciplinary_optimization_of_undersea_vehicles
(  0) 0)
|
| [4] |
YUKISH M, BENNETT L, SIMPSON T W. Requirements on MDO imposed by the undersea vehicle conceptual design problem[C]//Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization. Long Beach, CA, U.S.A., 2000. https://www.researchgate.net/publication/269224418_Requirements_on_MDO_imposed_by_the_undersea_vehicle_conceptual_design_problem
(  0) 0)
|
| [5] |
李学斌, 甘霖. AUV总体概念设计中的多学科和多目标优化研究[J]. 海洋技术, 2008, 27(2): 77-82. LI Xuebin, GAN Lin. Study on multi-disciplinary design and multi-objective problem in conceptual design of AUV[J]. Ocean technology, 2008, 27(2): 77-82. DOI:10.3969/j.issn.1003-2029.2008.02.018 (  0) 0)
|
| [6] |
王鹏, 宋保维, 胡海豹, 等. 基于子空间近似算法的鱼雷总体多学科设计优化[J]. 弹箭与制导学报, 2007, 27(5): 200-202. WANG Peng, SONG Baowei, HU Haibao, et al. Multidisciplinary design optimization of torpedo general design based on subspace approximating optimization[J]. Journal of projectiles, rockets, missiles and guidance, 2007, 27(5): 200-202. DOI:10.3969/j.issn.1673-9728.2007.05.061 (  0) 0)
|
| [7] |
宋保维, 杜伟, 高智勇, 等. 基于协同优化的鱼雷多学科设计优化[J]. 鱼雷技术, 2009, 17(6): 7-11. SONG Baowei, DU Wei, GAO Zhiyong, et al. Multidisciplinary design optimization of torpedo general design based on collaborative optimization[J]. Torpedo technology, 2009, 17(6): 7-11. DOI:10.3969/j.issn.1673-1948.2009.06.002 (  0) 0)
|
| [8] |
刘蔚.多学科设计优化方法在7000米载人潜水器总体设计中的应用[D].上海: 上海交通大学, 2007. LIU Wei. Application of MDO method to 7000m HOV general design[D]. Shanghai: Shanghai Jiao Tong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10248-2008052032.htm (  0) 0)
|
| [9] |
操安喜, 崔维成. 潜水器多学科设计中的多目标协同优化方法[J]. 船舶力学, 2008, 12(2): 294-304. CAO Anxi, CUI Weicheng. Multi-objective collaborative optimization in multidisciplinary design for submersible[J]. Journal of ship mechanics, 2008, 12(2): 294-304. DOI:10.3969/j.issn.1007-7294.2008.02.019 (  0) 0)
|
| [10] |
赵敏, 崔维成. BLISCO方法在载人潜水器设计中的应用[J]. 船舶力学, 2009, 13(2): 259-268. ZHAO Min, CUI Weicheng. Application of BLISCO to the multidisciplinary design of a HOV[J]. Journal of ship mechanics, 2009, 13(2): 259-268. DOI:10.3969/j.issn.1007-7294.2009.02.014 (  0) 0)
|
| [11] |
ZHAO Min, CUI Weicheng, LI Xiang. Multidisciplinary design optimization of a human occupied vehicle based on bi-level integrated system collaborative optimization[J]. China ocean engineering, 2015, 29(4): 599-610. DOI:10.1007/s13344-015-0042-y (  0) 0)
|
| [12] |
赵敏.两级集成系统协同优化方法及其在深海空间站总体概念设计中的应用[D].上海: 上海交通大学, 2009. ZHAO Min. Bi-level integrated system collaborative optimization method and its application to the overall conceptual design of deep sea space station[D]. Shanghai: Shanghai Jiao Tong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10248-2010033331.htm (  0) 0)
|
| [13] |
崔桐.微小型水下航行器多学科优化设计[D].哈尔滨: 哈尔滨工程大学, 2013. CUI Tong. Multidisciplinary design optimization for mini autonomous underwater vehicle[D]. Harbin: Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133759.htm (  0) 0)
|
| [14] |
蒋一, 孙寒冰, 邹劲, 等. 双断级滑行艇水动力特性数值研究[J]. 华中科技大学学报(自然科学版), 2015, 43(4): 74-78. JIANG Yi, SUN Hanbing, ZOU Jin, et al. Numerical simulation on hydrodynamic performances of double-stepped planing boat[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2015, 43(4): 74-78. (  0) 0)
|
| [15] |
崔维成, 马岭.潜水器设计中所要解决的水动力学问题[C]//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会论文集.北京, 2009: 9-29. CUI Weicheng, MA Ling. Hydrodynamic Problems involved in submersible design[C]//Proceedings of the 9th National Conference on hydrodynamics and the twenty-second National Symposium on water dynamics. Beijing, 2009: 9-29. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-SLDX200908001003.htm (  0) 0)
|
| [16] |
王集思. 基于FTP的校内资源共享系统的设计与实现[J]. 群文天地, 2012(22): 271-271. WANG Jisi. Design and implementation of campus resource sharing system based on FTP[J]. Folk art and literature, 2012(22): 271-271. (  0) 0)
|
| [17] |
赖宇阳, 姜欣, 方立桥, 等. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012: 1-10. LAI Yuyang, JIANG Xin, FANG Liqiao, et al. Parameter optimization theory and detailed solution of Isight[M]. Beijing: Beihang University Press, 2012: 1-10. (  0) 0)
|
| [18] |
刘峰, 王力丰, 韩端锋, 等. 载人潜器耐压球壳参数化设计与稳定性分析[J]. 海洋技术学报, 2015, 34(1): 32-37. LIU Feng, WANG Lifeng, HAN Duanfeng, et al. Parametric design and stability analysis of the pressure-proof spherical shell of the manned submersible[J]. Journal of ocean technology, 2015, 34(1): 32-37. (  0) 0)
|
| [19] |
郑向伟, 刘弘. 多目标进化算法研究进展[J]. 计算机科学, 2007, 34(7): 187-192. ZHENG Xiangwei, LIU Hong. Progress of research on multi-objective evolutionary algorithms[J]. Computer science, 2007, 34(7): 187-192. DOI:10.3969/j.issn.1002-137X.2007.07.050 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


