在铺设和服役期间,由于海流冲刷和海底地形起伏的影响,不可避免地会出现管道悬跨现象。当海流流经管道悬跨段时,结构后缘会出现交替的漩涡脱落,诱发管道发生垂向和流向的振动,加速了管道疲劳的进程。这种典型的流-固耦合现象称之为涡激振动(vortex-induced vibration, VIV)。VIV可造成管道严重的疲劳损伤、甚至断裂失效。
为深入探究VIV发生机理和振动特性,学术界和工程界开展了广泛研究,并取得大量研究成果[1-3]。海底悬跨管道两端跨肩处与土体直接接触,管-土耦合边界对悬跨管道VIV的影响不可忽略。何旭[4]利用土体弹簧模拟跨肩管-土作用,结合了VIVANA软件和有限元的梁单元研究了海底悬跨管道的涡激振动。Xiao[5]考虑了管土之间的相互作用,基于计算流体力学(computation fluid dynamic, CFD)方法模拟了海底悬跨管道的VIV特性。然而,已有研究大多将悬跨管道两端管-土作用边界处理为对称边界,未考虑更符合实际的非对称边界约束。徐万海等[6]分析了非对称边界条件下悬跨管道VIV特性,发现非对称边界的悬跨管道VIV响应的最大响应幅值及其位置,与对称边界条件下存在较大差异。海底悬跨管道的涡激振动疲劳受多种因素影响。Kapuria[7]采用DNV规范计算了两端跨肩处由弹性土体支撑的悬跨管道疲劳特性,分析了轴向力和土体刚度变化对海底悬跨管道疲劳寿命的影响规律。Dong[8]结合有限元与DNV规范,探讨了土体刚度和阻尼对管道疲劳寿命的影响机制,发现悬跨管道疲劳损伤随着土体刚度的增大而变小。Han[9]的研究表明高土体阻尼可减小悬跨管道跨肩和跨中处位移和应力,延长管道的使用寿命。Blanco[10]考虑了不同海床支撑和不同管土相互作用(刚度、阻尼、跨肩长度),分析了诸多因素作用下海底悬跨管道的疲劳寿命。
已有的海底悬跨管道的涡激振动疲劳特性研究,大多将悬跨两端跨肩处的土体作用简化为对称边界条件,并未考虑非对称边界的结构疲劳特性。在实际工程中,由于海底地形变化、海底冲刷或者海底土质分布不均,悬跨管道的两端跨肩处会存在不同埋深、不同土体支撑,悬跨两端更贴近非对称约束的情况。为了填补非对称边界悬跨管道疲劳研究领域的空白,本文考虑非对称边界的结构疲劳特性,并开展了非对称边界约束下海底悬跨管道VIV疲劳特性分析。
1 涡激振动的响应预报如图 1所示的海底悬跨管道可简化成Euler-Bernoulli梁,两端跨肩管-土作用采用两组土体弹簧模拟,分别设定为首、末端的扭转弹簧刚度为kr1、kr2,首、末端支撑弹簧刚度为kt1、kt2。漩涡脱落所产生的涡激升力:
| $ M\frac{{{\partial ^2}y}}{{\partial {t^2}}} + C\frac{{\partial y}}{{\partial t}} - T\frac{{{\partial ^2}y}}{{\partial {x^2}}} + EI\frac{{{\partial ^4}y}}{{\partial {x^4}}} = \frac{1}{2}{C_{\rm{L}}}\rho \mathit{\Omega }{V^2} $ | (1) |

|
Download:
|
| 图 1 海底悬跨管道结构示意 Fig. 1 Schematic diagram of a spanning submarine pipeline | |
式中:M是总质量,包括悬跨管道结构质量,管内流体质量以及外部附加水体质量;y为管道横流向位移;C为总阻尼,包括结构阻尼和水动力阻尼;T为轴向力;x为沿管道轴向坐标;E为材料弹性模量;I为截面转动模量;CL为升力系数;ρ为外界流体密度;Ω为管道的外径;V为来流速度。
采用Facchinetti提出的加速度耦合尾流振子模型描述海底悬跨管道后缘流场[11]。该振子模型运用经典的van der Pol方程模拟漩涡脱落的尾迹特性, 同时考虑与结构振动的耦合作用, 具有计算简单,精度相对较高等优点。控制方程为:
| $ \frac{{{\partial ^2}q}}{{\partial {t^2}}} + \theta {\omega _s}\left( {{q^2} - 1} \right)\frac{{\partial q}}{{\partial t}} + \omega _{\rm{s}}^2q = \frac{A}{\mathit{\Omega }}\frac{{{\partial ^2}y}}{{\partial {t^2}}} $ | (2) |
式中:q=2CL/CL0为无量纲尾流振子变量; CL0为固定刚性圆柱升力系数;ws为漩涡脱落频率,ws=2πStV/Ω,St为Strouhal数。参数A的取值[12]为:当Ur>5.0时A=10.0;当0<Ur≤5.0时(Ur为约化速度,Ur=V/(fnΩ),fn是管道振动的固有频率)A=4.0。根据管道的最大响应幅值与实验值相等的原则,确定模型参数θ[12]。
悬跨管道两端的边界条件可以表述为[13]:
首端:
| $ \left\{\begin{array}{l}{E I \frac{\partial^{2} y(0)}{\partial x^{2}}=k_{r 1} \frac{\partial y(0)}{\partial x}} \\ {T \frac{\partial y(0)}{\partial x}-E I \frac{\partial^{3} y(0)}{\partial x^{3}}=k_{t 1} y(0)}\end{array}\right. $ | (3) |
末端:
| $ \left\{\begin{array}{l}{E I \frac{\partial^{2} y(L)}{\partial x^{2}}=-k_{r 2} \frac{\partial y(L)}{\partial x}} \\ {T \frac{\partial y(L)}{\partial x}-E I \frac{\partial^{3} y(L)}{\partial x^{3}}=-k_{t 2} y(L) )}\end{array}\right. $ | (4) |
根据模态叠加原理,悬跨管道VIV响应位移可由多个模态组成。结合Runge-Kutta法计算求解管道VIV响应,具体过程可参见文献[6]。
2 悬跨管道的疲劳寿命计算方法 2.1 DNV规范目前,针对海底悬跨管道疲劳特性研究,大多采用挪威船级社(DNV)的RP-F105规范[14]。悬跨管道横向疲劳寿命TL为:
| $ {T_{\rm{L}}} = \frac{1}{{\int_0^{ + \infty } {\frac{{\left( {{f_{\rm{v}}}S_{{\rm{CF}}}^m} \right)}}{{\bar a}}} {\rm{d}}{\mathit{\boldsymbol{F}}_{{\rm{Uc}}}}}} $ | (5) |
式中:fv为振动频率;a为疲劳常量,基于相应的应力范围选取;m为疲劳指数; S-N曲线斜率的倒数;SCF为横流向应力范围,按下式计算:
| $ S_{\mathrm{CF}}=2 \psi_{\mathrm{CF}}(Y / \Omega) \alpha_{\mathrm{k}} \gamma_{\mathrm{s}} $ | (6) |
式中:ψCF为单位应力幅值; (Y/Ω)为横流向涡激振动响应幅值;αk为阻尼的幅值因子;γs为该应力范围内的安全系数。振动频率fv可表示为:
| $ f_{\mathrm{v}}=f_{n, \mathrm{CF}} \sqrt{\frac{\left(g_{\mathrm{s}} / g\right)+C_{\mathrm{a}}}{\left(g_{\mathrm{s}} / g\right)+C_{\mathrm{a}, \mathrm{CF}-\mathrm{RES}}}} $ | (7) |
式中:(gs/g)为质量比;Ca为附加质量系数;fn, CF为第n阶主控模态的固有频率;Ca, CF-RES为水动力附加质量系数。将式(6)、(7)代入式(5),即可得到悬跨管道的疲劳寿命。
直接运用DNV规范确定管道的疲劳损伤有诸多优点,但其局限性也十分明显,如仅可确定两端跨肩处为对称约束的悬跨管道最大疲劳损伤,不能获得非对称约束悬跨管道沿管长各点的疲劳损伤值,不能分析非对称边界条件的悬跨管道疲劳特性。本文以DNV规范为基础,结合理论分析,有效的弥补了仅依照DNV规范计算疲劳的局限性。
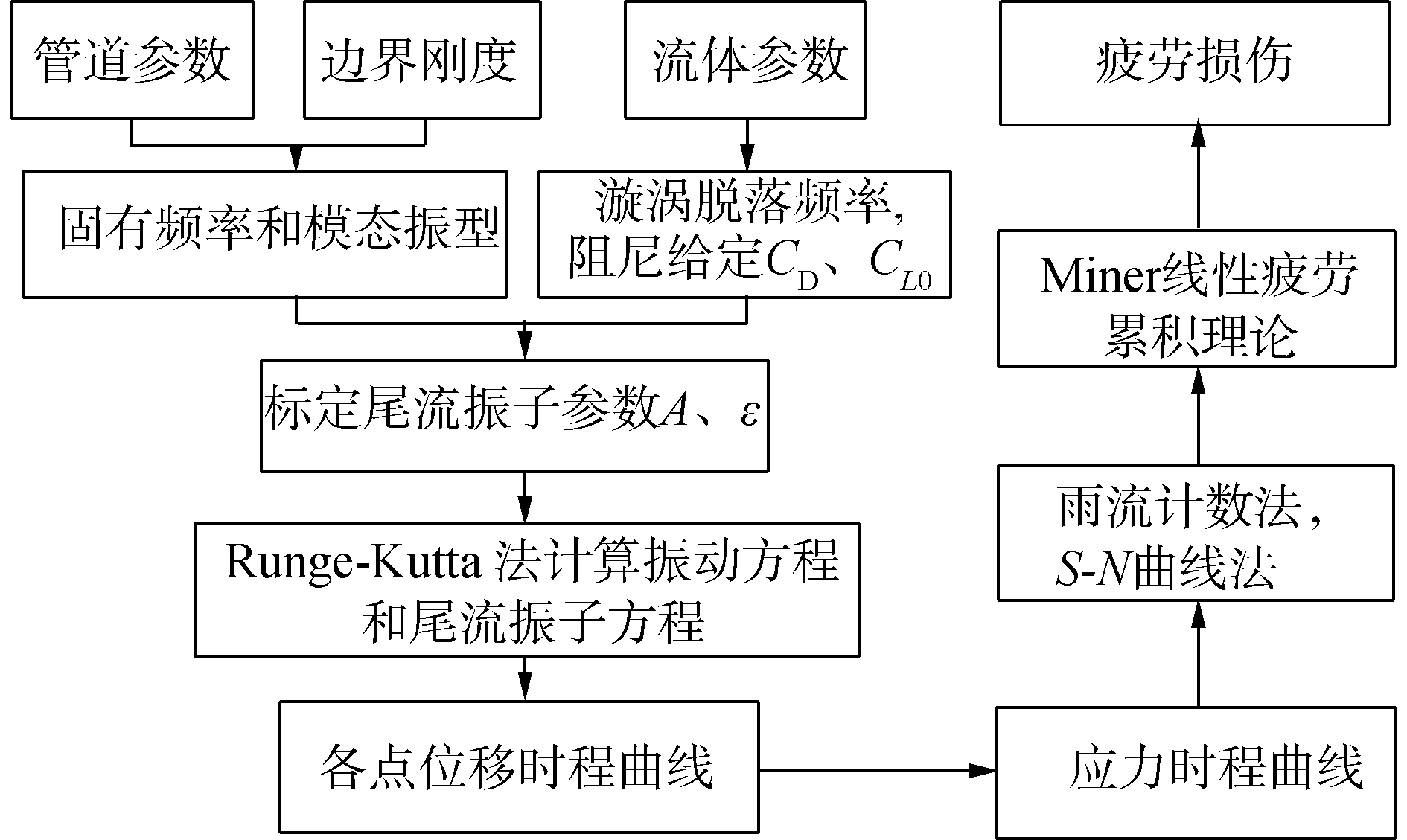
2.2 本文疲劳寿命计算方法本文对悬跨管道的疲劳损伤评估流程如图 2所示。首先对VIV预报得到的位移响应进行变换:
| $ \boldsymbol{\varepsilon}=R \sum\limits_{i=1}^{n} \varphi_{i}^{\prime \prime}(x) P_{i}(t) $ | (8) |
|
Download:
|
| 图 2 疲劳损伤计算流程 Fig. 2 Flowchart of fatigue damage calculation | |
式中:ε为应变;R为管道半径。将VIV位移转化为应变,并进一步转化为应力。根据雨流计数法对应力时程响应进行分解,得到各应力变化范围Si和循环次数ni。采用S-N曲线确定应力变化范围为Si时,悬跨管道上该点发生疲劳破坏所需循环次数Ni。S-N曲线的函数形式为:
| $ N=\left\{\begin{array}{ll}{a_{1} S^{-m_{1}},} & {S>S_{\mathrm{SW}}} \\ {a_{2} S^{-m_{2}},} & {S \leqslant S_{\mathrm{SW}}}\end{array}\right. $ | (9) |
式中:a1、a2为特征疲劳强度常数;m1、m2为疲劳指数;SSW为双斜率S-N曲线转折点处的应力值。DNV-RP-C203[15]根据海洋结构物所处环境和焊接类型等将S-N曲线分为不同等级。本文依据算例分析的管道参数,从规范中选取相对应的等级(a1=5.81×1011,m1=3;a2=4.04×1015,m2=5)。
根据Miner-Palmgren线性累积准则确定悬跨管道沿管长方向各点的疲劳损伤。其理论基础为应力变化范围Si对该位置造成的疲劳损伤度,等价于应力变化范围为Si的实际循环次数与结构在该应力变化范围下疲劳破坏所需的循环次数之比。所有比值线性叠加即为该点的疲劳损伤度:
| $ D_{\mathrm{t}}=\sum\limits_{i=1}^{K} \frac{n_{i}}{N_{i}} $ | (10) |
式中:Dt为累积疲劳损伤;ni为应力变化范围为Si的实际循环次数;Ni为单一应力变化范围Si作用下结构疲劳破坏所需的循环次数。年疲劳损伤值D[1/a]=365×24×3 600×Dt/t。年疲劳损伤的倒数即为悬跨管道上该点的疲劳寿命。
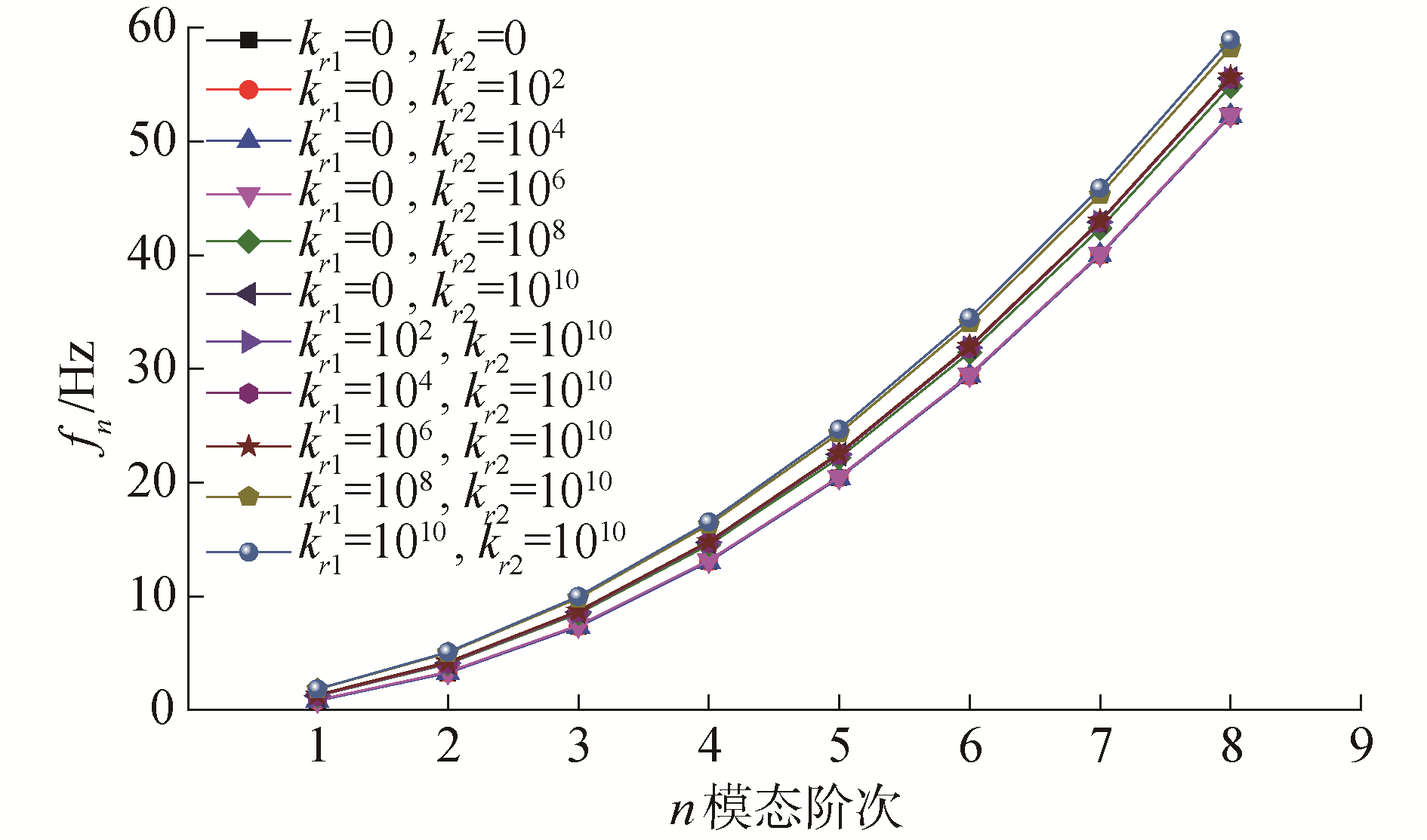
3 结果分析与讨论本节讨论非对称边界约束条件对疲劳损伤的影响。悬跨管道的结构参数物理量为:管道外径0.25 m;壁厚0.019 2 m;跨长25 m;轴向力500 N;结构单位长度质量107.2 kg/m;弯曲刚度1.96×107 N·m2;结构阻尼比0.003。非对称边界参照Yeganeh的研究结果选取[16],研究表明:扭转刚度为1010时为其极限值(对应海底岩石底质),悬跨管道的VIV响应并不会随其继续增大而发生变化。当两端支撑刚度kt1=kt2=1010,扭转刚度kr1=kr2=0时,对应简单支撑;扭转刚度kr1=kr2=1010时,对应固定支撑[6]。
图 3为非对称边界约束下悬跨管道的固有频率。在不同边界约束下,悬跨管道固有频率存在显著差异。随着边界约束强度增加,相同阶次的固有频率值也会随之增加,低阶固有频率略有增长,而高阶固有频率增长显著。
|
Download:
|
| 图 3 不同边界约束下悬跨管道的固有频率 Fig. 3 Natural frequencies of spanning pipelines with different boundary constraints | |
图 4为悬跨管道年疲劳损伤云图,显示了不同非对称边界条件下海底悬跨管道不同位置随流速变化的年均疲劳损伤情况,易于比较不同位置同流速或者不同流速下年均疲劳损伤值的大小。为了探究不同非对称边界条件下,海底悬跨管道疲劳特性,以及流速变化对疲劳损伤影响,列举了具有代表性的4种工况。对比发现,边界约束发生变化会导致沿管长方向的最大疲劳损伤位置以及年疲劳损伤率随之改变。

|
Download:
|
| 图 4 悬跨管道的年疲劳损伤云图 Fig. 4 Annual fatigue damage nephogram of spanning pipelines | |
为深入探究悬跨管道沿管长方向疲劳损伤趋势,绘制了对应不同流速和边界条件的疲劳损伤曲线图,如图 5、图 6所示。

|
Download:
|
| 图 5 末端刚度变化的悬跨管道疲劳损伤图 Fig. 5 Fatigue damage of spanning pipeline with the change of the end stiffness | |
|
Download:
|
| 图 6 首端刚度变化的悬跨管道疲劳损伤 Fig. 6 Fatigue damage of spanning pipeline with the change of the head stiffness | |
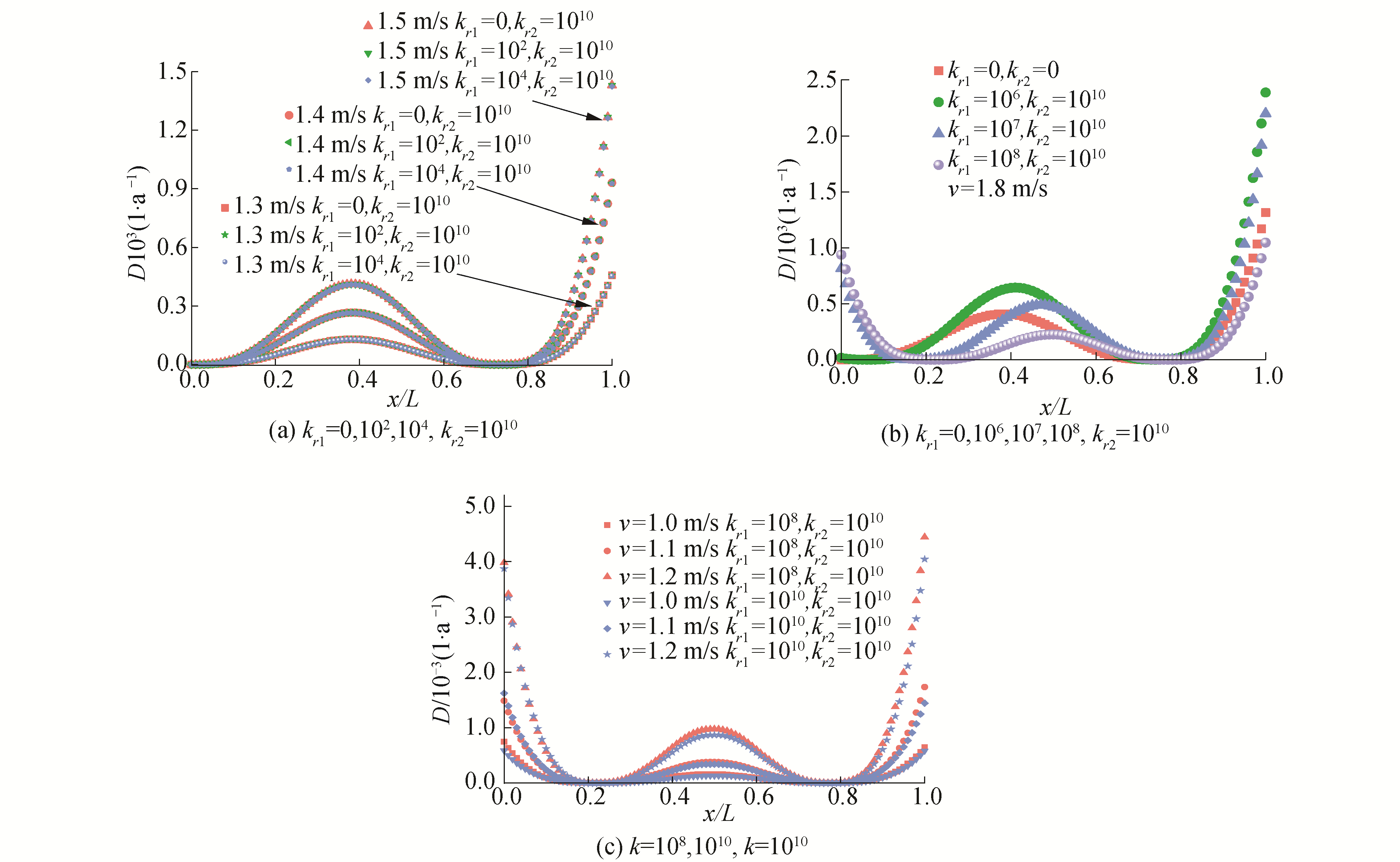
图 5给出首端简支、末端扭转刚度依次变大的海底悬跨管道沿管长方向疲劳损伤曲线。可以看到,当首端扭转刚度kr1=0、末端扭转刚度kr2=0,102,104时(如图 5(a)),疲劳损伤曲线变化趋势大致相同,最大损伤位置约在结构中点处,沿管长方向的疲劳损伤曲线呈现轴对称分布特性;当kr1=0、kr2=106时(如图 5(b)),最大损伤位置向首端移动,疲劳损伤曲线开始呈现非对称分布,且末端的疲劳损伤变大;当kr1=0、kr2=107时,疲劳损伤曲线发生显著变化。此边界约束条件下,管道末端疲劳损伤与中点偏首端处曲线极大值点的疲劳损伤差别不大;当kr1=0、kr2=108,1010时(如图 5(c)),疲劳损伤曲线的最大损伤位置位于管道末端且远大于极值点处损伤,曲线的极大值点继续向首部偏移,位于管长2/5处。
图 6为末端固支,首端扭转刚度依次增大的悬跨管道沿管长方向疲劳损伤曲线。可以发现:首端扭转刚度kr1<104时(如图 6(a)),疲劳损伤曲线与首端简支末端固支的情况极为相似。直到首端扭转刚度kr1=106时(如图 6(b)),疲劳曲线趋势才发生微小变化,最大极值点略微右移,首端的疲劳损伤相比简支时略大,最大疲劳损伤位置位于末端。首端扭转刚度kr1=107时,首端疲劳损伤与极大值点疲劳损伤相仿。首端扭转刚度kr1=108,1010时(如图 6(c)),两条沿管长方向的疲劳损伤曲线基本重合,最大疲劳位置位于两端,极大值点右移至结构中点处,曲线呈现轴对称分布。
综合图 4~6发现,两端扭转刚度发生变化,沿管长方向的疲劳损伤曲线的数值和趋势都相应的改变。但同一边界约束条件下,流速变化只会改变管道上各点的疲劳损伤值的大小,沿管长方向的疲劳损伤曲线的整体趋势并不改变。
图 7给出最大疲劳损伤随约化速度的变化关系。图 7(a)为首端简支、末端扭转刚度由0逐次增强到1010的情况,图 7(b)为末端固支、首端约束同样依次增强的情况。可以发现:不同边界约束条件下,悬跨管道最大疲劳损伤随约化速度变化趋势大致相同。当约化速度为一定值时,悬跨管道的最大疲劳损伤值随两端约束增强而增大;约化速度小于3.5时,疲劳损伤增长相对缓慢;当约化速度为3.5~4.0时,无论两端扭转约束大小,疲劳损伤均随约化速度变大而跳跃增长(约化速度增大0.5,对应的最大疲劳损伤值增长了近1 000倍);当约化速度为4.0~6.0时,变化趋势趋于平缓,疲劳损伤值达到一个峰值;而当约化速度大于6.0时,悬跨管道的最大疲劳损伤逐渐减小。

|
Download:
|
| 图 7 悬跨管道最大疲劳损伤随约化速度变化图 Fig. 7 Maximum fatigue damage versus reduced velocity of spanning pipelines | |
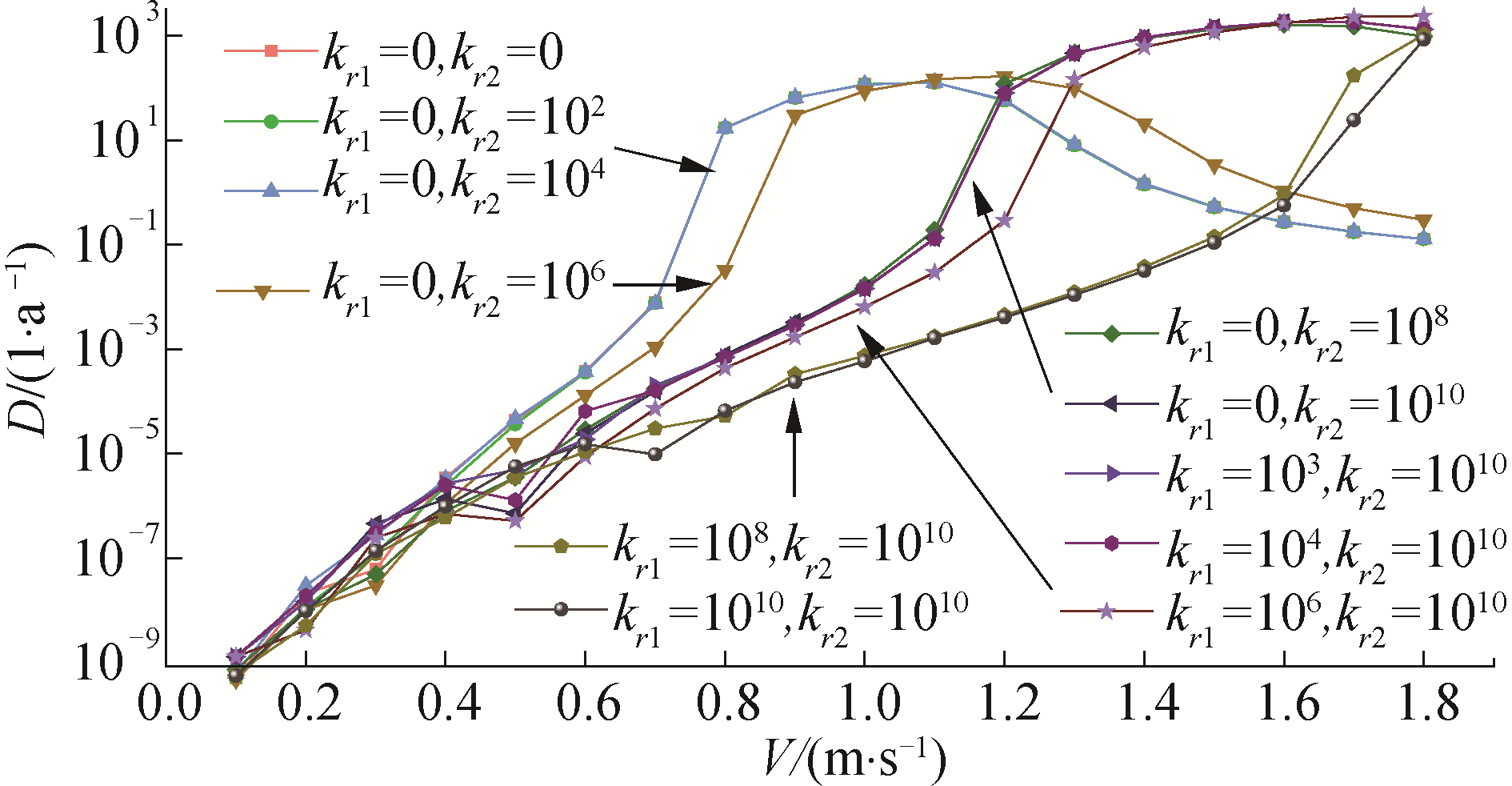
图 8给出流速对非对称边界约束的悬跨管道的疲劳损伤的影响曲线。当首端扭转刚度kr1=0、末端扭转刚度kr2=0, 102,104时,3条悬跨管道最大疲劳损伤曲线基本重合。当首端刚度kr1=0、末端刚度kr2=108,1010和首端kr1=102,104、末端kr2=1010时,4条曲线基本重合。当首端刚度kr1=108,1010、末端kr2=1010时,2条曲线亦基本重合。上述规律说明:相同海流流速下,扭转刚度在上述区间变化对悬跨管道疲劳损伤几乎没有影响。在相对较低流速的情况下(图 8中的流速低于1.1 m/s时),悬跨管道两端约束越强,其疲劳损伤值越小,疲劳寿命也更长。
|
Download:
|
| 图 8 悬跨管道最大疲劳损伤随流速变化 Fig. 8 Maximum fatigue damage versus flow velocity of spanning pipelines | |
1) 非对称边界约束变化会导致海底悬跨管道沿管长各点疲劳损伤值发生变化,疲劳损伤极大值点向约束相对减弱一端偏移。悬跨管道两端约束较强的一端比约束较弱的一端疲劳损伤值更大,疲劳寿命更短。
2) 边界固支时,最大疲劳损伤位于端部;边界简支时,最大疲劳损伤位于悬跨段中点处;而当一端简支、另一端处于简支和固支的过渡区域(末端扭转刚度约为107)时,悬跨管道最大疲劳损伤极大值点位于管长中点偏简支端位置,疲劳损伤的极大值与非简支端疲劳损伤值均较大。
3) 悬跨管道一端的扭转刚度小于临界区域时,可简化为简支端,扭转刚度在这一区间变化对沿管长方向的疲劳损伤曲线几乎没有影响。同理,当扭转刚度大于临界区域时,可简化为固支端。临界区域内(末端扭转刚度为106~108),沿管长方向的疲劳损伤曲线随扭转刚度的变化而显著变化。
| [1] |
SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(4): 389-447. DOI:10.1016/j.jfluidstructs.2004.02.005 (  0) 0)
|
| [2] |
KOUSHAN K. Vortex induced vibrations of free span pipelines[D]. Norway: Norwegian University of Science and Technology (NTNU), 2009: 1-217.
(  0) 0)
|
| [3] |
LARSEN C M, KOUSHAN K, PASSANO E. Frequency and time domain analysis of vortex induced vibrations for free span pipelines[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering. Oslo, Norway, 2002: 103-111.
(  0) 0)
|
| [4] |
何旭, 王永学, 李小超. 考虑管土作用海底管线涡激振动分析[J]. 中国海洋平台, 2011, 26(6): 21-26. HE Xu, WANG Yongxue, LI Xiaochao. Analysis of VIV for free spanning pipelines considering pipe-soil interaction[J]. China offshore platform, 2011, 26(6): 21-26. DOI:10.3969/j.issn.1001-4500.2011.06.005 (  0) 0)
|
| [5] |
XIAO Fei. CFD simulation of vortex-induced vibrations of free span pipelines including pipe-soil interactions[D]. College Station, TX, USA: Texas A&M University, 2015: 1-68.
(  0) 0)
|
| [6] |
徐万海, 谢武德, 高喜峰, 等. 非对称管-土边界的海底悬跨管道涡激振动特性[J]. 地震工程学报, 2014, 36(4): 773-777, 789. XU Wanhai, XIE Wude, GAO Xifeng, et al. Vortex-induced vibrations of a free-span submarine pipeline under asymmetric pipe-soil boundary conditions[J]. China earthquake engineering journal, 2014, 36(4): 773-777, 789. DOI:10.3969/j.issn.1000-0844.2014.04.0773 (  0) 0)
|
| [7] |
KAPURIA S, SALPEKAR V Y, SENGUPTA S. Fatigue due to vortex-induced cross flow oscillations in free spanning pipelines supported on elastic soil bed[C]//Proceedings of the Ninth International Offshore and Polar Engineering Conference. Brest, France, 1999: 197-203.
(  0) 0)
|
| [8] |
DONG Jie, CHEN Xuedong, WANG Bing, et al. The effect of soil on the structural response and fatigue life of free span for submarine pipeline[C]//Proceedings of ASME 2015 Pressure Vessels and Piping Conference. Boston, United States, 2015: V007T07A017.
(  0) 0)
|
| [9] |
HAN Yusha, CLUKEY E, RAVIRALA N, et al. Investigation of pipe-soil interaction on the fatigue life extension of subsea pipeline free spans[C]//Proceedings of the Twenty-Seventh International Ocean and Polar Engineering Conference. San Francisco, United States, 2017: 1171-1175.
(  0) 0)
|
| [10] |
CASANOVA E, BLANCO A. Effects of soil non-linearity on the dynamic behavior and fatigue life of pipeline spans subjected to slug flow[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China, 2010: 185-192.
(  0) 0)
|
| [11] |
FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(2): 123-140. DOI:10.1016/j.jfluidstructs.2003.12.004 (  0) 0)
|
| [12] |
XU Wanhai, WU Yingxiang, ZENG Xiaohui, et al. A new wake oscillator model for predicting vortex induced vibration of a circular cylinder[J]. Journal of hydrodynamics, 2010, 22(3): 381-386. DOI:10.1016/S1001-6058(09)60068-8 (  0) 0)
|
| [13] |
BAI Yong. Pipelines and risers[M]. New York: Elsevier Ocean Engineering Book Series, 2001: 1-495.
(  0) 0)
|
| [14] |
Det Norske Veritas. DNV-RP-F105, Free spanning pipelineS[S]. Norway: DNV, 2006.
(  0) 0)
|
| [15] |
Det Norske Veritas. DNV-RP-C203, Fatigue design of offshore steel structures[S]. Norway: DNV, 2010.
(  0) 0)
|
| [16] |
YEGANEH BAKHTIARY A, GHAHERI A, VALIPOUR R. Analysis of offshore pipeline allowable free span length[J]. International journal of civil engineering, 2007, 5(1): 84-91. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


