2. 北京精密机电控制设备研究所, 北京 100076
2. Beijing Research Institute of Precise Mechanical and Electronic Control Equipment, Beijing 100076, China
行星滚柱丝杠作为一种将旋转运动转化为直线运动的传动装置,具有承载力强、精度高、寿命长等特点,适宜应用在飞行器伺服舵机传动机构中。行星滚柱丝杠各部件之间通过空间曲面的多点接触传递作用力,具有非线性刚度,在其工作过程中承受较大轴向拉压力而产生较大的轴向变形,产生传递误差,影响飞行器伺服舵机系统的位置传递精度。准确的刚度模型是行星滚柱丝杠动力学建模的关键,为飞行器舵机系统的动力学分析提供基础。文献[1-10]主要针对行星滚柱丝杠的运动特性[1-2]、承载能力[3-4]、摩擦机理[5-6]、设计方法[7-8]以及承载效率计算[9-10]等方面进行研究,这些研究表明行星滚柱丝杠的传动精度与其轴向刚度有着紧密联系。靳谦忠等[11-12]、杨家军等[13]都依据赫兹接触理论,建立了行星滚柱丝杠轴向刚度数学模型,但所建立的模型都进行了简化,认为行星滚柱丝杠的接触方式与滚珠丝杠相同,影响了所建刚度模型的精度。付晓军等[14-15]研究了啮合特性对行星滚柱丝杠轴向刚度及传动效率的影响,为准确建立行星滚柱丝杠轴向刚度公式提供了参考。目前国内所使用的行星滚柱丝杠轴向刚度模型普遍是将行星滚柱丝杠的接触主曲率半径简化为滚珠的几何半径,因此会影响行星滚柱丝杠刚度模型的准确性。而Matthew等[16]所建立的行星滚柱丝杠轴向刚度模型较为准确,并对行星滚柱丝杠的动力学特性进行了仿真,但其螺纹刚度计算公式比较复杂,不方便快速计算。因此建立简单而准确的行星滚柱丝杠刚度模型是十分必要的。
本文采用空间微分几何方法描述了行星滚柱丝杠螺纹轮廓的几何模型以及螺纹的接触曲率半径,以赫兹接触理论建立了非标准螺纹的接触模型和轴向刚度模型,分析了螺纹接触角、滚柱数量以及丝杠偏心量对行星滚柱丝杠轴向刚度带来的影响,并通过行星滚柱丝杠刚度特性试验验证了本文的刚度模型的准确性。
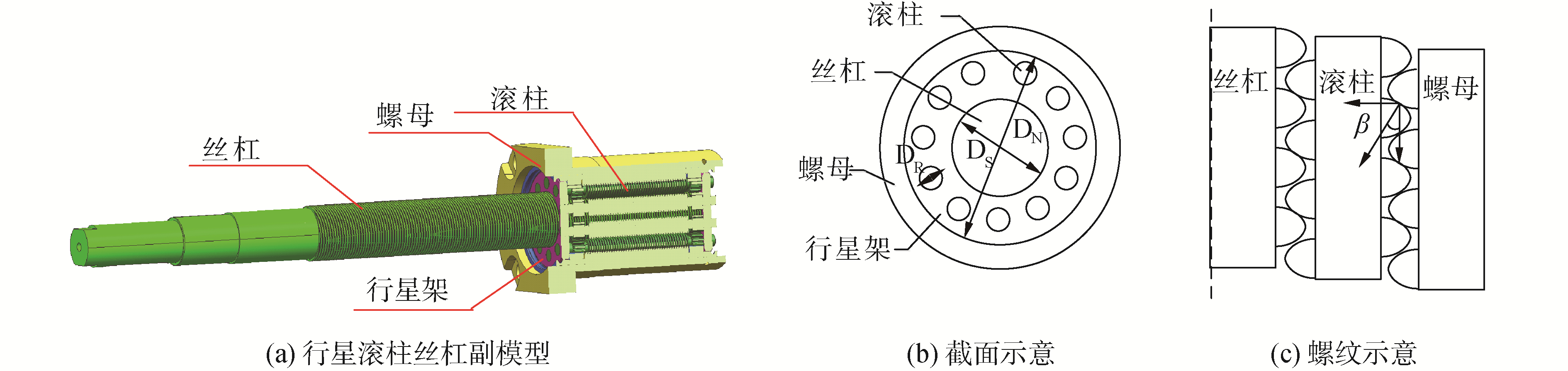
1 行星滚柱丝杠模型 1.1 行星滚柱丝杠结构模型图 1所示为行星滚柱丝杠结构示意图,其主要组成部分包括:丝杠、螺母、滚柱、行星架。结构中行星滚柱丝杠和滚柱有外螺纹,螺母有内螺纹。滚柱均匀分布在丝杠周围,通过螺纹进行运动传递。行星滚柱丝杠的螺母螺纹直径DN为35 mm,丝杠螺纹直径DR为21 mm,滚柱直径DS为7 mm,其中丝杠和螺母为5头螺纹,丝杠的螺纹升角为1.74°,螺母和滚柱的螺纹升角为1.04°。
|
Download:
|
| 图 1 行星滚柱丝杠结构模型示意 Fig. 1 Mechanical structure of planetary roller screw | |
行星滚柱丝杠的工作原理:工作过程中丝杠由电机驱动发生旋转;丝杠与滚柱接触,滚柱围绕自身轴线发生旋转,同时也围绕丝杠轴线公转并沿轴向进行直线运动;螺母在滚柱的带动下沿着丝杠的轴向做直线运动。行星滚柱丝杠螺母的轴向位移与丝杠转动角度的关系为:
| $ \begin{array}{*{20}{c}} {s = {D_{\rm{S}}} + {D_{\rm{R}}} = {P_{\rm{S}}}\frac{{{\theta _{{\rm{SC}}}}}}{{2{\rm{ \mathsf{ π} }}}} + {P_{\rm{R}}}\frac{{{\theta _{{\rm{RC}}}}}}{{2{\rm{ \mathsf{ π} }}}} = }\\ {\frac{{{\theta _{\rm{S}}}\left( {{r_{\rm{R}}}{P_{\rm{S}}} + {r_{\rm{S}}}{P_{\rm{R}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{r_{\rm{R}}}}}\left( {\frac{{{r_{\rm{S}}} + 2{r_{\rm{R}}}}}{{2{r_{\rm{S}}} + 2{r_{\rm{R}}}}}} \right)} \end{array} $ | (1) |
式中:θSC是丝杠接触弧形角;θRC为滚柱接触弧形角;PS为丝杠螺距;PR为滚柱螺距;s为螺母直线运动位移;rR为滚柱半径;rS为丝杠半径。
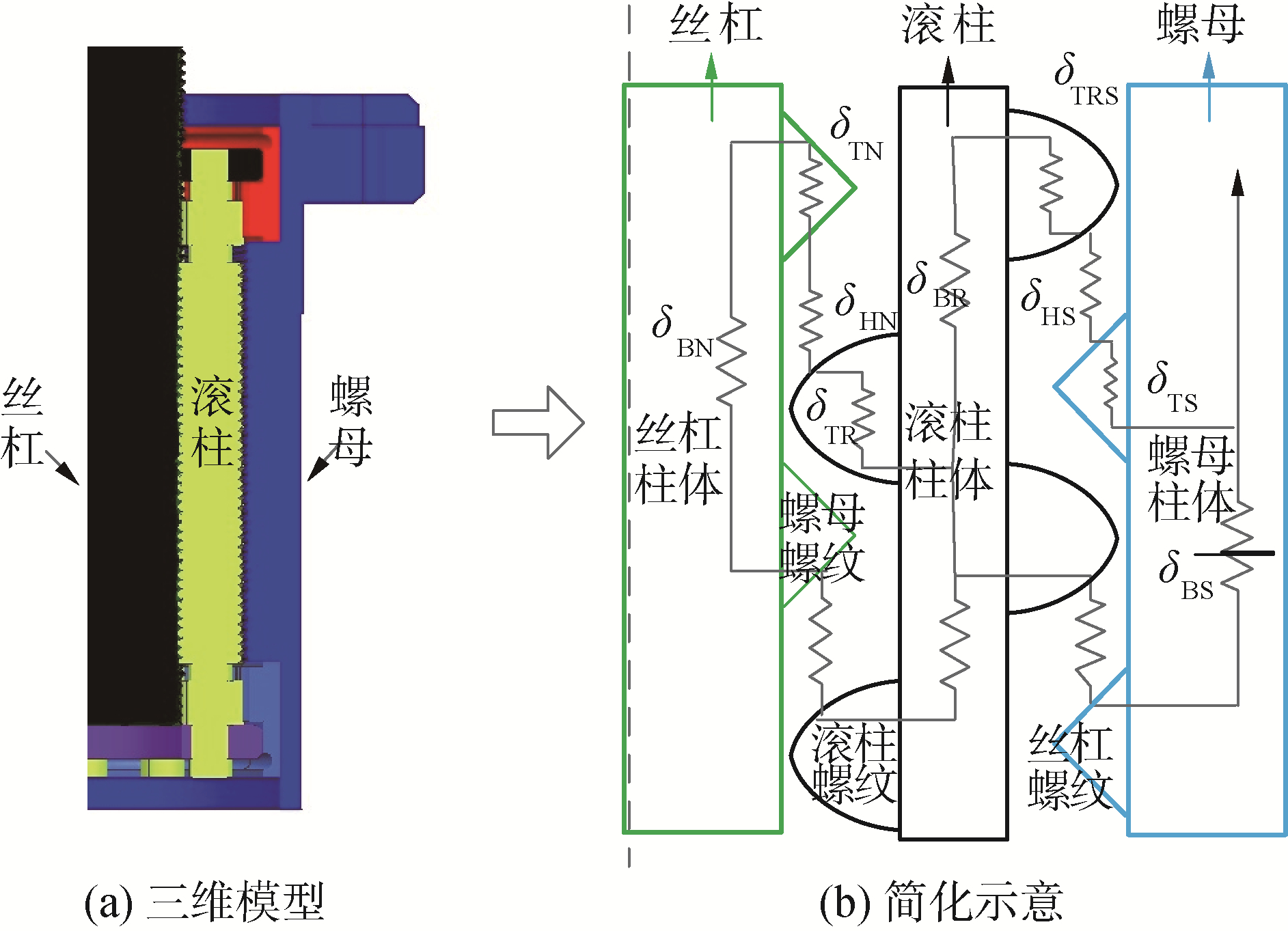
1.3 行星滚柱丝杠轴向刚度模型对行星滚柱丝杠进行简化,其简化模型示意图如图 2所示。图 2中行星滚柱丝杠模型发生接触的3个部分的连接顺序是螺母、滚柱和丝杠。从外由内,螺母实体与外部接触,螺母的螺纹与滚柱一侧螺纹接触,滚柱另一侧螺纹与丝杠的螺纹接触,丝杠本体承受负载。行星滚柱丝杠整体刚度是由螺母柱体刚度、螺母螺牙刚度、螺母-滚柱接触刚度、滚柱螺牙刚度、滚柱柱体刚度、丝杠-滚柱接触刚度、丝杠螺牙刚度和丝杠柱体刚度组成。图 2中δBN、δBR和δBS为螺母、滚柱和丝杠柱体变形;δHN、δHR和δHS为螺母、滚柱和丝杠接触变形;δTN、δTRN、δTRS和δTS为螺母、滚柱和丝杠螺牙变形。
|
Download:
|
| 图 2 行星滚柱丝杠三维模型和简化模型示意 Fig. 2 3D and a simplified model for planetary roller screw | |
丝杠、滚柱和螺母可以认为是外侧带有螺纹的圆柱体。由于柱体的刚度远高于整体轴向刚度,这部分圆柱体刚度对整个刚度模型影响并不大,因此可以进行一定程度的简化。根据文献[7],柱体的刚度可以表达成一个线性的拉压刚度,各部分柱体刚度公式分别为:
| $ k_{\mathrm{BS}}=\frac{E_{\mathrm{S}} A_{\mathrm{S}}}{p}, \quad k_{\mathrm{BN}}=\frac{E_{\mathrm{N}} A_{\mathrm{N}}}{p}, \quad k_{\mathrm{BR}}=\frac{n_{\mathrm{R}} E_{\mathrm{R}} A_{\mathrm{R}}}{p / 2} $ | (2) |
式中:ES、EN、ER分别为丝杠、螺母和滚柱的弹性模量;AS、AN、AR分别为丝杠螺母和滚柱的圆柱截面面积;p为行星滚柱丝杠的螺距。
1.3.2 行星滚柱丝杠接触刚度行星滚柱丝杠螺纹是非标准螺纹,丝杠和螺母的螺纹是直角三角螺纹,滚柱螺纹的上下表面截面分别是2个等半径的圆弧,其接触主曲率半径对于接触刚度影响较大。为得到行星滚柱丝杠螺纹的接触主曲率半径,需要建立螺纹接触面的数学模型,通过微分几何中曲面的2种基本形式得到螺纹接触表面的主曲率半径,使用Hertz接触理论可以得到接触刚度。滚柱螺纹的轮廓线方程:
| $ x^{2}+z^{2}=r_{\mathrm{p}}^{2} $ | (3) |
式中:rp为滚柱的螺纹轮廓半径,rp=rR/sinβs;βs为螺纹的接触角。
接触点在滚柱的螺纹上半面的坐标:
| $ \boldsymbol{r}=\left(a \cos \theta, a \sin \theta, \frac{L}{2 \pi} \theta+\sqrt{r_{p}^{2}-a^{2}}-\sqrt{r_{p}^{2}-r_{R}^{2}}+p\right) $ | (4) |
式中:a为接触点位置半径;θ为接触点位置轨道角;L为螺纹导程;p为螺纹螺距;rR为滚柱螺纹内径。
滚柱螺纹上半面接触点位置的法向量为:
| $ {\mathit{\boldsymbol{N}}_{{\rm{RT}}}} = \left[ {\begin{array}{*{20}{c}} {{S_{{\beta _{\rm{R}}}}}{C_{{\theta _{\rm{R}}}}} + {C_{{\beta _{\rm{R}}}}}{S_{{\alpha _{\rm{R}}}}}{S_{{\theta _{\rm{R}}}}}}\\ {{S_{{\beta _{\rm{R}}}}}{S_{{\theta _{\rm{R}}}}} - {C_{{\beta _{\rm{R}}}}}{S_{{\alpha _{\rm{R}}}}}{C_{{\theta _{\rm{R}}}}}}\\ {{C_{{\beta _{\rm{R}}}}}{C_{{\alpha _{\rm{R}}}}}} \end{array}} \right] $ | (5) |
式中:SβR表示的是滚柱接触角的正弦值;CθR表示的是轨道角的余弦值;SαR表示的是螺纹螺旋升角的正弦值。
同理可得丝杠和螺母螺纹上接触点坐标及法向量。根据微分几何中曲面的第1和第2基本形式方程:
| $ \left\{ \begin{array}{l} {E_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{r}}_{{\theta _{{\rm{bT/bB}}}}}}{\mathit{\boldsymbol{r}}_{{a_{{\rm{bT/bB}}}}}},{F_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{r}}_{{a_{{\rm{bT/bB}}}}}}{\mathit{\boldsymbol{r}}_{{\theta _{{\rm{bT/bB}}}}}}\\ {G_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{r}}_{{\theta _{{\rm{bT/bB}}}}}}{\mathit{\boldsymbol{r}}_{{a_{{\rm{bT/bB}}}}}},{L_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{N}}_{{\rm{bT/bB}}}}{\mathit{\boldsymbol{r}}_{a{a_{{\rm{bT/bB}}}}}}\\ {M_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{N}}_{{\rm{bT/bB}}}}{\mathit{\boldsymbol{r}}_{a{\theta _{{\rm{bT/bB}}}}}},{N_{{\rm{bT/bB}}}} = {\mathit{\boldsymbol{N}}_{{\rm{bT/bB}}}}{\mathit{\boldsymbol{r}}_{\theta {\theta _{{\rm{bT/bB}}}}}} \end{array} \right. $ | (6) |
式中下标bT/bB代表接触位置在螺纹面的上面或者下面。
将丝杠、滚柱和螺母螺纹面的曲面表达式代入到曲面的2类基本量表达式中,得到丝杠螺纹曲面上表面的2类基本量表达式[17]:
| $ \begin{array}{*{20}{c}} {{E_{{\rm{ST}}}} = 1 + T_{{\beta _{\rm{S}}}}^2,{F_{{\rm{ST}}}} = - \frac{{{L_{\rm{S}}}{T_{{\beta _{\rm{S}}}}}}}{{2{\rm{ \mathsf{ π} }}}},{G_{{\rm{ST}}}} = {u^2} + {{\left( {\frac{{{L_{\rm{S}}}}}{{2{\rm{ \mathsf{ π} }}}}} \right)}^2},}\\ {{L_{{\rm{ST}}}} = 0,{M_{{\rm{ST}}}} = - {C_{{\beta _{\rm{S}}}}}{S_{{\alpha _{\rm{S}}}}},{N_{{\rm{ST}}}} = - u{S_{{\beta _{\rm{S}}}}}} \end{array} $ |
式中下标ST代表丝杠螺纹曲面的上表面。根据同样的方法可以再得到滚柱和螺母的2类曲面表达形式,其中ERT、FRT、GRT、LRT、MRT、NRT和ENT、FNT、GNT、LNT、MNT、NNT均为微分几何中2类基本形式方程的系数。
设κ1和κ2为曲面上的2个主曲率,由高斯曲率以及平均曲率定义可以得:
| $ K=\kappa_{1} \kappa_{2}=\frac{L N-M^{2}}{E G-F^{2}} $ | (7) |
| $ H=\frac{1}{2}\left(\kappa_{1}+\kappa_{2}\right)=\frac{2 F M-(E N+G L)}{2\left(E G-F^{2}\right)} $ | (8) |
其中,曲面的主曲率为:
| $ \kappa_{1}=H+\sqrt{H^{2}-K}, \quad \kappa_{2}=H-\sqrt{H^{2}-K} $ | (9) |
曲面的2个主曲率半径为:
| $ R_{1}=\frac{1}{\kappa_{1}}, \quad R_{2}=\frac{1}{\kappa_{2}} $ | (10) |
1) 赫兹接触变形:
由赫兹接触公式可以得到:
| $ \begin{array}{*{20}{c}} {{\mathit{\Theta }_i} + {\chi _i} = \frac{1}{2}\left( {\frac{1}{{{R_{1{R_i}}}}} + \frac{1}{{{R_{2{R_i}}}}} + \frac{1}{{{R_{1i}}}} + \frac{1}{{{R_{2i}}}}} \right)}\\ {{\mathit{\Theta }_i} - {\chi _i} = }\\ {\quad \frac{1}{2}\left[ {{{\left( {\frac{1}{{{R_{1{R_i}}}}} - \frac{1}{{{R_{2{R_i}}}}}} \right)}^2} + {{\left( {\frac{1}{{{R_{1i}}}} - \frac{1}{{{R_{2i}}}}} \right)}^2} + } \right.}\\ {{{\left. {\left( {\frac{1}{{{R_{1{R_i}}}}} - \frac{1}{{{R_{2{R_i}}}}}} \right)\left( {\frac{1}{{{R_{1{R_i}}}}} - \frac{1}{{{R_{2{R_i}}}}}} \right)\cos \left( {2{\gamma _i}} \right)} \right]}^{\frac{1}{2}}}} \end{array} $ | (11) |
式中γ为两主曲率轴夹角;Θi、χi为曲率。
等效曲率半径:
| $ {R_{{E_i}}} = \frac{1}{2}{\left( {{\mathit{\Theta }_i}{\chi _i}} \right)^{ - \frac{1}{2}}} $ | (12) |
由赫兹接触理论得到接触变形为:
| $ {\delta _{\rm{H}}} = {F_2}{\left( {\frac{{9{P^2}}}{{16{E^{*2}}{R_{{E_i}}}}}} \right)^{\frac{1}{3}}}\cos \beta \cos \alpha $ | (13) |
| $ \frac{1}{E^{*}}=\frac{1-v_{1}^{2}}{E_{1}}+\frac{1-v_{2}^{2}}{E_{2}} $ | (14) |
式中:P为所受压力;F2为Hertz接触中的位移修正因子;E*为两接触物体等效弹性模量;E1和E2为两接触物体的弹性模量[18]。
1.3.3 行星滚柱丝杠螺牙刚度螺纹可以简化为圆柱体带有圆环。圆环受到集中载荷作用发生变形,变形的示意图如图 3所示。因此螺牙变形可以根据文献[19]得到:
| $ \delta_{T B}=-\frac{\omega a}{C_{8}}\left(\frac{r_{0} C_{9}}{b}-L_{9}\right) \frac{r^{2}}{D} F_{2}+\frac{\omega r_{0}}{b} \frac{r^{3}}{D} F_{3}-\omega \frac{r^{3}}{D} G_{3} $ | (15) |

|
Download:
|
| 图 3 环形板集中载荷示意 Fig. 3 Annular plate transversely load | |
式中:ω是螺纹所承受的集中载荷;r0是螺纹上所施加集中载荷位置的半径;t是圆环厚度;a是圆环外径;b是滚柱半径,C、D、F、G、L等参数是文献[19]中对应的系数表达式。
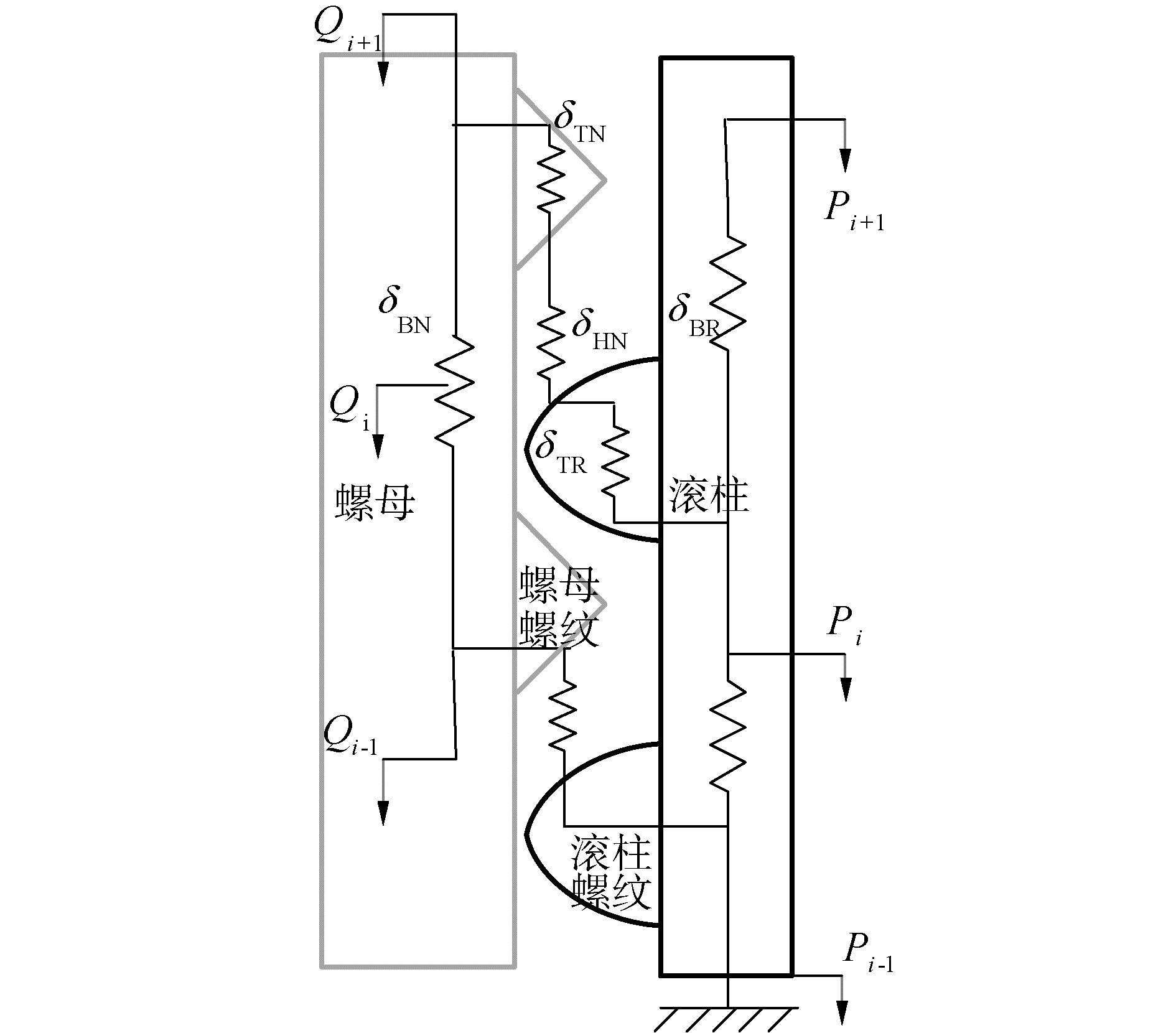
1.3.4 行星滚柱丝杠整体轴向刚度建立丝杠与滚柱接触时的变形协调方程,如图 4所示的为螺母和滚柱的第i和第i+1个螺纹。Qi+1为作用在第i+1啮合螺纹上的轴向载荷,Pi+1为作用在滚柱上第i+1轴段上的载荷,滚柱和螺母的螺纹接触模型如图 4所示。
|
Download:
|
| 图 4 滚柱与螺母螺纹接触模型 Fig. 4 Contact model of roller and nut thread | |
螺母和滚柱的螺纹变形总的变形量分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{\rm{N}}} = \Delta {s_{{\rm{NB}}i}} + \Delta {s_{{\rm{NT}}i}} + \Delta {s_{{\rm{NT}}i + 1}} + \Delta {s_{{\rm{NH}}i}}}\\ {{S_{\rm{R}}} = \Delta {s_{{\rm{RB}}i}} + \Delta {s_{{\rm{RT}}i}} + \Delta {s_{{\rm{RT}}i + 1}} + \Delta {s_{{\rm{RH}}i}}} \end{array}} \right. $ | (16) |
建立螺母与滚柱的变形协调方程表达式:
| $ \frac{{{Q_{i - 1}} - {Q_i}}}{{\frac{1}{{K_{{\rm{RT}}}^i}} + \frac{1}{{K_{{\rm{NT}}}^i}} + \frac{1}{{K_{\rm{H}}^i}}}} - \frac{{{Q_i} - {Q_{i + 1}}}}{{\frac{1}{{K_{{\rm{RT}}}^{i + 1}}} + \frac{1}{{K_{{\rm{NT}}}^{i + 1}}} + \frac{1}{{K_{\rm{H}}^{i + 1}}}}} = \frac{{{Q_i}}}{{K_{{\rm{NB}}}^{i + 1}}} + \frac{{{Q_i}}}{{K_{{\rm{RB}}}^i}} $ | (17) |
行星滚柱丝杠整体轴向刚度分为有螺纹接触部分轴向刚度和无螺纹接触部分轴向刚度。无螺纹接触部分刚度就是无负载端行星滚柱丝杠轴向刚度;有螺纹接触部分轴向刚度分由柱体刚度、螺纹变形刚度和螺纹接触刚度组成。式(17)为行星滚柱丝杠有螺纹接触部分变形协调方程,可以得到行星滚柱丝杠有螺纹接触部分的整体变形及其刚度Kt,无螺纹接触部分可视为圆柱体,刚度为:
| $ {K_{{\rm{nt}}}} = \frac{{EA}}{L} = \frac{{E{\rm{ \mathsf{ π} }}r_s^2}}{L} $ | (18) |
式中:Knt为无负载端行星滚柱丝杠轴向刚度;E为弹性模量;A为丝杠截面面积;L为丝杠无负载端的长度;rs为丝杠半径。
行星滚柱丝杠整体轴向刚度公式为:
| $ \frac{1}{K}=\frac{1}{K_{\mathrm{t}}}+\frac{1}{K_{\mathrm{nt}}} $ | (19) |
丝杠和滚柱螺纹螺牙整体刚度公式为:
| $ \frac{1}{K_{\mathrm{RNT}}}=\frac{1}{K_{\mathrm{RT}}^{i}}+\frac{1}{K_{\mathrm{NT}}^{i}}+\frac{1}{K_{\mathrm{H}}^{i}} $ | (20) |
同一平面上所有丝杠和滚柱的螺牙刚度以及接触刚度公式为:
| $ K_{{\rm{RNT}}}^A = K_{{\rm{RNT}}}^1 + K_{{\rm{RNT}}}^2 + \cdots + K_{{\rm{RNT}}}^n $ | (21) |
根据本文所建立的行星滚柱丝杠轴向刚度模型,针对模型中影响行星滚柱丝杠轴向刚度的参数,如滚柱数量、间隙以及接触角等参数进行仿真。
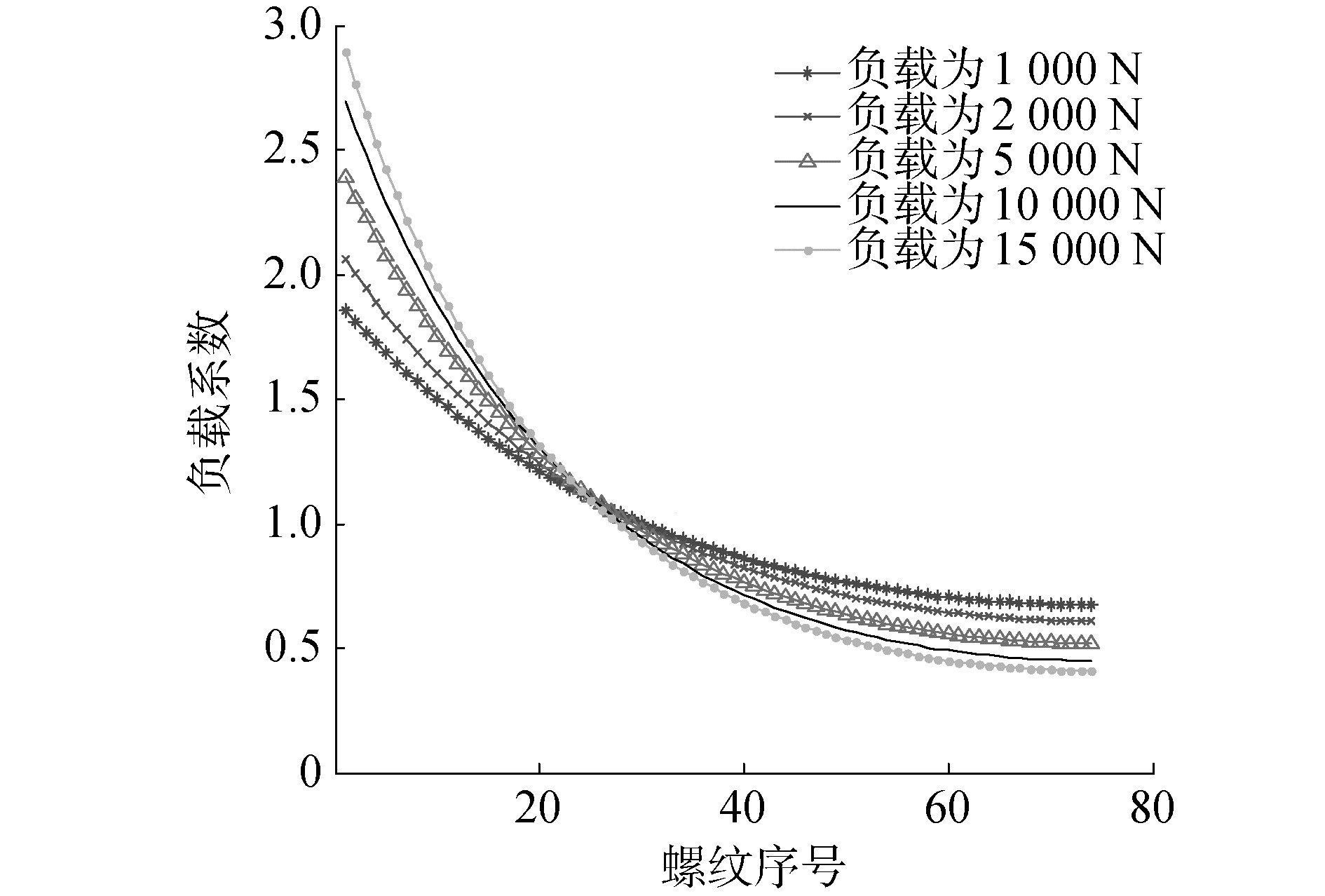
图 5所示为不同负载条件下,滚柱上螺纹所承受负载系数的分布。负载系数是螺纹实际所承受的负载与螺纹均载条件下的比值,而接触均载是指在理想状态下,行星滚柱丝杠上所有螺纹受到的负载均相同。从图 5中可以看出,当行星滚柱丝杠承受较大的负载时,螺纹承受的负载迅速随着螺纹的序号的增大而减小,会导致一端螺纹受力非常大,一端受力很小,容易导致丝杆一端远超丝杠承受极限而另一端还远未达到承受极限,不利于行星滚柱丝杠的安全;而从图 5中可以看出负载为1 000 N时螺纹整体负载系数变化平稳,因此载荷系数最大取值为2,可以保证行星滚柱丝杠整体范围内每个螺纹负载变化不大。因此假设行星滚柱丝杠所受负载为F,螺纹的抗压极限为p,应保证接触均载系数C小于p/2,而接触对数n应大于2F/p。
|
Download:
|
| 图 5 不同负载下负载系数随螺纹序号变化曲线 Fig. 5 Effect of roller number on planetary rollar screw axial stiffness | |
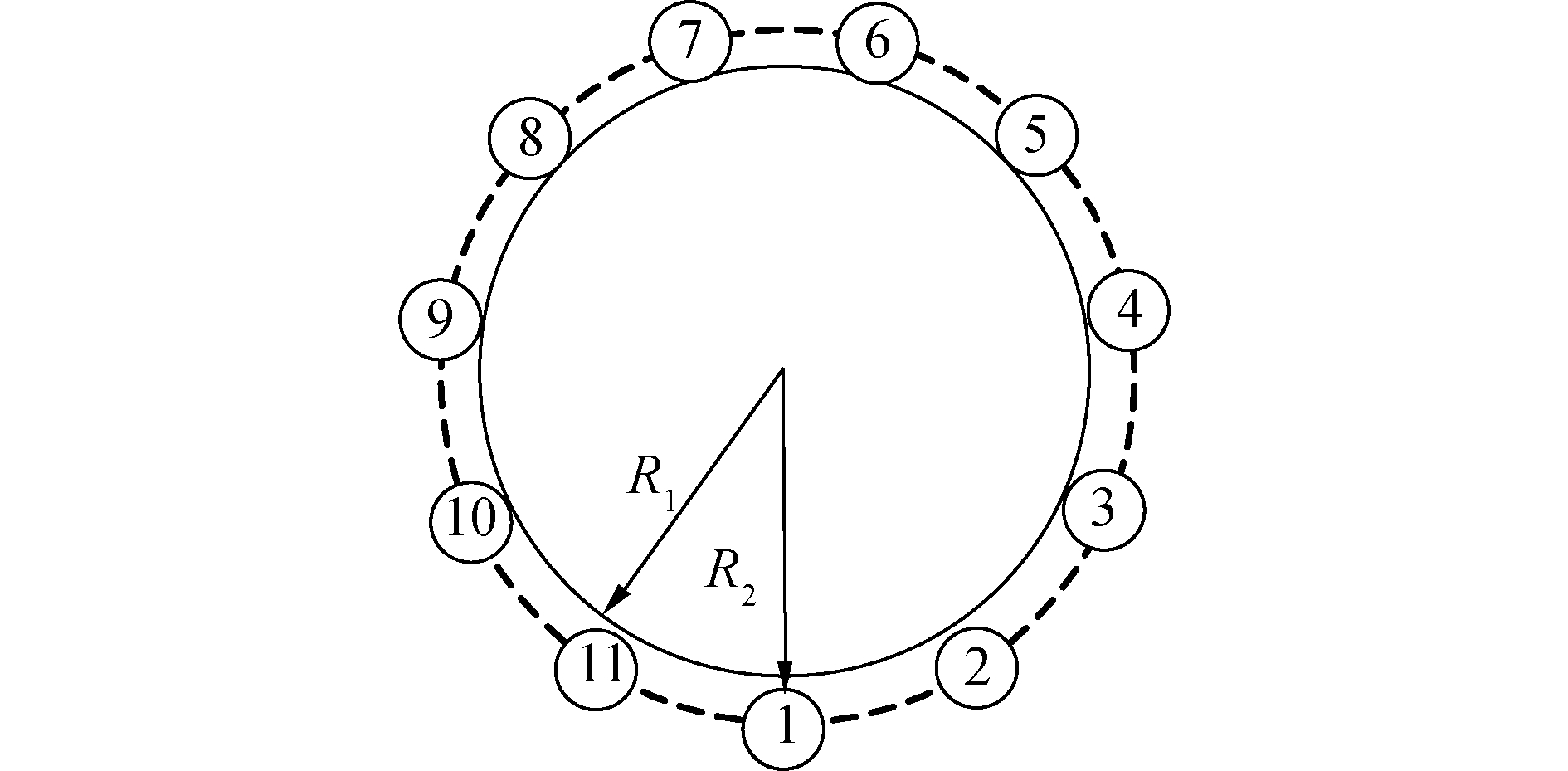
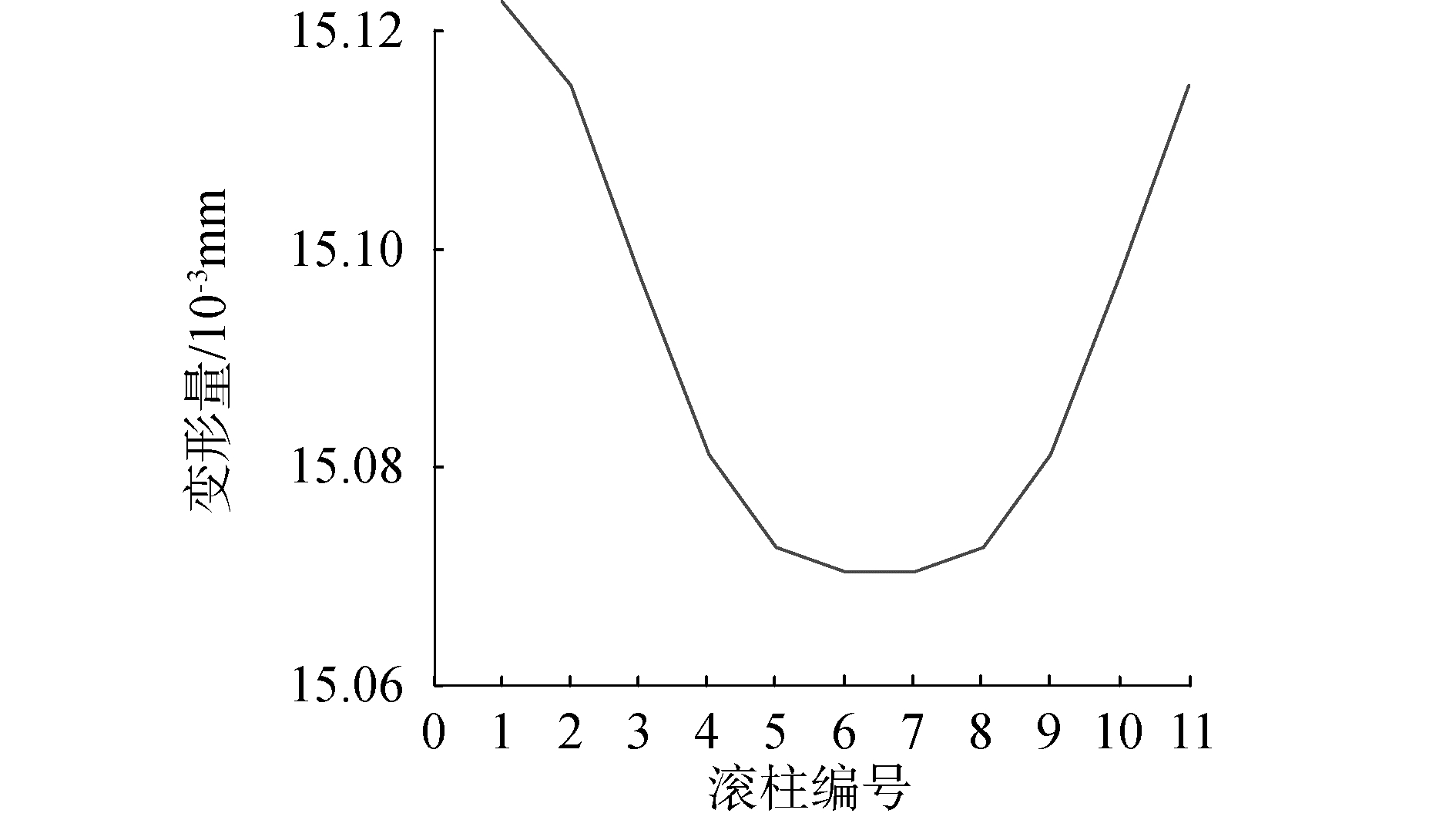
图 6所示为存在偏心量的滚柱按照圆形分布在丝杠周围。偏心量为丝杠轴线与滚柱轴线间实际距离与理想状态的偏差半径。偏心量的存在会对螺牙刚度产生影响。滚柱1有最大偏心量,2号滚柱到6号滚柱偏心量依次减小,7号滚柱到11号滚柱偏心量依次增大。图 7所示为受力70 000 N,有205个滚柱螺纹的行星滚柱丝杠在最大偏心量为0.09 mm时各滚柱的轴向变形量,从图 7中可以看出各个滚柱的相对变形量随偏心量的减小,滚柱的变形量减小。
|
Download:
|
| 图 6 滚柱的偏心分布 Fig. 6 Distribution of roller eccentricity | |
|
Download:
|
| 图 7 由偏心引起的各滚柱整体变形 Fig. 7 Roller deflection caused by eccentricity | |
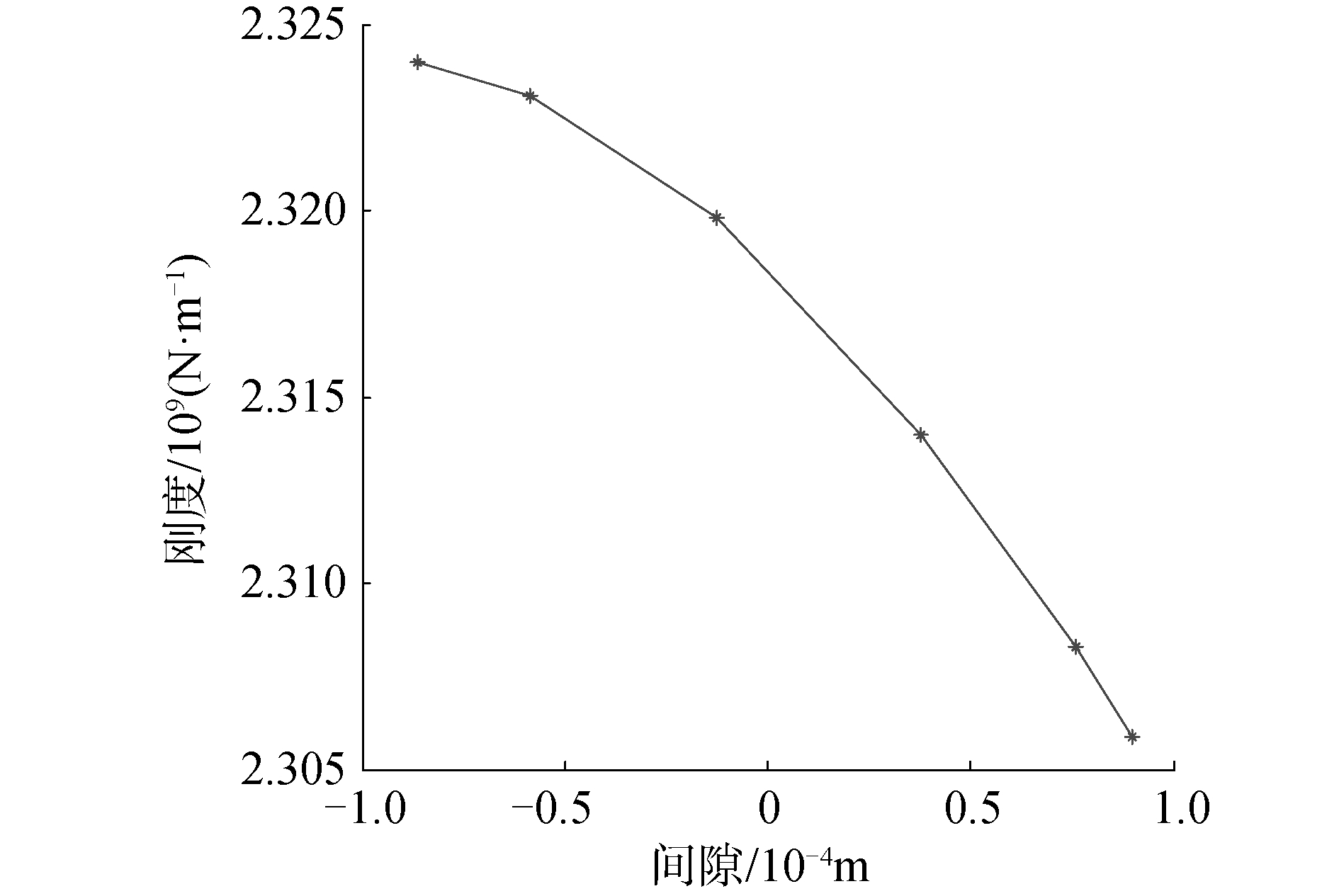
如图 8所示为间隙值对行星滚柱丝杠刚度的影响。假设当螺纹接触位置为螺纹中径时,接触螺纹之间的间隙为零,当接触位置偏向于外径时认为2螺纹的间隙为正,当间隙值为负数时,认为2螺纹接触位置更偏向于螺纹根部。从图 8中可以看出间隙值越大,整个行星滚柱丝杠轴向刚度越小,间隙值对行星滚柱丝杠轴向刚度的影响较小。
|
Download:
|
| 图 8 间隙值对行星滚柱丝杠刚度的影响 Fig. 8 Effect of clearance on PRS axial stiffness | |
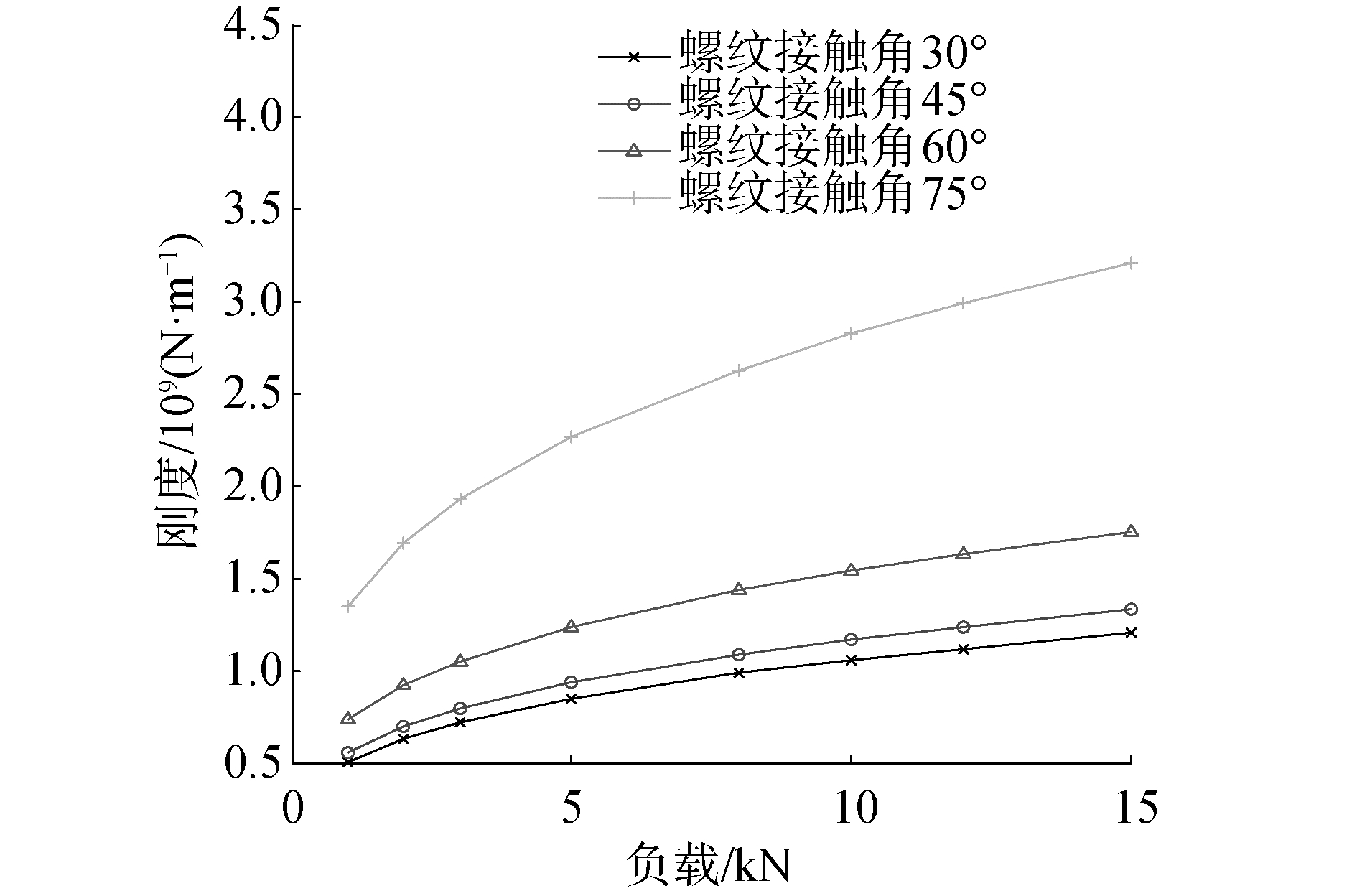
图 9所示为螺纹接触角对行星滚柱丝杠刚度的影响,从图 9中可以看出随着螺纹接触角的增大,螺纹的轴向刚度会增加。螺纹受力增加,根据赫兹接触理论,接触刚度会随负载增加而呈非线性增大。
|
Download:
|
| 图 9 接触角对行星滚柱丝杠刚度影响 Fig. 9 Effect of load on PRS axial stiffness | |
从图 10中可以看出滚柱个数对行星滚柱丝杠刚度影响非常大,滚柱个数越多, 行星滚柱丝杠的刚度越大,增加滚柱数量能够有效提高行星滚柱丝杠的轴向刚度。从结果中也可以看出,滚柱数量在负载较大的条件下对行星滚柱丝杠轴向刚度的影响比较大。

|
Download:
|
| 图 10 滚柱数对行星滚柱丝杠刚度影响 Fig. 10 Effect of roller number on PRS axial stiffness | |
行星滚柱丝杠刚度特性试验台如图 11所示。试验过程中施加扭矩,通过加载装置将扭矩转化为轴向压力并记录所施加轴向压力的大小。加载装置对丝杠施加轴向压力产生变形,通过使用涡流位移传感器测量丝杠产生的轴向变形,利用轴向压力和轴向变形计算行星滚柱丝杠的轴向刚度。在进行行星滚柱丝杠静刚度特性研究中,主要经验部件为2块支板和一块连接平板,其中支撑平板长宽厚分别为120、400、40 mm;连接平板为240、120、20 mm。试验使用涡流位移传感器和力传感器。涡流位移传感器的工作范围为0~1 mm,其灵敏度为0.062 5 mm/V;力传感器的工作范围为0~1 000 kg,灵敏度为0.02 kg/V。

|
Download:
|
| 图 11 行星滚柱丝杠刚度特性试验台示意和实物 Fig. 11 Sketch map and test rig of planctary roller scre waxial stiffness | |
行星滚柱丝杠试验台通过地脚螺栓固定在基础上,通过旋转加载装置对行星滚柱丝杠施加轴向载荷,位移挡板与丝杠固定在一起,通过测量位移挡板的运动位移,得到行星滚柱丝杠的轴向变形。试验装置中设置有防转连杆防止丝杠旋转,并设有保护装置保证丝杠垂直于地面。支撑平板的并联刚度为5.04×109 N/m,连接平板的变形并不会影响试验结果,通过手册得到行星滚柱丝杠整体轴向刚度为2×108~2.6×108 N/m,远小于支撑板刚度,因此可以忽略支撑平板对试验结果带来的影响。
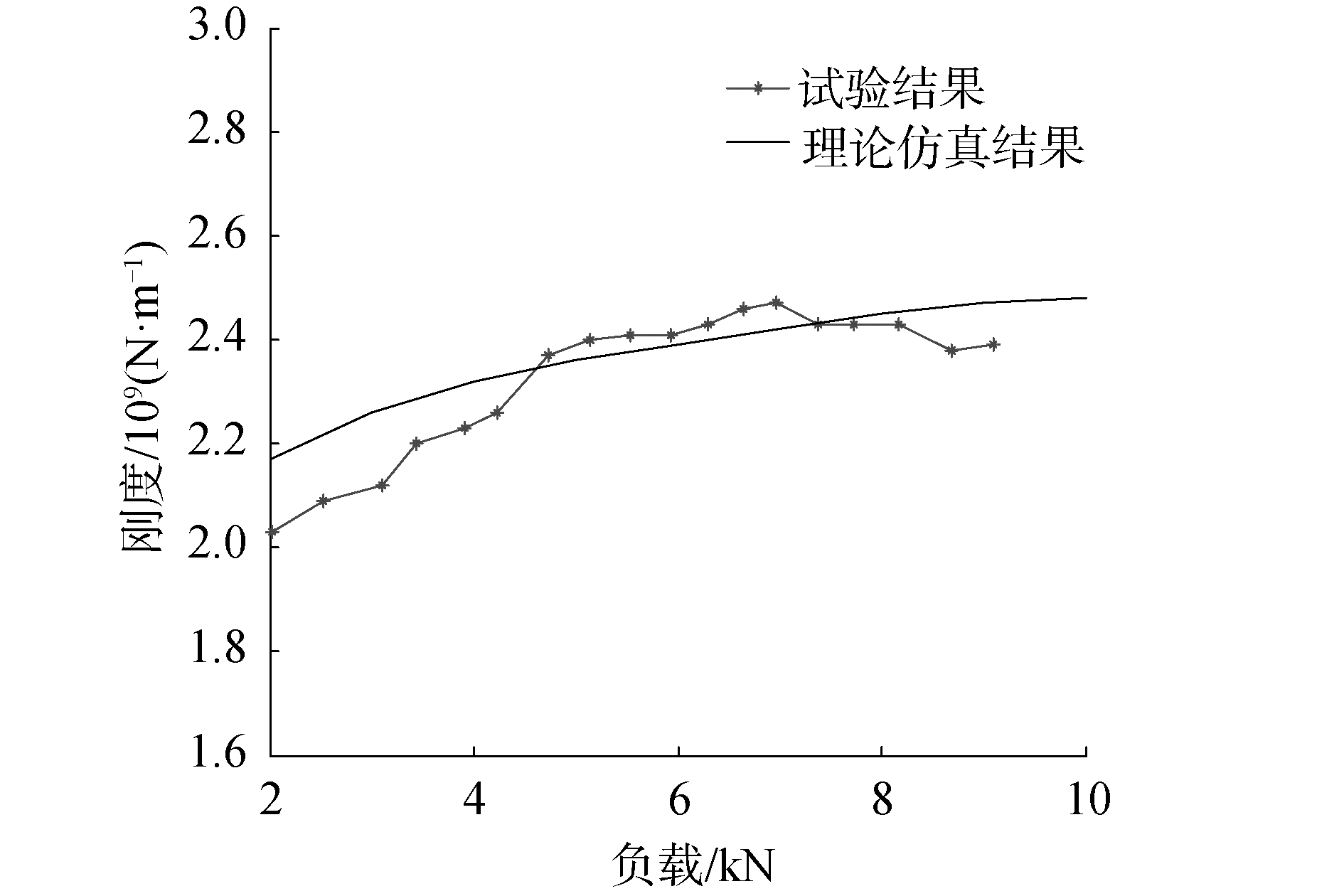
通过将行星滚柱丝杠轴向刚度试验和本文所使用的轴向刚度模型的结果进行对比,如图 12所示。为保证仿真结果与试验结果的可对比性,图 12两组数据均考虑了无螺纹接触部分丝杠轴向刚度带来的影响,从对比中可以看出,随着负载的增加,行星滚柱丝杠的轴向刚度在不断增加,当载荷达到一定程度后行星滚柱丝杠的轴向刚度趋于一个最大值。
|
Download:
|
| 图 12 行星滚柱丝杠轴向刚度试验与仿真结果对比 Fig. 12 Comparation of planetary roller screw axial stiffness experiment results and presented model simulation results | |
从图 12中可以看出本文所建立的刚度模型与试验结果比较接近。本文所建立的刚度模型可以考虑不同的结构参数对轴向刚度带来的影响,例如接触角、滚柱数量等参数。本文所建立的行星滚柱丝杠刚度模型有利于行星滚柱丝杠的参数化设计。
从图 12中可以看出本文所建立的刚度模型与试验结果之间最大误差为8%。本文建立的刚度模型仿真结果大于试验所测得行星滚柱丝杠的刚度。这是由于试验过程中,涡流位移传感器测量的是所有试验装置产生的变形,导致试验测得的变形要大于单独行星滚柱丝杠产生的变形,从而降低了行星滚柱丝杠的轴向刚度。
4 结论1) 相比于传统行星滚柱丝杠刚度模型,本文模型可以分析间隙、接触角以及滚柱数量等参数对行星滚柱丝杠轴向刚度的影响,从仿真结果中可以看出间隙会导致滚柱产生不同的变形,并且随着间隙增大行星滚柱丝杠刚度会减小;螺纹接触角和滚柱数量这2种设计参数越大,行星滚柱丝杠刚度越大;为快速而合理进行行星滚柱丝杠的参数化设计,过大的接触角会影响螺纹的传动,过小的接触角会影响行星滚柱丝杠整体的轴向刚度,因此综合考虑行星滚柱丝杠螺纹接触角45°为最优;滚柱数量会影响丝杠质量、转动惯量并会增大传动过程中的摩擦力,因此滚柱数量也需合理设计。
2) 搭建行星滚柱丝杠轴向刚度特性试验台,刚度特性试验结果与仿真结果误差为8%。通过与刚度试验结果对比,验证了本文所建立的行星滚柱丝杠刚度模型。
| [1] |
JONES M H, VELINSKY S A. Kinematics of roller migration in the planetary roller screw mechanism[J]. Journal of mechanical design, 2012, 134(6): 061006. DOI:10.1115/1.4006529 (  0) 0)
|
| [2] |
HOJJAT Y, AGHELI M M. A comprehensive study on capabilities and limitations of roller-screw with emphasis on slip tendency[J]. Mechanism and machine theory, 2009, 44(10): 1889-1899. (  0) 0)
|
| [3] |
VMOROZOV V V, ZHDANOV A V. Influence of the axial angle of screw profiles on the load capacity of roller-screw mechanisms[J]. Russian engineering research, 2015, 35(7): 477-480. DOI:10.3103/S1068798X1507014X (  0) 0)
|
| [4] |
ABEVI F, DAIDIE A, CHAUSSUMIER M, et al. Static load distribution and axial stiffness in a planetary roller screw mechanism[J]. Journal of mechanical design, 2016, 138(1): 012301. (  0) 0)
|
| [5] |
AURÉGAN G, FRIDRICI V, KAPSA P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332-333: 1176-1184. DOI:10.1016/j.wear.2015.01.047 (  0) 0)
|
| [6] |
杨家军, 杨保哲, 朱继生, 等. 预紧力对行星滚柱丝杠轴向变形及摩擦的影响[J]. 机械传动, 2011, 35(12): 16-18, 22. YANG Jiajun, YANG Baozhe, ZHU Jisheng, et al. Effect of preload on axial deformation and friction of planetary roller screw[J]. Journal of mechanical transmission, 2011, 35(12): 16-18, 22. DOI:10.3969/j.issn.1004-2539.2011.12.004 (  0) 0)
|
| [7] |
SANDU S, BIBOULET N, NELIAS D, et al. An efficient method for analyzing the roller screw thread geometry[J]. Mechanism and machine theory, 2018, 126: 243-264. DOI:10.1016/j.mechmachtheory.2018.04.004 (  0) 0)
|
| [8] |
MOROZOV V V, PANYUKHIN V I, ZHDANOV A V. Increasing the load capacity and rigidity of roller-screw mechanisms by adjusting the screw surfaces[J]. Russian engineering research, 2016, 36(5): 345-351. DOI:10.3103/S1068798X16050142 (  0) 0)
|
| [9] |
VELINSKY S A, CHU B, LASKY T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of mechanical design, 2008, 131(1): 011016. (  0) 0)
|
| [10] |
徐强, 王水铭, 赵国平, 等. PWG型差动丝杠摩擦转矩分析与效率求解[J]. 现代制造工程, 2016(5): 138-142, 62. XU Qiang, WANG Shuiming, ZHAO Guoping, et al. The analysis of friction torque and calculation of efficiency of PWG planetary roller screw[J]. Modern manufacturing engineering, 2016(5): 138-142, 62. (  0) 0)
|
| [11] |
靳谦忠, 杨家军, 孙健利. 滚珠丝杠副和行星式滚柱丝杠副静刚度的比较研究[J]. 机械科学与技术, 1999, 18(2): 230-232. JIN Qianzhong, YANG Jiajun, SUN Jianli. The comparative research on the static stiffness of ball screw and planetery roller screw[J]. Mechanical science and technology, 1999, 18(2): 230-232. DOI:10.3321/j.issn:1003-8728.1999.02.019 (  0) 0)
|
| [12] |
靳谦忠, 杨家军, 孙健利. 行星式滚柱丝杠副的摩擦机理研究[J]. 华中理工大学学报, 1998, 26(6): 82-83, 96. JIN Qianzhong, YANG Jiajun, SUN Jianli. The research on friction mechanism of the planetary roller screw[J]. Journal of Huazhong University of Science and Technology, 1998, 26(6): 82-83, 96. (  0) 0)
|
| [13] |
杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报(自然科学版), 2011, 39(4): 1-4. YANG Jiajun, WEI Zhenxing, ZHU Jisheng, et al. Calculation of load distribution of planetary roller screws and static rigidity[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(4): 1-4. (  0) 0)
|
| [14] |
付晓军, 刘更, 马尚君, 等. 行星滚柱丝杠副螺旋曲面啮合机理研究[J]. 机械工程学报, 2016, 52(3): 26-33. FU Xiaojun, LIU Geng, MA Shangjun, et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of mechanical engineering, 2016, 52(3): 26-33. (  0) 0)
|
| [15] |
付晓军, 刘更, 马尚君, 等. 考虑零件偏斜的行星滚柱丝杠副啮合特性研究[J]. 机械工程学报, 2017, 53(3): 25-33. FU Xiaojun, LIU Geng, MA Shangjun, et al. Meshing properties of planetary roller screw mechanism within misalignments[J]. Journal of mechanical engineering, 2017, 53(3): 25-33. (  0) 0)
|
| [16] |
JONES M H, VELINSKY S A. Stiffness of the roller screw mechanism by the direct method[J]. Mechanics based design of structures and machines:an international journal, 2014, 42(1): 17-34. DOI:10.1080/15397734.2013.839385 (  0) 0)
|
| [17] |
梅向明, 黄敬之. 微分几何[M]. 3版. 北京: 高等教育出版社, 2003. MEI Xiangming, HUANG Jingzhi. Differential geometry[M]. 3rd ed. Beijing: Higher Education Press, 2003. (  0) 0)
|
| [18] |
JOHNSON K L.接触力学[M].徐秉业, 罗学富, 刘信声, 等译.北京: 高等教育出版社, 1992. JOHNSON K L. Contact mechanics[M]. XU Bingye, LUO Xuefu, LIU Xinsheng, et al., trans. Beijing: Higher Education Press, 1992. (  0) 0)
|
| [19] |
YOUNG W C, BUDYNAS R G. Roark's formulas for stress and strain[M]. New York: McGraw-Hill, 1989.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


