2. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001
2. College of Automation, Harbin Engineering University, Harbin 150001, China
当今世界,综合电力推进系统以其经济性、环保性等诸多优势,正在逐步替代传统推进系统[1]。随着各种新能源的不断发现和应用,综合电力推进系统成为海、陆、空新型载具的主要推进系统。而对于新兴的综合电力推进系统,其风险性也大大区别于其他推进系统,传统的推进系统风险评估方法显然已经不再适用。
综合电力推进系统风险评估的早期研究来源于系统可靠性评估,又和故障相关技术有部分联系。美国海军致力于船舶综合电力推进系统可靠性的相关研究,主要侧重于各种新型电气设备和大功率武器和负载对综合电力推进系统可靠性的影响[2],以及新的配电网结构对综合电力推进系统的可靠性影响[3]。近年来,综合电力推进系统故障相关技术的研究成果较多,主要包括故障诊断以及进一步的故障定位技术[4-5]、故障控制管理技术[6-8]、故障预测技术[9]以及故障其他相关技术[10-12]。但是,可靠性评估和故障诊断相关技术只能对系统失效和系统故障做出分析判断,对后续产生的后果缺乏判断估计[13]。因此,为了能够更准确的对综合电力推进系统的各项性能进行研究,分析系统在不同工况下的运行情况以及存在的各种风险,并在各种风险发生后做出一系列决策分析,以及形成最佳风险对策组合,国内外学者不断地探索综合电力推进系统与风险评估方法之间的契合点[14-16],本文的风险预测评估方法也是在此基础上提出的。为验证本方法在外界环境影响下的有效性,本文以海情因素影响下的船舶综合电力推进系统为例进行了验证。
1 MHMM-Viterbi算法本文提出的MHMM-Viterbi算法,综合了隐性马尔科夫模型(hidden Markov model, HMM)算法、Viterbi算法和统计学理论,可以将评估对象内部状态转变与外界因素影响相结合,同时引入统计学原理,很大程度上消除了小概率事件,大大提高预测的准确性。建立评估对象的HMM模型,用5个元素来描述评估对象:隐含状态、可观测状态、初始状态概率矩阵、隐含状态概率转移矩阵、观测状态转移概率矩阵。
评估对象隐含状态S,即在模型中评估对象马尔科夫链的状态数,表达式为:
| $ S=\left\{S_{1}, S_{2}, \cdots, S_{M}\right\} $ | (1) |
时间t时刻的马尔科夫链的状态定义为:
| $ S_{t} \in\left(S_{1}, S_{2}, \cdots, S_{M}\right) $ | (2) |
评估对象可观测状态O,即模型中能被观测到的每个状态,表达式为:
| $ O=\left\{O_{1}, O_{2}, \cdots, O_{N}\right\} $ | (3) |
在t时刻的观测值可以被定义为,其中
| $ o_{t}=\left(O_{1}, O_{2}, \cdots, O_{N}\right) $ | (4) |
评估对象初始概率分布向量,表达式为
| $ \mathit{\boldsymbol{\pi }} = \left\{ {{\pi _1},{\pi _2}, \cdots ,{\pi _M}} \right\} $ | (5) |
| $ \mathit{\boldsymbol{\pi }} = P\left( {{q_t} = {S_i}} \right),\quad 1 \le i < M $ | (6) |
评估对象初始状态转移概率矩阵A,即评估对象从状态Si向状态Sj转移概率的矩阵,表达式为:
| $ \mathit{\boldsymbol{A}} = {\left( {{a_{ij}}} \right)_{M \times M}} $ | (7) |
| $ {a_{ij}} = P\left( {\left( {{q_{t + 1}} = {S_j}} \right)/\left( {{q_t} = {S_i}} \right)} \right),\quad 1 \le i,j \le M $ | (8) |
评估对象隐含状态转移概率矩阵B,即在外界因素为状态Ok时评估对象为状态Sj的转移概率,表达式为:
| $ \boldsymbol{B}=\left(b_{j k}\right)_{M \times N} $ | (9) |
| $ \left\{ {\begin{array}{*{20}{l}} {{b_{jk}} = P\left( {\left( {{o_i} = {O_k}} \right)/\left( {{q_t} = {S_j}} \right)} \right),}\\ {1 \le j < M,1 \le k < N} \end{array}} \right. $ | (10) |
因此,评估对象的隐性马尔科夫模型可以表示为λ=(M, N, π, A, B),或者可以简单表示为λ=(π, A, B)。即HMM可以被分为2个部分:第一部分就是由π和A表达的马尔科夫链,即状态序列。另一部分则是由B表达的随机过程,即外界因素状态序列。输出λ为一个时序序列。
接下来,根据评估对象的工作状态集合S={S1, S2, …, SM},在未来T时间内观察序列海况o={o1, o2, …, oN),与此同时,评估对象的预测序列Q=(q1, q2, …, qT),则时间T内单元状态转移情况如图 1所示。

|
Download:
|
| 图 1 时间T内单元状态转移图 Fig. 1 States transition diagram of unit in time T | |
如图 1所示,评估对象状态预测序列可描述为最大概率状态转移路径,即根据最大后验概率准则求取使P(Q|o)最大的预测序列Q,根据贝叶斯公式:
| $ P(Q | o)=(P(Q) P(o | Q)) / P(o) $ | (11) |
因为外界因素O已知,P(o)则已确定,因此预测序列Q的判定函数gQ(o):
| $ g_{Q}(o)=P(Q) P(Q | o) $ | (12) |
因此,只需根据观察序列O,求取预测序列Q,而使gQ(o)最大,则有:
| $ \begin{array}{c}{P(o | Q)=P\left(q_{1}, q_{2}, \cdots, q_{T}\right) P\left(q_{1}\right)} \\ {P\left(q_{2} | q_{1}\right) \cdots P\left(q_{T} | q_{T-1}\right)}\end{array} $ | (13) |
考虑到评估对象每一时刻状态的产生都是独立的,所以有:
| $ \begin{array}{*{20}{c}} {P(o|Q) = P\left( {{o_1},{o_2}, \cdots ,{o_T}} \right)P\left( {{q_1},{q_2}, \cdots ,{q_T}} \right) = }\\ {P\left( {{O_1}|{q_1}} \right)P\left( {{O_2}|{q_2}} \right) \cdots P\left( {{O_T}|{q_T}} \right)} \end{array} $ | (14) |
因此判定函数:
| $ \begin{array}{*{20}{c}} {{g_Q}(o) = P\left( {{q_1}} \right) \cdots P\left( {{q_T}|{q_{T - 1}}} \right)P\left( {{o_1}|{q_1}} \right) \cdots P\left( {{o_T}|{q_T}} \right) = }\\ {P\left( {{q_1}} \right)\prod\limits_{t = 2}^T P \left( {{q_t}|{q_{t - 1}}} \right)\prod\limits_{t = 1}^T P \left( {{o_t}|{q_t}} \right)} \end{array} $ | (15) |
对式(15)进行对数变化得:
| $ \begin{aligned} \ln q_{Q}=& \ln P\left(q_{1}\right)+\sum\limits_{i=2}^{T} \ln P\left(q_{t} | q_{t-1}\right)+\\ & \sum\limits_{t=1}^{T} \ln P\left(o_{t} | q_{t}\right) \end{aligned} $ | (16) |
式(16)中所需的参数均由HMM给出,因此通过式(16)可以求解预测序列Q,但是计算量太大,不便于实际应用,因此对式(16)进行变换得:
| $ \begin{aligned} \operatorname{ln}g_{Q}(o)=& \ln P\left(q_{1}\right)+\ln P\left(o_{1} | q_{1}\right)+\\ & \sum\limits_{i=2}^{T}\left(\ln P\left(q_{t} | q_{t-1}\right)+\ln P\left(o_{t} | q_{t}\right)\right) \end{aligned} $ | (17) |
式(17)将求取评估对象状态预测序列,分解为在每一时刻对每一状态求取子项lnP(qt|qt-1)+ lnP(ot|qt)的最大值,然后对所有时刻进行累加再进行判定。
最后,给定时间T,根据评估对象的HMM,采用Viterbi算法进行P次运算,得到P个评估对象状态预测序列,定义H为单元状态预测序列矩阵:
| $ \boldsymbol{H}=\left[H_{1}, H_{2}, \cdots, H_{i}, \cdots, H_{p}\right]^{\mathrm{T}} $ | (18) |
式中第i个单元状态预测序列可以表示为:
| $ H_{i}=\left\{S_{i_{1}}, S_{i_{2}}, \cdots, S_{i_{T}}\right\}, \quad i=1,2, \cdots, P $ | (19) |
所以有H为P×T的矩阵:
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{S_{11}}}& \cdots &{{S_{1T}}}\\ \vdots &{}& \vdots \\ {{S_{p1}}}& \cdots &{{S_{PT}}} \end{array}} \right] $ | (20) |
在应用MHMM-Viterbi算法进行评估对象异常状态预测时,必须要满足一个前提条件,即假设采用某一状态序列对评估对象在t时刻的状态进行分析,则要求在该状态序列的t-1时刻,评估对象必须处于正常状态,即:
| $ S_{i_{(t-1)}}=1 $ | (21) |
只有满足式(21)的评估对象状态预测序列才被筛选出来,对评估对象在t时刻的状态进行分析。
假设对评估对象在t时刻的状态进行分析,满足式(21)条件的状态预测序列的数量为Q,Q < P。对Q个状态预测序列在t时刻的状态进行统计,Q1为t时刻处于正常状态的评估对象状态预测序列的个数(在矩阵H中i列的值为1),以此类推,Qj为t时刻处于状态j的评估对象状态预测序列的个数(在矩阵H中i列的值为j, j < M), 因此,评估对象在t时刻处于异常状态的概率为:
| $ {f_t} = \frac{{\sum\limits_{j = 2}^M {{Q_J}} }}{Q} $ | (22) |
根据式(22), 从t=0到t=T时刻求取异常状态概率,则可以得到评估对象异常状态预测序列如下所示:
| $ F=\left\{f_{1}, f_{2}, \cdots, f_{T}\right\} $ | (23) |
MHMM-Viterbi算法将评估对象的内因和外因相结合,同时在很大程度上消除了小概率误差,使状态预测结果更准确。
2 综合电力推进系统风险预测评估方法在综合电力推进系统中,风险的来源主要是系统自身运行状态及周围环境的概率性而产生的局部系统故障,这种故障可能会导致整个系统瘫痪,因此风险评估就是对这种概率性的发生及导致的后果进行评估。
本文则提出一种多风险预测评估方法,即在外界环境影响下,系统所有单元可同时进行独立风险失效模拟,即多个单元可同时发生风险,并对多风险(如果只有一个单元发生风险,即为单风险)发生概率和风险后果进行分析评估。
综合电力推进系统风险预测评估方法主要包括系统拓扑建模、风险模拟、风险参数计算3部分组成。
2.1 综合电力推进系统拓扑建模在综合电力推进系统中,设备连接分为2种属性:1)物理连接属性,即不考虑设备的运行状态,只考虑设备之间的连接关系;2)电气连接属性,即设备运行时,各设备的电气参数及其相互之间的影响。而综合电力推进系统的风险拓扑建模既要体现出综合电力推进系统的物理连接属性,同时也是研究系统电气连接属性的基础。
风险拓扑建模原则如图 2所示,由3个部分组成:1)系统建模框架,即系统的基础拓扑模型;2)拓扑模型规范,即为了和建模目标一致,拓扑模型需要描述的系统性质;3)拓扑模型验证,即对拓扑模型规范的验证方法。在船舶综合电力推进系统中,基础拓扑模型根据船舶综合电力推进系统模型图建立;拓扑模型规范描述的两个系统性质,物理连接性质和电气连接性质;拓扑模型验证则是采用遍历算法对风险拓扑模型进行验证。

|
Download:
|
| 图 2 风险拓扑建模原则 Fig. 2 The principle for network topology modeling | |
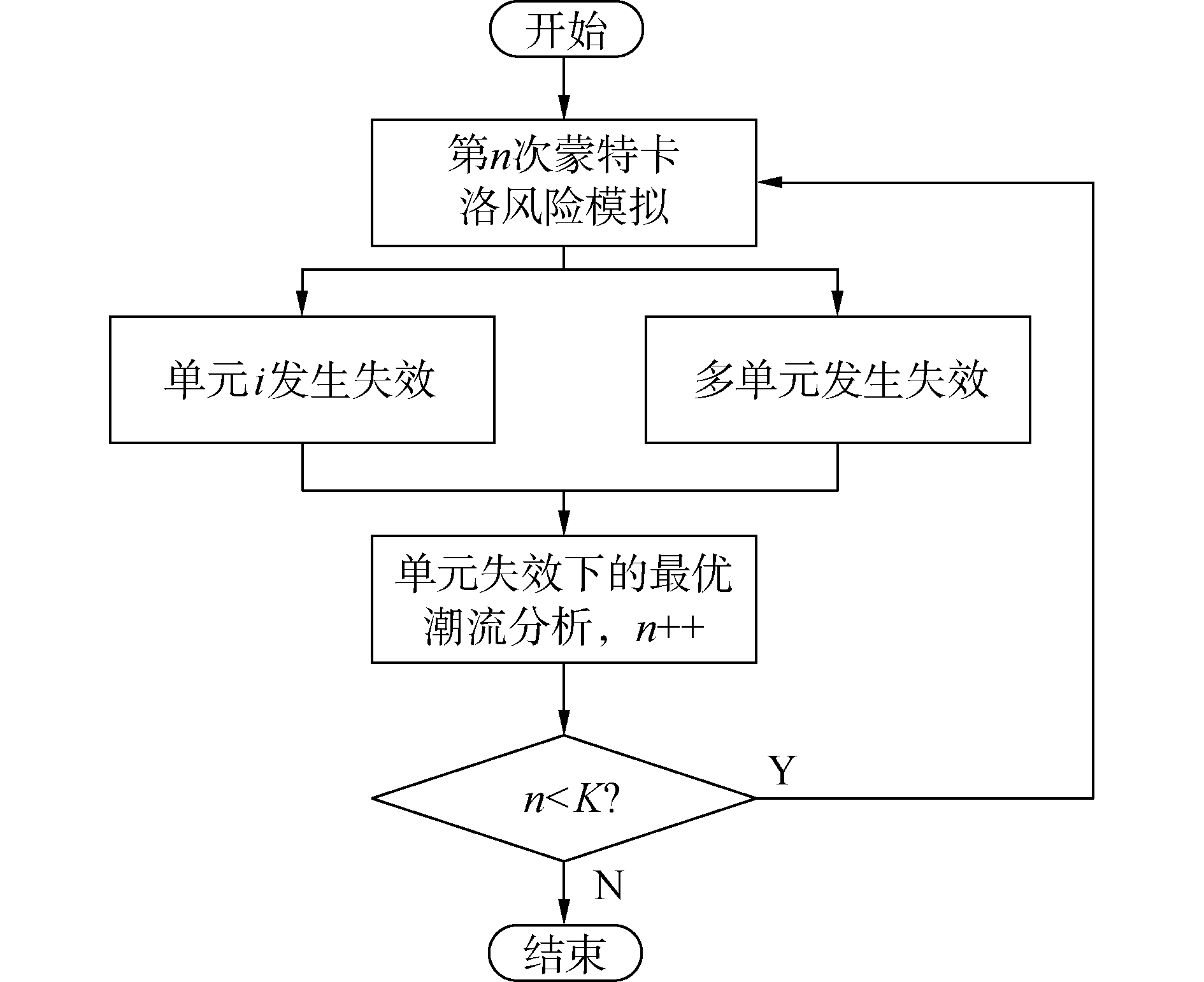
在完成综合电力推进系统风险拓扑建模的基础上,建立节点、支路、发电矩阵,完成正常状态下系统的潮流分析,作为风险比对基准参数。对综合电力推进系统进行风险模拟和分析具体流程如图 3所示。
|
Download:
|
| 图 3 系统风险模拟流程图 Fig. 3 The flow chart of system risk simulation | |
结合图 3所示,综合电力推进系统风险模拟的具体过程如下:
1) 单元失效模拟:对节点矩阵和支路矩阵的每个单元独立取[0, 1]的随机数,随机数小于单元失效率则认为该单元失效,反之则认为该单元未失效,单元失效模拟过程可以表达为:
| $ S_{i}=\left\{\begin{array}{ll}{1,} & {\lambda>a_{i}} \\ {0,} & {\lambda_{i} \leqslant a_{i}}\end{array}\right. $ | (24) |
式中:λi为单元i的失效率;ai为单元i取得的随机数;Si为单元i状态,失效状态为1,工作状态为0。
2) 单元失效后矩阵重组:首先对失效单元进行分类,确定单元所属矩阵,之后对综合电力推进系统拓扑模型进行该单元失效后的结构重组。
3) 单元失效下潮流分析:采用单元失效下的最优潮流分析方法,对单元失效下的重组节点矩阵、支路矩阵和发电矩阵进行潮流分析,潮流分析结果为各节点功率矩阵,矩阵参数包括节点类型、节点编号、节点实际注入有功、实际注入无功、负载有功、负载无功、实际电压和相角等参数。
4) 最后将单元失效引发风险后的潮流分析结果与正常工作状态下的潮流分析结果进行对比分析,则得到该次单元风险失效引发的系统风险评估结果。
2.3 综合电力推进系统风险评估参数计算综合电力推进系统风险评估结果是由系统的风险参数来表达的。在本文中,综合电力推进系统风险评估结果主要由3个风险评估参数来表达,分别为:系统风险发生概率(probability of risk occurrence, PRO)、系统期望缺供电力(expected demand not supplied,EDNS)、系统期望缺供电量(expected energy not supplied,EENS)。
根据综合电力推进系统风险模拟得到的系统参数,3个参数的计算表达式分别为:
1) 系统风险发生概率PRO。
系统风险发生概率,即为船舶综合电力推进系统工作时发生单元失效的概率。在船舶综合电力推进系统中,假设单元节点总数为NU,则有单元节点k的单元失效概率PROk可由下式表达:
| $ \mathrm{PRO}_{k}=\sum\limits_{i=1}^{N_{\mathrm{k}}} P_{i k} $ | (25) |
式中:Pik是与单元节点k处于失效停运状态i的概率;Nk为引起单元节点k削减单元的状态总数。
根据式(25),系统风险发生概率PRO为:
| $ \mathrm{PRO}=\sum\limits_{k=1}^{N_{\mathrm{U}}} \mathrm{PRO}_{k} $ | (26) |
2) 系统期望缺供电力EDNS。
系统期望缺供电力,即为船舶综合电力推进系统发生风险时,所损失的负载功率的期望值,假设系统的单元节点数为NU,则单元节点k的期望缺供电力EDNSk为:
| $ \mathrm{EDNS}_{k}=\sum\limits_{i=1}^{N_{k}} P_{i k} L_{k} $ | (27) |
式中:Lk为单元节点k的平均单元功率,MW。则系统期望缺供电力EDNS为:
| $ \mathrm{EDNS}=\sum\limits_{k=1}^{N_{\mathrm{U}}} \mathrm{EDNS}_{k} $ | (28) |
3) 系统期望缺供电量EENS。
系统期望缺供电量,即船舶综合电力推进系统在一定时间T内,由于风险引起单元失效而损失的电量的期望值。系统期望缺供电量一般可以由系统期望缺供电力乘以时间T得出,即:
| $ \mathrm{EENS}=\mathrm{EDNS} \times T $ | (29) |
系统期望缺供电量也可以由状态s的概率,状态s下的功率削减量以及时间T得出:
| $ \mathrm{EENS}=\sum\limits_{k=1}^{N_{\mathrm{U}}}\left(\sum\limits_{S \in F_{k}} P(s) C(s)\right) \times T $ | (30) |
式中:NU为单元节点集合;P(s)为系统处于状态s的概率; C(s)为状态s的功率削减量,MW; Fk为单元节点k全部失效状态的集合。
综合电力推进系统风险参数还包括系统期望单元失效频率和系统单元失效平均持续时间,本文中这2个参数用于对主要风险参数进行补充。
3 船舶综合电力推进系统风险预测评估本文以海情因素影响下的船舶综合电力推进系统为例,验证提出的风险预测评估方法。
3.1 综合电力推进系统风险评估参数计算船舶综合电力推进系统通常由发电模块、配电模块、能源管理模块、负载模块、储能模块、电力变换模块和推进模块组成。本文采用的船舶综合电力推进系统以美国DDG1000舰为原型,系统结构图如图 4所示。

|
Download:
|
| 图 4 船舶综合电力推进系统构成图 Fig. 4 The structure diagram of ship integrated electric propulsion system | |
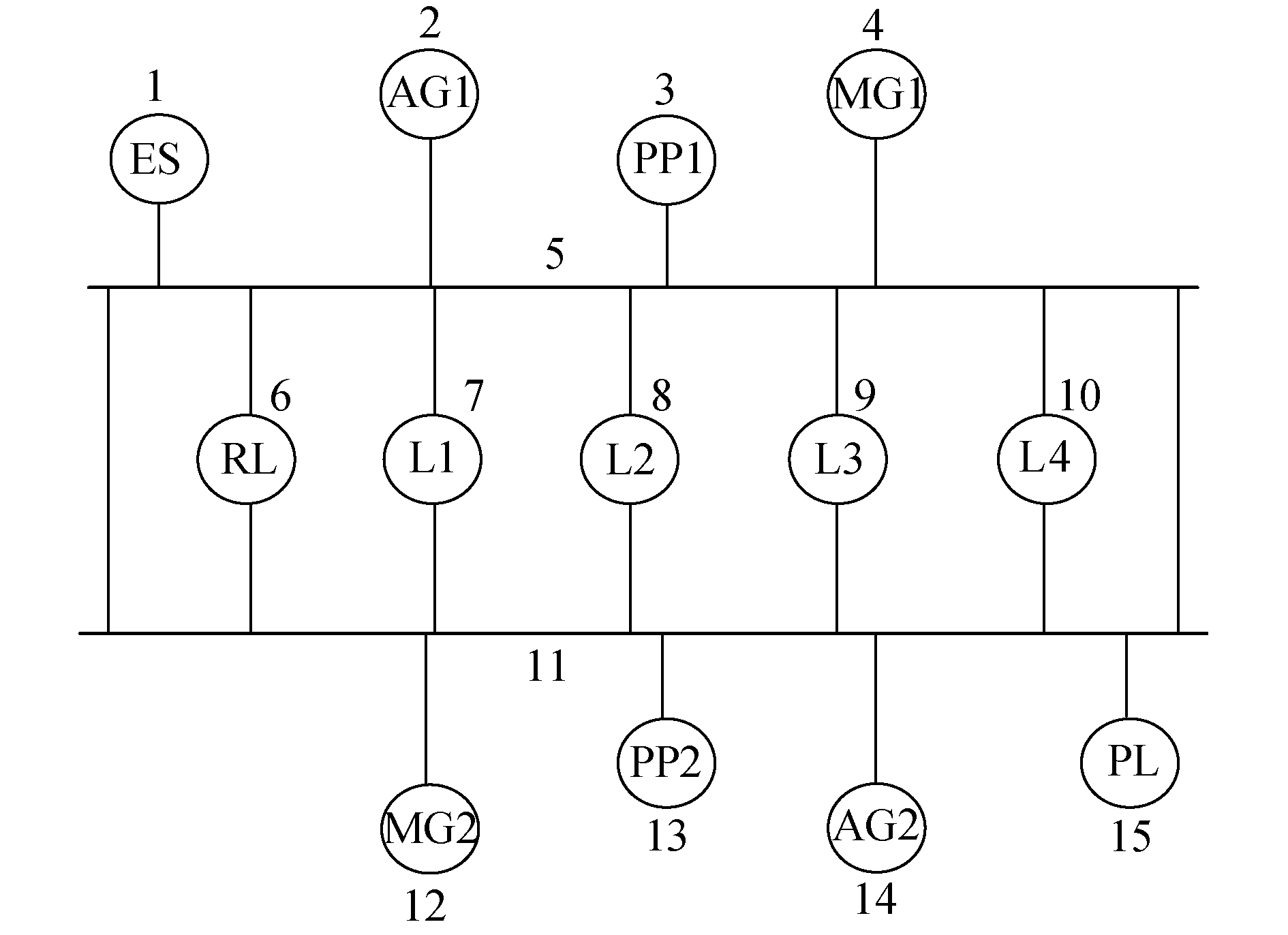
根据系统结构图,建立系统风险拓扑模型,模型包括系统风险拓扑图和风险评估节点、支路、发电矩阵,系统简略风险拓扑图如图 5所示。
|
Download:
|
| 图 5 船舶综合电力推进系统简略风险拓扑图 Fig. 5 The brief network topology figure of ship integrated electric propulsion system | |
风险评估节点、支路、发电矩阵,包括传统矩阵参数和风险参数,以风险评估节点矩阵为例,其包含的风险数据大部分来源于美国2013年的技术报告[17],其中不可用率和平均失效频率计算方法见参考文献[13]。风险评估拓扑模型将为船舶综合电力推进系统风险预测评估提供数据基础。
3.2 风险预测建模在本文中,观测量为船舶运行时的海况等级,观测序列N包括:O1(海况等级1~2级)、O2(海况等级3~4级)、O3(海况等级5~6级)、O4(海况等级7~9级),在t时刻的观测值可以被定义为Ot,其中,Ot∈(O1, O2, O3, O4)海况状态转移概率来源于中国某海域3 a的海况数据分析。
根据之前HMM的描述,在海情影响下,船舶综合电力推进系统风险评估中的HMM可以由一组状态转移概率和可观测特征分布概率来表达, 如图 6所示。

|
Download:
|
| 图 6 船舶综合电力推进系统单元HMM状态转换示意 Fig. 6 The state transition diagram of ship integrated electric propulsion system unit HMM | |
在图 6中,S1、S2、S3分别表示船舶综合电力推进系统风险评估的3个序列状态,每个状态则由一组可观测特征分布概率来表达。在船舶综合电力推进系统风险评估中,可观测特征为海况等级。图中箭头表示状态之间的转换关系, 箭头边的标号代表 2种状态之间的转移概率。例如,a12代表的状态1过渡到状态2的概率,概率值可以使用数值统计等方法通过可观察序列获得。
使用前述方法对采集到的各单元和子系统的工作状态数据进行分析,得到各子系统的状态转移概率和观测特征分布概率,这里以主推进电机MG1为例。
根据系统参数,主推进电机MG1的状态转移概率矩阵AMG1为:
| $ {\mathit{\boldsymbol{A}}_{MG1}} = \left[ {\begin{array}{*{20}{l}} {0.85}&{0.05}&{0.10}\\ {0.05}&{0.08}&{0.87}\\ {0.85}&{0.05}&{0.10} \end{array}} \right] $ | (31) |
MG1的可观测特征分布概率矩阵BMG1为:
| $ \boldsymbol{B}_{M G 1}=\left[ \begin{array}{cccc}{0.45} & {0.35} & {0.15} & {0.05} \\ {0.10} & {0.15} & {0.30} & {0.45} \\ {0.08} & {0.17} & {0.34} & {0.41}\end{array}\right] $ | (32) |
其中,状态转移的单位时间间距为1 h。
3.3 风险预测评估仿真根据船舶综合电力推进系统相关参数,采用风险预测评估方法,分别在满负载全速航行状态和半负载巡航状态下对船舶综合电力推进系统进行风险预测评估。设定预测时间为100 h,每个时间节点进行100次风险评估,每次风险评估中的蒙特卡洛模拟次数k为10 000。评估结果如图 7所示。

|
Download:
|
| 图 7 2种工况下PRO、EDNS与EENS曲线对比 Fig. 7 The PRO, EDNS and EENS curve contrast figure under two states | |
如图 7所示,综合电力推进船舶在满负载全速航行状态下,100 h内系统的风险发生概率PRO基本在2.59%~4.76%随海况状态变化波动,在半负载巡航状态下,100 h内系统的风险发生概率PRO基本在1.34%~2.56%随海况状态变化波动,符合船舶综合电力推进系统风险水平受海况影响的客观事实。
在满负载全速航行状态下,100 h内系统的期望缺供电力EDNS基本在0.81~1.53 MW范围随海况状态变化波动。在半负载巡航状态下,100 h内系统的期望缺供电力EDNS基本在0.39~0.73 MW范围随海况状态变化波动。
满负载全速航行状态下的期望缺供电量EENS要高于半负载巡航状态,根据之前计算的全系统数据,平均值约相差52.738 MW,而且从图上可以看出,全速航行状态下的期望缺供电力上下波动幅度较大。
这一结论与船舶综合电力推进系统在海上航行的实际情况相符合,本文的风险预测评估方法得到了验证。
4 结论1) 本文提出的基于MHMM-Viterbi算法的工作状态预测分析方法,将HMM算法、Viterbi算法与统计学理论相结合,可以对系统各单元和子系统在未来连续时间点所处的工作状态概率进行预测分析。
2) 本文提出的综合电力推进系统风险预测评估方法,能够对综合电力推进系统在未来一段时间内的风险进行预测和评估。该风险预测评估方法也适用于很多其他领域的系统,如果加入一些新的高速率智能算法,便可以实现对系统的实时风险预测评估。
| [1] |
DOERRY N, AMY J, KROLICK C. . History and the status of electric ship propulsion, integrated power systems, and future trends in the U.S. Navy[J]. Proceedings of the IEEE, 2015, 103(12): 2243-2251. DOI:10.1109/JPROC.2015.2494159 (  0) 0)
|
| [2] |
XIE Chuling, ZHANG Conghui. Research on the ship electric propulsion system network power quality with flywheel energy storage[C]//Proceedings of 2010 Asia-Pacific Power and Energy Engineering Conference. Chengdu, China, 2010: 1-3.
(  0) 0)
|
| [3] |
ZHOU Weiping, SUN Dongliang, WANG Jialin. Fault Diagnosis of ship power supply system based on grey correlation improved BP neural network[C]//Proceedings of 2015 Chinese Automation Congress. Wuhan, China, 2015: 1203-1208.
(  0) 0)
|
| [4] |
YANG Guang, WU Xiaoping, ZHANG Qi, et al. Fault diagnosis of ship main power system based on multi-layer fuzzy neural network[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation. Dalian, China, 2006: 5713-5717.
(  0) 0)
|
| [5] |
MEER J V, BENDRE A, KRSTIC S, et al. Improved ship power system-generation, distribution, and fault control for electric propulsion and ship service[C]//Proceedings of 2005 IEEE Electric Ship Technologies Symposium. Philadelphia, PA, USA, 2005: 284-291.
(  0) 0)
|
| [6] |
ANDRUS M, RAVINDRA H, HAUER J, et al. PHIL implementation of a MVDC fault management test bed for ship power systems based on megawatt-scale modular multilevel converters[C]//Proceedings of 2015 IEEE Electric Ship Technologies Symposium. Alexandria, VA, USA, 2015: 337-342.
(  0) 0)
|
| [7] |
MAQSOOD A, CORZINE K. The Z-source breaker for fault protection in ship power systems[C]//Proceedings of 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion. Ischia, Italy, 2014: 307-312.
(  0) 0)
|
| [8] |
WEI Gu, CHU Jianxin. Fault information model and maintenance cycle forecasting for ship's power system[C]//Proceedings of 2002 Annual Reliability and Maintainability Symposium. Seattle, WA, USA, 2002: 445-449.
(  0) 0)
|
| [9] |
DEO P R, SHAH T P, CHONG R. Ambient-temperature fault current limiter for electric ship power systems[C]//Proceedings of 2011 IEEE Electric Ship Technologies Symposium. Alexandria, VA, USA, 2011: 223-227.
(  0) 0)
|
| [10] |
SU C L, SU C Y, LEE C C, et al. Fault current limiter allocation in electric ship power systems[C]//2009 IEEE Electric Ship Technologies Symposium. Baltimore, MD, USA, 2009: 53-58.
(  0) 0)
|
| [11] |
ZHANG Yucheng, ALI H M, DOUGAL R A. Soft reclosing of fault current limiters in electric ship power systems[C]//Proceedings of 2011 IEEE Electric Ship Technologies Symposium. Alexandria, VA, USA, 2011: 244-247.
(  0) 0)
|
| [12] |
BILLINTON R. Composite system reliability evaluation[J]. IEEE transactions on power apparatus and systems, 1969. (  0) 0)
|
| [13] |
LI Wenyuan. Risk assessment of power systems:models, methods, and applications[M]. Hoboken, New Jersey: Wiley, 2014.
(  0) 0)
|
| [14] |
LI Wenyuan, LU Jiping. Risk evaluation of combinative transmission network and substation configurations and its application in substation planning[J]. IEEE transactions on power systems, 2005, 20(2): 1144-1150. DOI:10.1109/TPWRS.2005.846112 (  0) 0)
|
| [15] |
XING Bowen, LIU Sheng, CHEN Xiao, et al. Design of sensor data flow for ship information system[J]. Journal of ship production and design, 2017, 33(4): 310-316. DOI:10.5957/JSPD.150022 (  0) 0)
|
| [16] |
LIU Sheng, ZHI Pengfei, LI Bing, et al. A method of the simulation credibility analysis of ship electric propulsion system[C]//Proceedings of 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific. Beijing, China, 2014.
(  0) 0)
|
| [17] |
Improving the reliability of MVDC ship power system[R]. 2013.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


