目前,大部分有关车辆路径问题(vehicle routing problem, VRP)的研究是针对每个客户点的需求只能由一辆车服务,即需求不可拆分的问题类型。而实际中,允许对客户需求进行拆分运输的情况并不少见。且已有理论研究及事实证明,需求可拆分的运输方式有利于充分利用车辆装载能力和降低车辆行驶成本。这类问题被称为需求可拆分的车辆路径问题(split delivery vehicle routing problem, SDVRP)[1-2]。
目前有关SDVRP的研究文献中,大多数都是假设客户点的需求可按计量单位(件或个)连续拆分,即需求可连续拆分的问题类型。这种假设有其实际应用背景,但也有其局限性。在实际的货物运输和配送工作中,一般是以订单(批次)为单位组织的,而单位订单(批次)不可再被拆分。同时,各订单(批次)为相互独立的个体,所包含的需求量也不一定相同,即需求为离散的。例如,若某商品在销售及配送过程中要求以箱(订单)为最小单位进行,而单一订单(箱)中共包含商品12件(计量单位)。此时,客户需求只允许被拆分为以12为倍数的计件单位组合进行运输,即需求只允许以12个计量单位(件)为最小离散间隔进行拆分。需求进行离散拆分的另一种应用情况是不同货物需要的运输工具及装卸设备有所不同,将类型特性相同的货物作为同一订单进行分类运输,可提高物流作业效率。
目前,对于以离散方式进行拆分的SDVRP的研究仍然较少。Nakao等[3]首次提出需求可离散拆分的概念,定义这种新型的SDVRP为需求可离散拆分车辆路径问题(discrete split delivery vehicle routing problem, DSDVRP)。Salani等[4]提出了带时间窗的DSDVRP。Gulczynski等[5]则针对每一辆车给每一客户的送货量必须达到一个最小量要求的情形进行研究,将其称为带最小配送量的SDVRP(SDVRP-MDA)。Xiong等[6]在文献[5]的基础上进一步研究了SDVRP-MDA的解的下界。Han等[7]同样提出一种具有最小配送量限制的SDVRP,要求最小拆分量必须不大于被拆分客户总需求的50%。Wang等[8]以收益最大化(非总运输成本最小)的角度对SDVRP-MDA进行研究。向婷等[9]在研究SDVRP时考虑车辆载重的均衡性和可行解的特征,结合客户间的距离和载重,设定一个拆分阀值限定车辆载重范围,可视为一种特殊的最小拆分量限制。Archetti等[10]考虑实际操作中,不同种类货物所需的装卸工具及操作不同,设定相同种类货物不可拆分运输。符卓等[11]提出需求依订单拆分的车辆路径问题,即将各客户的离散需求看成相互独立的订单,并考虑软时间窗约束。Chen等[12]提出对客户需求进行预先特定拆分规则的拆分策略。
对于需求可拆分VRP的求解,无论是需求可连续拆分还是可离散拆分,若将各客户可拆分的需求视为相互独立的节点,且同客户节点间距离视为0,则可将问题转化为一般的VRP,用已有的算法求解。但正如上述相关文献中所指出,这样处理无疑将使属于NP-难的VRP的问题规模变得巨大而更难于求解。因此,一般都是根据问题的特点,设计有针对性的算法直接对原问题求解。
本文将在已有相关研究工作的基础上,给出DSDVRP描述及其数学模型;对比SDVRP分析总结DSDVRP特性,并针对其特性设计一种求解DSDVRP的禁忌搜索算法;采用不同规模的算例对算法进行测试,并对结果进行对比分析。
1 问题特点及数学模型 1.1 问题描述及数学模型DSDVRP可描述为:在满足车辆装载能力限制下,确定一组车辆行驶路线,使其从车场出发,依次访问各客户点(已知需求及位置),每个客户点的需求必须被满足且可由多辆车服务,最后返回车场,使运输总成本最小(如所使用的车辆数最少,车辆总行驶路程最短)。其中,若客户点的需求由多辆车共同完成,其需求拆分方式不得违背设定的离散拆分策略。
假设在完备图G=(V, E)中,V={0}∪N表示顶点集(0表示车场,N={1, 2,…, n}表示客户点集),E={(i, j) i, j∈V, i≠j}表示弧集。各弧(i, j)∈E对应一非负的权cij,表示车辆从顶点i到顶点j的行驶费用。车辆装载能力为Q,使用车辆数为K。Mi为客户点i的批订(订单)数,dim表示客户点i第m个订单(批次)的需求量,则
xijk:若车辆k从顶点i行驶到顶点j,其值为1;否则值为0。
yimk:若客户点i的第m批次(订单)由车辆k运送,其值为1;否则值为0。
于是,DSDVRP可用如下的数学模型来描述:
| $ \min Z = {P_1}K + {P_2}\sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {\sum\limits_{k = 1}^K {{c_{ij}}x_{ij}^k} } } $ | (1) |
| $ \begin{array}{l} {\rm{s}}.{\rm{t}}.\\ \;\;\;\;\;\;\;\sum\limits_{i = 0}^n {\sum\limits_{k = 1}^K {x_{ij}^k} } \ge 1, j = 1, 2, \cdots , \mathit{n} \end{array} $ | (2) |
| $ \sum\limits_{i = 1}^n {x_{i0}^k} = 1, k = 1, 2, \cdots , \mathit{K} $ | (3) |
| $ \sum\limits_{j = 1}^n {x_{0j}^k} = 1, k = 1, 2, \cdots , \mathit{K} $ | (4) |
| $ \sum\limits_{i = 0}^n {x_{ip}^k} = \sum\limits_{j = 0}^n {x_{pj}^k} , p = 1, 2, \cdots , \mathit{n}, k = 1, 2, \cdots , \mathit{K} $ | (5) |
| $ \sum\limits_{k = 1}^K {\sum\limits_{m = 1}^{{M_i}} {d_i^my_{im}^k} = {d_i}, i = } 1, 2, \cdots , \mathit{n} $ | (6) |
| $ \sum\limits_{i = 1}^n {\sum\limits_{m = 1}^{{M_i}} {d_i^my_{im}^k} } \le Q, k = 1, 2, \cdots , \mathit{K} $ | (7) |
| $ x_{ij}^k \in \left\{ {0, 1} \right\}, i, j = 0, 1, \cdots , n;k = 1, 2, \cdots , \mathit{K} $ | (8) |
| $ \begin{array}{l} y_{im}^k \in \left\{ {0, 1} \right\}, i = 1, 2, \cdots , n;m = 1, 2, \cdots , {\mathit{M}_i};\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1, 2, \cdots , \mathit{K} \end{array} $ | (9) |
式(1)表示最小化总运输成本的目标函数。总运输成本可从使用的车辆数(路径数)及总行驶费用两方面评价。通常认为,多用一辆车所产生的固定费用总是超过总行驶费用减少带来的节约,所以本文把最小化车辆使用数量作为第1层优化目标,最小化车辆行驶费用作为第2层优化目标,其中P1,P2(P1≫P2)与目标规划中的定义一样,为优先因子,是定性的概念,不赋予具体数值,只表示各目标的优先级。若固定费用和行驶费用都能准确度量,则也可以用统一的费用量纲表示,转化为单目标优化函数,直接进行求和比较优劣,如式(10)所示:
| $ {\rm{min}}\mathit{Z = }{\mathit{w}_1}K + {w_2}\sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {\sum\limits_{k = 1}^K {{c_{ij}}x_{ij}^k} } } $ | (10) |
式中:w1和w2分别表示单位车辆使用费和单位行驶距离行驶费用。例如Mitra[13]给出假设,拥有(租赁)一辆车及单位行驶路程的费用分别为100美元及0.1美元,此时可假设w1=100,w2=0.1。约束条件(2)确保每个客户点都有车辆进行服务,式(3)~(5)为汉密尔顿回路约束条件,式(6)表示每个客户点的需求必须得到满足,式(7)为车辆的装载能力约束。
1.2 问题特性根据已有研究可知,SDVRP最优解具有如下特性:1)SDVRP最优解中任意两条路径间最多只存在一个公共点[1-2];2)SDVRP最优解中需求拆分点个数少于路径数[14]。
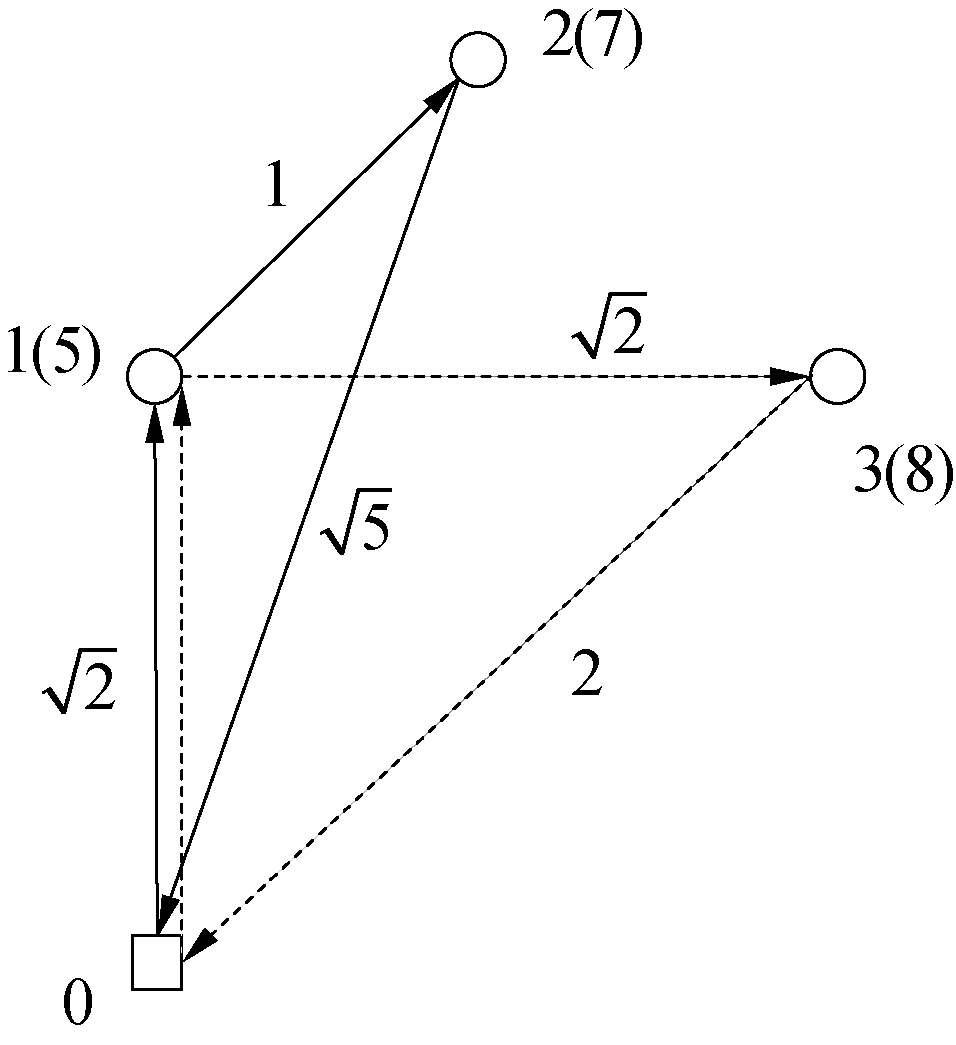
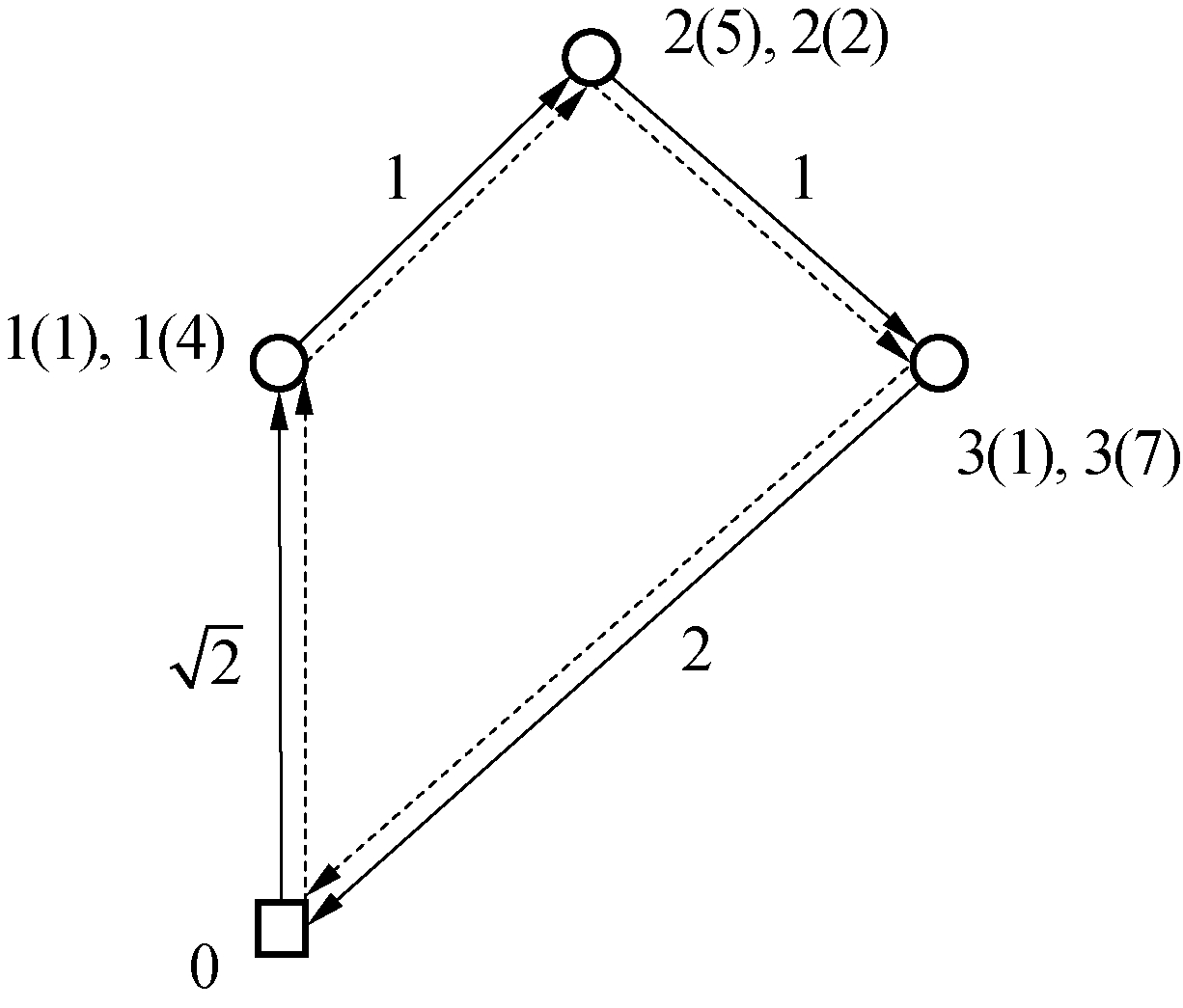
这是因为SDVRP中各客户需求可被连续拆分,可根据车辆剩余装载情况机动地对客户需求以任意方式(需求大小)进行拆分。如图 1所示,共有3个客户点(括号内数字为需求量),各弧旁数字为相邻点间距离。假设车辆装载能力为10,则所需最小车辆数为2。在相应的DSDVRP中,如图 2所示,各客户点的总需求量和车辆装载能力与图 1中的例子相同,但各客户需求均由2批(订单)组成(括号内为订单需求量)。采用动态规划算法可分别求得SDVRP及DSDVRP在使用最小车辆数且不超载的条件下的最优路径方案。
|
Download:
|
| 图 1 SDVRP最优路径方案 Fig. 1 Optimal solution to the SDVRP | |
|
Download:
|
| 图 2 DSDVRP最优路径方案 Fig. 2 Optimal solution to the DSDVRP | |
DSDVRP的上述路径方案中,各路径中各包含有3个拆分点,2条路径中公共点个数为3,大于路径数2,总路径长度为10.83,长于SDVRP总路径长度(9.48)。
路径1 0-1(3)-2(7)-0
路径2 0-1(2)-3(8)-0
路径1 0-1(1)-2(2)-3(7)-0
路径2 0-1(4)-2(5)-3(1)-0
对比SDVRP,DSDVRP及其最优解具有以下特性(cij、di和Q及其相关限制条件均相同的情况下):
1) 若R和R′分别为SDVRP和DSDVRP最优解中任意2条路径间存在的公共点数,存在R≤R′,即DSDVRP最优解中任意两条路径间可能存在多个公共点;
2) 若L和L′分别为SDVRP和DSDVRP最优解中需求拆分点个数,存在L≤L′,即DSDVRP最优解中拆分点个数可能多于路径数;
3) 若Z和Z′分别为SDVRP和DSDVRP的最优解对应的目标函数值,存在Z≤Z′,即DSDVRP最优解可能劣于SDVRP最优解;
4) 已知SDVRP为NP-难问题[1, 14],SDVRP是DSDVRP的特殊形式,所以DSDVRP同为NP-Hard问题。
2 禁忌搜索算法设计 2.1 解的表达方式本文在算法设计及求解过程的描述中,将各客户的离散需求看成相互独立的订单(批次),并视为相互独立的节点,同客户订单节点间距离视为0。例如,客户i的需求经拆分后生成Mi个订单,则本文将客户i的第m个订单需求描述为i(m)。因此,问题的解可表示为车场0及客户订单(批次)i(m),(i=1, 2, …, n; m=1, 2, …, Mi)的一个排列。如:
0-4(1)-4(3)-6(2)-0
表示某车辆从车场0出发,首先到达客户点4,服务其第1、3个订单(批次)货物,接着访问客户点6并服务其第2个订单(批次)货物后返回车场0。由此可知,问题解的表达中,2个“0”之间的客户点及其订单(批次)组成一条闭合路径。
2.2 初始解本文采用随机方式生成初始解。先对所有客户订单(批次)随机排序,构造一条包括车场及所有订单(批次)节点的大路径。在此基础上,对该路径顺序切割,即将路径中的某个连接断开,将该连接的2点直接与车场相连。切割依据(断点位置的确定)以路径中顺序装载的订单需求为基础,若车辆超载,则将造成超载的节点移出,并以此为新路径起点,继续构造新路径。以此类推,直至所有节点均被分配至指定路径为止。
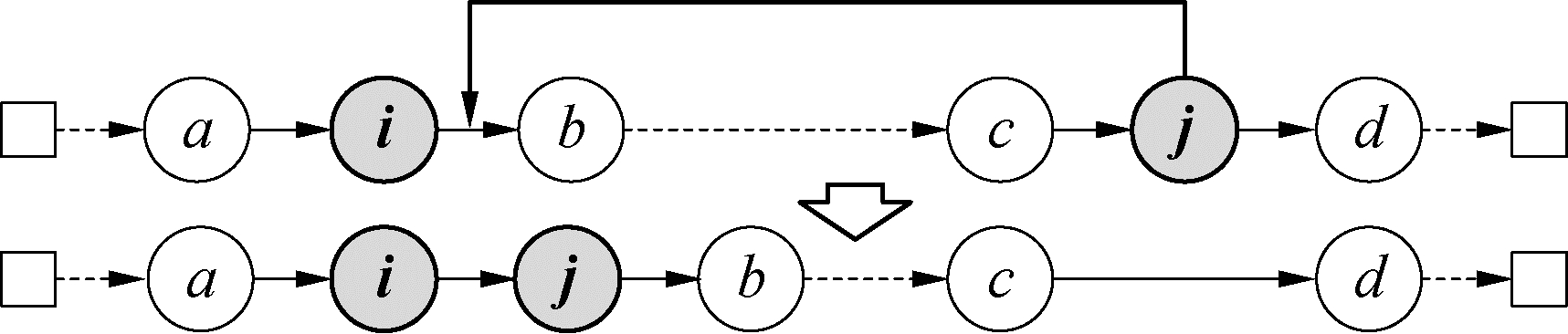
2.3 同客户节点合并操作由于路径构造时将所有离散的客户订单视为独立节点,故生成的路径中存在同客户订单被分散访问的情况。如图 3所示,节点i、j分别表示同客户的不同订单,路径中该客户点被先后访问了2次,增大了不必要的路径成本。为此本文设计同客户订单合并操作,对路径内相同客户的订单进行合并,避免不必要的路径成本,该操作为离散需求拆分的基本路径优化操作,为订单组合的操作奠定基础。
|
Download:
|
| 图 3 同客户节点合并操作 Fig. 3 Combination of items from the same customers | |
一般邻域操作中使用的操作对象为单一的客户节点,因DSDVRP中的实际个体为各客户订单节点,若简单将客户节点(该客户的全部订单)作为操作对象,则无法体现需求可拆分特性。但若将订单节点作为操作对象,因订单数量远大于客户数,将耗费大量的计算时间。故本文提出一种折中方式,设计同客户节点随机绑定操作,用于邻域操作中实际操作对象的生成及选择。具体操作方式为:在当前解中随机挑选可行的操作对象(节点),向前向后判断是否存在同客户节点。随后在同客户节点间随机选择若干个连续订单进行绑定,作为接下来邻域操作的实际操作对象。
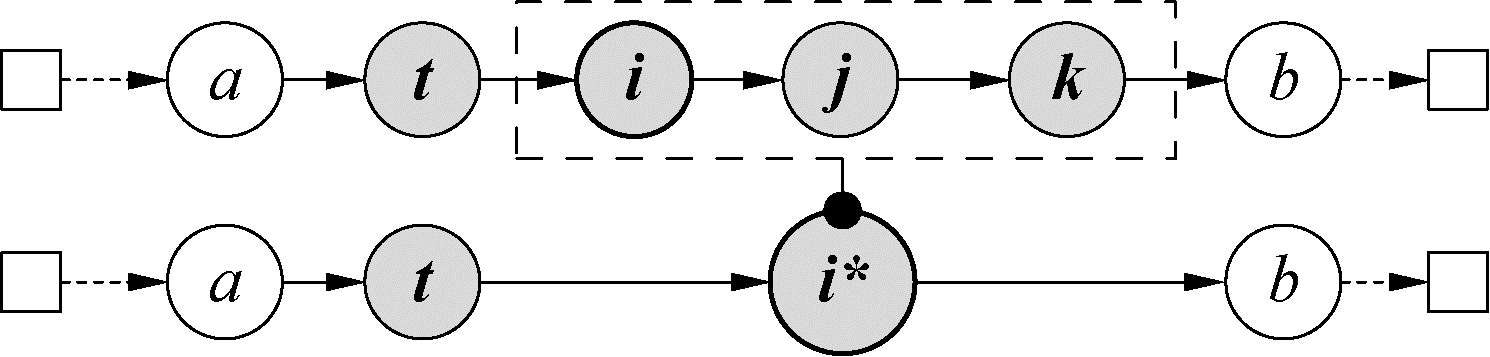
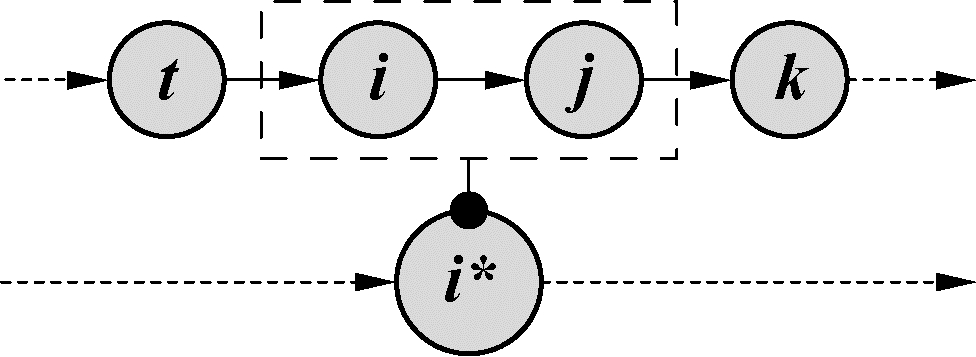
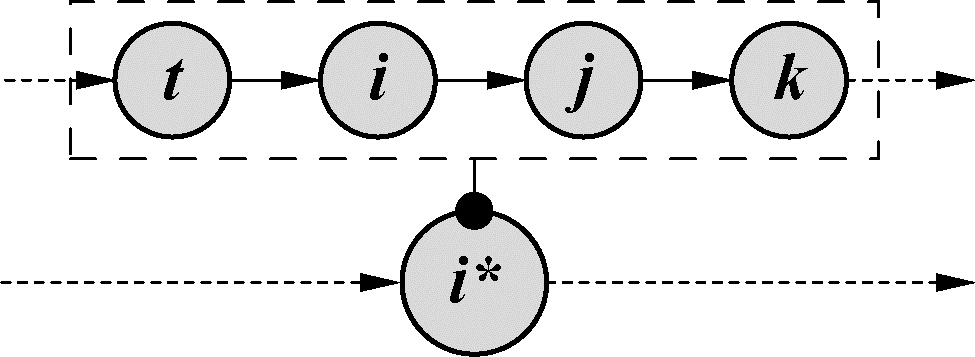
如图 4所示,挑选出的操作节点为i,经判断路径中t、i、j、k属于同一客户,t和k分别为起始同客户节点。i、j、k为随机挑选出的连续同客户订单节点,则在下一步邻域操作中将i、j、k绑定视为一个绑定节点i*进行操作。由此可知,经该操作确定的操作对象可能是单一订单节点,如图 5;可能是部分订单,如图 4和6;也可能是客户点(该客户的全部订单),如图 7,由此增大了操作对象的随机多样性。在下文若未特别说明,图中节点统一视为经绑定后的绑定节点。
|
Download:
|
| 图 4 同客户节点随机绑定操作 Fig. 4 Randomly binding of items from the same customers | |

|
Download:
|
| 图 5 单一订单节点 Fig. 5 A single item | |
|
Download:
|
| 图 6 部分订单 Fig. 6 Fractional items | |
|
Download:
|
| 图 7 全部订单 Fig. 7 All items | |
为增强算法的搜索能力,本文提出6种邻域操作构成混合邻域结构。其中包括2种线路内操作,3种线路间操作及1种路径消除操作。各邻域操作概述见表 1,下文中若未特别说明,所提到的路径,均为非空(访问节点数非零)路径。
| 表 1 邻域操作 Table 1 Neighborhood structure |
本文设计的禁忌搜索算法,在邻域搜索阶段随机选择线路内及线路间5种邻域操作中的一种,生成的解中使用的车辆数大于最小车辆数时,才调用路径消除操作,即合并2条路径。而正是路径消除操作的设计,使得问题在求解过程中向着路径数不断减少,最终达到使用车辆数最少的方向进行。通过多次参数设置及计算比较,兼顾求解质量及运算时间(后文参数取值同样基于此考虑),本算法设定候选解的个数为100+2n。
2.6 解的评价解的评价从解的目标函数值和解是否可行2方面进行。若某解中存在车辆的实际装载量超过车辆装载能力,则该解被视为不可行。本文借鉴Gendreu[15]设计的自适应惩罚机制,将算法设计为在邻域搜索过程中有条件地交替接受可行解和不可行解,以便对邻域空间充分搜索,避免过早地陷入局部最优,并试探通过不可行解的过渡,能否找到更好的可行解。因此,本文将解的评价设定为E=Z+p·Q*,其中,Q*为解中所有路径的总超载量。若解是可行的,则Q*=0。p∈[0.000 001, 200 000]为对单位超载量的惩罚系数,是一个自调整参数。开始时p=1。在其后的迭代过程中,若连续10次迭代中的所有解均为可行解,则将其值除以2;若连续10次迭代得到的解均为不可行解,则将其值乘以2。
2.7 禁忌规则本文针对线路内及线路间共5个邻域操作分别建立5个相互独立的n×n的二维矩阵禁忌表,其中n为客户点数。本算法采用动态禁忌长度,即随机选取长度在[5, 10]的禁忌期。每迭代一次,将当次邻域操作及其操作对象记录在其对应的禁忌表中,同时将禁忌表中其他被禁忌对象的禁忌期减去1,直至为0止。若某个禁忌解比到目前为止搜索到的“最好解”更优,则将该解解禁并接受为新的当前解和“最好解”;若所有候选解都被禁忌,则解禁最佳候选解,并接受为新的当前解。
2.8 终止条件当算法求得的“最好解”保持不变的连续迭代次数等于预先设定的最大迭代次数(4 000+10n)时,算法终止。
2.9 算法框架算法的基本框架描述如下:
初始化
读入相关数据及参数值;
随机生成初始解,
把该初始解设为当前解和“最好解”;
建立5种邻域操作的禁忌表;
While“最好解”保持不变的连续迭代次数未达到预先设定的最大迭代次数do
While没有达到候选解的预设数量do
在5种邻域操作中随机挑选一种,并随机选出对应邻域操作的操作对象
调用同客户节点绑定操作随机选择生成邻域操作的实际操作节点;
对当前解进行邻域变换操作;
若当前邻域操作为路径间操作,且当前解车辆数大于最小车辆数,执行路径消除操作;
调用同客户节点合并操作,生成新邻域解;
End;
更新当前解;
若某个候选解比当前取到的“最好解”更优,则更新最好解;
更新禁忌表;
若满足路径消除操作条件,对当前解进行规定操作,产生新的当前解;
End.
3 算例测试 3.1 离散拆分策略针对SDVRP,Chen等[12]提出了2种拆分策略,20/10/5/1和25/10/5/1。如20/10/5/1拆分策略中,规定所有客户需求只能被拆分为5类需求量不等的离散组合,且各组合按需求量大小具有降序等级,其中前4种(20/10/5/1)离散情况分别将各客户需求拆分为若干需求大小固定的订单,依次为车辆装载能力的20%、10%、5%及1%。最后一种离散情况只可能且最多只可以存在一个订单,该订单需求只可能小于车辆装载能力的1%。25/10/5/1的拆分原理类似。为简述方便,本文重新定义该离散拆分策略为20/10/5/1/x和25/10/5/1/x。某客户i的需求di用离散拆分策略分别生成5种离散需求种类Ws(20/10/5/1/x),s为20、10、5、1、x,其中生成的Ws的订单数量为Hs,其需求量为Ts。20/10/5/1/x离散规则见表 2所示。
| 表 2 20/10/5/1/x离散拆分规则 Table 2 Neighborhood structure |
本文所提出的求解DSDVRP的禁忌搜索算法采用Delphi 7.0编程,并在CPU为Core (TM) i7-4500U双核处理器(2.40 GHz),内存12.0 GB的微机上实现。为方便对比分析,本文采用Chen等[12]需求离散拆分策略分别对2组实验算例进行需求拆分,并测试求解。
3.2.1 实验1文献[16]的算例常被国内学者采用并进行SDVRP算法测试及对比。最新采用该算例测试的为姜婷[17],目前该算例得到的最佳计算结果来自向婷等[9]。文献[17]及文献[9]的研究均针对传统SDVRP,不同的是文献[9]中考虑了拆分阀值。本文分别采用20/10/5/1/x和25/10/5/1/x的拆分策略对文献[16]算例进行求解,结果见表 3所示。
| 表 3 实验1计算结果 Table 3 Solution to experiment 1 |
表 3中,计算得出总行驶路程分别为1 131.36和1 127.95,分别优于文献[17]的计算结果34.82%(20/10/5/1/x)和35.01%(25/10/5/1/x),同时比目前最好结果(文献[9])1721.70缩短了34.29%(20/10/5/1/x)和34.49%(25/10/5/1/x)。如第2节DSDVRP特性所述,DSDVRP最优解一般要大于或等于SDVRP的最优解,而本算法所求出结果甚至还优于文献[17]和[9],说明本文设计的禁忌搜索算法具有较优的性能。从表中可见,20/10/5/1/x拆分策略下客户点2、7、11分别被拆分2次(表中粗体标注,括号内为实际配送需求量),即被两辆车共同访问,客户点12被拆分3次。而25/10/5/1/x拆分策略下客户点4、5、7、12及13各被访问2次。
为检验本算法稳定性,对实验1的2组拆分算例进行10次运算测试,测试结果如表 4所示。
| 表 4 实验1运算结果 Table 4 Computational results of experiment 1 |
本文引用Yin等[18]提出的波动系数公式进行本算法运算稳定性评价:
| $ F = \frac{{{M_1} - {M_2}}}{A} \times 100\% $ | (11) |
式中:F为波动系数;M1为最大值;M2为最小值;A为平均值。
通过式(11)可得20/10/5/1/x及25/10/5/1/x策略下运算结果波动系数分别为2.15%及2.04%,证明本文算法稳定性良好。运算结果波动情况见图 5所示。

|
Download:
|
| 图 5 实验1运算结果波动情况 Fig. 5 Fluctuation of computational results of experiment 1 | |
Chen等[12]采用20/10/5/1/x和25/10/5/1/x拆分策略对文中算例生成订单。文中主要考虑实现车辆总行驶路程长度最短,故问题描述及模型建立中并不考虑最小车辆数限制,即最终求解结果中实际使用车辆数存在大于最小车辆数的情况。本算法对所有算例均求得最小车辆数。如表 5所示,对比文献[12],48.00%的算例(12个)的车辆数减少(因使用车辆数减少,总行驶路程可能增加),其中16.67%(2个)路径更短。车辆数相等的13个算例中,53.85%(7个)的解相等或更优(路径总行驶长度相等或更短)。总的来看,实验2中68.00%的算例的已知最好解得到改进(较文献[12]车辆数减少或总行驶路程缩短),或求得相同的解,见表 8中粗体标注。
| 表 5 实验2计算结果对比 Table 5 Comparison of the solutions to experiment 2 |
| 表 8 实验2运算结果 Table 8 Computational results of experiment 2 |
以S51D2为例,在20/10/5/1/x拆分策略下,本算法求得解无论在车辆数(车辆数减少1)还是总路程长度(缩短2.78)均优于文献[12]。已知S51D2中客户总需求量为1 415.00,车辆装载能力为160.00,本算法求得解中平均车辆装载量为157.22,车辆平均装载率为98.26%,比文献[12]中的88.44%提高了11.10%,如表 6所示。S51D2具体路径方案见表 7,其中客户点32、38、49分别被拆分2次(表中粗体标注,括号内为实际配送需求量)。
| 表 6 算例S51D2优化情况 Table 6 Improvement of instance S51D2 |
| 表 7 算例S51D2路径方案 Table 7 Solution to instance S51D2 |
本文所设计禁忌搜索算法的收敛情况,以S51D2为例,迭代过程中解的评价值变化情况如图 6所示。由图可知,算法收敛速度较快,收敛性较好。

|
Download:
|
| 图 6 S51D2解的评价值变化情况 Fig. 6 Development of objective function value of S51D2 | |
综上所述,本文所提出的禁忌搜索算法能够在可接受的计算时间内求解DSDVRP。已知DSDVRP最优解可能劣于SDVRP最优解的问题(详见2.2),本文算法仍能求得较相关文献更优的解,证明本文设计的禁忌搜索算法具有较优的性能。同时,通过波动系数的测试,进一步证明本文算法的稳定性。然而,因各客户点需求被拆分为若干独立订单,增加了数据规模(未拆分算例的3~5倍)。因此即使使用相同的原始算例进行测试,本文所需运算时间也要相应较长一些。
4 结论1) DSDVRP作为一种特殊的SDVRP,在问题性质及解的最优解特性上却存在明显差异。DSDVRP最优解中任意两条路径间可能存在多个公共点;DSDVRP最优解中拆分点个数可能多于路径数;DSDVRP最优解可能劣于SDVRP最优解。
2) DSDVRP中各客户需求以若干离散订单(批次)构成,针对此问题特性,本文提出特殊的禁忌搜索算法进行求解。通过不同数据规模的算例对所提出的算法进行测试,并将求解结果与相关文献中的结果进行比较。
3) 在DSDVRP最优解可能劣于SDVRP最优解的问题特性下,本文算法仍能求得更优解,证明本文设计的禁忌搜索算法具有较优的性能。为求解需求可离散拆分车辆路径问题提供了一种新的求解算法。
需求拆分不可避免地导致算例数据规模的成倍增长,大大增加了运算时间,在未来的研究中,应针对该问题改善算法性能。
| [1] |
DROR M, TRUDEAU P. Savings by split delivery routing[J]. Transportation science, 1989, 23(2): 141-145. DOI:10.1287/trsc.23.2.141 (  0) 0)
|
| [2] |
DROR M, TRUDEAU P. Split delivery routing[J]. Naval research logistics, 1990, 37(3): 383-402. DOI:10.1002/nav.v37.3 (  0) 0)
|
| [3] |
NAKAO Y, NAGAMOCHI H. A DP-based heuristic algorithm for the discrete split delivery vehicle routing problem[J]. Journal of advanced mechanical design, systems, and manufacturing, 2007, 1(2): 217-226. (  0) 0)
|
| [4] |
SALANI M, VACCA I. Branch and price for the vehicle routing problem with discrete split deliveries and time windows[J]. European journal of operational research, 2011, 213(3): 470-477. DOI:10.1016/j.ejor.2011.03.023 (  0) 0)
|
| [5] |
GULCZYNSKI D, GOLDEN B, WASIL E. The split delivery vehicle routing problem with minimum delivery amounts[J]. Transportation research part E:logistics and transportation review, 2010, 46(5): 612-626. DOI:10.1016/j.tre.2009.12.007 (  0) 0)
|
| [6] |
XIONG Yupei, GULCZYNSKI D, KLEITMAN D, et al. A worst-case analysis for the split delivery vehicle routing problem with minimum delivery amounts[J]. Optimization letters, 2013, 7(7): 1597-1609. DOI:10.1007/s11590-012-0554-9 (  0) 0)
|
| [7] |
HAN A F W, CHU Y C. A multi-start heuristic approach for the split-delivery vehicle routing problem with minimum delivery amounts[J]. Transportation research part E:logistics and transportation review, 2016, 88: 11-31. DOI:10.1016/j.tre.2016.01.014 (  0) 0)
|
| [8] |
WANG Xingyin, GOLDEN B, GULCZYNSKI D. A worst-case analysis for the split delivery capacitated team orienteering problem with minimum delivery amounts[J]. Optimization letters, 2014, 8(8): 2349-2356. DOI:10.1007/s11590-014-0752-8 (  0) 0)
|
| [9] |
向婷, 潘大志. 求解需求可拆分车辆路径问题的聚类算法[J]. 计算机应用, 2016, 36(11): 3141-3145. XIONG Ting, PAN Dazhi. Clustering algorithm for split delivery vehicle routing problem[J]. Journal of computer applications, 2016, 36(11): 3141-3145. DOI:10.11772/j.issn.1001-9081.2016.11.3141 (  0) 0)
|
| [10] |
ARCHETTI C, BIANCHESSI N, SPERANZA M G. A branch-price-and-cut algorithm for the commodity constrained split delivery vehicle routing problem[J]. Computers & operations research, 2015, 64: 1-10. (  0) 0)
|
| [11] |
符卓, 刘文, 邱萌. 带软时间窗的需求依订单拆分车辆路径问题及其禁忌搜索算法[J]. 中国管理科学, 2017, 25(5): 78-86. FU Zhuo, LIU Wen, QIU Meng. A tabu search algorithm for the vehicle routing problem with soft time windows and split deliveries by order[J]. Chinese journal of management science, 2017, 25(5): 78-86. (  0) 0)
|
| [12] |
CHEN Ping, GOLDEN B, WANG Xingyin, et al. A novel approach to solve the split delivery vehicle routing problem[J]. International transactions in operational research, 2017, 24(1/2): 27-41. (  0) 0)
|
| [13] |
MITRA S. A parallel clustering technique for the vehicle routing problem with split deliveries and pickups[J]. Journal of the operational research society, 2008, 59(11): 1532-1546. DOI:10.1057/palgrave.jors.2602500 (  0) 0)
|
| [14] |
ARCHETTI C, SAVELSBERGH M W P, SPERANZA M G. Worst-case analysis for split delivery vehicle routing problems[J]. Transportation science, 2006, 40(2): 226-234. DOI:10.1287/trsc.1050.0117 (  0) 0)
|
| [15] |
GENDREAU M, LAPORTE M G, POTVIN J Y. Metaheuristics for the Capacitated VRP[M]//TOTH P, VIGO D. The Vehicle Routing Problem. Philadelphia: SIAM monographs on discrete mathematics and applications, 2002: 129-154.
(  0) 0)
|
| [16] |
隋露斯, 唐加福.用蚁群算法求解需求可拆分车辆路径问题[C]//中国控制与决策会议.烟台, 2008: 997-1001. SUI Lusi, TANG Jiafu. Ant colony algorithm for split delivery vehicle routing problem[C]//China Control and Decision Conference. Yantai, 2008: 997-1001. (  0) 0)
|
| [17] |
姜婷. 求解需求可拆分车辆路径问题的人工蜂群算法[J]. 四川理工学院学报(自然科学版), 2017, 30(3): 6-9. JIANG Ting. Artificial bee colony algorithm for split delivery vehicle routing problem[J]. Journal of Sichuan University of Science & Engineering (natural science edition), 2017, 30(3): 6-9. (  0) 0)
|
| [18] |
YIN Chuanzhong, BU Lei, Gong Haitao. Mathematical model and algorithm of Split load vehicle routing problem with simultaneous delivery and pickup[J]. International journal of innovative computing, information and control, 2013, 9(11): 4497-4508. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


