2. 中海油研究总院有限责任公司, 北京 100028
2. CNOOC Research Institute Co., Ltd., Beijing 100028, China
Spar平台在波频范围内具有良好的运动性能以及深水立管技术适应性,是目前深海油气开发中的一种重要的平台形式[1]。Spar平台固有周期较大,在长周期涌浪作用下,平台的垂荡运动会失稳,发生非线性参激-内共振纵摇运动[2]。
Rho等[3]发现当Spar平台纵摇固有周期大约是垂荡固有周期两倍,且垂荡运动幅值达到一个临界值时,会引起大幅的不稳定纵摇运动。Hong等[4]通过实验研究了Spar平台在垂荡共振波浪下的极端运动,结果表明平台发生大幅的不稳定纵摇运动。Neves等[5]采用模型实验对一圆筒进行了研究,结果表明当纵摇固有周期为垂荡固有周期两倍,大幅的垂荡运动很容易引起模型不稳定的横摇或者纵摇运动。赵晶瑞等[6]利用模型实验研究了传统Spar平台的非线性内共振运动。刘丽琴等[7]通过模型实验研究了Truss Spar的非线性内共振响应特性,并与数值结果进行了对比,得到平台失稳的参数域。Yang等[8]针对Spar平台单自由度模型,对非规则波下Spar平台参数激励运动做了敏感性分析。刘树晓等[9]考虑了二阶波浪力的影响,研究了Spar平台在随机波中垂荡-纵摇非线性耦合运动。
之前大量的研究将Spar平台的非线性运动采用单自由度的Mathieu方程,或者垂荡-纵摇耦合的二自由度模型。实际上除了垂荡和纵摇,非线性耦合运动也会出现在横摇模态。在实验中,横摇模态甚至占据主导地位。有必要关注垂荡、横摇和纵摇三个模态的运动,研究其在发生非线性共振时的运动响应规律及能量在各个模态的渗透机理。
本文对一座垂荡-横摇-纵摇固有频率比接近2:1:1的Spar平台进行模型实验,研究其在规则波中的非线性耦合运动行为。通过实验得到了Spar平台在不同海况下的非线性运动特性,揭示了发生非线性运动时能量在三个模态的渗透规律,获得了平台发生不稳定运动的参数域。
1 试验环境及模型参数本模型试验在天津大学船舶与海洋工程系水池进行。水池长137 m、宽7 m、深3 m。水池拥有摇摆式造波机,可以制造波长为2~12 m的规则波。试验通过浪高仪测量和CDSP数据采集仪测量波浪参数,通过光学非接触式六自由度运动测量系统测量模型运动响应。本次模型试验在规则波中进行,不考虑风载荷和流载荷。
此次模型试验,根据Hong等[5]的Spar平台作为试验参考原型,选取模型缩尺比k为120:1,平台主体的各项技术参数如表 1所示。
| 表 1 Spar平台技术参数表 Table 1 Parameters of Spar platform |
Spar平台模型如图 1所示。平台主体由一圆筒型硬舱构成,下设两块垂荡板。

|
Download:
|
| 图 1 Spar平台模型 Fig. 1 Scaled model of Spar platform | |
试验开始前调整Spar模型重量和重心位置。之后将模型和测量系统布置在拖车上(图 2)。模型通过4根弹簧—钢丝绳水平系泊固定在拖车上。平台上设置3个点光源,与拖车上的测量设备配合记录Spar平台6个自由度的运动,拖车上设置录像设备记录实验流程。

|
Download:
|
| 图 2 Spar平台、信号测量设备及数据采集设备 Fig. 2 Layout of Spar platform, signal measuring equipment and data acquisition equipment | |
通过静水中测量Spar各个模态的自由衰减运动,记录平台各模态的时间历程曲线,通过数据分析可以得到Spar平台各个模态的固有周期和阻尼。
图 3为实验得到的Spar平台在静水中自由衰减时间历程曲线,通过频谱分析得到平台的固有周期。根据式(1)、(2)计算各个模态的线性阻尼系数:

|
Download:
|
| 图 3 自由衰减曲线 Fig. 3 Free decay curve | |
| $ \xi = \frac{1}{N}\ln \frac{{{y_i}}}{{{y_{i + N}}}} $ | (1) |
| $ \xi \approx \frac{\zeta }{{2\pi }} $ | (2) |
式中:yi为时间历程曲线上第i个周期的峰值;N为截取的周期数;ξ为对数衰减率;ζ为阻尼比。
表 2为实验得到的Spar平台各个模态的固有周期和阻尼比。
| 表 2 平台垂荡、横摇和纵摇固有周期和阻尼比 Table 2 Natural periods and damping ratio |
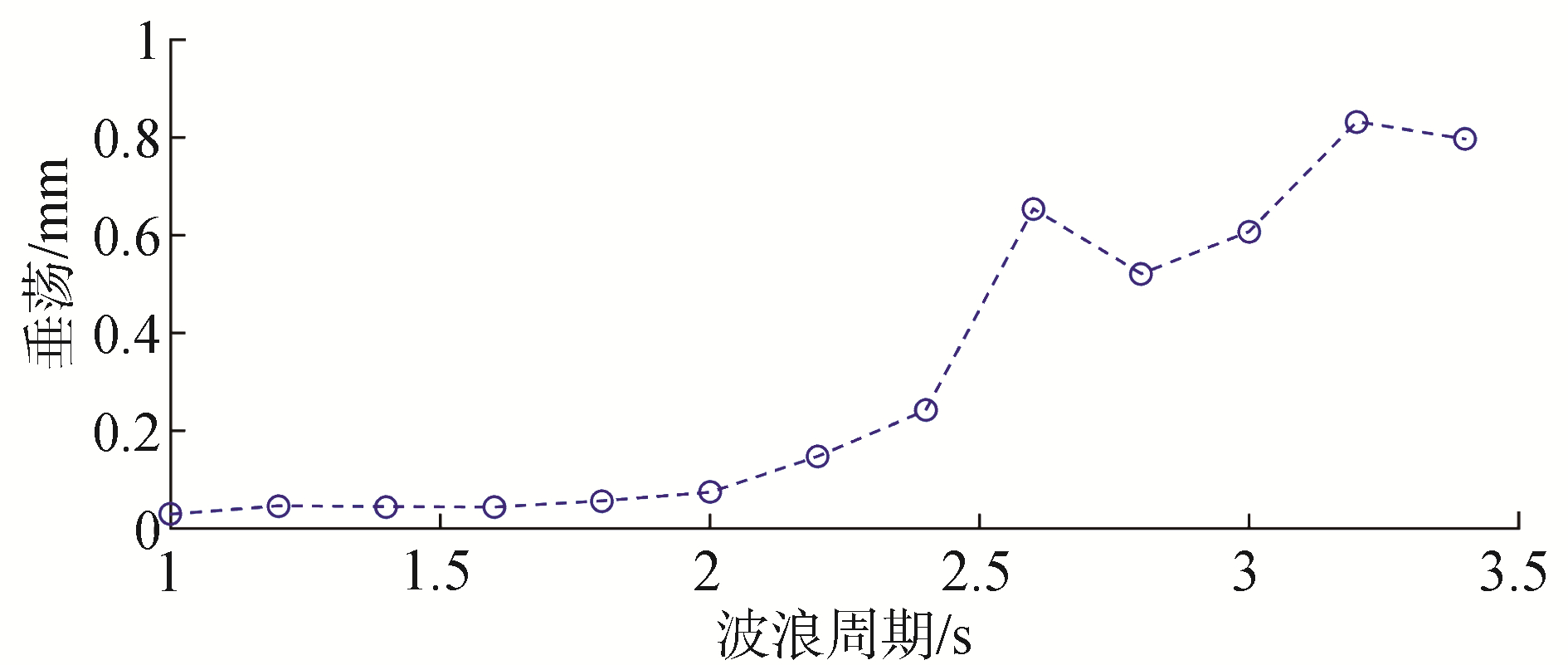
在相同波高(40 mm),不同波浪周期下测量Spar平台垂荡、横摇和纵摇模态的运动响应。图 4为Spar平台垂荡模态的幅值—频率响应曲线。可以看到在垂荡固有周期附近垂荡运动的幅值并没有出现峰值,而是出现了不规则的幅值跳跃现象,此时平台运动失稳,发生非线性内共振响应。
|
Download:
|
| 图 4 垂荡频率响应曲线 Fig. 4 Frequency response curve of heave motion | |
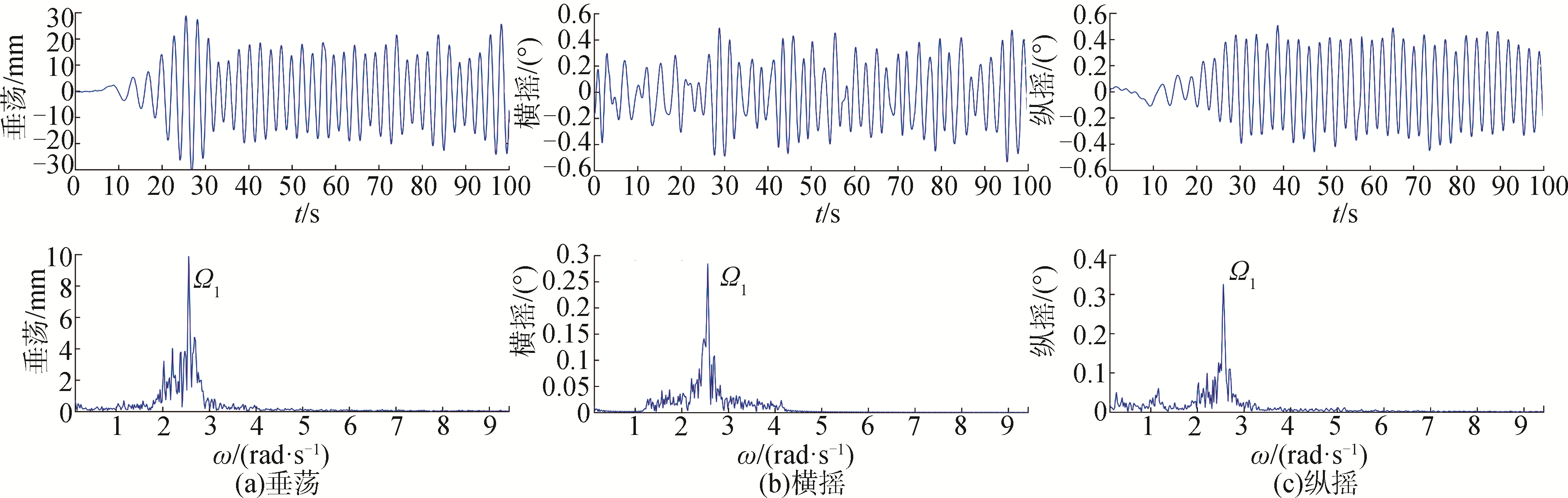
图 5~7为相同波高,不同入射波浪周期情况下Spar平台各模态的时间历程和频谱图。
|
Download:
|
| 图 5 时间历程曲线和频谱图,波浪周期2.4 s,波高41.1 mm Fig. 5 The time history curves and frequency spectrum, wave period 2.4 s, wave height 41.1 mm | |

|
Download:
|
| 图 6 时间历程曲线和频谱图,波浪周期1.89 s,波高40.0 mm Fig. 6 The time history curves and frequency spectrum, wave period 1.89 s, wave height 40.0 mm | |
|
Download:
|
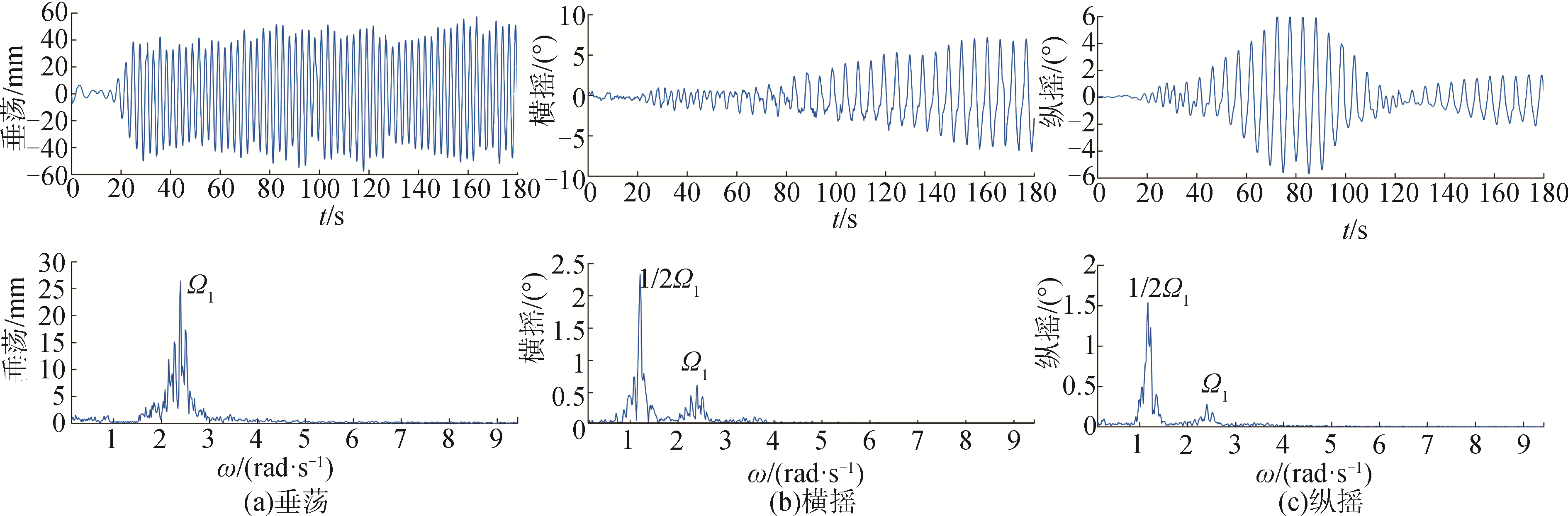
| 图 7 时间历程曲线和频谱图,波浪周期2.6 s,波高40.5 mm Fig. 7 The time history curves and frequency spectrum, wave period 2.6 s, wave height 40.5 mm | |
入射波浪周期为2.4 s时(图 5),平台发生线性强迫运动,各个模态运动频率等于波浪频率,运动幅值很小,垂荡为15 mm,纵摇和横摇幅值分别为0.4°和0.3°。
入射波浪周期为1.89 s时(图 6),横摇和纵摇模态出现了1/3 Ω1亚谐频率运动,垂荡模态出现了1/3 Ω1和2/3Ω1亚谐频率运动。平台在该种海况下发生组合共振运动现象。此时入射波浪频率接近垂荡和横摇(或者纵摇)频率之和。纵摇运动幅值不超过1.5°,横摇运动幅值超过4°,说明发生组合共振时,能量主要在横摇模态释放。
入射波浪周期为2.6 s时(图 7),横摇和纵摇模态发生大幅的1/2 Ω1亚谐频率运动。横摇幅值达到7°,纵摇幅值达到6°。垂荡模态以波浪频率做强迫运动。平台此时发生非线性内共振运动,垂荡模态运动失稳,能量向横摇和纵摇模态转移。
由图 7的时间历程曲线能得到Spar平台发生内共振运动时的能量转移情况:在内共振情况下,垂荡运动能量首先饱和,多余的能量向纵摇模态转移,从0~80 s纵摇模态激起大幅的1/2亚谐纵摇运动,幅值从0°迅速增大到6°,此时横摇模态响应很小,横摇运动幅值不超过2°;然后纵摇模态的能量向横摇模态转移,80 s之后纵摇模态运动幅值衰减,横摇模态运动幅值增大,最终引起大幅的1/2亚谐横摇运动。该结论与文献[10]解析和数值模拟的结果一致:Spar平台发生非线性内共振运动时,垂荡模态的能量饱和,多余的能量会向横摇或者纵摇模态转移,并以1/2亚谐运动的形式释放。对于纵摇模态,纵摇波浪力矩频率是亚谐频率的2倍,对1/2亚谐运动起阻碍作用,对于横摇模态没有波浪外激力的干扰,因此多余的能量更容易在横摇模态释放。在实验中可以看到Spar平台最终会发生大幅的横摇运动,而纵摇模态运动幅值相对较小。
Spar平台发生内共振响应时,能量的渗透过程和初始条件有关[10]。为了验证该结论实验设置了相同海况不同初值条件的对比实验,实验结果如图 8所示。

|
Download:
|
| 图 8 初始条件对能量渗透的作用,波浪周期2.6 s,波高40.5 mm Fig. 8 Effect of initial conditions on energy penetration, wave period 2.6 s, wave height 40.5 mm | |
图 8(a)为初始状态没有干扰,从静止状态开始造波,记录实验结果,从图中可以看到在80 s之前垂荡模态多余的能量首先向纵摇模态转移,引起大幅的1/2纵摇亚谐运动,横摇的运动幅值很小,80 s之后纵摇运动幅值减小横摇模态幅值增大,能量从纵摇模态向横摇模态转移。
图 8(b)给Spar平台一个初始4°的横摇扰动,然后造波,记录实验结果。从图中可以看到,发生内共振运动时,垂荡模态多余的能量直接向横摇模态转移,引起大幅的1/2亚谐横摇运动,纵摇模态的运动幅值很小,与图 8(a)稳定后的结果一致。
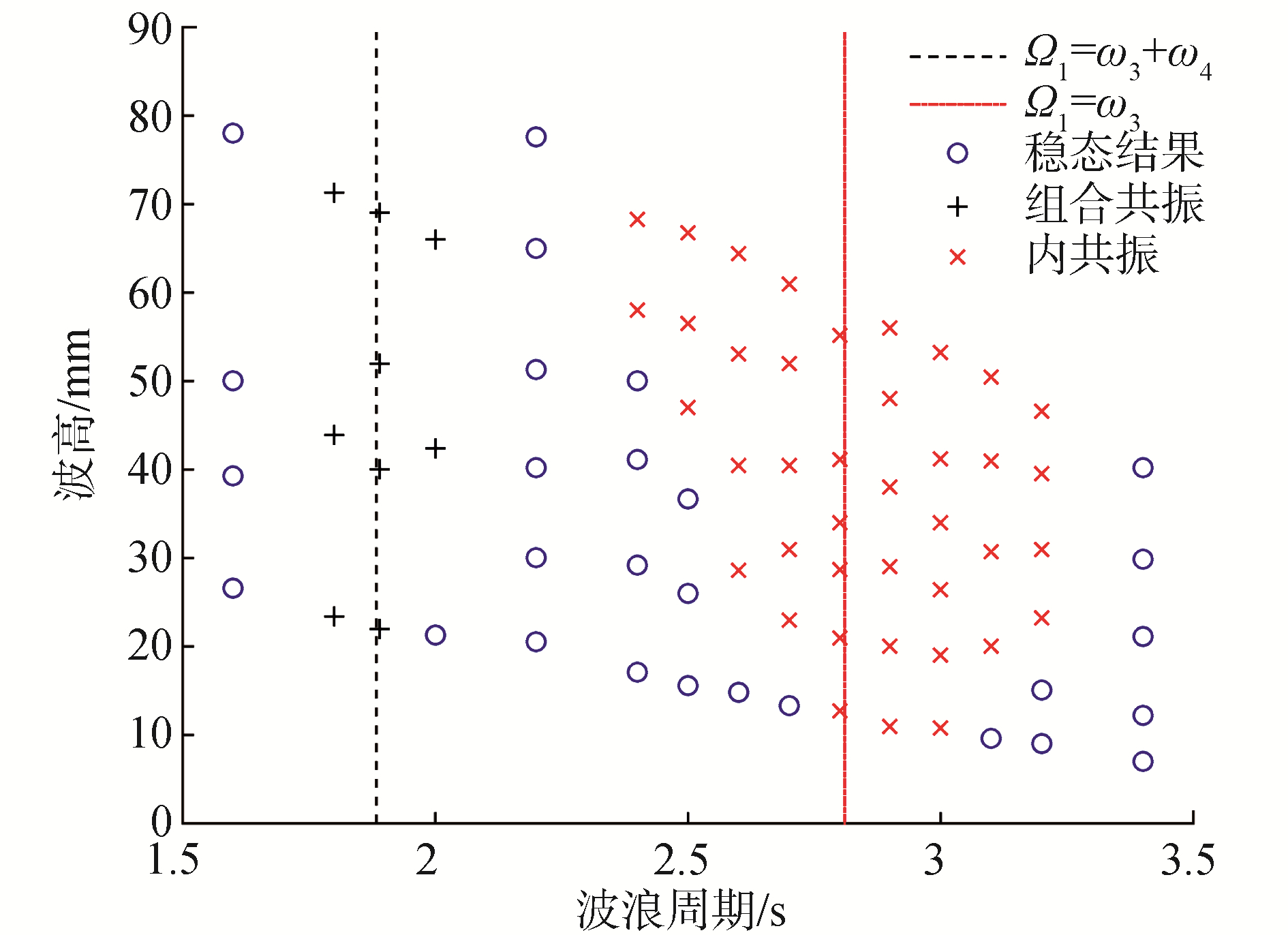
图 9为试验测得Spar平台发生组合共振和内共振时不稳定参数区域。圆圈表示稳定的线性强迫运动(对应于图 5所示的结果),加号表示非线性组合共振运动(对应于图 6所示的结果),叉号表示非线性内共振运动(对应于图 7所示的结果)。
|
Download:
|
| 图 9 组合共振和内共振不稳定参数域 Fig. 9 Unsteady parameter field of combination resonance and internal resonance | |
Spar平台在入射波浪频率接近1.89 s时发生非线性组合共振,如图虚线表示入射波浪频率等于垂荡与横摇(或者纵摇)频率之和。平台在入射波浪频率接近垂荡固有频率时发生非线性内共振运动,点划线为入射波浪频率等于横摇(或者纵摇频)率。图中可以看出组合共振频率带宽相比内共振较窄。
3 结论1) 入射波浪频率接近垂荡固有频率时,Spar平台发生非线性内共振运动,引起大幅的1/2亚谐横摇和纵摇运动。入射波浪频率接近垂荡固有频率和横摇(或者纵摇)频率之和时,Spar平台发生非线性组合共振,引起1/3亚谐横摇和纵摇运动。
2) 当入射波浪频率在垂荡固有频率附近逐渐变化时,平台运动运动幅值会出现跳跃现象。这种现象会导致平台在海上作业时的运动突变,不利于平台的安全生产。
3) 内共振不稳定参数域相对组合共振参数域较大,波高相同,内共振引起的平台运动幅值也较大。
4) 在内共振情况下,Spar平台垂荡模态达到能量饱和状态,多余的能量先向纵摇模态转移,再向横摇模态转移,最终引起横摇模态大幅的1/2亚谐频率运动。
5) 能量渗透过程与初始条件和平台各模态的阻尼有关。平台发生非线性内共振运动时,能量在阻尼最小的模态以1/2亚谐运动的形式释放。对于Spar平台,纵摇模态上受到纵摇波浪力矩的阻碍作用,因此纵摇模态能量会向横摇模态转移,引起大幅的横摇亚谐运动。当Spar平台初始横摇模态受到扰动时,垂荡模态能量会直接向横摇模态转移。
| [1] |
RIJKEN O R, NIEDZWECKI J M. Dynamic response and runup on spar platforms[C]//The Sixth International Offshore and Polar Engineering Conference. Los Angeles, USA, 1996: 289-295.
(  0) 0)
|
| [2] |
HASLUM H A, FALTINSEN O M. Alternative shape of spar platforms for use in hostile areas[C]//Offshore Technology Conference. Houston, Texas, 1999: 217-228.
(  0) 0)
|
| [3] |
RHO J B, CHOI H S, SHIN H S, et al. An experimental study for mooring effects on the stability of spar platform[C]//The Thirteenth International Offshore and Polar Engineering Conference. Honolulu, Hawaii, 2003: 285-288.
(  0) 0)
|
| [4] |
HONG Y P, LEE D Y, CHOI Y H, et al. An experimental study on the extreme motion responses of a SPAR platform in the heave resonant waves[C]//The Fifteenth International Offshore and Polar Engineering Conference. Seoul, Korea, 2005: 225-232..
(  0) 0)
|
| [5] |
NEVES M A S, SPHAIER S H, MATTOSO B M, et al. On the occurrence of Mathieu instabilities of vertical cylinders[C]//ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal, 2008: 619-627.
(  0) 0)
|
| [6] |
赵晶瑞.经典式Spar平台非线性耦合动力响应研究[D].天津: 天津大学, 2010. ZHAO Jingrui. Study on nonlinear coupling dynamic response of a classic spar platform[D]. Tianjin: Tianjin University, 2010. (  0) 0)
|
| [7] |
ZHAO Jingrui, TANG Yougang, SHEN Wenjun. A study on the combination resonance response of a classic spar platform[J]. Journal of vibration and control, 2010, 16(14): 2083-2107. DOI:10.1177/1077546309349393 (  0) 0)
|
| [8] |
LIU Liqin, ZHOU Bin, TANG Yougang. Study on the nonlinear dynamical behavior of deepsea Spar platform by numerical simulation and model experiment[J]. Journal of vibration and control, 2014, 20(10): 1528-1537. DOI:10.1177/1077546312472917 (  0) 0)
|
| [9] |
YANG Hezhen, XU Peiji. Effect of hull geometry on parametric resonances of spar in irregular waves[J]. Ocean engineering, 2015, 99: 14-22. DOI:10.1016/j.oceaneng.2015.03.006 (  0) 0)
|
| [10] |
LIU Shuxiao, TANG Yougang, LI Wei. Nonlinear random motion analysis of coupled heave-pitch motions of a spar platform considering 1st-order and 2nd-order wave loads[J]. Journal of marine science and application, 2016, 15(2): 166-174. DOI:10.1007/s11804-016-1349-7 (  0) 0)
|
| [11] |
WEI Li, TANG Yougang, LIU Liqin, et al. Heave-roll-pitch coupled nonlinear internal resonance response of a spar platform considering wave and vortex exciting loads[J]. Journal of ocean university of China, 2017, 16(2): 209-222. DOI:10.1007/s11802-017-3151-9 (  0) 0)
|
| [12] |
LI Wei, TANG Yougang, LIU Liqin, et al. Internal resonances for heave, roll and pitch modes of a spar platform considering wave and vortex-induced loads in the main roll resonance[J]. China ocean engineering, 2017, 31(4): 408-417. DOI:10.1007/s13344-017-0047-9 (  0) 0)
|
| [13] |
LI Wei, TANG Yougang, WANG Bin, et al. Internal resonances for the heave roll and pitch modes of a spar platform considering wave and vortex exciting loads in heave main resonance[J]. Journal of marine science and application, 2018, 17: 265-272. DOI:10.1007/s11804-018-0023-7 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


