入水砰击现象在海洋工程领域中十分常见,如海浪对海洋平台下甲板和立柱的的砰击,船舶航行时船艏与水面的拍击等。砰击产生的压力载荷会对结构物造成不利影响,引起结构物的变形和破坏,甚至导致严重的事故。因此入水砰击问题在工程设计中越来越引起人们的重视,许多学者都对该热点问题进行了研究与分析。自Karmam [1]利用动量守恒定理计算物体入水砰击载荷以来,结构的入水砰击问题得到了广泛而深入的研究。Wagner[2]在Karman的基础上引入势流理论,为后续的许多理论模型奠定了基础。Chuang[3]在试验中首先发现空气垫在平底结构的入水过程中起着非常重要的作用,对平底结构的入水问题进行了一系列的试验。Huera[4]对平底板以一定角度入水的斜向入水砰击进行了试验研究,当入水角度小于5°时,空气垫现象非常明显。Scolan[5]将Wagner相当平板理论拓展到三维入水问题中,对轴对称钝体问题进行渐近分析得到解析解。闫发锁等[6]以Wagner的入水砰击理论为基础,提出了在考虑流固耦合情况下楔形体砰击压力的计算方法。并且通过试验的对比分析,得出了完整的计算压力的方法。卢炽华等[7]通过非线性伯努利方程,将流体域边界元方程与结构有限元方程耦合求解,并考虑了自由表面的非线性边界条件。陈震等[8]利用MSC.Dytran仿真软件对二维楔形体入水问题进行了数值模拟仿真研究,阐述了空气垫和重力对砰击时液面的变化和根部的喷射的影响。Peseux[9]采用有限元方法计算了刚性、弹性物体的砰击问题,并进行实验对比研究,对于刚性物体,计算结果与实验值吻合的较好,对于弹性体则出现了新的情况,需要进一步研究。许凯玮[10]研究了板架入水过程中其高频弹性振动对流体力的影响,将双渐近法应用于二维弹性楔形体入水问题,提出了一种可以求解弹性结构入水砰击问题的方法。杨衡[11]通过考虑结构运动非线性的伯努利方程将流体域控制方程与结构弹性动力响应方程耦合求解,结果表明,流固耦合效应对弹性结构入水砰击载荷及结构弹性动力响应影响不可忽略。近年来学者对三维物体的砰击问题探讨越来越多,Troesch[12]分别用切片法与三维面元法计算了球体的特例,并与实验值进行比较,很明显三维法算得的砰击载荷较为准确,而以切片法所得值明显偏大。三维物体的砰击问题最大的难点在于自由面的处理,特别是端部,流体更容易逃逸,三位效应显著。
本文在Wagner理论的基础上,采用数值仿真计算的方法研究三维刚性立柱体结构的入水砰击问题,分析了纵倾角和入水速度对砰击压力峰值大小与分布的影响,讨论了空气垫在小角度纵倾角入水时的作用。
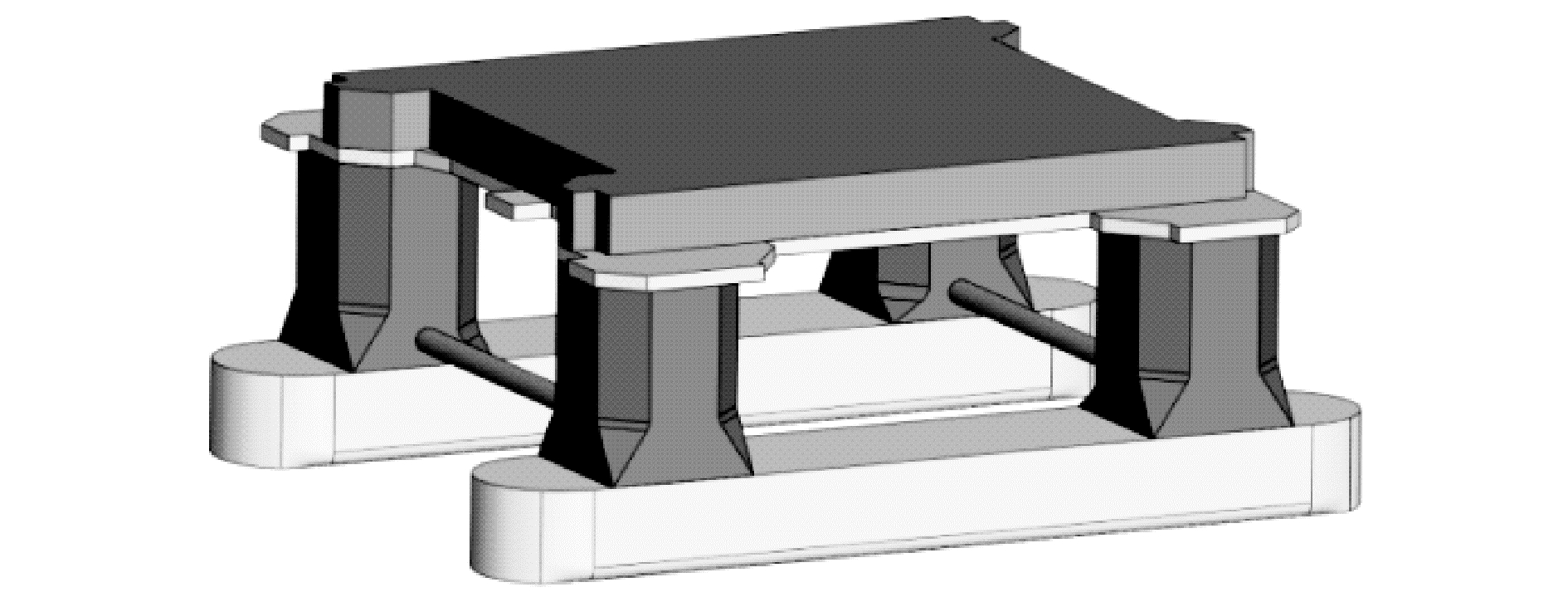
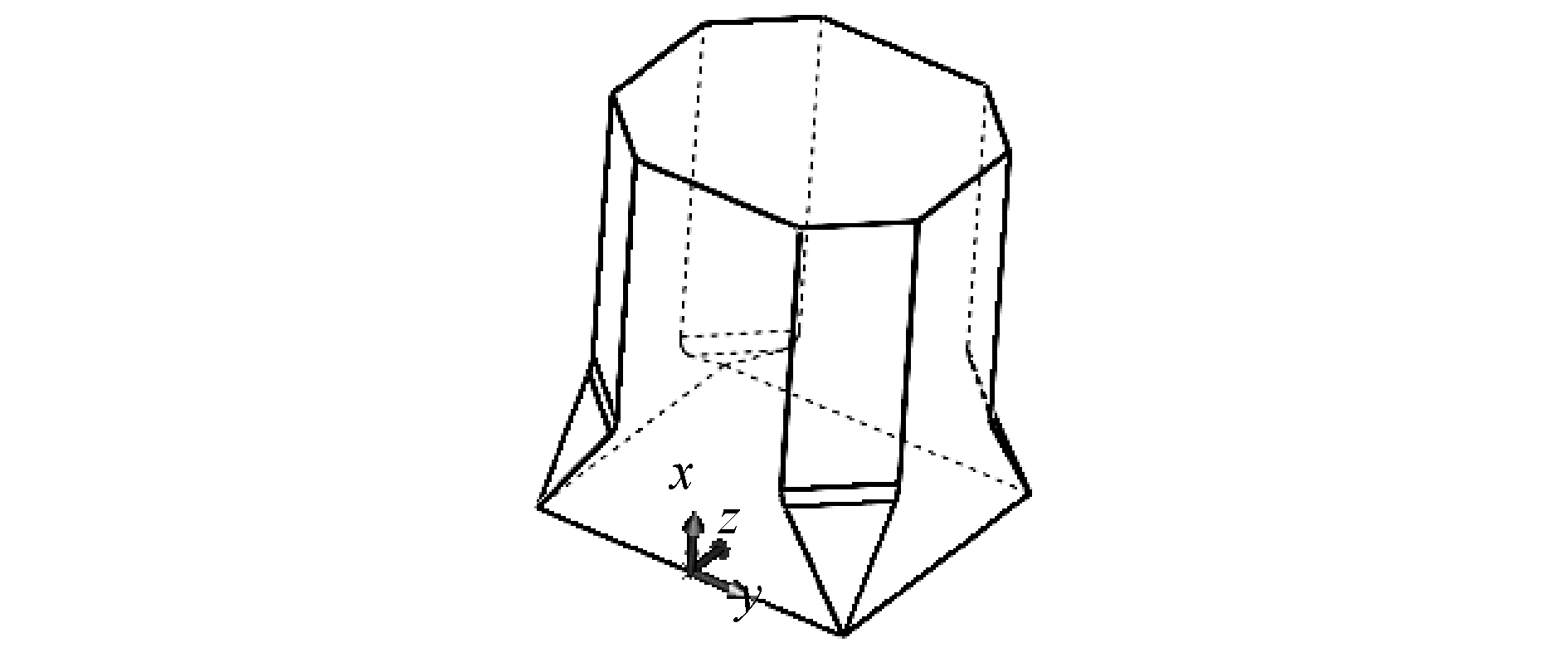
1 半潜式平台立柱体结构砰击模型的建立 1.1 立柱模型为了研究半潜式平台的立柱砰击特性,从半潜式平台中提取立柱作为研究对象,半潜式平台的三维模型见图 1。图 2给出了半潜式平台立柱体三维模型图,立柱体下基座为矩形,与下甲板连接面为八边形,立柱体结构为三维柱体,入水砰击时三维效应显著。立柱高16.9 m;横截面长与宽分别为13.65 m和12.35 m。
|
Download:
|
| 图 1 半潜式平台三维模型 Fig. 1 Three dimensional model of semi submersible platform | |
|
Download:
|
| 图 2 立柱体三维模型图 Fig. 2 Three dimensional model of column body | |
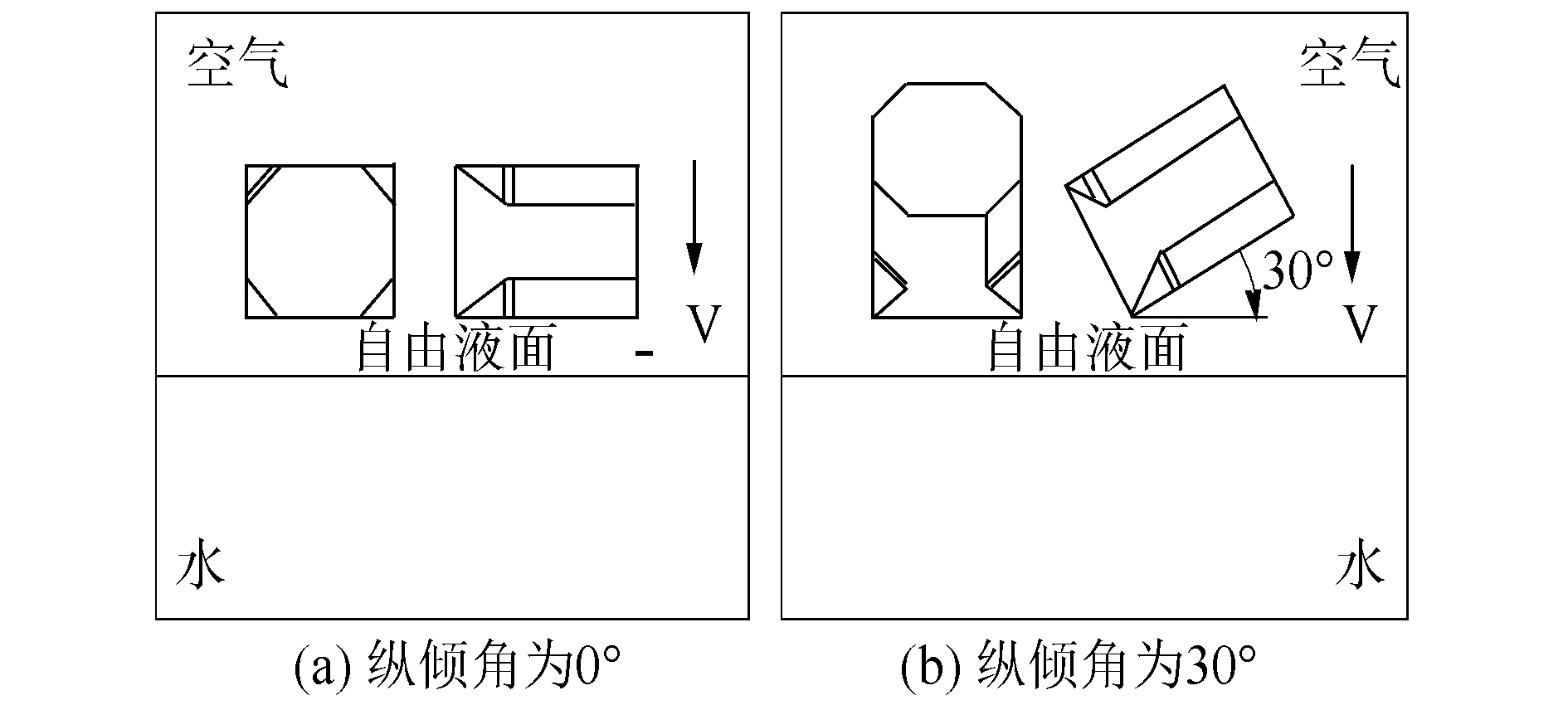
立柱悬于自由液面以上,以恒定速度v下落,图 3为立柱体结构入水砰击示意图。基于粘性流体理论开展数值计算,立柱结构计算域统一为11.5 m×10 m×7 m。图 4为立柱体结构计算域网格划分图,为了更加精确地捕捉砰击载荷,在立柱入水砰击面与自由液面处进行了加密处理,动量方程采用中心差分格式离散;自由面采用混合自由面捕捉与重构相结合格式离散。
|
Download:
|
| 图 3 平台立柱入水砰击示意 Fig. 3 Schematic diagram of platform column slamming into water | |

|
Download:
|
| 图 4 立柱计算域网格划分图 Fig. 4 Grid partition diagram of column computation domain | |
立柱体结构入水纵倾角度设为β。纵倾角0°≤β≤30°,间隔Δβ=5°,纵倾角β=3°为特殊纵倾角。入水速度1≤v≤6 m/s,Δv=1,工况编号为B1~B48。
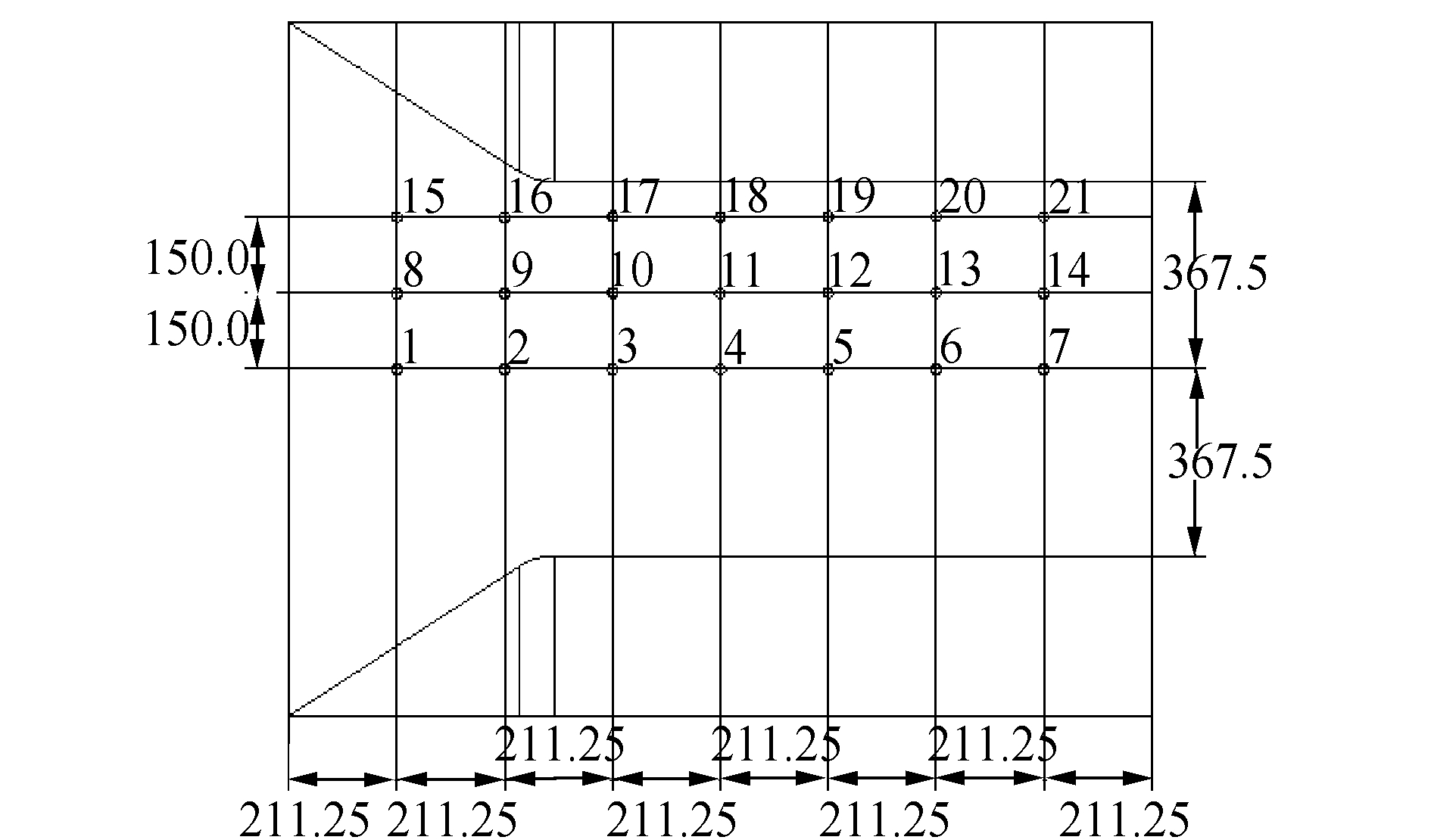
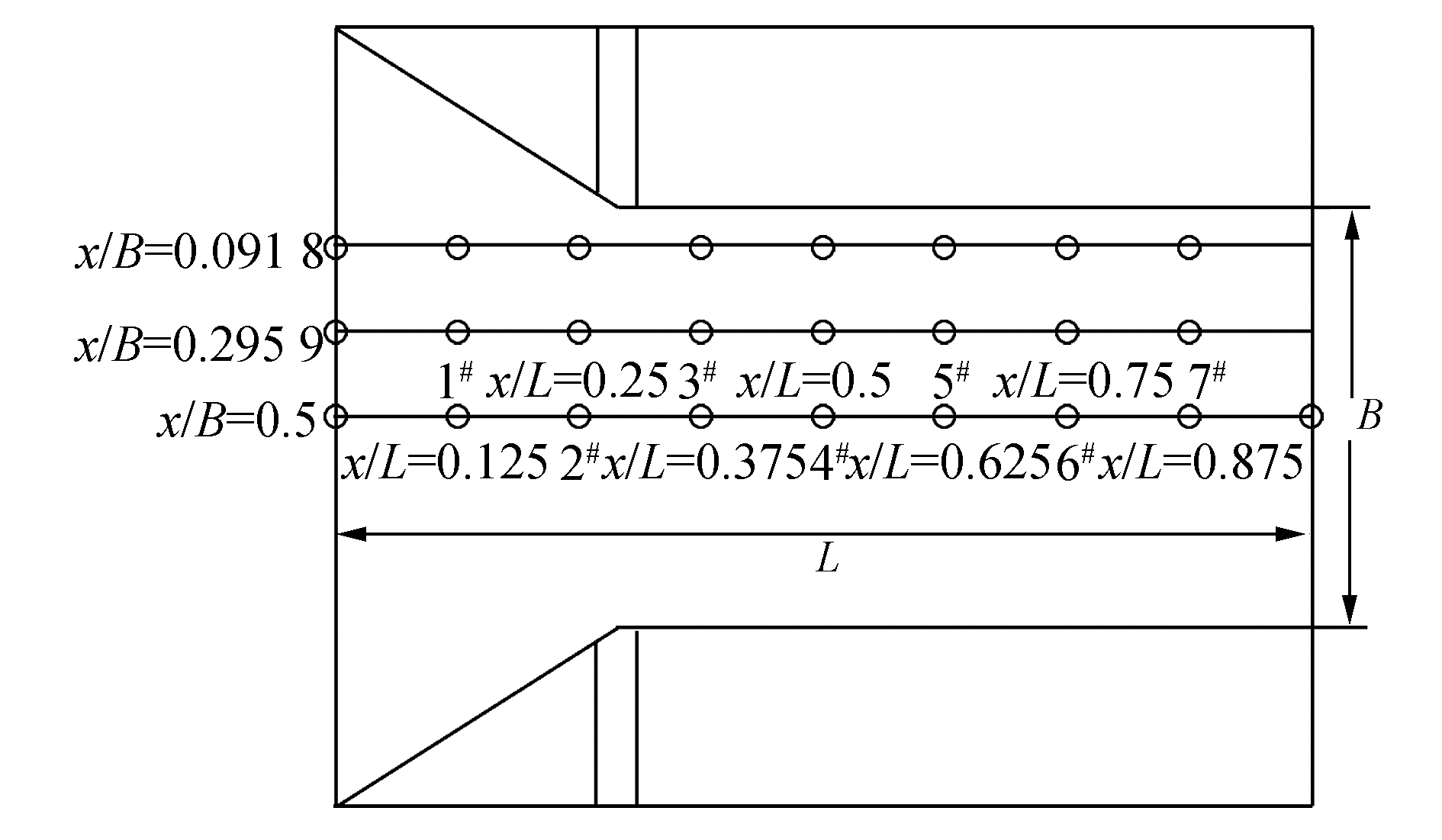
为了监测入水面砰击载荷瞬态压力,入水面设置压力监测点。立柱入水面具有对称性,压力测点布置见图 5, 测点编号为1#~21#。为更好的反映出砰击载荷在入水面上随空间位置变化的趋势,对监测点位置进行无量纲化处理,入水面长度L和宽度B进行归一化处理。沿着L方向划分为x/L为0.125、0.25、0.375、0.5、0.625、0.75、0.875,沿着宽度方B划分x/B为0.091 8、0.295 9、0.5,具体如图 6所示。
|
Download:
|
| 图 5 立柱监测点分布 Fig. 5 Distribution chart of map of column monitoring points | |
|
Download:
|
| 图 6 立柱监测点无量纲示意 Fig. 6 Non dimensional sketch column monitoring points | |
根据冲量入水砰击理论,砰击压力峰值可以表示为:
| $ {p_p} = k\rho \mathit{\boldsymbol{v}}_e^2 $ | (1) |
式中:ρ为水的密度;ve为结构体入水速度;k为结构体入水砰击压力系数。系数k反映了不同入水角度及速度对砰击压力峰值的影响程度。
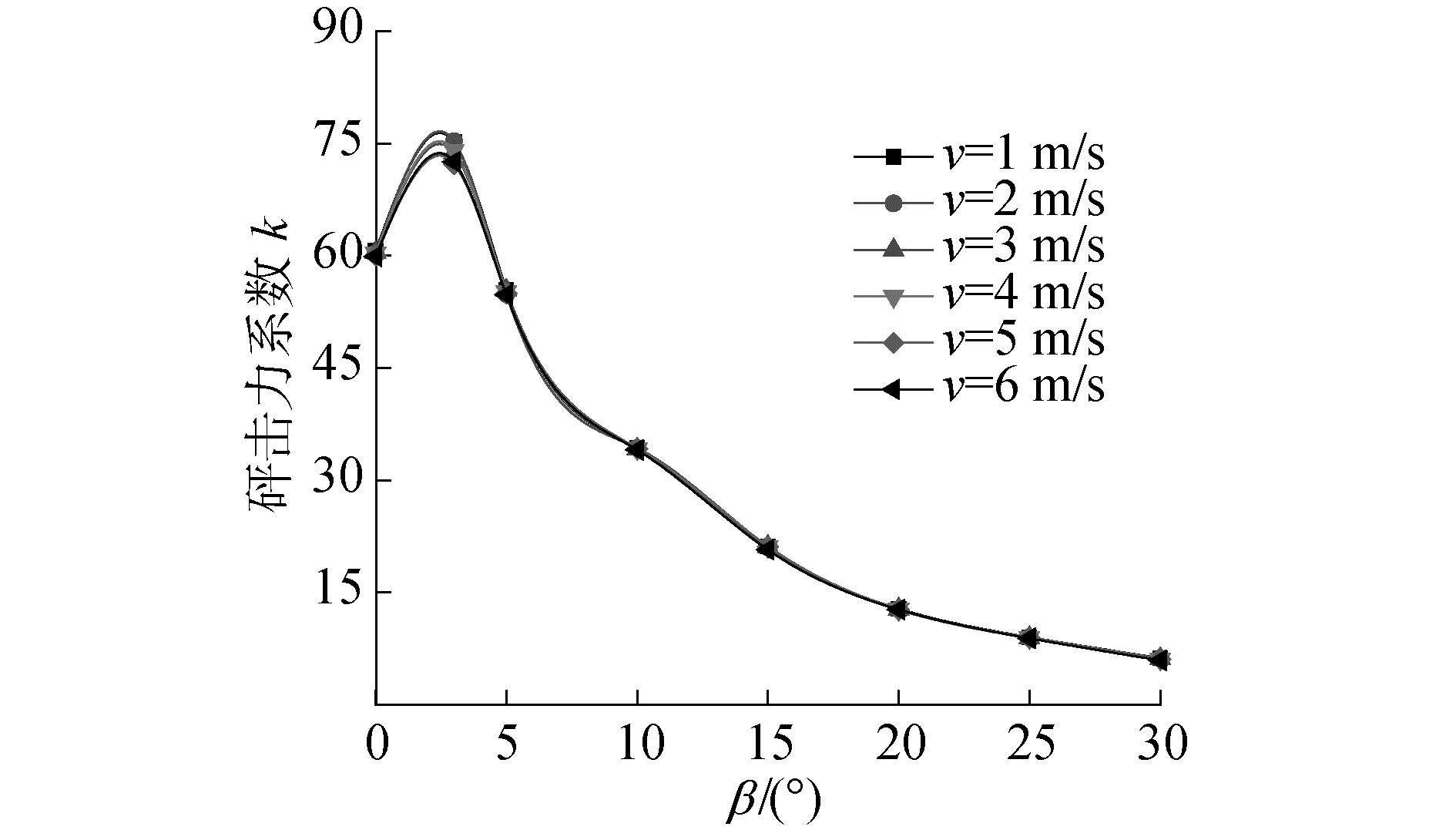
图 7为不同入水速度下最大砰击压力系数k随斜升角β变化的曲线。从图中可以直观看出:在不同的入水速度下,砰击压力系数k随着入水角度的增加先增大后减小,k值均在2°≤β≤4°出现最大值,这是空气垫的阻塞效应引起的砰击压力数值增加。在β>5°时空气从结构边缘处迅速逃逸,空气垫的缓冲效应消失,砰击压力主要为结构与水之间相互作用的动力效应,不同速度下的k值曲线基本重合。当结构物小角度入水时,速度v对砰击力系数k存在一定影响,这是因为结构物高速入水时可以有效抑制气体逃逸,使气垫效应相对低速时更加显著。当β>5°时,速度对k值的影响基本可以忽略。
|
Download:
|
| 图 7 不同入水速度下监测点最大砰击力系数k随纵倾角β变化曲线 Fig. 7 The maximum slamming force coefficient k of the monitoring point with the change of the inclination angle curve at different water entry speeds | |
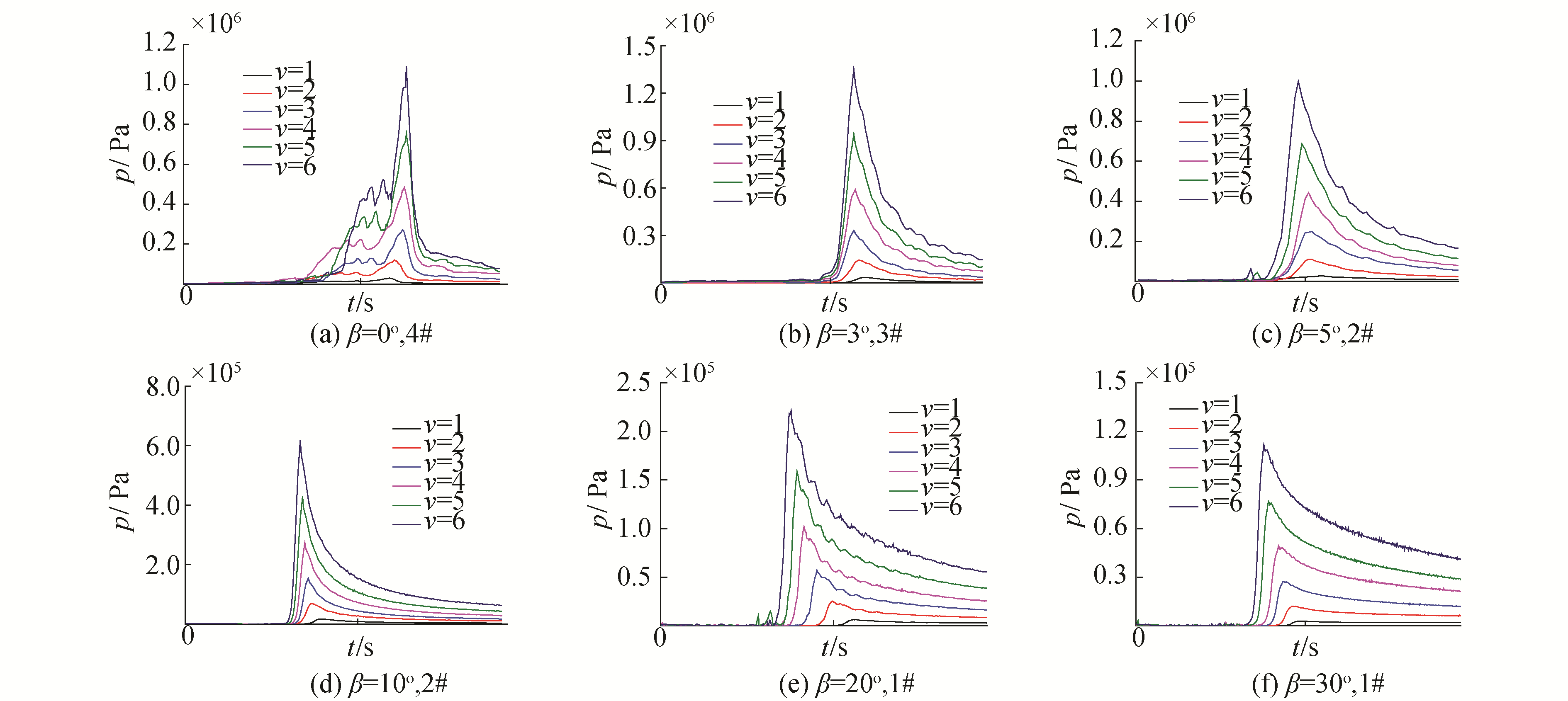
图 8为立柱在不同纵倾角、不同入水速度下测得的最大砰击压力监测点的历时曲线图。从图中可以看出:在纵倾角相同时,不同速度下最大砰击压力发生的位置相同,当纵倾角改变时,最大砰击压力发生的位置不同,随着纵倾角增大不断向边缘扩散,从β=0°中心处的4#监测点转移到β=30°边缘处的1#监测点,纵倾角直接影响了最大砰击压力发生的空间位置。
|
Download:
|
| 图 8 立柱体结构在不同纵倾角、不同入水速度下最大砰击压力监测点历时曲线 Fig. 8 Time history curve of maximum slamming pressure monitoring point of column structure under different angle and different water entry speed | |
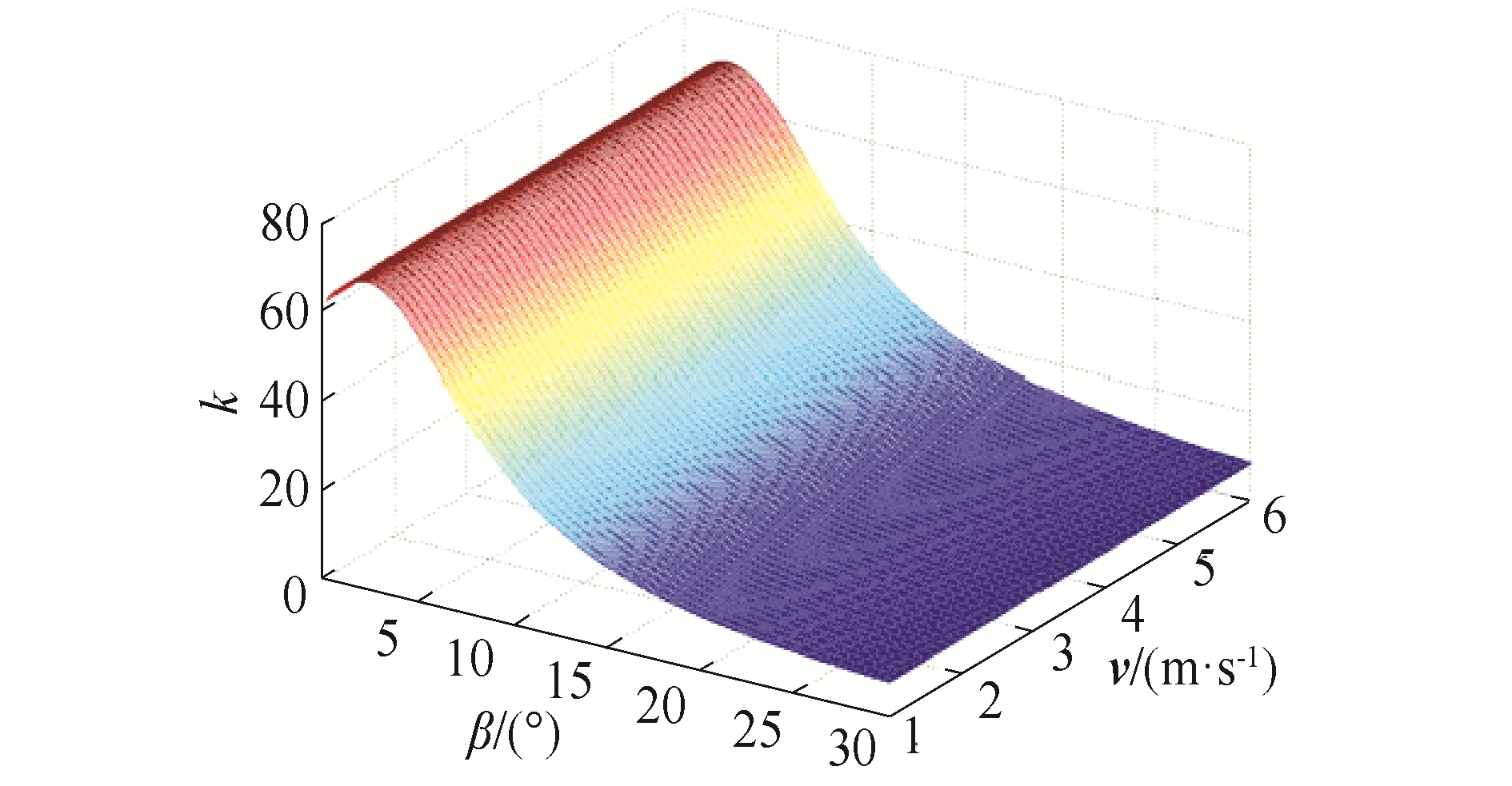
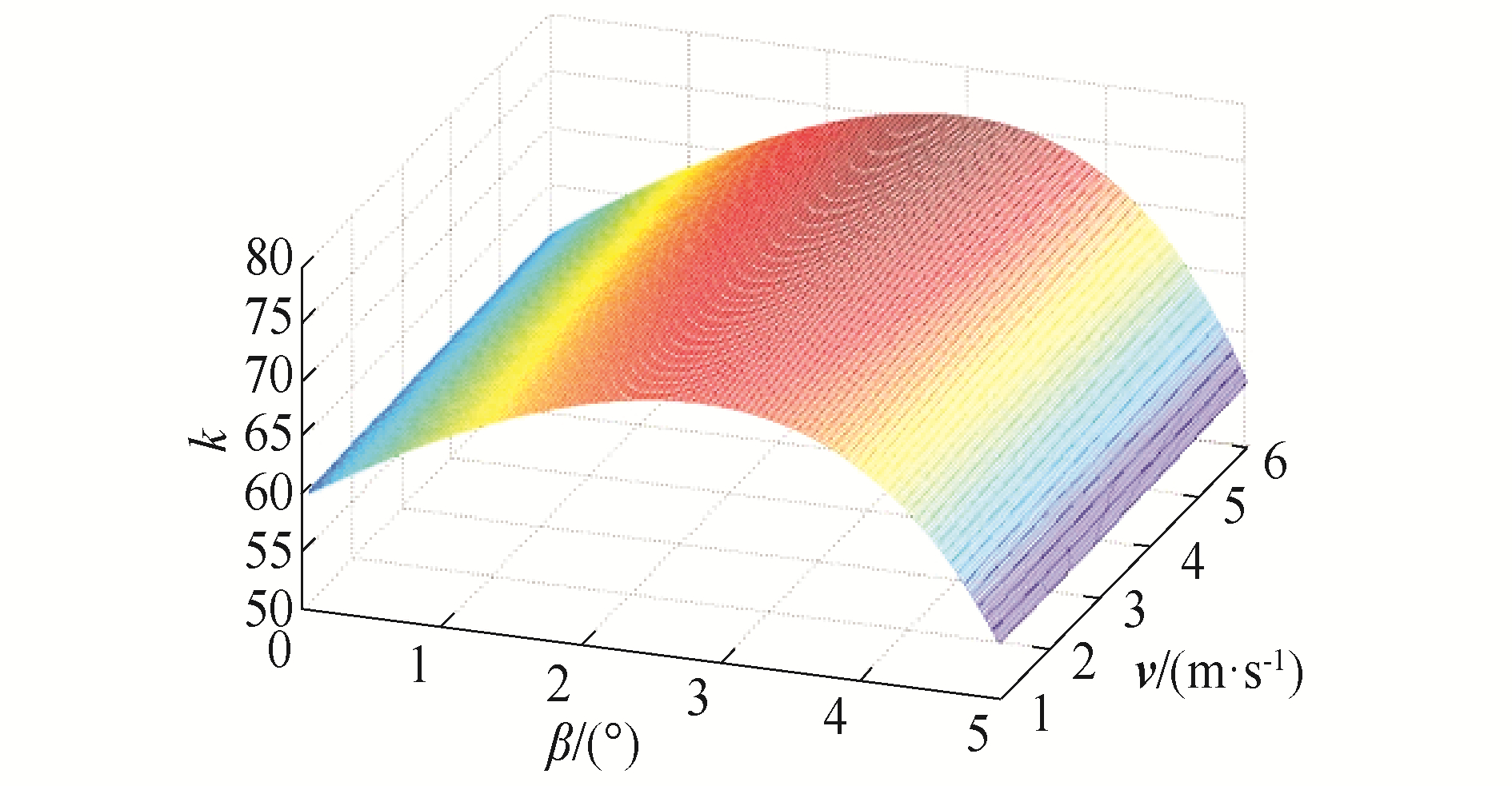
为量化倾角β和入水速度v对最大砰击力系数k的影响,对最大砰击力系数k值进行三维曲面拟合,如图 9所示,表 1、表 2为最大k值拟合公式。由于小角度入水时速度v对最大砰击力系数k值的影响是不可忽略的,因此采用分段函数,当β<5°时k值同时由v和β共同决定,图 10为β<5°时k值曲面图。当β≥5°时,速度项可以忽略,主要由入水角决定。通过该k值公式及其拟合的k值曲面,可以快速得到不同情况下的最大砰击力系数k值,从而可以迅速化解出作用在立柱结构面上的最大的砰击压力的大小。
|
Download:
|
| 图 9 不同纵倾角和入水速度下最大k值曲面图 Fig. 9 Maximum k surface figure at different longitudinal angles and water entry speeds | |
| 表 1 β<5°最大k值曲面拟合公式 Table 1 Surface fitting formula of maximum k value of β < 5° |
| 表 2 β≥5°最大k值曲面拟合公式 Table 2 Surface fitting formula of maximum k value of β≥5° |
|
Download:
|
| 图 10 β<5°最大k值曲面图 Fig. 10 Maximum k value surface graph of β < 5° | |
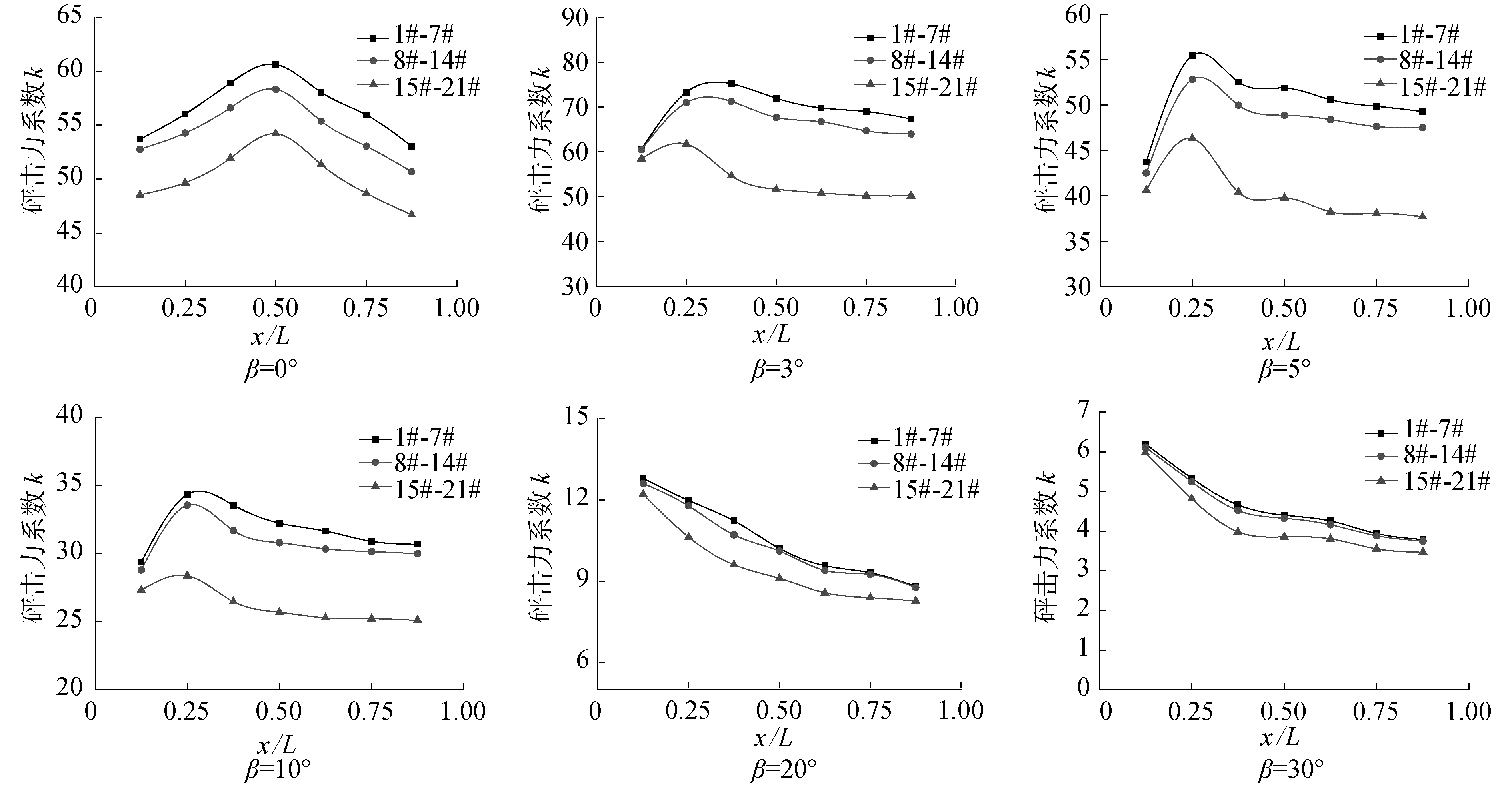
图 11为v=6 m/s时,β为0°、3°、5°、10°、20°、30°入水面上21个压力监测点测得的最大砰击压力系数k值随x/L变化的曲线图。由图可见:中线上的1#~7#测点的k值最大,随着宽度B向两边逐渐减小,但k值曲线的变化规律与中线处监测点的变化规律基本一致,这种变化规律不随入水角度β的改变而改变。在长度L方向上,由于受到纵倾角β的影响,k值峰值出现的位置发生变化,随着纵倾角的增大不断向边缘扩散。
|
Download:
|
| 图 11 不同纵倾角下k值曲线图 Fig. 11 k curves of different inclination angles | |
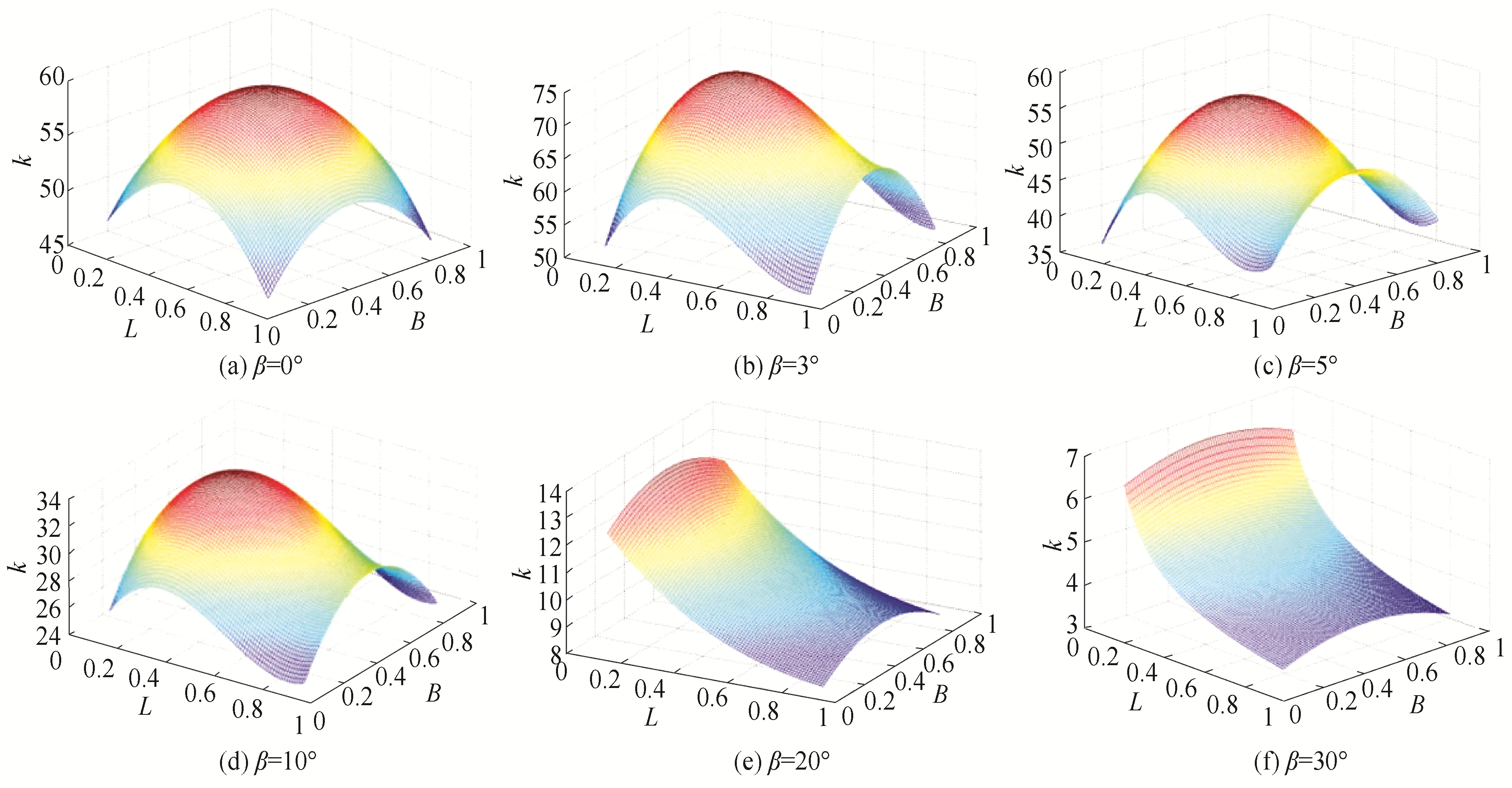
为量化空间位置对k值分布规律的影响,根据6种纵倾角下的k值及其对应的空间位置进行三维曲面拟合,3种纵倾角下的k值曲面图以及k值曲面拟合公式如图 12和表 3~8所示。
|
Download:
|
| 图 12 k值曲面图及投影图 Fig. 12 k valued surface graph | |
| 表 3 β=0°曲面拟合公式 Table 3 Fitting formula of the surface of the β=0° |
| 表 4 3°曲面拟合公式 Table 4 Fitting formula of the surface of the β=3° |
| 表 5 5°曲面拟合公式 Table 5 Fitting formula of the surface of the β=5° |
| 表 6 10°曲面拟合公式 Table 6 Fitting formula of the surface of the β=10° |
| 表 7 20°曲面拟合公式 Table 7 Fitting formula of the surface of the β=20° |
| 表 8 30°曲面拟合公式 Table 8 Fitting formula of the surface of the β=30° |
1) 立柱体结构入水砰击压力系数与入水角度密切相关。入水角度直接影响最大砰击压力发生的空间位置和量值;砰击压力系数在入水角2°~3°时达到最大值,约为77。
2) 当入水角β<5°时,由于受到空气垫的影响,入水速度对砰击压力系数的影响不可忽略,当入水角β>5°时,入水速度对砰击压力系数影响可以忽略。
3) 在砰击面上砰击压力系数k值的空间分布规律:在宽度方向B上,最大k值出现的区域均集中的x/B=0.5的中线上,向边缘发展时逐渐减小,与入水角度β无关。入水角β直接决定最大砰击压力系数k在x/L的长度方向上分布。
| [1] |
VON KARMAN T. The impact on seaplane floats during landing[R]. Technical Notes No.321. Washington: National Advisory Committee for Aeronautics, 1929.
(  0) 0)
|
| [2] |
WAGNER H. Uber stoss-und gleitvorgange an der oberflache von flussigkeiten[J]. Zeitschrift für angewandte mathematik und mechanik, 1932, 12(4): 193-215. DOI:10.1002/(ISSN)1521-4001 (  0) 0)
|
| [3] |
CHUANG S L. Experiments on slamming of wedges-shaped bodies[J]. Journal of ship research, 1967, 112(3): 190-198. (  0) 0)
|
| [4] |
HUERA-HUARTE F J, JEON D, GHARIB M. Experimental investigation of water slamming loads on panels[J]. Ocean engineering, 2011, 38(11/12): 1347-1355. (  0) 0)
|
| [5] |
SCOLAN Y M, KOROBKIN A A. Three-dimensional theory of water impact. Part 1. Inverse wagner problem[J]. Journal of fluid mechanics, 2001, 440: 293-326. (  0) 0)
|
| [6] |
闫发锁, 董丽娜, 顾学康, 等. 计及流固耦合时楔形结构的冲击压力计算[J]. 哈尔滨工程大学学报, 2007, 28(11): 1202-1205. YAN Fasuo, DONG Lina, GU Xuekang, et al. Effects of fluid-solid interaction on calculations of slamming pressure for wedged structures[J]. Journal of Harbin Engineering University, 2007, 28(11): 1202-1205. DOI:10.3969/j.issn.1006-7043.2007.11.003 (  0) 0)
|
| [7] |
卢炽华, 何友声. 二维弹性结构入水冲击过程中的流固耦合效应[J]. 力学学报, 2000, 32(3): 129-140. LU Chihua, HE Yousheng. Coupled analysis of nonlinear interaction between fluid and structure during impact[J]. Acta mechanica sinica, 2000, 32(3): 129-140. (  0) 0)
|
| [8] |
陈震, 肖熙. 空气垫在平底结构入水砰击中作用的仿真分析[J]. 上海交通大学学报, 2005, 39(5): 670-673. CHEN Zhen, XIAO Xi. Simulation analysis on the role of air cushion in the slamming of a flat-bottom structure[J]. Journal of Shanghai Jiao Tong University, 2005, 39(5): 670-673. DOI:10.3321/j.issn:1006-2467.2005.05.002 (  0) 0)
|
| [9] |
TROESCH A W, KANG C. Hydrodynamic impact loads on three-dimensional bodies[C]//Proceedings of the 16th Symposium on Naval Hydrodynamics. Berkeley, CA, USA, 1987.
(  0) 0)
|
| [10] |
许凯玮.板架结构自由入水耦合数值模拟方法研究[D].哈尔滨工程大学, 2018. XU Kaiwei. Research on numerical simulation method of freeentry coupling of plate frame structure[D]. Harbin Engineering University, 2018. (  0) 0)
|
| [11] |
杨衡, 孙龙泉, 龚小超, 等. 弹性结构入水砰击载荷特性三维数值模拟研究[J]. 振动与冲击, 2014, 33(19): 28-34. YANG Heng, SUN Longquan, GONG xiaochao, et al. Three dimensional numerical simulation study on the characteristics of water slamming load of elastic structures[J]. Journal of vibration and shock, 2014, 33(19): 28-34. (  0) 0)
|
| [12] |
PESEUX B, GORNET L, DONGUY B. Hydrodynamic impact:numerical and experimental investigations[J]. Journal of fluids and structures, 2005, 21(3): 277-303. DOI:10.1016/j.jfluidstructs.2005.04.011 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


