2. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300072;
3. 宁夏大学 土木与水利工程学院, 宁夏 银川 750021
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;
3. School of Civil Engineering and Hydraulic Engineering, Ningxia University, Yinchuan 750021, China
以重要海岸工程作为一级节点,同时增设二级甚至多级人工节点,如离岸潜堤,构建海岸整体防护体系,是目前海岸工程防护的新思路[1]。与出水堤相比,潜堤结构兼顾防护性和观赏性,造价更低,有利于港湾内外水体的正常交换,更符合海岸带可持续发展的理念。
由于潜堤具备固边界、不同流速汇合及自由表面这3个黏性流体中涡漩生成的基本条件,导致其所受载荷及局部冲刷方式与出水堤有极大不同。例如,长江口深水航道治理工程北导堤半圆型沉箱出现的局部破坏,即发生于寒潮大浪作用下的淹没工况[2]。此外,由于波能在反射波和透射波的不同分配,潜堤向海侧的冲刷将减弱,向岸侧的冲刷可能性则上升[3]。
随着实验仪器及数值技术的进步,学术界逐渐尝试从流场内部结构出发来解释潜堤的工作机理。Ting等[4]采用激光多普勒流速仪(laser doppler velocimtry, LDV)量测了非破碎波通过不透水矩形潜堤时的流场,发现Keulegan-Carpenter数越大,潜体表面的流体分离区域越宽,涡流强度相应增大。Lin等[5]联合运用粒子图像测速技术(paricle image velocimetry, PIV)、激光诱导荧光技术(laser induced fluorescence, LIF)和质点追踪技术(particle tracing, PT)研究了孤立波作用下矩形潜堤周围的紊动射流现象。Poupardin等[6]借助PIV技术分析了波浪振荡流在水下平板上下游边缘处形成的环流系统,观测到下游涡对导致强烈的向下射流,可能引起底床冲刷或淤积,上游涡对则表现为水平对流,对底床无影响。
早期数值分析多以无旋势流理论为架构,如Rey等[7],但难以捕捉到前述试验所展现的紊动效应。因此,近年来研究者们往往是通过求解描述不可压缩黏性流体运动的Navier-Stokes方程(navier stockes, N-S)来探讨潜堤附近的流场。如孤立波-矩形潜堤[8],非破碎波-不透水双列矩形潜堤[9],非对称结构的涡流三维效应[10],相对干舷高度对矩形潜堤涡场的影响[11]等。基于无网格拉格朗日涡法(lagrangian vortex method, LVM)研究波浪-水下立板相互作用的涡场[12],基于非静压模型研究不规则波-光滑潜堤相互作用过程中的波周期变化[13]等,也得到了较好的结果。
初始潜堤型式以矩形为主,随着水动力理论和工程技术的发展,逐渐出现了更适于深水环境的新型低反射结构,如削角堤[14]、梯形堤[15]、半圆堤[16]和弧面堤[17]等。弧面堤是从半圆堤基础上开发出来的新型结构型式,相对后者拥有更小的底面尺寸和基床体积,经济性更好。截止目前,弧面堤的研究集中于波浪反射和透射[18]、波浪力[19]、波浪爬高和落深[20]。
比较新型弧面潜堤(半流线型)与传统矩形潜堤(钝形),前者反射波能更少,透射更多,更有可能造成堤后堤脚冲刷和堤背波压脉动,这些表现与潜堤周围的涡流结构有密切关联。因此,本文的目的是借助数值波浪水槽对比研究2种堤型周围的涡流形成机制及表现形式。首先,简要介绍了数值波浪水槽的理论基础。其次,详细阐述了数值模型的设计和参数选择。之后,从波面、速度场、涡量场3方面对比分析了弧面潜堤与矩形潜堤的涡流结构。
1 数值模拟的建立数值模型以描述不可压缩黏性流体的Navier-Stokes方程为基础,采用k-ε紊流模型封闭紊动应力项,流体体积法(volume of fluid, VOF)追踪自由表面[21]。孔隙介质内部流动采用Darcy-Brinkman-Forchheimer层紊混合渗流模型描述[22]。这一数值模式已应用于多个波浪-建筑物相互作用问题中,详细求解方法可参考文献[23-24]:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 $ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + {g_i} + \frac{1}{\rho }\frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} $ | (2) |
式中:下标i,j=1,2,3代表三维情况;t为时间;ui为速度分量;p为压力;ρ为流体密度;gi为重力加速度;τij为应力张量。
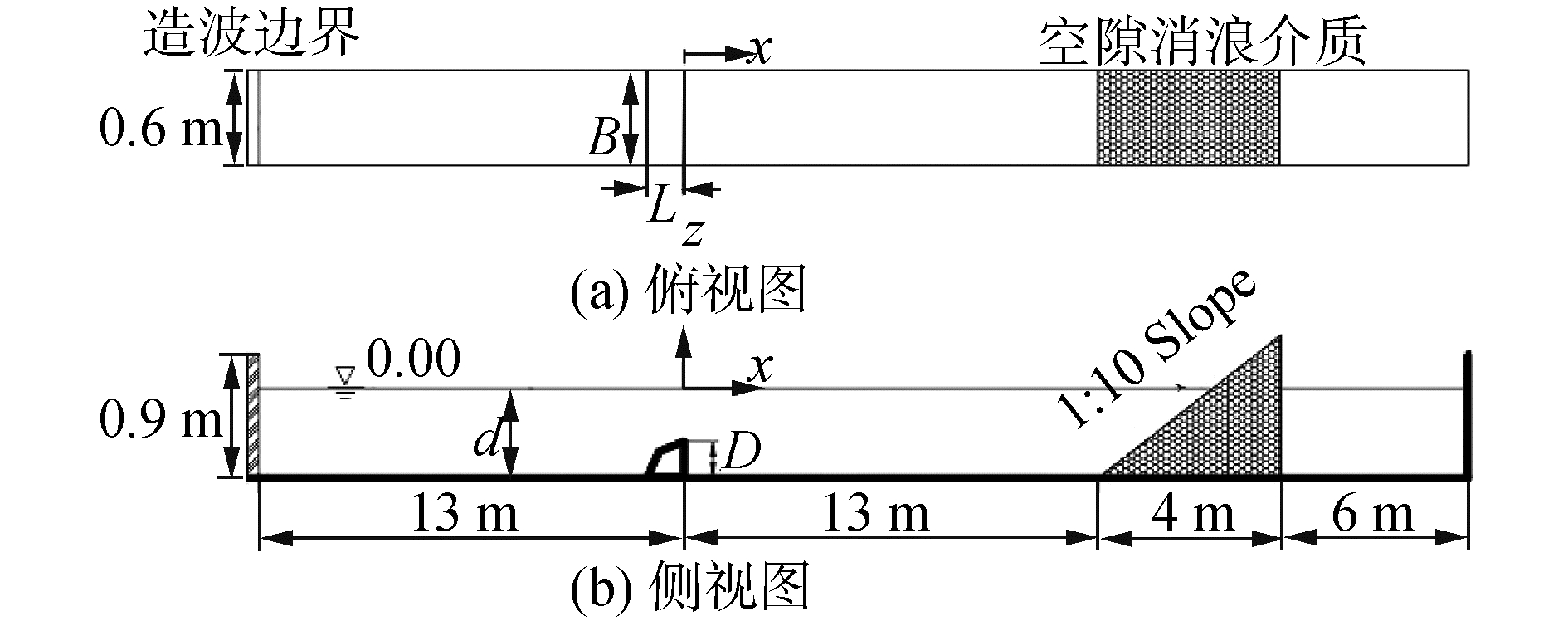
为便于比较,模型设计参考文献[25]的椭圆余弦波-矩形潜堤相互作用PIV试验,如图 1所示。水槽左端为造波边界,右侧为开放出流边界,采用Sommerfeld辐射条件,底部为固边界,其余均为对称边界[26]。入射波形为椭圆余弦波,水深d=0.24 m,波高H=0.036 m,周期T=2.0 s,波长L=2.94 m,水质点运动轨迹直径S=0.069 m。潜堤高度D=0.12 m。x=0置于堤背,顺浪向为正,z=0置于静水面,向上为正。
|
Download:
|
| 图 1 数值水槽布置示意图 Fig. 1 Sketch of wave flume with a quartercircular breakwater | |
网格设定参考相昌盛[27]所建立的三维数值波浪水槽,采用不均匀网格,建筑物和自由表面附近加密,最小网格尺寸为Δxmin=Δzmin =0.002 m。模拟时长36 s。
开放出流边界的消浪是决定数值波浪水槽模拟精度的关键问题之一。Sommerfeld辐射边界条件适合小振幅线性波,但对波浪-建筑物相互作用后强烈变形的波面消浪效果一般,应辅以海绵层、孔隙介质结构等消波方式。张婷[28]研究了消浪孔隙介质的孔隙率、粒径、坡度对消波效果的影响,认为孔隙率0.8和粒径0.1 mm的组合最优。同时提出,对于长周期波,可采用减缓斜坡坡度的方法来减小端部反射。李世森等[29]在数值水槽末端设置了具有垂向渐变孔隙率的结构,结果表明该方法对规则波消波效果良好。本文参照文献[30],在建筑物后、水槽尾端前增加一段多孔介质斜坡结构(坡度1:10),用于吸收端部反射波,如图 1所示。
为了验证消浪效果,仅在数值水槽中放入多孔消浪介质结构(无模型建筑物),测得不同孔隙率时水槽右端的反射系数,在孔隙率为0.3、0.4、0.5和0.8的情况下,反射系数分别为0.44、0.28、0.42和0.31。反射系数Kr=Hr/Hi,Hr为多孔消浪介质结构前的反射波高,采用三点法[31]得到,Hi为入射波高。数据表明,孔隙率0.4时的消浪效果最好,且满足《波浪模型试验规程》“尾部消浪装置需消除90%以上反射波的要求”,故本文多孔消浪介质结构的孔隙率选为0.4。
图 2比较了x=0处的模拟波面(放入多孔消浪介质结构,无模型建筑物)与理论波面,两者吻合良好。

|
Download:
|
| 图 2 模拟造波与理论波面对比(x=0) Fig. 2 Comparison of the predicted and numerical surface elevations for wave generation(x=0) | |
图 3比较了波浪越过两种潜堤后的波面变化,采样位置选择在距离造波边界55倍水深处(x=0.2 m)。可以看出,波面均未发生明显的破碎现象,但波谷变得更为平缓,波高减小,说明部分波能在越堤过程中损耗。弧面潜堤后的波谷呈现更为明显的非线性,表明更多的能量从低频向高频转换。

|
Download:
|
| 图 3 波浪越堤后的波面比较(x=0.2 m) Fig. 3 Comparison of the transmitted surface elevations for submerged vertical and quartercircular breakwaters (x=0.2 m) | |
本节从速度场角度分析波浪与潜堤的作用过程。选取第6个波越堤过程的记录,此时传到建筑物周围的波浪已稳定,且计算域内的波浪场还未受到尾端反射的干扰,数据准确性高。
在堤背处(x=0)观测一个完整周期的波面,分别采集对应波面上相位a~i时刻的堤身周围速度分布。首先与Chang等[25]的矩形潜堤PIV测速结果进行比较,如图 4所示。由图 4可以看出,数值模拟结果与PIV测速结果吻合良好。相对而言,受限于较粗的分辨率和后处理时的数据平滑技术,邻近建筑物的区域PIV测速结果不准确,数值计算则不受这一限制,可以更精确地模拟建筑物附近的流场。在波谷越堤时刻(相位a),高速流体主要集中在堤顶,流速为负向,有一个顺时针涡在堤顶上方,并向上游传递,这是由前一个波形成的(见相位h),同时有一个逆时针涡在堤顶形成,这是由堤角流体的分离造成的。在相位c时刻,水流开始转向,波峰开始通过堤背。从相位d时刻开始,涡流区域转到了堤后,堤角流体开始分离,形成一个顺时针涡。为了展示这一过程,纵轴坐标下移6 cm。从相位e~f可以看出,这一强涡由堤顶的分离射流引起,其中心与堤背的水平距离约为半个水质点运动轨迹(水质点运动轨迹直径S=0.069 m)。在相位g时刻,此顺时针涡逐渐开始消散。相位h对应波峰向波谷的转换阶段,此时顺时针涡向上传递,与逆时针涡相互作用变弱。相位i与相位a对应,堤角和堤背处的流体分离均形成了逆时针涡。

|
Download:
|
| 图 4 矩形潜堤各相位时刻的速度场比较 Fig. 4 Comparison of captured by PIV and numerical velocity fields at phase a to phase h for submerged vertical breakwater | |
图 5给出了波谷越堤时刻矩形潜堤与弧面潜堤周围的速度分布。可以看出,弧面潜堤上方的逆时针涡流的强度更大,并趋向上游移动,而矩形潜堤的逆时针涡流则趋向上方移动。此时,矩形潜堤的涡流中心与堤顶的距离约为0.14S(S=0.069 m),而弧面潜堤的涡流中心与堤顶的距离约为0.3S。

|
Download:
|
| 图 5 波谷越堤时刻的速度场比较(相位a) Fig. 5 Comparison of numerical velocity fields at wave trough (phase a) for submerged vertical and quartercircular breakwaters | |
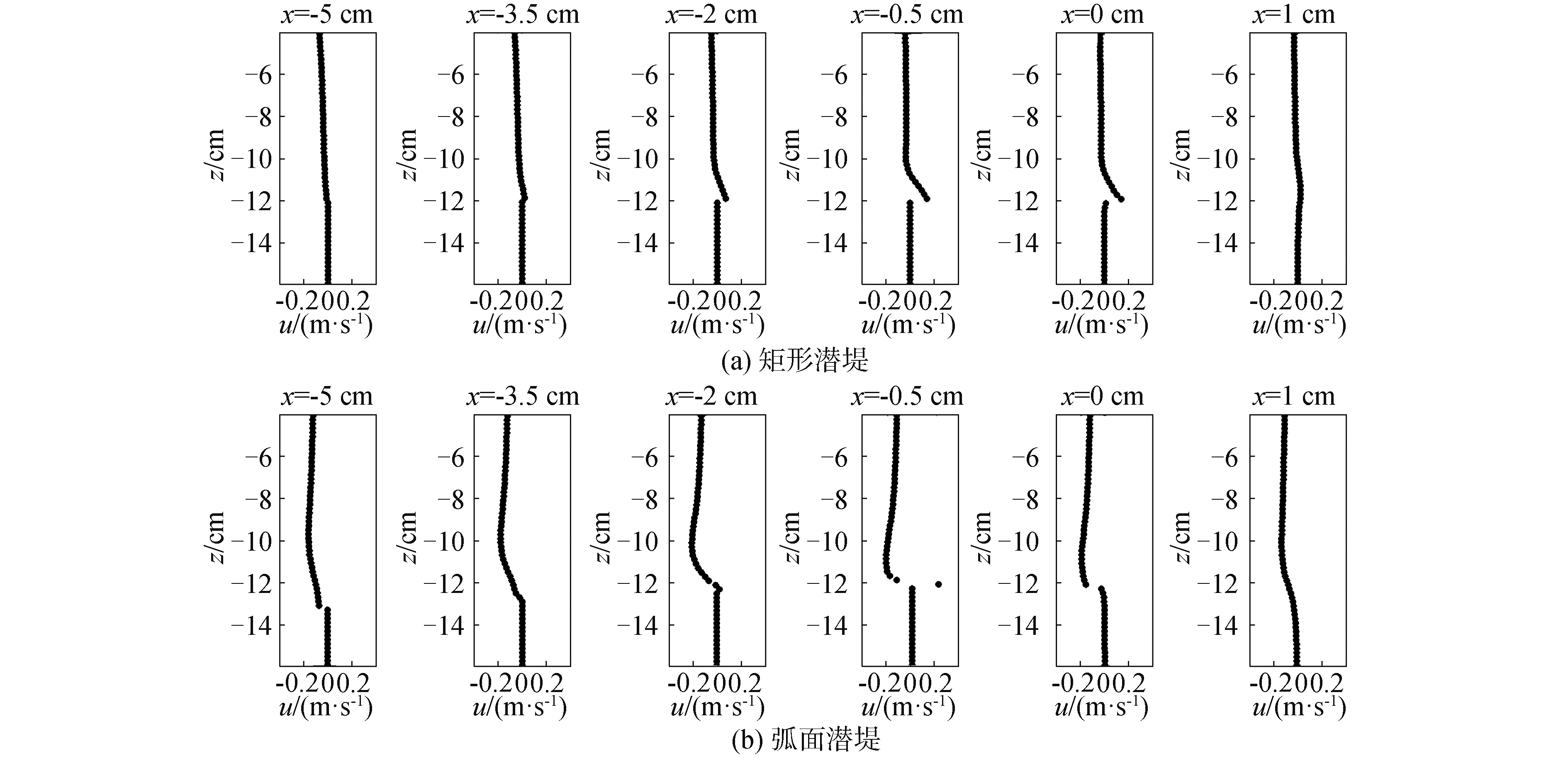
为了描述流体分离现象,图 6和图 7分别给出了波谷越堤时刻堤身周围不同位置处(-5~1 cm)的水平及垂向速度沿水深的分布。由图 6可以看出,矩形潜堤堤顶的水平速度在x=-3.5 cm处发生转向(由负转正),而弧面潜堤堤顶的水平速度在x=-2 cm处发生转向(由负转正),且在x=0处迅速转回。图 7显示,矩形潜堤堤顶的垂向速度在x=0处发生转向(由负转正),而弧面潜堤堤顶的垂向速度在x=-0.5 cm处发生转向(由负转正)。
|
Download:
|
| 图 6 波谷越堤时刻水平速度沿水深的分布 Fig. 6 Horizontal velocity profile along water depth at wave trough (相位a;水平速度顺波向为正) (phase a; going positive downstream) | |

|
Download:
|
| 图 7 波谷越堤时刻垂向速度沿水深的分布 Fig. 7 Vertical velocity profile along water depth at wave trough (相位a;垂向速度向上为正) (phase a; going positive upward) | |
图 8给出了波峰越堤时刻矩形潜堤与弧面潜堤周围的速度分布。可以看出,弧面潜堤后方涡流内的流速量值更大。此时,矩形潜堤的涡流中心与堤背的水平距离约为0.5S(S=0.069 m),而弧面潜堤的涡流中心与堤背的水平距离约为0.6S。

|
Download:
|
| 图 8 波峰越堤时刻的速度场比较(相位e) Fig. 8 Comparison of numerical velocity fields at wave crest (phase e) for submerged vertical and quartercircular breakwaters | |
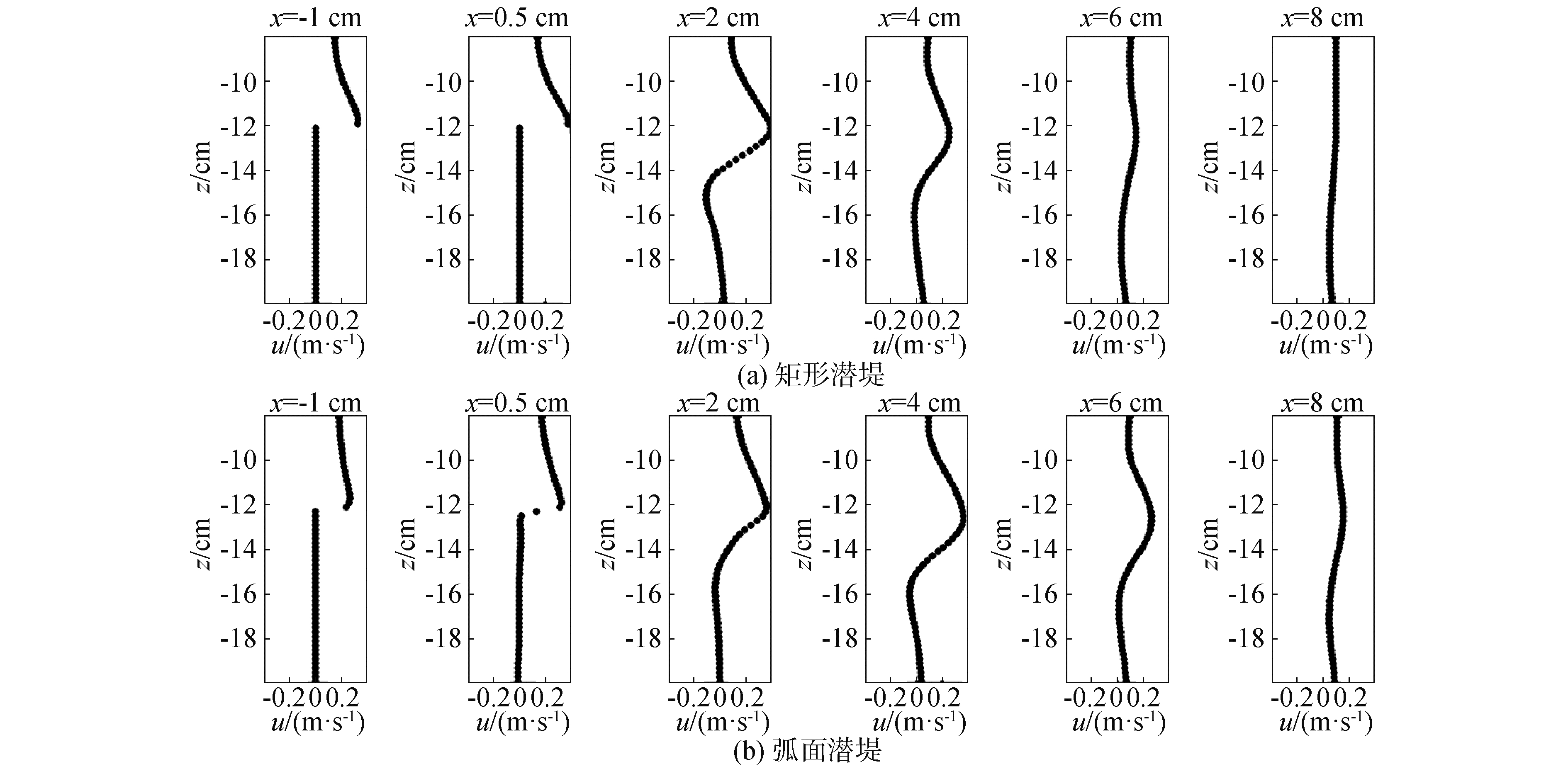
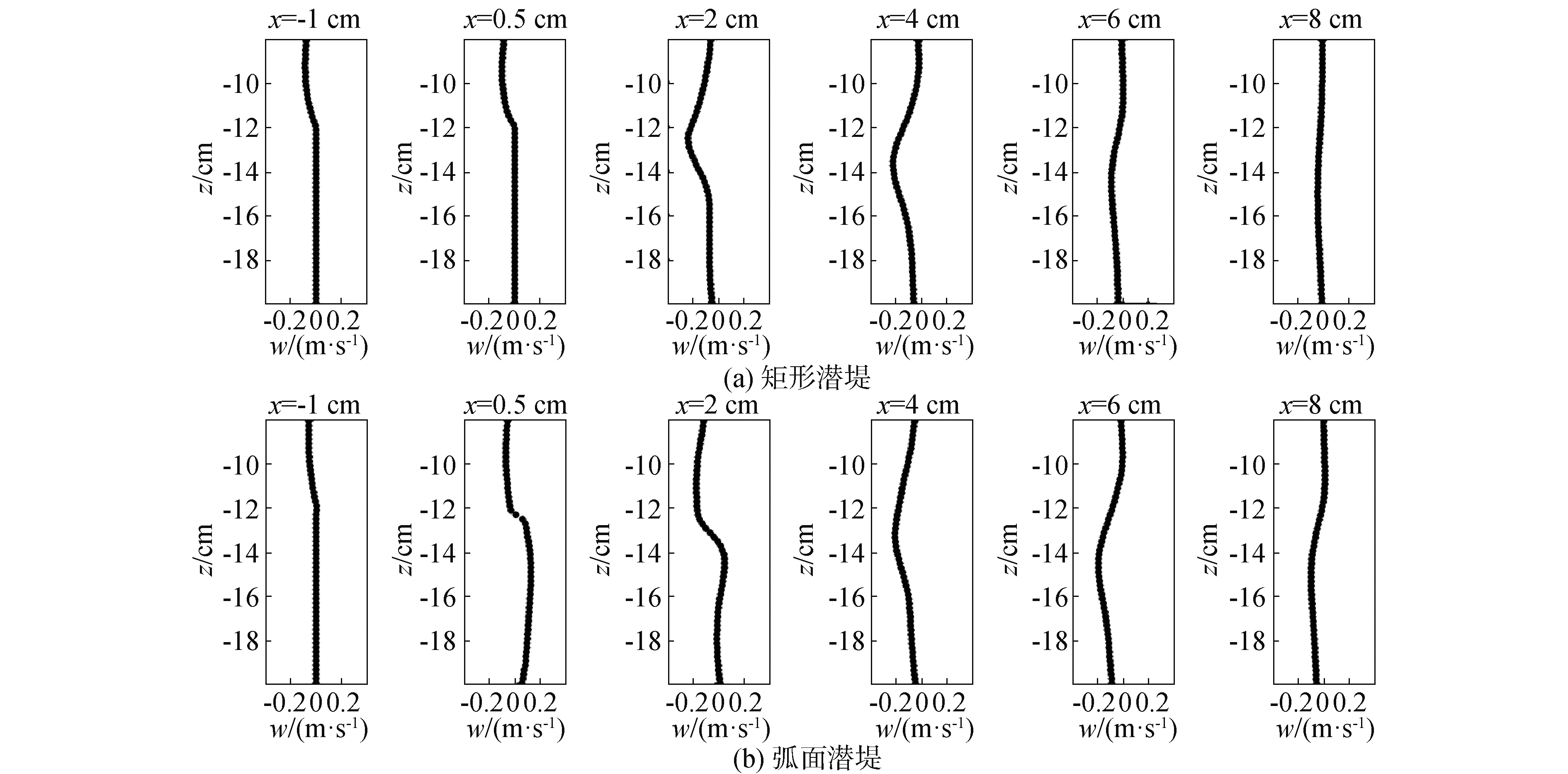
图 9和图 10分别给出了波峰越堤时刻堤身周围不同位置处(-2~8 cm)的水平及垂向速度沿水深的分布。由图 9可以看出,矩形潜堤背浪堤角后的水平速度在x=2 cm处发生转向(上正下负),弧面潜堤背浪堤角后的水平速度在x=4 cm处发生转向(上正下负)。图 10显示,矩形潜堤和弧面潜堤背浪堤角后的垂向速度均在x=2 cm处发生转向(上负下正),但弧面潜堤的垂向速度量值明显更大。
|
Download:
|
| 图 9 波峰越堤时刻水平速度沿水深的分布 Fig. 9 Horizontal velocity profile along water depth at wave crest (相位e;水平速度顺波向为正) (phase e; going positive downstream) | |
|
Download:
|
| 图 10 波峰越堤时刻垂向速度沿水深的分布 Fig. 10 Vertical velocity profile along water depth at wave crest (相位e;垂向速度向上为正) (phase e; going positive upward) | |
本节从涡量场角度分析涡流的演化过程。与图 4类似,采集一个波周期内各相位时刻(a~i)的涡量分布(图 11)。

|
Download:
|
| 图 11 各相位时刻的涡量场比较 Fig. 11 Comparison of numerical vorticity fields at different phases | |
可以看出,弧面潜堤和矩形潜堤的涡量演变过程类似。在波谷越堤时刻(相位a),背浪堤角上方正涡量聚集为一个逆时针涡,背浪堤角处逐渐产生负涡量,形成一个很小的顺时针涡。在向波峰爬升过程中(相位b~d),逆时针涡逐渐消散,顺时针涡范围先逐步增大后也开始消散,它们均向上游移动。到达波峰时刻(相位e),堤顶涡量基本消散。由于此时速度转向,背浪堤角处发生流体分离,产生顺时针负涡,且逐渐扩大,向堤后扩散,为了展示这一过程,将纵轴坐标下移6 cm。弧形潜堤在波谷向波峰转换的过程中,率先发生流体分离(相位c),形成顺时针涡,各过程均先于矩形潜堤发生。相位f~h对应波峰向波谷的转换,顺时针涡逐渐顺流传递并消散,堤顶涡量变化更为显著,已开始形成逆时针涡,弧面潜堤堤后的涡扩散范围更大,速度更快。相位i与相位a对应,表示前一个波谷越堤时的涡量场。
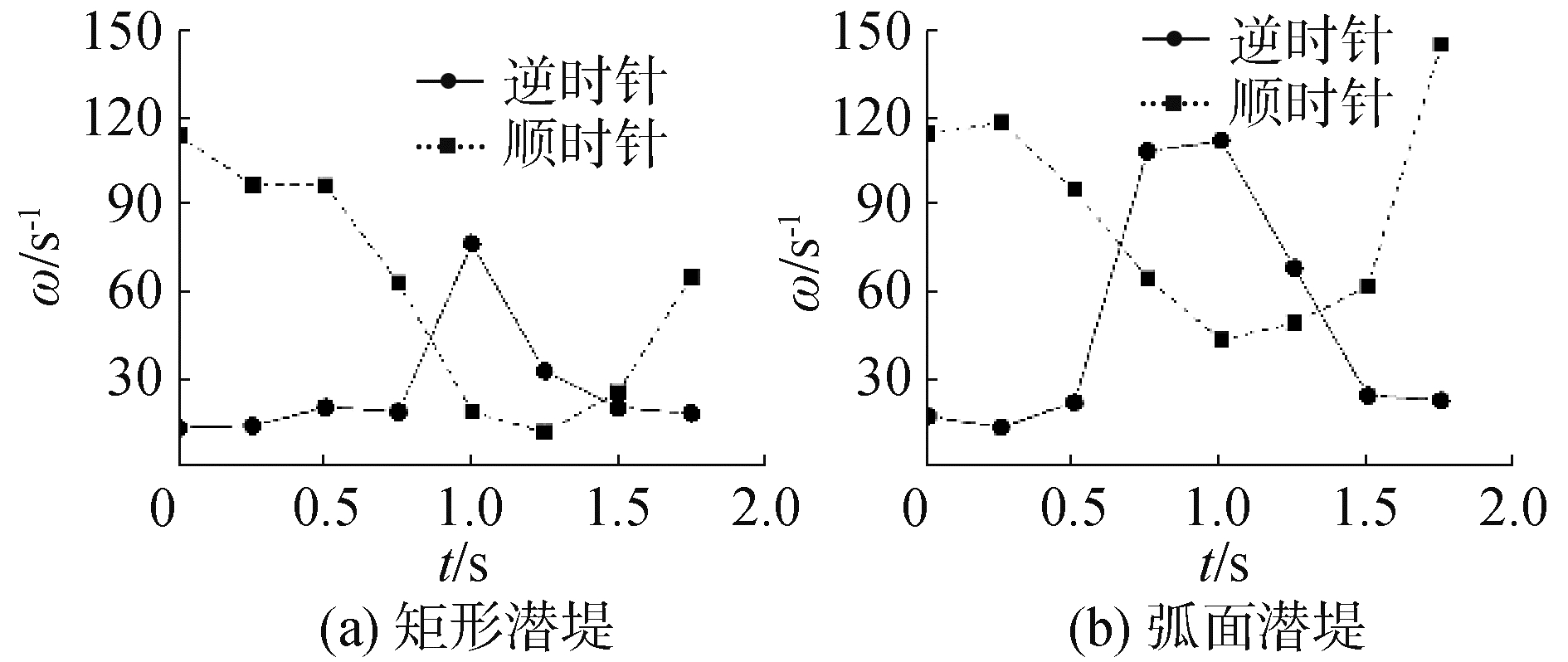
为了演示一个周期内涡流的强度变化,选取区间范围-1~8 cm,定义范围内各相位时刻顺时针(或逆时针)最大涡量的绝对值为涡强ω,并取10个周期的平均值以减小数据波动。图 12展示了各相位时刻的顺时针涡强和逆时针涡强的变化过程。可以看出,从波谷到波峰的过程(相位a~e),顺时针涡强呈减小趋势,逆时针涡强呈上升趋势。从波峰到波谷的过程(相位e~h),顺时针涡强呈上升趋势,逆时针涡强则呈减小趋势。总体而言,顺时针涡强的极值大于逆时针涡强,且弧面潜堤的顺时针和逆时针涡强的极值均高于矩形潜堤。
|
Download:
|
| 图 12 各相位时刻的背浪面涡强比较 Fig. 12 Comparison of leeside vortex intensities at different phases | |
1) 无模型建筑物时的反射测试表明,斜坡式多孔消波介质可有效减小数值波浪水槽属端反射,本文工况下,最优孔隙率为0.4。
2) 堤后波面的比较表明,弧面潜堤后的波谷非线性更为明显,预示更多能量向高频转换。
3) 速度场的比较表明,弧面潜堤发生流体分离及堤后涡流速度转向的位置距堤背更近,其涡流泄放过程较之矩形潜堤更剧烈。
4) 涡量场的比较表明,弧面潜堤的涡流强度更大,扩散范围更宽,消散更为迅速,表明更为强烈的波能损耗。
| [1] |
左其华, 窦希萍, 段子冰. 我国海岸工程技术展望[J]. 海洋工程, 2015, 33(1): 1-13. ZUO Qihua, DOU Xiping, DUAN Zibing. Prospects of coastal engineering technology in China[J]. The ocean engineering, 2015, 33(1): 1-13. (  0) 0)
|
| [2] |
范期锦, 李乃扬. 长江口二期工程北导堤局部破坏的原因及对策[J]. 中国港湾建设, 2004(2): 1-8. FAN Qijin, LI Naiyang. The reasons & countermeasures for north bank's part failure in the second phase regulation project of Yangtze Estuary[J]. China harbour engineering, 2004(2): 1-8. DOI:10.3969/j.issn.1003-3688.2004.02.001 (  0) 0)
|
| [3] |
YOUNG D M, TESTIK F Y. Onshore scour characteristics around submerged vertical and semicircular breakwaters[J]. Coastal engineering, 2009, 56(8): 868-875. DOI:10.1016/j.coastaleng.2009.04.003 (  0) 0)
|
| [4] |
TING F C K, KIM Y K. Vortex generation in water waves propagating over a submerged obstacle[J]. Coastal engineering, 1994, 24(1/2): 23-49. (  0) 0)
|
| [5] |
LIN Chang, CHANG S C, HO T C, et al. Laboratory observation of solitary wave propagating over a submerged rectangular dike[J]. Journal of engineering mechanics, 2006, 132(5): 545-554. DOI:10.1061/(ASCE)0733-9399(2006)132:5(545) (  0) 0)
|
| [6] |
POUPARDIN A, PERRET G, PINON G, et al. Vortex kinematic around a submerged plate under water waves. Part Ⅰ:Experimental analysis[J]. European journal of mechanics-B/fluids, 2012, 34: 47-55. DOI:10.1016/j.euromechflu.2012.02.003 (  0) 0)
|
| [7] |
REY V, BELZONS M, GUAZZELLI E. Propagation of surface gravity waves over a rectangular submerged bar[J]. Journal of fluid mechanics, 1992, 235: 453-479. DOI:10.1017/S0022112092001186 (  0) 0)
|
| [8] |
CHANG Kuangan, HSU T J, LIU P L F. Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle:part Ⅰ. Solitary waves[J]. Coastal engineering, 2001, 44(1): 13-36. DOI:10.1016/S0378-3839(01)00019-9 (  0) 0)
|
| [9] |
HSU T W, HSIEH C M, HWANG R R. Using RANS to simulate vortex generation and dissipation around impermeable submerged double breakwaters[J]. Coastal engineering, 2004, 51(7): 557-579. DOI:10.1016/j.coastaleng.2004.06.003 (  0) 0)
|
| [10] |
HUR D S, MIZUTANI N, KIM D S. Direct 3-D numerical simulation of wave forces on asymmetric structures[J]. Coastal engineering, 2004, 51(5/6): 407-420. (  0) 0)
|
| [11] |
JIANG Xuelian, WU Miling, LI Yanbao. Study on flow field around vertical breakwater under different overtopping conditions based on numerical simulation[J]. China ocean engineering, 2010, 24(4): 641-651. (  0) 0)
|
| [12] |
CHANG Kaohao, LIN Mengyu, HUANG L H. Modified Lagrangian vortex method with improved boundary conditions for water waves past a thin bottom-standing barrier[J]. International journal for numerical methods in fluids, 2015, 77(4): 183-205. DOI:10.1002/fld.v77.4 (  0) 0)
|
| [13] |
张娜, 张庆河, 邹国良, 等. 越浪堤后透射波周期特性研究[J]. 哈尔滨工程大学学报, 2017, 38(11): 1715-1720. ZHANG Na, ZHANG Qinghe, ZOU Guoliang, et al. Study on transmitted mean wave period after low-crested breakwater[J]. Journal of Harbin Engineering University, 2017, 38(11): 1715-1720. (  0) 0)
|
| [14] |
HOSOYAMADA T, TAKAHASHI S. Calculation of wave forces on caisson breakwater using the nonlinear boundary element method and its application for vertical and sloping caisson[J]. Coastal engineering in Japan, 1993(40): 726-730. (  0) 0)
|
| [15] |
VAN DER MEER J W, DAEMEN I F R. Stability and wave transmission at low-crested rubble-mound structures[J]. Journal of waterway, port, coastal, and ocean engineering, 1994, 120(1): 1-19. (  0) 0)
|
| [16] |
TANIMOTO K, YOSHINOTO N, NAMERIKAWA N, et al. Hydraulic characteristics and design wave forces of semicircular caisson breakwaters[J]. Coast. eng., JSCE, 1987(34): 551-55. (  0) 0)
|
| [17] |
谢世楞, 李炎保, 吴永强, 等. 圆弧面防波堤波浪力初步研究[J]. 海洋工程, 2006, 24(1): 14-18. XIE Shileng, LI Yanbao, WU Yongqiang, et al. Preliminary research on wave forces on quarter circular breakwater[J]. The ocean engineering, 2006, 24(1): 14-18. DOI:10.3969/j.issn.1005-9865.2006.01.003 (  0) 0)
|
| [18] |
SHI Yanjiao, WU Miling, JIANG Xuelian, et al. Experimental researches on reflective and transmitting performances of quarter circular breakwater under regular and irregular waves[J]. China ocean engineering, 2011, 25(3): 469. DOI:10.1007/s13344-011-0038-1 (  0) 0)
|
| [19] |
QIE Luwen, ZHANG Xiang, JIANG Xuelian, et al. Research on partial coefficients for design of quarter-circular caisson breakwater[J]. Journal of marine science and application, 2013, 12(1): 65-71. (  0) 0)
|
| [20] |
BINUMOL S, RAO S, HEGDE A V. Runup and Rundown characteristics of an emerged seaside perforated quarter circle breakwater[J]. Aquatic procedia, 2015, 4: 234-239. DOI:10.1016/j.aqpro.2015.02.032 (  0) 0)
|
| [21] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of computational physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 (  0) 0)
|
| [22] |
LIN Pengzhi, KARUNARATHNA S A. Numerical study of solitary wave interaction with porous breakwaters[J]. Journal of waterway, port, coastal, and ocean engineering, 2007, 133(5): 352-363. DOI:10.1061/(ASCE)0733-950X(2007)133:5(352) (  0) 0)
|
| [23] |
LIU P L F, WU T R, RAICHLEN F, et al. Runup and rundown generated by three-dimensional sliding masses[J]. Journal of fluid mechanics, 2005, 536: 107-144. DOI:10.1017/S0022112005004799 (  0) 0)
|
| [24] |
HU Kaicheng, HSIAO S C, HWUNG H H, et al. Three-dimensional numerical modeling of the interaction of dam-break waves and porous media[J]. Advances in water resources, 2012, 47: 14-30. DOI:10.1016/j.advwatres.2012.06.007 (  0) 0)
|
| [25] |
CHANG Kuangan, HSU T J, LIU P L F. Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle:part Ⅱ:Cnoidal waves[J]. Coastal engineering, 2005, 52(3): 257-283. DOI:10.1016/j.coastaleng.2004.11.006 (  0) 0)
|
| [26] |
郭晓宇.数值波浪水槽及其应用研究[D].上海: 上海交通大学, 2011. GUO Xiaoyu. Studies on numerical wave flume and its application[D]. Shanghai: Shanghai Jiao Tong University, 2011. (  0) 0)
|
| [27] |
相昌盛.三维数值波浪水槽的构建及其应用研究[D].青岛: 中国海洋大学, 2013. XIANG Changsheng. Generation of the three dimensional numerical wave tank and study of its application[D]. Qingdao: Ocean University of China, 2013. (  0) 0)
|
| [28] |
张婷, 张庆河, 韩涛. 数值波浪水槽中的斜坡式孔隙结构规则波消波研究[J]. 广东水利水电, 2010(10): 43-46. ZHANG Ting, ZHANG Qinghe, HAN Tao. Regular wave absorption research on inclined porous structure in a numerical wave tank[J]. Guangdong water resources and hydropower, 2010(10): 43-46. DOI:10.3969/j.issn.1008-0112.2010.10.013 (  0) 0)
|
| [29] |
李世森, 江鸣. 数值波浪水槽末段孔隙结构消波性能的研究[J]. 港工技术, 2012, 49(5): 1-4. LI Shisen, JIANG Ming. Study on wave-absorbing performance of porosity solid in end-piece of numerical wave flume[J]. Port engineering technology, 2012, 49(5): 1-4. DOI:10.3969/j.issn.1004-9592.2012.05.001 (  0) 0)
|
| [30] |
詹杰民, 董志.黏性数值波浪水槽的多孔介质消波方法[C]//第十四届中国海洋(岸)工程学术讨论会论文集.呼和浩特, 2009: 437-441. ZHAN Jiemin, DONG Zhi. Performance of a porous wave absorber in a viscous numerical wave flume[C]//Proceedings of the 14th China Ocean and Coastal Engineering. Hohhot, 2009: 437-441. (  0) 0)
|
| [31] |
MANSARD E P D, FUNKE E R. The measurement of incident and reflected spectra using a least squares method[C]//Proceedings of the 17th International Conference on Coastal Engineering. Sydney, 1980, 1: 154-172.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


