2015年8·12天津港大爆炸事故引发了社会对港口危险化学品(危化品)物流安全问题的高度重视。天津港大爆炸事故经调查发现众多问题,其中天津市交通运输委员会作为天津港危险化学品经营管理行业主管部门,违规发放经营许可证,监管不严是导致事故发生的主要原因。随着我国经济的不断发展,工业化不断深入,危险化学品物流行业呈现出危险化学品需求量大、种类多和危险性强等特点,且通过港口进行中长距离的异地危险化学品物流运输不断增加。目前,港口频频发生危化品事故,凸显我国港口危化品物流安全监督管理形势严峻,严重影响港口的安全运作和社会的安定。因此,如何通过博弈论中的演化机制刻画港口管理者与危化品物流企业间的关系,使港口危化品物流参与双方充分博弈,进而对港口危化品物流企业形成良好的激励与引导机制十分重要。
近年来危化品需求旺盛,但事故频发,围绕危化品运输安全问题开展了一系列研究[1-3]。文献[4-6]对危化品事故进行统计分析,以研究其发生规律和原因等。针对危化品物流中存在的风险,学者提出相应的安全运输策略或对事故分析方法[7-9]。还有一些学者针对危险货物运输风险,提出新的联运模式或采用射频技术降低风险或者采用系统动力学等方法进行管理风险[10-12]。而国内外学者关于博弈论应用的研究很多,学者们运用博弈理论分析了网络或供应链中的合作问题[13-14]。采用博弈论研究竞争风险以及资源分配问题[15-16]。利用博弈论研究情感预测算法和策略协同进化关系[17-18]。还有学者基于博弈论研究了政府监管策略对企业或第三方监管机构策略的影响[19-21]。上述关于博弈论研究多侧重于食品安全等政府博弈,较少关注港口危化品物流方面,且鲜有研究从演化机理出发对港口危化品风险进行管理。因此,本文构建演化博弈模型,并考虑政府监管策略和事故发生率两个因素对港口企业的影响机理,通过数值仿真更直观地反映出不同监管策略和事故发生率下政府和企业策略演化规律,剖析不同策略下存在的问题,进而为政府监管提供思考。
1 演化博弈模型的构建 1.1 模型假设及符号定义为便于对港口危化品政府监管机构和港口危化品物流企业之间的演化博弈模型进行分析,对模型参数及符号说明见表 1,并进行如下假设:
| 表 1 港口危化品物流企业和政府演化博弈支付矩阵 Table 1 Evolutionary game payoff matrix of port hazardous chemicals management enterprises and government |
1) 有2个有限理性的局中人:港口危化品物流企业和和政府监管机构;
2) 博弈模型为非对称博弈;
3) 模型中局中人的信息为不完全信息。
在此博弈模型中,危化品物流企业设施和工人安全投入为a,港口危化品物流企业正常经营的收入为r,港口危化品物流企业设施不安全的罚款为m,政府监管部门严格监管付出的成本为c,发生事故给政府带来的负面声誉为b,事故发生概率为p,事故发生造成的损失为f。
假设港口危化品物流企业重视经营安全问题,设施安全的比例为x,那么设施不安全的比例为1-x,政府监管部门对港口危化品物流企业严格监管的比例为y,则宽松监管的比例为1-y。港口危化品物流企业和政府演化博弈支付矩阵如表 1。
1.2 复制动态方程的建立港口危化品企业选择设施安全的期望收益:
| $ {u_{A1}} = y(r - a) + (1 - y)(r - a) $ | (1) |
港口危化品企业选择设施不安全的期望收益:
| $ {u_{A2}} = r - pf - my $ | (2) |
港口危化品企业选择设施安全和设施不安全的平均期望收益:
| $ {{\bar U}_A} = x{u_{A1}} + (1 - x){u_{A2}} $ | (3) |
港口危化品企业选择设施安全比例的复制动态过程为:
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = F(x, y) = x(1 - x)(my + pf - a) $ | (4) |
政府监管部门选择严格监管的期望收益:
| $ {u_{B1}} = - cx + (1 - x)(m - c) $ | (5) |
政府监管部门选择宽松监管的期望收益:
| $ {u_{B2}} = - pb(1 - x) $ | (6) |
政府监管部门选择严格监管和宽松监管的平均期望收益:
| $ {{\bar U}_B} = y{u_{B1}} + (1 - y){u_{B2}} $ | (7) |
政府监管部门选择严格监管的复制动态过程:
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = H(x, y) = x(1 - x)(my + pf - a) $ | (8) |
根据式(4)和(8)得系统的雅可比矩阵J为:
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {(1 - 2x)(my + pf - a)}&{mx(1 - x)}\\ { - (m + pb)y(1 - y)}&{(1 - 2y)[ - (m + pb)x + m - c + pb]} \end{array}} \right] $ | (9) |
矩阵J的行列式为:
| $ \begin{array}{l} {\rm{tr}}\mathit{\boldsymbol{J}} = (1 - 2x)(my + pf - a)(1 - 2y) \cdot \\ \;\;\;\;\;\;\;[ - (m + pb)x + m - c + pb] \end{array} $ | (10) |
根据微分方程稳定性定理,演化稳定策略对较小的干扰具有稳定性,在数学上,F(x, y)的导数必须小于0,即矩阵J的行列式大于0,矩阵的迹小于0。令F(x, y)=0,同时H(x, y)=0,求得系统的5个平衡点,分别为:(0,0)、(0,1)、(1,0)、(1,1)、(x0,y0),
情况1:当pf-a>0且m-c+pb>0时,此时的稳定点为(1,0)即(设施安全,宽松监管)。
情况2:当pf-a>0且m-c+pb<0时,此时的稳定点为(1,0),即(设施安全,宽松监管)。
情况3:当pf-a<0且m-c+pb>0,m+pf-a>0时,此时系统没有稳定点,可得该情况条件下没有稳定策略。
情况4:当pf-a<0且m-c+pb>0,m+pf-a<0时,此时的稳定点为(0,1),即(设施不安全,严格监管)。
情况5:当pf-a<0且m-c+pb<0,m+pf-a>0时,此时的稳定点为(0,0),即(设施不安全,宽松监管)。
情况6:当pf-a<0且m-c+pb<0,m+pf-a<0时,此时的稳定点为(0,0),即(设施不安全,宽松监管)。
2 数值仿真 2.1 演化稳定策略下的模型仿真根据演化模型对危化品物流企业和政府监管机构双方策略建模分析,为进一步探讨危化品企业策略的选择和监管机构策略选择之间的关系,采用数值仿真进一步观察双方行为的演化机制。基于Matlab软件,资金为万元,港口危化品物流企业采取设施安全的比例x分别为0.1、0.3、0.7和0.9,参数设置如表 2所示,演化结果如图 1和2所示。
| 表 2 港口危化品物流企业和政府监管相关参数设置 Table 2 Parameter setting of port hazardous chemicals management enterprises and gerernment regulators |
|
Download:
|
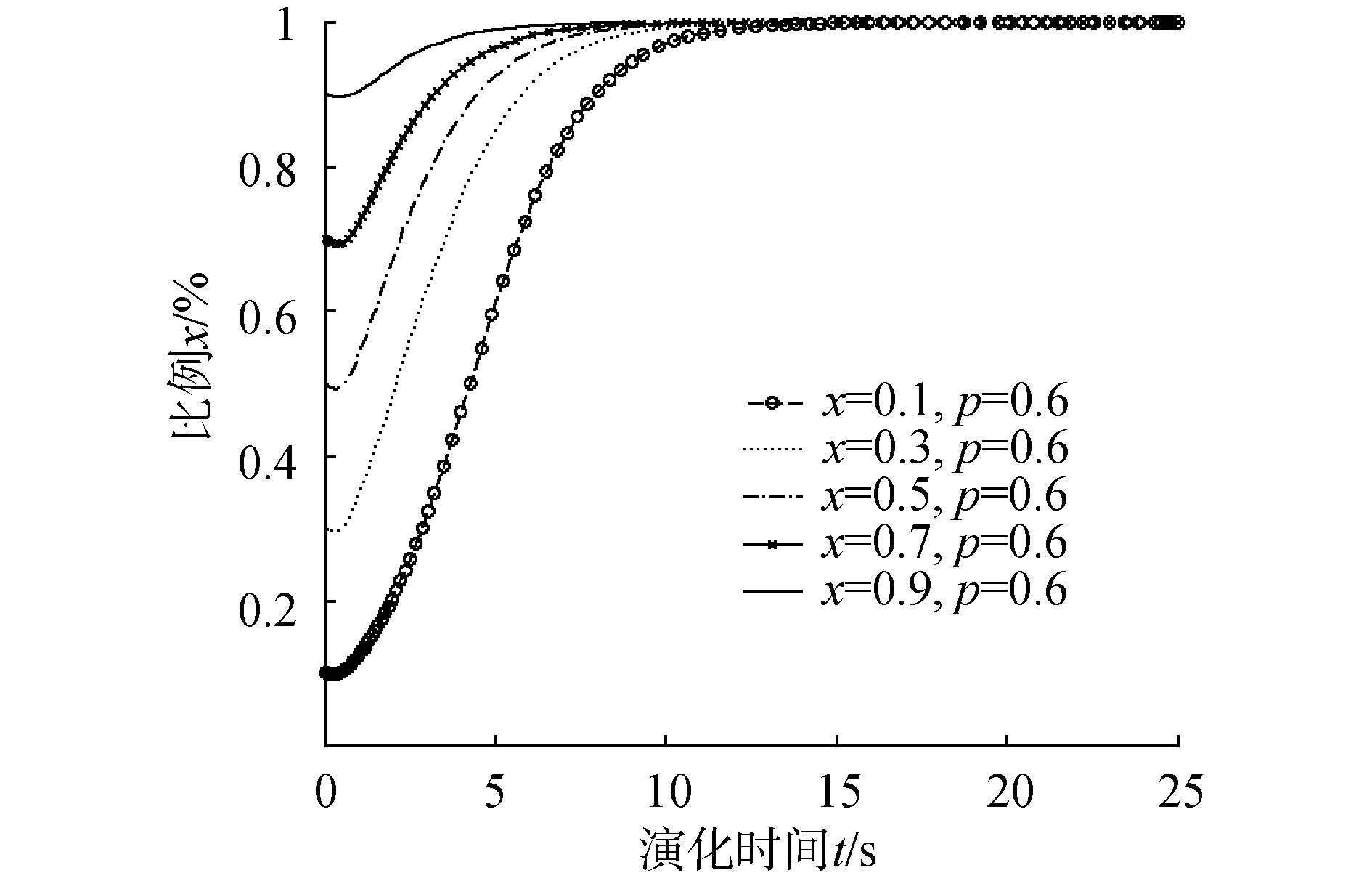
| 图 1 情况1和2港口危化品企业采取设施安全策略演化 Fig. 1 Case 1 and 2 probability change of port hazardous chemicals enterprises take facility safety policy | |
|
Download:
|
| 图 2 情况3和4港口危化品企业采取设施安全策略演化 Fig. 2 Case 3 and 4 probability change of port hazardous chemicals enterprises take facility safety policy | |
情况1条件下如图 1所示,港口危化品物流企业采取安全设施的比例x的取值分别为0.1、0.3、0.5、0.7和0.9,监管部门采取严格监管的比例y为0.2。在这一过程中,港口危化品物流企业采取设施安全进行经营的比例从0.1到0.9,演化结果向1趋近,也就是当监管部门采取宽松监管的概率较大时,港口危化品物流企业一开始采取何种策略,通过演化博弈结果显示最终将趋向于设施安全策略。此时,需要满足的条件是事故发生时造成的损失大于企业加大设施和工人安全保障费用投入,同时企业设施不安全条件下被监管发现的罚款以及发生事故时给政府带来的负面影响之和大于政府投入的监管成本。演化博弈结果趋向于企业采取设施安全,政府监管部门采取宽松监管策略。
在情况2条件下仿真结果与情况1一致,如图 1所示,政府监管部门采用严格监管比例仍为0.2,改变其他参数设置如表 3,演化博弈结果仍为设施安全和宽松监管。说明企业对于设施安全进行的投入成本和事故发生带来的损失之间的关系影响演化结果。
| 表 3 港口危化品物流企业和政府监管相关参数设置 Table 3 Parameter setting of port hazardous chemicals meragerment enterprises and government regulators |
在情况3条件下,改变参数设置如表 3中情况3,结果如图 2所示。事故发生时造成的损失小于企业加大设施和工人安全保障费用投入,同时企业设施不安全条件下被监管发现的罚款以及发生事故时给政府带来的负面影响之和大于政府投入的监管成本,企业设施不安全条件下被监管发现的罚款以及发生事故时给企业带来的损失之和小于企业投入的安全成本。演化结果港口危化品物流企业采取设施安全进行经营的比例从不同初始值趋向于0。最终博弈结果为设施不安全和严格监管。
在情况4条件下改变参数设置如表 3中情况4,仿真结果与情况3一致,如图 2所示。在这个过程中,满足的条件是事故发生造成的损失小于企业加大设施和工人安全保障费用投入,同时企业设施不安全条件下被监管发现的罚款以及发生事故时给政府带来的负面影响之和小于政府监管成本。最终演化博弈结果为设施不安全,宽松监管。这个情况下的演化结果不是想要的理想状态,因此,为了使演化向更理想的状态发展,需要满足相应条件。
一般认为企业收入增加会增加安全成本投入,但仿真结果表明,在港口危化品监管过程中,港口危化品物流企业是否采取设施安全策略与其经营收入无关,而与其加大安全设施投入的成本和事故发生造成的损失关系密切;政府是否采取严格监管行为,与其需要投入的监管成本和事故发生造成的损失以及对危化品物流企业设施不安全的处罚相关。
2.2 考虑政府监管比例和事故发生概率的模型仿真上述研究发现政府监管严格与否和事故发生概率的大小直接影响企业策略选择。在此,进一步考虑事故发生概率变化时以及政府监督检查概率波动对港口危化品企业的策略选择的影响。仿真设置同上,参数如表 3,仿真结果如图 3~5。
|
Download:
|
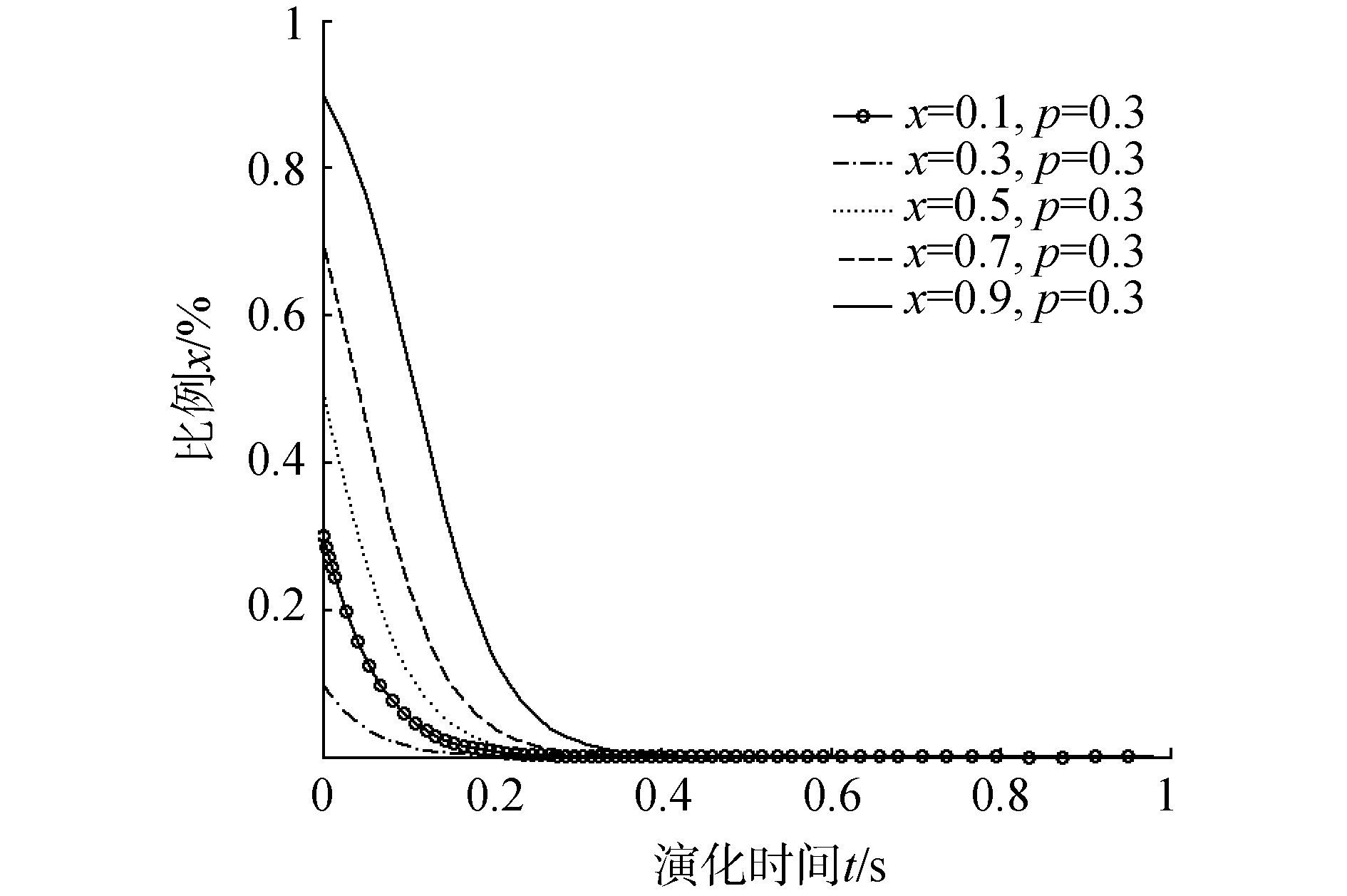
| 图 3 p=0.2时港口危化品企业采取设施安全策略演化 Fig. 3 Probability change of port hazardous chemicals enterprises take facility safety policy when p=0.2 | |
|
Download:
|
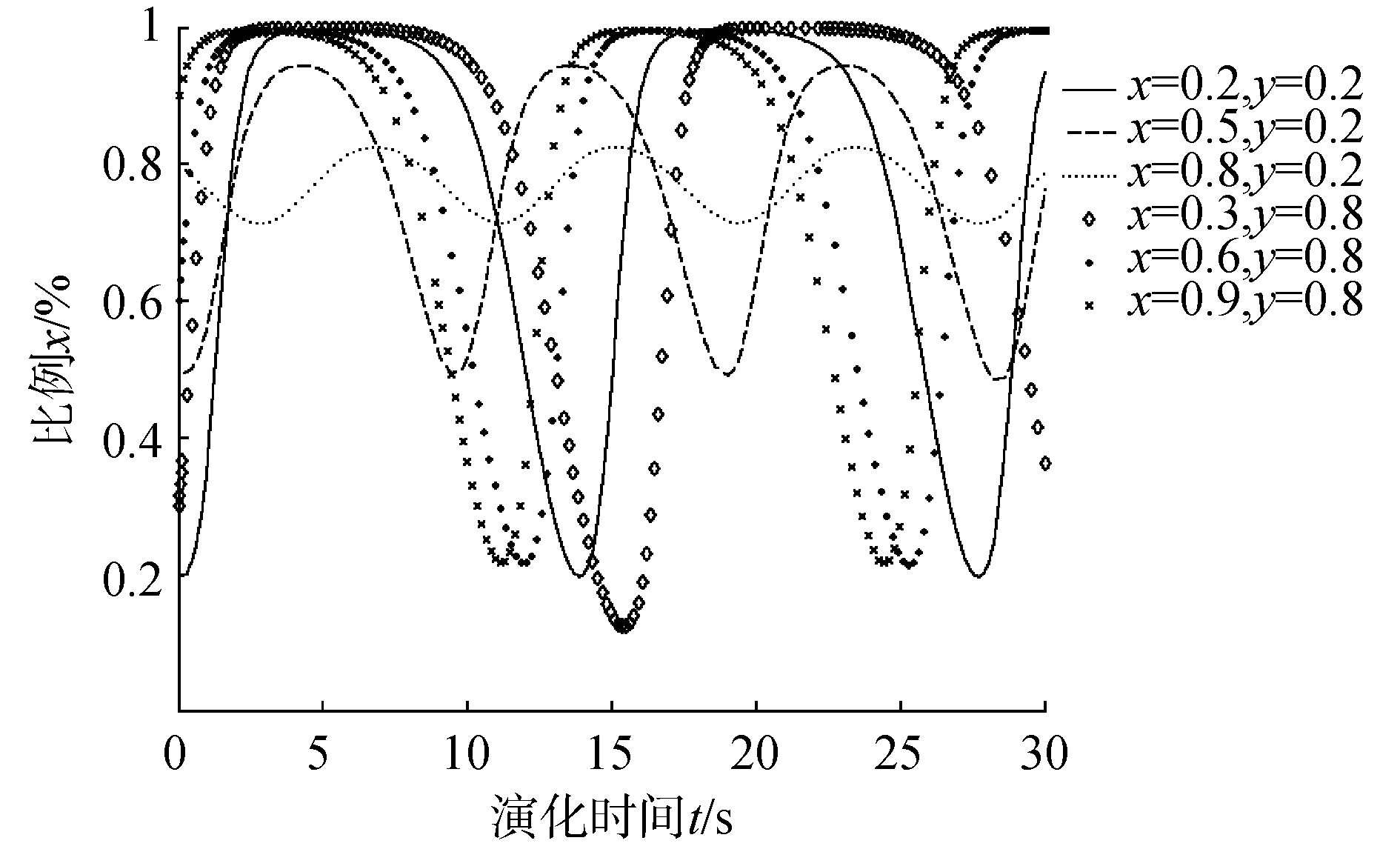
| 图 4 p=0.3时港口危化品企业采取设施安全策略演化 Fig. 4 Probability change of port hazardous chemicals enterprises take facility safety policy when p=0.3 | |
|
Download:
|
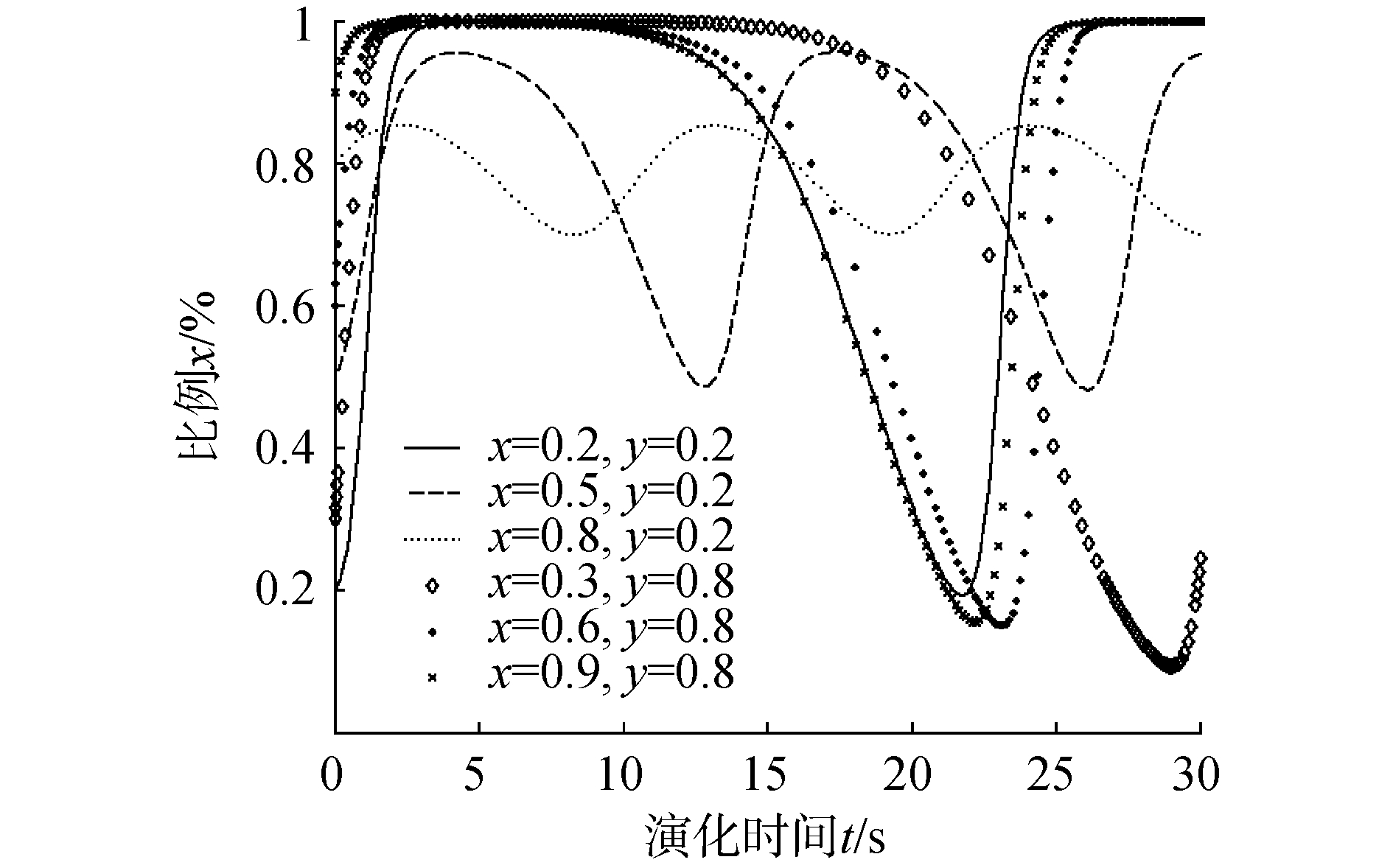
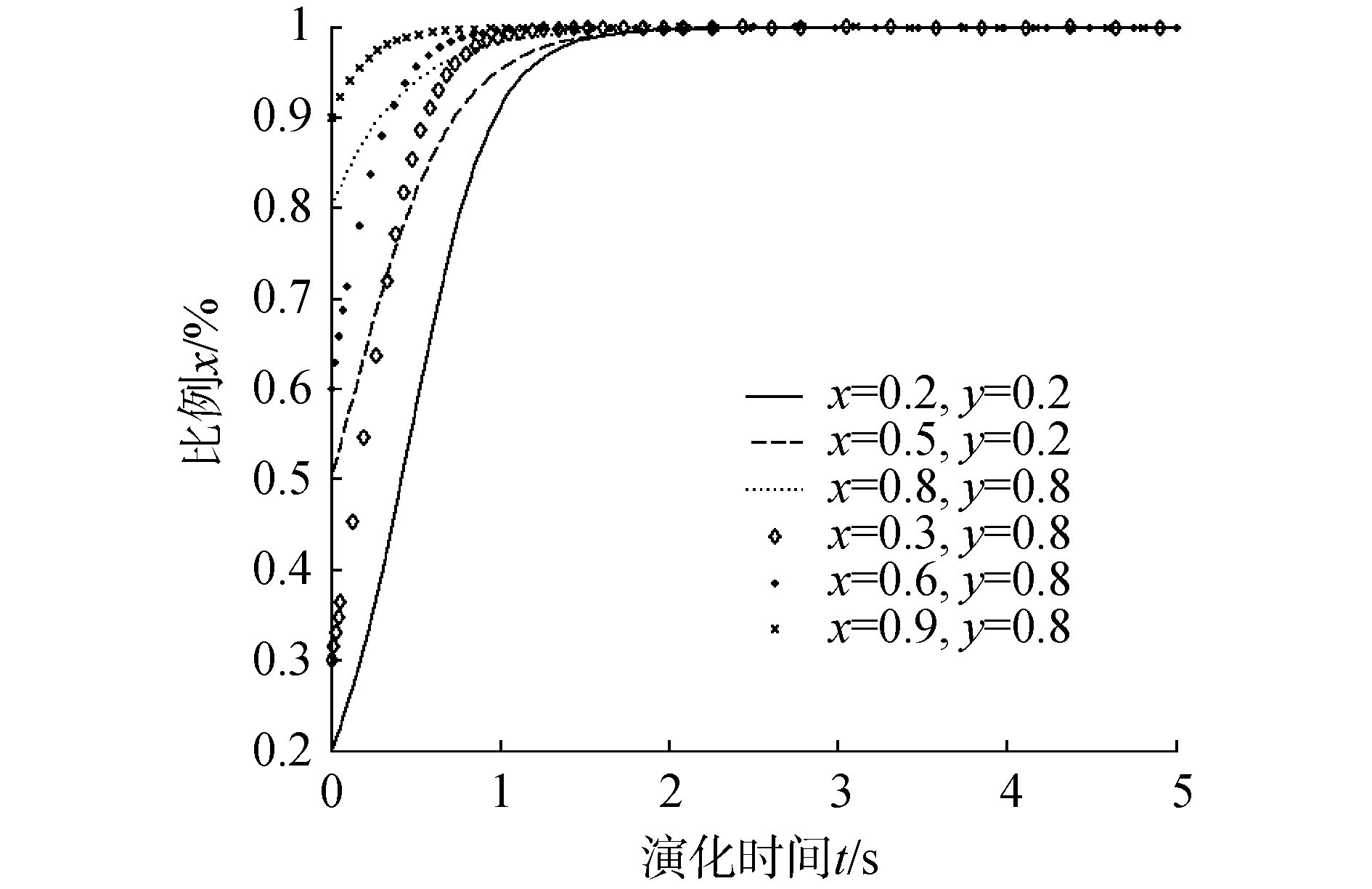
| 图 5 p=0.8时港口危化品企业采取设施安全策略演化 Fig. 5 Probability change of port hazardous chemicals enterprises take facility safety policy when p=0.8 | |
如图 3,当政府采取严格监督检查的比例y为0.2时,如图中x为0.2、0.5和0.8,企业采取设施安全的比例在0到1之间波动;当y增加到0.8时,如图中x为0.3、0.6和0.9,企业选择设施安全的比例呈现先上升,后波动的趋势。即企业开始有0.1的概率加大投入确保设施安全,随着时间的推移,企业采取设施安全的比例逐渐为1,但随着双方继续博弈,企业选择设施安全的比例呈现波动趋势。这表明政府采取严格监督检查的比例增加时,企业为减少受到的惩罚,会在短时间内先增加设施安全投入和人员培训,以应对政府的严格监管。
如图 4,当政府采取严格监管比例y为0.2时,如图中x为0.2、0.5和0.8,企业采取设施安全的策略的比例在0到1之间波动,与事故发生概率为0.2时相比,企业选择设施安全的比例在演化时间10之前有所上升,但后期仍呈波动趋势;当y增加到0.8时,如图中x为0.3、0.6和0.9,企业选择设施安全的比例在一段时间内趋于1,这段时间会增加设施安全投入和人员培训以应对政府监管,这段时间比y为0.2时更长,但后期仍会转向设施不安全策略。这表明政府采取严格监督检查的比例和事故发生概率增加时,企业为减少受到的惩罚和损失,会在一定时间内采取设施安全策略应对监管风险。
当危化品事故发生概率不断上升到0.8时,如图 5所示,这时无论政府采取严格监管的比例为0.2或0.8,随着时间推移,港口危化品企业很快选择重视安全问题,使得生产环境趋于安全范围,以减少事故发生。说明当事故发生率较高时,无论政府采取严格监管的概率大或小,企业都会重视安全经营,加大设施投入和人员培训等,以获得正常经营收入。
一般认为,如果使港口危化品企业更倾向于选择安全合法经营,应加大政府严格监管的力度。但上述研究发现结论并不如此,此种现象称为悖论,政府和企业之间的演化模型体现了监管悖论现象。
3 结论1) 港口企业采取何种策略与其经营收入无关,而与事故损失和设施安全投入成本有关。当危化品物流企业发生事故时造成的损失大于港口危化品物流企业对重视设施安全进行投资的成本时,存在演化稳定策略设施安全和宽松监管。当危化品物流企业对设施安全投资成本过高时,企业容易选择忽略安全问题。
2) 我国港口危化品监管过程中,事故发生率和政府采取严格监管的概率对港口危化品企业采取何种策略产生影响。当事故发生概率较高时,无论政府选择何种监管方式,企业都选择设施安全。政府严格监管的比例短期内对企业策略选择产生较大影响,长期对企业策略选择的影响减弱。
3) 演化仿真结果表明,港口危化品监管中存在“监管悖论”现象。即政府采取严格监管策略不会使企业一直采取设施安全策略。政府采取严格监管策略时,短期间港口企业会先增加设施安全投入和人员培训,以应对政府的严格监管,但后期又会转向设施不安全策略。
| [1] |
JIANG Mingwei, YING Ming. Study on route selection for hazardous chemicals transportation[J]. Procedia engineering, 2014, 71: 130-138. DOI:10.1016/j.proeng.2014.04.019 (  0) 0)
|
| [2] |
YU Lean, LI Ling, TANG Ling. What can mass media do to control public panic in accidents of hazardous chemical leakage into rivers? A multi-agent-based online opinion dissemination model[J]. Journal of cleaner production, 2017, 143: 1203-1214. DOI:10.1016/j.jclepro.2016.11.184 (  0) 0)
|
| [3] |
DUAN Weili, CHEN Guohua, YE Qing, et al. The situation of hazardous chemical accidents in China between 2000 and 2006[J]. Journal of hazardous materials, 2011, 186(2/3): 1489-1494. (  0) 0)
|
| [4] |
李健, 王雅洁, 吴军, 等. 零星危险化学品快递运输风险博弈分析[J]. 中国安全生产科学技术, 2016, 12(3): 108-114. LI Jian, WANG Yajie, WU Jun, et al. Game analysis on risk in express transportation of sporadic hazardous chemicals[J]. Journal of safety science and technology, 2016, 12(3): 108-114. (  0) 0)
|
| [5] |
ZHANG Heda, ZHENG Xiaoping. Characteristics of hazardous chemical accidents in China:A statistical investigation[J]. Journal of loss prevention in the process industries, 2012, 25(4): 686-693. DOI:10.1016/j.jlp.2012.03.001 (  0) 0)
|
| [6] |
ELLIS J. Analysis of accidents and incidents occurring during transport of packaged dangerous goods by sea[J]. Safety science, 2011, 49(8/9): 1231-1237. (  0) 0)
|
| [7] |
BU Quanmin, WANG Zhanjun, Tong Xing. Research on cause analysis and safety management for road transportation accidents of dangerous chemicals[J]. Applied mechanics and materials, 2013, 361-363: 2282-2286. DOI:10.4028/www.scientific.net/AMM.361-363 (  0) 0)
|
| [8] |
SI Hu, JI Hong, ZENG Xiaohong. Quantitative risk assessment model of hazardous chemicals leakage and application[J]. Safety science, 2012, 50(7): 1452-1461. DOI:10.1016/j.ssci.2012.01.011 (  0) 0)
|
| [9] |
李建民, 齐迹, 郑中义. 不确定条件下海上危化品运输安全演变机理[J]. 哈尔滨工程大学学报, 2014, 35(6): 707-712. LI Jianmin, QI Ji, ZHENG Zhongyi. Safety evolution mechanism for the maritime dangerous chemical transportation system under uncertainty conditions[J]. Journal of Harbin Engineering University, 2014, 35(6): 707-712. (  0) 0)
|
| [10] |
WANG Xuefeng, XIE Jiajia, LIU Yinghui. RFID application in dangerous chemicals safety management[J]. Applied mechanics and materials, 2012, 198-199: 1261-1264. DOI:10.4028/www.scientific.net/AMM.198-199 (  0) 0)
|
| [11] |
帅斌, 黄丽霞. 危险货物运输风险评估研究动态[J]. 中国安全科学学报, 2014, 24(7): 50-56. SHUAI Bin, HUANG Lixia. Developments in research on assessment of risk in hazardous materials transportation[J]. China safety science journal, 2014, 24(7): 50-56. (  0) 0)
|
| [12] |
余乐安, 李玲, 武佳倩, 等. 基于系统动力学的危化品水污染突发事件中网络舆情危机应急策略研究[J]. 系统工程理论与实践, 2015, 35(10): 2687-2697. YU Lean, LI Ling, WU Jiaqian, et al. Emergency policy exploration for network public opinion crisis in water pollution accident by hazardous chemicals leakage based on systematic dynamics[J]. Systems engineering-theory & practice, 2015, 35(10): 2687-2697. DOI:10.12011/1000-6788(2015)10-2687 (  0) 0)
|
| [13] |
SEREDYNSKI M, BOUVRY P. Analysing the development of cooperation in MANETs using evolutionary game theory[J]. Journal of supercomputing, 2013, 63(3): 854-870. DOI:10.1007/s11227-012-0769-7 (  0) 0)
|
| [14] |
JI Ping, MA Xin, LI Gang. Developing green purchasing relationships for the manufacturing industry:An evolutionary game theory perspective[J]. International journal of production economics, 2015, 166: 155-162. DOI:10.1016/j.ijpe.2014.10.009 (  0) 0)
|
| [15] |
CHEUNG M, ZHUANG Jun. Regulation games between government and competing companies:Oil spills and other disasters[J]. Decision analysis, 2012, 9(2): 156-164. DOI:10.1287/deca.1120.0233 (  0) 0)
|
| [16] |
PODIMATA M V, YANNOPOULOS P C. Evolution of game theory application in irrigation systems[J]. Agriculture and agricultural science procedia, 2015, 4: 271-281. DOI:10.1016/j.aaspro.2015.03.031 (  0) 0)
|
| [17] |
LUO Chao, ZHANG Xiaolin, ZHENG Yuanjie. Chaotic evolution of prisoner's dilemma game with volunteering on interdependent networks[J]. Communications in nonlinear science and numerical simulation, 2017, 47: 407-415. DOI:10.1016/j.cnsns.2016.12.004 (  0) 0)
|
| [18] |
ZHANG Kangjie, CHENG Hongyan. Co-evolution of payoff strategy and interaction strategy in prisoner's dilemma game[J]. Physica A:statistical mechanics and its applications, 2016, 461: 439-445. DOI:10.1016/j.physa.2016.04.045 (  0) 0)
|
| [19] |
张国兴, 高晚霞, 管欣. 基于第三方监督的食品安全监管演化博弈模型[J]. 系统工程学报, 2015, 30(2): 153-164. ZHANG Guoxing, GAO Wanxia, GUAN Xin. Evolutionary game model of food safety supervision based on the third-party intendance[J]. Journal of systems engineering, 2015, 30(2): 153-164. (  0) 0)
|
| [20] |
刘家国, 王军进, 周欢, 等. 基于安全风险等级的港口危化品监管问题研究[J]. 系统工程理论与实践, 2018, 38(5): 1141-1152. LIU Jiaguo, WANG Junjin, ZHOU Huan, et al. Research on supervision problems of port hazardous chemicals base on security risk level[J]. Systems engineering-theory & practice, 2018, 38(5): 1141-1152. (  0) 0)
|
| [21] |
程永波, 李婷, 陈洪转, 等. 复杂产品共性技术研发的政府最优成本补贴[J]. 哈尔滨工程大学学报, 2015, 36(3): 432-436. CHENG Yongbo, LI Ting, CHEN Hongzhuan, et al. The optimal government cost subsidies for R & D of the complex product generic technology[J]. Journal of Harbin Engineering University, 2015, 36(3): 432-436. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


