2. 安徽师范大学 数学计算机科学学院, 安徽 芜湖 241003
2. School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China
集成电路技术高速发展,互连线层数不断增加,每一层互连线的温度都不相同[1-3]。互连线温度的不同,导致了互连线的电阻、电容、电感出现变化,这些变化直接影响了信号完整性问题。由于高频时存在的趋肤效应,也影响了电阻、电感的变化[4-5]。这些因素都引起互连线上信号的波形发生变化,对高速集成电路产生很坏的影响,尤其是对频率和温度比较敏感的互连层更是如此。如果在设计阶段没有考虑这些因素的影响,很有可能设计的产品不符合要求。在高速电路中,信号完整性中的延迟和串扰问题最为突出。
很多文献研究了互连线上信号的延时和串扰[6-9],但是很少有人考虑温度和频率对互连线的影响。多层互连中,每一层温度不相同,而且在高频信号作用下,信号延时和串扰需要进行详细的研究,考虑在不同温度、不同频率、不同负载情况下的情形。
1 温度特性集成电路中每层的温度不同,对电路的影响也不同。温度对电容、电阻和电感有不同的影响,需要区别对待。
1.1 各层互连线的温度假设芯片表面温度均匀分布,温度为T0,第i层互连线的温度为Ti,电流密度是Ji。互连线的宽度为wi,长度为li,厚度为hi,互连线之间的间距为di,热传导系数为km。
第i层互连线上面几层传递的热量引起的附加电流密度为ΔJi,它与其上各层互连线的宽度、厚度和长度、线间距离以及上一层的互连线热扩散特征长度有关。第i层与第i-1层金属之间电介质层厚度为hinsi,有效热传导系数为kinse,第i-1层金属温度为Ti-1。
热扩散特征长度Ldi与ρ、β、hi、kinse、km、J、hinsi有关,其中ρ代表 0 ℃时的金属电阻率,β代表金属电阻率的温度系数。
式(1)给出了多层金属线上各层的平均温度[10]:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;{T_i} = {T_i} - 1 + \rho {\left( {{J_i} + \Delta {J_i}} \right)^2} \times \\ \left( {{h_{{\rm{insi}}}}/{k_{{\rm{inse}}}} \times {h_i}} \right) \times \left[ {1 - {\rm{tanh}}\left( {{l_i}/2{L_{{\rm{di}}}}} \right)/\left( {{l_i}/2{L_{{\rm{di}}}}} \right)} \right] \end{array} $ | (1) |
电容、电阻、电感都和温度有关,但温度对它们的影响不同。电容和温度的关系可由式(2)表示:
| $ {T_{{\rm{cc}}}} = {T_{{\rm{cc}}}}\left( {{\rm{th}}} \right) + {T_{{\rm{cc}}}}\left( {{\rm{sc}}} \right) + {T_{{\rm{cc}}}}\left( {{\varepsilon _{{\rm{ox}}}}} \right) $ | (2) |
式中:第1项是由于热膨胀引起的电容平板面积和电介质厚度的改变;第2项是温度引起空间电容的改变;第3项是由于温度对介电常数的影响。对于金属电容器,这个值一般在30~50×10-6/℃[11]。
电阻和温度的关系为:
| $ {T_{{\rm{rc}}}} = {T_{{\rm{rc}}}}\left( {{\rm{th}}} \right) + {T_{{\rm{rc}}}}\left( \rho \right) $ | (3) |
式中:Trc(th)是金属的热膨胀引起的变化;Trc(ρ)是电阻率随温度的改变。对于金属铜,这个值一般在4 000×10-6/℃左右[10]。
电感和温度的关系为:
| $ {T_{{\rm{lc}}}} = {T_{{\rm{lc}}}}\left( {{\rm{th}}} \right) + {T_{{\rm{lc}}}}\left( {{\rm{in}}} \right) $ | (4) |
式中:Tlc(th)表示金属随温度而膨胀,由此引起电感发生变化;Tlc(in)表示随着温度的升高,引起趋肤深度的增加。电感的温度系数一般在50~70×10-6/℃[12]。
2 频率对电阻、电感的影响由于趋肤效应的存在,互连线的电阻和电感都与频率有关系。趋肤深度定义为当电流密度衰减到初值的1/e(即衰减1/e=-8.7 dB)时的穿透距离,其与频率具有如下关系:
| $ \delta = \sqrt {\rho /{\rm{ \mathsf{ π} }}f\mu } $ | (5) |
式中f、ρ、μ分别为频率、导体电阻率及介质磁导率。
电阻可由式(6)计算[13]得:
| $ R = \left( {l/w} \right) \times \sqrt {{\rm{ \mathsf{ π} }}f\rho \mu } $ | (6) |
由于频率的影响,互连线自感的计算如下[14]:
| $ \begin{array}{l} {L_s} = \left( {{\mu _0}/2\pi } \right) \times (l \times {\rm{ln}}\left( {2l/\left( {w + t} \right)} \right) + \\ \left. {0.5l + {\rm{ }}0.223{\rm{ }}5\left( {w + t} \right) - {\mu _r}\left( {0.25 - X} \right)} \right) \end{array} $ | (7) |
| $ X = \left\{ \begin{array}{l} 0.473{\rm{ }}2x, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x < 0.5\\ 0.057{\rm{ }}8x - 0.189{\rm{ }}7, \;\;\;\;\;0.5 \le x \le 1\\ 0.25, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x > 1 \end{array} \right. $ |
式中x=δ/0.223 5(w+t)。
频率对电容的改变很小,几乎可以不考虑。
3 信号完整性实验和分析实验采用0.13 μm 1P6M N阱CMOS逻辑工艺,假设芯片表面温度为绝对温度398 K,对这6层用式(1)分别计算每层的温度,依次为402.27、405.20、406.58、418.81、420.10、421.18 K。
第1~4层金属互连线厚度小于0.25 μm,当互连线上信号的频率从1~100 GHz变化时,由于铜的趋肤深度大于互连线的厚度,所以不用考虑趋肤效应。第5层互连线厚度2 μm,需要考虑趋肤效应;第5层互连线温度比芯片表面温度高20.1 K,需考虑温度效应。由于第5层互连线具有典型的代表性,用第5层互连做以下实验。
3.1 实验模型随着VLSI芯片集成度的不断提高,互连线的寄生耦合效应已不能被忽略,但由于相邻互连线对较远线的屏蔽效应,只需考虑相邻线间的串扰。在CMOS集成电路里中,驱动源有驱动电阻,负载端为电阻或电容。
对一根互连线可以有很多方法来建模,不同的方法有着不同的精度,计算量相差很大。RC模型易于计算,但相对不太准确,对于高频电路和较长的连线,电感效应非常显著,RLC模型通过考虑了电感的影响而增加了准确度。互连线是有损传输线,可用足够数量的RLC线元近似表示,在此采用二阶n节RLC集总电路模型来近似,如图 1。

|
Download:
|
| 图 1 互连线等效模型 Fig. 1 Interconnection equivalent model | |
图 1中,L1为攻击线,L2为受害线;Cc为单位长度耦合电容,Cg为单位长度接地电容;r为单位长度电阻,li为单位长度自感;lm为单位长度互感;Gg为接地电导,dx=l/n为每个线元的长度;Vin为信号源;Rs1和Rs2分别为信号源电阻和受害线的源端电阻;Z1和Z2分别为攻击线和受害线的负载。
采用n节RLC集总电路模型近似互连线时,必须确保模型的带宽大于信号的带宽,即要求[15]:
| $ n > 3.5{T_D}/{R_T} $ | (8) |
式中:TD为信号延迟;RT为信号的上升时间;本文中n为6。
电阻随温度的上升而增加,由于趋肤效应,它随频率的增加而增大;电容随温度的上升而减小,但与频率几乎无关;电感随温度的上升而增加,随频率的增加而减小,并且二者的影响程度接近。
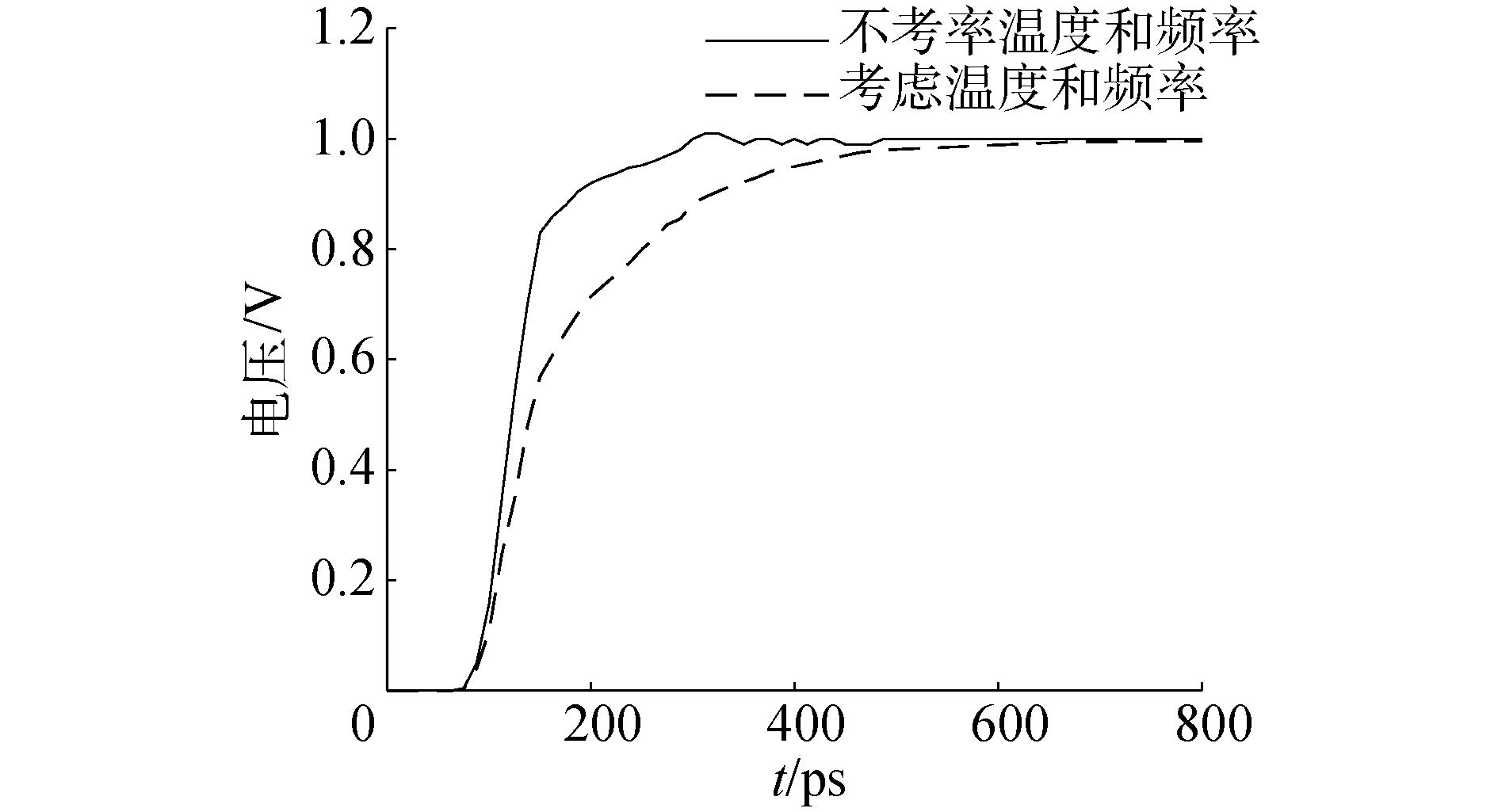
3.2 信号延迟的实验结果及分析定义延迟时间为输出信号值从10%上升到90%的时间。首先,信号上升时间为0.05 ns,在这个上升时间下,对5 000 μm长的互连线做信号延迟实验,其中驱动电阻为100 Ω,负载为0.1 pF电容,选用Synopsys公司的Hspice工具进行仿真,实验结果如图 2。
|
Download:
|
| 图 2 电容负载时的延迟 Fig. 2 Delay in capacitance load | |
从图 2中可以看出,在信号上升时间为0.05 ns时,考虑趋肤效应和温度效应,输出端(图 1中的out节点)的延迟时间是208 ps,没有考虑温度和频率影响的信号延迟是87 ps,延迟时间相差121 ps。如此大的时延差,使得设计人员要想设计合格的产品,必须考虑频率和温度的影响。
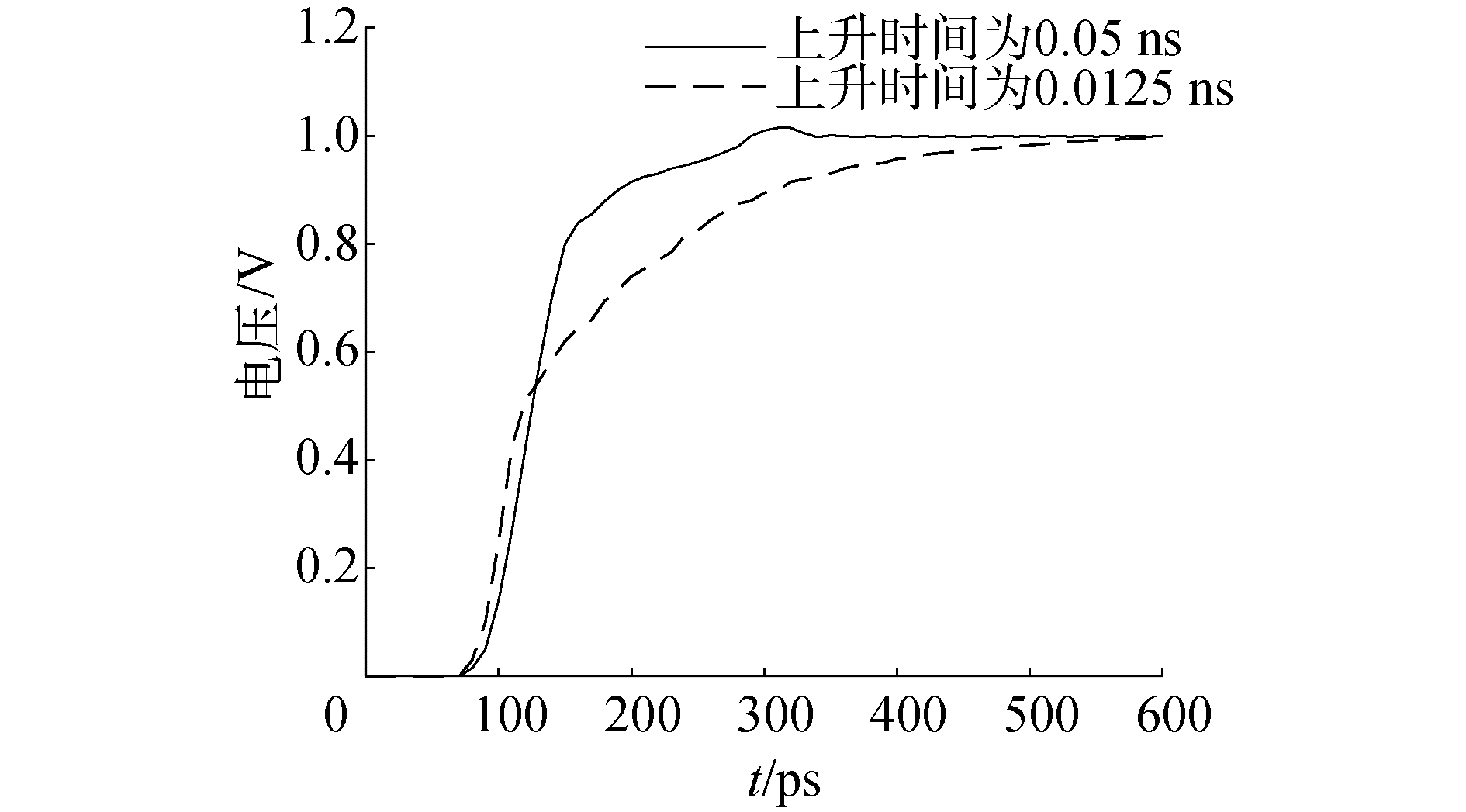
信号上升时间分别为0.05 ns和0.012 5 ns,互连线长5 000 μm,驱动电阻为100 Ω,负载为0.1 pF电容,对这2个信号上升时间都考虑频率和温度的影响,实验结果如图 3。
|
Download:
|
| 图 3 信号上升时间的影响 Fig. 3 Influence of signal rising time | |
从图 3中看出,信号上升时间为0.05 ns时,信号延迟为90 ps。信号上升时间为0.012 5 ns时,信号延迟为201 ps,可见负载相同,信号上升时间越快,信号延迟越大。
以上实验都是电容负载,在此选用电阻负载分析信号延迟。给定信号上升时间为0.05 ns,互连线长5 000 μm,驱动电阻和负载电阻都是100 Ω,实验结果如图 4。

|
Download:
|
| 图 4 电阻负载时的信号延迟 Fig. 4 Delay in resistance load | |
从图 4中看出,考虑了温度和频率影响的信号延迟为42 ps,没有考虑温度和频率影响的信号延迟为40 ps,可见电阻负载对信号延迟影响不大。
频率和温度对互连线的电阻影响都很大,对电感的影响正好相反,频率对电容几乎没有影响,只有温度对电容有影响。通过实验发现,信号延迟对容性负载比较敏感,对电阻负载几乎没有影响。在设计高速集成电路时要详细,认真考虑温度和频率对信号延迟的影响。
3.3 信号串扰的实验结果及分析对1 000 μm长的2条相邻互连线做信号串扰实验,信号源为一脉冲信号,幅值为1.2 V,攻击线的源电阻和受害线的源端电阻都为125 Ω,NTF表示既不考虑温度也不考虑频率时的近端串扰,OT为仅考虑温度变化时的近端串扰,OF为仅考虑频率效应时的近端串扰,TF表示同时考虑温度效应和频率效应时的曲线。
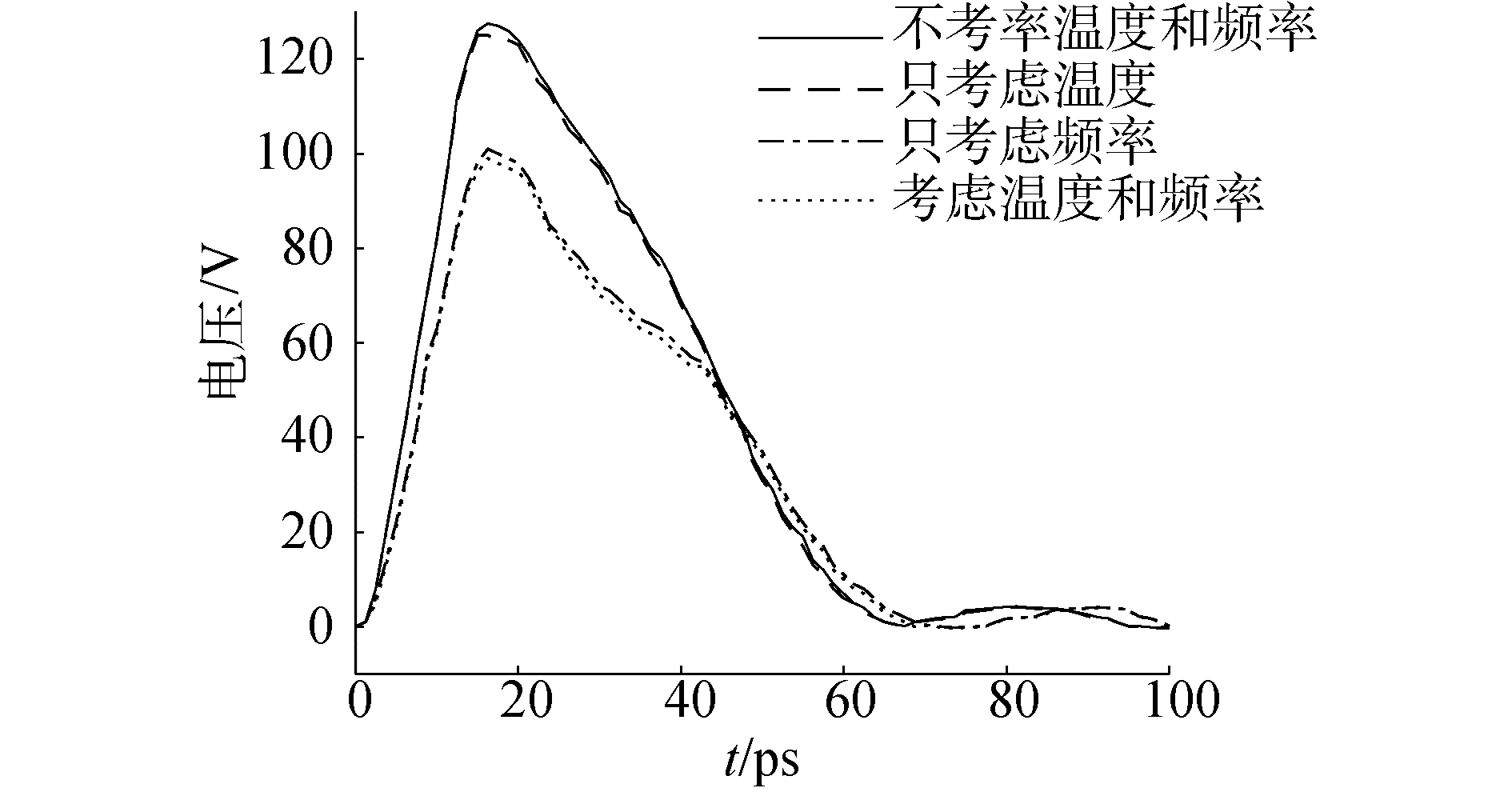
信号的上升时间为12.5 ps,2条互连线的负载都为125 Ω的电阻,攻击线在受害线近端(图 1中的near节点)引起的串扰如图 5所示。温度使电阻变化较大,电容和电感变化很小,OT曲线和NTF曲线相比有一点减小,峰值减小1.4 mV;频率使电阻变化很大,电容和电感变化很小,OF曲线和NTF曲线相比有较大的减小,峰值减小27.3 mV;温度和频率共同作用,使得电阻变化很大,电容变化很小,电感变化更小,TF曲线和OF曲线相比有一点减小,峰值减小1.8 mV。由于频率和温度共同作用,使得电阻变化很大,电容变化小,电感几乎不变,所以考虑了温度和频率的近端串扰反而变小,这对于实际电路是有利的。
|
Download:
|
| 图 5 电阻负载时的近端串扰 Fig. 5 Near-end crosstalk in resistance load | |
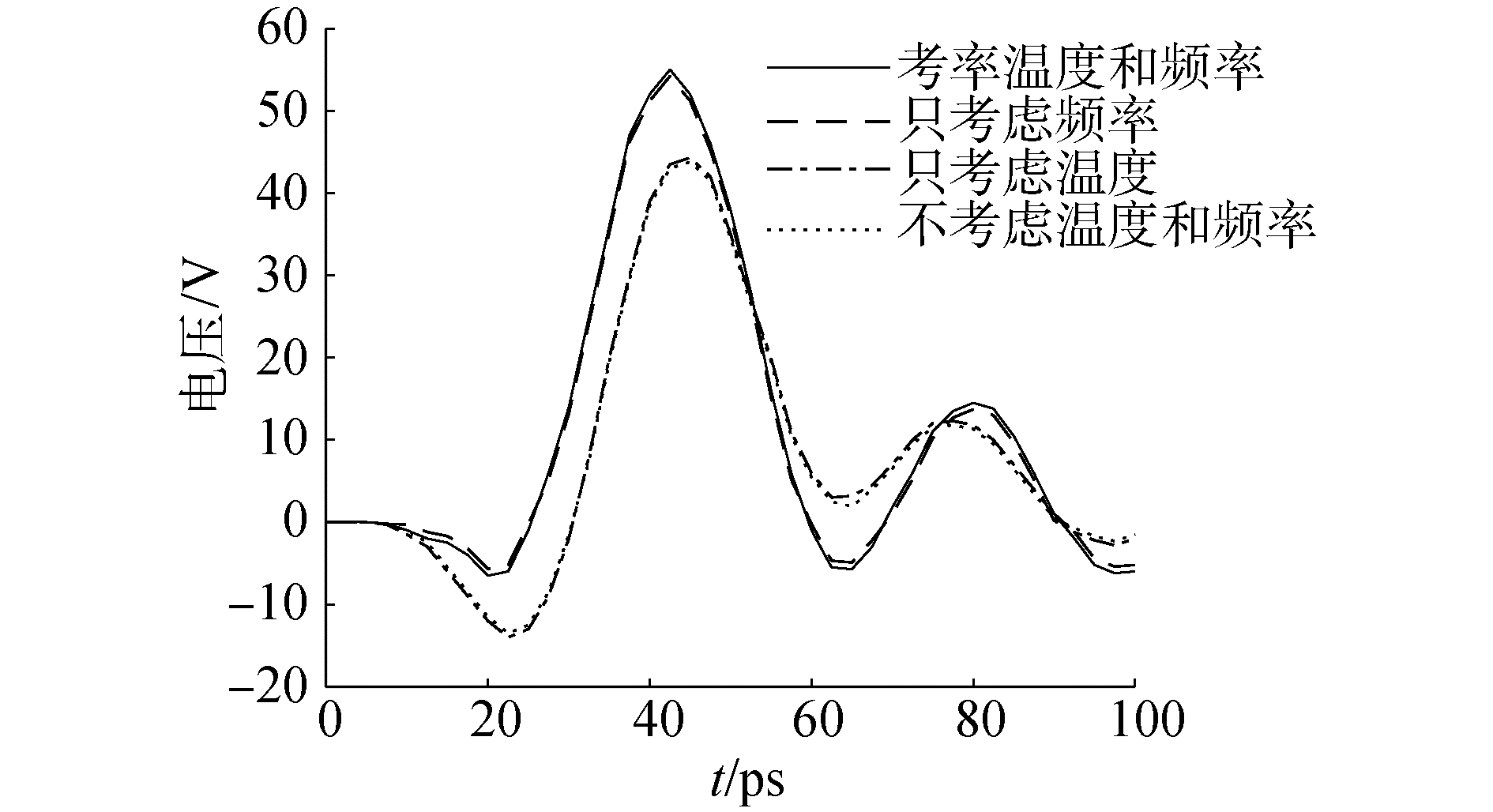
攻击线在受害线远端(图 1中的far节点)引起的串扰如图 6所示。温度使电容有一定的变化,但变化较小,电感的变化也较小,电阻有所增加,OT曲线和NTF曲线相比有一些增大,峰值增加0.8 mV;频率使电阻显著增大,OF曲线和NTF曲线相比有较大的增加,峰值增加9.2 mV;温度和频率共同作用时,电阻变化最大,TF曲线和NTF曲线相比增加也最大,峰值增加9.8 mV。远端串扰由互连线的互容决定,由于频率和温度共同作用,耦合电容减小,耦合到受害线上的电流减小,但电阻显著增大,而远端的阻抗由互连线的阻抗决定,二者的乘积使远端串扰增大,这对于实际电路是不利的。
|
Download:
|
| 图 6 电阻负载时的远端串扰 Fig. 6 Far-end crosstalk in resistance load | |
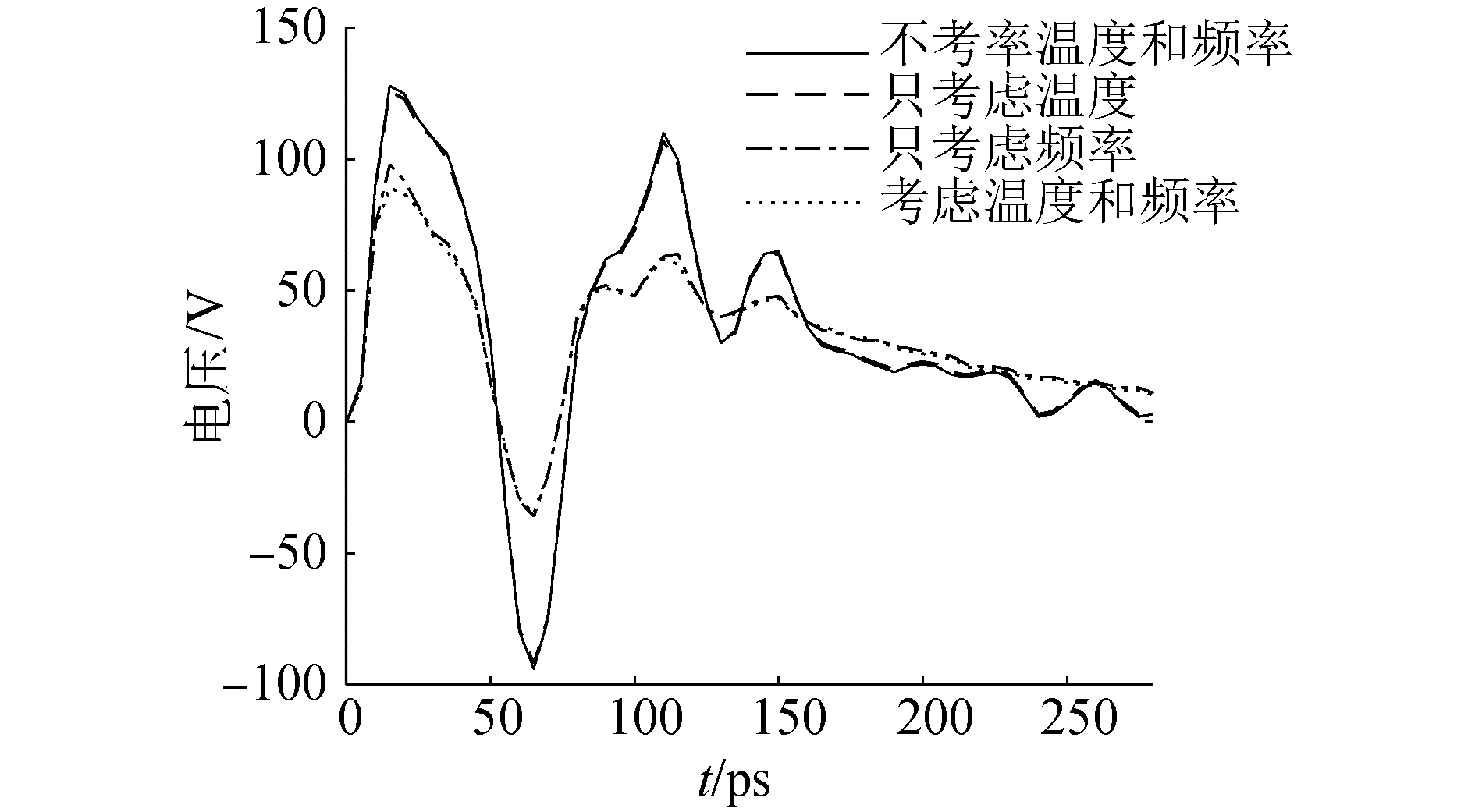
图 5和图 6都是负载是电阻的情况,负载是电容时,信号的上升时间为12.5 ps,2条互连线的负载都为0.2 pF的电容,攻击线在受害线近端引起的串扰如图 7所示。由于负载是电容,互连线间的互容变化量相对负载电容很小,串扰由互连线的电阻决定,互连线电阻大,串扰就小,互连线电阻小,串扰就大。温度使电阻有一定量的变大,OT曲线和NTF曲线相比有一些减小,峰值减小3 mV;频率对电阻影响很大,OF曲线和NTF曲线相比有较大的减小,峰值减小49.5 mV;温度和频率共同作用时,电阻变化最大,TF曲线和NTF曲线相比减小也最大,峰值减小51.0 mV。
|
Download:
|
| 图 7 电容负载时的近端串扰 Fig. 7 Near-end crosstalk in capacitance load | |
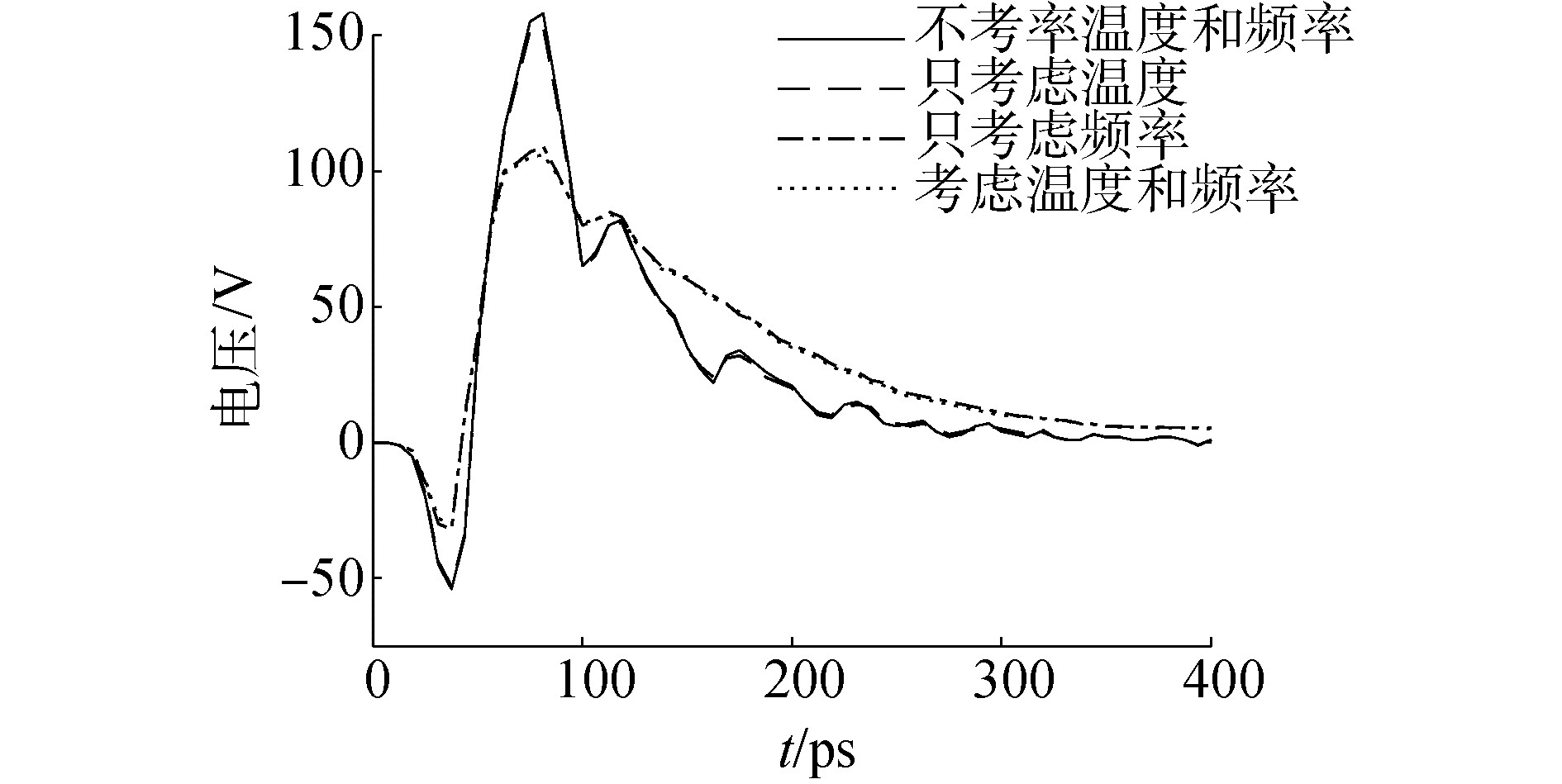
电容负载时攻击线在受害线远端引起的串扰如图 8所示。温度的增加使电阻有所增大,电容减小,OT峰值比NTF峰值小1.4 mV。频率的增加使电阻显著增大,OF峰值比NTF峰值小27.9 mV。在温度和频率的共同作用下,TF峰值比NTF峰值小29.7 mV。在温度和频率的共同作用下,电阻增大,耦合电容减小,耦合到受害线上的电流减小,负载电容上的电荷减少,远端串扰减小。
|
Download:
|
| 图 8 电容负载时的远端串扰 Fig. 8 Far-end crosstalk in capacitance load | |
从以上试验可以看出,温度和频率的共同影响使得相邻2条互连线之间串扰有相应的变化,在实际的电路设计中,毫伏级的差异,很可能使得设计失败,所以在具体应用中要充分考虑温度和频率对串扰的共同影响,设计出合格的产品。本文的试验模型可以用于实际设计中,对实际电路有一定指导意义。
4 结论在0.13 μm 1P6M N阱CMOS逻辑工艺下,对温度和频率敏感的第5层互连线进行了信号完整性的研究。
1) 在不同负载和不同信号上升时间的情况下,温度和频率对信号延迟的存在影响。在电容负载下温度和频率对信号的延迟影响很大,而在电阻负载下的影响很小。
2) 在短的信号上升时间和不同负载的情况下,温度和频率对互连线上信号近端串扰和远端串扰存在影响。温度对串扰的影响较小,而由于电流的趋附效应,频率对串扰的影响较大。
3) 在负载是电阻情况下,由于温度和频率对电阻,电容和电感有不同的影响,近端串扰减小,峰值减少29.1 mV,而远端串扰增大,峰值增加9.8 mV;在负载是电容情况下,近端串扰和远端串扰由互连线电阻决定,互连线电阻越大串扰越小,所以在考虑温度和频率影响时,近端串扰和远端串扰都减小,峰值分别减少51.0 mV和29.7 mV。本文结果可为超大规模集成电路中互连线的设计提供参考依据。片上互连线的层数越来越多,下一步可对层间互连线之间的影响做进一步研究。
| [1] |
ZHANG B, CARISEY Y C P, DAMIAN A, et al. 3D interconnect technology based on low temperature copper nanoparticle sintering[C]//Proceedings of the 17th International Conference on Electronic Packaging Technology. Wuhan, China, 2016: 1163-1167. http://www.researchgate.net/publication/308989429_3D_interconnect_technology_based_on_low_temperature_copper_nanoparticle_sintering
(  0) 0)
|
| [2] |
HUANG Mingliang, ZHANG Zhijie, ZHAO Ning, et al. Reverse polarity effect in Cu/Sn-9Zn/Ni interconnect under high current density at high temperature[C]//Proceedings of the 15th International Conference on Electronic Packaging Technology. Chengdu, China, 2014: 433-436. https://www.researchgate.net/publication/286227830_Reverse_polarity_effect_in_CuSn-9ZnNi_interconnect_under_high_current_density_at_high_temperature
(  0) 0)
|
| [3] |
ALIZADEH A, SARVARI R. On temperature dependency of delay for local, intermediate, and repeater inserted global copper interconnects[J]. IEEE transactions on very large scale integration (VLSI) systems, 2015, 23(12): 3143-3147. DOI:10.1109/TVLSI.2014.2379954 (  0) 0)
|
| [4] |
SATHYAKAM P U, KARTHIKEYAN A, RAJESH J K, et al. Reduction of crosstalk in mixed CNT bundle interconnects for high frequency 3D ICs and SoCs[C]//Proceedings of 2014 International Conference on Advances in Electrical Engineering. Vellore, India, 2014: 1-3. https://www.researchgate.net/publication/261435516_Reduction_of_crosstalk_in_mixed_CNT_bundle_interconnects_for_high_frequency_3D_ICs_and_SoCs
(  0) 0)
|
| [5] |
ZHENG Lei, FERRARA A R, WEISSHAAR A. Scalable modeling of resistive losses 1n on-chip interconnects at mm-wave frequencies[C]//Proceedings of 2016 IEEE MTT-S International Microwave Symposium. San Francisco, USA, 2016: 1-4. https://www.researchgate.net/publication/306117078_Scalable_modeling_of_resistive_losses_1n_on-chip_interconnects_at_mm-wave_frequencies
(  0) 0)
|
| [6] |
CHTOUROU S, ABID M, MARRAKCHI Z, et al. The effect of interconnect depopulation on FPGA performances in terms of power, area and delay[C]//Proceedings of 2016 International Conference on High Performance Computing & Simulation. Innsbruck, Austria, 2016: 104-111.
(  0) 0)
|
| [7] |
SHI Feng, WU Xuebin, YAN Zhiyuan. Improved analytical delay models for RC-coupled interconnects[J]. IEEE transactions on very large scale integration (VLSI) systems, 2014, 22(7): 1639-1644. DOI:10.1109/TVLSI.2013.2275071 (  0) 0)
|
| [8] |
BARANNYK L L, TRAN H H, NGUYEN L V, et al. Delay estimation using SVD-based causal Fourier continuations for high speed interconnects[C]//Proceedings of the IEEE 24th Electrical Performance of Electronic Packaging and Systems. San Jose, USA, 2015: 225-228. https://www.researchgate.net/publication/283347895_Delay_Estimation_Using_SVD-Based_Causal_Fourier_Continuations_for_High_Speed_Interconnects
(  0) 0)
|
| [9] |
SAHA S K, AHMED B, LIU Jiangjiang. A survey on interconnect encoding for reducing power consumption, delay, and crosstalk[C]//Proceedings of the 2nd International Conference on Electrical Information and Communication Technologies. Khulna, Bangladesh, 2015: 7-12. https://www.researchgate.net/publication/304297002_A_survey_on_interconnect_encoding_for_reducing_power_consumption_delay_and_crosstalk
(  0) 0)
|
| [10] |
CHIANG T Y, SARASWAT K C. Closed-form analytical thermal model for accurate temperature estimation of multilevel ULSI Interconnects[C]//Proceedings of 2003 Symposium on VLSI Circuits. Digest of Technical Papers. Kyoto, Japan, 2003: 275. https://www.researchgate.net/publication/4028202_Closed-form_analytical_thermal_model_for_accurate_temperature_estimation_of_multilevel_ULSI_interconnects
(  0) 0)
|
| [11] |
COLDREN L A, BARVE A V. On-chip VCSEL interconnects enabled by 3-D interposer-based integration and polarization modulation[C]//Proceedings of 2015 IEEE Summer Topicals Meeting Series. Nassau, Bahamas, 2015: 150-151. https://www.researchgate.net/publication/308839768_On-chip_VCSEL_interconnects_enabled_by_3-D_interposer-based_integration_and_polarization_modulation
(  0) 0)
|
| [12] |
DARABI H. Radio frequency integrated circuits and systems[M]. California: Cambridge University Press, 2015.
(  0) 0)
|
| [13] |
NDAGIJIMANA F. Signal integrity:from high-speed to radiofrequency applications[M]. Hoboken, NJ: Wiley-ISTE, 2014.
(  0) 0)
|
| [14] |
QI Xiaoning, WANG Gaofeng, YU Zhiping, et al. On-chip inductance modeling and RLC extraction of VLSI interconnects for circuit simulation[C]//Proceedings of IEEE 2000 Custom Integrated Circuits Conference. Orlando, USA, 2000: 487-490. http://www.researchgate.net/publication/3852739_On-chip_inductance_modeling_and_RLC_extraction_of_VLSIinterconnects_for_circuit_simulation
(  0) 0)
|
| [15] |
BOGATIN E. Signal and power integrity:simplified[M]. 2nd ed. Upper Saddle River: Prentice Hall, 2009.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


