2. 哈尔滨工程大学 科学技术研究院, 黑龙江 哈尔滨 150001
2. Research Institute of Science and Technology, Harbin Engineering University, Harbin 150001, China
随着武器系统的发展,近程搜索雷达的俯仰角度覆盖越来越大,频率范围越来越宽,测角精度要求也越来越高。因此,需要对影响测角精度的各种误差进行分析、修正[1-4]。目前使用与研制的近程搜索雷达中,出于降低成本等方面的考虑,还较多采用串馈形式的一维有源相扫相控阵天线,它们在仰角方向上进行相位扫描形成多个接收波束覆盖探测空域,在方位上进行机械扫描[5-7]。为了满足空域覆盖要求,雷达阵面还会倾斜一定角度放置。由于色散角和倾斜角的存在,如果处理不当就会给雷达方位、俯仰测角带来误差[8-10]。另外,在雷达远场测试中往往将雷达旋转90°,通过专用工装垂直固定于天线测试转台上,俯仰维方向图测试通过转动转台方位来实现的测试方法,这也会给雷达测角带来误差。本文针对以上3个方面进行了推导,并给出了修正公式,相比常规方法[8-9],无需复杂的坐标变换,不需要分步修正,计算量小。对符合方位上频率扫描、俯仰同时多波束[11-15]、测试方法同本文的搜索雷达,给出了一个综合的修正公式,可以直接计算出3个误差源情况下目标在雷达球坐标下的方位、俯仰值。通过对雷达检飞数据分析,验证了修正算法的正确性、有效性。
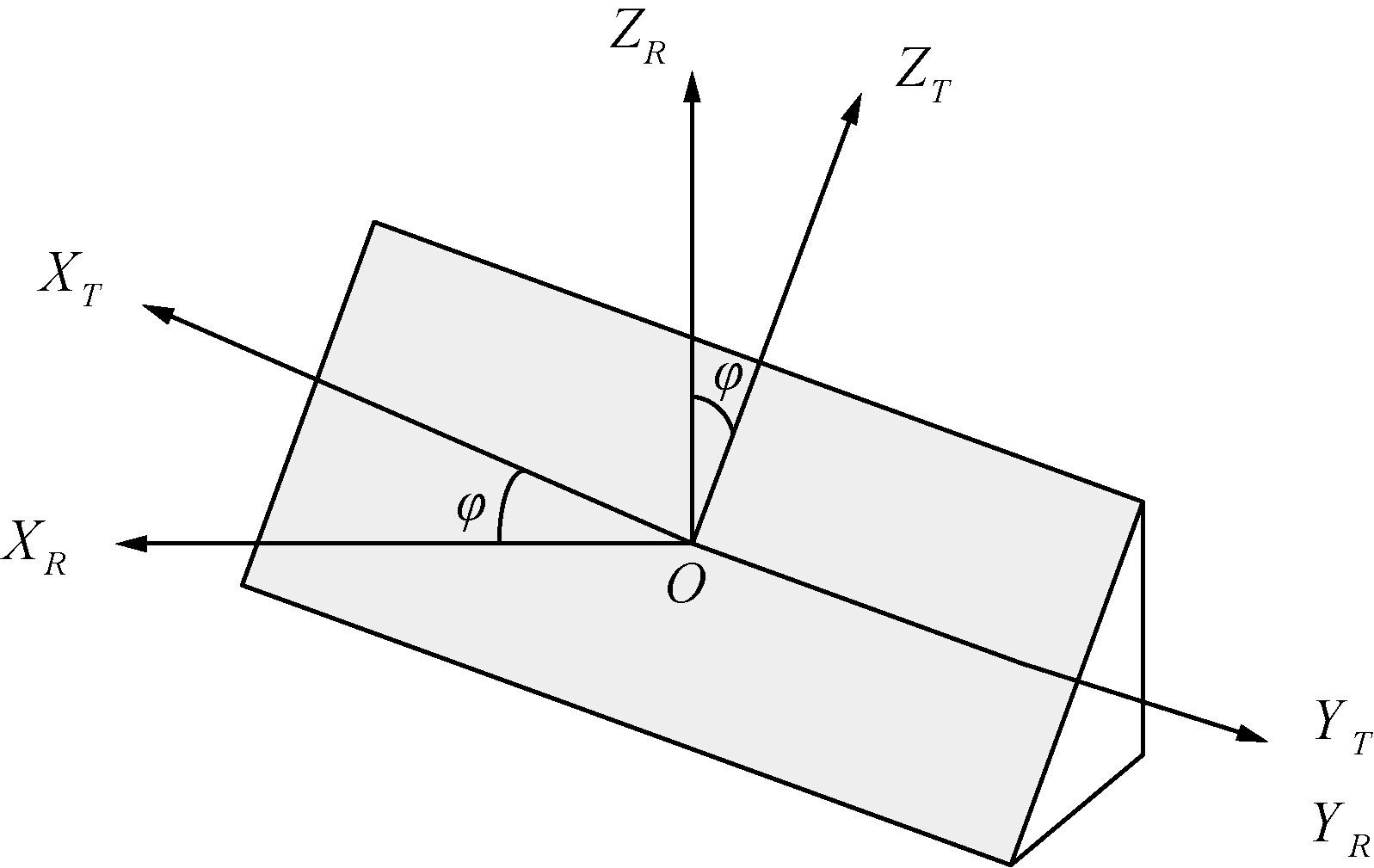
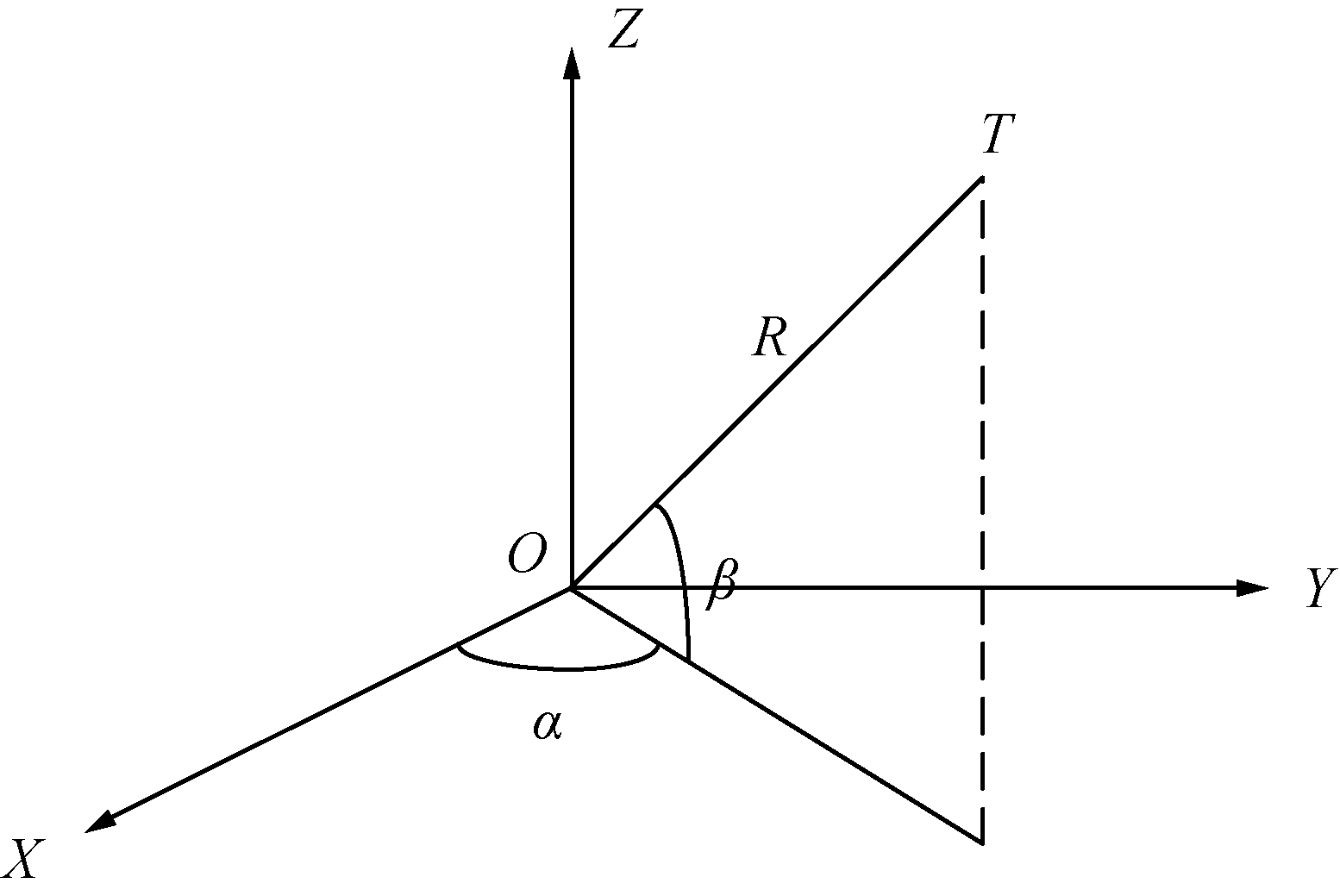
1 坐标系定义天线阵面直角坐标系(XT,YT,ZT)的定义为:YT轴和ZT轴位于天线阵面平面内, XT轴指向天线阵面的法向方向; YT轴与地面平行,ZT轴沿阵面向上与XT轴YT轴垂直。XTYTZT构成右手坐标系,如图 1所示。天线阵面球坐标系(R,α,β)的定义为:α为阵面方位角; OT在XTOYT平面上的投影与天线阵面直角坐标系XT轴的夹角;β为阵面俯仰角; OT与XTOYT平面的夹角[9],如图 2所示。
|
Download:
|
| 图 1 直角坐标系定义示意 Fig. 1 Rectangular coordinate definition diagram | |
|
Download:
|
| 图 2 球坐标系定义示意 Fig. 2 Spherical coordinate definition diagram | |
雷达直角坐标系的坐标原点O与天线阵面直角坐标系坐标原点重合。雷达直角坐标系(XR,YR,ZR)的定义为:XROYR平面与地面平行;ZR轴垂直向上;XRYRZR构成右手坐标系,如图 1所示。雷达球坐标系(R,α′,β′)的定义为:α′为雷达方位角;OT在XROYR平面上的投影与雷达直角坐标系XR轴的夹角;β′为雷达俯仰角;OT与XROYR平面的夹角;如图 2所示。
2 测角误差源分析与研究 2.1 色散角导致的方位、俯仰测角误差为了提高雷达的抗干扰能力,雷达会进行频率捷变,当雷达信号频率改变后,串馈形式一维有源相扫相控阵雷达方位上相邻天线辐射单元的相位差会发生变化,如果方位上没有移相器,将会导致天线波束指向发生偏移,每个频点将会对应一个色散角。由于色散角的存在,不同俯仰的方位指向在天线阵面球坐标系下会发生偏移。
天线在YTOZT平面上放置,XT轴和天线的法线重合,如图 3所示。天线坐标系下方位角α定义为:以OYT为中心轴,以方位角余角为锥角的圆锥体,波束中心在这个圆锥上的所有波束方位角都是α。天线坐标系下俯仰角β定义为:以OZT为中心轴,以俯仰角余角为锥角的圆锥体,波束中心在这个圆锥上的所有波束俯仰角都是β。因此,当色散角为α时,在俯仰维形成的多个波束是在以OYT为中心轴,以方位角余角为锥角的圆锥面上排布。在天线阵面球坐标系下,这就造成了不同俯仰角方位角不同,如图 3所示。
|
Download:
|
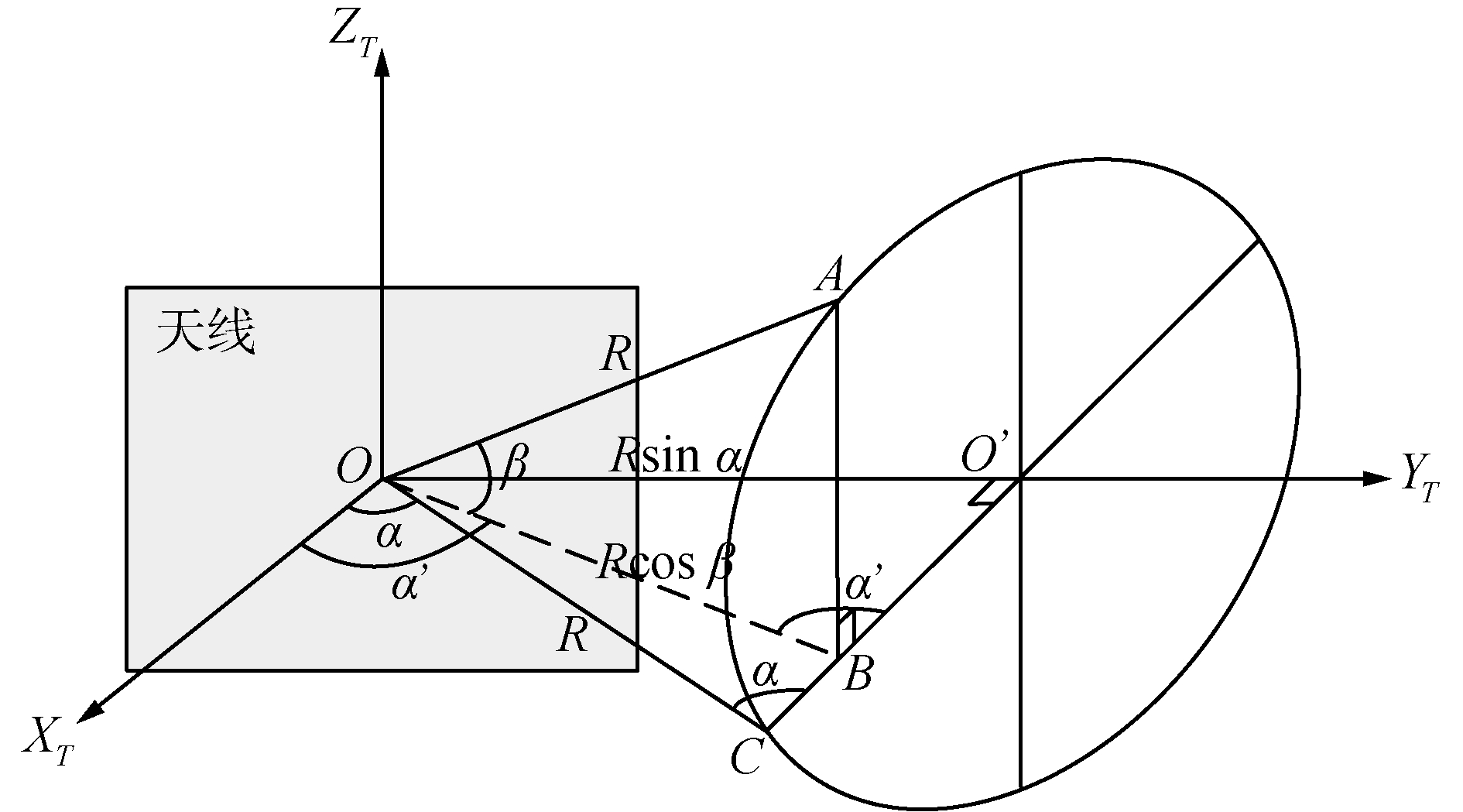
| 图 3 色散角导致的测角误差几何关系 Fig. 3 Geometric relationship of the angle error due to dispersion angle | |
当色散角为α,目标处于A点,俯仰角为β时,在天线阵面球坐标系下方位角变为α′。图 3中,以O′为圆心、以O′C为半径的圆是以OO′为中心轴、以90°-α为圆锥角的圆锥底面,O′C是圆锥底面和XTOYT平面的交线,OO′⊥O′C,AB⊥O′C,AB⊥OO′,因此AB垂直XTOYT平面。∠OCO′=α;OA=OC=R,OO′=Rsinα,OB=Rcosβ,∠OBO′=α′,
| $ \alpha ^\prime = {\rm{arcsin}}\left( {\frac{{{\rm{sin}}\alpha }}{{{\rm{cos}}\beta }}} \right) $ | (1) |
式(1)适用于串馈形式一维有源相控阵雷达,方位上频率扫描、俯仰上同时多波束情况,在色散角存在的情况下,在天线坐标系下不同俯仰的目标,目标方位在天线阵面球坐标系下的修正公式。
2.2 天线倾斜导致的方位、俯仰测角误差为了满足空域探测要求,一维有源相控阵雷达天线往往要往后倾斜一定的角度,由于色散角的存在,目标在雷达球坐标系下的俯仰就不能是天线阵面球坐标系下的俯仰值简单地加上倾斜角度,需要做坐标旋转。一般坐标旋转方法为将天线坐标系(R,α,β)首先转成天线阵面直角坐标系,然后进行坐标旋转变为雷达直角坐标系,最后再变换成雷达球坐标系下坐标(R,α′,β′)。本文直接推导了雷达球坐标系下坐标与天线坐标系坐标、倾斜角度之间的关系。
当目标在天线坐标系下色散角为α,目标处于A点,俯仰角为β,天线旋转φ时,目标在雷达球坐标系下方位角变为α′,俯仰角变为β′,如图 4所示。图 4中,以O′为圆心、以O′C为半径的圆是以OO′为中心轴、以90°-α为圆锥角的圆锥底面,O′C是圆锥底面和XTOYT平面的交线,OO′⊥O′C,AB⊥O′C,AB⊥OO′,因此AB垂直XTOYT平面。O′D是圆锥底面和XROYR平面的交线,OO′⊥O′D,AD⊥O′D,AD⊥OO′,因此AD垂直XROYR平面。∠OCO′=α;OA=OC=R,OO′=Rsinα,AO′=CO′=Rcosα,∠BOA=β,AB=Rsinβ,θ=∠AO′B,设θ为中间变量,∠ODO′=α′,∠DOA=β′,∠DO′B=φ,O′D=AO′cos(θ+φ)=Rcosαcos(θ+φ),AD=AO′sin(θ+φ)=Rcosαsin(θ+φ),得出:
| $ \left\{ \begin{array}{l} {\rm{sin}}\theta = \frac{{AB}}{{AO^\prime }} = \frac{{{\rm{sin}}\beta }}{{{\rm{cos}}\alpha }}\\ \theta = {\rm{arcsin}}\left( {\frac{{{\rm{sin}}\beta }}{{{\rm{cos}}\alpha }}} \right) \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} {\rm{tan}}\alpha ^\prime = \frac{{OO^\prime }}{{O^\prime D}} = \frac{{{\rm{sin}}\alpha }}{{{\rm{cos}}\alpha {\rm{cos}}\left( {\theta + \varphi } \right)}}\\ \alpha ^\prime = {\rm{arctan}}\left( {\frac{{{\rm{sin}}\alpha }}{{{\rm{cos}}\alpha {\rm{cos}}\left( {\theta + \varphi } \right)}}} \right) \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} {\rm{sin}}\beta ^\prime = \frac{{AD}}{{AO}} = {\rm{cos}}\alpha {\rm{sin}}\left( {\theta + \varphi } \right)\\ \beta ^\prime = {\rm{arcsin}}\left( {{\rm{cos}}\alpha {\rm{sin}}\left( {\theta + \varphi } \right)} \right) \end{array} \right. $ | (4) |

|
Download:
|
| 图 4 倾斜角导致的测角误差几何关系 Fig. 4 Geometric relationship of the angle error due to radar tilt angle | |
式(2)、(3)、(4)适用于串馈形式一维有源相控阵雷达,方位上频率扫描、俯仰上同时多波束,雷达倾斜安装且存在色散角情况时,目标方位、俯仰在天线坐标系下检测值与目标在雷达球坐标系下方位、俯仰值之间的关系公式。
2.3 天线测试方法导致的方位、俯仰测角误差研究为了验证雷达是否满足指标设计要求,会对雷达进行一系列的测试,测试内容包括接收方向图、发射方向图、测角曲线等。不同的安装方式、不同的测试方法都会给测角带来一定的误差。大多数一维相扫近程搜索雷达远场测试往往采用将雷达(含天线和收发系统)旋转90°,通过专用工装垂直固定于天线测试转台上,俯仰维方向图测试通过转动转台方位来实现的方法。不同色散角下的俯仰维方向图通过转动转台俯仰使波束指向远场测试信号源,此时转台方位转动平面和远场测试信号源不在一个平面内,转台方位转动的角度θ不能等同于天线阵面球坐标下目标的俯仰角度β,用这种测试方法给雷达俯仰角的测试带来误差。本文分析了转台方位转动角度θ和目标在天线阵面球坐标系下俯仰角度β的关系,并对其进行了修正。
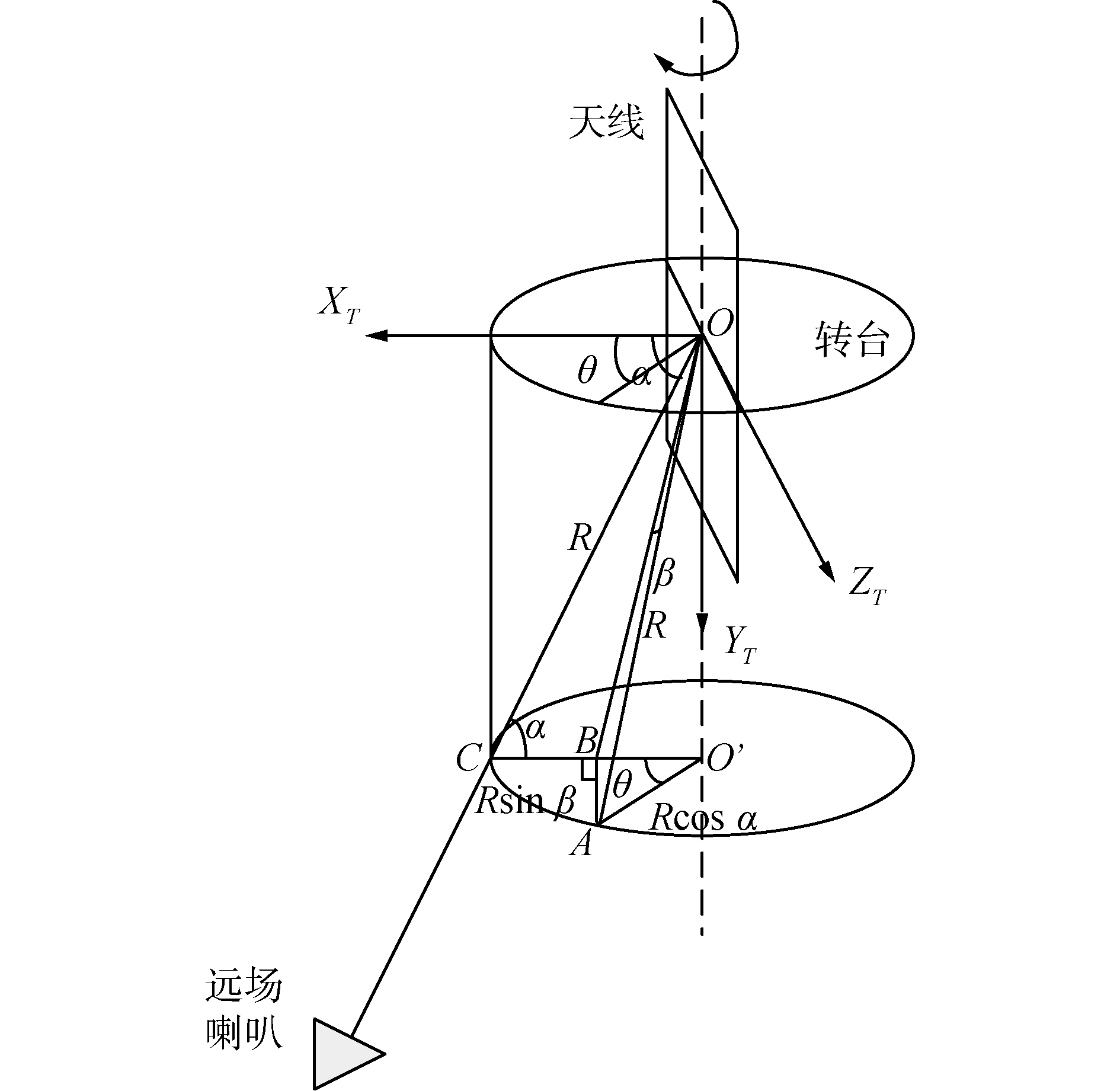
天线阵面垂直与测试转台安装,天线阵面法线为XT轴,当色散角为α,转台方位转动θ时,目标处于A点,目标在天线坐标系下的俯仰角为β,如图 5所示。图 5中,以O′为圆心、以O′C为半径的圆是以OO′为中心轴、以90°-α为圆锥角的圆锥底面,O′C是圆锥底面和XTOYT平面的交线,OO′⊥O′C,AB⊥O′C,OO′⊥AB,因此AB垂直XTOYT平面。∠OCO′=α;OA=OC=R,O′A=O′C=Rcosα,AB=Rsinβ,
| $ \left\{ \begin{array}{l} {\rm{sin}}\beta = {\rm{sin}}\theta {\rm{cos}}\alpha \\ \beta = {\rm{arcsin}}\left( {{\rm{sin}}\theta {\rm{cos}}\alpha } \right) \end{array} \right. $ | (5) |
|
Download:
|
| 图 5 雷达测试方法导致的测角误差几何关系 Fig. 5 Geometric relationship of the angle error due to radar test method | |
式(5)适用于串馈形式一维有源相控阵雷达,方位上频率扫描、俯仰上同时多波束,且在雷达方向图测试时将雷达旋转90°,通过专用工装垂直固定于天线测试转台上,俯仰维方向图测试通过转动转台方位来实现,且以转台方位为真值的情况,目标在天线坐标下俯仰与俯仰测试值之间的修正公式。
观察图 4、5可以发现,图 5中中间变量θ就是转台方位旋转角度,即俯仰测试值。因此,式(3)、(4)直接给出了目标在雷达球坐标下方位值、俯仰值与色散角、雷达倾斜角度、俯仰测试值之间的关系,每个频率的色散角可以测得。式(3)、(4)可以改为:
| $ \alpha ^\prime = {\rm{arctan}}\left( {\frac{{{\rm{sin}}\alpha }}{{{\rm{cos}}\alpha {\rm{cos}}\left( {\beta + \varphi } \right)}}} \right) $ | (6) |
| $ \beta ^\prime = {\rm{arcsin}}\left( {{\rm{cos}}\alpha {\rm{sin}}\left( {\beta + \varphi } \right)} \right) $ | (7) |
式中α、β为目标在天线坐标系测得的方位、俯仰值,α′、β′为目标在雷达球坐标系下方位、俯仰值,φ为雷达倾斜角,式(6)、式(7)给出了以上3种情况下的误差修正。
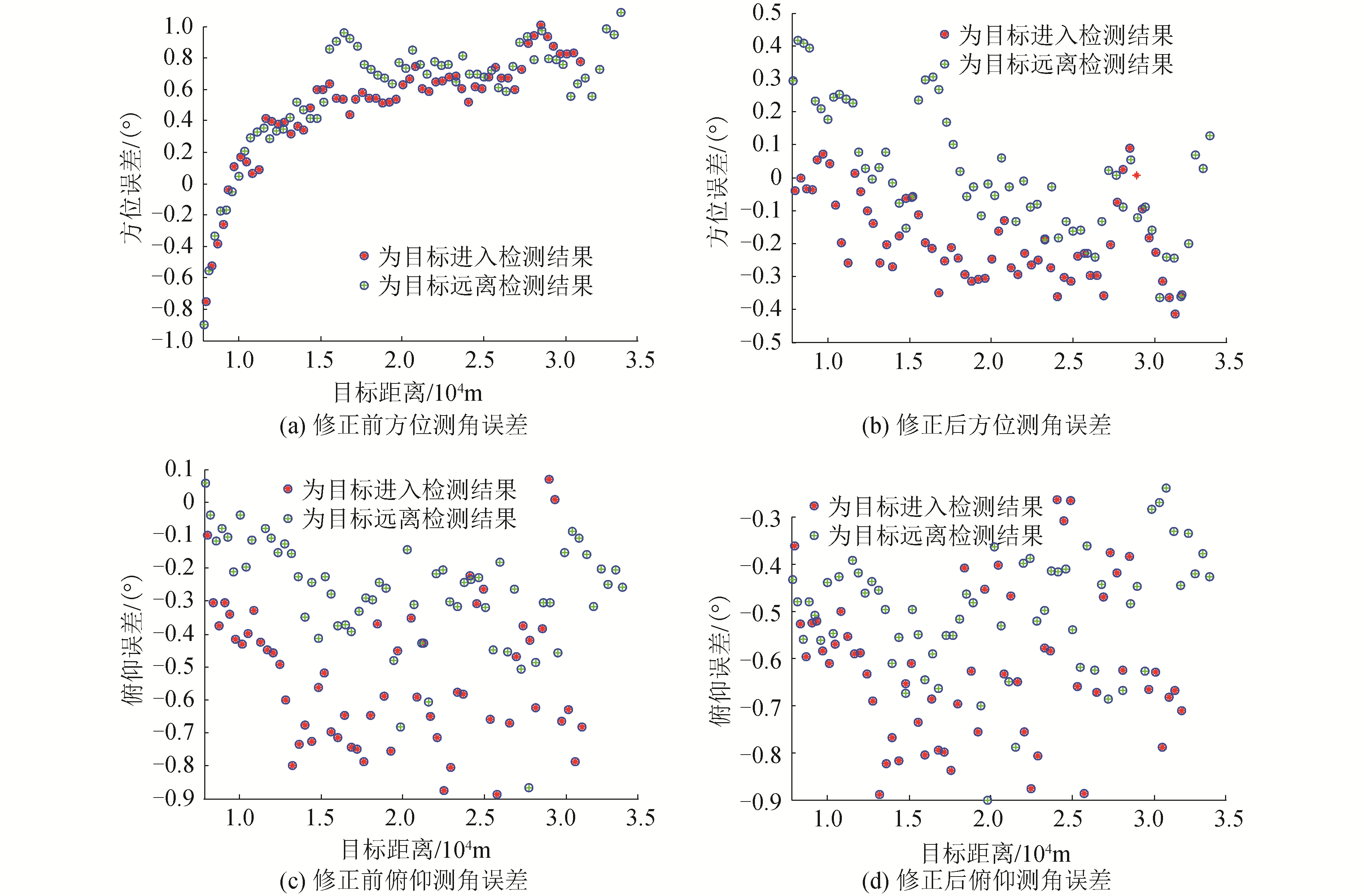
2.4 检测结果及分析该方法在雷达产品上进行了验证,达到了理想的效果。雷达放置在航路的中间位置,雷达倾斜角度为11.5°,检飞时采用频率的色散角为9°。图 6给出了雷达检飞数据修正前后的检测结果,修正前雷达方位角度为色散角与码盘角度之和,俯仰角度为天线坐标系下目标检测角度与倾斜角之和,修正后雷达方位角度为式(6)结果与码盘角度之和,修正后俯仰角度为式(7)结果。
|
Download:
|
| 图 6 修正前后参数变化 Fig. 6 Change of parameters before and after correction | |
通过图 6可以看出修正前后方位角误差变化明显,修正前目标越近、俯仰角度越大、方位测角误差越大,修正后方位测角方差改善显著,和式(6)完全符合,式(6)中cos(β+φ)在分母上,俯仰角度β越大,cos(β+φ)越小,不修正和真值的误差就越大。
通过图 6可以看出修正前后俯仰角误差变化并不明显,与式(7)完全符合,色散角越小,对俯仰造成的误差越小。
3 结论本文对串馈形式一维有源相扫搜索雷达测角误差源进行了分析与研究:
1) 方位测角误差和色散角、目标俯仰角有关,在色散角不为零的情况下,目标在天线阵面球坐标系下的方位测角误差会随着俯仰角的增大而变大,随着色散角与俯仰角的同时增大,方位测角误差将迅速增加。
2) 雷达球坐标系下测角误差和雷达倾斜角度有关,色散角、倾斜角度越大,方位、俯仰测角误差将随目标俯仰角度的增加而增大。
方向图测试方法也会给雷达测角带来误差,误差大小和色散角有关。
| [1] |
李杰涛, 陈国际, 李伟, 等. DBF同时多波束测角方法研究及工程实现[J]. 火控雷达技术, 2013, 42(2): 19-22. LI Jietao, CHEN Guoji, LI Wei, et al. Study on DBF simultaneous multi-beam angle measuring method and its implementation in engineering[J]. Fire control radar technology, 2013, 42(2): 19-22. DOI:10.3969/j.issn.1008-8652.2013.02.006 (  0) 0)
|
| [2] |
朱伟, 陈伯孝, 周琦. 两维数字阵列雷达的数字单脉冲测角方法[J]. 系统工程与电子技术, 2011, 33(7): 1503-1509. ZHU Wei, CHEN Baixiao, ZHOU Qi. Angle measurement method with digital monopulse for2-dimensional digital array radar[J]. Systems engineering and electronics, 2011, 33(7): 1503-1509. DOI:10.3969/j.issn.1001-506X.2011.07.14 (  0) 0)
|
| [3] |
陈知明, 魏述刚. 相控阵雷达测角误差自适应计算方法[J]. 现代雷达, 2013, 35(7): 13-15. CHEN Zhiming, WEI Shugang. Self-adaptive calculation method of angel error curvemeasurement for phased array antenna[J]. Modern radar, 2013, 35(7): 13-15. DOI:10.3969/j.issn.1004-7859.2013.07.004 (  0) 0)
|
| [4] |
华瑶. 一种高效的高精度相控阵雷达工程测角方法[J]. 微波学报, 2016, 32(4): 88-91. HUA Yao. A high effective and high precision engineering calculation method of angel error curve measurement for phased array radar[J]. Journal of microwaves, 2016, 32(4): 88-91. (  0) 0)
|
| [5] |
张光义, 赵玉洁. 相控阵雷达技术[M]. 北京: 电子工业出版社, 2006: 12.
(  0) 0)
|
| [6] |
SKOLNIK M I. Radar handbook[M]. 2nd ed. New York: McGraw-Hill, 1990.
(  0) 0)
|
| [7] |
SKOLNIK M I.雷达手册[M].王军, 林强, 译.北京: 电子工业出版社, 2003: 7. SKOLNIK M I. Radar handbook[M]. WANG Jun, LIN Qiang, trans. Beijing: Publishing House of Electronics Industry, 2003: 7. (  0) 0)
|
| [8] |
郦能敬. 对空情报雷达的测量精度分析[J]. 雷达科学与技术, 2005, 3(1): 1-10. LI Nengjing. Analysis of measurement accuracy of air surveillance radar[J]. Radar science and technology, 2005, 3(1): 1-10. DOI:10.3969/j.issn.1672-2337.2005.01.001 (  0) 0)
|
| [9] |
温丹昊, 马敏, 刘志高. 相控阵雷达波束调度中的三维坐标转换方法[J]. 科技论坛, 2012(12): 25-26. (  0) 0)
|
| [10] |
张军, 刘衍, 赵迎超. 天线与转台之间的坐标关系[J]. 火控雷达技术, 2007, 36(1): 30-32. ZHANG Jun, LIU Yan, ZHAO Yingchao. Coordinate relation between antenna and turntable[J]. Fire control radar technology, 2007, 36(1): 30-32. DOI:10.3969/j.issn.1008-8652.2007.01.007 (  0) 0)
|
| [11] |
韩彦明, 陈希信. 自适应和差波束形成与单脉冲测角研究[J]. 现代雷达, 2010, 32(12): 44-47. HAN Yanming, CHEN Xixin. A study on adaptive sum and difference beamforming and monopulse angle estimation[J]. Modern radar, 2010, 32(12): 44-47. DOI:10.3969/j.issn.1004-7859.2010.12.010 (  0) 0)
|
| [12] |
NIELSEN R O. Accuracy of angle estimation with monopulse processing using two beams[J]. IEEE transactions on aerospace and electronic systems, 2001, 37(4): 1419-1423. DOI:10.1109/7.976976 (  0) 0)
|
| [13] |
SKOLNIK M I. Introduction to radar systems[M]. 3rded. New York: McGraw-Hill Education, 2002: 1-10.
(  0) 0)
|
| [14] |
杨晓倩, 刘海波, 姜菡, 等. 基于数字阵列雷达的单脉冲测角技术研究[J]. 空军预警学院学报, 2013, 27(3): 184-187. YANG Xiaoqian, LIU Haibo, JIANG Han. Study of mono-pulse angle measurement based on digital array radar[J]. Journal of air force early warning academy, 2013, 27(3): 184-187. (  0) 0)
|
| [15] |
甘明. 基于相控阵天线单脉冲测角算法的测角精度研究[J]. 现代电子技术, 2013, 36(7): 89-93. GAN Ming. Research on precision of monopulse angle measurement based on phased array antenna[J]. Modern electronics technique, 2013, 36(7): 89-93. DOI:10.3969/j.issn.1004-373X.2013.07.028 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


