MIMO技术由于其分集传输和多路复用的特点，在频谱利用率和链接的可靠性方面性能都有显著的提高^[1]。而中继协作MIMO技术自从被Sendonaris等首次提出后，因其具有提高系统容量、频谱利用率和增大系统覆盖范围等特点吸引了无线通信领域研究者们的兴趣。另外，放大转发(amplify-and-forward, AF)中继协议因其具有较低的计算复杂度和较小的传输时延而受到较多的关注^[2]。因此，结合中继技术和MIMO技术的MIMO中继技术被认为是下一代无线通信领域最具有应用前景的技术之一。特别地，因为考虑直传链路的多用户MIMO AF中继系统可以明显地提高通信质量，所以，越来越多的学者对此产生兴趣。

近年来，多用户MIMO中继系统中的预编码算法的设计问题一直备受关注，预编码算法是解决无线通信中多用户MIMO信道干扰问题的主要方法，也是提高无线通信系统性能的关键技术之一。对于多用户MIMO AF中继系统，Khandaker等^[3]针对上行的多用户MIMO中继系统，提出一种基于MMSE设计准则的预编码算法，联合优化了发射端，中继节点和接收端的预编码矩阵；基于最小SMSE设计准则且在没有考虑中继节点的情况下，文献[4]提出一种联合发射预编码矩阵和接收滤波矩阵的迭代算法。文献[3]和[4]都是在发射端为多用户的情况下展开的研究。然而，在满足功率限制的条件下，文献[5]在由一个基站、一个中继节点和多个用户组成的系统模型下，提出了一种联合预编码算法。另外，文献[5]还研究了基站的预编码设计和中继节点的预编码设计这2种特殊情况。为了减小计算复杂度，文献[6]对于多用户对MIMO AF中继系统，提出了2种子优化非迭代设计方案。然而，上述提到的文献均没有考虑发射端和接收端用户之间的直传链路。到目前为止，仅有少量的文献考虑直传链路对系统性能的贡献。在基于MMSE设计准则下，文献[7-8]针对包含直传链路的三节点双向的MIMO AF中继系统，提出了一种预编码算法，但是算法不适合应用到多用户MIMO AF中继系统中。文献[9]基于系统容量和MSE这2个设计准则，设计了一种考虑直传链路的联合预编码算法。不同于文献[9]，在包含直传链路的多用户MIMO AF中继系统中，一种加权合速率(weighted sun rate, WSR)最大化的联合预编码算法在文献[10]中被提出，算法考虑将最初的优化问题等效为容易处理的问题模型，且实现简单。

本文考虑了所有通信节点均配备多天线且包含直传链路的发射/接收端多用户MIMO AF中继系统模型，在所有发射端的用户和中继节点满足功率限制条件下，研究了一种发射端的用户集中优化的联合预编码问题。目前，没有文献对包含直传链路的发射/接收端多用户MIMO AF中继系统的预编码算法进行研究，而且多用户之间的通信更加具有实际的应用意义。基于这些，本文首先将系统所有发射端的用户看成一个整体，即将发射单流信号的多用户等效为一个发射多流信号的基站，以一种集中优化的方式处理所有发射端用户的子预编码矩阵。其次，提出一种有效的联合预编码算法，结合标准的SDP凸优化模型和迭代思想，简化了算法设计的数学推导过程，算法交替迭代至所有预编码矩阵的优化值。最后，本文提出的算法与文献[6]的2个非迭代设计和文献[10]的迭代算法进行性能比较。

1 多用户MIMO AF中继系统模型

本文考虑了一个包含直传链路的多用户MIMO AF中继系统模型，模型由K个发射端的用户、K个接收端的用户和一个中继节点组成。如图 1所示，发射端的用户和接收端的用户配备相同的天线数为N_k(k=1, 2, …, K)，中继节点配备N_r根天线。在该通信系统中，第k个发射端的用户通过中继节点或者直接将信息发送给第k个接收端的用户。对于任意一个接收端的用户来说，最终在接收端接收到的信息不仅会有相应的发射端的用户发送的有用信息，还会有来自发射端其他用户的干扰信息。因此，本文将所有发射端的用户等效为一个传输多信息流的基站，基站将所有发射端的用户发送的单信息流进行同时传输。为简化分析，本文假设系统工作在半双工模式下，信息由发射端的用户通过2个传输时隙发送到接收端的用户，并假设每个时隙内的信道状态信息(channel state information, CSI)保持不变。

在第1个传输时隙内，第k个发射端的用户将原始的单流信号s_k∈C^N_k×1(k=1, 2, …, K)经过发射预编码矩阵${\mathit{\boldsymbol{B}}_k} \in {\rm{ }}{{\bf{C}}^{{N_b} \times {N_k}}}({N_b} = \sum\limits_{k = 1}^K {{N_k}} )$处理后得到发送信号x_k=B_ks_k∈ C^N_b×1，信号x_k被同时发送给中继节点和第k个接收端的用户。其中，原始信号s_k满足的功率限制条件为R_sk=Ε[s_ks_k^H]=I_Nk。令${\mathit{\boldsymbol{s}}^{\rm{T}}} \buildrel \Delta \over = {\rm{ }}[\mathit{\boldsymbol{s}}_1^{\rm{T}} \cdots \mathit{\boldsymbol{s}}_k^{\rm{T}} \cdots {\rm{ }}\mathit{\boldsymbol{s}}_K^{\rm{T}}] \in {{\bf{C}}^{1 \times {N_b}}}$为所有发射端的用户的信号，即等效基站的原始多流信号，且信号s满足的功率限制条件为Ε[ss^H]=I_Nb。第1个时隙内，中继节点和第k个接收端的用户接收到的信号分别为y_r∈ C^N_r×1和y_k¹∈ C^N_k×1，具体表达式为：

$ {\mathit{\boldsymbol{y}}_r} = \mathit{\boldsymbol{HBs}} + {\mathit{\boldsymbol{n}}_r} = \mathit{\boldsymbol{H}}\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}} + {\mathit{\boldsymbol{n}}_r} $

(1)

$ \mathit{\boldsymbol{y}}_k^1 = \underbrace {{\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}}_{有用信号} + \underbrace {{\mathit{\boldsymbol{T}}_k}\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{s}}_i}} }_{干扰信号} + \mathit{\boldsymbol{n}}_k^1 $

(2)

式中：H∈C^N_r×N_b是等效后的基站到中继节点的MIMO信道矩阵；$\mathit{\boldsymbol{B}} \buildrel \Delta \over = [{\mathit{\boldsymbol{B}}_1}, \cdots, {\mathit{\boldsymbol{B}}_k}, \cdots, {\mathit{\boldsymbol{B}}_K}] \in {{\bf{C}}^{{N_b} \times {N_b}}}$是等效后基站的预编码矩阵，矩阵B由所有发射端用户的子预编码矩阵构成。等效后的基站到第k个接收端用户之间的MIMO信道矩阵为T_k∈C^N_k×N_b(k=1, 2, …, K)。另外，n_r∈C^N_r×1和n_k¹∈C^N_k×1分别为中继节点和第k个接收端用户处的复加性高斯白噪声(AWGN)，且满足均值为零、方差矩阵分别为Ε[n_rn_r^H]=σ_r²I_Nr和Ε[n_k¹(n_k¹)^H]=σ_k²I_Nk，σ_r²和σ_k²分别为中继节点和第k个接收端用户处的噪声功率。

在第2个传输时隙内，中继节点通过中继预处理矩阵F∈C^N_r×N_r对接收信号y_r进行处理，并转发给所有的接收端用户，第k个接收端的用户接收到的信号y_k²可表示为：

$ \mathit{\boldsymbol{y}}_k^2 = \underbrace {{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}}_{有用信号} + \underbrace {\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}{\mathit{\boldsymbol{B}}_i}{s_i}} }_{干扰信号} + {\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{n}}_r} + \mathit{\boldsymbol{n}}_k^2 $

(3)

式中：G_k∈C^N_k×N_r(k=1, 2, …, K)为中继节点到第k个接收端用户的MIMO信道矩阵；n_k²∈C^N_k×1为第k个接收端用户在第2个传输时隙内的复AWGN，且满足均值为零、方差矩阵为Ε[n_k²(n_k²)^H]=σ_k²I_Nk；P_r为中继节点处最大的发射功率。那么，中继节点处的功率限制条件可具体表达为：

$ {\rm{tr}}\left( {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}} + \sigma _r^2{\mathit{\boldsymbol{I}}_{{N_r}}}} \right){\mathit{\boldsymbol{F}}^{\rm{H}}}} \right) \le {P_r} $

(4)

结合表达式(2)和(3)，第k个接收端的用户在2个传输时隙内接收的信号y_k¹和y_k²可以表达为：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_k} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}_k^1}\\ {\mathit{\boldsymbol{y}}_k^2} \end{array}} \right] = \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_k}}\\ {{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}} \end{array}} \right]{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k}}_{有用信号} + \underbrace {\sum\limits_{i = 1,i \ne k}^K {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_k}}\\ {{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}} \end{array}} \right]{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{s}}_i}} }_{干扰信号} + }\\ {\underbrace {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{F}}}&\mathit{\boldsymbol{I}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{n}}_k^1}\\ {{\mathit{\boldsymbol{n}}_r}}\\ {\mathit{\boldsymbol{n}}_k^2} \end{array}} \right]}_{噪声}} \end{array} $

(5)

式中：本文定义${\mathit{\boldsymbol{\overline H}} _k} = {[{\mathit{\boldsymbol{T}}_k}\;\;{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}]^{\rm{T}}}$ (k=1, 2, …, K)为等效后的基站到第k个接收端用户之间的等效信道矩阵；${\mathit{\boldsymbol{\overline n}} _k} = {[\mathit{\boldsymbol{n}}_k^1\;\;{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{n}}_r} + {\boldsymbol{n}}_k^2]^{\rm{T}}}$ (k=1, 2, …, K)为等效后的基站到第k个接收端用户之间的等效噪声。那么，表达式(5)可进一步表达为：

$ {\mathit{\boldsymbol{y}}_k} = {{\mathit{\boldsymbol{\bar H}}}_k}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k} + \sum\limits_{i = 1,i \ne k}^K {{{\mathit{\boldsymbol{\bar H}}}_k}{\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{s}}_i}} + {{\mathit{\boldsymbol{\bar n}}}_k} $

(6)

在第k个接收端用户处用滤波矩阵W_k∈C^N_k×2N_k(k=1, 2, …, K)对信号s_k进行估计：

$ {{\mathit{\boldsymbol{\bar s}}}_k} = {\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{y}}_k} $

(7)

式中第k个接收端用户处的滤波矩阵W_k由第1个传输时隙的滤波矩阵W_1k∈C^N_k×N_k和第2个传输时隙的滤波矩阵W_2k∈C^N_k×N_k组成。根据文献[11]的MMSE接收滤波理论，第k个接收端用户处的滤波矩阵W_k的表达式可表达为：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_k} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{1k}}}&{{\mathit{\boldsymbol{W}}_{2k}}} \end{array}} \right] = \arg \mathop {\min }\limits_{{W_k}} {\rm{E}}\left[ {\left\| {{\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{s}}_k}} \right\|_2^2} \right] = }\\ {\mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}{{\left( {{{\mathit{\boldsymbol{\bar H}}}_k}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}} + {\mathit{\boldsymbol{Z}}_k}\mathit{\boldsymbol{Z}}_k^{\rm{H}}} \right)}^{ - 1}}} \end{array} $

(8)

式中：Z_kZ_k^H=diag(σ_k²I_Nk, σ_k²I_Nk+σ_r²G_kFF^HG_k^H)。根据表达式(5)和表达式(8)，第k个接收端用户处的均方误差矩阵MSE_k的具体表达式为：

$ \begin{array}{*{20}{c}} {{\rm{MS}}{{\rm{E}}_k} = {\rm{E}}\left[ {\left( {{\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{s}}_k}} \right){{\left( {{\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{s}}_k}} \right)}^{\rm{H}}}} \right] = }\\ {{\mathit{\boldsymbol{I}}_{{N_k}}} - {\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}} + }\\ {{\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}} + {\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{Z}}_k}\mathit{\boldsymbol{Z}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}}} \end{array} $

(9)

2 基于SMSE最小化的联合预编码设计

这部分主要设计了一种发射端的用户集中优化的联合预编码算法，在保证系统SMSE最小化的前提下，将所有传输单流信号的发射端用户等效为一个传输多流信号的基站，通过预编码算法获得所有发射端用户的子预编码矩阵B_k，接收端用户的滤波矩阵W_k和中继收发矩阵F的优化值。具体优化问题为：

$ \mathop {\min }\limits_{\scriptstyle{B_k},F,{W_k}\atop {\scriptstyle {k = 1,2, \cdots ,K}}} \sum\limits_{k = 1}^K {{\rm{tr}}\left( {{\rm{MS}}{{\rm{E}}_k}} \right)} $

(10)

$ {\rm{s}}.{\rm{t}}.\;\;\;{\rm{tr}}\left( {{\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{B}}_k^{\rm{H}}} \right) \le {P_s} $

(11)

$ {\rm{tr}}\left( {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}} + \sigma _r^2{\mathit{\boldsymbol{I}}_{{N_r}}}} \right){\mathit{\boldsymbol{F}}^{\rm{H}}}} \right) \le {P_r} $

(12)

显然，对于矩阵变量B_k、F和W_k，优化问题(10)~(12)是一个非凸的问题，所以不能直接获得每个优化变量的全局优化值。对此，我们设计了一个有效的发射端的用户集中优化的迭代算法，通过求解下面几个子凸优化问题获得优化变量B_k、F和W_k的局部优化表达式。最后，通过算法交替迭代至收敛，获得每个优化变量矩阵的局部优化值。

2.1 发射端用户的子预编码矩阵的优化设计

给定矩阵变量F和W_k后，将表达式(9)代入到目标函数表达式(10)中，原多优化变量的优化问题，就可转化为只有发射端用户的子预编码矩阵B_k(k=1, 2, …, K)一个优化变量的优化问题，仅以B_k为优化变量的优化方程可以表示为：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\begin{array}{*{20}{c}} {{B_k}}\\ {k = 1,2, \cdots ,K} \end{array}} \sum\limits_{k = 1}^K {{\rm{tr}}\left( {{\mathit{\boldsymbol{I}}_{{N_k}}} - {\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}} + } \right.} }\\ {\left. {{\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}} + {\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{Z}}_k}\mathit{\boldsymbol{Z}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}}} \right)} \end{array} $

(13)

$ {\rm{s}}.{\rm{t}}.{\rm{tr}}\left( {{\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{B}}_k^{\rm{H}}} \right) \le {P_s} $

(14)

对于上述在给定矩阵变量F和W_k下的关于矩阵变量B_k的优化问题，暂时忽略中继节点处的功率限制条件，因为该条件可以通过后续的迭代过程得到满足。显而易见，问题(13)~(14)是关于矩阵变量B_k的凸优化问题。

为了求解上述关于矩阵变量B_k的凸优化问题，本文采用传统的凸优化求解方法K.K.T条件求解其优化值^[12]。首先构造有关B_k的拉格朗日函数为：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{{B_k}}} = \sum\limits_{k = 1}^K {{\rm{tr}}\left( {{\mathit{\boldsymbol{I}}_{{N_k}}} - {\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}} + } \right.} }\\ {\left. {{\mathit{\boldsymbol{W}}_k}{{\mathit{\boldsymbol{\bar H}}}_k}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}}} \right) + {\lambda _{{B_k}}}\left( {{\rm{tr}}\left( {{\mathit{\boldsymbol{B}}_k}\mathit{\boldsymbol{B}}_k^{\rm{H}}} \right) - {P_s}} \right)} \end{array} $

(15)

式中：λ_Bk≥0(k=1, 2, …, K)是与功率限制条件(14)有关的拉格朗日系数。由于表达式(9)中的W_kZ_kZ_k^HW_k^H与矩阵变量B_k无关，因此在关于矩阵变量B_k的拉格朗日函数中忽略不考虑。通过拉格朗日乘数法求得的矩阵变量B_k的优化表达式为：

$ {\mathit{\boldsymbol{B}}_k} = \sum\limits_{j = 1}^K {{{\left( {\mathit{\boldsymbol{\bar H}}_j^{\rm{H}}\mathit{\boldsymbol{W}}_j^{\rm{H}}{\mathit{\boldsymbol{W}}_j}{{\mathit{\boldsymbol{\bar H}}}_j} + {\lambda _{{B_k}}}{\mathit{\boldsymbol{I}}_{{N_b}}}} \right)}^{ - 1}}\mathit{\boldsymbol{\bar H}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_k^{\rm{H}}} $

(16)

在求解表达式(16)的过程中，应用了矩阵运算规则：$\frac{\partial \text{tr}({{Z}^{\dagger }}\mathit{\boldsymbol{A}})}{\partial {{Z}^{*}}}=\mathit{\boldsymbol{A}}$和$\frac{\partial \text{tr}(\mathit{\boldsymbol{AZ}}{{\mathit{\boldsymbol{Z}}}^{\dagger }}\mathit{\boldsymbol{B}})}{\partial {{Z}^{*}}}=\mathit{\boldsymbol{BAZ}}$。其中，未知的拉格朗日系数λ_Bk通过二分法算法获得。

2.2 中继收发矩阵的优化设计

给定矩阵变量B_k和W_k(k=1, 2, …, K)，将表达式(9)代入目标函数表达式(10)中，原优化问题就可转化为只有中继收发矩阵F一个优化变量的问题，仅以F为优化变量的优化方程可进一步转化为：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_F \sum\limits_{k = 1}^K {{\rm{tr}}\left( {{\mathit{\boldsymbol{I}}_{{N_k}}} - {\mathit{\boldsymbol{W}}_{1k}}{\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{T}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} - {\mathit{\boldsymbol{W}}_{2k}}{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FH}}{\mathit{\boldsymbol{B}}_k} - } \right.} }\\ {\mathit{\boldsymbol{B}}_k^{\rm{H}}{\mathit{\boldsymbol{H}}^{\rm{H}}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{G}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}} + {\mathit{\boldsymbol{W}}_{2k}}{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FHB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{T}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + {\mathit{\boldsymbol{W}}_{1k}}{\mathit{\boldsymbol{T}}_k}}\\ {\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{G}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}} + {\mathit{\boldsymbol{W}}_{2k}}{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{FHB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{G}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}} + }\\ {{\mathit{\boldsymbol{W}}_{1k}}{\mathit{\boldsymbol{T}}_k}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{T}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + \sigma _r^2{\mathit{\boldsymbol{W}}_{2k}}{\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{G}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}} + \sigma _k^2}\\ {\left. {{\mathit{\boldsymbol{W}}_{1k}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + \sigma _k^2{\mathit{\boldsymbol{W}}_{2k}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}}} \right)} \end{array} $

(17)

$ {\rm{s}}.{\rm{t}}.{\rm{tr}}\left( {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}} + \sigma _r^2{\mathit{\boldsymbol{I}}_{{N_r}}}} \right){\mathit{\boldsymbol{F}}^{\rm{H}}}} \right) \le {P_r} $

(18)

与优化问题(13)~(14)一样，优化问题(17)~(18)是关于矩阵变量F的凸优化问题。Matlab仿真软件下的CVX优化工具箱可以高效地求解复杂的凸优化问题，K.K.T条件在求解凸优化问题时需要做大量的数学推导，算法复杂度高。因为CVX工具箱只可以优化特定的凸优化问题，所以需要将优化问题(17)~(18)转化成一个SDP问题后，再去优化矩阵变量F。首先，根据下面的运算规则^[13]：

$ {\rm{tr}}\left( {{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{D}}} \right) = {\left( {{\rm{vec}}\left( \mathit{\boldsymbol{C}} \right)} \right)^{\rm{T}}}{\rm{vec}}\left( \mathit{\boldsymbol{D}} \right) $

(19)

$ {\rm{tr}}\left( {{\mathit{\boldsymbol{C}}^{\rm{H}}}\mathit{\boldsymbol{DCA}}} \right) = {\rm{vec}}{\left( \mathit{\boldsymbol{C}} \right)^{\rm{H}}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}} \otimes \mathit{\boldsymbol{D}}} \right){\rm{vec}}\left( \mathit{\boldsymbol{C}} \right) $

(20)

令${\mathit{\boldsymbol{M}}_k} \buildrel \Delta \over = {\mathit{\boldsymbol{W}}_{2k}}{\mathit{\boldsymbol{G}}_k}$，V_k=W_1kT_k和f=vec(F)，关于中继收发矩阵F的目标函数表达式(17)可进行分解为：

$ {\rm{tr}}\left( {{\mathit{\boldsymbol{M}}_k}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{M}}_k^{\rm{H}}} \right) = {\mathit{\boldsymbol{f}}^{\rm{H}}}\left( {{\mathit{\boldsymbol{I}}_{{N_r}}} \otimes \left( {\mathit{\boldsymbol{M}}_k^{\rm{H}}{\mathit{\boldsymbol{M}}_k}} \right)} \right)\mathit{\boldsymbol{f}} $

(21)

$ \begin{array}{*{20}{c}} {{\rm{tr}}\left( {{\mathit{\boldsymbol{M}}_k}\mathit{\boldsymbol{FH}}{\mathit{\boldsymbol{B}}_k}} \right) = {\rm{tr}}\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{M}}_k}\mathit{\boldsymbol{F}}} \right) = }\\ {{{\left( {{\rm{vec}}\left( {{{\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{M}}_k}} \right)}^{\rm{T}}}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{f}}} \end{array} $

(22)

$ \begin{array}{*{20}{c}} {{\rm{tr}}\left( {{\mathit{\boldsymbol{M}}_k}\mathit{\boldsymbol{FHB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{V}}_k^{\rm{H}}} \right) = {{\left( {{\rm{vec}}\left( {{{\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{V}}_k^{\rm{H}}{\mathit{\boldsymbol{M}}_k}} \right)}^{\rm{T}}}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{f}}}\\ {{\rm{tr}}\left( {{\mathit{\boldsymbol{M}}_k}\mathit{\boldsymbol{FHB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{M}}_k^{\rm{H}}} \right) = {\mathit{\boldsymbol{f}}^{\rm{H}}}\left( {{{\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}} \right)}^{\rm{T}}}} \right.}\\ {\left. { \otimes \left( {\mathit{\boldsymbol{M}}_k^{\rm{H}}{\mathit{\boldsymbol{M}}_k}} \right)} \right)\mathit{\boldsymbol{f}}} \end{array} $

(24)

令$\mathit{\boldsymbol{R}} \buildrel \Delta \over = \mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}} + \sigma _r^2{\mathit{\boldsymbol{I}}_{{N_r}}}$，中继功率限制条件的表达式(18)左边一项可以通过矩阵运算法则(19)~(20)进一步转化为：

$ {\rm{tr}}\left( {\mathit{\boldsymbol{FR}}{\mathit{\boldsymbol{F}}^{\rm{H}}}} \right) = {\mathit{\boldsymbol{f}}^{\rm{H}}}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{{N_r}}}} \right)\mathit{\boldsymbol{f}} $

(25)

另外，为简化最终的优化问题，定义下面几个变量替换：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_k} \buildrel \Delta \over = \left( {{{\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}} \right)}^{\rm{T}}} + \sigma _r^2{\mathit{\boldsymbol{I}}_{{N_r}}}} \right) \otimes \left( {\mathit{\boldsymbol{M}}_k^{\rm{H}}{\mathit{\boldsymbol{M}}_k}} \right)}\\ {{\mathit{\boldsymbol{a}}_k} \buildrel \Delta \over = {\rm{vec}}\left( {{{\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{M}}_k}} \right)}^{\rm{T}}}} \right)}\\ {{\mathit{\boldsymbol{b}}_k} \buildrel \Delta \over = {\rm{vec}}\left( {{{\left( {\mathit{\boldsymbol{HB}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{V}}_k^{\rm{H}}{\mathit{\boldsymbol{M}}_k}} \right)}^{\rm{T}}}} \right)}\\ {{t_k} \buildrel \Delta \over = {\rm{tr}}\left( {{\mathit{\boldsymbol{I}}_{{N_r}}} - {\mathit{\boldsymbol{W}}_{1k}}{\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}\mathit{\boldsymbol{T}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + {\mathit{\boldsymbol{W}}_{1k}}{\mathit{\boldsymbol{T}}_k}\mathit{\boldsymbol{B}}} \right.}\\ {\left. {{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{T}}_k^{\rm{H}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + \sigma _k^2{\mathit{\boldsymbol{W}}_{1k}}\mathit{\boldsymbol{W}}_{1k}^{\rm{H}} + \sigma _k^2{\mathit{\boldsymbol{W}}_{2k}}\mathit{\boldsymbol{W}}_{2k}^{\rm{H}}} \right)} \end{array} $

(26)

将表达式(21)~(26)代入到优化问题(17)~(18)中，则与中继收发矩阵F相关的优化问题可进一步转化为：

$ \mathop {\min }\limits_f \sum\limits_{k = 1}^K {\left( {{\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{U}}_k}\mathit{\boldsymbol{f}} + \mathit{\boldsymbol{a}}_k^{\rm{H}}\mathit{\boldsymbol{f}} + {\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_k} + \mathit{\boldsymbol{b}}_k^{\rm{H}}\mathit{\boldsymbol{f}} + {\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{b}}_k} + {\mathit{\boldsymbol{t}}_k}} \right)} $

(27)

$ {\rm{s}}.{\rm{t}}.{\mathit{\boldsymbol{f}}^{\rm{H}}}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{{N_r}}}} \right)\mathit{\boldsymbol{f}} \le {P_r} $

(28)

为进一步将非凸的优化问题转化为标准的SDP问题，根据舒尔补定理，引入辅助变量p_k(k=1, 2, …, K)且满足p_k≥tr(MSE_k)，基于MSMSE准则的关于矩阵变量F的优化问题可进一步转化为如下等价的SDP问题：

$ \mathop {\min }\limits_{\mathop {f,{p_k},}\limits_{k = 1,2, \cdots ,K} } \sum\limits_{k = 1}^K {{p_k}} $

(29)

$ {\rm{s}}.{\rm{t}}.\left[ {\begin{array}{*{20}{c}} {{P_r}}&{{\mathit{\boldsymbol{f}}^{\rm{H}}}}\\ \mathit{\boldsymbol{f}}&{{{\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{{N_r}}}} \right)}^{ - 1}}} \end{array}} \right] \ge 0 $

(30)

$ \left[ {\begin{array}{*{20}{c}} {{p_k} - \mathit{\boldsymbol{a}}_k^{\rm{H}}\mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_k} - \mathit{\boldsymbol{b}}_k^{\rm{H}}\mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{f}}^{\rm{H}}}{\mathit{\boldsymbol{b}}_k} - {\mathit{\boldsymbol{t}}_k}}&{{\mathit{\boldsymbol{f}}^{\rm{H}}}\mathit{\boldsymbol{U}}_k^{{\rm{1}}/2}}\\ {\mathit{\boldsymbol{U}}_k^{{\rm{H}}/2}\mathit{\boldsymbol{f}}}&{{\mathit{\boldsymbol{I}}_{{N_r}}}} \end{array}} \right] \ge 0 $

(31)

上述优化问题(29)~(31)是CVX可以解决的标准SDP问题，CVX优化工具箱^[14]会识别标准的SDP问题且自动调用内点法对该问题进行求解，简化了以往求解此类优化问题时所需要的大量数学运算。

2.3 联合迭代算法

综上所述，当接收端的用户采用MMSE接收滤波矩阵W_k(k=1, 2, …, K)时，最初的基于MSMSE准则的联合优化问题被转化为2个子优化问题，然后单独优化发射端用户的子预编码矩阵B_k(k=1, 2, …, K)和中继收发矩阵F的优化形式。前面已经具体介绍了每个子凸优化问题的求解思路和设计过程，在包含直传链路的发射/接收端多用户的MIMO AF中继系统中，对于预编码矩阵B_k、F和W_k的优化问题，一种基于MSMSE准则的联合迭代预编码算法如下。

基于MSMSE准则的联合迭代算法

1) 初始化：B_k和F的初始值满足功率限制条件，设最大迭代次数为I_max，迭代终止门限为ε，迭代次数初始化n=1；

2) 给定B_k⁽ⁿ⁾和F⁽ⁿ⁾，根据表达式(8)计算所有接收端用户的接收滤波矩阵W_k⁽ⁿ⁾；

3) 给定F⁽ⁿ⁾和W_k⁽ⁿ⁾，通过求解表达式(16)更新所有发射端用户的子预编码矩阵B_k⁽ⁿ⁺¹⁾；

4) 根据更新后的B_k⁽ⁿ⁺¹⁾和W_k⁽ⁿ⁾，通过求解表达式(29)~(31)的SDP问题获得更新后的中继收发矩阵F⁽ⁿ⁺¹⁾；

5) 判断如果‖B_k⁽ⁿ⁺¹⁾-B_k⁽ⁿ⁾‖²≤ε且‖F⁽ⁿ⁺¹⁾-F⁽ⁿ⁾‖≤ε或者n>I_max，结束迭代；否则，跳转2)继续迭代直到满足收敛条件。

因为上述算法在每次更新W_k、B_k和F时，对应的表达式(8)、式(16)和式(29)~(31)都是非负的且单调递减，所以上述联合迭代预编码算法满足收敛条件，且算法总是收敛到优化值点。另外，算法在每一次迭代过程中，主要的算法复杂度式求解表达式(29)~(31)的SDP问题来更新F，然而求解B_k和W_k的算法复杂度与求解SDP问题的复杂度相比可以忽略不计，因此每次迭代过程的算法复杂度可以近似为O((N_r²+1)^4.5)^[15]。

3 仿真结果

在数值仿真过程中，假设所有的MIMO信道(包括H、G_k和T_k(k=1, 2, …, K))均服从准静态独立同分布的瑞利衰落模型，所有的噪声(包括n_r和n_k(k=1, 2, …, K))均为零均值的加性白噪声，且所有通信节点的噪声功率归一化，即σ_r²=σ_k²=1。为简化分析，在下面的论述中用SNR表示所有通信链路的信噪比，即SNR=SNR_sr=SNR_rd=SNR_sd。根据系统模型中对所有节点配备天线数的情况说明，下面给出具体的仿真参数设置：发射端的用户数和接收端的用户数均为K=4，且所有的用户都配备2根天线，即N_k=2，中继节点配备的天线数为N_r=8。

为进一步验证所提算法性能上的优越性，首先将提出的算法与下面的4种优化算法在系统SMSE性能和系统BER性能上进行了比较分析。其中，4种比较算法如下：

1) MSMSE w/o DL算法:一种基于MSMSE设计准则的联合迭代算法，该算法没有考虑发射端与接收端之间的直传链路，系统模型是多用户通过中继节点的协作通信；

2) WSR算法^[10]：一种基于WSR准则的联合迭代算法，该算法考虑发射端与接收端之间的直传链路，系统模型是一个基站和多个用户之间通过中继节点的协作通信；

3) ZF-CI算法^[6]：迫零信道反转算法，一种多用户对间点对点中继系统中的非迭代算法。其中，${\mathit{\boldsymbol{F}}^{({\rm{ZF}})}} = \sum\limits_{k = 1}^K {\mathit{\boldsymbol{B}}_k^{\left( {{\rm{ZF}}} \right)}{\mathit{\boldsymbol{W}}_k}}, \mathit{\boldsymbol{B}}_k^{\left( {{\rm{ZF}}} \right)} = \mathit{\boldsymbol{Q}}_k^{\left( {{\rm{ZF}}} \right)}\mathit{\boldsymbol{U}}_k^{\left( {{\rm{ZF}}} \right)}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k^{\left( {{\rm{ZF}}} \right)1/2}$；

4) MMSE-CI算法^[6]：最小均方误差信道反转算法，一种多用户对间点对点中继系统中的非迭代算法。其中，${\mathit{\boldsymbol{F}}^{({\rm{MMSE}})}} = \sum\limits_{k = 1}^K {\mathit{\boldsymbol{B}}_k^{\left( {{\rm{MMSE}}} \right)}{\mathit{\boldsymbol{W}}_k}}, \mathit{\boldsymbol{B}}_k^{\left( {{\rm{MMSE}}} \right)} = \mathit{\boldsymbol{Q}}_k^{\left( {{\rm{MMSE}}} \right)}\mathit{\boldsymbol{U}}_k^{\left( {{\rm{MMSE}}} \right)}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k^{\left( {{\rm{MMSE}}} \right)1/2}$。

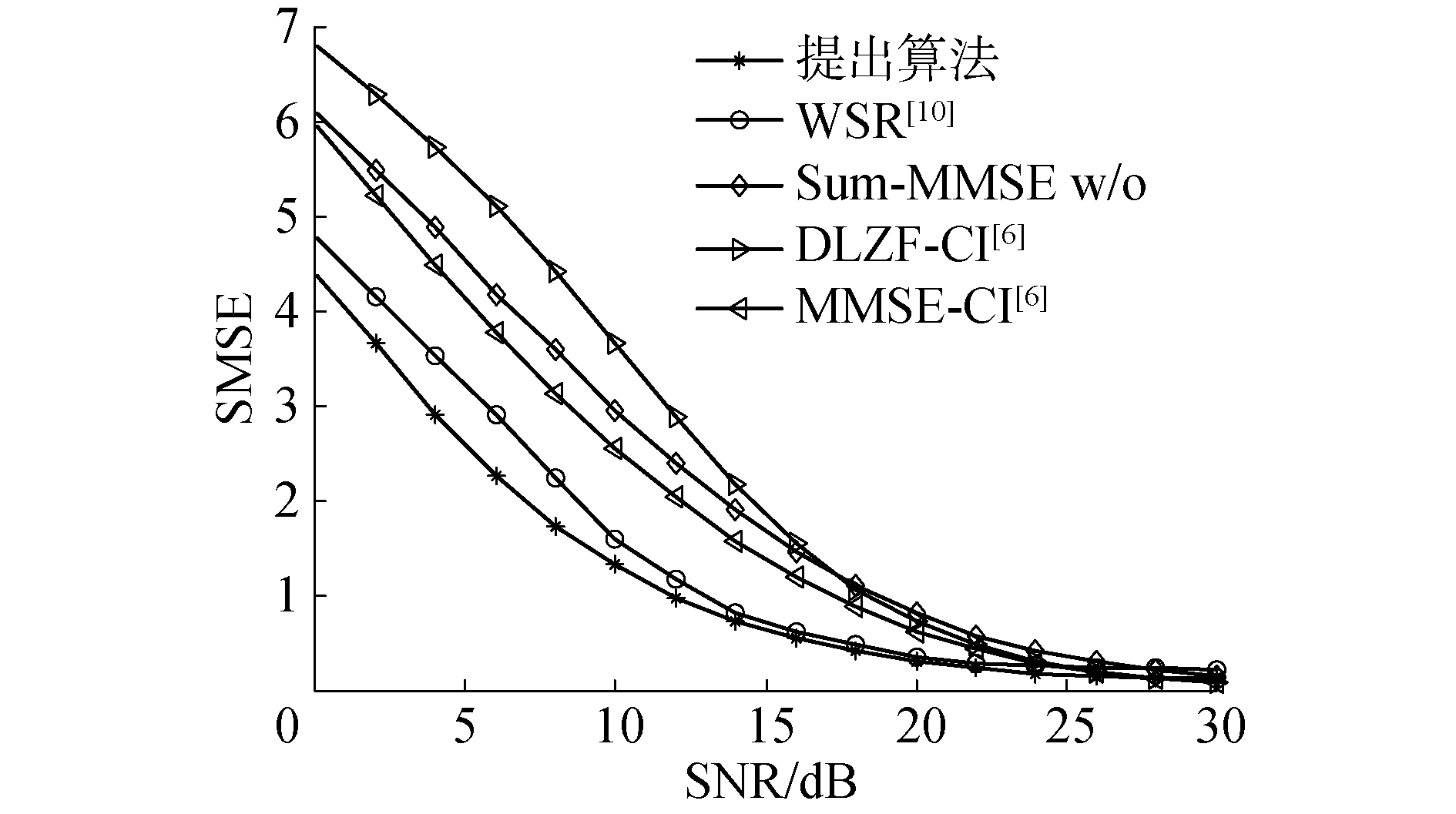
图 2为包含直传链路的发射/接收端多用户MIMO AF中继系统中的SMSE性能随SNR变化的算法比较曲线图。从仿真图中可以明显地看出，本文提出的迭代算法在整个SNR范围内，SMSE性能最优，并且随着SNR的增加，算法的SMSE值接近于0。在所有的算法仿真曲线中，WSR算法与提出算法的SMSE性能相近，文献[6]中的非迭代ZF-CI算法的SMSE性能最差。在低SNR情况下，例如SNR=0时，提出算法的SMSE值低于ZF-CI算法的SMSE值约为2.5。另外，从仿真图中可以得出2个结论：1)提出算法与没有考虑直传链路的MSMSE w/o DL算法相比，算法可以明显地降低系统的SMSE值；2)尽管文献[6]中提出的2个非迭代算法，ZF-CI算法和MMSE-CI算法减小了迭代算法的计算复杂度，但它们的系统SMSE性能曲线却明显高于提出的算法，尤其在SNR取值较低的情况下。

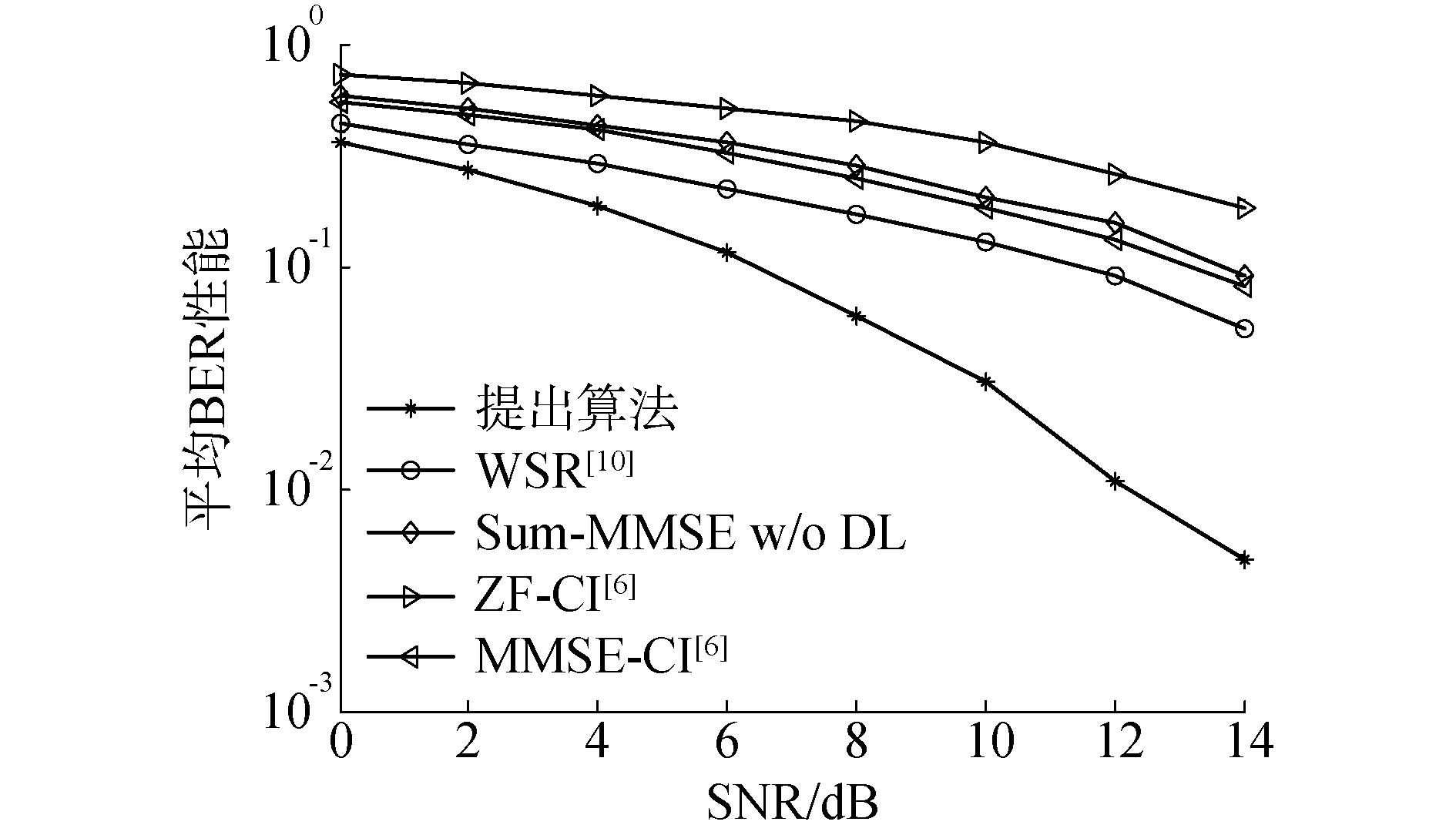
图 3为提出算法与其他4种算法在低SNR情况下的BER性能曲线图，信号调制方式为QPSK。由仿真结果图可知，提出算法的系统BER性能明显优于其他4种算法的BER性能，其他4种算法的BER性能相近，并且提出算法的BER性能随着SNR的增加显著提高。

随着SNR值的增加系统的SMSE值在减小，并且SNR取值的不同将直接影响着算法的收敛速度。例如，在低SNR情况下，提出算法在6次迭代以后收敛；在高SNR的情况下，提出算法在4次迭代以内就可以达到收敛。因此，提出算法仅仅需要较少的迭代次数就可以实现较好的SMSE性能，同时也表明了提出算法有较低的计算复杂度和较小的处理延迟。

在不同的SNR情况下，提出算法的SMSE性能的收敛情况如图 4所示。仿真图给出了提出的算法分别在SNR=10 dB、SNR=20 dB和SNR=30 dB 3种情况下，系统SMSE性能随算法迭代次数变化的仿真曲线。从仿真图中可以看出，随着SNR值的增加系统的SMSE值在减小，即系统的SMSE值与SNR值成反比。并且SNR取值的不同将直接影响着算法的收敛速度，在低SNR情况下，提出算法在6次迭代以后收敛；在高SNR的情况下，提出算法在4次迭代以后能够快速地收敛。因此，提出算法仅仅需要较少的迭代次数就可以实现较好的SMSE性能。同时也表明了提出算法有较低的计算复杂度和较小的延迟。

为进一步验证提出算法的优越性，在不同用户数的情况下，即K的取值分别为K=2和K=4。图 5和图 6分别给出了提出算法的系统SMSE性能随着SNR变化的曲线图和提出算法的系统SMSE性能随着迭代次数变化的曲线图。从图 5中可以得出，当SNR增加时，系统的SMSE性能曲线有明显的下降趋势，并且不同用户数下的SMSE取值最终都趋近于0；从图 6中可以得出，用户数多的算法其收敛速度也是最快的。

4 结论

对于包含直传链路的发射/接收端多用户MIMO AF中继系统，提出一种发射端用户集中优化的联合预编码算法。

1) 算法首先将发射单流信号的多用户等效为一个发射多流信号的基站，然后根据等效的通信模型，基于MSMSE准则的算法将原来三变量非凸的优化问题转化为单变量的凸优化问题进行求解。

2) 对于发射端的用户子预编码矩阵B_k(k=1, 2, …, K)的优化问题，通过传统的K.K.T条件求解所有的B_k的优化表达式。

3) 中继收发矩阵F的子优化问题被转化成为一个标准的SDP问题，对于中继收发矩阵F的SDP问题，通过CVX优化工具箱自动识别并求解出局部最优解，最后所有优化矩阵联合迭代至收敛获得最优解。

4) 考虑到现有的文献忽略直传链路对系统性能的贡献，本文将直传链路的作用考虑到发射/接收端多用户MIMO AF中继系统中，可以明显地提高了系统的性能。仿真结果表明，提出算法的SMSE性能和BER性能均优于现有的联合预编码算法，而且算法具有快速的收敛速度。