2. 大连海事大学 船舶h与海洋工程学院, 辽宁 大连 116026
2. School of Naval Architecture and Ocean Engineering, Dalian Maritime University, Dalian 116026, China
圆碟形水下滑翔机对比鱼雷形水下滑翔机,其外形不仅左右对称,前后、上下也对称,具有全向运动的特性,机动性极强。日本较早提出了圆碟形水下滑翔机的设计,主要应用于虚拟锚泊,对指定海域进行监测,其设计方案已经完成了海试试验,证实了圆碟形设计理念的可行性,但其设计方案中的姿态调节机构和浮力调节机构复杂,需要多个电机同时运作才能实现姿态和净浮力的调节[1-2]。美国研究开发了一款带尾翼的碟形水下滑翔机Discus[3],它的坐底稳定性好,海底海流阻力低。国内的一些大学和研究人员也相继开始研究碟形外观的水下机器人或潜水器,王天[4]、张超[5]研究了碟形水下机器人,针对其特殊外形进行了航姿控制系统的研究,但水下机器人配备了螺旋桨或喷水推进装置,结构同样复杂。张怀新等[6]在鱼雷形水下机器人的基础上进行扁平化,提出一种圆碟形水下机器人,并对该机器人进行了水动力试验与数值计算,证实其具有良好的水动力性能[7]。文献[8]提出一种碟形潜水器的概念,并对其水动力性能、稳定性和机动性进行了仿真分析,但其提出的碟形潜水器只是每一站的剖面为椭圆形,外形仍与常规水下滑翔机的鱼雷形外观相似。赵宝强等[9]自主设计了碟形水下滑翔器原理样机,并进行了建模与仿真,证实了碟形水下滑翔器的可行性。
升阻比和稳定性分别影响水下滑翔机航行效率与运动控制,螺旋运动半径、螺距和周期反映滑翔机小空间内的机动能力,但目前对于碟形水下滑翔机而言,上述3点的研究均处于空白。因此,本文研究圆碟形水下滑翔机垂直面、空间运动的性能和受到外界小幅扰动后的稳定性是非常有必要的。
1 圆碟形水下滑翔机运动控制方程本文定义圆碟形水下滑翔机6个自由度的运动分别为:进退、横移、升沉、横倾、纵倾和回转运动,各运动状态的描述如表 1所示。
| 表 1 滑翔机六自由度运动描述 Table 1 Description of glider′s six degrees of freedom motion |
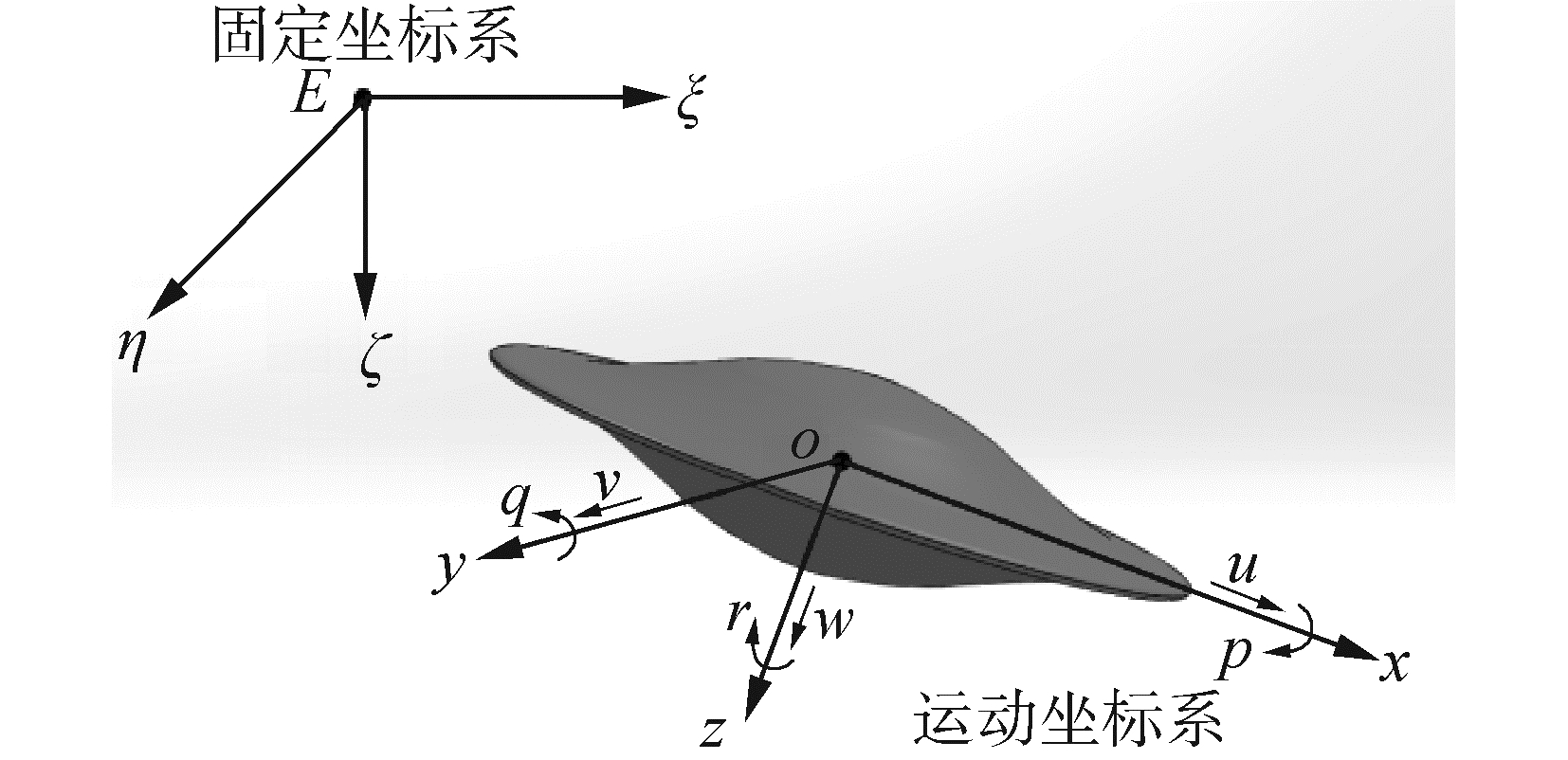
参考水下运载器坐标的定义[10],本文采用的坐标系如图 1所示,包含固定坐标系和运动坐标系。图 1中,E-ξηζ为固定坐标系,建立在海平面上;E选为海面上一点,Eξ轴和Eζ轴在同一水平面上,Eξ轴指向滑翔机主要的前进方向,Eη轴与Eξ轴垂直,Eζ轴与Eξη坐标平面垂直,正方向指向地心,使坐标系E-ξηζ为一个右手系;o-xyz为运动坐标系,固结在滑翔机上,原点o取在滑翔机的浮心上,ox轴取在纵中剖面内,指向滑翔机的主要前进方向,oy轴垂直于纵中剖面,指向ox轴在水平面内顺时针旋转90°的方向,oz轴位于纵中剖面内,与平面xoy垂直,其正方向使坐标系o-xyz为一个右手系。
|
Download:
|
| 图 1 坐标系系统 Fig. 1 Coordinate system | |
假定固定坐标系E-ξηζ与运动坐标系o-xyz的原点E和o已经重合,通过3次旋转变换可以使2个坐标系相互重合,流程为:1)坐标系oξηζ绕oζ轴旋转ψ角,得到坐标系ox1y1ζ;2)坐标系ox1y1ζ绕oy1轴旋转θ角,得到坐标系ox1y1z1;3)坐标系ox1y1z1绕ox轴旋转φ角,得到坐标系oxyz。
3次旋转变换中,角度φ称为横倾角,θ称为俯仰角,ψ称为回转角,三者统称为欧拉角,记做Λ=[φ θ ψ]T。定义了欧拉角后,可以用旋转变换矩阵REB来描述圆碟形水下滑翔机在运动坐标系下位置到固定坐标系的转换[11]。本文采用简化表示:c·=cos(·),s·=sin(·),t·=tan(·),矩阵REB为:
| $ {\mathit{\boldsymbol{R}}_{EB}} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\psi {\rm{c}}\theta }&{{\rm{c}}\psi {\rm{s}}\theta - {\rm{s}}\psi {\rm{c}}\varphi }&{{\rm{c}}\psi {\rm{s}}\theta {\rm{c}}\varphi + {\rm{s}}\psi {\rm{s}}\varphi }\\ {{\rm{s}}\psi {\rm{c}}\theta }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{s}}\varphi + {\rm{c}}\psi {\rm{c}}\varphi }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{c}}\varphi - {\rm{c}}\psi {\rm{s}}\varphi }\\ { - {\rm{s}}\theta }&{{\rm{c}}\theta {\rm{s}}\varphi }&{{\rm{c}}\theta {\rm{c}}\varphi } \end{array}} \right] $ | (1) |
圆碟形水下滑翔机在运动过程中,运动坐标系固结在滑翔机浮心位置。根据表 1中的参数设定,用向量b=[ξ η ζ]T表示固定坐标系下滑翔机浮心(运动坐标系原点)的位置向量,v=[u v w]T和ω=[p q r]T分别表示运动坐标系下滑翔机的平移线速度和旋转角速度向量。滑翔机的运动学方程表达为:
| $ \mathit{\boldsymbol{\dot b}} = {\mathit{\boldsymbol{R}}_{EB}}\mathit{\boldsymbol{v}} $ | (2) |
| $ {{\mathit{\boldsymbol{\dot R}}}_{EB}} = {\mathit{\boldsymbol{R}}_{EB}}\mathop {\mathit{\boldsymbol{\omega }}}\limits^ \wedge $ | (3) |
式中运算符“∧”表示叉乘运算,可将REB与ω之间的叉乘运算转换成点乘运算[11]。运动坐标系中滑翔机角速度与欧拉角速率之间的关系为:
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varLambda} }} = {\mathit{\boldsymbol{R}}_{\mathit{\Lambda }B}}\mathit{\boldsymbol{\omega }} $ | (4) |
式中:RΛB表示运动坐标系中角速度与固定坐标系中姿态角速率之间的转换矩阵,其表达式为:
| $ {\mathit{\boldsymbol{R}}_{\mathit{\Lambda }B}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - {\rm{s}}\theta }\\ 0&{{\rm{c}}\varphi }&{{\rm{s}}\varphi {\rm{c}}\theta }\\ 0&{ - {\rm{s}}\varphi }&{{\rm{c}}\varphi {\rm{c}}\theta } \end{array}} \right] $ | (5) |
将式(1)代入式(2),式(5)代入式(4)中,得到圆碟形水下滑翔机的运动学方程:
| $ \left[ {\begin{array}{*{20}{c}} {\dot \xi }\\ {\dot \eta }\\ {\dot \zeta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\psi {\rm{c}}\theta }&{{\rm{c}}\psi {\rm{s}}\theta - {\rm{s}}\psi {\rm{c}}\varphi }&{{\rm{c}}\psi {\rm{s}}\theta {\rm{c}}\varphi + {\rm{s}}\psi {\rm{s}}\varphi }\\ {{\rm{s}}\psi {\rm{c}}\theta }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{s}}\varphi + {\rm{c}}\psi {\rm{c}}\varphi }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{c}}\varphi - {\rm{c}}\psi {\rm{s}}\varphi }\\ { - {\rm{s}}\theta }&{{\rm{c}}\theta {\rm{s}}\varphi }&{{\rm{c}}\theta {\rm{c}}\varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u\\ v\\ w \end{array}} \right] $ | (6) |
| $ \left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&{ - {\rm{s}}\theta }\\ 0&{{\rm{c}}\varphi }&{{\rm{s}}\varphi {\rm{c}}\theta }\\ 0&{ - {\rm{s}}\varphi }&{{\rm{c}}\varphi {\rm{c}}\theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] $ | (7) |
圆碟形水下滑翔机的运动可分为非定常运动段和定常运动段,并且滑翔机长时间处于定常运动段。在定常运动状态下,忽略滑翔机各部分质量的重心的细微变化,各部分质量与滑翔机保持相对静止状态,此时圆碟形水下滑翔机可看做一个六自由度单刚体模型。根据刚体动力学理论,得到圆碟形水下滑翔机动力学方程:
| $ m\left[ {\frac{{\delta U}}{{\delta t}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{U}} + \frac{{\delta \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}{{\delta t}} \times {\mathit{\boldsymbol{R}}_G} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{R}}_G}} \right)} \right] = {\mathit{\boldsymbol{F}}_\mathit{\Sigma }} $ | (8) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_G}\frac{{\delta \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}{{\delta t}} + {\mathit{\boldsymbol{R}}_G} \times m\left( {\frac{{\delta \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}{{\delta t}} + {\mathit{\boldsymbol{R}}_G}} \right) + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{J}}_G}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times }\\ {\left[ {{\mathit{\boldsymbol{R}}_G} \times m\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{R}}_G}} \right)} \right] + {\mathit{\boldsymbol{R}}_G} \times m\frac{{\delta U}}{{\delta t}} + {\mathit{\boldsymbol{R}}_G} \times }\\ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times m\mathit{\boldsymbol{U}}} \right) = {\mathit{\boldsymbol{T}}_\mathit{\Sigma }}} \end{array} $ | (9) |
式中:m为滑翔机的总质量;U为滑翔机运动坐标系中重心的速度向量;Ω为滑翔机角速度向量;RG为重心G在运动坐标系中的位置向量;JG为滑翔机对原点在重心的坐标系的惯量矩阵;J为滑翔机惯量矩阵;F为滑翔机所受外力;T为滑翔机所受合外力对原点的力矩。
1.3 运动控制方程圆碟形水下滑翔机的姿态调整系统中的滑块布置在圆环形轨道之上,滑块的旋转角度对滑翔机重心的影响为:
| $ \begin{array}{l} {x_G} = \frac{{{m_b}{x_{rb}} + {m_{s1}}{x_{s1}} + {m_{s2}}{x_{s2}}}}{m} = \\ \;\;\;\;\frac{{{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}}}{m} \end{array} $ |
| $ \begin{array}{l} {y_G} = \frac{{{m_{rb}}{y_{rb}} + {m_{s1}}{y_{s1}} + {m_{s2}}{y_{s2}}}}{m} = \\ \;\;\;\;\frac{{{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{c}}{\theta _{s2}}}}{m} \end{array} $ |
| $ {z_G} = \frac{{{m_{rb}}{z_{rb}} + {m_{s1}}{z_{s1}} + {m_{s2}}{z_{s2}}}}{m} = \frac{{{m_{rb}}{z_{rb}}}}{m} $ |
式中:mrb为滑翔机(除去滑块)的质量;ms1和ms2分别为2个滑块的质量;(xrb, yrb, zrb)、(xs1, ys1, zs1)和(xs2, ys2, zs2)分别为滑翔机(除去滑块)和2个滑块在运动坐标系中的重心坐标;rs为滑块所在轨道的半径;θs1和θs2分别为2个滑块绕轴oz的旋转角度。
综合上述推导,参考国内外相关研究机构在水下滑翔机动力学模型方面的研究[1, 12],得到圆碟形水下滑翔机的运动控制方程,将线性项移至方程左端,非线性项留在方程右端,方程用矩阵形式表示为:
| $ \left[ {\begin{array}{*{20}{c}} {m + {A_{11}}}&0&0&0&{m{z_G}}&{ - m{y_G}}\\ 0&{m + {A_{22}}}&0&{ - m{z_G}}&0&{m{x_G}}\\ 0&0&{m + {A_{33}}}&{m{y_G}}&{ - m{x_G}}&0\\ 0&{ - m{z_G}}&{m{y_G}}&{{I_{xx}} + {A_{44}}}&0&0\\ {m{z_G}}&0&{ - m{x_G}}&0&{{I_{yy}} + {A_{55}}}&0\\ { - m{y_G}}&{m{x_G}}&0&0&0&{{I_{zz}} + {A_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot u}\\ {\dot v}\\ {\dot w}\\ {\dot p}\\ {\dot q}\\ {\dot r} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_x}}\\ {{F_y}}\\ {{F_z}}\\ {{M_x}}\\ {{M_y}}\\ {{M_z}} \end{array}} \right] $ | (10) |
式中:
| $ \begin{array}{l} {F_x} = - \left( {m + {A_{33}}} \right)qw + \left( {m + {A_{22}}} \right)rv + \left( {{m_{rb}}{x_{rb}} + } \right.\\ \;\;\;\;\;\;\;\left. {{m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}} \right)\left( {{q^2} + {r^2}} \right) - {m_{rb}}{z_{rb}}pr - \\ \;\;\;\;\;\;\;{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{c}}{\theta _{s2}}pq - \left( {m - } \right.\\ \;\;\;\;\;\;\;\left. {p\nabla } \right)g{\rm{s}}\theta + {X_{uu}}{u^2} + {X_{ww}}{w^2} \end{array} $ | (11) |
| $ \begin{array}{l} {F_y} = - \left( {m + {A_{11}}} \right)ru + \left( {m + {A_{33}}} \right)pw + \left( {{m_{rb}}{x_{rb}} + } \right.\\ \;\;\;\;\;\;\;\left. {{m_{s1}}{y_{s1}} + {m_{s2}}{y_{s2}}} \right)\left( {{p^2} + {r^2}} \right) - \left( {{m_{rb}}{x_{rb}} + } \right.\\ \;\;\;\;\;\;\;\left. {{m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}} \right)pq - \left( {{m_{rb}}{z_{rb}}} \right)qr - \\ \;\;\;\;\;\;\;\left( {m - p\nabla } \right)g{\rm{s}}\varphi {\rm{c}}\theta + {Y_v}v + {Y_{\left. v \right|\left. v \right|}}\left. v \right|\left. v \right| \end{array} $ | (12) |
| $ \begin{array}{l} {F_z} = - \left( {m + {A_{22}}} \right)pv + \left( {m + {A_{11}}} \right)qu + \left( {{m_{rb}}{z_{rb}}} \right)\left( {{p^2} + } \right.\\ \;\;\;\;\;\;\left. {{q^2}} \right) - \left( {{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}} \right)pr + \\ \;\;\;\;\;\;\left( {{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{c}}{\theta _{s2}}} \right)qr + \\ \;\;\;\;\;\;\;\left( {m - p\nabla } \right)g{\rm{c}}\varphi {\rm{c}}\theta + {Z_w}w \end{array} $ | (13) |
| $ \begin{array}{l} {M_x} = \left( {{m_{rb}}{z_{rb}}} \right)\left( {ru - pw} \right) - \left( {{I_{zz}} - {I_{yy}} + {A_{55}} - } \right.\\ \;\;\;\;\;\;\;\left. {{A_{66}}} \right)qr - \left( {{A_{33}} - {A_{22}}} \right)vw + \left( {{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + } \right.\\ \;\;\;\;\;\;\;\left. {{m_{s2}}{r_s}{\rm{c}}{\theta _{s2}}} \right)\left( {qu - pv} \right) - \left( {{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + } \right.\\ \;\;\;\;\;\;\;\left. {{m_{s2}}{r_s}{\rm{c}}{\theta _{s2}} - \rho \nabla {y_B}} \right)g{\rm{c}}\varphi {\rm{c}}\theta - \left( {{m_{rb}}{z_{rb}} - } \right.\\ \;\;\;\;\;\;\;\left. {\rho \nabla {z_B}} \right)g{\rm{s}}\varphi {\rm{c}}\theta + {K_p}p + {K_{\left. p \right|\left. p \right|}}\left. p \right|\left. p \right| \end{array} $ | (14) |
| $ \begin{array}{l} {M_y} = \left( {{m_{rb}}{z_{rb}}} \right)\left( {rv - qw} \right) - \left( {{I_{xx}} - {I_{zz}} + {A_{44}} - {A_{66}}} \right)pr - \\ \;\;\;\;\;\;\;\;\;\left( {{A_{11}} - {A_{33}}} \right)uw + \left( {{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}} \right)\left( {pv - qu} \right) - \left( {{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{m_{s2}}{r_s}{\rm{s}}{\theta _{s2}} - \rho \nabla {x_B}} \right)g{\rm{c}}\varphi {\rm{c}}\theta - \left( {{m_{rb}}{z_{rb}} - \rho \nabla {z_B}} \right)g{\rm{s}}\theta + \\ \;\;\;\;\;\;\;\;\;{M_w}w + {M_q}q + {M_{\left. q \right|\left. q \right|}}\left. q \right|\left. q \right| \end{array} $ | (15) |
| $ \begin{array}{l} {M_z} = \left( {{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}}} \right)\left( {pw - ru} \right) - \\ \;\;\;\;\;\;\;\;\left( {{I_{yy}} - {I_{xx}} - {A_{44}} + {A_{55}}} \right)pq - \left( {{A_{22}} - {A_{11}}} \right)uv + \\ \;\;\;\;\;\;\;\;\left( {{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{c}}{\theta _{s2}}} \right)\left( {pw - rv} \right) - \\ \;\;\;\;\;\;\;\;\left( {{m_{rb}}{x_{rb}} + {m_{s1}}{r_s}{\rm{s}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{s}}{\theta _{s2}} - \rho \nabla {x_B}} \right)g{\rm{s}}\varphi {\rm{c}}\theta - \\ \;\;\;\;\;\;\;\;\left( {{m_{rb}}{y_{rb}} + {m_{s1}}{r_s}{\rm{c}}{\theta _{s1}} + {m_{s2}}{r_s}{\rm{c}}{\theta _{s2}} - \rho \nabla {y_B}} \right)g{\rm{s}}\theta + \\ \;\;\;\;\;\;\;\;{N_r}r + {N_{\left. r \right|\left. r \right|}}\left. r \right|\left. r \right| \end{array} $ | (16) |
式中:
圆碟形水下滑翔机运动控制方程用来研究从控制参数输入到滑翔机达到定常运动状态的过程,根据仿真结果总结圆碟形水下滑翔机控制参数对运动性能的影响。
2.1 垂直面内运动圆碟形水下滑翔机的部分参数见表 2,运动仿真算例初始参数见表 3,其中表 3中各参数均在运动坐标中描述。
| 表 2 圆碟形水下滑翔机的部分参数 Table 2 Partial parameters of disc type underwater glider |
| 表 3 仿真算例初始参数 Table 3 Initial parameters of the simulation |
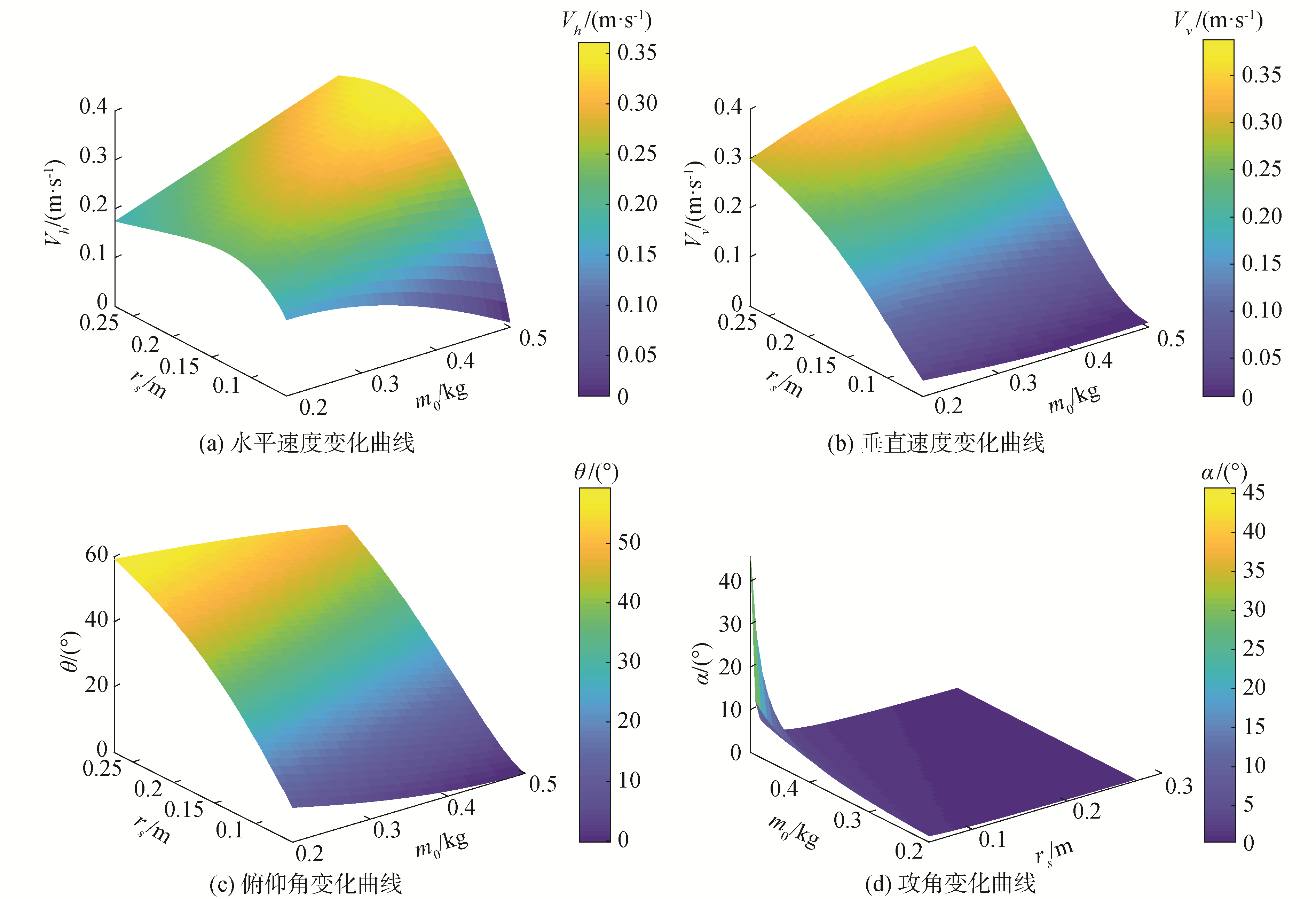
对圆碟形水下滑翔机的特征参数、状态参数与时间的关系以及各参数之间的耦合关系进行了仿真分析,仿真结果如图 2所示。本文研究的滑翔机特征参数为滑块重心在运动坐标系ox轴上的偏移量rs和净浮力质量m0,状态参数包含滑翔机运动中的速度Vh与Vv、攻角α和俯仰角θ。
|
Download:
|
| 图 2 仿真结果 Fig. 2 Simnlation results | |
从图 2(a)可以看出,Vh随m0的增大而增大,随rs的增大而先增大后减小,在某一位置时达到最大。从图 2(b)可以看出,rs与m0对Vv均有影响,但rs的影响更加显著。Vv随rs的增加而显著增大,随m0增大而增大,但变化幅度较小,且rs较小时,其数值基本恒定。
从图 2可以看出,rs对θ的影响更加显著。当rs一定时,θ随m0的增大有减小的趋势,但变化幅度细微;当m0一定时,θ随着rs的增加而显著增大。从图 2(a)可以看出,α的大小主要由rs决定,m0的影响较小;当m0为一定值时,α随着rs的增大,逐渐接近于一个较小的常值;而当rs一定时,随着m0的增大,α基本不变。
以净浮力质量为0.4 kg时的滑翔机垂直面运动为例,表 4与表 5分别为滑块重心偏移量在0.158~0.181 m与0.055~0.082 m范围内变化时滑翔机垂直面内运动的仿真结果,分别对应滑块旋转30°~35°与10°~15°。
| 表 4 垂直面运动仿真结果A Table 4 Vertical plane simulation results A |
| 表 5 垂直面运动仿真结果B Table 5 Vertical plane simulation results B |
结合图 2和表 4得到,圆碟形水下滑翔机滑翔角大小在35.4°~36.4°范围内,水平速度达到最大,此时为最大水平速度滑翔状态;根据表 5得到,圆碟形水下滑翔机滑翔角大小为6.9°时,升阻比最大,此时为最小阻力滑翔状态。文献[13]以SLOCUM为例,提到滑翔机速度为1.5 kn,攻角为4.3°时对应最大升阻比,根据文献提供的数据算得升阻比约为4.53;文献[14-16]的研究表明采用传统对称构型的高展弦比水翼的鱼雷形水下滑翔机最大升阻比只能达到5左右。相比于鱼雷形水下滑翔机,全翼身形的圆碟形水下滑翔机的最大升阻比达到了8.7,在滑翔相同水平距离时需要更小的垂直深度,有利于其在有限水深的水域中灵活地运动。
2.2 垂直面内受小幅干扰运动圆碟形水下滑翔机工作环境为深海,外部环境比较稳定,故假定圆碟形水下滑翔机垂直面定常运动时受到外界干扰为小幅扰动。小幅扰动表现为滑翔机的横倾角φ瞬时变化一个角度δ,本节研究此后滑翔机的运动状态。
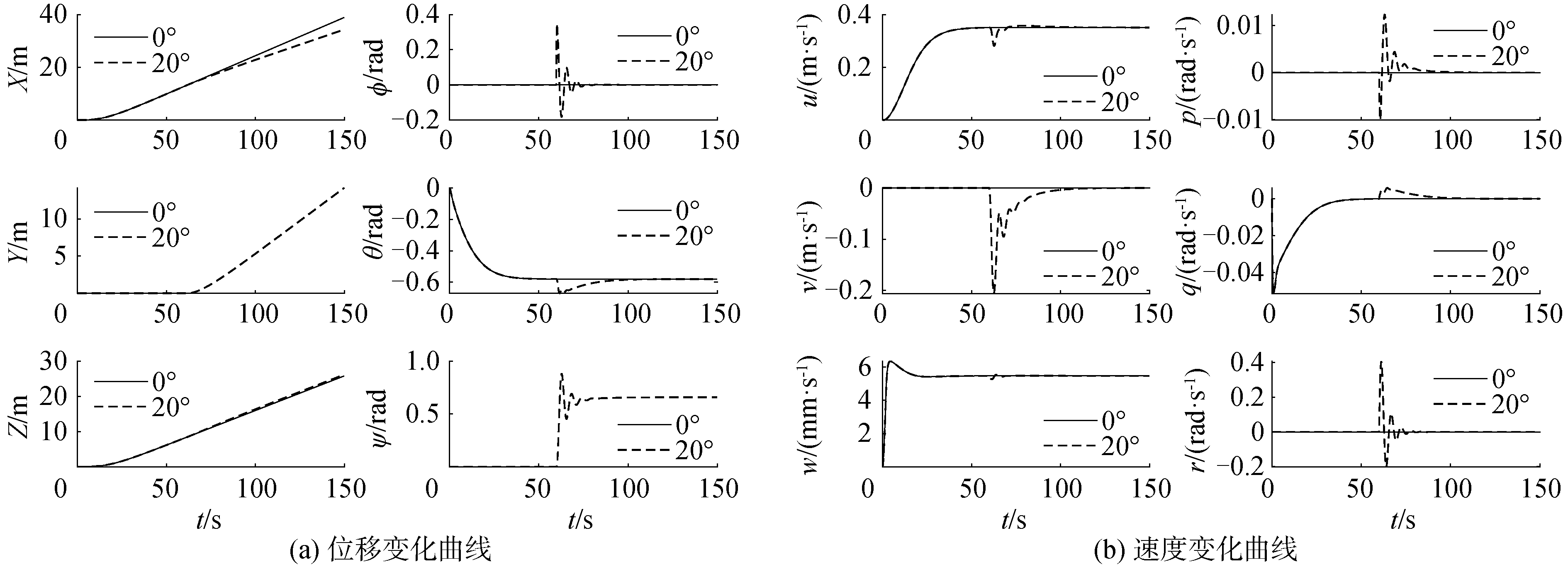
设定净浮力质量为0.4 kg,滑块旋转角度为34°,外界干扰引起的角度δ为0°~20°,图 6为滑翔机运动状态变化情况,图 7为滑翔机受干扰后φ与δ的关系。
|
Download:
|
| 图 6 滑翔机受扰动后运动状态 Fig. 6 Motion states of the glider after disturbance | |

|
Download:
|
| 图 7 φ、ψ与δ的关系曲线 Fig. 7 Relationship between φ, ψ and δ | |
图 6显示,圆碟形水下滑翔机受到小幅干扰后,横倾角φ能够迅速恢复至扰动前的状态,同时产生一定的回转角度ψ;图 7显示受到小幅扰动后滑翔机的横倾角φ均能恢复到扰动前的状态,回转角度ψ与扰动角度δ成正比。仿真结果表明圆碟形水下滑翔机在小幅干扰下具有一定的稳定性,与鱼雷形水下滑翔机[17]相比,其全翼身外形带来的较大阻尼有利于系统快速恢复稳定;另一方面,圆碟形水下滑翔机的全翼身对称外形使其在xoz平面和yoz平面内的运动特性相同,在受到外界小幅扰动(横倾角或俯仰角发生瞬时变化)后2个平面内的运动特性依然相同,横摇角和俯仰角均能较快地恢复到稳定状态,而鱼雷形水下滑翔机则不同,鱼雷形水下滑翔机受到小幅扰动后横摇角恢复速度与俯仰角恢复速度相差较大。
2.3 螺旋运动通过对圆碟形水下滑翔机的数学模型的仿真可以看到滑翔机的螺旋运动状态,同时也可以通过解析这些动力学方程来说明螺旋运动状态是如何通过调整滑块旋转角度和净浮力质量等控制参数而变化的。本节以最小阻力滑翔状态和最大水平速度滑翔状态为例,研究圆碟形水下滑翔机回转运动性能。
在螺旋运动仿真模型中,设定浮力调节系统提供的净浮力质量固定为0.4 kg,分别在滑块旋转11°和34° 2种工况下,改变滑翔机重心在轴oy上的偏心量,仿真得到螺旋运动的螺旋半径、螺距、周期和重心偏移量之间的关系,如图 8所示。图 9为滑块旋转34°,y轴偏心0.003 m时的螺旋运动轨迹曲线。

|
Download:
|
| 图 8 螺旋运动参数随偏心量变化情况 Fig. 8 The spiral motion parameters vary with offset | |

|
Download:
|
| 图 9 螺旋运动轨迹 Fig. 9 Spiral trajectory | |
仿真结果表明,在2种工况下,螺旋运动的半径、螺距和周期均随着y轴方向重心偏移量的增大而减小;而在偏心量一定的情况下,滑块旋转34°工况中螺旋运动特征参数相对于11°工况下特征参数均较大,为了验证结果变化规律的准确性,设定净浮力质量为0.4 kg,y轴方向偏心量为0.003 m,分别对滑块旋转10°~35°工况下的滑翔机螺旋运动进行仿真,结果如表 6所示。
| 表 6 螺旋运动仿真结果 Table 6 Spiral motion simulation results |
仿真结果显示,当y轴偏心量一定时,随着滑块旋转角度的增加,螺旋运动半径、螺距和周期均逐渐增大。
文献[18]对鱼雷形水下滑翔机的螺旋定常运动进行了模型仿真,结果显示:单独调节旋转质量块旋转角度时,当旋转角度为20°左右时,螺旋运动的半径和周期达到最低,其中半径约为20 m,螺距约为100 m,周期约为0.6×104 s;单独调节净重力时,螺旋运动的半径和周期变化不明显,净重力为0.222 3 kg时,半径约为18 m,螺距约为100 m,周期约为0.75×104 s。而圆碟形水下滑翔机调控其滑块旋转较小角度时,螺旋运动的特征参数远小于文献中的鱼雷形水下滑翔机螺旋运动特征参数最优值,对比表明圆碟形水下滑翔机螺旋运动所需空间尺度极小。
3 结论1) 圆碟形水下滑翔机在最小阻力滑翔状态时,升阻比大于传统对称构型高展弦比的鱼雷形水下滑翔机的升租比,这为其带来了较高的航行效率,滑翔相同水平距离时所需要的垂向空间尺度更小,对降低水下滑翔机能耗、提升续航力、拓展浅水应用领域提供了新的研究思路。
2) 圆碟形水下滑翔机垂直面内的运动受到外界小幅干扰后具有一定稳定性,能快速恢复到稳定状态。研究结果不仅为水下滑翔机圆碟形外形设计的可行性提供佐证,更为圆碟形水下滑翔机垂直面内运动稳定性的深入研究提供理论基础。
3) 相比鱼雷形水下滑翔机,圆碟形水下滑翔机螺旋运动的半径、螺距和周期更小,完成螺旋运动所需空间尺度极小,大幅提升了水下滑翔机在小空间内的机动能力,弥补了鱼雷形水下滑翔机仅能在大范围水域内运动的不足。
| [1] |
NAKAMURA M, HYODO T, KOTERAYAMA W. "LUNA" testbed vehicle for virtual mooring[C]//Proceedings of the Seventeenth International Offshore and Polar Engineering. Lisbon, Portugal, 2007: 1130-1137.
(  0) 0)
|
| [2] |
NAKAMURA M, KOTERAYAMA W, INADA M, et al. Disk-type underwater glider for virtual mooring and field experment[J]. International journal of offshore and polar engineering, 2009, 19(1): 66-70. (  0) 0)
|
| [3] |
NIEWIADOMSKA K, JONES C, WEBB D. Design of a mo-bile and bottom-resting autonomo-us un-derwater gliding vehicle[C]//Proceeding of the 13th International Symposium on Unmanned Untethered Submersible Technology. Durham New Hampshire: Autonomous Undersea Systems Institute, 2003.
(  0) 0)
|
| [4] |
王天.新型碟形水下机器人及其航姿预测控制系统研究[D].哈尔滨: 哈尔滨工程大学, 2013: 21-34. WANG Tian. Researches on a novel dish-like underwater robot and attitude predictive control[D]. Harbin: Harbin Engineering University, 2013: 21-34. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133980.htm (  0) 0)
|
| [5] |
张超.圆碟形水下机器人的设计及运动控制[D].哈尔滨: 哈尔滨工程大学, 2013: 15-24. ZHANG Chao. The design and motion control of round dish-shaped underwater vehicle[D]. Harbin: Harbin Engineering University, 2013: 15-24. http://cdmd.cnki.com.cn/article/cdmd-10217-1014133456.htm (  0) 0)
|
| [6] |
张怀新, 潘雨村. 圆碟形潜水器阻力性能研究[J]. 上海交通大学学报, 2006, 40(6): 978-982, 987. ZHANG Huaixin, PAN Yucun. The resistance performance of a dish-shaped underwater vehicle[J]. Journal of Shanghai Jiao Tong university, 2006, 40(6): 978-982, 987. DOI:10.3321/j.issn:1006-2467.2006.06.023 (  0) 0)
|
| [7] |
张怀新, 潘雨村. CFD在潜艇外形方案比较中的应用[J]. 船舶力学, 2006, 10(4): 1-8. ZHANG Huaixin, PAN Yucun. Application CFD to compare submarine hull forms[J]. Journal of ship mechanics, 2006, 10(4): 1-8. DOI:10.3969/j.issn.1007-7294.2006.04.001 (  0) 0)
|
| [8] |
张新曙.碟形潜水器概念研究[D].上海: 上海交通大学, 2003: 24-29, 54-58. ZHANG Xinshu. Concept study of dish-spaped underwater vehicle[D]. Shanghai: Shanghai Jiao Tong University, 2003: 24-29, 54-58. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y490287 (  0) 0)
|
| [9] |
赵宝强. 碟形水下滑翔机动态稳定性建模仿真研究[J]. 舰船科学技术, 2016, 38(7): 82-86. ZHAO Baoqiang. Study of modeling and simulation of disc-underwater glider dynamic stability[J]. Ship science and technology, 2016, 38(7): 82-86. DOI:10.3404/j.issn.1672-7619.2016.07.018 (  0) 0)
|
| [10] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 10-12.
(  0) 0)
|
| [11] |
GOLDSTEIN H, REVIEWER V T. Classical mechanics[J]. Physics Today, 1952, 5(9): 19. DOI:10.1063/1.3067728 (  0) 0)
|
| [12] |
张晶.潜艇运动建模及简化技术研究[D].哈尔滨: 哈尔滨工程大学, 2009: 11-22. ZHANG Jing. A research on modeling and simplifying of the moving submarine[D]. Harbin: Harbin Engineering University, 2009: 11-22. http://cdmd.cnki.com.cn/article/cdmd-10217-2009157204.htm (  0) 0)
|
| [13] |
MAHMOUDIAN N, GEISBERT J, WOOLSEY C. Dynamics & control of underwater gliders Ⅰ: steady motions[R]. Blacksburg, VA: Virginia Polytechnic Institute & State University, 2007.
(  0) 0)
|
| [14] |
赵宝强. 水下滑翔机水平固定翼设计[J]. 舰船科学技术, 2016, 38(1): 103-107. ZHAO Baoqiang. The horizontal fixed wing design of underwater glider[J]. Ship science and technology, 2016, 38(1): 103-107. DOI:10.3404/j.issn.1672-7649.2016.1.022 (  0) 0)
|
| [15] |
武建国, 陈超英, 王树新, 等. 混合驱动水下滑翔器滑翔状态机翼水动力特性[J]. 天津大学学报, 2010, 43(1): 84-89. WU Jianguo, CHEN Chaoying, WANG Shuxin, et al. Hydrodynamic characteristics of the wings of hybrid-driven underwater glider in glide mode[J]. Journal of Tianjin University, 2010, 43(1): 84-89. DOI:10.3969/j.issn.0493-2137.2010.01.014 (  0) 0)
|
| [16] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 829-837. LI Zhiwei, CUI Weicheng. Overview on the hydrodynamic performance of underwater gliders[J]. Journal of ship mechanics, 2012, 16(7): 829-837. DOI:10.3969/j.issn.1007-7294.2012.07.014 (  0) 0)
|
| [17] |
王振宇.翼型水下滑翔机性能数值优化与运动特性问题研究[D].沈阳: 中国科学院沈阳自动化研究所, 2018: 79-86. WANG Zhenyu. Research on hydrodynamic performance optimization and dynamic behaviors for fly-wing structure underwater gliders[D]. Shenyang: Shenyang Institution Automation Chinese Academy of Sciences, 2018: 79-86. http://ir.sia.ac.cn/handle/173321/21758/browse;jsessionid=4940C0119FCEB38EC693E664A55D56CA?type=dateissued (  0) 0)
|
| [18] |
赵宝强, 王晓浩, 姚宝恒, 等. 水下滑翔机三维定常运动建模与分析[J]. 海洋技术学报, 2014, 33(1): 11-18. ZHAO Baoqiang, WANG Xiaohao, YAO Baoheng, et al. Three-dimensional steady motion modeling and analysis for underwater gliders[J]. Journal of ocean technology, 2014, 33(1): 11-18. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


