2. 哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
卫星的姿态控制问题在航天技术的发展与应用中得到了大量的关注与研究,而PD控制作为发展最成熟、应用最广泛的一种控制方法得到了深入而大量的研究。Wie等[1-2]在早期的研究中,针对航天器的姿态控制问题设计了PD控制律,并给出了几种典型的Lyapunov函数,给出了一些通用的稳定性证明方法。在近期的研究中,Forbes等[3]针对航天器的姿态控制问题提出了一种无源PD控制律,在这篇文章中,方向余弦矩阵被视为比例项引入控制律中。
尽管PD控制存在着结构简单、物理意义清晰、鲁棒性强等优势,但其存在着以下几个方面的弊端:1)收敛速率慢,姿态角速度的急剧下降导致了四元数收敛速率的变慢;2)没有有效利用已知信息,实际控制中系统转动惯量并非完全未知,然而PD控制律则完全忽视系统的转动惯量值;3)初始控制力矩过大,同时随着状态的减小, 控制力矩急剧下降,对于控制律的利用效率较低。同时,考虑到卫星运行过程中过大的角速度会导致姿态确定精度的急剧下降,甚至星敏感器的失效,因此有必要对卫星的姿态角速度进行限制,而传统的PD控制则存在着角速度较大的缺陷,针对以上几方面的缺陷,有必要对PD控制器进行改进。
针对PD控制器的收敛速率问题,Verbin[4-6]应用Back-stepping方法,设计了具有快速收敛特性的角速度曲线,并设计控制律实现实际状态对于设计的参考轨迹的跟踪。在文献[4]和[6]中对于卫星的角速度限制进行了讨论,而在文献[4]和[5]中则对卫星的控制力矩限制进行了讨论。但值得注意的是,文献[4-6]中均缺少对于系统转动惯量不确定性的讨论。Cao等[7]针对转动惯量具有不确定性和外部干扰力矩的情形针对卫星姿态控制设计了时间较优的控制律,并对于卫星的时间最优角加速度与角速度进行了规划。针对卫星角速度受限问题,Hu等[8-9]基于滑模控制与退步法为柔型卫星设计了姿态控制律。针对控制力矩受限问题,Boskovic等[10]设计了一种鲁棒姿态跟踪控制律。除了在航天领域,PD控制器在其他方面也得到了广泛的应用与讨论。Su等[11]针对四旋翼飞行器的姿态控制设计了非线性PD控制器,在这篇文章中系统状态经过非线性变换之后才输入到控制器当中,从而系统的稳定性得到了增强。Li等[12]基于遗传算法对PD控制器的参数进行了优化,在该文章中指出了控制器各项对于系统性能的影响,并给出针对收敛时间与稳态精度的参数优化方案。文献[13-14]针对直升机的姿态控制设计了模糊PD控制器,考虑到直升机飞行时受到的干扰远多于卫星,作者对经典PD控制器进行了改进以增强其对于各类扰动的鲁棒性。
在本研究中,针对控制力矩与角速度受限的情形,对于传统PD控制律进行了改进,给出了一种时间较优的滑模面,同时在不改变稳定性证明方法的前提下设计了PD+控制器,实现系统状态沿着所设计的滑模面运动。给出了控制力矩饱和的解决方案,并讨论了姿态角速度与控制参数之间的关系。最后通过仿真验证本文所提出算法的有效性。
1 动力学与运动学模型| $ \mathit{\boldsymbol{J\dot \omega }} + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} = \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}} $ | (1) |
式中:ω为姿态角速度;J为系统转动惯量矩阵;u为控制力矩;d为有上界的位置干扰力矩且满足‖d‖ < d。三维向量r的叉乘矩阵r×定义如下:
| $ {\mathit{\boldsymbol{r}}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {r_3}}&{{r_2}}\\ {{r_3}}&0&{ - {r_1}}\\ { - {r_2}}&{{r_1}}&0 \end{array}} \right] $ | (2) |
叉乘矩阵r×的奇异值λ(r×)满足:
| $ \lambda \left( {{\mathit{\boldsymbol{r}}^ \times }} \right) = 0, \pm \left\| \mathit{\boldsymbol{r}} \right\|,{\lambda _{\max }}\left( {{\mathit{\boldsymbol{r}}^ \times }} \right) = \left\| \mathit{\boldsymbol{r}} \right\| $ | (3) |
一般来说,在实际控制过程中卫星的转动惯量矩阵不是精确已知的,假定:
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{\hat J}} + \mathit{\boldsymbol{\tilde J}} $ | (4) |
式中:J为转动惯量真实值;
基于欧拉轴/角的卫星姿态运动学模型为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot e}} = \frac{1}{2}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} - {\mathit{\boldsymbol{e}}^ \times }\cot \frac{\varphi }{2}} \right)\mathit{\boldsymbol{\omega }}\\ \dot \varphi = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\omega }} \end{array} \right. $ | (5) |
考虑到在φ=0时模型(5)会出现奇异性,引入姿态四元数定义如下:
| $ \mathit{\boldsymbol{q}} = {\left[ {\begin{array}{*{20}{c}} {{q_0}}&{\mathit{\boldsymbol{q}}_v^{\rm{T}}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {\cos \frac{\varphi }{2}}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}\sin \frac{\varphi }{2}} \end{array}} \right]^{\rm{T}}} $ | (6) |
注意到q与-q表示同一姿态,因此在本文中假定q0≥0。
基于姿态四元数的姿态运动学模型为[12]:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot q}}}_0} = - \frac{1}{2}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }}\\ {{\mathit{\boldsymbol{\dot q}}}_v} = \frac{1}{2}\left( {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{\omega }} = \frac{1}{2}\mathit{\boldsymbol{F\omega }} \end{array} \right. $ | (7) |
式中矩阵F的奇异值满足:
| $ \left\{ \begin{array}{l} \lambda \left( \mathit{\boldsymbol{F}} \right) = \left| {{q_0}} \right|,1\\ {\lambda _{\max }}\left( \mathit{\boldsymbol{F}} \right) = 1 \end{array} \right. $ | (8) |
为简化后文书写,以λM(A)和λm(A)分别表示矩阵A的最大奇异值和最小奇异值。
2 PD+姿态跟踪控制器传统的PD控制器由微分项、比例项组成,一般来说,比例项系数越大,系统的收敛速度也会越快,但会加剧系统状态的振荡,而微分项的引入则会减弱系统的振荡并增强系统稳定性,但微分项的引入则会减小姿态角速度,从而导致姿态四元数收敛速率的下降。与此同时,PD控制律的另一优势在于完全不需要系统转动惯量值,从而对系统转动惯量的误差具有鲁棒性。但考虑到实际中角速度模型并非完全的黑箱模型,系统转动惯量矩阵也并非完全未知,这也意味着传统的PD控制并未完全利用已知信息。
基于上述讨论,本文所提出的控制律采用的结构如下:
| $ \mathit{\boldsymbol{u}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_1} + {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_1} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right),\;\;\;\;\;\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \ge \bar q\\ {\mathit{\boldsymbol{u}}_2} + {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_2} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right) - \\ \;\;\;\;\left( {{k_2}/2} \right)\lambda \left| {{q_0}} \right|\left\| \omega \right\|{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right),\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| < \bar q \end{array} \right. $ | (9) |
式中:q为正常数;λ满足λ≥λM(
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_1} = - {k_d}\mathit{\boldsymbol{\omega }} - \left( {{k_1}{k_d}/\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|} \right){\mathit{\boldsymbol{q}}_v}\\ {\mathit{\boldsymbol{u}}_2} = - {k_d}\mathit{\boldsymbol{\omega }} - \frac{{{k_2}}}{2}{q_0}\mathit{\boldsymbol{\hat J\omega }} - {k_2}{k_d}{\mathit{\boldsymbol{q}}_v} \end{array} \right. $ | (10) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1} = \left( {\mathit{\boldsymbol{\hat J\omega }} - \frac{1}{2}\mathit{\boldsymbol{\hat Js}} - \frac{1}{2}\cot \frac{\varphi }{2}{\mathit{\boldsymbol{e}}^ \times }\mathit{\boldsymbol{\hat Js}}} \right) - }\\ {\lambda \left( {\left\| \mathit{\boldsymbol{\omega }} \right\| + \frac{1}{2}\left( {1 + \cot \frac{\varphi }{2}} \right)\left\| \mathit{\boldsymbol{s}} \right\|} \right){\mathop{\rm sgn}} \left( {{{\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }} \right)}^{\rm{T}}}} \right)} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_2} = \left( {\mathit{\boldsymbol{\hat J\omega }} - \frac{1}{2}\mathit{\boldsymbol{\hat Js}}} \right) - }\\ {\lambda \left( {\left\| \mathit{\boldsymbol{\omega }} \right\| + \frac{1}{2}\left\| \mathit{\boldsymbol{s}} \right\|} \right){\mathop{\rm sgn}} \left( {{{\left( {\mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{\omega }}^ \times }} \right)}^{\rm{T}}}} \right)} \end{array} $ | (12) |
在式(11)、(12)中,滑模面s定义如下:
| $ \mathit{\boldsymbol{s}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\mathit{\boldsymbol{\omega }}_e} + {k_1}{\mathit{\boldsymbol{e}}_e},\\ {\mathit{\boldsymbol{\omega }}_e} + {k_2}{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}, \end{array}&\begin{array}{l} \left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\| \ge \bar q\\ \left\| {{\mathit{\boldsymbol{q}}_{{\rm{ev}}}}} \right\| < \bar q \end{array} \end{array}} \right. $ | (13) |
| $ {k_2} = {k_1}/\bar q $ | (14) |
由控制器(13)可以看到,本文所提出的控制器由3项组成,ui为常规的PD控制项,在‖qv‖范数较大时,PD项中的微分项固定,而比例项则是时变的,在‖qv‖范数较小时,PD项与常规PD项不同之处在于引入了系统转动惯量的估计值;ω的符号函数项的作用是消除位置干扰力矩对系统的影响;本文所提出的控制律与传统PD控制主要不同之处在于ω×r项与s的符号函数项,这一项的作用在于使得系统状态能够沿着滑模面(13)收敛,从而实现收敛速率的提升与收敛时间的估计,这一性质将在后文给出证明。
在给出本文控制器结构之后,接下来将给出控制器(9)的稳定性证明与性能分析。
2.1 控制器稳定性证明为证明控制器(9)的稳定性,首先需要给出一个引理。
引理1 系统(1)、(7)在如下结构的控制律作用下全局一致渐进稳定:
| $ \mathit{\boldsymbol{u}} = - {k_d}\mathit{\boldsymbol{\omega }} - {k_p}{\mathit{\boldsymbol{q}}_v} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right) + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{r}} $ | (15) |
式中:kd、kp为任意正常数;r为任意三维向量。
证明 选取Lyapunov函数如下并对其求导可以得到:
| $ {\mathit{\boldsymbol{V}}_1} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{J\omega }}/2 + 2{k_p}\left( {1 - {q_0}} \right) $ | (16) |
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} - 2{k_p}{{\mathit{\boldsymbol{\dot q}}}_0} = }\\ {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) + {k_p}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }} = }\\ { - {k_d}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} - {k_p}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{r}} + {k_p}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }} + }\\ {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{d}} - \bar d{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right) = }\\ { - {k_d}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} \le 0} \end{array} $ | (17) |
从而系统(1)、(7)在控制律(15)的作用下一致渐进稳定,引理1证毕。
对比控制律(9)与控制律(15),可以看到在‖qev‖≥q时二者形式完全相同,在‖qev‖ < q时二者的不同之处在于s的符号函数项,考虑到:
| $ \left\| { - \frac{{{k_2}}}{2}\lambda \left| {{q_0}} \right|} \right\|\mathit{\boldsymbol{\omega }}\left\| {{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right)} \right\| \le - \frac{{\sqrt 3 }}{2}{k_2}\lambda \left\| \mathit{\boldsymbol{\omega }} \right\| $ | (18) |
因此只需选择控制参数满足:
| $ {k_d} + \frac{{{k_2}}}{2}\sqrt {1 - {{\bar q}^2}} {\lambda _m}\left( {\mathit{\boldsymbol{\hat J}}} \right) - \frac{{\sqrt 3 }}{2}{k_2}\lambda > 0 $ | (19) |
控制器(13)中的比例项与微分项系数均为正,从而系统(1)、(7)在控制器(13)的作用下全局一致渐近稳定。
2.2 控制器性能分析本文所提出的控制器(13)能够使得系统状态沿着滑模面(18)运行,从而实现系统收敛速率的提升。接下来对这一性质进行证明。
选取Lyapunov函数如下:
| $ {V_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Js}}/2 $ | (20) |
在‖qev‖≥q阶段对其求导,并考虑到系统状态较大时干扰力矩远小于控制律中的比例项与微分项,忽略d与d项,可以得到:
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} + {\mathit{\boldsymbol{k}}_1}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot e}} = }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) + \frac{{{k_1}}}{2}{s^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} - \cot \left( {\frac{\varphi }{2}} \right){\mathit{\boldsymbol{e}}^ \times }} \right)\omega \approx }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - {k_d}\mathit{\boldsymbol{\omega }} - \left( {{k_1}{k_d}/\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|} \right){\mathit{\boldsymbol{q}}_v} + {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_1} - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) + }\\ {\frac{{{k_1}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} - \cot \left( {\frac{\varphi }{2}} \right){\mathit{\boldsymbol{e}}^ \times }} \right)\mathit{\boldsymbol{\omega }} = }\\ { - {\mathit{\boldsymbol{k}}_d}{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{k}}_1}\mathit{\boldsymbol{e}}} \right) + {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_1} - {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + }\\ {\frac{{{k_1}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{e}}^ \times }\mathit{\boldsymbol{\omega }} - \frac{{{k_1}}}{2}\cot \left( {\frac{\varphi }{2}} \right){\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{e}}^ \times }{\mathit{\boldsymbol{e}}^ \times }\mathit{\boldsymbol{\omega }} = - {k_d}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} - }\\ {{k_1}\lambda \left( {\left\| \mathit{\boldsymbol{\omega }} \right\| + \frac{1}{2}\left( {1 + \cot \frac{\varphi }{2}} \right)\left\| \mathit{\boldsymbol{s}} \right\|} \right){\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }}\\ {{\mathop{\rm sgn}} \left( {{{\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }} \right)}^{\rm{T}}}} \right) + }\\ {{k_1}{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\left( { - \mathit{\boldsymbol{\tilde J\omega }} + \frac{1}{2}\mathit{\boldsymbol{\tilde Js}} + \frac{1}{2}{\mathit{\boldsymbol{e}}^ \times }\mathit{\boldsymbol{\tilde J}}s\cot \frac{\varphi }{2}} \right) \le }\\ { - {k_d}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} \le 0} \end{array} $ | (21) |
在‖qev‖ < q阶段对其求导,忽略干扰力矩,可以得到
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} + {k_2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot q}}}_v} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) + \frac{{{k_2}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{q}}_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{\omega }} \approx }\\ {{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - {k_d}\mathit{\boldsymbol{\omega }} - {k_2}{k_d}{\mathit{\boldsymbol{q}}_v} + {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_2} - \frac{{{k_2}}}{2}{\lambda _1}\left| {{\mathit{\boldsymbol{q}}_0}} \right|\left\| \mathit{\boldsymbol{\omega }} \right\|{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) + \frac{{{k_2}}}{2}{q_0}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\omega + }}\frac{{{k_2}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Jq}}_v^ \times \mathit{\boldsymbol{\omega }} = }\\ { - {k_2}{\lambda _2}\left( {\left\| \mathit{\boldsymbol{\omega }} \right\| + \frac{1}{2}\left\| \mathit{\boldsymbol{s}} \right\|} \right)\mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{\omega }}^ \times }{{{\mathop{\rm sgn}} }^{\rm{T}}}\left( {\mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{\omega }}^ \times }} \right) - {k_d}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} + {k_2}\mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{\omega }}^ \times }\left( { - \mathit{\boldsymbol{\tilde J\omega }} + \frac{1}{2}\mathit{\boldsymbol{\tilde Js}}} \right) + }\\ {\frac{{{k_2}}}{2}{q_0}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\omega }} - \frac{{{k_2}}}{2}{\lambda _1}\left| {{\mathit{\boldsymbol{q}}_0}} \right|\left\| \mathit{\boldsymbol{\omega }} \right\|{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) \le - {k_d}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} \le 0} \end{array} $ | (22) |
通过(21)、(22)可以看到滑模状态s一致渐进稳定,从而系统状态将沿着本文所设计的滑模面(13)收敛。同时值得注意的是滑模面(13)分为2阶段,在第1阶段姿态角速度为匀速,这就避免了传统PD控制律中角速度下降过快导致的四元数收敛速率变慢的问题。同时,在滑模面的第2阶段收敛速率为指数收敛,选择合适的控制参数即可实现对于收敛时间的估计。
3 角速度与控制力矩限制在卫星的运行过程中,过大的角速度会导致星敏感器的失效与姿态确定系统精度的急剧下降,因此有必要对卫星的姿态角速度进行限制。同时,卫星的控制执行机构所能提供的控制力矩有限,因此同样有必要对控制力矩的范数进行限制。为了讨论姿态角速度与控制参数之间的关系,首先需要给出一个引理。
引理2 对于系统(1),若控制律结构为:
| $ \mathit{\boldsymbol{u}} = - {k_d}\mathit{\boldsymbol{\omega }} - {k_p}{\mathit{\boldsymbol{q}}_v} + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{r}} $ | (23) |
角速度初值满足
| $ \left\| \mathit{\boldsymbol{\omega }} \right\| \le \frac{{{k_p}}}{{{k_d}}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} $ | (24) |
证明 定义σ如下:
| $ \sigma = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{J\omega }} $ | (25) |
从而有:
| $ \sqrt {{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)} \left\| \mathit{\boldsymbol{\omega }} \right\| \le {\sigma ^{1/2}} \le \sqrt {{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)} \left\| \mathit{\boldsymbol{\omega }} \right\| $ | (26) |
对求导并代入控制律(23)可以得到:
| $ \begin{array}{*{20}{c}} {\dot \sigma = 2{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} = }\\ {2{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( { - {k_d}\mathit{\boldsymbol{\omega }} - {k_p}{\mathit{\boldsymbol{q}}_v} + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}} \right) = }\\ { - 2{k_d}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{\omega }} - 2{k_p}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{q}}_v} \le }\\ { - 2{k_d}\frac{\sigma }{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} + 2{k_p}\frac{{{\sigma ^{1/2}}}}{{\sqrt {{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)} }}} \end{array} $ | (27) |
对于系统:
| $ \dot \sigma = - 2{k_d}\frac{\sigma }{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} + 2{k_p}\frac{{{\sigma ^{1/2}}}}{{\sqrt {{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)} }} $ | (28) |
其平衡点为:
| $ {\sigma ^{1/2}} = \frac{{{k_d}}}{{{k_p}}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{\sqrt {{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)} }} $ | (29) |
从而若系统(28)初值小于其平衡点,则恒有:
| $ {\sigma ^{1/2}} \le \frac{{{k_d}}}{{{k_p}}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{\sqrt {{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)} }} $ | (30) |
注意到性质(26),从而有:
| $ \left\| \mathit{\boldsymbol{\omega }} \right\| \le \frac{{{k_d}}}{{{k_p}}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} $ | (31) |
引理2证毕。
假定系统所允许的角速度上限为ω,考虑到角速度饱和时干扰力矩可近似忽略不计,同时注意到控制律(9)的结构,因此选取控制参数时只需满足:
| $ \begin{array}{*{20}{c}} {\frac{{{k_1}}}{{\bar q}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} \le \bar \omega }\\ {\frac{{2{k_2}{k_d}}}{{2{k_d} + {k_2}\left( {{\lambda _m}\left( {\mathit{\boldsymbol{\hat J}}} \right) - \sqrt 3 \lambda } \right)}}\frac{{{\lambda _M}\left( \mathit{\boldsymbol{J}} \right)}}{{{\lambda _m}\left( \mathit{\boldsymbol{J}} \right)}} \le \bar \omega } \end{array} $ | (32) |
即可严格意义上保证‖ω‖≤ω。
值得注意的是,不等式(32)在最极端情形下给出的参数要求,而在一般情况下,
| $ \frac{{{k_p}}}{{{k_d}}} \le \frac{{\left\| \mathit{\boldsymbol{\omega }} \right\|}}{{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|}} $ | (33) |
即可保证在角速度到达其极值时不再增加。代入控制律(9),可以得到
| $ {k_1} \le \bar \omega $ | (34) |
通过式(32)与(34)可以看到,式(32)是对于姿态控制参数的严格要求,而式(34)则是一种较为近似的约束。
在给出卫星角速度与控制参数之间的关系之后,接下来需要对控制力矩进行讨论。
改写控制律(9)为:
| $ \mathit{\boldsymbol{u}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\rho _1}{\mathit{\boldsymbol{u}}_1} + {\mathit{\boldsymbol{\tau }}_1},\\ {\rho _2}{\mathit{\boldsymbol{u}}_2} + {\mathit{\boldsymbol{\tau }}_2}, \end{array}&\begin{array}{l} \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \ge \bar q\\ \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| < \bar q \end{array} \end{array}} \right. $ | (35) |
式中:ρi为待定控制增益系数;τi定义为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\tau }}_1} = {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_1} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right)\\ {\mathit{\boldsymbol{\tau }}_2} = {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{r}}_2} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right) - \frac{{{k_2}}}{2}\lambda \left| {{q_0}} \right|\left\| \mathit{\boldsymbol{\omega }} \right\|{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) \end{array} \right. $ | (36) |
为保证控制力矩不超过系统上限,选取合适的控制参数使得‖τi‖ < u,同时定义ρi如下:
| $ \begin{array}{*{20}{c}} {{\rho _i} = }\\ {\left\{ \begin{array}{l} \frac{{ - \mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{\tau }}_i} + \sqrt {{{\left( {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{\tau }}_i}} \right)}^2} + {{\mathit{\boldsymbol{\bar u}}}^2} - {{\left\| {{\mathit{\boldsymbol{\tau }}_i}} \right\|}^{\rm{2}}}} }}{{{{\left\| {{\mathit{\boldsymbol{u}}_i}} \right\|}^2}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| \ge \bar u\\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| < \bar u \end{array} \right.} \end{array} $ | (37) |
通过式(37)可以看到,控制增益系数ρi的本质是当控制力矩范数不超过系统上限时,维持控制律(9)不变,而当控制力矩范数超过系统上限时,对控制律(9)中的比例项与微分项进行成比例缩小,使得控制力矩维持在系统上限。
4 仿真与分析一般而言,能够进行快速机动的敏捷卫星转动惯量矩阵通常较小,为100 kg·m2以内,同时控制力矩上界通常在0.1 N·m左右,同时卫星进行姿态机动的最大角速度约为0.1 rad/s量级,同时考虑到kd、k1、q的选取应当使得系统能够沿着前文所述的滑模面运动,并尽可能停留在匀速运动阶段,综上所述,选取仿真参数如下:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{J}} = {\rm{diag}}\left( {25,20,15} \right){\rm{kg}} \cdot {{\rm{m}}^2}\\ \mathit{\boldsymbol{\hat J}} = {\rm{diag}}\left( {24,21,16} \right){\rm{kg}} \cdot {{\rm{m}}^2} \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \bar d = {10^{ - 5}}{\rm{N}} \cdot {\rm{m}},\bar u = 0.5{\rm{N}} \cdot {\rm{m}},\bar \omega = 0.1\;{\rm{rad}}/{\rm{s}}\\ {k_d} = 20,{k_1} = 0.1,\bar q = 0.1,{k_2} = 1,\lambda = 2\\ \mathit{\boldsymbol{\omega }} = {\left[ {\begin{array}{*{20}{c}} {0.07}&{ - 0.05}&{ - 0.04} \end{array}} \right]^{\rm{T}}}{\rm{rad}}/{\rm{s}}\\ \mathit{\boldsymbol{q}} = {\left[ {\begin{array}{*{20}{c}} {0.4}&{0.2}&{0.4}&{ - 0.8} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (38) |
通过对约束条件(32)与(34)的验证可以看到,本小节仿真参数并不满足严格约束(32),但满足近似约束(34)。
为说明本文提出控制律的性能,以相同参数的传统PD控制律(36)作为对比:
| $ \mathit{\boldsymbol{u}} = - {k_d}\mathit{\boldsymbol{\omega }} - {k_p}{\mathit{\boldsymbol{q}}_v} - \bar d{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{\omega }} \right) $ | (39) |

|
Download:
|
| 图 1 经典PD控制器的姿态角速度曲线 Fig. 1 Curve of angular velocity under standard PD controller | |
|
Download:
|
| 图 2 经典PD控制器的姿态四元数曲线 Fig. 2 Curve of attitude quaternion under standard PD controller | |
由图 1、2可以看到传统PD控制律虽能使状态收敛,但收敛时间在50 s左右,5 s之后角速度开始急剧下降,这也导致了四元数的收敛速率急速下降。同时由图 3可以看到控制力矩范数在前5 s严重超过系统上限,同时前10 s角速度范数同样超过系统上限。总的来说,传统的PD控制律存在着明显的缺陷,接下来给出相同参数下本文提出的控制律(35)的收敛时间估计与仿真图。

|
Download:
|
| 图 3 经典PD控制器的控制力矩及角速度范数曲线 Fig. 3 Curve of control torque norm and angular velocity norm under standard PD controller | |
由于滑模面(13)第1阶段为匀速段,从而收敛时间t1为:
| $ {t_1} = \frac{{2\arcsin \left( {\left\| \mathit{\boldsymbol{q}} \right\|} \right) - 2\arcsin \left( {\mathit{\boldsymbol{\bar q}}} \right)}}{{{k_1}}} \approx 21.18 $ | (40) |
在滑模面的2阶段,定义V如下并对其求导:
| $ V = \mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{q}}_v} $ | (41) |
| $ \dot V = 2\mathit{\boldsymbol{q}}_v^{\rm{T}}{{\mathit{\boldsymbol{\dot q}}}_v} = - {k_2}{q_0}\mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{q}}_v} \approx - {k_2}V $ | (42) |
从而在滑模面(13)的第2阶段‖qv‖收敛至10-6精度范围内的时间t2约为:
| $ {t_2} \approx \frac{1}{{{k_2}}}\ln \left( {\frac{{{{\bar q}^2}}}{{{{10}^{ - 12}}}}} \right) \approx 23.02 $ | (43) |
考虑到系统在控制力矩饱和阶段(多出现于系统到达滑模面之前或匀速段)对控制参数的缩小会使得系统收敛速率下降,因此对收敛时间估计为:
| $ t \approx {t_1} + {t_2} + \Delta t = {t_1} + {t_2} + \varepsilon {t_1} $ | (44) |
式中ε为时间增益系数,此处选取为0.1,从而可以得到系统总的收敛时间估计为:
| $ t \approx 46.3\;{\rm{s}} $ | (45) |
接下来给出本文所提出的考虑角速度与控制力矩限制的控制律(35)的仿真图。
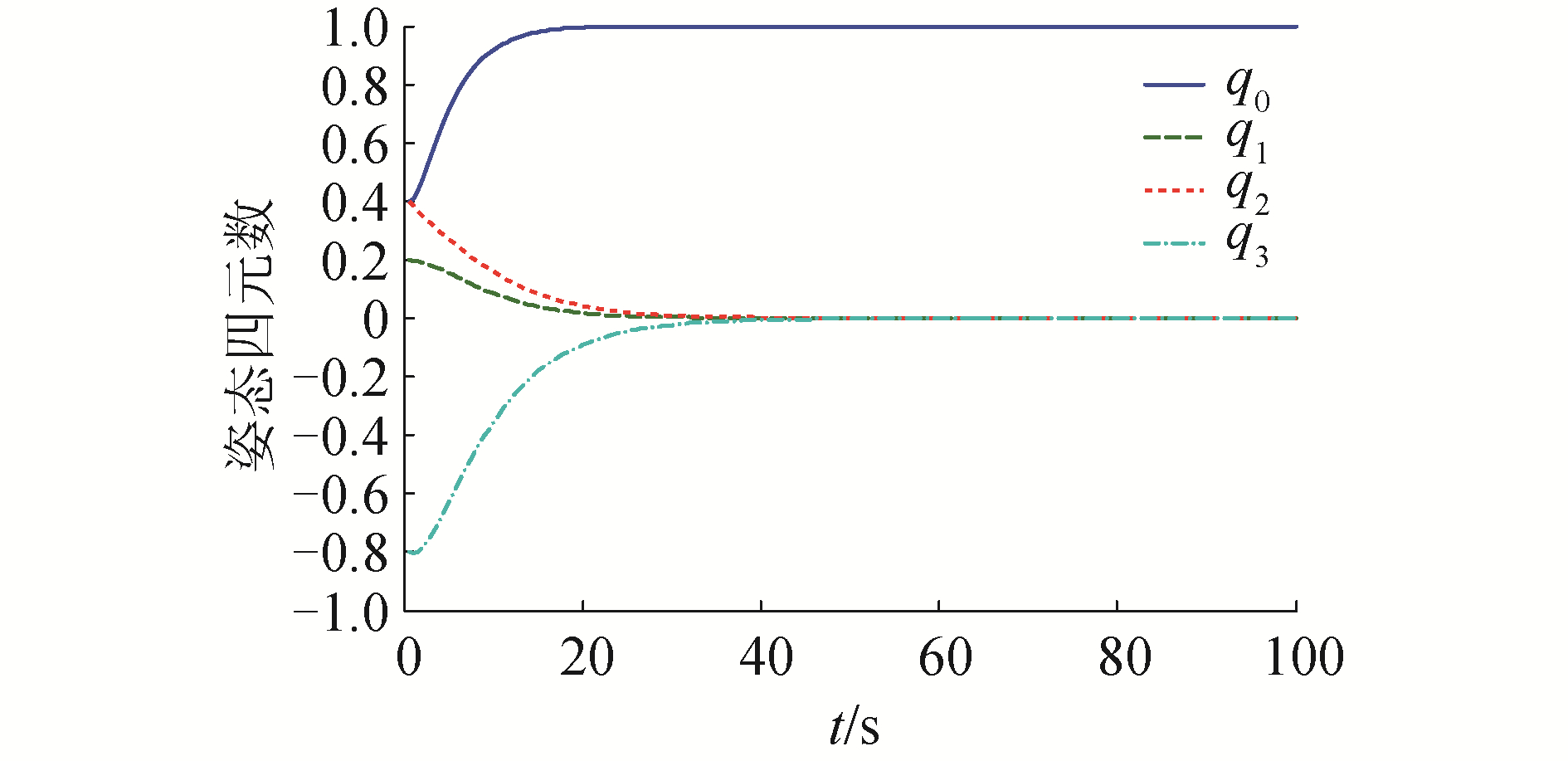
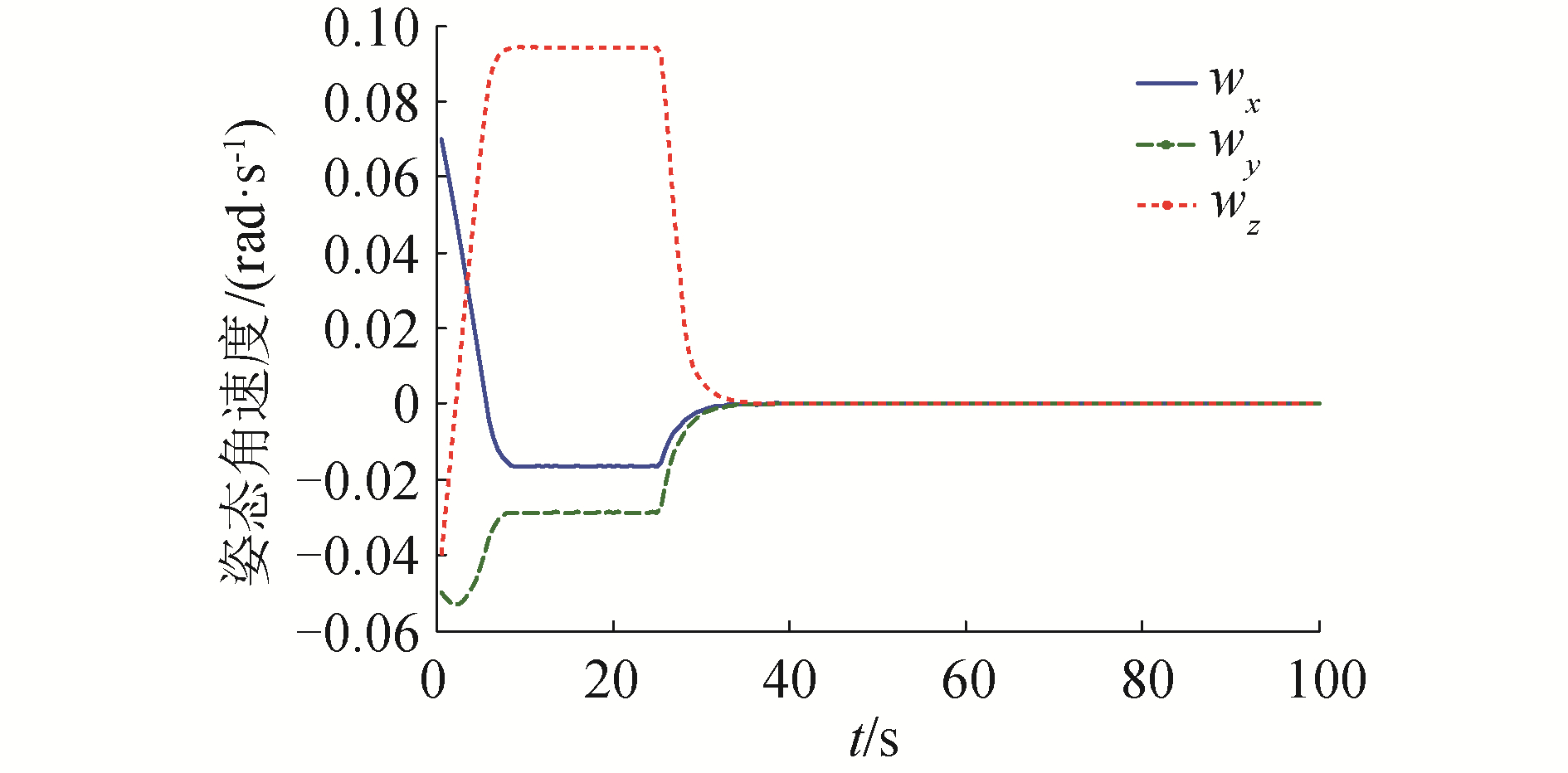
由图 4与图 5可以看到系统状态在35 s左右收敛,收敛时间相比较于传统的PD控制得到了很大的缩短,与此同时,可以看待系统在5 s左右角速度趋于匀速,开始进入本文所设计的滑模面(13),25 s左右开始减速,在匀速段的时间约为20 s,而在45 s时qv的精度为10-6,总的收敛时间约等于前文所估算的收敛时间t,从而说明本文所设计的控制律能够使得系统状态沿着滑模面(13)运行,同时根据滑模面(13)得到系统的收敛时间估计。由图 6可以看到系统控制力矩全程未超过系统上限。值得注意的是,针对角速度的限制,本文所采用的对参数的约束为较为宽松的不等式(34),在系统初始角速度值即为系统幅值的情形下,依然保证了整个控制过程中角速度范数并未超过系统上限,从而也说明了本文所提出的控制算法对角速度限制的有效性。
|
Download:
|
| 图 4 PD+控制器的姿态角速度曲线 Fig. 4 Curve of angular velocity under PD+ controller | |

|
Download:
|
| 图 5 PD+控制器的姿态四元数曲线 Fig. 5 Curve of attitude quaternion under PD+ controller | |

|
Download:
|
| 图 6 PD+控制器的控制力矩及角速度范数曲线 Fig. 6 Curve of control torque norm and angular velocity norm under PD+ controller | |
1) 通过使系统尽量停留在匀速运动阶段能够大幅度提升系统收敛速率;
2) 实时放大比例项、并在控制器中添加角速度叉乘项能够避免在远离平衡点时减速过快;
3) 对微分项进行放大能够解决角速度超过系统上界的问题;
4) PD+控制器中,对微分项与比例项进行成比例放缩并不改变系统稳定性,并能够解决控制力矩饱和问题。
| [1] |
WIE B, BARBA P M. Quaternion feedback for spacecraft large angle maneuvers[J]. Journal of guidance, control, and dynamics, 1985, 8(3): 360-365. DOI:10.2514/3.19988 (  0) 0)
|
| [2] |
WIE B, WEISS H, ARAPOSTATHIS A. Quarternion feedback regulator for spacecraft eigenaxis rotations[J]. Journal of guidance, control, and dynamics, 1989, 12(3): 375-380. DOI:10.2514/3.20418 (  0) 0)
|
| [3] |
FORBES J R. Passivity-based attitude control on the special orthogonal group of rigid-body rotations[J]. Journal of guidance, control, and dynamics, 2013, 36(6): 1596-1605. DOI:10.2514/1.59270 (  0) 0)
|
| [4] |
VERBIN D, LAPPAS V J. Rapid rotational maneuvering of rigid satellites with hybrid actuators configuration[J]. Journal of guidance, control, and dynamics, 2013, 36(2): 532-547. DOI:10.2514/1.56405 (  0) 0)
|
| [5] |
VERBIN D, LAPPAS V J. Rapid rotational maneuvering of rigid satellites with reaction wheels[J]. Journal of guidance, control, and dynamics, 2013, 36(5): 1538-1544. DOI:10.2514/1.58155 (  0) 0)
|
| [6] |
VERBIN D, LAPPAS V J, BEN-ASHER J Z. Time-efficient angular steering laws for rigid satellite[J]. Journal of guidance, control, and dynamics, 2011, 34(3): 878-892. DOI:10.2514/1.48154 (  0) 0)
|
| [7] |
CAO Xibin, YUE Chengfei, LIU Ming, et al. Time efficient spacecraft maneuver using constrained torque distribution[J]. Acta astronautica, 2016, 123: 320-329. DOI:10.1016/j.actaastro.2016.03.026 (  0) 0)
|
| [8] |
HU Qinglei. Robust adaptive backstepping attitude and vibration control with L2-gain performance for flexible spacecraft under angular velocity constraint[J]. Journal of sound and vibration, 2009, 327(3/4/5): 285-298. (  0) 0)
|
| [9] |
HU Qinglei, LI Bo, ZHANG Youmin. Robust attitude control design for spacecraft under assigned velocity and control constraints[J]. ISA transactions, 2013, 52(4): 480-493. DOI:10.1016/j.isatra.2013.03.003 (  0) 0)
|
| [10] |
BOSKOVIC J D, LI Saiming, MEHRA R K. Robust tracking control design for spacecraft under control input saturation[J]. Journal of guidance, control, and dynamics, 2004, 27(4): 627-633. DOI:10.2514/1.1059 (  0) 0)
|
| [11] |
宿敬亚, 樊鹏辉, 蔡开元. 四旋翼飞行器的非线性PID姿态控制[J]. 北京航空航天大学学报, 2011, 37(9): 1054-1058. SU Jingya, FAN Penghui, CAI Kaiyuan. Attitude control of quadrotor aircraft via nonlinear PID[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1054-1058. (  0) 0)
|
| [12] |
李玥, 孙健国. 基于遗传算法的航空发动机多目标优化PID控制[J]. 航空动力学报, 2008, 23(1): 174-178. LI Yue, SUN Jianguo. Multi-objective optimization of aeroengine PID control based on multi-objective genetic algorithms[J]. Journal of aerospace power, 2008, 23(1): 174-178. (  0) 0)
|
| [13] |
SAKAMOTO T, KATAYAMA H, ICHIKAWA A. Attitude control of a helicopter model by robust PID controllers[C]//Proceedings of 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control. Munich, Germany, 2006.
(  0) 0)
|
| [14] |
ZHANG Le, BI Shaojie, YANG Hong. Fuzzy-PID control algorithm of the helicopter model flight attitude control[C]//2010 Chinese Control and Decision Conference. Xuzhou, China, 2010.
(  0) 0)
|
| [15] |
WU Shunan, RADICE G, SUN Zhaowei. Robust finite-time control for flexible spacecraft attitude maneuver[J]. Journal of aerospace engineering, 2014, 27(1): 185-190. DOI:10.1061/(ASCE)AS.1943-5525.0000247 (  0) 0)
|
| [16] |
ZHANG Le, BI Shaojie, YANG Hong. Fuzzy-PID control algorithm of the helicopter model flight attitude control[C]//2010 Chinese Control and Decision Conference. Xuzhou, China, 2010.
(  0) 0)
|
| [17] |
LI You, YE Dong, SUN Zhaowei. Robust finite time control algorithm for satellite attitude control[J]. Aerospace science and technology, 2017, 68: 46-57. DOI:10.1016/j.ast.2017.05.014 (  0) 0)
|
| [18] |
LI You, SUN Zhaowei, YE Dong. Time efficient robust PID plus controller for satellite attitude stabilization control considering angular velocity and control torque constraint[J]. Journal of aerospace engineering, 2017, 30(5): 04017030. DOI:10.1061/(ASCE)AS.1943-5525.0000743 (  0) 0)
|
| [19] |
LI You, YE Dong, SUN Zhaowei. Time efficient sliding mode controller based on Bang-Bang logic for satellite attitude control[J]. Aerospace science and technology, 2018, 75: 342-352. DOI:10.1016/j.ast.2017.12.042 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


