2. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150080, China
我国广大城市经济和城镇化处于高速发展阶段,当面临地震灾害时,作为生命线工程系统的重要组成部分,要求城市桥梁具有足够的地震安全性。如果桥梁在地震中受到了严重破坏,会造成交通中断,影响抗震救灾工作的进行。而桥梁在使用期内,当经历了自然老化、车辆荷载、外界环境等影响,其地震安全性水平尚不明确。所以有必要对桥梁的地震安全性进行分析和评价。目前国内外对桥梁的地震安全水平进行了广泛的研究,包括震害预测、地震易损性、抗震设计、抗震加固与维护等内容。姜淑珍等[1]介绍了城市桥梁的6种预测方法,通过实际桥梁的震害与回归统计法的预测进行比较,检验了回归统计法的可靠性;王东升等[2]根据不同桥梁的分类标准,建立了桥梁震害预测的一般流程,并通过实例,简要介绍了各类震害预测方法的应用;Choi等[3]通过实验和数值模拟建立了美国某地区常见桥梁的分析模型,给出其易损性曲线,并利用易损性分析,量化地评价了桥梁的修复加固手段;文献[4]总结了地震作用下钢筋混凝土桥梁主要构件的理论易损性曲线的建立方法及基本步骤,并通过构件预计结构整体的易损性;文献[5]阐述了日本高速道路桥梁抗震设计的发展历程以及我国公路桥梁抗震设计值得借鉴之处;美国在1995年出版了公路桥梁抗震评估与加固方面的指导手册。此外,地震可靠度理论从结构或构件在地震作用下完成预定功能的可能性出发,通过比较失效概率的大小,计算结构或构件的可靠度,以此评估结构或构件的安全水平[6]。但是该理论应用的常规方法往往以结构或构件是否发生完全破坏为界限,给出其失效的可能性大小,并没有量化地给出结构或构件出现其他损伤状态的可能性大小,以及对应的功能履行情况,更没有给出直观的安全指标评价安全性。所以本文基于可靠度理论的方法,研究并计算出钢筋混凝土梁式桥主要构件可能出现的各种损伤状态下的可靠度,定义了安全评价指标,对主要构件和桥梁系统的地震安全性进行了评价。
1 桥梁的破坏机理在地震作用下,桥梁产生的地震惯性力主要作用于上部结构,并通过支座传递给墩柱,最后由墩柱传递给基础和地基[7]。而这一惯性力,主要取决于上部结构的质量、下部结构的刚度以及支座的连接条件,支撑上部结构的支座可以对其产生一定的隔震作用,在地震反应分析以及模型的建立中,通常将上部结构视为有质量的点(刚体),其在地震中自身的破坏并不常见,多发生移位(包括落梁)和碰撞破坏。但上部结构是桥梁履行使用功能的主要构件,它的严重破坏将直接导致桥梁通行能力的丧失。而支座特别是板式橡胶支座的主要破坏形式为支座移位,它的破坏会使结构的传力路径改变,引起上部结构的移位、落梁等震害。桥墩是支承上部结构的主要构件,它承担着结构的地震惯性力,在地震作用下会产生较大的弯矩和剪力,发生弯曲破坏和剪切破坏。基础震害隐蔽性的特征使得其在震后不易发现,修复困难,应尽量避免,在地震安全性分析评价中的地位也较为突出。因此本文从对桥梁的破坏程度和使用功能造成重要影响的角度出发,选取上部结构、支座、桥墩和基础为研究对象。
2 地震可靠度理论可靠度是指结构或构件在规定的时间和条件下,完成预定功能的概率[6]。而结构的地震可靠度分析,是研究结构在地震作用下,在地震持续时间内不发生破坏的可能性,这种分析方法的评价指标可以通过建立功能函数, 并用可靠度来表示[8]。桥梁可靠度分析采用的方法主要有一次二阶矩法、蒙特卡罗法、响应面法等[6]。一次二阶矩法计算可靠度时,要求结构的功能函数均是随机变量的显式函数,但是在地震可靠度分析中,桥梁的地震反应与设计时所需的基本变量之间的函数关系一般不能用显式表达,即功能函数是隐式的,因此无法运用一次二阶矩法等传统方法进行计算,而响应面法却可以很好地求解此类问题。相比于蒙特卡罗法,应用响应面法在进行确定性有限元分析时需要的模拟次数取决于输入随机变量的个数,而蒙特卡罗法却需要进行大量的有限元模拟,当随机变量个数不是太多时,响应面法比蒙特卡罗法计算效率更高。另外,考虑计算结果的精度要求,响应面法(集成化响应面法)可以将数值模拟过程通过非线性拟合转化为近似的算术函数进行大量计算,所以极大地提高了计算效率[9]。
2.1 集成化响应面法所谓集成化响应面法是将有限单元法、响应面法和蒙特卡罗法结合使用的一种方法[9]。该方法首先设计一系列的随机变量值,每组变量值组成一个试验点,然后逐点进行有限单元计算得到对应的响应值,通过这些变量值和响应值可以拟合为一个显式函数
| $ \hat T\left( x \right) = a + \sum\limits_{i = 1}^n {{b_i}{x_i}} + \sum\limits_{i = 1}^n {{c_i}x_i^2} $ | (1) |
或
| $ \hat T\left( x \right) = a + \sum\limits_{i = 1}^n {{b_i}{x_i}} + \sum\limits_{i = 1}^n {{c_i}x_i^2} + \sum\limits_{i = 1}^n {\sum\limits_{j < i}^n {{d_{ij}}{x_i}{x_j}} } $ | (2) |
式中:
可靠度分析中可将结构或构件的破坏程度划分为3个等级[10]:
| $ \begin{array}{*{20}{c}} {\left\{ {{B_1},{B_2},{B_3}} \right\} = \left\{ {无损伤,轻微或中等损伤,} \right.}\\ {\left. {严重损伤或破坏} \right\}} \end{array} $ | (3) |
式中的3个破坏等级对应的构件或结构的功能函数可以分别描述为:
B1:结构或构件的强度不超过弹性极限、变形小于弹性允许变形,形成非结构损伤;
B2:结构或构件的强度超过弹性极限或变形大于弹性允许变形,但变形小于弹塑性允许变形,形成结构性损伤;
B3:结构或构件变形大于弹塑性允许变形,具有结构性损伤。
前文提到了本文仅研究桥墩、支座、上部结构和基础的安全性水平,在分析了钢筋混凝土梁式桥的破坏机理后,本文对上部结构的移位、碰撞破坏通过支座的剪切变形和损伤程度来粗略模拟,因为对于钢筋混凝土连续梁桥,纵向主梁之间可以认为是没有空隙的,那么支座产生的位移变形等效为上部结构的位移,所以可以通过支座的变形判断上部结构是否发生移位或者碰撞,通过支座的损伤情况判断上部结构的损伤情况,即当支座处于无损伤状态时, 上部结构也视为基本完好,当支座发生轻微或中等损伤时,认为上部结构也将产生轻微或中等破坏,可能发生移位和碰撞破坏,而当支座发生严重损伤或破坏时,认为上部结构将发生严重破坏,发生碰撞甚至落梁。针对构件不同的受力情况及破坏状态,参考文献[11]结合我国规范,定义了桥墩、支座和基础2种损伤极限状态的功能函数,即损伤初形成极限状态和损伤形成后极限状态的功能函数。
2.3.1 损伤初形成极限状态定义损伤初形成时的极限状态,对桥墩来说是塑性铰截面位置出现塑性变形时,也就是作用在塑性铰区的弯矩首次达到弯矩屈服强度的点,对支座来说是剪切变形达到100%的时候[11],对群桩基础来说是作用于群桩对称线处的桩顶弯矩将造成桩的弯曲开裂的时候。该极限状态下构件将基本保持完好,形成非结构性损伤,给出桥墩、支座和基础的极限状态功能函数:
| $ {Z_{D1}} = {M_{yD}} - {M_s} $ | (4) |
| $ {Z_{D2}} = {\mu _1} - {\mu _z} $ | (5) |
| $ {Z_{D3}} = {M_{c1}} - {M_{s2}} $ | (6) |
式中:MyD表示桥墩弯矩的首次屈服强度;Ms表示作用在桥墩塑性铰区的弯矩;Mc1为桩弯矩的首次屈服强度;Ms2是作用于群桩中心线的桩顶弯矩;μ1为支座剪切应变等于100%时的相对位移延性比,通常取μ1=1;μz为支座的相对位移延性比,可以表示为[12-13]:
| $ {\mu _z} = {u_{\max }}/{X_E} $ | (7) |
式中:umax为地震作用下支座的相对位移;XE为剪切应变等于100%时,支座在不同作用效应组合下的相对位移。
2.3.2 损伤形成后极限状态定义损伤形成后极限状态,对于桥墩的塑性铰区截面来说已经进入弹塑性变形阶段,所以这个阶段桥墩的极限状态由弯矩屈服强度、名义抗剪强度和变形来决定,对支座来说是其剪切应变超过100%时的情况,对群桩基础来说假定会发生屈服和剪切破坏,屈服点是所有的桩都将发生弯曲破坏或者作用在某一排的桩顶作用力达到最大容许强度[14],这个阶段桩基础的极限状态由弯矩屈服强度、剪切屈服强度和轴向容许承载力决定。该极限状态下构件将产生轻微损伤、中等损伤、严重损伤或倒塌4种状态,因此给出桥墩、支座和基础在该极限状态下的功能函数[11, 15]:
| $ {Z_1} = {M_u} - {M_s} $ | (8) |
| $ {Z_2} = {V_n} - V $ | (9) |
| $ {Z_3} = {\mu _2} - {\mu _d} $ | (10) |
式中:Mu表示桥墩的能力弯矩;Vn表示桥墩的名义抗剪强度[11];V表示桥墩塑性铰区所受的剪力;μ2为桥墩的容许相对位移延性比;μd为桥墩的相对位移延性比,可用式(11)表示[16]:
| $ {\mu _d} = \Delta /{\Delta _{cy1}} $ | (11) |
式中:Δ为墩顶响应最大相对位移;Δcy1为钢筋首次屈服时墩顶相对位移。
| $ {Z_4} = {\mu _3} - {\mu _z} $ | (12) |
| $ {Z_5} = {M_y} - {M_{s2}} $ | (13) |
| $ {Z_6} = {V_{c2}} - {V_{s2}} $ | (14) |
| $ {Z_7} = {P_0} - {P_H} $ | (15) |
式中:μ3为支座在该极限状态下的容许相对位移延性比;μz为支座在地震作用下的相对位移延性比;My表示桩的能力弯矩;Vc2为桩的抗剪强度;Vs2为作用于桩的横向力;PH为作用于桩身的轴压力;P0为容许的轴向承载能力,表示为:
| $ {P_0} = \frac{1}{2}u\sum\limits_{i = 1}^n {{q_{ik}}{l_i}} + {A_p}{m_0}\lambda \left\{ {\left[ {{f_{a0}}} \right] + {k_2}{\gamma _2}\left( {h - 3} \right)} \right\} $ | (16) |
根据所给的功能函数,并结合其定义和抗震规范的要求[12, 17],划分桥墩、支座和桩基础不同损伤状态的破坏准则,如表 1所示。
| 表 1 桥墩、支座和桩基础由功能函数定义的损伤状态 Table 1 Damage states determined by functions of piers and bearings |
表中:μcy1为钢筋首次屈服位移延性比;μc4为墩柱截面边缘混凝土压应变达到0.004时的位移延性比;μx为支座剪切应变等于200%时的位移延性比[13];定义My1为桩的截面边缘混凝土压应变达到0.004时的弯矩。这些量可以通过结构的有限元分析获得。为了计算桥墩、支座和基础的功能函数(非显式),结合上文提到的集成化响应面法,可以给出桥墩、支座和桩基础在损伤初形成时的功能函数:
| $ \begin{array}{*{20}{c}} {{Z_{D1}} = {\alpha _{D1}}{{\hat T}_{D1}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_{D2}} = {\alpha _{D2}}{{\hat T}_{D2}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_{D3}} = {\alpha _{D3}}{{\hat T}_{D3}}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} \end{array} $ | (17) |
式中:αD1、αD2为考虑计算式不确定性的系数;
桥墩、支座和基础在损伤形成后的功能函数为:
| $ \begin{array}{*{20}{c}} {{Z_1} = {\alpha _1}{{\hat T}_1}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_2} = {\alpha _2}{{\hat T}_2}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_3} = {\alpha _3}{{\hat T}_3}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_4} = {\alpha _4}{{\hat T}_4}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_5} = {\alpha _5}{{\hat T}_5}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_6} = {\alpha _6}{{\hat T}_6}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)}\\ {{Z_7} = {\alpha _7}{{\hat T}_7}\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)} \end{array} $ | (18) |
构件在设计基准期内发生3个破坏等级的失效概率为:
| $ \begin{array}{l} {P_f}\left( {{B_i}} \right) = P\left( {{I_s}} \right){P_{{I_s}}}\left( {{B_i}} \right) + P\left( {{I_o}} \right){P_{{I_o}}}\left( {{B_i}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;P\left( {{I_l}} \right){P_{{I_l}}}\left( {{B_i}} \right) \end{array} $ | (19) |
式中:Is、Io、Il分别表示多遇地震、设防地震和罕遇地震;PIs(Bi)、PIo(Bi)、PIl(Bi)分别为地震烈度Is、Io和Il下构件发生Bi级破坏的失效概率(i=1, 2, 3);P(Is)、P(Io)和P(Il)分别为地震烈度Is、Io和Il在设计基准期内发生的概率,可近似表示为:
| $ \begin{array}{*{20}{c}} {P\left( {{I_s}} \right) = {P_l}\left( {{I_o} - 0.77} \right)}\\ {P\left( {{I_o}} \right) = {P_l}\left( {{I_o} + 0.5} \right) - {P_l}\left( {{I_o} - 0.77} \right)}\\ {P\left( {{I_l}} \right) = 1 - {P_l}\left( {{I_o} + 0.5} \right)} \end{array} $ | (20) |
式中:Pl(i)为最大地震烈度在设计基准期50 a内发生的概率,由文献[15]中的公式计算得到。本文计算中多遇地震和偶遇地震分别取:Is=Io-1.55, Il=Io+1.0。
则抗震结构或构件在使用期的可靠度Ps可表示为[6]:
| $ {P_s} = 1 - {P_f} = 1 - \int_0^\infty {{P_f}\left( {R < S\left| a \right.} \right)f\left( a \right){\rm{d}}a} $ | (21) |
式中:Pf是结构或构件在使用期限内发生破坏的概率, 即功能函数Z < 0的概率;S为结构响应;R为结构抗力;f(a)为结构或构件所在地区使用期限内最大地震动强度参数的概率密度;a为地震动强度参数。
实际计算地震可靠度时,在某一地震强度下,需要先用FEM法得到若干结构随机参数和与之对应的结构响应的样本点,并拟合得到响应面函数(RSM法),进而得到功能函数,确定好MCS法所需的模拟次数后,在响应面上用Matlab程序获得不同损伤状态下功能函数小于零时的累积次数,其与模拟次数之比即为失效概率,进而可得到构件不同损伤状态对应的地震可靠度。
3 钢筋混凝土梁式桥的地震安全性参考结构安全性的概念,定义桥梁的地震安全性:在规定期限内,在正常施工和使用条件下,当遭遇指定强度的地震直接或间接作用时,桥梁局部可以发生一定程度的损伤,但仍能保证足够的通行能力。而可靠度理论考虑变量的不确定性,计算结构在生命周期里发生不利事件如结构损伤的概率,通过比较概率的大小,并转化为地震安全评价指标,由此评定结构的安全水平。总之,基于可靠度理论的研究方法可以使人们了解结构的安全水平是否满足要求。但该理论往往只是给出了结构发生完全破坏的可能性大小,并没有量化地给出结构出现其他损伤状态的可能性大小。所以基于可靠度理论,本文给出了钢筋混凝土梁式桥的桥墩、支座和基础可能出现的各种损伤状态下的可靠度,并定义了评价构件安全性的量化指标,给出了计算步骤,以此来直观地分析和评价构件的地震安全性。对于已建桥梁,本文仅考虑对结构抗力产生重要影响的混凝土和钢筋的强度以及计算模式的不确定性,将其作为可靠度分析时的随机输入变量。
3.1 安全评价指标安全评价指标是评价结构或构件是否安全的指标。本文定义构件的安全指标表达式为:
| $ S = \sum\limits_{i = 1}^3 {{P_s}\left( {{B_i}} \right){K_{{B_i}}}} $ | (22) |
式中:Ps(Bi)为构件在设计基准期内的不同损伤程度的可靠度概率值,i=1, 2, 3;B1、B2、B3等级分别代表无损伤、轻微或中等损伤、严重损伤或破坏;KBi为Bi种破坏等级下的安全系数,参考易损性分析方法中的经验法、规范校核法等对破坏程度的量化表示;本文给出其与破坏程度的对应关系如下:0.95—B1;0.725—B2;0.275—B3。S为安全性评价指标,参考文献[6]中对Ps(Bi)的大致说明,并结合KBi可以计算出不同破坏程度对应的S范围,根据上文对不同损伤程度的描述,本文给出桥梁构件的安全水平划分如表 2所示。
| 表 2 桥梁构件的安全水平划分 Table 2 Safety level division of bridge components |
为了评价桥梁系统的地震安全性,结构需要通过体系的可靠度分析计算出较为准确的系统可靠度。但对既有桥梁的结构系统可靠度以现有理论来说较难准确得到,而国内外近年来对其的研究仍然处于探索阶段,研究尚不成熟。故本文利用桥梁主要构件的安全指标得到桥梁系统的安全等级,以此评定桥梁系统的地震安全性。
为了方便对桥梁体系的地震安全性进行评估,参照层次分析法的思想,定义桥梁体系中的桥墩单元、支座单元、基础单元分别由若干桥墩构件、支座构件和基础构件组成。给出桥梁单元的安全等级划分如表 3。同时本文将桥梁的地震安全性水平相应地划分为3个等级。因为3个单元地震安全等级的任意一个组合有33种情况,对这27种单元安全等级组合情况下的桥梁系统地震安全等级的具体划分和对应的桥梁整体通行能力整理如表 4。
| 表 3 桥梁单元的安全等级划分 Table 3 Safety grade division of the bridge units |
| 表 4 桥梁系统的安全等级划分 Table 4 Safety grade division of the bridge structure |
钢筋混凝土连续梁桥地震安全性评价分析的主要计算步骤为[8-9, 16]:
1) 根据式(20)计算地震烈度Is、Io和Il在设计基准期内发生的概率P(Is)、P(Io)和P(Il)。
2) 确定需要输入的随机变量和输出变量。本文采用表 5中的输入变量,并由拉丁超立方抽样法(LHS)获得。输出变量根据不同功能函数的表现形式,一般取为结构或构件在地震激励下的响应,本文为桥墩的弯矩、剪力、相对位移延性比、支座的相对位移延性比、基础的弯矩、剪力和轴力。输出变量可以按照反应谱法或其他动力方法进行FEM分析得到。本文算例采用规范反应谱法进行确定性分析。
| 表 5 随机变量统计特征 Table 5 Statistics of random variables |
3) 根据桥墩、支座和基础的功能函数(4)~(6)、(8)~(14),运用RSM法构造不同地震烈度Is、Io和Il下的响应面函数
4) 根据响应面分析得到的近似函数
5) 得到PIs(Bi)、PIo(Bi)、PIl(Bi)后,按式(19)计算构件设计基准期内发生3个破坏等级的失效概率,然后用式(21)求出构件的可靠度。
6) 用安全评价指标计算式(22)将构件的可靠度转化为安全评价指标,评价构件的安全等级。根据表 3、4评价桥梁单元和系统的安全等级。
综上,给出钢筋混凝土梁式桥安全性评价模型如图 1。

|
Download:
|
| 图 1 钢筋混凝土梁式桥地震安全性评价模型 Fig. 1 Model of Seismic safety evalution of the reinforced concrete beam bridge | |
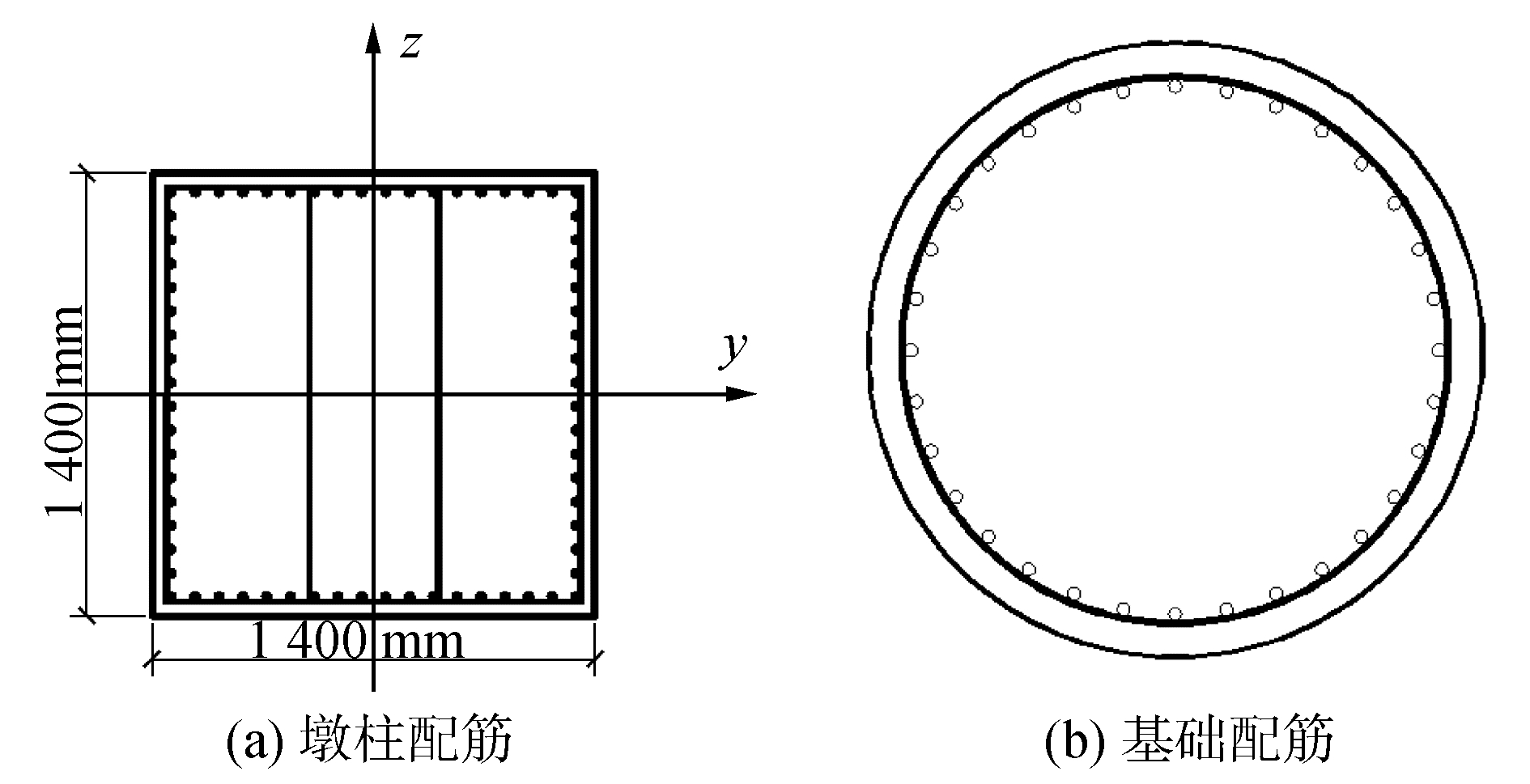
参考文献[16]给出的算例,已知一座40 m×5跨的钢筋混凝土连续梁桥,桥面幅宽12 m,支承采用板式橡胶支座,桥墩形式为T型,高7.5 m,箱型截面,基础为现场灌注桩,直径为1.2 m。桥墩、桩基础按C30混凝土模拟,主筋和箍筋采用HRB335钢筋。墩柱截面的主筋直径为ϕ28 mm,箍筋直径为ϕ16 mm,基础采用的主筋直径为ϕ22 mm,箍筋直径为ϕ16 mm,给出桥墩和基础的截面配筋图如图 2。抗震设防分类为乙类,相应的特征周期为0.40 s,场地类型为Ⅱ类,设防烈度为7度设防(0.10 g)。设计基准期为100 a,地震反应谱采用《城市桥梁抗震设计规范》(2011)。本桥属于中小跨度桩基桥梁,考虑桩基边界条件,在顺桥方向上用承台底6个自由度的弹簧刚度模拟桩土相互作用,图 3为该桥的有限元模型。该桥按照抗震规范进行两阶段设计,采用Midas Civil用规范反应谱方法计算了顺桥向桥墩和支座在设计地震下的内力和变形响应(包括弯矩、剪力、位移)。给出桥梁结构随机变量如表 5所示[11, 16]。因为桥梁是对称结构,故仅计算了P1和P2桥墩、上部支座B1、B2、B3和群桩基础S1、S2、S3的安全指标,并给出了桥梁整体的安全等级。
|
Download:
|
| 图 2 墩柱及基础配筋 Fig. 2 Pier and foundation reinforcement | |
|
Download:
|
| 图 3 钢筋混凝土连续梁桥有限元模型 Fig. 3 Finite element model of the reinforced concrete continuous beam bridge | |
根据式(20),多遇地震烈度Is、设防地震烈度Io和罕遇地震烈度Il在设计基准期内发生的概率见表 6。
| 表 6 地震烈度的发生概率 Table 6 The probabilities of seismic intensities |
根据构件地震安全性的计算步骤2)~4),计算桥墩和支座在不同地震烈度下发生Bi级破坏的失效概率PIs(Bi)、PIo(Bi)、PIl(Bi),这里按照精度要求,确定MCS模拟次数为10万次[6],计算结果见表 7~9。
| 表 7 桥墩在不同地震烈度下不同破坏等级的失效概率 Table 7 The failure probability of piers under different seismic intensities |
| 表 8 支座在不同地震烈度下不同破坏等级的失效概率 Table 8 The failure probability of bearings under different seismic intensities |
| 表 9 基础在不同地震烈度下不同破坏等级的失效概率 Table 9 The failure probability of foundations under different seismic intensities |
根据步骤5),桥墩、支座和基础在设计基准期内发生不同种损伤时的地震可靠度见表 10~表 12。
| 表 10 桥墩在设计基准期内发生不同种损伤情况可靠度 Table 10 The reliability of different damages of piers in the design period |
| 表 11 支座在设计基准期内发生不同种损伤情况可靠度 Table 11 The reliability of different damages of bearings in the design period |
| 表 12 基础在设计基准期内发生不同破坏等级的可靠度 Table 12 The reliability of different damages of foundations in the design period |
根据步骤6),给出桥墩、支座和基础的地震安全性评价指标,如表 13所示。根据表 2~4,得到该桥所有单元和该桥系统的安全等级,计算结果如表 14。
| 表 13 构件的安全性评价指标 Table 13 Safety evaluation index of components |
| 表 14 桥梁单元和系统的安全等级 Table 14 Safety grades of the bridge structure and its components |
从表 7中可得到桥墩P1、P2在小震下没有损伤产生,在中震下产生B2级破坏的概率非常小,而在大震下保持基本完好的概率较大,为0.914 6和0.925 5,进入屈服阶段的概率较小,分别为0.135 3和0.174 8。从表 8中可以看出,支座B1、B2、B3在小震和中震下将保持基本完好,但支座B2在中震下有发生B2级破坏的可能性,概率很小,为0.015 4,在大震下发生非结构性损伤的可能性较大(0.999 6、0.930 7和0.984 5),发生B2级破坏的可能性较小(0.160 4、0.089 1和0.000 9),出现严重损伤或破坏的概率为0。从表 9中可以看出,基础S1、S2、S3在小震下将保持基本完好,在中震下基础S1、S2有发生B2级破坏的可能性,但概率很小,为0.063 3和0.084 2,在大震下基础S1、S2、S3发生B1级损伤的可能性较大(0.989 9、0.923 3和0.921 9),发生B2级破坏的可能性较小(0.022 5、0.116 9和0.116 1),出现B3级破坏的概率为0。从表 10~12可以看出,在三水准地震作用下,桥墩、支座和基础在设计基准期内发生不同破坏等级的可靠度都比较高,说明达到了设计要求,B3级破坏对应的可靠度更是达到了1,说明构件不会出现严重损伤或破坏。从表 2和表 13可以得出:桥墩P1、P2在使用周期内没有结构性损伤,属于Ⅰ级安全,可以正常使用;支座B1、B2、B3产生B1级损伤,在地震作用下将会产生非结构性损伤,保持基本完好,而上部结构的主梁之间也将保持基本完好,属于Ⅰ级安全,可以正常使用;基础S1、S2、S3产生B1级损伤,属于Ⅰ级安全,可以正常使用。从表 14可以得出:桥墩单元、支座单元和基础单元的安全等级均为Ⅰ级,所以桥梁系统的安全等级也为“好”,可以正常通行,说明该桥在设计基准期内地震作用下的安全水平较高。
5 结论1) 以可靠度理论作为出发点,定义了地震安全评价指标和桥梁单元,以此评价桥梁的地震安全性,判断其损伤程度、安全等级和履行功能情况。通过算例,从理论上验证了改进该理论后评价桥梁地震安全性的可行性。
2) 以往应用可靠度理论只是给出了构件或结构发生完全破坏的可能性,本文结合破坏准则,采用不同损伤极限状态下的功能函数,可以分析出构件不同破坏等级发生的可能性,并给出相应的安全水平和功能,为桥梁的加固维修、抗震救灾等提供了参考。
由于桥梁在地震作用下破坏机理复杂,除桥梁构件的安全性外还有很多因素需要考虑,如地基土液化等问题,因此想要对桥梁系统的地震安全性水平进行更加精确地评价仍需进一步研究。
| [1] |
姜淑珍, 林均岐. 城市桥梁震害预测方法的探讨[J]. 世界地震工程, 2004, 20(4): 64-66. JIANG Shuzhen, LIN Junqi. Study on seismic damage predicting methods of bridges in cities[J]. World information on earthquake engineering, 2004, 20(4): 64-66. DOI:10.3969/j.issn.1007-6069.2004.04.011 (  0) 0)
|
| [2] |
王东升, 冯启民. 桥梁震害预测方法[J]. 自然灾害学报, 2001(3): 113-118. WANG Dongsheng, FENG Qimin. Seismic damage assessment methods for bridges[J]. Journal of natural disasters, 2001(3): 113-118. DOI:10.3969/j.issn.1004-4574.2001.03.020 (  0) 0)
|
| [3] |
CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones[J]. KSCE journal of civil engineering, 2003, 7(1): 41-51. DOI:10.1007/BF02841989 (  0) 0)
|
| [4] |
陈亮. 钢筋混凝土桥梁地震易损性分析方法[J]. 上海公路, 2007, 3: 48-51. CHEN Liang. Seismic fragility analytical methodology for reinforced concrete bridges[J]. Shanghai Highways, 2007, 3: 48-51. (  0) 0)
|
| [5] |
王占飞, 张济宁, 赵乃志. 日本高速道路桥梁抗震设计方法的研究[J]. 世界桥梁, 2008, 4: 13-15. WANG Zhanfei, ZHANG Jining, ZHAO Naizhi. Study of seismic design methods for expressway bridges in japan[J]. World Bridges, 2008, 4: 13-15. (  0) 0)
|
| [6] |
武清玺. 结构可靠度理论、方法及应用[M]. 北京: 科学出版社, 2004: 39-84. WU Qingxi. Structural reliability theory, method and application[M]. Beijing: Science Press, 2004: 39-84. (  0) 0)
|
| [7] |
叶爱君. 桥梁抗震[M]. 北京: 人民交通出版社, 2011: 14-32. YE Aijun. Seismic design of bridges[M]. Beijing: China Communications Press, 2011: 14-32. (  0) 0)
|
| [8] |
陈文元, 赵雷, 钟强文, 等. 基于响应面法的连续刚构地震可靠度分析[J]. 地震工程与工程振动, 2009, 29(3): 45-50. CHEN Wenyuan, ZHAO Lei, ZHONG Qiangwen, et al. Seismic reliability analysis of rigid frame bridge based on response surface method[J]. Journal of Earthquake Engineering & Engineering Vibration, 2009, 29(3): 45-50. (  0) 0)
|
| [9] |
程进. 基于响应面法的几何非线性结构概率响应分析[J]. 同济大学学报(自然科学版), 2006, 34(9): 1147-1151. CHENG Jin. Probabilistic response analysis of geometrically nonlinear structures based on systematic response surface method[J]. Journal of Tongji University(Natural science), 2006, 34(9): 1147-1151. DOI:10.3321/j.issn:0253-374X.2006.09.003 (  0) 0)
|
| [10] |
欧进萍, 段宇博. 高层建筑结构的抗震可靠度分析与优化设计[J]. 地震工程与工程振动, 1995, 15(1): 1-13. OU Jinping, DUAN Yubo. Seismic reliability analysis and optimum design of tall buildings[J]. Earthquake Engineering & Engineering Vibration, 1995, 15(1): 1-13. (  0) 0)
|
| [11] |
Motoyuki Suzuki, Mitsuyoshi Akiyama, Yasunori Yamazaki, et al. Method of evaluating earthquake safety of RC bridge system based on reliability theory[J]. Concrete Library International of JSCE, 2001, 38: 33-50. (  0) 0)
|
| [12] |
JTC/TB02-01-2008.公路桥梁抗震设计细则[S].北京: 人民交通出版社, 2008. JTC/TB02-01-2008. Guidelines for seismic design of highway bridges[S]. Beijing: China Communications Press, 2008. (  0) 0)
|
| [13] |
谢旭. 桥梁结构地震响应分析与抗震设计[M]. 北京: 人民交通出版社, 2006: 311-313. XIE Xu. Seismic response analysis and seismic design of bridge structures[M]. Beijing: China Communications Press, 2006: 311-313. (  0) 0)
|
| [14] |
ASSOCIATION J R. Specifications forhighway bridges, Part Ⅳ substructures[M]. Japan: Maruzen, 1996.
(  0) 0)
|
| [15] |
SUZUKI M, AKIYAMA M, YAMAZAKI Y. Safety evaluation method of structural system and its application to seismic design of RC bridge pier[J]. Concrete library international of JSCE, 1997, 32: 43-68. (  0) 0)
|
| [16] |
李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报, 2012, 45(10): 152-160. LI Lifeng, WU Wenpeng, HUANG Jiamei, et al. Study on system vulnerability of medium span reinforced concrete continuous girder bridge under earthquake excitation[J]. China Civil Engineering Journal, 2012, 45(10): 152-160. (  0) 0)
|
| [17] |
ZHAO Jun, LIN Junqi, LIU Jinlong, et al. Study on safety level of RC beam bridges under earthquake[C]//ACNCIS, 2017, Zhengzhou: AIP Comference Proceedings.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


