在恶劣海况或高速状态下,船体局部结构与波浪之间常发生剧烈的砰击现象,如多体船的湿甲板结构、滑行艇的底部结构等。作用于船身的砰击压力载荷具有压力峰值大、传播速度快的特点,再加之轻质复合材料的应用,结构的弹性变形与流体之间更易产生耦合作用,这种流固耦合现象在船舶与海洋工程领域常称之为“水弹性”问题。
楔形剖面是高速船舶的典型剖面形式,因此,在砰击问题研究中,楔形体入水冲击模型被广泛地采用。Faltinsen[1]结合正交板理论和Wagner解析砰击模型[2]分析了双体船湿甲板的砰击响应。闫发锁等[3]采用相似的方法计算了考虑流固耦合影响时,楔形体入水冲击的砰击压力;Korobkin等[4]分析了简支边界下板条梁在波浪拍击作用下的结构响应,流场采用解析Wagner理论进行求解,结构响应利用伯努利欧拉梁理论进行分析;Khabakhpasheva等[5]同样基于Wagner理论和梁理论分析了二维楔形体入水冲击的水弹性响应,并进一步给出3种近似求解方法,讨论了不同耦合程度下各方法的求解精度;Stenius等[6]利用LS-DYNA软件分析了二维弹性楔形体入水冲击的流固耦合机理;Das等[7]采用相似的方法分析了夹层板结构的入水冲击响应;Piro等[8]采用有限体积方法分析了二维弹性楔形体入水和出水过程中的振动响应;王文华等[9]采用一种新型的CFD方法分析了各状态参数对弹性楔形体入水性能的影响。
综合来看,按照流场的求解方法不同,弹性楔形体入水冲击的水弹性分析方法可分为基于解析砰击模型的分析方法[1-5]和基于计算流体力学的分析方法[6-9]。基于计算流体力学的分析方法需对流体域进行离散,流场的求解通常耗时较长;而基于解析砰击模型的分析方法,虽然可以高效地实现流场的求解,但现有方法常需要结构模型具有解析振型,因此只适用于简单的结构形式。借鉴解析砰击模型在水弹性分析中的应用思路,本文结合有限元方法的离散模态信息和解析水动力模型,系统地建立了楔形体入水冲击的水弹性分析方法。相比于已有的基于解析砰击模型的分析方法,该方法采用有限元法给出的结构离散振型,不需要结构振型的解析表达式,适用范围更广;与计算流体力学的分析方法相比,该方法无需进行流体域的离散,计算效率更高。本文首先推导了二维弹性楔形体入水冲击的控制方程,并给出了数值求解思路;进而对该方法进行了收敛性分析和理论验证;最后,以具有复杂边界形式的楔形体为例进行分析。
1 水弹性分析 1.1 结构动力学方程基于有限元理论,将结构离散为具有有限自由度的系统,从而给出弹性楔形体无阻尼振动的动力学方程[10]:
| $ \mathit{\boldsymbol{M\ddot U}} + \mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{P}} $ | (1) |
式中:M为结构的质量矩阵;K为结构的刚度矩阵;P为结构所承受的分布外力矩阵。
当采用模态叠加法求解动力响应分析时,砰击载荷作用下系统的节点位移U可表达为:
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{DP}} = \sum\limits_{r = 1}^m {{\mathit{\boldsymbol{D}}_r}{p_r}\left( t \right)} $ | (2) |
式中:D为系统的固有振型矩阵;P为广义主坐标列阵;m为用于结构分析的模态数目;Dr表示第r阶模态的固有振型;pr(t)表示第r阶模态在结构响应中的贡献量。在式(1)左右两端同时乘以DT,并将式(2)代入式(1),可以得出结构系统的主坐标运动方程式:
| $ \mathit{\boldsymbol{a\ddot p}} + \mathit{\boldsymbol{cp}} = \mathit{\boldsymbol{Z}} $ | (3) |
式中:a为结构广义质量矩阵,a=DTMD;c为结构广义刚度矩阵,c=DTKD;Z为广义分布力矩阵,Z=DTp。
采用正交的固有振型,并引入质量归一化,则有:
| $ \mathit{\boldsymbol{D}}_r^{\rm{T}}\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{D}}_r} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ 1, \end{array}&\begin{array}{l} r \ne s\\ r = s \end{array} \end{array}} \right. $ |
| $ \mathit{\boldsymbol{D}}_r^{\rm{T}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{D}}_r} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ \omega _r^2, \end{array}&\begin{array}{l} r \ne s\\ r = s \end{array} \end{array}} \right. $ |
式中ωr为第r阶模态的固有频率。
当通过流场的求解确定作用于结构的广义力Z量值后,即可得到各阶振动模态的主坐标,从而可以利用模态叠加法确定关注的结构响应。
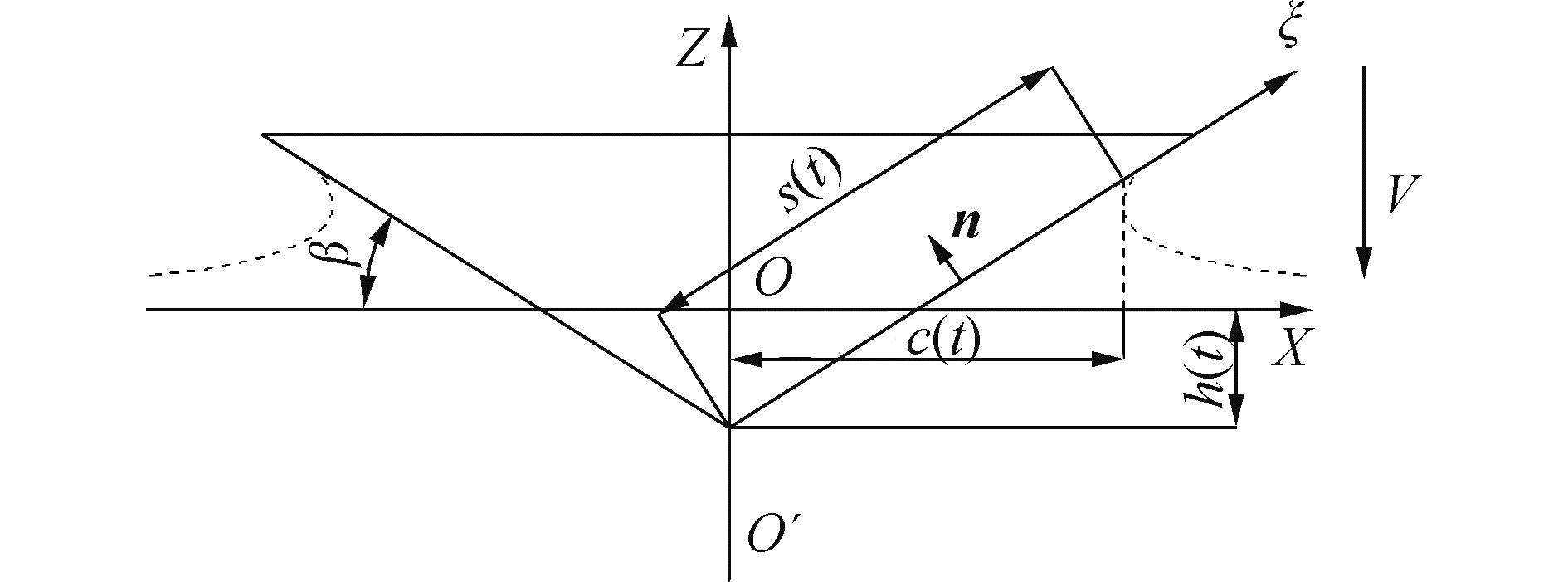
1.2 弹性结构的广义力如图 1所示,初始时刻t=0,流体静止,OX轴与初始静水面重合,楔形剖面与静水面的交点位于XOZ平面的原点O处。o′ξ轴沿着楔形体的斜边方向,初始时刻,o′与原点o重合。c(t)为水平方向的浸湿半宽,s(t)为沿着斜边的浸湿长度。V为楔形体垂直入水的恒定速度。基于Wagner砰击理论,假定流体为不可压缩的理想流体,并忽略重力的影响,则浸湿表面上流体的速度势可以近似的表达为:
|
Download:
|
| 图 1 入水砰击的坐标系与参数 Fig. 1 Coordinates and parameters of water entry | |
| $ \varphi \left( {x,0,t} \right) = - V\sqrt {{c^2}\left( t \right) - {x^2}} $ | (4) |
剖面浸湿半宽变化速度为:
| $ c\left( t \right) = \frac{{{\rm{ \mathsf{ π} }}V}}{{2\tan \beta }} $ | (5) |
由
| $ \varphi \left( {\xi ,0,t} \right) = - V\cos \beta \sqrt {{s^2}\left( t \right) - {\xi ^2}} $ | (6) |
| $ \dot s\left( t \right) = \frac{{{\rm{ \mathsf{ π} }}V}}{{2\sin \beta }} $ | (7) |
由于楔形体的弹性效应,结构自身的振动也会改变结构与流体之间的砰击速度。文献[1]的耦合交界面条件,引入浸湿表面的平均振动速度
| $ \varphi \left( {\xi ,0,t} \right) = \left( { - V \cdot \cos \beta + \bar {\dot w}\left( {s\left( t \right)} \right)} \right) \cdot \sqrt {{s^2}\left( t \right) - {\xi ^2}} $ | (8) |
式中:Vcosβ为整体砰击速度在楔形体表面法向方向的分量;
则考虑弹性效应后的浸湿弧长变化速度为:
| $ \begin{array}{*{20}{c}} {\dot s\left( t \right) = \frac{{{\rm{ \mathsf{ π} }} \cdot \left( {V\cos \beta - \bar {\dot w}\left( {s\left( t \right)} \right)} \right)}}{{2\sin \beta cos\beta }} = }\\ {\frac{{{\rm{ \mathsf{ π} }} \cdot \left( {V\cos \beta - \bar {\dot w}\left( {s\left( t \right)} \right)} \right)}}{{\sin \left( {2\beta } \right)}}} \end{array} $ | (9) |
由伯努利方程,忽略压力表达式中的速度势梯度平方项,可得楔形体湿表面压力沿o′ξ轴的表达式为:
| $ \begin{array}{*{20}{c}} {P\left( {\xi ,t} \right) = - \rho \frac{{\partial \varphi }}{{\partial t}} = - \rho \bar {\ddot w}\left( {s\left( t \right)} \right) \cdot \sqrt {{s^2}\left( t \right) - {\xi ^2}} = }\\ { - \rho \left[ { - V\cos \beta + \bar {\dot w}\left( {s\left( t \right)} \right)} \right] \cdot \frac{{s\left( t \right)}}{{\sqrt {{s^2}\left( t \right) - {\xi ^2}} }} \cdot \dot s\left( t \right)} \end{array} $ | (10) |
式中
由式(10)可以看出,Wagner模型的弹性体周围流场压力主要由2项组成,其中,
为便于推导,可以将弹性体周围的流场进一步划分为:刚体冲击对应的压力项Pr(ξ, t)、弹性效应对应的压力项Pe(ξ, t)2个部分,即P(ξ, t)=Pr(ξ, t)+Pe(ξ, t),则有:
| $ \begin{array}{*{20}{c}} {{P_r}\left( {\xi ,t} \right) = \rho V \cdot \cos \beta \cdot \frac{{s\left( t \right)}}{{\sqrt {{s^2}\left( t \right) - {\xi ^2}} }} \cdot \dot s\left( t \right)}\\ {{P_e}\left( {\xi ,t} \right) = - \rho \bar {\ddot w}\left( {s\left( t \right)} \right) \cdot \sqrt {{s^2}\left( t \right) - {\xi ^2}} - }\\ {\rho \bar {\dot w}\left( {s\left( t \right)} \right) \cdot \frac{{s\left( t \right)}}{{\sqrt {{s^2}\left( t \right) - {\xi ^2}} }} \cdot \dot s\left( t \right)} \end{array} $ |
入水砰击过程中,流体的砰击压力垂直于楔形体表面的法向方向,因此,在流体广义力计算时,仅需考虑沿着法线方向的振动位移。若第i阶振动模态下,沿着斜边法向方向的位移振型为ψi(ξ),则在斜边浸湿长度为s(t)时,对应的广义砰击力为:
| $ {f_i}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {P\left( {\xi ,t} \right) \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi } $ |
令
| $ \begin{array}{l} {f_{{\rm{exc}},i}}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {{P_r}\left( {\xi ,t} \right) \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi } \\ {f_{{\rm{ela}},i}}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {{P_e}\left( {\xi ,t} \right) \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi } \end{array} $ |
式中:fexc, i(s(t))为楔形体剖面的广义激励力,其只与剖面的振型和刚性剖面所受的砰击压力有关,与剖面的弹性振动无关;fela, i(s(t))为弹性效应引起的广义水动力:
| $ \begin{array}{*{20}{c}} {{f_{{\rm{ela}},i}}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {\left[ { - \rho \bar {\ddot w}\left( {s\left( t \right)} \right) \cdot \sqrt {{{\left( {{s^k}\left( t \right)} \right)}^2} - {\xi ^2}} - } \right.} }\\ {\left. {\rho \bar {\dot w}\left( {s\left( t \right)} \right) \cdot \frac{{s\left( t \right)}}{{\sqrt {{{\left( {s\left( t \right)} \right)}^2} - {\xi ^2}} }} \cdot \dot s\left( t \right)} \right] \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi } \end{array} $ | (11) |
可以看出,fela, i(s(t))与弹性剖面的瞬时平均振动速度
| $ \left\{ \begin{array}{l} \bar w\left( {s\left( t \right)} \right) = \sum\limits_{j = 1}^m {{{\bar \psi }_j}\left( {s\left( t \right)} \right)} \cdot {p_j}\left( t \right)\\ \bar {\dot w}\left( {s\left( t \right)} \right) = \sum\limits_{j = 1}^m {{{\bar \psi }_j}\left( {s\left( t \right)} \right)} \cdot {{\dot p}_j}\left( t \right)\\ \bar {\ddot w}\left( {s\left( t \right)} \right) = \sum\limits_{j = 1}^m {{{\bar \psi }_j}\left( {s\left( t \right)} \right)} \cdot {{\ddot p}_j}\left( t \right) \end{array} \right. $ | (12) |
式中:s(t)为浸湿的楔形体斜边长度;m为计及的弹性模态的数目;
| $ {{\bar \psi }_j}\left( {s\left( t \right)} \right) = \int_0^{s\left( t \right)} {\frac{{{\psi _j}\left( \xi \right)}}{{s\left( t \right)}}{\rm{d}}\xi } $ |
将式(12)代入式(11),弹性效应引起的广义力可以进一步表达为:
| $ \begin{array}{*{20}{c}} {{f_{{\rm{ela}},i}}\left( {s\left( t \right)} \right) = - \sum\limits_{j = 1}^m {{A_{ij}}\left( {s\left( t \right)} \right)} \cdot {{\ddot p}_j}\left( t \right) - }\\ {\sum\limits_{j = 1}^m {{B_{ij}}\left( {s\left( t \right)} \right)} \cdot {{\dot p}_j}\left( t \right)} \end{array} $ |
式中:Aij(s(t))为楔形体斜边浸湿长度s(t)时的广义流体附加质量;Bij(s(t))为楔形体斜边浸湿长度为s(t)时的广义流体附加阻尼。其表达式应为:
| $ {A_{ij}}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {\rho {{\bar \psi }_j}\left( {s\left( t \right)} \right)} \cdot \sqrt {{{\left( {s\left( t \right)} \right)}^2} - {\xi ^2}} \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi $ |
| $ \begin{array}{*{20}{c}} {{B_{ij}}\left( {s\left( t \right)} \right) = \int\limits_0^{s\left( t \right)} {\rho {{\bar \psi }_j}\left( {s\left( t \right)} \right)} \cdot \frac{{s\left( t \right)}}{{\sqrt {{{\left( {s\left( t \right)} \right)}^2} - {\xi ^2}} }} \cdot }\\ {\dot s\left( t \right) \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi } \end{array} $ |
那么,在第i阶振动模态下,楔形体剖面对应的广义砰击力为:
| $ \begin{array}{*{20}{c}} {{f_i}\left( {s\left( t \right)} \right) = - \sum\limits_{j = 1}^m {{A_{ij}}\left( {s\left( t \right)} \right)} \cdot {{\ddot p}_j}\left( t \right) = }\\ { - \sum\limits_{j = 1}^m {{B_{ij}}\left( {s\left( t \right)} \right)} \cdot {{\dot p}_j}\left( t \right) + {f_{{\rm{exc}},i}}\left( {s\left( t \right)} \right)} \end{array} $ | (13) |
将式(13)代入式(3),可得弹性楔形体入水冲击的水弹性方程:
| $ \left( {\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{\ddot p}} + \mathit{\boldsymbol{B\dot p}} + \mathit{\boldsymbol{cp}} = {\mathit{\boldsymbol{F}}_{{\rm{exc}}}} $ | (14) |
式中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{A_{11}}\left( t \right)}& \cdots &{{A_{1m}}\left( t \right)}\\ \vdots &{}& \vdots \\ {{A_{m1}}\left( t \right)}& \cdots &{{A_{mm}}\left( t \right)} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{B_{11}}\left( t \right)}& \cdots &{{B_{1m}}\left( t \right)}\\ \vdots &{}& \vdots \\ {{B_{m1}}\left( t \right)}& \cdots &{{B_{mm}}\left( t \right)} \end{array}} \right]; $ |
引入
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot p}}}\\ {\mathit{\boldsymbol{\dot q}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{q}}\\ {\frac{{{\mathit{\boldsymbol{F}}_{{\rm{exc}}}} - \mathit{\boldsymbol{Bq}} - \mathit{\boldsymbol{cp}}}}{{\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{A}}}}} \end{array}} \right] $ | (15) |
每个时间步上还需要求解各个剖面
在数值求解过程中,需要在每个时间步上更新矩阵Fexc、A、B和
|
Download:
|
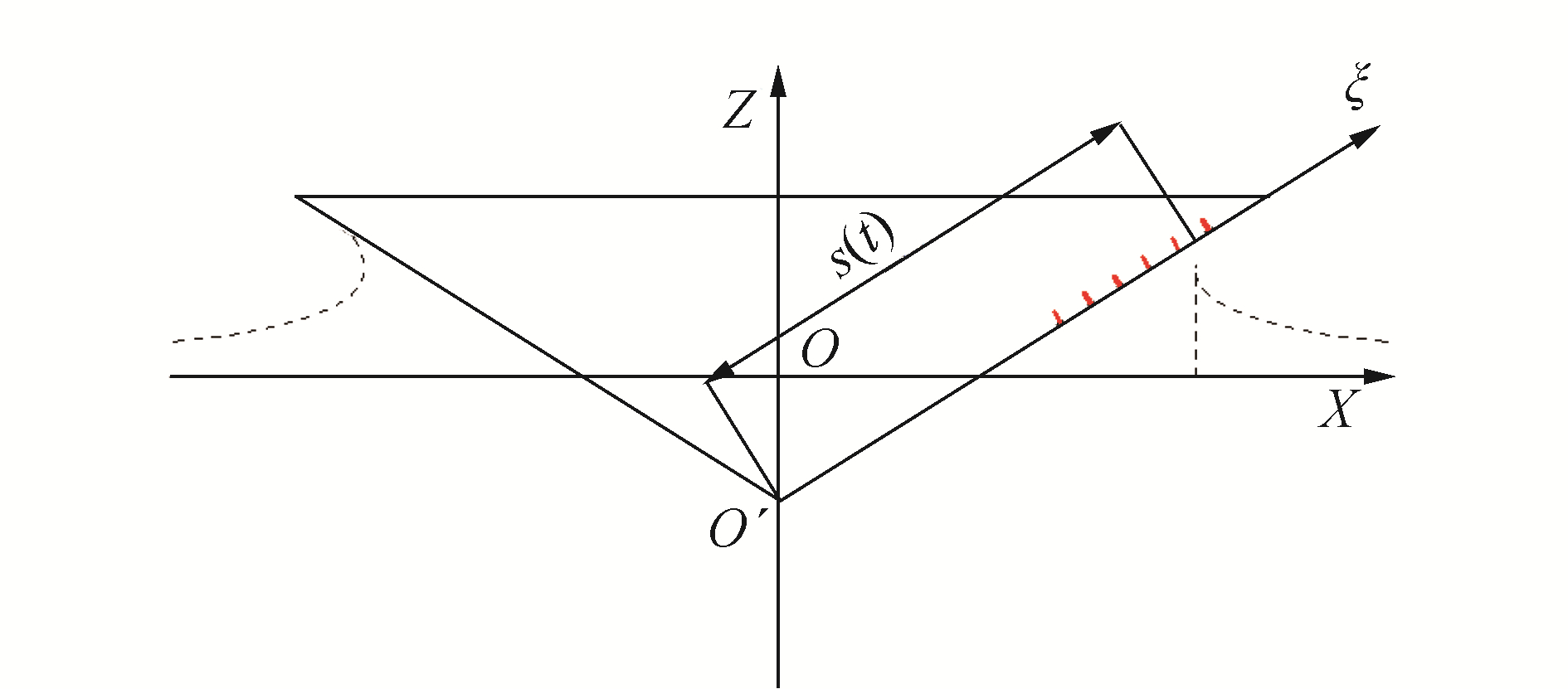
| 图 2 线元网格与浸湿长度的关系 Fig. 2 Relationship between mesh element and wetted length | |
为解决上述问题,以第i阶弹性模态为例,预先计算一系列s值下的下列各式的函数值:
| $ {T_{1,i}}\left( {{s^k}} \right) = \int\limits_0^{{s^k}} {\sqrt {{{\left( {{s^k}} \right)}^2} - {\xi ^2}} } \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi $ |
| $ {T_{2,i}}\left( {{s^k}} \right) = \int\limits_0^{{s^k}} {\frac{{{s^k}}}{{\sqrt {{{\left( {{s^k}} \right)}^2} - {{\left( \xi \right)}^2}} }}} \cdot {\psi _i}\left( \xi \right){\rm{d}}\xi $ |
| $ {T_{3,i}}\left( {{s^k}} \right) = {{\bar \psi }_j}\left( {{s^k}} \right) = \int_0^{{s^k}} {\frac{{{\psi _j}\left( \xi \right)}}{{{s^k}}}{\rm{d}}\xi } $ |
式中sk取值恰好位于线元的边界处。
当t时刻s(t)位于线元的中间时,采用线性插值的方法确定瞬时时刻的上述积分T1, i(s(t))、T2, i(s(t))、T3, i(s(t)),则t时刻Aij(s(t))、Bij(s(t))和fexc, i(s(t))可以表达为:
| $ {A_{ij}}\left( s \right) = \rho {T_{3,i}}\left( s \right){T_{1,i}}\left( s \right) $ |
| $ {B_{ij}}\left( s \right) = \rho {T_{3,i}}\left( s \right){T_{2,i}}\left( s \right)\dot s\left( t \right) $ |
| $ {f_{{\rm{exc}},i}}\left( s \right) = \rho V\cos \beta \cdot {T_{2,i}}\left( s \right) \cdot \dot s\left( t \right) $ |
可以看出,利用上述方法更新水弹性方程(14)中的相应系数,避免了每个时间步上网格的重新划分和积分的求解,加快了计算速度。
3 收敛性分析对本文方法中涉及到的楔形体网格离散数目和计算模态数目进行收敛性分析。计算中,楔形体的模态分析利用商业有限元软件Nastran来实现。有限元模型中的网格划分密度与广义力积分中所采用的离散密度相一致,便于直接利用模态分析中的节点振型进行广义力的计算。文献[11]确定弹性楔形体的计算参数,其中,楔形体底升角为10°,斜边长度L=0.5 m,板条梁的厚度为h=18 mm,结构材料为钢材,密度为7 850 kg/m3,弹性模量E=210 GPa,流体的密度为1 000 kg/m3,板条梁两端取为简支边界。楔形体的冲击速度为4 m/s。本文采用壳单元进行板条梁的建模,建模中板条梁的宽度取值为0.04 m,并且沿着宽度方向仅划分一个网格。
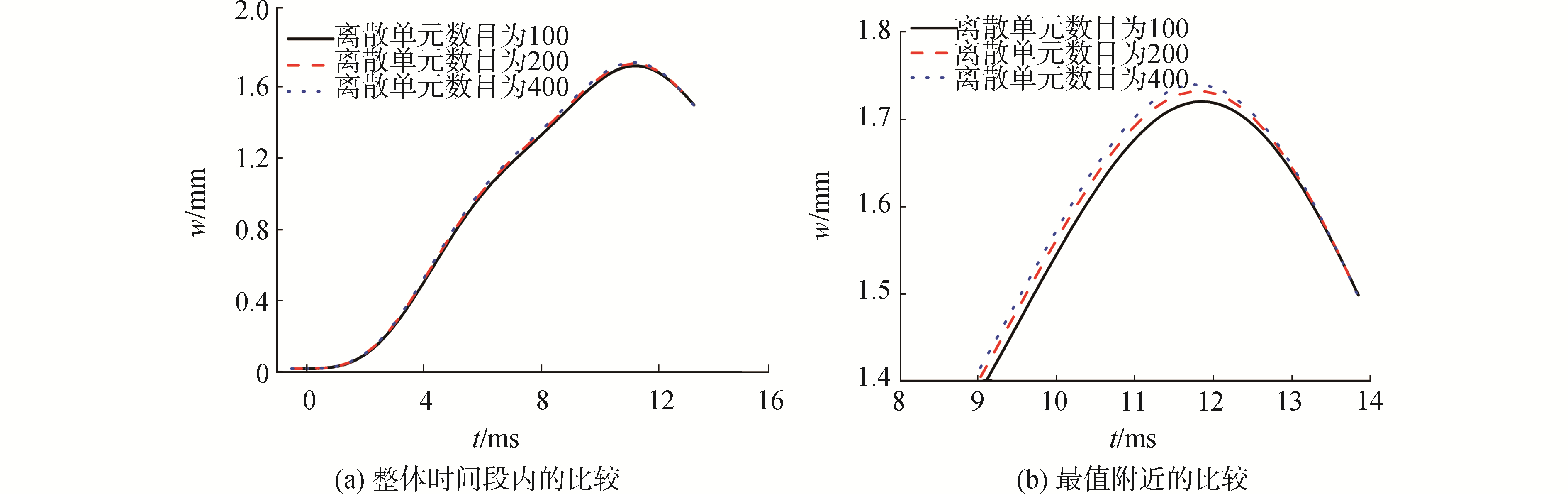
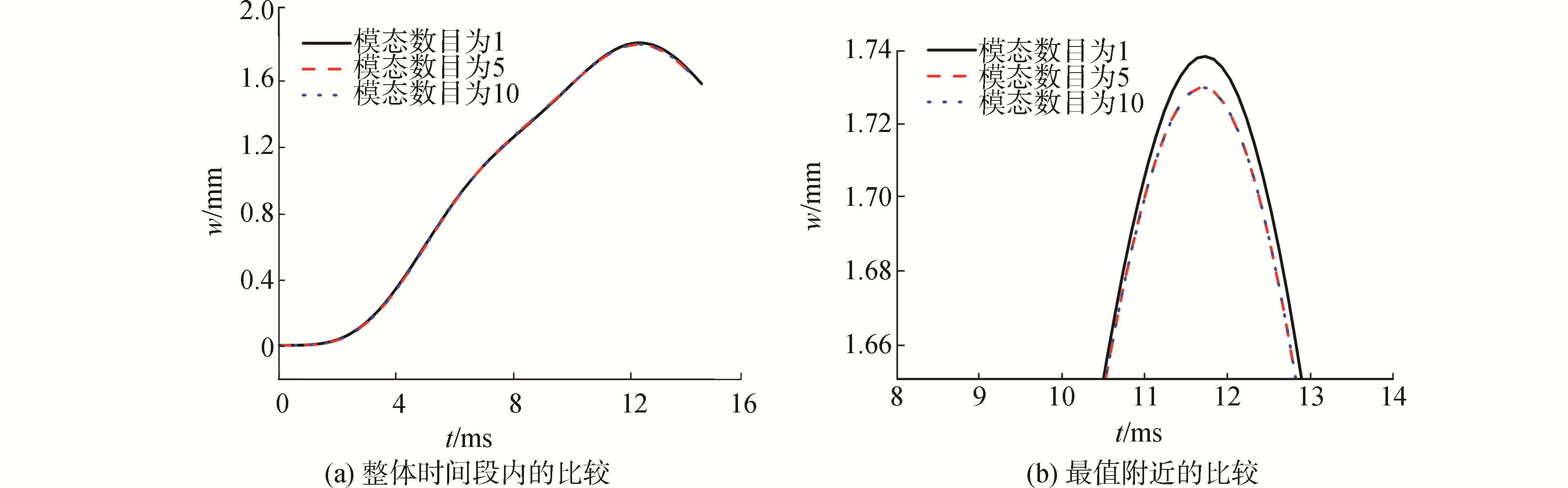
将楔形体的斜边分别离散为100、200和400等份进行计算,用于计算的模态数目为前10阶模态。得到楔形体斜边中心位置处,沿着斜边法线方向的振动位移,如图 3所示。可以看出,不同网格密度下的振动响应十分接近,200与400等份之间的偏差为0.43%。将楔形体的斜边离散为200份,用于计算的模态数目分别为前1、5和10阶模态,得到楔形体斜边中心位置处,沿着斜边法线方向的振动位移,如图 4所示。可以看出,不同计算模型下的振动响应十分接近,5阶与10阶计算模型的振动响应偏差为0.006%。总体看来,本文算法具有较好的网格收敛性和模态收敛性,后续将斜边划分为200等份,并取前10阶振动模态。
|
Download:
|
| 图 3 网格密度的收敛性 Fig. 3 Convergence of mesh density | |
|
Download:
|
| 图 4 模态数目的收敛性 Fig. 4 Convergence of mode number | |
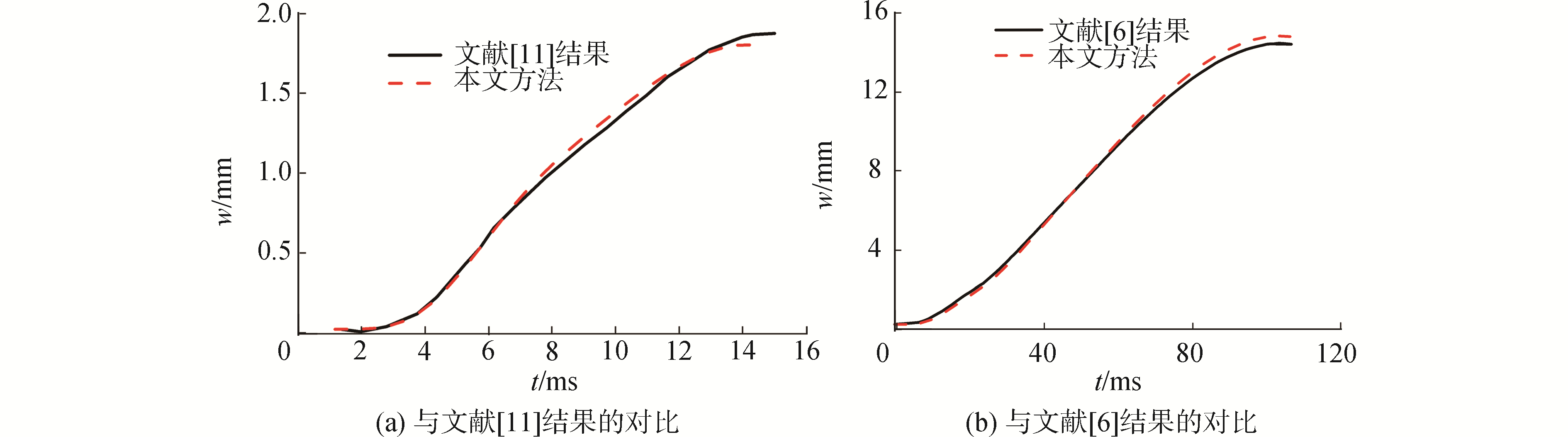
文献[6, 11]给出了弹性楔形体入水冲击时,斜边中心位置处的位移响应。为进一步验证本文的数值方法,将本文方法应用于文献的算例,并与文献结果进行对比。图 5(a),为本文方法与文献[11]的对比,其中,文献结果取自文献[11]中的图 6。图 5(b),为本文方法与文献[6]的对比,其中,文献解取自文献[6]中的图 12(a)。总体看来,本文分析方法与文献结果吻合较好,验证了本文方法的正确性。
|
Download:
|
| 图 6 边界条件 Fig. 6 Boundary condition | |
滑行艇底部纵桁位置可视为板条梁的简支支座[6],对应图 6所示的复杂边界形式的板条梁模型。其中,楔形体底升角为10°,斜边长度L=0.951 m,板条梁的厚度为h=10 mm,结构材料的密度为1 840/m3,弹性模量E=240 GPa,流体的密度为1 000 kg/m3。楔形体的冲击速度为5 m/s。P1~P6分别在板条梁的8等分位置。楔形体的斜边方向划分为400等份。通过模态分析,得到各阶模态的振型、固有频率、广义质量、广义刚度信息,如图 7和表 1。这里仅列出前4阶振型。

|
Download:
|
| 图 7 模态振型 Fig. 7 Mode shapes | |
| 表 1 模态信息 Table 1 Modal information |
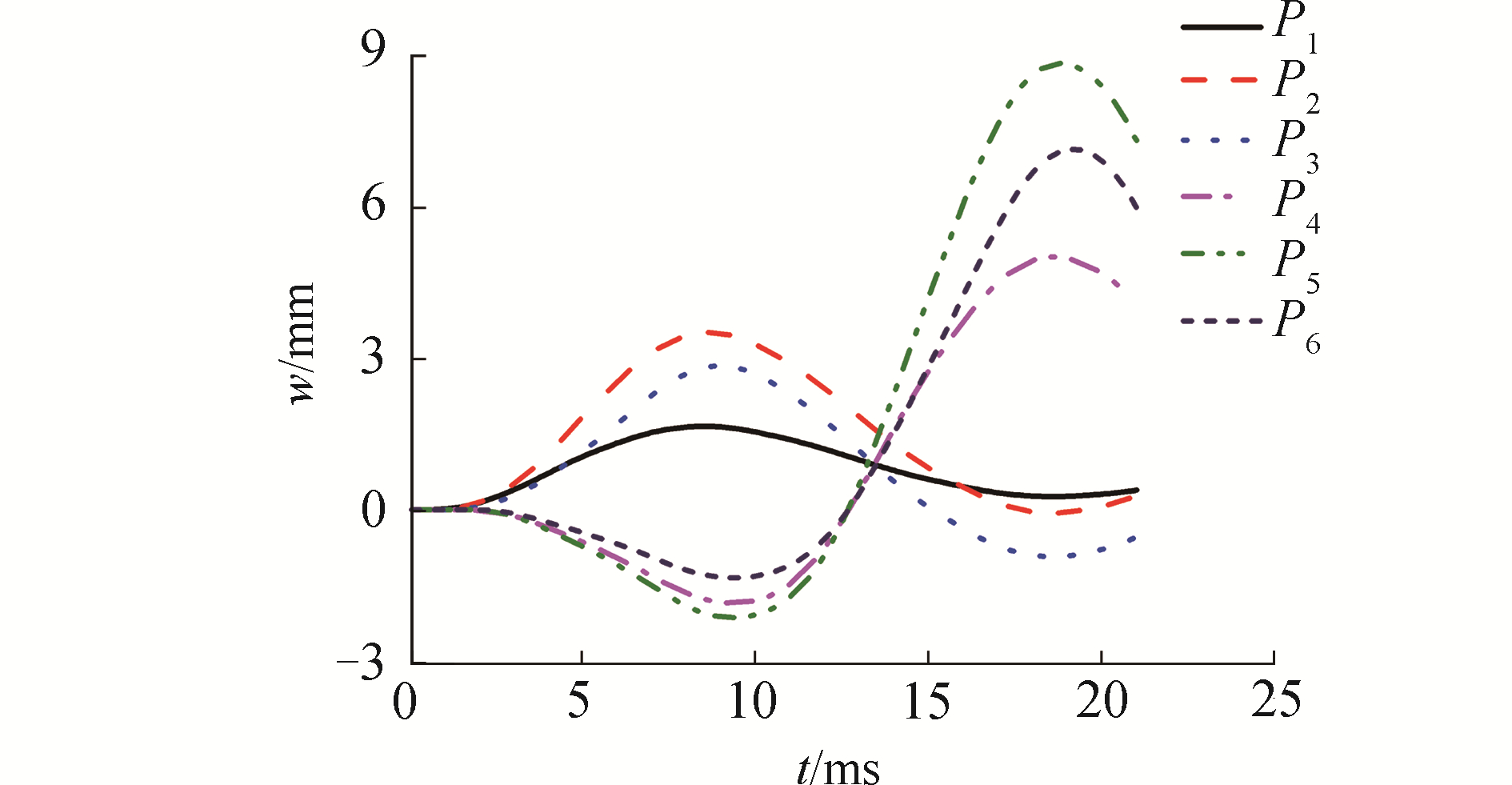
选取前10阶模态用于计算,得到P1~P6位置沿着斜边法线方向的振动位移响应,如图 8。可以看出,在入水冲击的初始阶段,砰击压力主要作用于板条梁的前半段,P1~P3位置产生向上的位移,而受中间简支支座的影响,P4~P5位置产生向下的位移;随着砰击压力逐步作用于板条梁的后半段,P4~P6位置也将产生较大的向上位移。得到各阶振动模态的主坐标,如图 9所示,可以看出,前4阶模态在砰击响应中起到主要贡献作用,第10阶模态主坐标几乎为零,因此,选取前10阶模态已足以反映出入水冲击过程中的楔形体响应特征。
|
Download:
|
| 图 8 位移响应 Fig. 8 Displacement response | |

|
Download:
|
| 图 9 主坐标响应 Fig. 9 Principal coordinate response | |
1) 本文基于Wagner水动力模型和有限元模态信息,系统地建立了二维楔形体入水冲击的水弹性方法。该方法避免了解析结构振型的推导,更加适用于复杂的结构形式。
2) 通过对比不同网格密度和模态数目下的计算结果,验证了该方法的收敛性。通过与文献结果的对比,验证了该方法的正确性。以具有复杂边界形式的楔形体为例,合理地分析了入水砰击过程中的结构振动响应,体现了该方法的优越性。
在当前有限元方法广泛应用的基础上,本文的水弹性方法后续可进一步推广到三维复杂板架结构入水砰击响应的研究,具有较强的工程应用潜力。
| [1] |
FALTINSEN O M. Water entry of a wedge by hydroelastic orthotropic plate theory[J]. Journal of ship research, 1999, 43(3): 180-193. (  0) 0)
|
| [2] |
WAGNER H. Über stoß-und gleitvorgänge an der oberflache von flüssigkeite[J]. Zeitschrift fur angewandte mathematik und mechanik, 1932, 12(4): 193-215. DOI:10.1002/(ISSN)1521-4001 (  0) 0)
|
| [3] |
闫发锁, 董丽娜, 顾学康, 等. 计及流固耦合时楔形结构的冲击压力计算[J]. 哈尔滨工程大学学报, 2007, 28(11): 1202-1205. YAN Fasuo, DONG Li'na, GU Xuekang, et al. Effects of fluid-solid interaction on calculations of slamming pressure for wedged structures[J]. Journal of Harbin Engineering University, 2007, 28(11): 1202-1205. DOI:10.3969/j.issn.1006-7043.2007.11.003 (  0) 0)
|
| [4] |
KOROBKIN A A, KHABAKHPASHEVA T I. Regular wave impact onto an elastic plate[J]. Journal of engineering mathematics, 2006, 55(1/2/3/4): 127-150. (  0) 0)
|
| [5] |
KHABAKHPASHEVA T I, KOROBKIN A A. Elastic wedge impact onto a liquid surface:Wagner's solution and approximate models[J]. Journal of fluids and structures, 2013, 36: 32-49. DOI:10.1016/j.jfluidstructs.2012.08.004 (  0) 0)
|
| [6] |
STENIUS I, ROSÉN A, KUTTENKEULER J. Hydroelastic interaction in panel-water impacts of high-speed craft[J]. Ocean engineering, 2011, 38(2/3): 371-381. (  0) 0)
|
| [7] |
DAS K, BATRA R C. Local water slamming impact on sandwich composite hulls[J]. Journal of fluids and structures, 2011, 27(4): 523-551. DOI:10.1016/j.jfluidstructs.2011.02.001 (  0) 0)
|
| [8] |
PIRO D J, MAKI K J. Hydroelastic analysis of bodies that enter and exit water[J]. Journal of fluids and structures, 2013, 37: 134-150. DOI:10.1016/j.jfluidstructs.2012.09.006 (  0) 0)
|
| [9] |
王文华, 黄一, 王言英, 等. 弹性楔形体各状态参数对入水运动性能的影响[J]. 船舶力学, 2014, 18(11): 1320-1330. WANG Wenhua, HUANG Yi, WANG Yanying, et al. Effect of status parameters for elastic wedge on dynamic performance of water-entry[J]. Journal of ship mechanics, 2014, 18(11): 1320-1330. DOI:10.3969/j.issn.1007-7294.2014.11.007 (  0) 0)
|
| [10] |
李辉.船舶波浪载荷的三维水弹性分析方法研究[D].哈尔滨: 哈尔滨工程大学, 2009. LI Hui. 3-D hydroelasticity analysis method for wave loads of ship[D]. Harbin: Harbin Engineering University, 2009. http: //cdmd.cnki.com.cn/Article/CDMD-10217-1011021322.htm (  0) 0)
|
| [11] |
SHAMS A, PORFIRI M. Treatment of hydroelastic impact of flexible wedges[J]. Journal of fluids and structures, 2015, 57: 229-246. DOI:10.1016/j.jfluidstructs.2015.06.017 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40