船舶操纵性能与船舶的实际营运密切相关,良好的操纵性能可以保证船舶在航行过程中的安全。负责海事安全的国际海事组织于2002年底通过了《船舶操纵性标准》决议[1],对不同船型的操纵性指标做出了规定和安全性建议。船舶设计人员在设计船舶时不仅要满足船舶快速性要求,还要满足操纵性要求。即在船舶设计初期,设计人员需要评估所设计船舶的操纵性能,以降低船舶运营生命周期中出现安全事故的几率。因此在船舶设计的初始阶段,一个准确评估船舶操纵性能的研究方法极其重要。
目前船舶操纵问题的研究有很多种方法,第25届国际拖曳水池会议船舶操纵技术委员会根据已有的研究汇总了主流的船舶操纵性预报方法,主要有直接预报法、基于系统的研究方法和CFD数值模拟方法三种[2]。其中,直接预报的方法包括:根据已有数据库进行插值估算、实船海试和自航模试验等。系统方式的操纵性预报方法则是基于操纵性数学模型,利用预报的水动力系数/导数,获得船舶操纵性指数,该方法主要集中在水动力系数/导数的获取方式上,包括约束船模试验(captive model test)、自航船模试验(free-running ship model test)及系统辨识方法预报等。CFD数值研究主要分为对约束船模和自航船模两种操纵试验的数值模拟。
具体来讲,经验估算方法可以快速地给出船舶的操纵性指标,但受限于已有母型船的试验数据,当船型出现较大的差异时,其预报精度就会存在问题;实船海试可以提供最为可靠精确的操纵数据,但是实船海试成本巨大,并且已有船型不属于船舶设计的范畴,因此应用最为广泛的是船模试验以及数值模拟船模操纵试验两种研究方法,两者均是通过不同的船舶操纵运动响应,预报对应的船舶操纵性能。
船模试验方法包括约束船模试验和自航船模试验。约束船模试验方法,包括静态的斜拖试验(oblique towing test)、动态的平面运动机构试验(planar motion mechanism test)和旋转试验(circular motion test)等。约束船模试验在装备了特定船模控制设备的拖曳水池中完成,可以测量得出一系列的船舶操纵性数学模型中所需的水动力导数值。但该方法需要对船体模型进行大量的强迫运动试验,最终通过操纵性数学模型仿真得到船舶操作性能结果,但是得到的操纵性结果精度与系列试验工况数量及设计息息相关,存在费用与适用性的矛盾。另外,约束船模试验的完成需要对试验方法、结果分析等具有丰富经验的人员才能保证其可信度。自航船模试验方法是采用在一定缩尺比下船体、螺旋桨和舵的模型,螺旋桨旋转速度和舵角的变化通过对应的标准操纵性试验进行控制,实现在物理操纵水池中进行标准操纵试验,如典型Z形操纵试验、自由回转试验等,进而完成船舶操纵性能的预报。该方法能真实反映船模在实际工作环境中操纵性能,因此具有很高的可信性,而且可针对目标问题给出直接的结果。但该方法需要较大的试验水池,精确的螺旋桨和舵的控制系统以及船体六自由度运动测量设备,试验成本高昂。总体而言,船模试验方法目前仍然大部分用于船舶设计的后期验证工作。
通过数值计算方法预报船舶操纵性能由来已久,从船舶操纵运动方程出发的传统的操纵性数学模型方法已经被广泛的应用,且该方法发展的较为成熟。当前,随着高性能计算机的快速发展以及数值方法的日臻完善,计算流体力学(CFD)方法在船舶水动力学领域,尤其是船舶操纵运动的数值预报方面取得了突飞猛进的成果。通过CFD方法进行船舶操纵运动过程中的全粘性流场数值求解,可以给出丰富的流场数据,能够系统地分析操纵运动中船舶的水动力变化,因此该方法具备很大潜力和工程应用前景。本文将从基于CFD方法进行船舶操纵运动数值模拟方面综述其国内外的研究进展,包括约束船模操纵运动数值模拟和自航船模操纵运动数值模拟两个方面。最后,根据现有的CFD数值模拟研究,简述了当前船舶操纵运动数值研究的挑战和未来的研究趋势。
1 约束船模操纵运动数值模拟研究目前,国内外采用粘性流场模拟复杂船型在约束船模操纵试验中的水动力特性,从模拟手段上大致可以分为三种形式,分别为自主开发的CFD程序、通用商业软件以及开源软件平台。(本节将分别从约束船模静态操纵试验和动态操纵运动的数值模拟两个方面进行分别介绍。)
1.1 约束船模静态操纵试验数值模拟研究进展日本的Ohmori[3]基于有限体积法自主开发了求解不可压两相流的CFD求解器WISDAM-V,采用网格整体运动的方法来处理船体的操纵运动,用Density-Function方法来处理自由界面,模拟了两个不同艉部线型的船型SR221 A和SR221B的静态斜拖试验(OTT),考虑了0°、3°、6°和9°四个漂角的工况,并且给出了船体侧向力和转艏力矩的数值和试验的对比结果,初步验证了采用CFD方法数值研究操纵性的可行性,文中并没有给出根据计算结果推导出的水动力导数,但是为数值研究此类问题提供了示范。Tahara等[4]采用自主开发的程序求解非定常RANS方程,湍流模型采用Baldwin-Lomax模型,对S60船型在Fr为0.16及0.36、漂角0°和10°工况下的斜拖试验进行了数值模拟,并且同试验结果进行了对比验证,文中还通过5种不同密度的网格进行了数值的不确定性分析。Hajivand等[5]采用开源OpenFOAM平台,进行了DTMB船模的静态斜拖试验的数值模拟,求解中分别采用的定常求解器LTSInterFoam,非定常求解器interFoam和考虑动网格技术的interDyMFoam求解器进行数值模拟,研究发现定常流动求解器可以更快的达到收敛,但是预报精度最差,考虑浮态变化的动网格求解器精度最高,但是计算最耗时。Abbas等[6]针对大型油轮KVLCC2在6°和12°漂角下的斜拖问题,研究了不同求解模型,如RANS方法结合不同湍流模型(SA模型和k-ω SST模型)、传统的分离涡(DES)方法,以及改进的延迟模式的分离涡(IDDES)方法,对静态斜拖试验数值模拟精度的影响,计算中忽略了自由面的影响,采用开源CFD平台OpenFOAM进行数值计算。根据计算结果发现,RANS方法预报船舶水动力精度可以接受,但是在预报船艉伴流的非定常特性时较差,而IDDES方法则可以捕捉更为精确船艉非定常泻涡特性。
美国爱荷华大学船舶水动力学研究团队基于有限差分法自主开发了船舶水动力学求解器CFDShip-Iowa,并在船舶操纵性领域进行了广泛的应用,Simonsen等[7]采用非定常RANS方法数值模拟了带静态舵的斜拖试验,文中采用k-ω SST湍流模型对Esso Osaka的裸船体模型以及带附体的模型进行了数值求解,计算中忽略自由面的影响。此外,文中对带舵的斜拖试验数值模拟进行了数值不确定性分析,发现尽管斜拖试验的部分工况没有达到收敛性要求,但是当前数值方法总体上可以很好的模拟出斜拖试验过程中的水动力变化。Simonsen等[8]采用同样的求解器在相同工况下进一步研究了带附体船体的流场特性,通过对斜拖工况下船体两侧涡量场的对比分析,可以看出明显的不对称特性,并且可以看出由舭龙骨导致的涡结构。此外,通过不同漂角工况下的计算结果对比,可以看出漂角对摩擦力的影响较小,而对船体表面的压力影响较大。Pinto-Heredero等[9]采用CFDShip-Iwoa求解器进行了Wigley船型在漂角10°~60°的斜拖试验数值模拟,不同于其他学者,文中采用了两相流模型,自由面采用level-set方法进行捕捉,同时文中还分别采用了RANS和DES两种方法进行了数值求解,但是限于当时的计算能力,网格量最大仅为140万,因此文中只是进行了简单的定性上的分析。Ismail等[10]采用同样的数值求解器,分析了不同的对流项离散格式对斜拖试验计算结果的影响,文中试验模型采用KVLCC2油轮,计算中对流项的离散格式分别选用了线性和非线性的总变差减小(TVD)格式,对裸船体模型在0°和12°漂角工况下的斜拖试验进行了数值模拟,得出了对于船舶水动力预报中采用2阶TVD格式可以更精确地预报出船体受力的结论。Xing等[11]同样采用CFD Ship-Iowa求解器对大型油轮KVLCC2进行了不同漂角(0°、12°、30°)的斜拖工况数值模拟,文中湍流解析采用分离涡模型(DES),为了能够更为精确的解析在大漂角斜拖工况下的流动分离现象以及船体周围的精细涡结构,总计算网格量达到了1 300万,计算中仍然采用叠模形式,忽略自由面,同前面Ismail等在160万网格规模上的计算精度对比可以看出显著的提升,证实了采用更为精细的网格和分离涡模拟方法,可以模拟出斜拖工况下的精确伴流场信息。Stern等[12]在总结了当前采用CFD方法数值模拟操纵问题的方法,给出了采用分离涡方法以及更细网格可以给出更为精确的数值求解结果的结论。
国内学者针对静态约束模试验也进行了广泛的研究,田喜民等[13]采用商业软件FLUENT对大型油轮KVLCC2进行了斜拖试验的全粘性流场的数值预报,计算得到了不同漂角时的横向水动力、艏摇力矩、船体表面压力分布及艉流场,通过将计算结果与试验结果进行比较,验证了文中计算方法的有效性,文中分别采用k-ω SST和RNG k-ε两种湍流模式进行了水动力计算及流场数值模拟,通过将其结果与试验结果进行比较,得出了SST模型较RNG模型更为适合于实际船型的斜航运动粘性水动力计算和流场数值模拟的结论。万德成等[14]采用非定常RANS方法对大型油轮KVLCC2船型在不同漂角下的斜拖试验进行了数值模拟,计算中湍流模型采用两方程的k-ω SST模型,并且分别进行了深水和浅水两种工况下的船体周围粘性流场数值计算,模拟出了浅水工况下船体的吸底效应,并且给出了大量的船体周围流场信息,分析了不同漂角,不同水深下的船体水动力变化。王建华等[15]采用上海交通大学船海计算水动力学研究中心(CMHL)基于开源CFD平台OpenFOAM自主开发的面向船舶与海洋工程的水动力学求解器naoe-FOAM-SJTU,数值模拟了某船型在6个漂角工况(2°、4°、6°、8°、10°和12°)下的斜拖试验,计算中采用非定常RANS方法,湍流模型采用k-ω SST模型,精确地预报了在斜拖工况下的船体侧向力、转艏力矩等,并且预报的水动力导数值同试验结果吻合良好,验证了当前方法对静态约束模试验数值模拟的可靠性,并对不同漂角下的船体泻涡进行了分析,如图 1所示。冯松波等[16]采用商业软件FLUENT对KVLCC2模型进行了0°和12°两种工况下的斜拖试验数值模拟,计算中压力速度耦合采用SIMPLEC算法,湍流模型采用RNG k-ε模型,文中给出了三套不同网格密度的数值计算结果,并进行了网格收敛性分析,数值模拟中考虑了舵角为0时不同漂角下以及不同舵角、不同漂角下作用在船-舵系统上的横向力和转艏力矩,并对计算结果进行了分析。刘义等[17]采用商业软件STAR CCM+进行了标准船模KCS在不同漂角下的斜拖试验数值模拟,计算了不同舵角工况,并且计算模型中考虑了船舶的升沉和纵摇运动,通过对比固定船体运动的数值预报结果发现,考虑真实斜拖试验中船舶的浮态变化,可以更高精度的预报船体受到的水动力。
从斜拖试验的CFD数值模拟研究现状可以看出,国外采用自主开发的CFD求解器进行该问题的研究较为广泛,自主开发程序可以针对特定问题进行求解器的适应性改造,例如开发适用于大漂角斜拖工况下对应大分离流动更为精确的DES求解模型,提高数值预报精度。而国内大部分的研究还仍然基于商业软件进行,不利于对特定问题进行深入的求解分析。而目前采用开源的CFD软件平台,如OpenFOAM,也可以利用平台已有的基本数值离散格式和算法,根据问题需求进行求解器的升级改造,从而更有针对性的进行深入研究分析,因此采用这种方式的研究越来越多。
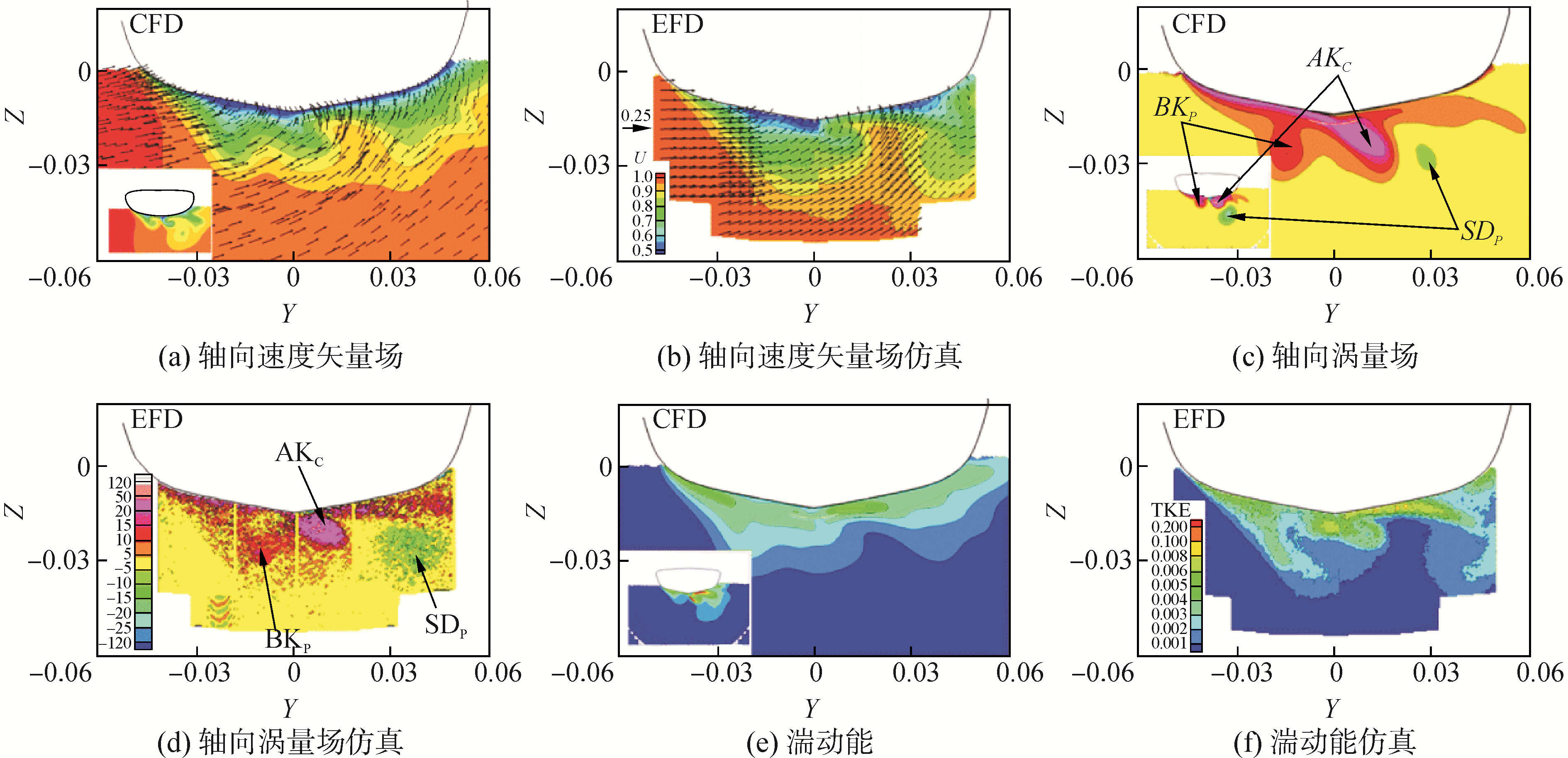
1.2 约束船模动态操纵运动数值模拟研究进展约束船模动态操纵运动包括平面运动机构试验中的纯横荡试验(pure sway test)、纯摇艏试验(pure yaw test)等。动态试验更为复杂,要求精确的预报出整个动态操纵运动过程中的船舶水动力变化,因此对数值计算要求更高。采用CFD手段对动态约束模试验的研究可以考虑在复杂操纵运动过程中船体周围的粘性效应,进而提升整体的水动力预报精度,因此粘性CFD数值预报可以作为一种有效的研究手段补充或者替代初步设计阶段的模型试验。国际上针对此类动态约束船模操纵运动提供了大量的标准船模试验数据,可以用于CFD数值模拟方法预报精度的验证,如国际船舶操纵运动数值模拟方法研讨会SIMMAN会议,针对标准船模大型邮轮KVLCC1/KVLCC2、集装箱船KCS和水面舰船DTMB5415,提供了多家单位的约束船模操纵试验数据,用于不同研究单位基于CFD方法进行的操纵运动数值模拟的结果对比。Cura-Hochbaum等[18]对KVLCC1的油轮模型进行了基于RANS方法的动态约束船模操纵运动试验数值模拟,预报了对应的水动力导数,并且通过水动力导数,基于操纵性模型模拟得出了自由回转和Z形操纵运动的轨迹,同自航模试验结果吻合较好,验证了采用RANS方法进行数值预报操纵运动的可靠性。Simonsen等[19]利用自主开发求解器CFDShip-Iowa,数值模拟了静态和动态PMM试验,并且分别采用CFD计算得的和试验测量得到的水动力导数,根据分离型操纵性数学模型,对KCS船模在静水中的回转操纵和Z形操纵试验进行模拟。Sakamoto等[20-21]针对国际操纵性研讨会提供的标准船模DTMB5415,采用自主开发程序CFDShip-Iwoa进行了静态和动态的PMM试验数值模拟,数值预报得到的操纵运动相关的水动力导数,并且同试验结果进行对比分析,给出了数值结果的验证与确认,通过系列的PMM试验数值仿真,表明大部分线性水动力导数数值预报精度较高,同试验值的误差在10%以内,而非线性水动力导数的预报结果同试验值误差较大。同时,文中还对不同形式操纵运动下的详细流场信息进行了分析,如图 2所示,包括自由面兴波、船体周围涡量场等。通过局部流场的变化解释了不同操纵运动过程中的水动力变化。Kim等[22]采用自主开发的基于RANS方法的求解器SHIP_Motion模拟了KCS船模不同形式的平面运动机构试验,包括动态纯横荡试验和纯摇艏试验,数值计算中湍流模型采用动态亚格子DSGS模型,计算网格为结构化网格,有限体积法进行空间离散。数值预报的静态试验和动态纯横荡试验的水动力导数值同试验结果吻合良好,但是纯摇艏试验的预报结果有一定误差。Jin等[23]针对标准船模KVLCC2的纯横荡运动进行了CFD数值模拟,计算采用商业软件STAR CCM+,研究中侧重于分析了不同船模尺度对预报结果的影响,并且进行了实尺度的数值模拟。通过研究发现,船模尺度下的流场更容易受湍流模型的影响,即数值粘性的不精确导致的误差。RoyChoudhury等[24]采用商业软件SHIPFLOW进行了KVLCC2船模纯摇艏和带漂角摇艏等多种操纵运动的数值模拟,并且研究了深水和浅水两种工况下操纵运动过程中的水动力特性,探讨了CFD方法在不同水深操纵运动数值模拟的可行性。
|
Download:
|
| 图 2 纯首摇操纵运动中尾部伴流场数值模拟结果同试验值对比[21] Fig. 2 Wake flow comparisons between CFD and experiments during pure yaw test[21] | |
近些年来,国内也有很多学者进行了动态约束模试验的数值研究。杨勇等[25]通过求解非定常RANS方程,选取k-ω SST湍流模型,采用全六面体网格进行离散,在忽略自由面兴波影响的情况下,对KVLCC1裸船体在深水和浅水中的PMM试验纯横荡运动粘性流场进行了数值模拟,计算了作用在船体上的水动力和力矩,通过将计算结果与现有的试验数据对比,验证了文中方法的有效性,在此基础上,根据水动力和力矩计算结果,计算得到了船舶横荡运动线性水动力导数。程捷等[26]通过商业软件FLUENT提供的动网格功能对DTMB5415模型的平面运动机构试验中的动态纯横荡和纯摇艏试验进行了数值模拟,忽略了自由面兴波,计算得到的侧向力及转首力矩的变化与实验结果趋势一致,但是鉴于忽略自由面、固定船体纵倾和升沉等简化,预报精度有待提高。刘小健等[27]对不同航速和水深工况下的船舶纯横荡试验进行了数值模拟,数值计算采用基于OpenFOAM开发的水动力学求解器naoe-FOAM-SJTU,求解非定常RANS方程,湍流模型为k-ω SST模型,采用动态变形网格处理船体横荡运动,计算结果表明在浅水工况下船舶的侧向力和转首力矩会明显增大,数值预报水动力变化趋势同试验结果保持一致,但动态变形网格处理船舶的大幅操纵运动导致预报结果同试验值有一定偏差。王建华成等[28]采用自主开发的结合重叠网格技术的船舶水动力学求解器naoe-FOAM-SJTU,模拟了标准船模DTMB5415的纯摇艏操纵运动,其中采用重叠网格技术模拟船舶的大幅度操纵运动,并且放开船体的纵倾和升沉运动,同试验保持一致,模拟了最大摇艏角度为10.2°工况下的三种纯首摇操纵运动,其中通过调整横荡和首摇运动的相位达到纯摇艏工况对应的每个时刻船体坐标系下没有侧向速度的要求,数值预报的相关水动力导数通过最小二乘法回归获得,CFD求解得到的线性水动力导数与试验值相比误差在10%以内,非线性水动力导数值误差在20%以内,达到了国际上的同等预报水平。刘晗等[29]基于计算流体力学技术对限宽水域中的平面运动机构试验进行了数值模拟,在对有限宽度水域的PMM试验的动态模拟上,使用了混合动网格技术,数值计算结果与循环水槽PMM试验结果对比证明采用该方法有效,继而模拟不同宽度水域中的PMM试验,分析船舶水动力随运动速度变化的关系,结果表明,限宽水域中水动力随运动速度变化的非线性特征更为显著,船舶操纵加速度导数增大,该研究为限制水域的平面运动机构试验提供了参考。郭海鹏等[30]采用商业软件STAR CCM+数值模拟了标准船模ONRT的旋转试验、静态斜拖试验和纯横摇试验的操纵运动,数值回归得到了操纵性水动力导数值,并且用四自由度的MMG模型仿真出了船舶的25°自由回转和20/20 Z形操纵运动,预报的运动轨迹同试验值吻合良好,验证了采用CFD方法数值模拟约束船模操纵运动试验得到的操纵性导数值的可靠性。
通过上述动态约束船模操纵运动的数值模拟研究进展来看,基于RANS方程配合k-ω SST湍流模型求解的CFD方法应用最为广泛,通过数值模拟结果同试验数据的对比,验证了采用自主开发的CFD软件,商业软件以及基于开源平台进行二次开发的求解器均可以较好的进行船舶操纵运动的数值模拟。并且数值模拟中考虑船舶的升沉和纵倾变化可以得到更好的预报结果,相对于传统的动态变形网格方法,动态重叠网格在进行大幅度的船舶操纵运动数值模拟中预报精度更高。
2 自航船舶操纵运动数值模拟研究通过CFD数值模拟自航船舶的不同操纵运动可以预报出船舶的运动轨迹、典型操纵参数,如超越角、纵距、横距等,直接反映船舶的操纵性能。因此自航船舶的操纵运动数值模拟研究是目前的研究热点。基于CFD方法的自航船舶操纵运动数值模拟的技术难题是如何进行船桨舵系统复杂运动和流场的同时求解,而船桨舵系统中船后尾流场中旋转螺旋桨的直接数值模拟则最为复杂和耗时。从现有的研究来看,自航船舶操纵运动的CFD数值模拟研究从对螺旋桨模拟形式的不同,大致可以分为不依赖螺旋桨几何模型的体积力方法和直接构建螺旋桨几何模型进行模拟的两种方法,而第二种方法中又可以根据不同的动网格处理方式分为滑移网格法和重叠网格方法。
2.1 体积力方法传统的体积力方法,一般是在动量方程中添加源项,替代螺旋桨旋转对周围流场的影响。体积力的计算方法有叶素动量理论(blade element momentum)、等推力面模型(equivalent thrust disk)、升力面和升力线模型(lifting-surface/line)等。螺旋桨体积力模型简单易实施,并且计算量小,因此被广泛应用到船舶自航推进和操纵运动的数值模拟。Stern等[31]将船舶艉部流场和螺旋桨考虑为一个轴对称的控制体,采用基于升力面模型的体积力方法进行了带螺旋桨船舶的数值计算。Kawamura等[32]采用类似的方式,通过迭代法实现了船和螺旋桨之间相互配合的数值模拟。Choi等[33-34]采用商业软件FLUENT和开发的螺旋桨体积力模型,对多种船型进行了带螺旋桨船舶的自航推进计算。Phillips等[35]实现了基于叶素动量理论的螺旋桨体积力模型同RANS方程的结合,并且进行了固定舵角下的KVLCC2船和桨的配合计算,预报了船舶操纵性数学模型中的水动力系数值。Phillips等[36]采用三种不同形式的螺旋桨体积力模型,等推力面模型、Hough和Ordway体积力模型和叶素动量理论体积力模型,研究了螺旋桨和后面舵的水动力特性,采用等推力面模型,由于忽略了桨的扭矩,因此预报的桨后舵的阻力精度很差,因此不推荐采用此种体积力模型,Hough和Ordway体积力模型和叶素动量理论体积力模型均可以准确的预报出舵面上的压力分布,但是前者只适用于桨对舵的影响研究,而不能计及舵对桨的影响,而叶素动量理论和RANS方法的耦合方式可以考虑到桨舵间的相互影响,因此更适用于船桨舵配合下的自航船舶水动力性能研究。Simonsen等[37]采用基于势流理论的体积力模型替代船后螺旋桨,采用迭代方式实现RANS方法流场和螺旋桨体积力的耦合求解,并且将该方法应用到带附体的油轮Esso Osaka的操纵运动数值求解,并且分析了船、桨、舵间的相互干扰情况,为自航船舶操纵性的研究提供了可行性示范。Carrica等[38]同样采用文献[31]的体积力模型,数值计算采用CFDShip-Iowa V4,湍流模型采用混合k-ω和k-ε模型,自由面采用Level-set方法进行捕捉,采用动态重叠网格技术处理大幅度的船舶操纵运动,模拟了不同航速下(Fr=0.25,Fr=0.41)的自由回转(35°舵角)和Z形操纵(20/20),同时进行了波浪工况下的计算,文中数值预报的操纵性参数同试验值的误差在10%以内,指出预报误差的主要原因在于简化的螺旋桨体积力模型,简化模型忽略了由于真实旋转桨导致的对船体运动的阻尼以及桨受到的侧向力影响等。Dubbioso等[39]采用自主开发的CFD求解器χnavis数值模拟了双桨双舵的船型Z形操纵运动,数值计算中采用有限体积法进行空间离散,数值求解非定常RANS方程,湍流模型采用一方程的SA模型,螺旋桨采用改进的体积力模型,修正了由于舵影响导致的桨水动力变化,数值模型了典型20/20 Z形操纵,对比了数值预报的超越角同试验值的差别,第一超越角同试验值吻合良好,但是第二超越角预报结果偏大,证实了修正形式的螺旋桨体积力模型还有待改进。Broglia等[40-41]采用上述改进的螺旋桨体积力模型,分别进行了单独舵和双舵情况下的双桨推进船舶的自由回转试验数值模拟,数值模拟得到的船体运动轨迹同试验进行了对比,误差在10%以内,证实了通过改进的体积力模型改善船舶操纵运动数值预报精度,文中同时分析船体不同部分对操纵运动中的水动力贡献。
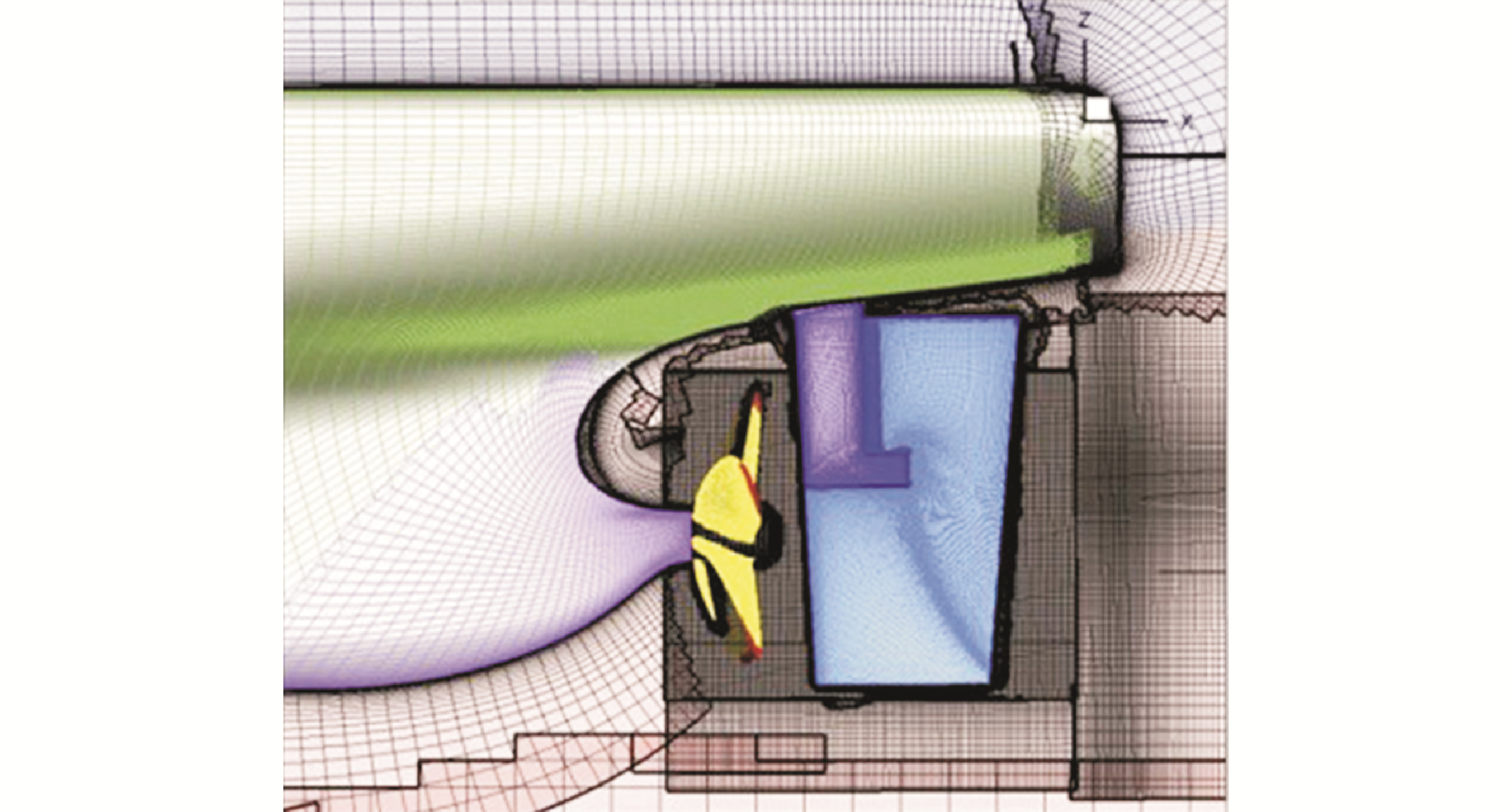
Mofidi等[42]实现了基于涡格法(vorice lattice method)的升力面螺旋桨体积力求解模型PUF-14,同CFD求解器REX相结合,每个时间步内进行CFD流场数据同螺旋桨区域的交互,可以充分考虑船艉伴流的变化以及船桨间的干扰。该方法与直接模拟旋转螺旋桨情况下KCS船模Z形操纵运动结果进行对比,通过详细的桨舵周围伴流分布,如图 3所示,发现该方法可以较为精确的捕捉操纵运动过程中的船桨舵间的干扰。体现出了开发精确的体积力模型进行自航船舶操纵运动的数值模拟具有很高的可靠性。

|
Download:
|
| 图 3 考虑伴流干扰影响的体积力模型数值模拟伴流场结果同旋转螺旋桨模拟结果对比[42] Fig. 3 Comparisons of wake flow between improved body force model and fully discretized propeller model[42] | |
体积力方法由于不需要进行真实螺旋桨转动的数值模拟,因此该方法不需要划分螺旋桨的网格,计算所需的网格量显著减小,时间步长也可以放大,有利于对此类问题进行快速的数值预报。但是采用这种方法应该考虑更为精确的体积力模型,充分考虑到船艉伴流的不均匀性以及船和舵对桨的干扰,从而最大程度上还原船体和舵对螺旋桨的流场干扰,提高整体数值计算精度。
2.2 滑移网格方法由于体积力方法在计算精度上的有一定的缺陷,因此想要获得更为精确的船桨舵配合下的船舶操纵运动数值预报,需要直接构建螺旋桨模型,进行旋转螺旋桨的数值模拟。通过直接对船体、螺旋桨和舵进行网格的划分,进行船体运动和船后螺旋桨和舵等转动的数值计算,从而精确预报船、桨、舵周围流场干扰和水动力变化。随着高性能计算平台的飞速发展以及数值方法的日臻完善,对船桨舵系统的直接离散化求解已经成为现实。
滑移网格(sliding mesh)方法是目前广泛采用的螺旋桨网格运动求解方法。该方法对螺旋桨周围划定一个控制域,一般为圆柱体,圆柱体表面作为滑移边界连接内部旋转域和外部的固定域,通过这个滑移边界实现旋转螺旋桨的网格同外部船体网格的连接,并完成流场信息传递。除此之外,常用的螺旋桨计算方法中的多重参考系(MRF)方法与滑移网格方法类似。该方法同样是分区域进行计算,移动区域内设置旋转坐标系,但在计算中该区域内网格没有发生旋转运动。多重参考系方法计算时收敛速度快,但是由于计算的是稳态流动,无法对螺旋桨的非定常流动进行模拟,因此计算精度要低于滑移网格方法。目前,采用滑移网格技术实现船后螺旋桨转动的数值模拟研究较多。
Lübke[43]使用商业软件CFX和滑移网格方法对一固定姿态的KCS船型在不考虑自由面的工况下进行了带螺旋桨的自航计算。Queutey等[44]针对哥德堡船舶CFD研讨会上的标准算例,采用自主开发的CFD求解器ISIS-CFD求解流场,计算中采用同位网格技术,有限体积法离散求解RANS方法,结合采用滑移网格方法模拟船后螺旋桨的转动,对固定姿态的KCS进行了自航的数值模拟,与Lübke数值计算不同的是,这里考虑了自由面的影响,自由面通过VOF方法进行捕捉,此外,数值模拟中采用了自适应网格加密技术,改进了计算的精度。Seo等[45]使用通用商业软件FLUENT,采用混合形式网格划分方法,即船艏部和艉部以及螺旋桨周围采用非结构网格,其他部分采用结构化网格,并且采用滑移网格方法实现船后螺旋桨的转动,自由面求解采用VOF方法结合高精度离散算法,数值预报的伴流分数和推进系数同试验值吻合较好。Badoe等[46]基于开源CFD平台OpenFOAM进行了船桨舵配合下的数值模拟研究,其中桨的转动通过滑移网格技术实现,计算中进行了不同漂角下的数值模拟,分析了不同来流对船后桨舵干扰间的影响,初步实现了对船桨舵配合下的操纵运动的数值仿真。Moctar等[47]采用滑移网格方法分别构建直接旋转的螺旋桨和舵计算网格,滑移界面均为圆柱面,如图 4所示,进行了双桨双舵DTC船模Z形操纵运动的直接数值模拟,并且对比了采用滑移网格方法和MRF方法进行螺旋桨模拟方式对计算结果的影响,证实了采用滑移网格方法进行船桨舵配合下的大幅度操纵运动直接数值模拟的可行性。
国内在采用滑移网格方法进行船桨舵配合数值模拟研究也有很多相关的工作,张志荣[48]分别使用体积力模型(Hough和Ordway模型)和滑移网格法求解螺旋桨处流场,数值计算采用商业软件FLUENT,对KCS船型的船、桨配合进行数值计算,并进行了详细的数值不确定性验证和确认分析,证实了CFD方法在数值预报船桨配合问题上的可靠性。沈海龙等[49]基于分离涡(DES)模型和滑移网格方法,对带桨的KCS船进行了数值模拟,得出了船体和螺旋桨的相互干扰,对湍流边界层影响不大,但是对船体和桨叶上的表面压力分布影响较大的结论。沈兴荣等[50-51]均应用FLUENT软件的滑移网格技术,进行了带螺旋桨带舵船舶的全粘性流场计算。
目前,滑移网格方法作为一种有效的研究手段,已经被广泛地应用于船、桨、舵配合的数值计算中,具有较高的数值预报精度,可以精确地捕捉船、桨、舵之间的粘性流场干扰,但是现有基于滑移网格的研究大部分仍然采用通用的商业软件,并且只是针对较为简化的固定航线的自航运动数值预报。由于船舶六自由度运动同船后桨和舵的滑移网格区域结合需要对软件进行大规模的程序改造,而商业软件的封闭性限制了这方面的发展,因此在自航船舶操纵运动中的应用还很少。但是已有学者通过自主开发的程序实现了基于滑移网格技术进行自航船舶操纵运动直接数值模拟,因此说明该方法未来在船舶操纵运动数值模拟研究中有很大的发展潜力和空间。
2.3 重叠网格方法在现有研究当中,重叠网格方法在船、桨、舵配合以及三者运动耦合直接数值模拟中应用最为广泛。它不仅能够处理船体的六自由度运动,还能在船体运动的基础上同时处理螺旋桨和舵的旋转运动。Carrica等[52]结合重叠网格的水动力学求解器CFDShip-Iwoa,实现了自航船舶操纵运动的数值模拟,直接构建基于几何体的船体、螺旋桨和舵离散模型,采用重叠网格方法处理自航操纵运动工况下的船桨舵耦合运动,进行了KVLCC船型的Z形操纵运动和自由回转运动的数值模拟。Mofidi等[53]采用同样的求解器和数值方法进行了典型10/10 Z形操纵试验和修正型的15/1 Z形操纵试验的数值模拟,数值预报的船体运动及操纵性参数同试验结果吻合良好,并且对自航操纵运动过程中的详细流场进行了分析,指出更为精确的流动求解模型可以提高船舶操纵运动的预报精度。
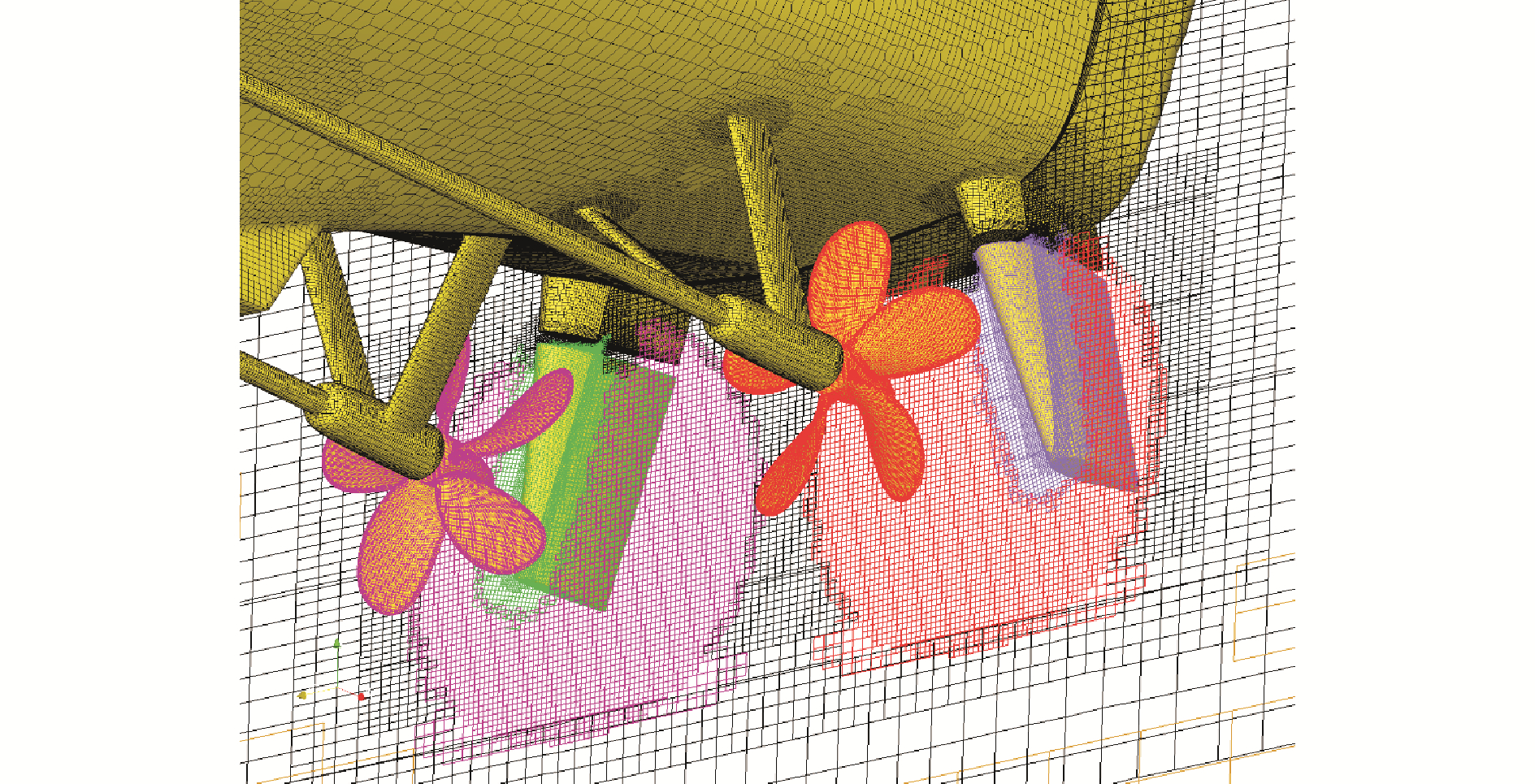
Broglia等[40-41]分别进行了单独舵和双舵情况下的双桨推进船舶的自由回转试验数值模拟,舵和船体的运动则采用动态重叠网格进行处理,数值模拟得到的船体运动轨迹同试验进行了对比,同时对比了单舵和双舵情况下的自由回转运动轨迹以及回转降速、漂角和横摇等历时曲线,分析了整个回转运动过程中的舵力和船体、附体侧向力变化,文中指出在双桨情况下,舵的存在会强烈干扰螺旋桨所受到的载荷。Carrica等[54]采用重叠网格方法实现了对浅水工况下的大型集装箱船KCS船桨舵配合下的自航和修正型20/5 Z形操纵试验的直接数值模拟,并且文中首次完成了对基于重叠网格技术的船桨舵配合数值模拟的网格收敛性验证,使用的三套计算网格量分别为870万、2 460万和7 130万,计算网格分布如图 5所示。并行规模达到500核以上,网格收敛性研究表明对自航数值模拟呈现一致收敛,但是针对Z形操纵工况,部分参数呈现出振荡收敛的情况,甚至部分参数没有达到收敛性要求,证实了进行基于重叠网格方法的自航船舶操纵性网格收敛性研究较为困难。
前文的研究学者,不论是基于有限差分求解器,还是有限体积的求解器,都是采用基于结构化网格的重叠网格技术,沈志荣等[55]在OpenFOAM中引入了适用于全非结构化网格的重叠网格模块(见图 6),开发了船舶水动力学求解器naoe-FOAM-SJTU,该求解器实现了流场求解进程和重叠网格插值信息计算进程的并行化求解,并且应用到KCS带桨自航和Z形操纵运动的数值模拟,验证了在相对较为粗糙的非结构网格情况下也可以得出较为精确的预报结果。王建华等[56]在此基础上,进行了全附体双桨双舵ONRT船模的自由自航试验,并进行了35°舵角工况下的自由回转试验数值模拟,预报的自航点和回转操纵性特征参数同试验结果吻合良好,进一步验证了naoe-FOAM-SJTU求解器对全附体船,尤其是双桨双舵船型自航操纵问题的适用性。
目前,部分学者将重叠网格方法应用到了波浪中的操纵运动数值模拟研究。Carrica等[38]实现了波浪工况下自航船舶的自由回转和Z形操纵运动的数值模拟,但是其中桨的模型仍是采用的是体积力模型。王建华等[57]采用自主开发的三维数值造波消波模块实现了船桨舵配合下在迎浪工况下的直接数值模拟,数值预报的船体运动响应,航速等参数同东京2015年CFD船舶水动力学研讨会上所提供的试验数据吻合良好,拓展了naoe-FOAM-SJTU求解器在波浪中自航的应用功能。
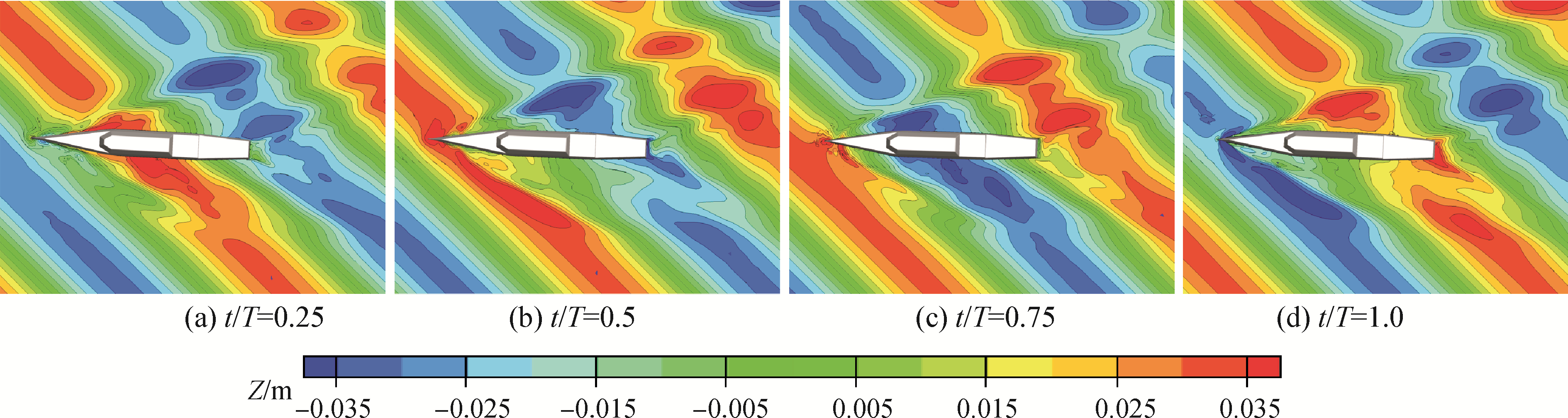
王建华等[58]在自主开发的水动力学求解器naoe-FOAM-SJTU基础上,基于重叠网格技术和多级物体运动模块开发了船舶航向保持控制器,并且研究了不同浪向下自航船舶艏向角变化以及通过自动舵控制实现航向保持的性能,将现有的自航船舶操纵运动数值模拟扩展到了复杂的波浪工况中(见图 7、8)。Shen等[59]实现了自航船舶在迎浪和艉斜浪工况下的航向保持数值模拟,并且同东京CFD研讨会上的标准船舶试验数据进行了对比,验证了重叠网格处理大幅度船舶操纵运动的可靠性。王建华等[60]采用自主开发naoe-FOAM-SJTU求解器,实现了全附体船舶ONRT在波浪工况下的Z形操纵运动的直接数值模拟,并且同静水工况下的自航船舶Z形操纵数值预报结果进行了对比,探究了波浪对Z形操纵运动的影响。
|
Download:
|
| 图 7 自航船舶在首斜浪工况一个波浪周期内自由面变化[58] Fig. 7 Wave elevation of free running ship in bow quartering waves in one wave period[58] | |
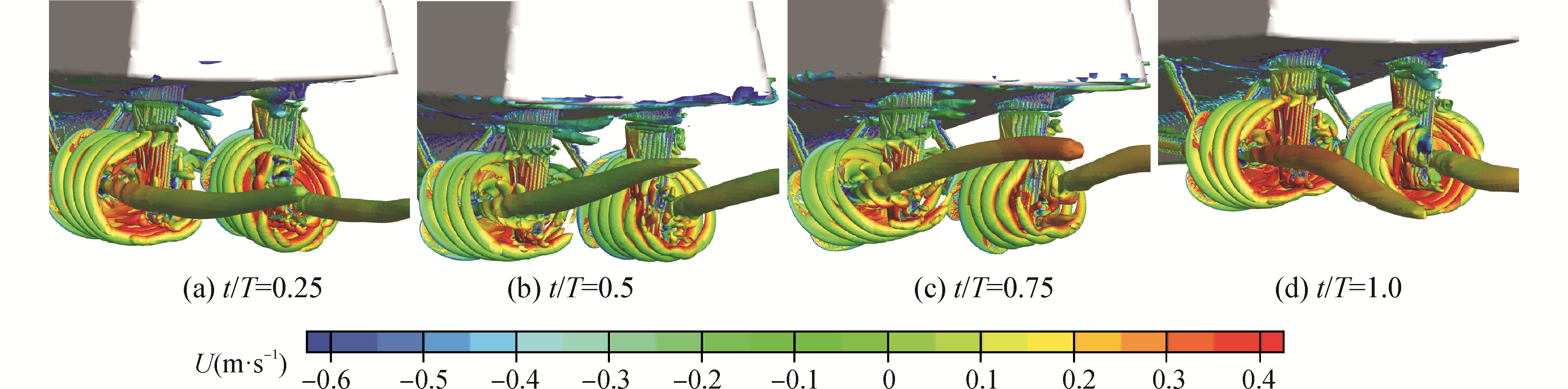
|
Download:
|
| 图 8 自航船舶在首斜浪工况下一个周期内船桨舵周围涡量场变化[58] Fig. 8 Vortical structures around ship hull propeller and rudder in one wave period[58] | |
根据上述研究学者基于重叠网格技术进行的船、桨、舵耦合运动以及自航操纵运动数值模拟的研究成果,证明了基于重叠网格技术的CFD数值模拟方法在自航船舶操纵运动数值预报中应用最为广泛也最为适用,同时具有较高的预报精度,是目前最具发展潜力和工程应用前景的研究方法。
3 总结和研究展望综合当前基于CFD方法的船舶操纵操纵运动数值模拟研究进展,国内外研究学者在约束船模操纵运动试验的数值模拟方面开展了深入的研究。其中,约束船模静态操纵试验数值研究开展较早,约束船模动态操纵运动的数值模拟研究也已经广泛的开展。从CFD数值模拟研究的方法来看,国外采用自主开发的CFD软件进行操纵运动的研究较为广泛,自主开发程序可以针对特定问题进行求解器的适应性改造,提高数值预报精度。而一般商业软件只提供部分的用户接口,无法对软件进行深度的适应性改造,不利于对特定问题进行深入的求解分析。目前采用开源的CFD软件平台,例如OpenFOAM,进行船舶操纵运动数值模拟的研究逐渐增多,该方式可以利用平台已有的基本数值离散格式和算法,根据问题需求进行求解器的功能拓展,例如复杂操纵运动求解模块、高精度的湍流求解模型等,从而更有针对性的进行深入研究分析。从采用的数值方法来看,流场求解从最初的准定常方法转向非定常流场求解,在操纵运动数值模拟中,除去平面的操纵运动之外,考虑船舶的升沉和纵倾运动可以有效的提高精度;RANS方法结合两方程的k-ω SST湍流模型在数值模拟中应用最为广泛,但是目前混合RANS/LES方法,也称为分离涡模拟(DES)方法,由于其可以更为精确的预报操纵运动中大流动分离现象,因此得到了更多的应用;计算所用的网格量也从百万量级逐渐转向千万量级。但是,由于约束船模操纵运动属于间接的操纵性研究方法,需要结合操纵性数学模型才能够完整的预报船舶的操纵运动参数,因此,基于CFD方法的船舶操纵运动逐步转向带桨带舵的自航船舶操纵运动数值模拟研究方面。
基于CFD方法进行自航船舶操纵运动数值模拟的三种方法中,简化的体积力模型,不需要构建旋转螺旋桨网格,可以显著减小计算量,能够进行快速的船舶操纵运动数值预报,但是传统的简化体积力模型,没有考虑船艉伴流同螺旋桨间的干扰,因此预报精度受限。但是现在的螺旋桨体积力模型正在逐渐改进完善,通过CFD数值计算和螺旋桨求解的交互,充分考虑到船艉伴流的不均匀性,从而最大程度上还原船体和舵对螺旋桨的流场干扰,提高整体数值计算精度,因此发展更精确的螺旋桨体积力模型是未来进行自航船舶操纵运动数值预报的高效手段。
滑移网格方法通过滑移界面,可以实现船后螺旋桨和舵的转动模拟,目前采用该方法的研究更多的用于处理准定常运动轨迹下的船桨舵配合研究,不过已经有国外学者实现了基于滑移网格方法的船桨舵配合下自航船舶操纵运动的数值模拟,因此该方法在未来带桨带舵船舶操纵运动的数值模拟研究中仍然具有较大的发展潜力。
目前为止,重叠网格方法在自航船舶操纵运动数值模拟研究中应用最为广泛,数值预报精度较高,能够最大程度上的还原操纵运动中船桨舵相互干扰,但是当前由于重叠网格方法涉及到插值信息的计算,因此并行计算效率相对于其他方法较低,并且由于要对船桨舵所有运动部件进行网格划分,计算量较大,存在计算效率不足的情况,未来需要开展对该方法在并行计算效率优化的研究。
当前国内外研究学者基于CFD方法进行自航船舶操纵运动数值预报的研究主要集中在静水工况下,第28届ITTC会议中,专门成立了波浪中操纵性专业委员会[61],强调了波浪中操纵问题的重要性,该问题也是未来船舶水动力学领域重要的研究方向。因此,基于CFD方法数值模拟研究接下来的研究方向应该是波浪中船舶的操纵运动的数值预报,并且进行这种复杂工况数值计算的不确定性分析。此外,船桨舵配合下的复杂流场的细节分析仍需要进行流场求解模型的进一步完善;同时现有的研究中,针对船舶操纵运动的数值模拟仍停留在模型尺度,未来应该发展实尺度下的船舶操纵运动的数值模拟方法,构建超高雷诺数流动的湍流求解模型,研究实尺度下操纵运动特性,更好的为船舶设计服务。
| [1] |
IMO. MSC. 137(76), Standards for ship manoeuvrability[S]. IMO, 2002.
(  0) 0)
|
| [2] |
ITTC. Final report and recommendations to the 25th ITTC[C]//Proceedings of the 25th International Towing Tank Conference. Fukuoka, Japan, 2008.
(  0) 0)
|
| [3] |
OHMORI T. Finite-volume simulation of flows about a ship in maneuvering motion[J]. Journal of marine science and technology, 1998, 3(2): 82-93. DOI:10.1007/BF02492563 (  0) 0)
|
| [4] |
TAHARA Y, LONGO J, STERN F. Comparison of CFD and EFD for the Series 60 CB=0.6 in steady drift motion[J]. Journal of marine science and technology, 2002, 7(1): 17-30. DOI:10.1007/s007730200010 (  0) 0)
|
| [5] |
HAJIVAND A, MOUSAVIZADEGAN S H. Virtual simulation of maneuvering captive tests for a surface vessel[J]. International journal of naval architecture and ocean engineering, 2015, 7(5): 848-872. DOI:10.1515/ijnaoe-2015-0060 (  0) 0)
|
| [6] |
ABBAS N, KORNEV N. Validation of hybrid URANS/LES methods for determination of forces and wake parameters of KVLCC2 tanker at manoeuvring conditions[J]. Ship technology research, 2016, 63(2): 96-109. DOI:10.1080/09377255.2016.1157275 (  0) 0)
|
| [7] |
SIMONSEN C D, STERN F. Verification and validation of RANS maneuvering simulation of Esso Osaka:effects of drift and rudder angle on forces and moments[J]. Computers & fluids, 2003, 32(10): 1325-1356. (  0) 0)
|
| [8] |
SIMONSEN C D, STERN F. Flow pattern around an appended tanker hull form in simple maneuvering conditions[J]. Computers & fluids, 2005, 34(2): 169-198. (  0) 0)
|
| [9] |
PINTO-HEREDERO A, XING T, STERN F. URANS and DES analysis for a Wigley hull at extreme drift angles[J]. Journal of marine science and technology, 2010, 15(4): 295-315. DOI:10.1007/s00773-010-0092-z (  0) 0)
|
| [10] |
ISMAIL F, CARRICA P M, XING T, et al. Evaluation of linear and nonlinear convection schemes on multidimensional non-orthogonal grids with applications to KVLCC2 tanker[J]. International journal for numerical methods in fluids, 2010, 64(8): 850-886. (  0) 0)
|
| [11] |
XING T, BHUSHAN S, STERN F. Vortical and turbulent structures for KVLCC2 at drift angle 0, 12, and 30 degrees[J]. Ocean engineering, 2012, 55: 23-43. DOI:10.1016/j.oceaneng.2012.07.026 (  0) 0)
|
| [12] |
STERN F, AGDRUP K, KIM S Y, et al. Experience from SIMMAN 2008-the first workshop on verification and validation of ship maneuvering simulation methods[J]. Journal of ship research, 2011, 55(2): 135-147. (  0) 0)
|
| [13] |
田喜民, 邹早建, 王化明. KVLCC2船模斜航运动粘性流场及水动力数值计算[J]. 船舶力学, 2010, 14(8): 834-840. TIAN Ximin, ZOU Zaojian, WANG Huaming. Computation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion[J]. Journal of ship mechanics, 2010, 14(8): 834-840. (  0) 0)
|
| [14] |
MENG Qingjie, WAN Decheng. Numerical simulations of viscous flow around the obliquely towed KVLCC2M model in deep and shallow water[J]. Journal of hydrodynamics, ser. B, 2016, 28(3): 506-518. DOI:10.1016/S1001-6058(16)60655-8 (  0) 0)
|
| [15] |
WANG Jianhua, LIU Xiaojjian, WAN Decheng. Numerical simulation of an oblique towed ship by naoe-FOAM-SJTU solver[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. Kona, Big Island, Hawaii, USA, 2015.
(  0) 0)
|
| [16] |
冯松波, 邹早建, 邹璐. KVLCC2船-舵系统斜航水动力数值计算[J]. 上海交通大学学报, 2015, 49(4): 470-474. FENG Songbo, ZOU Zaojian, ZOU Lu. Numerical calculation of hydrodynamic forces on a KVLCC2 hull-rudder system in oblique motion[J]. Journal of Shanghai jiaotong university, 2015, 49(4): 470-474. (  0) 0)
|
| [17] |
LIU Yi, ZOU Lu, ZOU Zaojian. Computational fluid dynamics prediction of hydrodynamic forces on a manoeuvring ship including effects of dynamic sinkage and trim[J]. Proceedings of the institution of mechanical engineers, part M:journal of engineering for the maritime environment, 2017. DOI:10.1177/1475090217734685 (  0) 0)
|
| [18] |
CURA-HOCHBAUM A. On the numerical prediction of the ship's manoeuvring behaviour[J]. Ship science & technology, 2011, 5(9): 27-39. (  0) 0)
|
| [19] |
SIMONSEN C D, OTZEN J F, KLIMT C, et al. Maneuvering predictions in the early design phase using CFD generated PMM data[C]//Proceedings of the 29th Symposium on Naval Hydrodynamics. Gothenburg, Sweden, 2012: 26-31.
(  0) 0)
|
| [20] |
SAKAMOTO N, CARRICA P M, STERN F. URANS simulations of static and dynamic maneuvering for surface combatant:part 1. Verification and validation for forces, moment, and hydrodynamic derivatives[J]. Journal of marine science and technology, 2012, 17(4): 422-445. DOI:10.1007/s00773-012-0178-x (  0) 0)
|
| [21] |
SAKAMOTO N, CARRICA P M, STERN F. URANS simulations of static and dynamic maneuvering for surface combatant:part 2. Analysis and validation for local flow characteristics[J]. Journal of marine science and technology, 2012, 17(4): 446-468. DOI:10.1007/s00773-012-0184-z (  0) 0)
|
| [22] |
KIM H, AKIMOTO H, ISLAM H. Estimation of the hydrodynamic derivatives by RANS simulation of planar motion mechanism test[J]. Ocean engineering, 2015, 108: 129-139. DOI:10.1016/j.oceaneng.2015.08.010 (  0) 0)
|
| [23] |
JIN Yuting, DUFFY J, CHAI Shuhong, et al. URANS study of scale effects on hydrodynamic manoeuvring coefficients of KVLCC2[J]. Ocean engineering, 2016, 118: 93-106. DOI:10.1016/j.oceaneng.2016.03.022 (  0) 0)
|
| [24] |
ROYCHOUDHURY S, DASH A K, NAGARAJAN V, et al. CFD simulations of steady drift and yaw motions in deep and shallow water[J]. Ocean engineering, 2017, 142: 161-184. DOI:10.1016/j.oceaneng.2017.06.058 (  0) 0)
|
| [25] |
杨勇, 邹早建, 张晨曦. 深浅水中KVLCC船体横荡运动水动力数值计算[J]. 水动力学研究与进展, 2011, 26(1): 85-93. YANG Yong, ZOU Zaojian, ZHANG Chenxi. Calculation of hydrodynamic forces on a KVLCC hull in sway motion in deep and shallow water[J]. Chinese journal of hydrodynamics, 2011, 26(1): 85-93. (  0) 0)
|
| [26] |
程捷, 张志国, 蒋奉兼, 等. 平面运动机构试验的数值模拟[J]. 水动力学研究与进展, 2013, 28(4): 460-464. CHENG Jie, ZHANG Zhiguo, JIANG Fengjian, et al. Numerical simulation of the planar motion mechanism tests[J]. Chinese journal of hydrodynamics, 2013, 28(4): 460-464. (  0) 0)
|
| [27] |
LIU Xiaojian, FAN Sheming, WANG Jianhua, et al. Hydrodynamic simulation of pure sway tests with ship speed and water depth effects[C]//Proceedings of the 25th International Offshore and Polar Engineering Conference. Kona, Big Island, Hawaii, USA, 2015.
(  0) 0)
|
| [28] |
王建华, 万德成. 基于重叠网格技术数值模拟船舶纯摇艏运动[J]. 水动力学研究与进展, 2016, 31(5): 567-574. WANG Jianhua, WAN Decheng. Numerical simulation of pure yaw motion using dynamic overset grid technology[J]. Chinese journal of hydrodynamics, 2016, 31(5): 567-574. (  0) 0)
|
| [29] |
刘晗, 马宁, 邵闯, 等. 限宽水域中船舶平面运动机构试验及水动力导数数值模拟[J]. 上海交通大学学报, 2016, 50(1): 115-122. LIU Han, MA Ning, SHAO Chuang, et al. Numerical simulation of planar motion mechanism test and hydrodynamic derivatives of a ship in laterally restricted water[J]. Journal of Shanghai jiaotong university, 2016, 50(1): 115-122. (  0) 0)
|
| [30] |
GUO Haipeng, ZOU Zaojian. System-based investigation on 4-DOF ship maneuvering with hydrodynamic derivatives determined by RANS simulation of captive model tests[J]. Applied ocean research, 2017, 68: 11-25. DOI:10.1016/j.apor.2017.08.006 (  0) 0)
|
| [31] |
STERN F, KIM H T, PATEL V C, et al. A viscous-flow approach to the computation of propeller-hull interaction[J]. Journal of ship research, 1988, 32(4): 246-262. (  0) 0)
|
| [32] |
KAWAMURA T, MIYATA H, MASHIMO K. Numerical simulation of the flow about self-propelling tanker models[J]. Journal of marine science and technology, 1997, 2(4): 245-256. DOI:10.1007/BF02491531 (  0) 0)
|
| [33] |
CHOI J E, KIM J H, LEE H G, et al. Computational predictions of ship-speed performance[J]. Journal of marine science and technology, 2009, 14(3): 322-333. DOI:10.1007/s00773-009-0047-4 (  0) 0)
|
| [34] |
CHOI J E, MIN K S, KIM J H, et al. Resistance and propulsion characteristics of various commercial ships based on CFD results[J]. Ocean engineering, 2010, 37(7): 549-566. DOI:10.1016/j.oceaneng.2010.02.007 (  0) 0)
|
| [35] |
PHILLIPS A B, TURNOCK S R, FURLONG M. Evaluation of manoeuvring coefficients of a self-propelled ship using a blade element momentum propeller model coupled to a Reynolds averaged Navier Stokes flow solver[J]. Ocean engineering, 2009, 36(15/16): 1217-1225. (  0) 0)
|
| [36] |
PHILLIPS A B, TURNOCK S R, FURLONG M. Accurate capture of propeller-rudder interaction using a coupled blade element momentum-RANS approach[J]. Ship technology research, 2010, 57(2): 128-139. DOI:10.1179/str.2010.57.2.005 (  0) 0)
|
| [37] |
SIMONSEN C D, STERN F. RANS Maneuvering simulation of Esso Osaka with rudder and a body-force propeller[J]. Journal of ship research, 2005, 49(2): 98-120. (  0) 0)
|
| [38] |
CARRICA P M, ISMAIL F, HYMAN M, et al. Turn and zigzag maneuvers of a surface combatant using a URANS approach with dynamic overset grids[J]. Journal of marine science and technology, 2013, 18(2): 166-181. DOI:10.1007/s00773-012-0196-8 (  0) 0)
|
| [39] |
DUBBIOSO G, DURANTE D, BROGLIA R. Zig-zag maneuver simulation by CFD for tanker like vessel[C]//Proceedings of the 5th International Conference on Computational Methods in Marine Engineering. Hamburg, Germany, 2013: 29-31.
(  0) 0)
|
| [40] |
BROGLIA R, DUBBIOSO G, DURANTE D, et al. Turning ability analysis of a fully appended twin screw vessel by CFD. Part Ⅰ:Single rudder configuration[J]. Ocean engineering, 2015, 105: 275-286. DOI:10.1016/j.oceaneng.2015.06.031 (  0) 0)
|
| [41] |
DUBBIOSO G, DURANTE D, DI MASCIO A, et al. Turning ability analysis of a fully appended twin screw vessel by CFD. Part Ⅱ:Single vs. twin rudder configuration[J]. Ocean engineering, 2016, 117: 259-271. DOI:10.1016/j.oceaneng.2016.03.001 (  0) 0)
|
| [42] |
MOFIDI A, MARTIN J E, CARRICA P M. Propeller/rudder interaction with direct and coupled CFD/potential flow propeller approaches, and application to a zigzag manoeuvre[J]. Ship technology research, 2018, 65(1): 10-31. DOI:10.1080/09377255.2017.1399970 (  0) 0)
|
| [43] |
LVBKE L O. Numerical simulation of the flow around the propelled KCS[C]//Proceedings of CFD Workshop 2005. Tokyo, Japan, 2005: 9-11.
(  0) 0)
|
| [44] |
QUEUTEY P, DENG G, WACKERS J, et al. Sliding grids and adaptive grid refinement for RANS simulation of ship-propeller interaction[J]. Ship technology research, 2012, 59(2): 44-57. DOI:10.1179/str.2012.59.2.004 (  0) 0)
|
| [45] |
SEO J H, SEOL D M, LEE J H, et al. Flexible CFD meshing strategy for prediction of ship resistance and propulsion performance[J]. International journal of naval architecture and ocean engineering, 2010, 2(3): 139-145. DOI:10.2478/IJNAOE-2013-0030 (  0) 0)
|
| [46] |
BADOE C E, PHILLIPS A B, TURNOCK S R. Influence of drift angle on the computation of hull-propeller-rudder interaction[J]. Ocean engineering, 2015, 103: 64-77. DOI:10.1016/j.oceaneng.2015.04.059 (  0) 0)
|
| [47] |
EL MOCTAR O, LANTERMANN U, MUCHA P, et al. RANS-based simulated ship maneuvering accounting for hull-propulsor-engine interaction[J]. Ship technology research, 2014, 61(3): 142-161. DOI:10.1179/str.2014.61.3.003 (  0) 0)
|
| [48] |
张志荣, 李百齐, 赵峰. 螺旋桨/船体粘性流场的整体数值求解[J]. 船舶力学, 2004, 8(5): 19-26. ZHANG Zhirong, LI Baiqi, ZHAO Feng. Integral calculation of viscous flow around ship hull with propeller[J]. Journal of ship mechanics, 2004, 8(5): 19-26. (  0) 0)
|
| [49] |
沈海龙, 苏玉民. 基于滑移网格技术的船桨相互干扰研究[J]. 哈尔滨工程大学学报, 2010, 31(1): 1-7. SHEN Hailong, SU Yumin. Use of the sliding mesh technique to analyze interaction between ship hulls and propellers[J]. Journal of Harbin engineering university, 2010, 31(1): 1-7. (  0) 0)
|
| [50] |
沈兴荣, 冯学梅, 蔡荣泉. 均流中大型集装箱船桨舵干扰粘性流场的数值计算研究[J]. 船舶力学, 2009, 13(4): 540-550. SHEN Xingrong, FENG Xuemei, CAI Rongquan. Numerical study on the interaction between propeller and rudder of ultra-large container ship in uniform viscous flow[J]. Journal of ship mechanics, 2009, 13(4): 540-550. (  0) 0)
|
| [51] |
杜云龙, 陈霞萍, 陈昌运. 某船及其改型船桨舵数值模拟与性能比较[J]. 水动力学研究与进展, 2013, 28(5): 566-574. DU Yunlong, CHEN Xiaping, CHEN Changyun. Numerical simulation and comparison of performance for a bulk carrier with two different hull lines[J]. Chinese journal of hydrodynamics, 2013, 28(5): 566-574. (  0) 0)
|
| [52] |
CARRICA P M, STERN F. DES simulations of KVLCC1 in turn and zigzag maneuvers with moving propeller and rudder[C]//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods. Lyngby, Denmark, 2008.
(  0) 0)
|
| [53] |
MOFIDI A, CARRICA P M. Simulations of zigzag maneuvers for a container ship with direct moving rudder and propeller[J]. Computers & fluids, 2014, 96: 191-203. (  0) 0)
|
| [54] |
CARRICA P M, MOFIDI A, ELOOT K, et al. Direct simulation and experimental study of zigzag maneuver of KCS in shallow water[J]. Ocean engineering, 2016, 112: 117-133. DOI:10.1016/j.oceaneng.2015.12.008 (  0) 0)
|
| [55] |
SHEN Zhirong, WAN Decheng, CARRICA P M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering[J]. Ocean engineering, 2015, 108: 287-306. DOI:10.1016/j.oceaneng.2015.07.035 (  0) 0)
|
| [56] |
WANG Jianhua, ZHAO Weiwen, WAN Decheng. Free maneuvering simulation of ONR Tumblehome using overset grid method in naoe-FOAM-SJTU solver[C]//Proceedings of the 31th Symposium on Naval Hydrodynamics. Monterey, USA, 2016.
(  0) 0)
|
| [57] |
王建华, 万德成. 全附体ONRT船模在波浪中自航的数值模拟[J]. 应用数学和力学, 2016, 37(12): 1345-1358. WANG Jianhua, WAN Decheng. Investigations of self-propulsion in waves of fully appended ONR Tumblehome model[J]. Applied mathematics and mechanics, 2016, 37(12): 1345-1358. (  0) 0)
|
| [58] |
WANG Jianhua, ZOU Lu, WAN Decheng. CFD simulations of free running ship under course keeping control[J]. Ocean engineering, 2017, 141: 450-464. DOI:10.1016/j.oceaneng.2017.06.052 (  0) 0)
|
| [59] |
SHEN Zhirong, KORPUS R. Numerical Simulations of Ship Self-Propulsion and Maneuvering Using Dynamic Overset Grids in OpenFOAM[C]//Proceedings of the Tokyo 2015 A Workshop on CFD in Ship Hydrodynamics. Tokyo, Japan, 2015.
(  0) 0)
|
| [60] |
WANG Jianhua, WAN Decheng, YU Xingguo. Standard zigzag maneuver simulations in calm water and waves with direct propeller and rudder[C]//Proceedings of the 27th International Ocean and Polar Engineering Conference. San Francisco, CA, USA, 2017.
(  0) 0)
|
| [61] |
ITTC. Tasks and Structure of the 29th ITTC Technical Committees and Groups[C]//Proceedings of the 28th International Towing Tank Conference. Wuxi, China, 2017, Ⅰ: 393-408.
(  0) 0)
|
| [73] |
WANG Jianhua, WAN Decheng. CFD simulations of ship maneavering motion[J]. Journal of Harbin Engineering University, 2018, 39(5): 813-824. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39