钻取采样是月球、火星以及其他外星体探测任务中获取岩石样本的有效方式[1]。从前苏联的Luna系列到美国的好奇号,人类不断探索外星体极端环境下的钻探技术,寻求更便捷、更有效的采样方式。美国喷气与推进实验室的研究人员率先研发了基于压电驱动的冲击式超声波钻探器(ultrasonic/sonic driller/corer,USDC)。USDC有三个关键组件:压电换能器、自由质量块和钻具。在高频交流电压激励下,压电换能器末端产生超声频振动(几十千赫兹),并与自由质量块发生冲击碰撞,使其在压电换能器与钻具之间作往复运动,以驱动钻具作高频振动(几百~几千赫兹),达到破碎岩石的目的[2]。与电磁电机驱动的传统钻探器相比,采用超声波技术的钻探器具有结构简单、体积小、能耗低、所需钻压力小、无需润滑等特点[3]。USDC既可安装在微型着陆器上,又可搭载在小型巡视机器人上进行原位探测[4]。Chang等[5]为降低压电换能器的轴向长度,提出了具有折叠式构型变幅杆的压电换能器。Harkness等[6]在500 ℃高温环境下对所采用的压电陶瓷的性能进行了测试,结果表明钻探器能够适应金星的温度环境。Jpl[7]还研制出内部具有样芯保持及依靠楔形断芯功能的取芯钻具,成功实现了岩石的钻进取芯。
自Jpl首次将超声波技术应用到地外天体采样任务中以来,超声波钻进取芯装置的研究备受许多国家研究人员的关注。Potthast等[8-9]提出采用球形自由质量块的方案,研究了自由质量块的混沌运动。Harkness等[10]提出采用多个球形自由质量单元的结构形式。研究指出自由质量单元的外径对钻探效率的影响显著,而自由质量单元的个数对其影响较小[10]。Budairi等[11]提出了一种可实现钻具冲击运动及回转运动的纵扭复合型压电换能器,文献[12]在此基础上研究了超声波钻探器的控制方法。英国Magna Parva公司与ESA合作研发了用于火星表面探测的超声波钻探器。研究了安装方式对钻进效果的影响规律。钻取直径为10 mm、长度12 mm的冰芯只需20 s,钻进效果显著[13]。俄罗斯比斯克超声技术中心的研究人员研制出一种采用压电换能器直接钻进的钻探器。在45 W的输出功率下,对模拟月壤的最大钻进速率为25 mm/min[14-16]。郭俊杰等[17-21]亦对超声波钻探器进行了跟踪研究,取得了显著成果。
上述超声波钻探器均是通过自由质量块将压电换能器末端的超声频振动转化为钻具的高频振动。本文拟提出一种不含自由质量块的直驱式超声波钻探器。压电换能器变幅杆直接与钻具发生冲击碰撞,将冲击能量传递给钻具以驱动钻具破碎岩石。
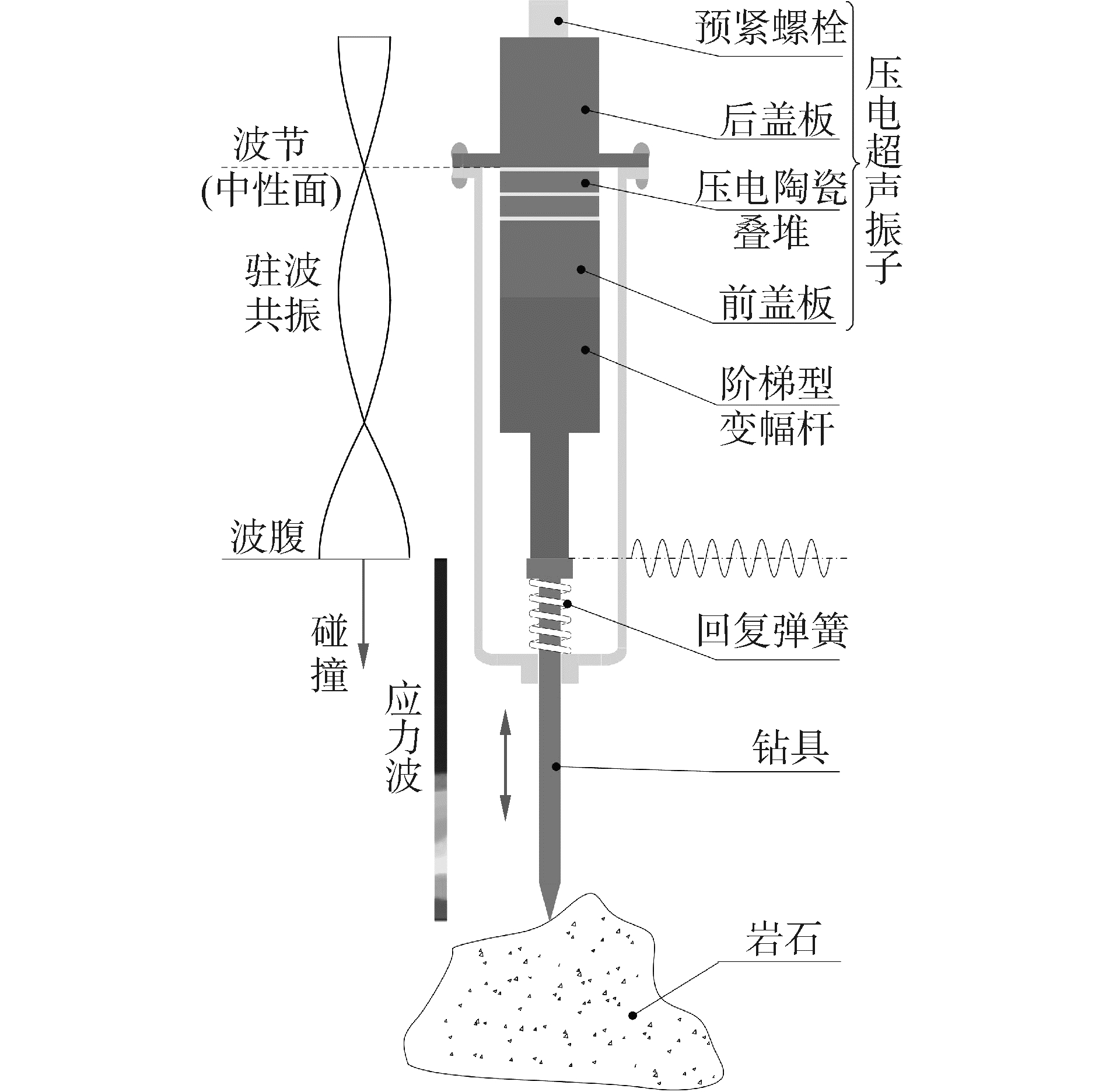
1 超声波钻探器工作原理及换能器设计 1.1 超声波钻探器工作原理本文提出的压电换能器变幅杆直接驱动钻具的超声波钻探器的工作原理如图 1所示。两片纵向极化的带孔压电陶瓷片组成压电陶瓷叠堆;陶瓷叠堆的前后两侧分别是前盖板、后盖板;预紧螺栓将后盖板、压电陶瓷叠堆、前盖板连为一体,使压电陶瓷叠堆始终处于压缩状态;预紧螺栓、后盖板、压电陶叠堆及前盖板组成了压电超声振子。由于压电陶瓷叠堆具有逆压电效应,在超声频交流电激励下压电超声振子产生几千赫兹到几万赫兹的超声频机械振动。阶梯型变幅杆将压电超声振子的超声频机械振动的振幅放大,形成驻波共振。变幅杆底端作为输出端与钻具发生冲击碰撞,使钻具内部产生应力波并传递到钻具与岩石接触表面。当岩石接触面应力超过岩石强度极限时,岩石发生破碎。
|
Download:
|
| 图 1 超声波钻探器工作原理 Fig. 1 Principle of ultrasonic drilling device | |
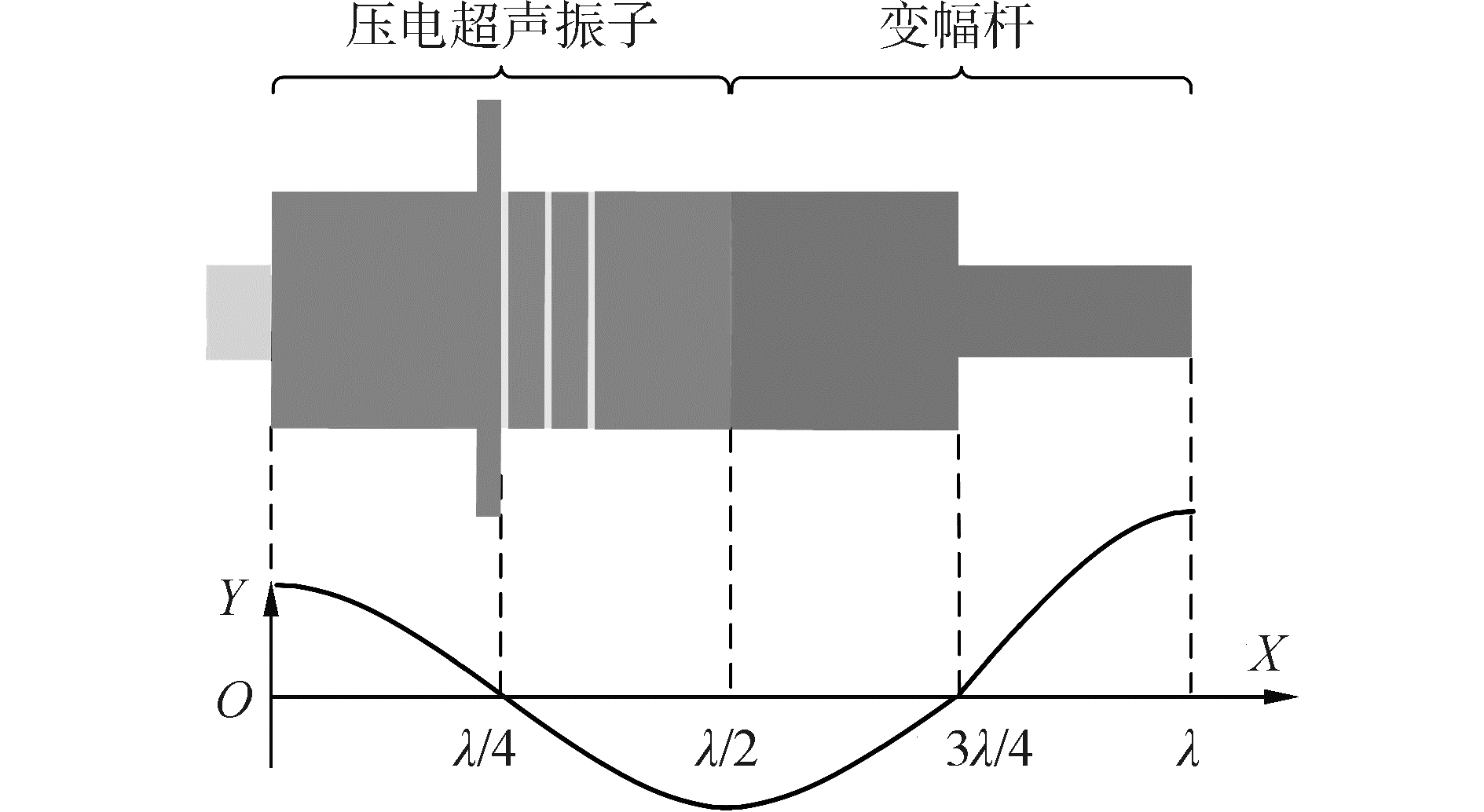
作为超声波钻探器的驱动单元,压电换能器由压电超声振子与变幅杆两部分组成。当激励信号频率与压电超声振子的纵振谐振频率相同时,压电超声振子产生共振。此时振子输出端的纵向振幅达到最大值。变幅杆的作用是放大压电超声振子输出端的振幅。本文使用的压电换能器为全波长谐振系统,如图 2所示。设定换能器的理论工作频率为25 kHz,借助驻波共振原理确定振子结构尺寸。
|
Download:
|
| 图 2 全波长驱动原理示意图 Fig. 2 Driving principle with full wavelength | |
压电超声振子由前盖板、压电陶瓷叠堆、后盖板及预紧螺栓组成。忽略压电陶瓷叠堆中空特性,假设超声波振子的前盖板、压电陶瓷叠堆及后盖板均为连续弹性介质。
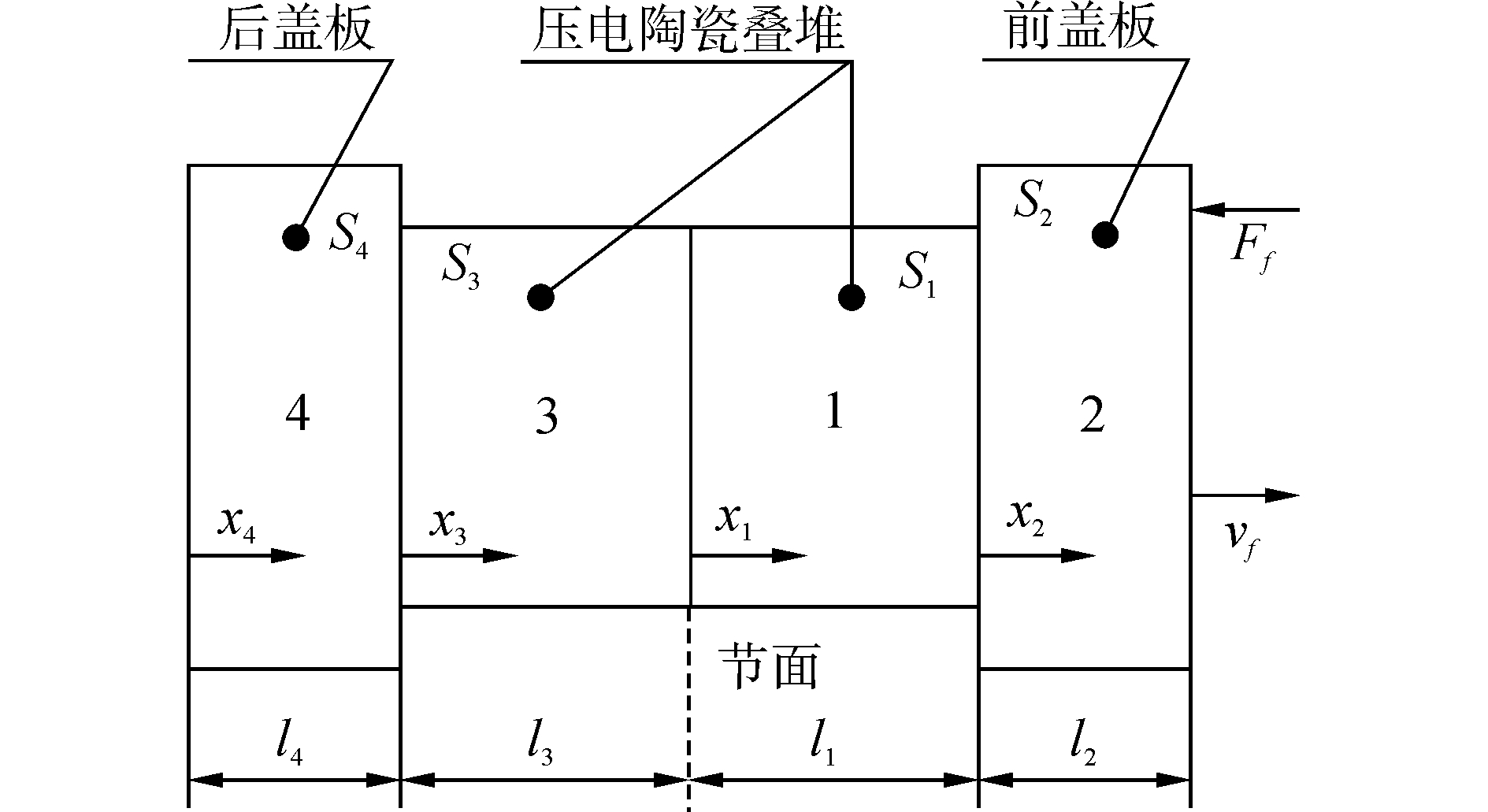
假定压电超声振子的节面存在于压电陶瓷叠堆中间位置,将压电超声振子看作由四个单元组成,如图 3所示。1、3单元为压电材料,2、4单元分别为前盖板及后盖板。虚线表示的节面将压电超声振子分为左右两部分。根据胡克定律及牛顿第二运动定律,振子各部分任意一点xn的振速方程为
| $ \frac{{{\partial ^2}{v_n}}}{{\partial x_n^2}} + k_n^2{v_n} = 0\;\;\;\;\left( {n = 1,2,3,4} \right) $ | (1) |
|
Download:
|
| 图 3 压电超声振子组成示意图 Fig. 3 Composition of ultrasonic transducer | |
式中:vn为点xn处振速,kn为振子各单元内波数。方程(1)的通解为
| $ {v_n}\left( {{x_n}} \right) = {A_n}\sin \left( {{k_n}{x_n}} \right) + {B_n}\cos \left( {{k_n}{x_n}} \right) $ | (2) |
| $ {F_n}\left( {{x_n}} \right) = - {\rm{j}}{Z_n}\left( {{A_n}\cos \left( {{k_n}{x_n}} \right) - {B_n}\sin \left( {{k_n}{x_n}} \right)} \right) $ | (3) |
式中:Fn(xn)为xn处拉力;An、Bn为待定系数;Zn为振子内各单元的特定声阻抗,Zn=ρncnSn;ρn为振子各单元材料密度;cn为振子各单元声速;Sn为振子各单元横截面积。
由动力学边界条件及式(2)、(3),得到压电超声振子节面左右两侧单元的振动频率方程:
| $ \tan \left( {{k_1}{l_1}} \right)\tan \left( {{k_2}{l_2}} \right) = \frac{{{Z_1}}}{{{Z_2}}} $ | (4) |
| $ \tan \left( {{k_3}{l_3}} \right)\tan \left( {{k_4}{l_4}} \right) = \frac{{{Z_3}}}{{{Z_4}}} $ | (5) |
压电超声振子性能的评价指标为前后盖板输出端振速比。假设振子节面处弹性力连续,则由式(1)、(4)、(5)得到前后盖板输出端振速比为
| $ \left| {\frac{{{v_f}}}{{{v_b}}}} \right| = \frac{{{Z_3}}}{{{Z_1}}}\frac{{\sin \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_3}{l_3}} \right)}}\frac{{\sqrt {1 + {{\left( {\frac{{{Z_1}}}{{{Z_2}}}} \right)}^2}{{\cot }^2}\left( {{k_1}{l_1}} \right)} }}{{\sqrt {1 + {{\left( {\frac{{{Z_3}}}{{{Z_4}}}} \right)}^2}{{\cot }^2}\left( {{k_3}{l_3}} \right)} }} $ | (6) |
式中:vf为前盖板端面振速,vb为后盖板端面振速。
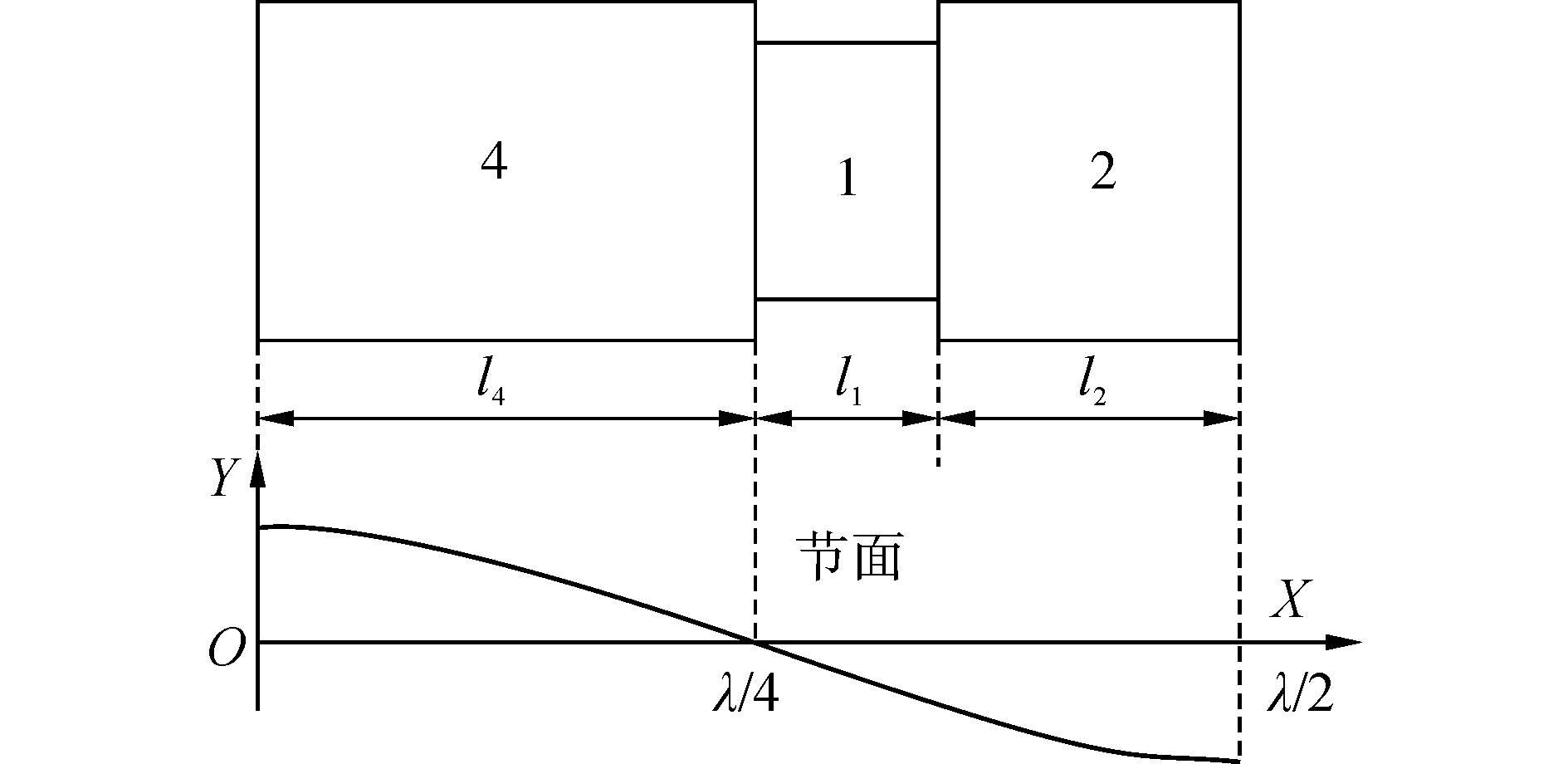
由式(6)可知,k3l3越小前后盖板端面振速之比越大。当k3l3=0时,前后盖板端面振速之比最大。此时,节面位于压电陶瓷与后盖板的结合面处,如图 4所示。
|
Download:
|
| 图 4 节面设置示意图 Fig. 4 Site of nodal plane | |
为提高前后振速比,前盖板材料的特性声阻抗应愈小愈好,后盖板的材料的特性声阻抗应尽可能大[16]。需满足:
| $ {Z_2} < {Z_1} < {Z_4} $ | (7) |
取20号钢作为后盖板材料,钛合金作为前盖板材料,20号钢作为预紧螺栓材料,压电陶瓷采用PZT-4型陶瓷环片。压电超声振子各部分材料属性如表 1所示。陶瓷叠堆由2片外径为25 mm,内径为12 mm,厚度为3 mm的陶瓷环片组成。
| 表 1 压电超声振子材料属性 Tab.1 Property of material for ultrasonic transducer |
PZT-4型压电陶瓷材料的功率容量一般取2~3 W/(cm3·kHz)[22]。本文中压电陶瓷片的功率容量取2 W/(cm3·kHz)。压电换能器的理论设计谐振频率25 kHz。单片陶瓷可允许的最大功率为57 W,压电陶瓷叠堆可承受的最大功率为114 W。
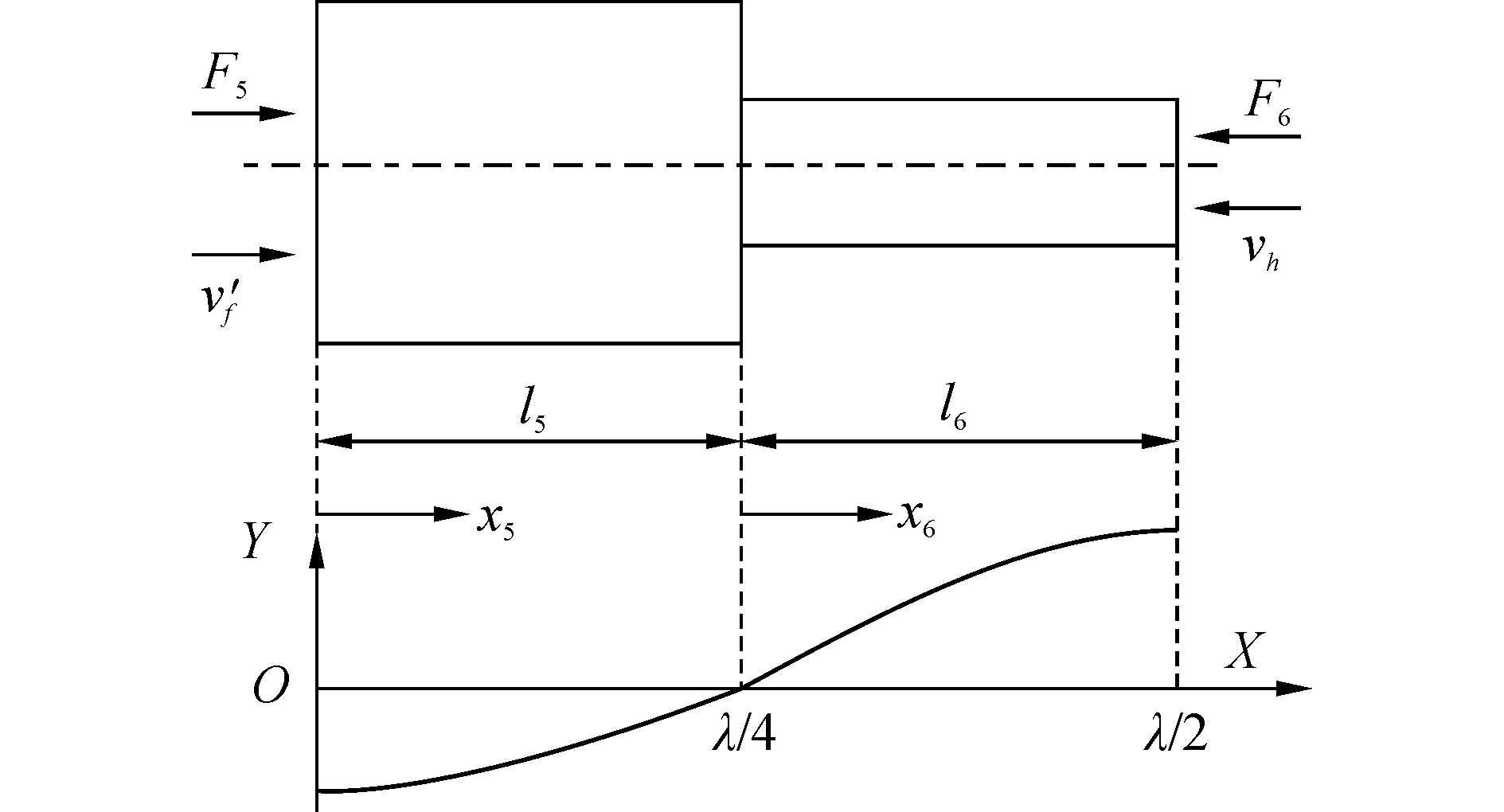
1.2.2 变幅杆动力学模型变幅杆的作用是放大压电超声振子前盖板的振动幅值。由弹性材料应力、力、节面之间关系可知,通过改变弹性体截面尺寸,可放大弹性体内应力波的振幅及波速。本文利用全波长共振原理设计阶梯型变幅杆构型,如图 5所示。
|
Download:
|
| 图 5 阶梯型变幅杆 Fig. 5 Stepped horn of ultrasonic transducer | |
假设阶梯型变幅杆为连续弹性体,变幅杆内各点的运动满足振动方程(1)。由边界条件及式(2)、(3)得到阶梯型变幅杆的振动频率方程为
| $ {Z_5}\tan \left( {{k_5}{l_5}} \right) + {Z_6}\tan \left( {{k_6}{l_6}} \right) = 0 $ | (8) |
式中:k5为5单元内波数,k6为6单元内波数,Z5为5单元的特征声阻抗,Z6为6单元的特征声阻抗。
变幅杆输出端振速放大倍数为
| $ \left| {\frac{{{v_h}}}{{{v_f}}}} \right| = \frac{{{Z_5}}}{{{Z_6}}}\sin \left( {{k_5}{l_5}} \right)\;\;\sqrt {1 + {{\left( {\frac{{{Z_6}}}{{{Z_5}}}} \right)}^2}{{\cot }^2}\left( {{k_5}{l_5}} \right)} $ | (9) |
式中vh为变幅杆输出端振速。
由式(9)可知,当k5l5=π/2,即l5=λ5/4时,振幅放大系数最大,此时放大系数为
| $ {\left| {\frac{{{v_h}}}{{{v_f}}}} \right|_{\max }} = \frac{{{Z_5}}}{{{Z_6}}}=\frac{{{\rho _5}{c_5}{S_5}}}{{{\rho _6}{c_6}{S_6}}} $ | (10) |
式中:S5为变幅杆大径端横截面积,S6为变幅杆小径端横截面积。
由于阶梯型变幅杆的大径端与小径端采用同一材料,因此放大倍数仅取决于断面半径比。当大径端与小径端的半径比大于5时会导致边界弹性力不连续[22]。本文中阶梯型变幅杆的大径端直径与压电陶瓷片外径相同,为25 mm;小径端的直径为8 mm;变幅杆大径端与小径端的长度均为50 mm。
压电陶瓷材料抗张强度约为2×107~5×107 N/m2,抗压强度约为抗张强度的10倍左右[23],高频工作压电陶瓷所承受的预紧力应大于20 MPa[24]。设定压电陶瓷预紧力P1为20~30 MPa,以避免陶瓷材料工作在交变拉压应力状态,影响工作寿命。
根据基本力学公式
| $ F' = {P_1}{A_1} $ | (11) |
式中:F′为预紧螺栓预紧力,A1为陶瓷片面积。
根据拧紧力矩Mt的计算公式
| $ {M_{\rm{t}}} = KF'D $ | (12) |
式中:K为拧紧力系数,K=0.18;D为螺纹公称直径,D=10 mm。
根据式(12),拧紧力矩13.6 Nm·m≤Mt≤20.4 Nm·m,本文中设定预紧螺栓的拧紧力矩为20 N·m。
2 变幅杆与钻具碰撞过程分析在高频交流信号激励下,变幅杆输出端作高频简谐振动并与钻具发生碰撞冲击,将机械能传递给钻具,以驱动钻具作冲击运动,进而冲击破碎岩石。研究变幅杆与钻具的碰撞过程可揭示直驱式超声波钻探器内部的能量传递规律,为钻探器的优化设计提供理论依据。
2.1 变幅杆与钻具碰撞接触模型假设碰撞过程中变幅杆末端的运动不受碰撞的影响,变幅杆末端的运动可视为简谐运动[5],其运动方程为
| $ {u_h}\left( t \right) = - {u_0}\cos \left( {\omega t} \right) $ | (13) |
式中:u0为变幅杆输出端简谐振动幅值,ω为变幅杆谐振角频率。
变幅杆末端与钻具碰撞前后的运动速度满足动量守恒定律,可表示为
| $ {m_h}{v_h} + {m_{ds}}{v_{ds}} = {m_h}{{v'}_h} + {m_{ds}}{{v'}_{ds}} $ | (14) |
式中:mh为变幅杆参与碰撞的质量,vh为碰撞前变幅杆输出端的运动速度,mds为钻具质量,vds为碰撞前钻具的运动速度,v′h为碰撞后变幅杆输出端的运动速度,v′ds为碰撞后钻具的运动速度。
碰撞过程中的恢复系数表示为
| $ e = \frac{{{{v'}_{ds}} - {{v'}_h}}}{{{v_h} - {v_{ds}}}} $ | (15) |
由式(14)、(15)得到碰撞后钻具的运动速度:
| $ {{v'}_{ds}} = \frac{{{m_h}{v_h} + {m_{ds}}{v_{ds}} + e{m_h}\left( {{v_h} - {v_{ds}}} \right)}}{{{m_h} + {m_{ds}}}} $ | (16) |
由于变幅杆的质量远大于钻具的质量,因而忽略钻具质量相关项将式(16)进一步简化为
| $ {{v'}_{ds}} = - e{v_{ds}} + \left( {1 + e} \right){v_h} $ | (17) |
钻具与变幅杆发生碰撞后的运动可视为含阻尼的单自由度运动。钻具的运动方程为
| $ {m_{ds}}\ddot x + c\dot x + kx = k{x_0} $ | (18) |
式中:x为钻具的位移,c为阻尼系数,k为弹簧刚度,x0为弹簧预压缩量。
由式(13)、(17)、(18)得到变幅杆与钻具第n次碰撞之后钻具的运动方程
| $ x\left( t \right) = {A_0} + {A_n}{{\rm{e}}^{ - at}}\sin \left( {{\omega _d}t + {\varphi _n}} \right) $ | (19) |
式中:A0为平衡位置坐标,An为振动幅值,ωd为振动角频率,φn为初始相位角。
根据上述分析结果,基于Matlab对变幅杆-钻具的碰撞过程进行仿真分析。仿真过程中变幅杆的谐振频率为25 kHz,谐振幅值为37.5 μm;弹簧的刚度系数为1 000 N/m,弹簧的预压缩量为5 mm;钻具的质量为5 g。
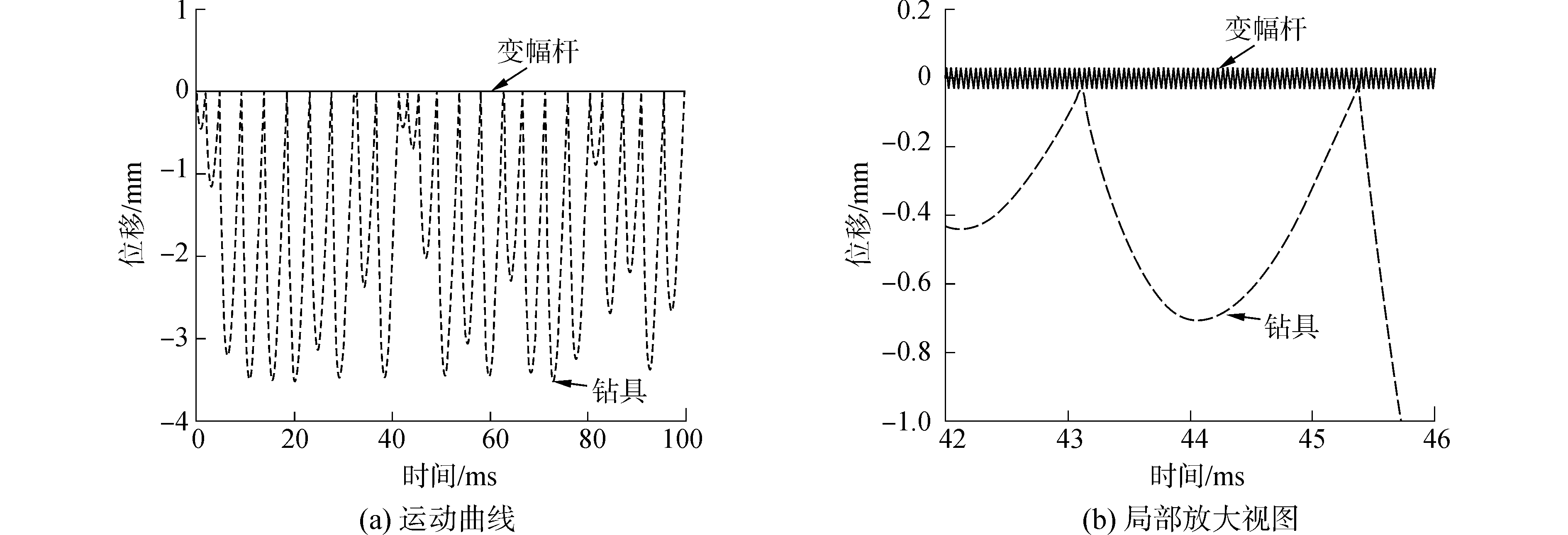
图 6(a)所示为弹性恢复系数e=0.1,阻尼比ζ=0.1时变幅杆与钻具的运动曲线。图 6(b)为图 6(a)中虚线框部分的局部放大视图。在0.1 s的时间内,变幅杆与钻具一共发生了26次碰撞,冲击频率约为260 Hz。变幅杆输出端的运动为超声频小振幅(微米级)的简谐运功。通过冲击碰撞,压电换能器变幅杆驱动钻具作高频大振幅(毫米级)的含阻尼自由运动。
|
Download:
|
| 图 6 变幅杆与钻具的运动曲线及局部放大视图 Fig. 6 Positions of ultrasonic horn and drill rod versus time and partly enlarged view | |
本文提出的超声波钻探器依靠钻具对岩石的冲击作用达到破碎岩石的效果。变幅杆与钻具每次冲击碰撞过程中,传递到钻具的能量为
| $ \Delta E = \frac{1}{2}{m_{ds}}\left( {v{'}_{ds}^2 - v_{ds}^2} \right) $ | (20) |
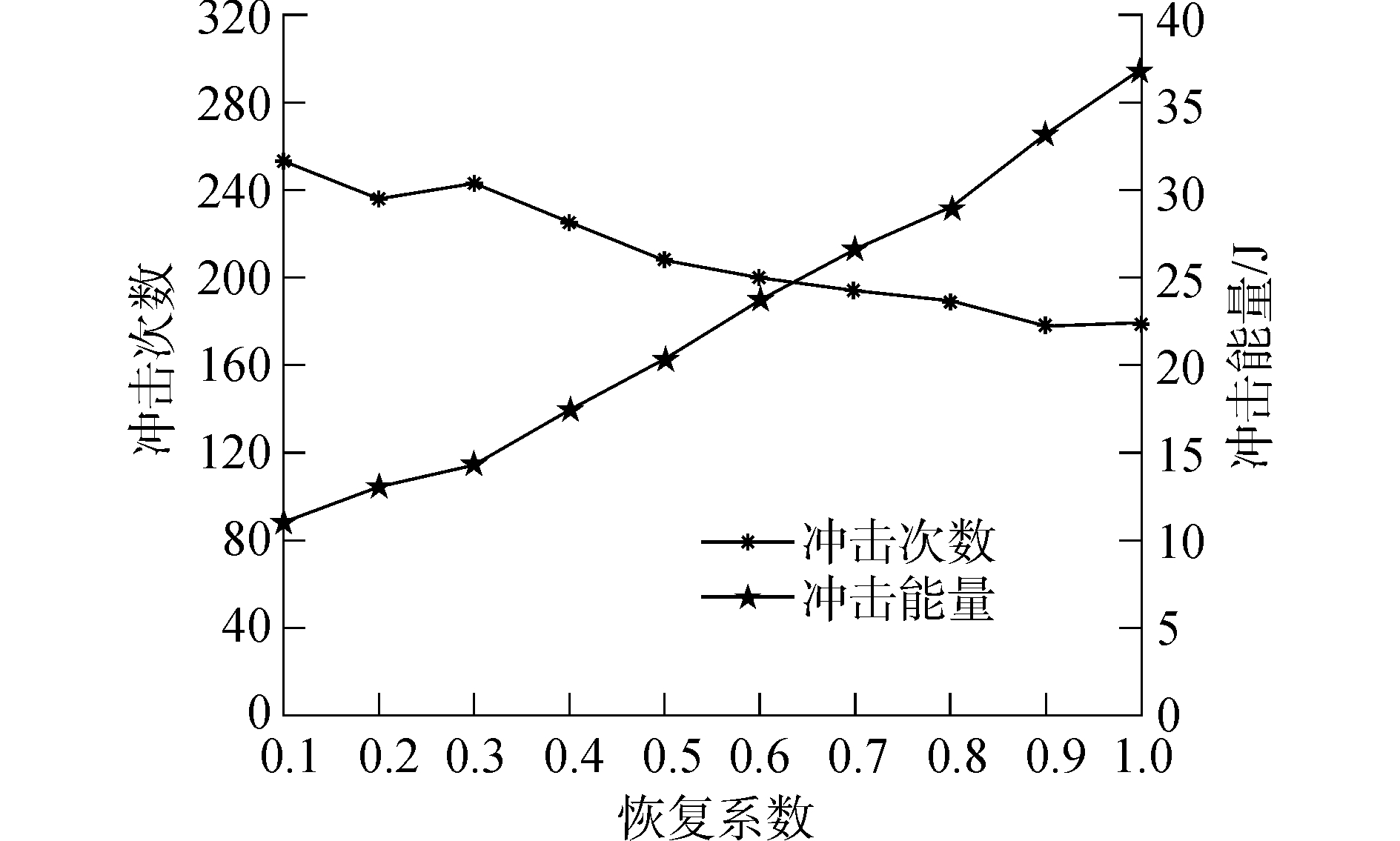
由式(17)及式(20)可知,恢复系数是影响能量传递的重要因素。恢复系数对单位时间内的冲击次数及冲击能量影响的仿真分析结果如图 7所示。随恢复系数的增大,单位时间内变幅杆对钻具的冲击次数减少,传递到钻具的能量随之增大。由于变幅杆与钻具的实际碰撞过程属于非弹性碰撞,恢复系数0 < e < 1。当e无限接近于1时,单位时间内传递到钻具的冲击能量最大。
|
Download:
|
| 图 7 恢复系数对单位时间内冲击次数及冲击能量的影响 Fig. 7 Number of impacts and impact energy per second for different coefficients of restitution | |
1) 压电换能器谐振频率测试
利用阻抗分析仪测试压电换能器的谐振频率。测试结果如图 8所示。压电换能器的谐振频率为24.47 kHz,与理论设计值(25 kHz)相接近。

|
Download:
|
| 图 8 压电换能器谐振频率测试结果 Fig. 8 Resonance frequency of ultrasonic transducer | |
2) 压电换能器输出端面振幅测试
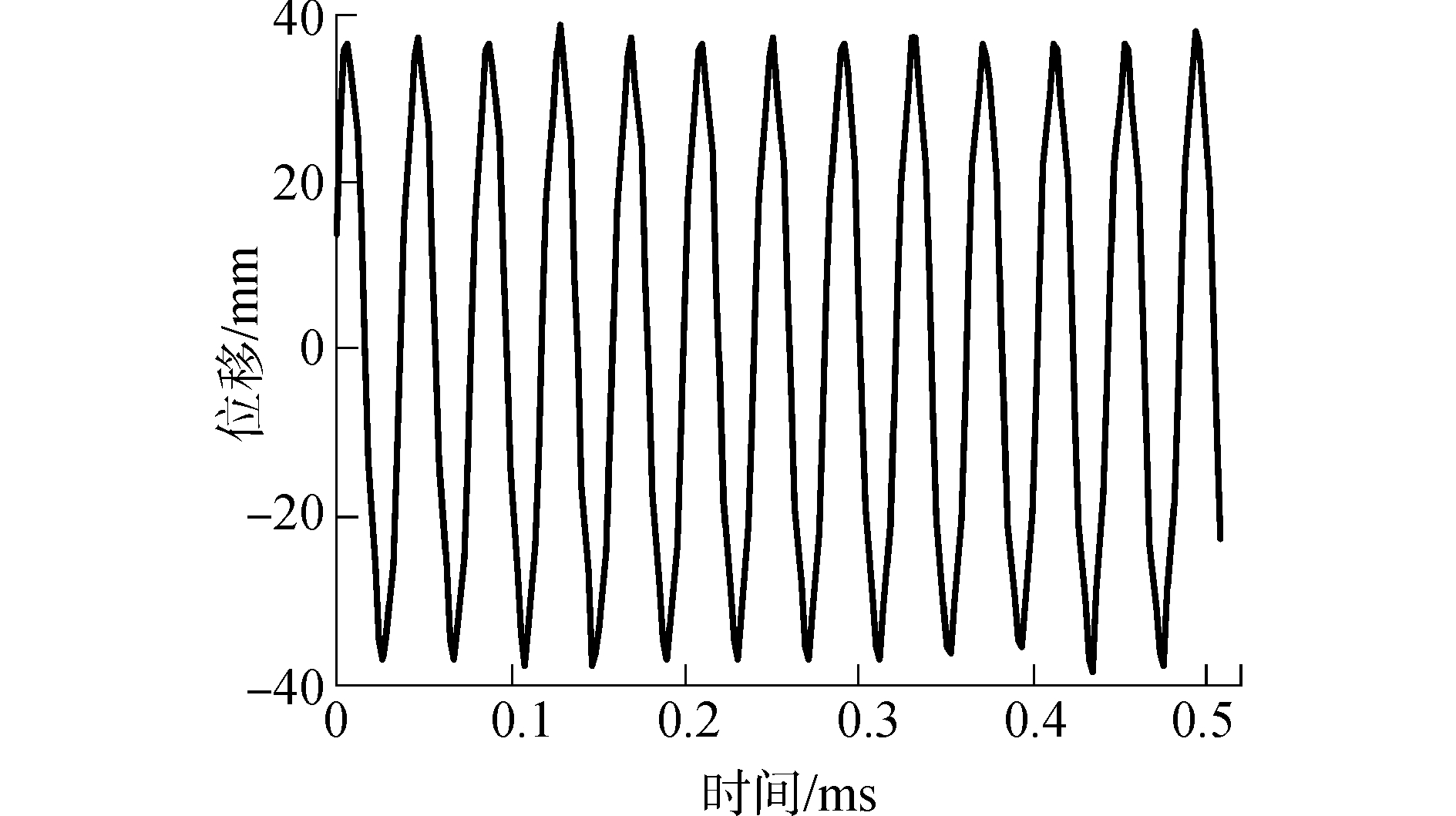
本文提出的钻探器依靠压电换能器变幅杆输出端直接与钻具发生冲击碰撞来传递能量,驱动钻具破碎岩石。变幅杆输出端简谐运动的幅值能反映压电换能器的驱动能力。在压电换能器谐振频率已知的基础上,进一步测试变幅杆输出端的振幅。利用基恩士LK-H020型激光位移传感器测试变幅杆输出端的简谐振动。变幅杆输出端简谐运动的振幅为37.5 μm,如图 9所示。
|
Download:
|
| 图 9 压电换能器输出端振幅测试结果 Fig. 9 Amplitude test of output of ultrasonic transducer | |
为测试超声波钻探器对岩石的钻进性能,搭建了超声波钻探器测试系统,如图 10所示。该系统由工控机、控制箱、函数信号发生器、压电陶瓷驱动电源、钻进实验台等组成。

|
Download:
|
| 图 10 超声钻探器测试系统 Fig. 10 A test system for ultrasonic drilling tool | |
超声波钻探器依靠钻具与岩石的高频冲击作用破碎岩石,因此钻具需具有一定的强度与韧性。钻探器的钻具材料为40Cr,直径为3 mm。以可钻性等级为5级的砂岩作为钻进对象。
1) 超声波钻探器钻进能力测试
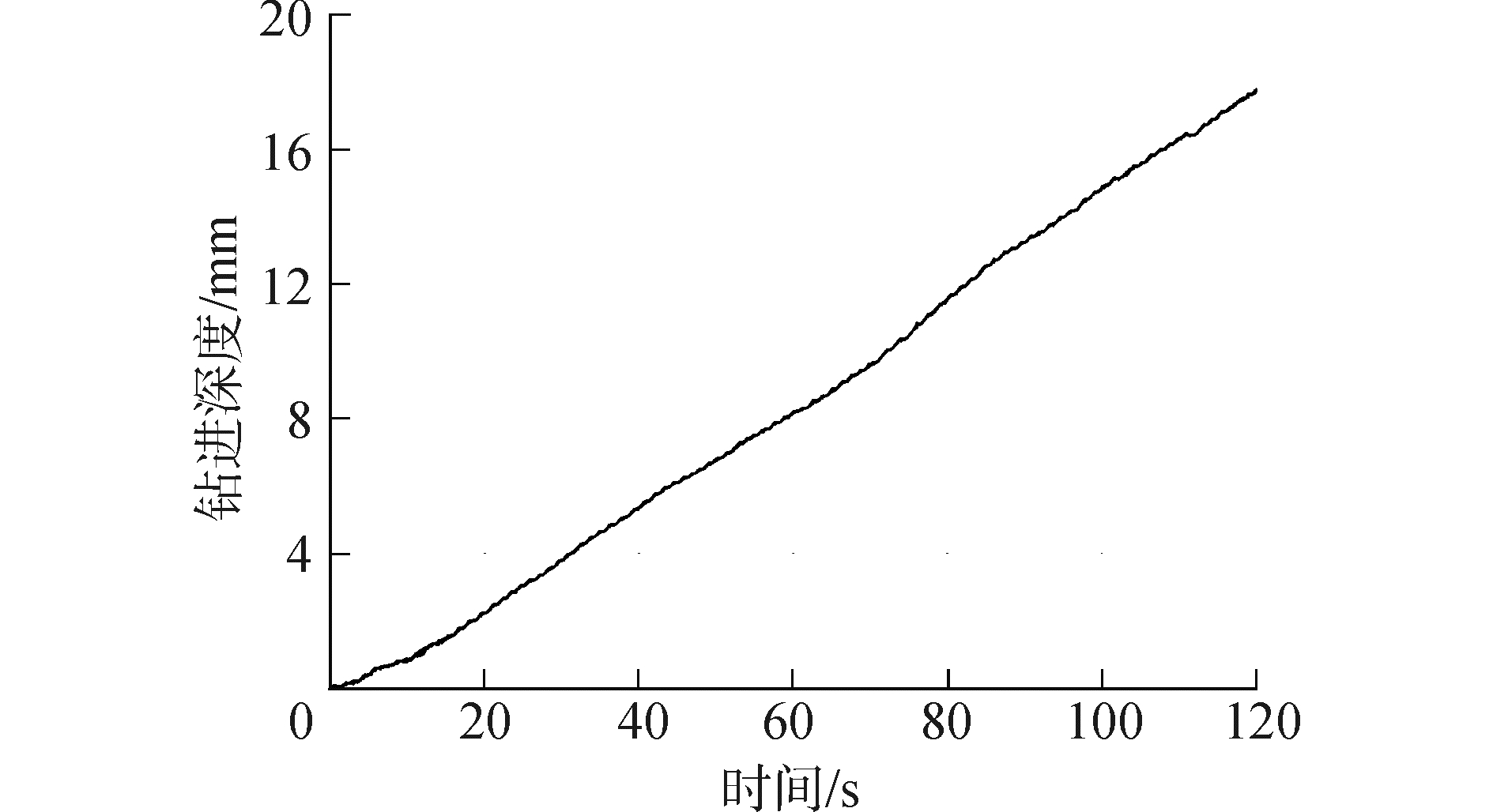
设定钻具的长度为65 mm,钻压力为1.6 N,钻进时间为120 s。图 11所示为钻进过程中的钻进深度-时间曲线。由实验结果可知:钻进时间为120 s时,钻进深度达到了17.6 mm。实验结果表明本文提出的直驱式超声波钻探器对可钻性等级为5级的砂岩可有效钻进。
|
Download:
|
| 图 11 钻进深度-时间曲线 Fig. 11 Drilling depth to time | |
2) 钻压力对钻探器钻进性能影响测试
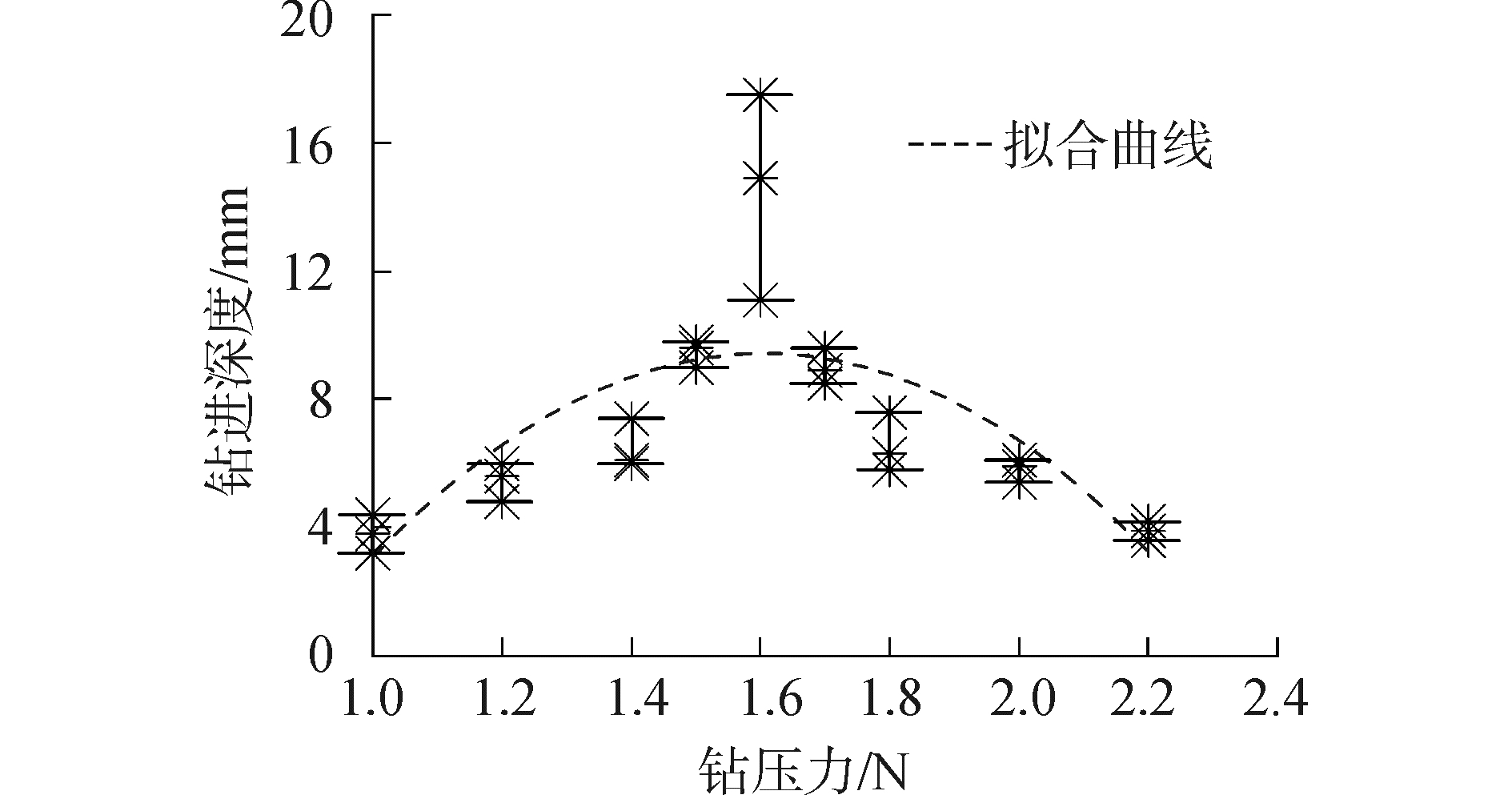
为研究钻压力对超声波钻探器钻进效率的影响规律,钻进实验台采用恒钻压力模式控制超声波钻探器的进给运功。分别在不同钻压力下对同一岩石样本钻进120 s,对比钻进结束时的钻进深度。图 12所示为不同钻压力对应的钻进深度。实验结果表明:对于直径为3 mm,长度为65 mm的钻具,在钻压力为1.6 N时对砂岩的钻进效果最优。此时的最大钻进深度为17.6 mm,钻进速率为8.8 mm/min。
|
Download:
|
| 图 12 不同钻压力对应的钻进深度 Fig. 12 Drilling depth for different drill preload | |
3) 钻具长度对钻探器钻进性能影响测试
钻具长度对钻探器的钻进效果有一定的影响。图 13所示为直径为3 mm,长度为90 mm的钻具在不同钻压力下对砂岩钻进120 s时的钻进深度。由实验结果可知:钻压力对长度为90 mm的钻具的钻进速率影响较大。在钻压力为1.6 N时,钻进深度为1.76 mm,钻进速率为0.88 mm/min。

|
Download:
|
| 图 13 长度为90 mm的钻具在不同钻压力下的钻进深度 Fig. 13 Drilling depth for different drill preload with length of drill rod being 90 mm | |
对比图 12与图 13的实验结果可知:直径均为3 mm时,长度为65 mm的钻具对砂岩的钻进速率是长度为90 mm的钻具对砂岩的钻进速率的10倍。因此,对于本文提出的直驱式超声波钻探器,钻具的直径均为3 mm时,长度较短的钻具具有较优的钻进效果。
4 结论1) 恢复系数对单位时间内的冲击次数及传递到钻具的冲击能量影响显著。
2) 钻探器采用直径为3 mm,长度为65 mm的钻具时,在1.6 N的钻压力下,对可钻性等级为5级的砂岩的最大钻进速率达到了8.8 mm/min。证明本文提出的直驱式超声波钻探器在轴向钻压力较小时便具有较好的钻进效果。
3) 对于直驱式超声波钻探器,钻具的长度对钻探器的钻进效率影响较大。钻具的直径均为3 mm时,长度较短的钻具具有较优的钻进效果。
| [1] |
ZACNY K, BAR-COHEN Y, BRENNAN M, et al. Drilling systems for extraterrestrial subsurface exploration[J]. Astrobiology, 2008, 8(3): 665-706. DOI:10.1089/ast.2007.0179 (  0) 0)
|
| [2] |
SHERRIT S, DOLGIN B P, BAR-COHEN Y, et al. Modeling of horns for sonic/ultrasonic applications[C]//Proceedings of 1999 IEEE Ultrasonics Symposium. Caesars Tahoe, USA, 1999: 647-651.
(  0) 0)
|
| [3] |
BAR-COHEN Y, SHERRIT S, BAO Xiaoqi, et al. Subsurface sampler and sensors platform using the ultrasonic/sonic driller/corer (USDC)[C]//Proceedings of SPIE 6529, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2007. San Diego, USA, 2007: 65290E.
(  0) 0)
|
| [4] |
BAR-COHEN Y, SHERRIT S, DOLGIN B P, et al. Ultrasonic/sonic driller/corer (USDC) as a sampler for planetary exploration[C]//Proceedings of 2001 IEEE Aerospace Conference. Big Sky, USA, 2001: 263-271.
(  0) 0)
|
| [5] |
CHANG Z, SHERRIT S, BAO Xiaoqi, et al. Design and analysis of ultrasonic horn for USDC (ultrasonic/sonic driller/corer)[C]//Proceedings of SPIE 5388, Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies. Pasadena, USA, 2004: 320-326.
(  0) 0)
|
| [6] |
HARKNESS P, LUCAS M. A brief overview of space applications for ultrasonics[J]. Ultrasonics, 2012, 52(8): 975-979. DOI:10.1016/j.ultras.2012.09.004 (  0) 0)
|
| [7] |
BAR-COHEN Y, CHANG Z, SHERRIT S, et al. The ultrasonic/sonic driller/corer (USDC) as a subsurface drill, sampler, and lab-on-a-drill for planetary exploration applications[C]//Proceedings of SPIE 5762, Smart Structures and Materials 2005: Industrial and Commercial Applications of Smart Structures Technologies. San Diego, USA, 2005: 152-159.
(  0) 0)
|
| [8] |
POTTHAST C, TWIEFEL J, WALLASCHEK J. Modelling approaches for an ultrasonic percussion drill[J]. Journal of sound and vibration, 2007, 308(3/4/5): 405-417. (  0) 0)
|
| [9] |
NEUMANN N, SATTEL T, WALLASCHEK J. On set-oriented numerical methods for global analysis of non-smooth mechanical systems[J]. Journal of vibration and control, 2007, 13(9/10): 1393-1405. (  0) 0)
|
| [10] |
HARKNESS P, LUCAS M, CARDONI A. Architectures for ultrasonic planetary sample retrieval tools[J]. Ultrasonics, 2011, 51(8): 1026-1035. DOI:10.1016/j.ultras.2011.06.001 (  0) 0)
|
| [11] |
AL-BUDAIRI H, LUCAS M, HARKNESS P. A design approach for longitudinal-torsional ultrasonic transducers[J]. Sensors and actuators A (physical), 2013, 198: 99-106. DOI:10.1016/j.sna.2013.04.024 (  0) 0)
|
| [12] |
LI Xuan, WORRALL K, HARKNESS P, et al. A motion control system design for an ultrasonic planetary core drill (UPCD) unit[C]//AIAA SPACE 2015 Conference and Exposition. Pasadena, USA, 2015.
(  0) 0)
|
| [13] |
THOMAS P N H. Magna Parva and ESA's ultrasonic drill tool for planetary surface exploration[C]//Proceedings of the 12th Biennial International Conference on Engineering, Construction, and Operations in Challenging Environments; and Fourth NASA/ARO/ASCE Workshop on Granular Materials in Lunar and Martian Exploration. Honolulu, USA, 2010: 1235-1245.
(  0) 0)
|
| [14] |
KHMELEV V N, KHMELEV S S, KHMELEV M V, et al. Development of ultrasonic specifically drilling technology and improvement of construction of ultrasonic machine tools[C]//Proceedings of the 13th IEEE International Conference and Seminar of Young Specialists on Micro/Nanotechnologies and Electron Devices. Erlagol, Russia, 2012: 179-182.
(  0) 0)
|
| [15] |
KHMELEV V N, GENNE D V, KHMELEV S S, et al. Studies of functional possibilities of model sample of the ultrasonic apparatus for drilling of the simulator of lunar soil[C]//Proceedings of the 14th International Conference of Young Specialists on Micro/nanotechnologies and Electron Devices. Novosibirsk, Russia, 2013: 123-127.
(  0) 0)
|
| [16] |
KHMELEV V N, NESTEROV V A, KHMELEV S S, et al. The development of experimental sample of ultrasonic equipment for the intake of lunar soil[C]//Proceedings of the 13th IEEE International Conference and Seminar of Young Specialists on Micro/nanotechnologies and Electron Devices. Erlagol, Russia, 2012: 162-169.
(  0) 0)
|
| [17] |
郭俊杰, 黄卫清, 李志荣. 一种新型的超声波/声波钻探器[J]. 压电与声光, 2008, 30(5): 579-581. GUO Junjie, HUANG Weiqing, LI Zhirong. A new ultrasonic/sonic drilling device[J]. Piezoelectrics & acoustooptics, 2008, 30(5): 579-581. (  0) 0)
|
| [18] |
杨康. 基于超声波/声波能量耦合机理的钻探器研究[D]. 南京: 南京航空航天大学, 2012: 37-51. YANG Kang. Research on drilling corer based on ultrasonic/acoustic energy coupling mechanism[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012: 37-51. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041081.htm (  0) 0)
|
| [19] |
陈超, 杨康. 超声波/声波钻探器的设计与试验[J]. 振动、测试与诊断, 2013, 33(2): 252-257. CHEN Chao, YANG Kang. Design and experiment of ultrasonic/sonic drilling device[J]. Journal of vibration, measurement & diagnosis, 2013, 33(2): 252-257. (  0) 0)
|
| [20] |
梁彩红, 韦旌坤, 史立京, 等. 超声波取样钻机电耦合特性研究[J]. 探矿工程:岩土钻掘工程, 2015, 42(11): 46-49. LIANG Caihong, WEI Jingkun, SHI Lijing, et al. Research on electromechanical coupling properties of the ultrasonic/sonic driller/corer (USDC)[J]. Exploration engineering:rock & soil drilling and tunneling, 2015, 42(11): 46-49. (  0) 0)
|
| [21] |
梁彩红. 联接方式对太空超声取样钻性能影响的研究[D]. 北京: 中国地质大学(北京), 2015: 54-55. LIANG Caihong. Research on the impact of ultrasonic/sonic driller/corer (USDC)'s connection mode[D]. Beijing: China University of Geosciences (Beijing), 2015: 54-55. http://cdmd.cnki.com.cn/Article/CDMD-11415-1015391299.htm (  0) 0)
|
| [22] |
陈桂生. 超声换能器设计[M]. 北京: 海洋出版社, 1984: 108-235.
(  0) 0)
|
| [23] |
林书玉. 夹心式功率超声压电陶瓷换能器的工程设计[J]. 声学技术, 2006, 25(2): 160-164. LIN Shuyu. Design of sandwich piezoelectric ceramic ultrasonic transducer[J]. Technical acoustics, 2006, 25(2): 160-164. (  0) 0)
|
| [24] |
SHERRIT S, BAO Xiaoqi, BADESCU M, et al. Monolithic rapid prototype flexured ultrasonic horns[C]//Proceedings of 2010 IEEE Ultrasonics Symposium. Piscataway, San Diego, USA, 2010: 886-889.
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


