2. 中国航空工业空气动力研究院, 辽宁 沈阳 110034
2. AVIC Aerodynamic Research Institute, Shenyang 110034, China
在现代航空航天飞行器发展过程中,随着技术的进步与发展,研究中所涉及到的气动弹性问题越来复杂,由此所带来的非线性问题也越来越多。由于非线性问题带来的极限环振荡现象往往会引起结构疲劳,进而造成结构损伤乃至结构失效。因此,近年来关于非线性气动弹性力学的研究逐渐成为一个热点[1]。根据诱发非线性气弹问题的因素,将非线性问题分为气动非线性和结构非线性2类。气动非线性问题主要由跨声速时激波运动以及流动分离引发的非线性。结构非线性主要有几何大变形引发的几何非线性问题和间隙引起的非线性问题。由于装配问题,或者长时间的使用磨损导致操纵面铰链处普遍存在间隙,空中客车民用运输机曾出现操纵面间隙非线性引发的极限环振荡现象[2]。在F-22和F-35战斗机的设计过程中,对控制面间隙进行了大量的计算和试验研究[3]。这些研究表明了间隙的存在对飞行器的气弹特性有重要影响。为了减弱间隙所带来的极限环振荡引起的问题,美国军用标准MIL-A-8870要求所有全动控制面的间隙角不超过0.034°[4]。FAA同样采用了此类军标的技术要求,但是由于加工技术的限制,间隙角的要求往往很难达到,因此针对操纵面间隙问题的研究值得重视。
为了探究间隙非线性对气弹系统的影响,文献[5-7]针对低速带后缘操纵面的二维翼型进行了一系列的数值和试验研究,贺顺等[8]通过降阶模型方法研究了间隙非线性对气弹系统在跨音速阶段的影响,胡海岩等[9]总结了近期间隙非线性问题的研究进展。但目前的研究大多是采用较低精度方法对非定常气动力进行建模,本文采用基于非定常RANS方程耦合结构运动方程建立的高精度时域气动弹性分析方法进行间隙非线性问题的研究,计算了带后缘操纵面二元翼段的颤振速度,通过描述函数方法对间隙非线性问题进行处理,得到间隙非线性带来的一系列极限环振荡现象,通过频谱分析得到系统的主要作用频率。并探究了预加载方法对改善间隙非线性对颤振特性影响的作用。
1 非定常气动力求解 1.1 控制方程本文采用课题组开发的程序TeAM进行非定常气动力求解,该程序控制方程是三维可压缩非定常积分形式的N-S方程,在直角坐标系下其表达式为:
| $ \iiint\limits_\Omega {\left( {\frac{{\partial Q}}{{\partial t}} + \frac{{\partial \left( {F - {F_v}} \right)}}{{\partial x}} + \frac{{\partial \left( {G - {G_v}} \right)}}{{\partial y}} + \frac{{\partial \left( {H - {H_v}} \right)}}{{\partial z}}} \right){\text{d}}\mathit{\Omega }} = 0 $ | (1) |
式中:Q为守恒变量;F、G和H为无黏通量;Fv、Gv和Hv为黏性通量。方程空间离散无粘通量项采用Roe格式,粘性通量项采用中心格式进行空间离散,时间推进方法采用伪时间步法进行迭代求解,应用了多重网格及并行计算技术等进行加速求解,湍流模型采用Menter k-ω SST模型。边界条件包括物面边界条件、对称边界以及远场无反射边界条件等[10]。
1.2 非定常气动力验证非定常气动力的准确计算是研究气动弹性气特性的基础,本文以NACA0012跨声速强迫振动为例, 验证所采用非定常气动力计算方法的准确性。计算模型转轴位置以及力矩计算参考点均设在0.25倍弦长处。翼型强迫运动形式为:
| $ \alpha \left( t \right) = {\alpha _0} + {\alpha _m}\sin \left( {\omega t} \right),k = \omega b/{V_\infty } $ | (2) |
式中:b为翼型半弦长;V∞为来流速度;ω为翼型振动圆频率;Ma∞=0.755, α0=0.016°, αm=2.51°, k=0.081 4,计算采用的真实的时间步长为0.000 1 s,计算网格如下图 1所示,采用C型网格,单元数为7.15万。

|
Download:
|
| 图 1 NACA0012翼型网格示意 Fig. 1 Grid of NACA0012 | |
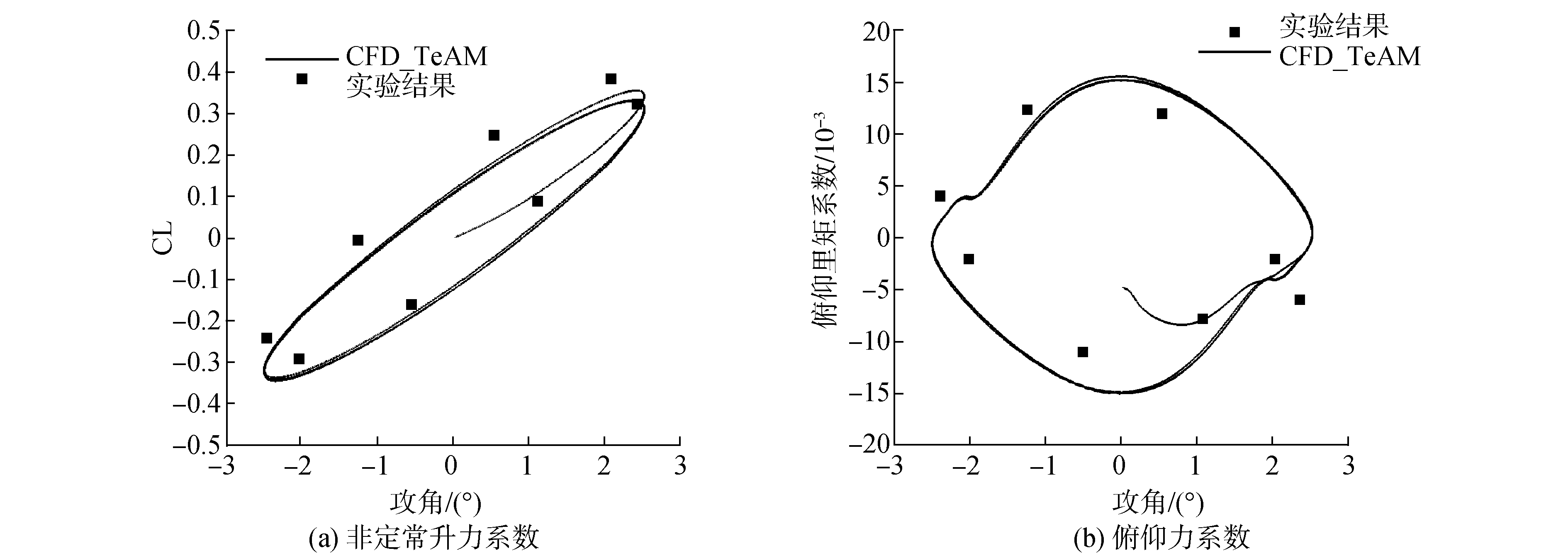
计算结果如图 2所示,分别为非定常升力系数与俯仰力矩系数随着攻角的变化情况,非定常气动力计算结果与实验[11]符合很好,证明该非定常气动力求解程序可以用以后续的气弹分析。
|
Download:
|
| 图 2 非定常升力系数和俯仰力矩系数随攻角变化 Fig. 2 Coefficients of lift and pitch moment change along with the angle of attack | |
对于气动弹性求解系统,除了非定常气动力求解模块之外,结构运动方程的求解同样不可缺少,结构运动方程通常写为[12]:
| $ \mathit{\boldsymbol{M\ddot q}} + \mathit{\boldsymbol{D\dot q}} + \mathit{\boldsymbol{Kq}} = \mathit{\boldsymbol{f}} $ | (3) |
一阶常微分方程组的时间求解方法较为成熟,因此将上式转化为状态空间方程的形式, 通过时间推进方法进行求解,如下所示:
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bf}} $ | (4) |
式中:
| $ \mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{q}}\\ {\mathit{\boldsymbol{\dot q}}} \end{array}} \right];\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&\mathit{\boldsymbol{I}}\\ { - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{K}}}&{ - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{D}}} \end{array}} \right];\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}\\ {{\mathit{\boldsymbol{M}}^{ - 1}}} \end{array}} \right] $ |
采用二阶Euler预估-校正方法[6]进行时间推进,形式如下:
预测:
| $ {{\mathit{\boldsymbol{\tilde x}}}^{n + 1}} = {\mathit{\boldsymbol{x}}^n} + \frac{1}{2}\mathit{\boldsymbol{A}}\left( {3{\mathit{\boldsymbol{x}}^n} - {\mathit{\boldsymbol{x}}^{n - 1}}} \right) + \frac{1}{2}\mathit{\boldsymbol{B}}\left( {3{\mathit{\boldsymbol{f}}^n} - {\mathit{\boldsymbol{f}}^{n - 1}}} \right) $ |
修正:
| $ {\mathit{\boldsymbol{x}}^{n + 1}} = {\mathit{\boldsymbol{x}}^n} + \frac{1}{2}\mathit{\boldsymbol{A}}\left( {{{\mathit{\boldsymbol{\tilde x}}}^{n + 1}} + {\mathit{\boldsymbol{x}}^n}} \right) + \frac{1}{2}{\mathit{\boldsymbol{B}}}\left( {{{\mathit{\boldsymbol{\tilde f}}}^{n + 1}} + {\mathit{\boldsymbol{f}}^n}} \right) $ |
对于带操纵面的二维翼型沉浮/俯仰/操纵面偏转三自由度颤振问题,结构矩阵、模态位移和广义力定义如下:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} M&{{S_\alpha }}&{{S_\beta }}\\ {{S_\alpha }}&{{I_\alpha }}&{{I_\beta } + b\left( {{a_f} - a} \right){S_\beta }}\\ {{S_\beta }}&{{I_\beta } + b\left( {{a_f} - a} \right){S_\beta }}&{{I_\beta }} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{D_h}}&{}&{}\\ {}&{{D_\alpha }}&{}\\ {}&{}&{{D_\beta }} \end{array}} \right],\mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{K_h}}&{}&{}\\ {}&{{K_\alpha }}&{}\\ {}&{}&{{K_\beta }} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{q}} = \left[ {\begin{array}{*{20}{c}} h\\ \alpha \\ \beta \end{array}} \right],\mathit{\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} { - L}\\ {{M_y}}\\ {{M_\beta }} \end{array}} \right] $ |
式中:h为沉浮位移,向下为正;α为俯仰角,抬头为正;β为操纵面偏转角,顺时针为正;M为整个弹性系统的质量;Sα和Iα分别为关于弹性轴的一阶、二阶惯性矩;Sβ和Iβ分别为操纵面关于铰链轴的一阶、二阶惯性矩;a和af分别是弹性轴和操纵面铰链轴的位置;Dh和Dα分别为沉浮和俯仰阻尼;Dβ为操纵面偏转的阻尼;Kh和Kα分别为沉浮和扭转刚度;Kβ为关于铰链轴的扭转刚度;L为升力;My为俯仰力矩;Mβ为操纵面铰链力矩。将第1个方程除以mb,第2个和第3个方程除以mb2,时间通过俯仰频率无量纲处理τ=ωαt,重新整理得到无量纲形式表达式如下:
| $ \mathit{\boldsymbol{\tilde M}} = \left[ {\begin{array}{*{20}{c}} {M/m}&{{x_\alpha }}&{{x_\beta }}\\ {{x_\alpha }}&{r_\alpha ^2}&{r_\alpha ^2 + b\left( {{a_f} - a} \right){x_\beta }}\\ {{x_\beta }}&{r_\alpha ^2 + b\left( {{a_f} - a} \right){x_\beta }}&{r_\beta ^2} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\tilde D}} = \left[ {\begin{array}{*{20}{c}} {{\zeta _h}}&{}&{}\\ {}&{{\zeta _\alpha }}&{}\\ {}&{}&{{\zeta _\beta }} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\tilde K}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\omega _h}/{\omega _\alpha }} \right)}^2}}&{}&{}\\ {}&{r_\alpha ^2}&{}\\ {}&{}&{r_\beta ^2{{\left( {{\omega _\beta }/{\omega _\alpha }} \right)}^2}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{\tilde q}} = \left[ {\begin{array}{*{20}{c}} {h/b}\\ \alpha \\ \beta \end{array}} \right],\mathit{\boldsymbol{\tilde f}} = \frac{{V_f^2}}{{\rm{ \mathsf{ π} }}}\left[ {\begin{array}{*{20}{c}} { - {C_l}}\\ {2{C_m}}\\ {2{C_{{m_\beta }}}} \end{array}} \right] $ |
式中:m为翼型质量;b为参考长度(弦长的1/2);弹性轴和质心的无量纲距离xα=Sα/mb;操纵面转轴和操纵面质心xβ=Sβ/mb;沉浮、俯仰和操纵面偏转阻尼系数ζα=Dh/2mωh;ζα=Dα/2Iαωα和ζβ=Dβ/Iβωβ;沉浮、俯仰和操纵面偏转自然频率

|
Download:
|
| 图 3 带后缘操纵面二维翼型的几何和结构参数的定义 Fig. 3 Geometry and structural definition of foil with actor | |
为了研究间隙非线性问题,杜克大学Conner等[14]和Tang等[6]对带后缘操纵面的NACA0012翼型开展了一系列的试验研究,试验结果包括线性系统(无间隙非线性)颤振边界和不同间隙角情况下的极限环振荡,如图 4[13]所示。
|
Download:
|
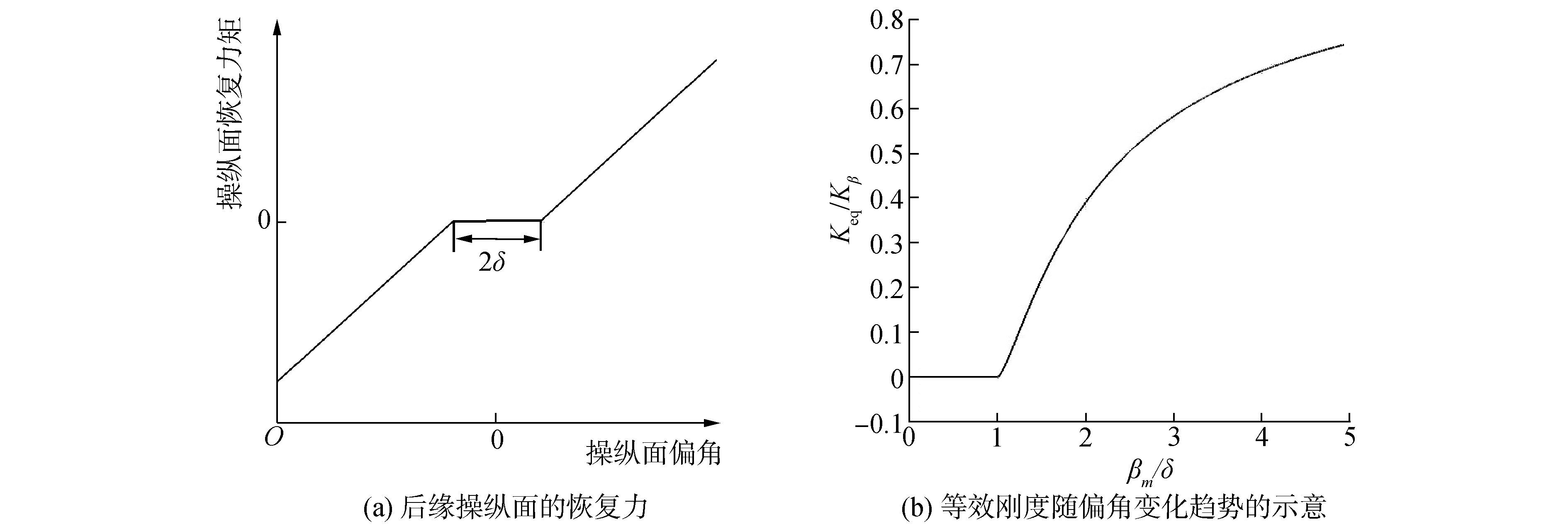
| 图 4 后缘操纵面的恢复力矩和等效刚度随偏角变化趋势的示意 Fig. 4 The recovery moment and equivalent stiffness of the trailing edge control surface change along with the angle of attack | |
图 4(a)为后缘操纵面恢复力矩随偏角的变化趋势,写成公式为:
| $ {\tau _\beta } = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0,\\ {K_\beta }\left( {\beta - \delta } \right), \end{array}&\begin{array}{l} \left| \beta \right| \le \delta \\ \left| \beta \right| > \delta \end{array} \end{array}} \right. $ |
式中:Kβ为线性后缘偏转刚度;δ定义间隙非线性存在的范围,为间隙角的一半。基于描述函数方法能够得到等效刚度,首先假设俯仰角是简谐变化:
| $ \beta = {\beta _m}\sin \left( {\omega t} \right) $ | (5) |
然后对一个周期内的恢复力矩积分,得到:
| $ {\tau _{\beta ,eq}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}/\omega } {{\tau _\beta }\left( t \right)\sin \left( {\omega t} \right){\rm{d}}t} $ | (6) |
将上式除以俯仰角振幅即可得到等效刚度:
| $ {K_{eq}} = {\tau _{\beta ,eq}}/{\beta _m} $ | (7) |
等效刚度Keq/Kβ随操纵面偏角振幅βm/δ的变化趋势如图 4(b)所示。
该构型的结构参数为:M/m=2.172, xα=0.434, xβ=0.019 96, rα=0.732 1, rβ=0.113 97, a=-1.0, af=1.0,沉浮、俯仰和操纵面偏转3个模态的自然频率分别为ωh=6.769 2 Hz, ωα=8.379 8 Hz, ωβ=17.385 9 Hz, 各模态阻尼系数ζh=0.011 3, ζα=0.016 26, ζβ=0.011 5, 质量比μ=25.24。注意ζh、ζα、ζβ分别是3个耦合自由度的阻尼系数,首先需要将之转换到[h, α, β]坐标系:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{D \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{c}} {2{m_h}{{\omega '}_h}{\zeta _h}}&{}&{}\\ {}&{2{m_\alpha }{{\omega '}_\alpha }{\zeta _\alpha }}&{}\\ {}&{}&{2{m_\beta }{{\omega '}_\beta }{\zeta _\beta }} \end{array}} \right] $ |
式中:mh、mα、mβ是模态质量;ω′h、ω′α、ω′β是耦合频率。矩阵Φ=[φhφαφβ]如下:
| $ \omega _i^2\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{\varphi }}_i} = \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{\varphi }}_i},\;\;\;\;i = h,\alpha ,\beta $ | (8) |
这样就能得到[h, α, β]坐标系下的阻尼矩阵D,建立三自由度气动弹性系统。Conner等[14]、Tang等[6]分别基于线性气动力理论,利用描述函数方法和特征模态降阶模型对NACA0 012间隙非线性问题开展研究,计算结果与试验结果较为吻合。本文后续将采用RANS方法进行带后缘操纵面的二元机翼的颤振速度预测,并分析由间隙非线性带来的极限环振荡行为以及间隙非线性对颤振特性的影响等问题。
3.2 间隙非线性带来的极限环振荡采用与1.2节相同的C型计算网格,网格的弦向和法向维度是425×101,其中流向有337点在翼型表面,自由来流速度为5~25 m/s,基于弦长的雷诺数等于0.52×106。虽然雷诺数较低,但是风洞的来流湍流度较大(≈1%),因此翼型表面不会出现大范围的层流区,本文直接采用全湍假设,计算步长为5×10-5 s。
对于间隙角δ=0°的线性系统,颤振速度和频率如表 1所示,计算结果与试验的颤振速度差别在15%以上。根据参考文献[14]修正沉浮、俯仰及操纵面偏转3个自由度的刚度后,得到的颤振速度与试验结果的误差由13.77%减小至5.34%,颤振频率的误差由11.52%减小至2.56%。
| 表 1 颤振速度和频率的对比及刚度修正的影响 Table 1 Comparison of flutter speed and frequency and the effect of stiffness correction |
然后研究气弹系统中间隙非线性导致的极限环振荡行为。本文分别取3种间隙角构型进行计算,文献[14]研究了3种间隙角构型gap1、gap2和gap3的间隙角δ分别为±1.15°、±1.83°和±2.12°,为节省计算时间本文取gap1和gap3进行研究。Conner等[14]提供了在不同来流速度下振荡频率及各模态位移均方根的试验结果,其中沉浮位移、俯仰角和操纵面偏转角的均方根定义为:
| $ {h_{{\rm{rms}}}} = \sum\limits_{n = {N_1} + 1}^{{N_2}} {\sqrt {{{\left( {h\left( {{t_n}} \right) - {h_{{\rm{avg}}}}} \right)}^2}/\left( {{N_2} - {N_1}} \right)} /\left( {b\delta } \right)} $ |
| $ {\alpha _{{\rm{rms}}}} = \sum\limits_{n = {N_1} + 1}^{{N_2}} {\sqrt {{{\left( {\alpha \left( {{t_n}} \right) - {\alpha _{{\rm{avg}}}}} \right)}^2}/\left( {{N_2} - {N_1}} \right)} /\delta } $ |
| $ {\beta _{{\rm{rms}}}} = \sum\limits_{n = {N_1} + 1}^{{N_2}} {\sqrt {{{\left( {\beta \left( {{t_n}} \right) - {\beta _{{\rm{avg}}}}} \right)}^2}/\left( {{N_2} - {N_1}} \right)} /\delta } $ |
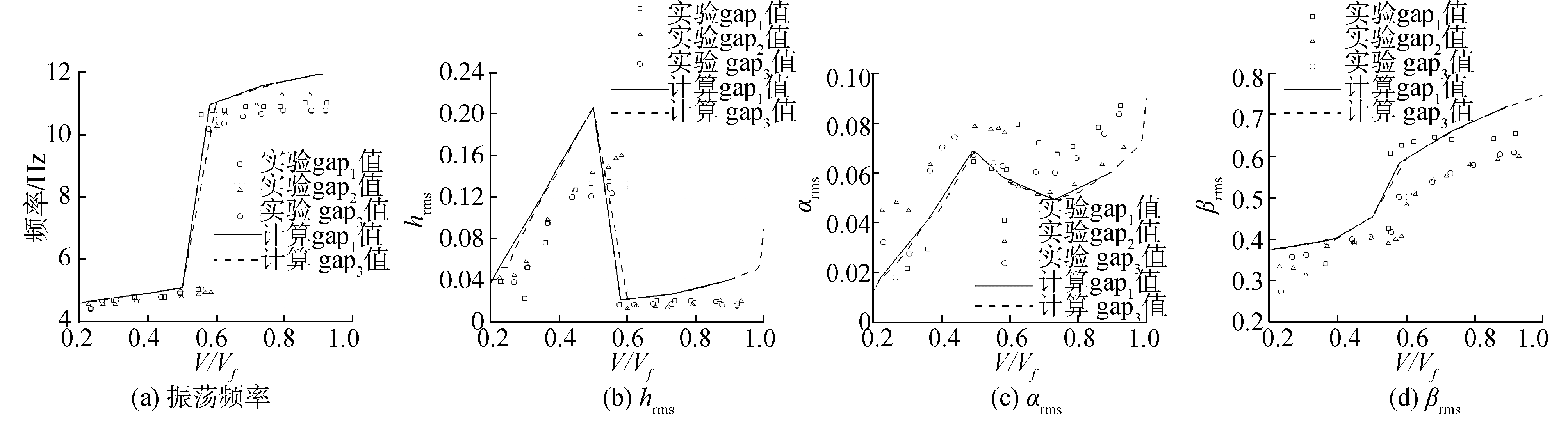
式中:N1+1至N2为若干个运动周期的计算步数。振荡频率及各模态位移均方根的结果对比如图 5所示,计算结果与试验值吻合较好。
|
Download:
|
| 图 5 振荡频率及各模态位移均方根的试验结果与计算结果对比 Fig. 5 Comparison of the oscillation frequency and the mean square of the modal displacement with the experiment results | |
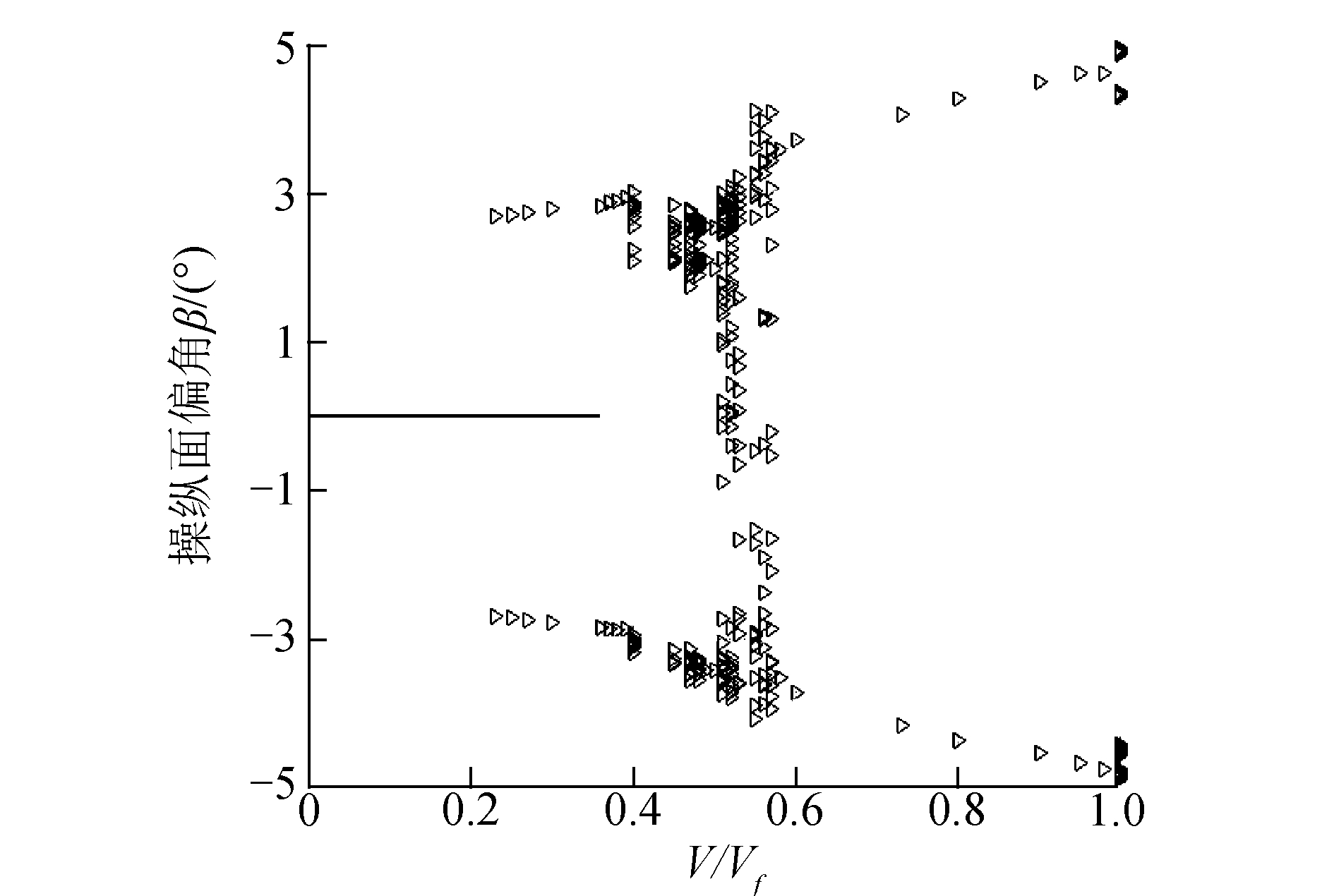
文献[14]在不同来流速度(由小到大)下出现了5种典型的响应:衰减振荡、低频对称LCO、非周期响应、低频非对称LCO和高频LCO。本文以gap3为例进行分析,图 6为后缘操纵面偏角的分岔图,当来流速度比0.23≤V/Vf≤0.36时,系统处于亚临界Hopf分岔,较大的初始扰动(
|
Download:
|
| 图 6 后缘操纵面偏角的分岔 Fig. 6 Bifurcation of skew angle of trailing edge control surface | |

|
Download:
|
| 图 7 来流速度比V/Vf=0.27时后缘操纵面偏角的相图和频谱能量分布 Fig. 7 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.27 | |
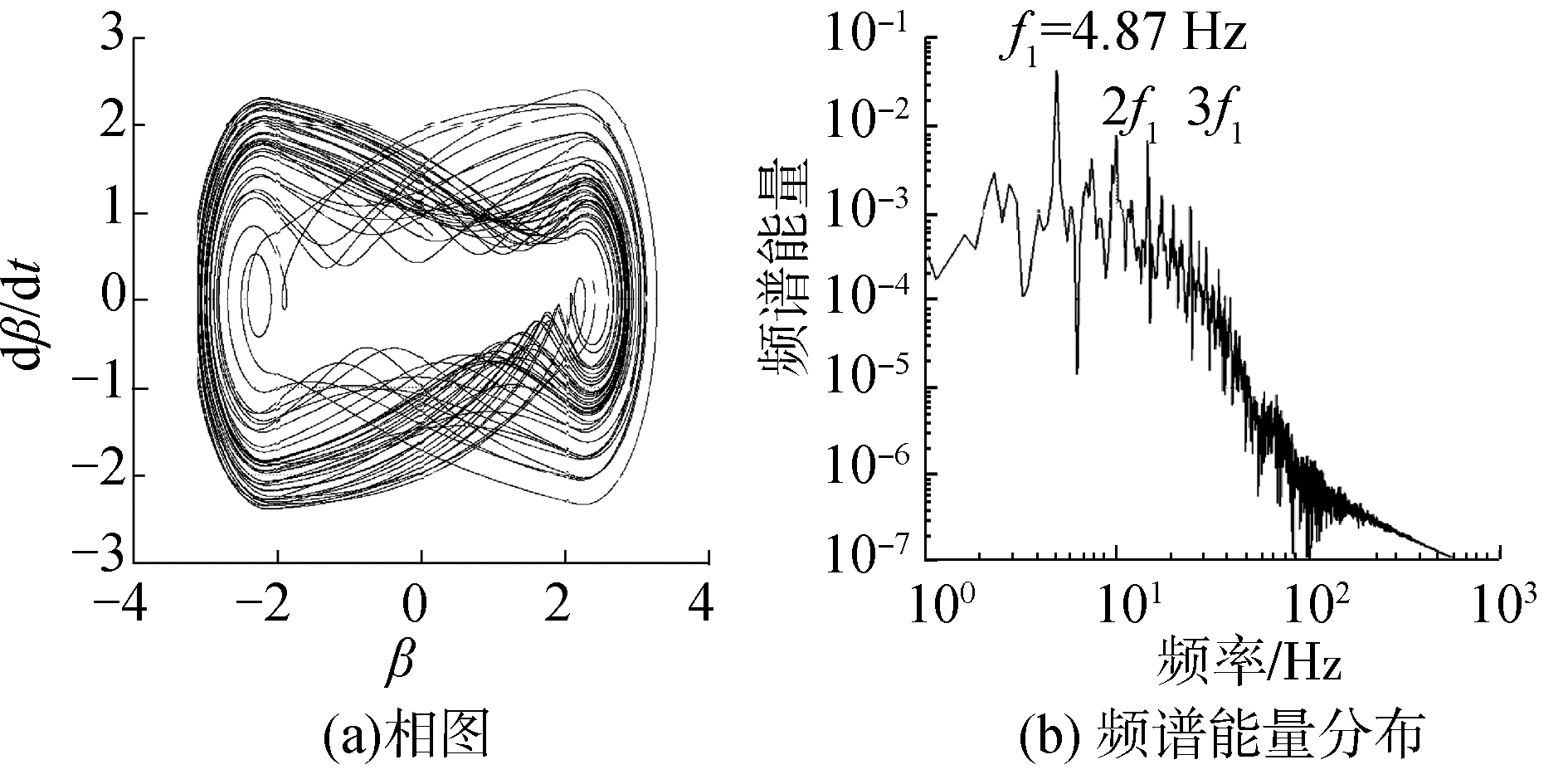
|
Download:
|
| 图 8 来流速度比V/Vf=0.40时后缘操纵面偏角的相图和频谱能量分布 Fig. 8 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.40 | |
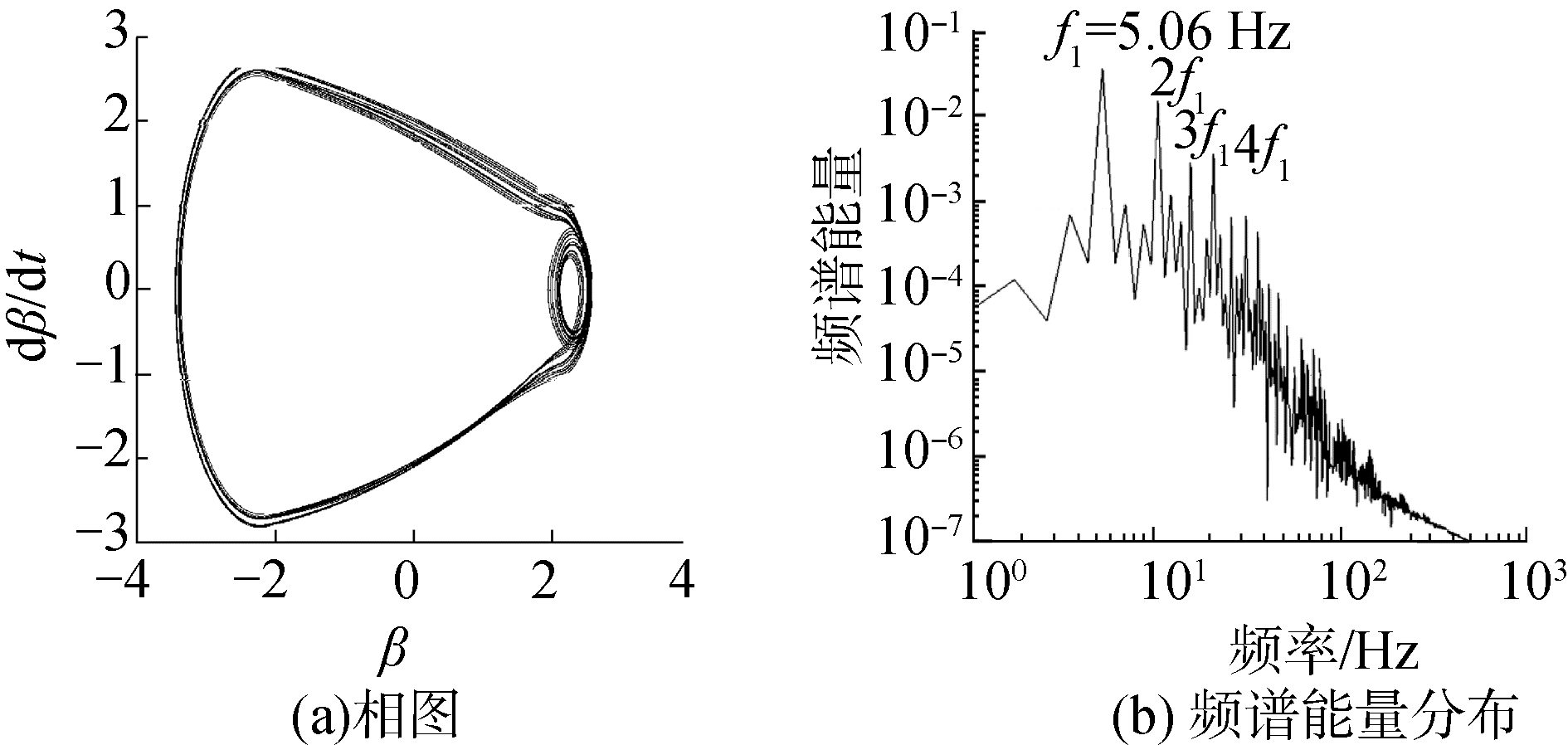
|
Download:
|
| 图 9 来流速度比V/Vf=0.49时后缘操纵面偏角的相图和频谱能量分布 Fig. 9 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.49 | |
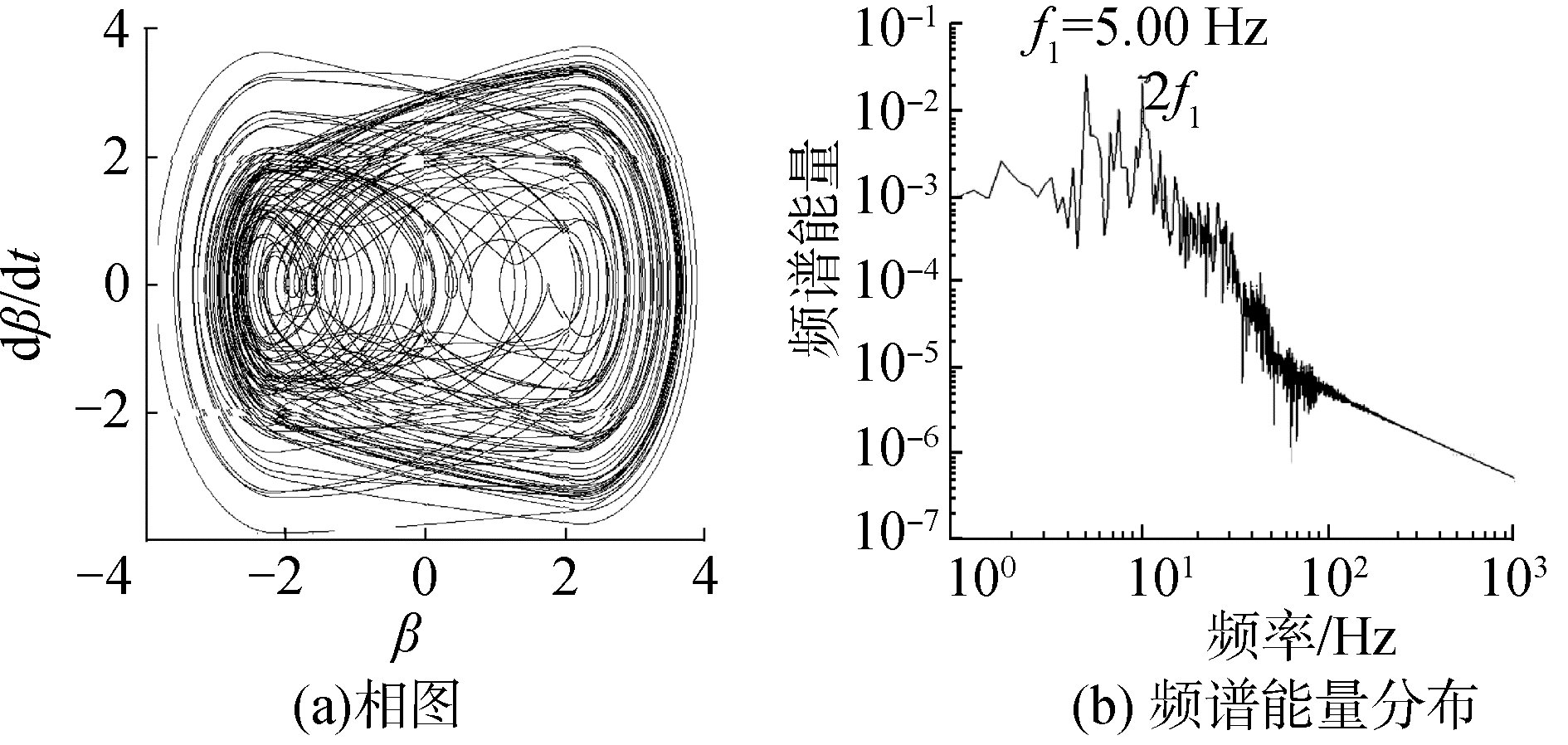
|
Download:
|
| 图 10 来流速度比V/Vf=0.52时后缘操纵面偏角的相图和频谱能量分布 Fig. 10 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.52 | |
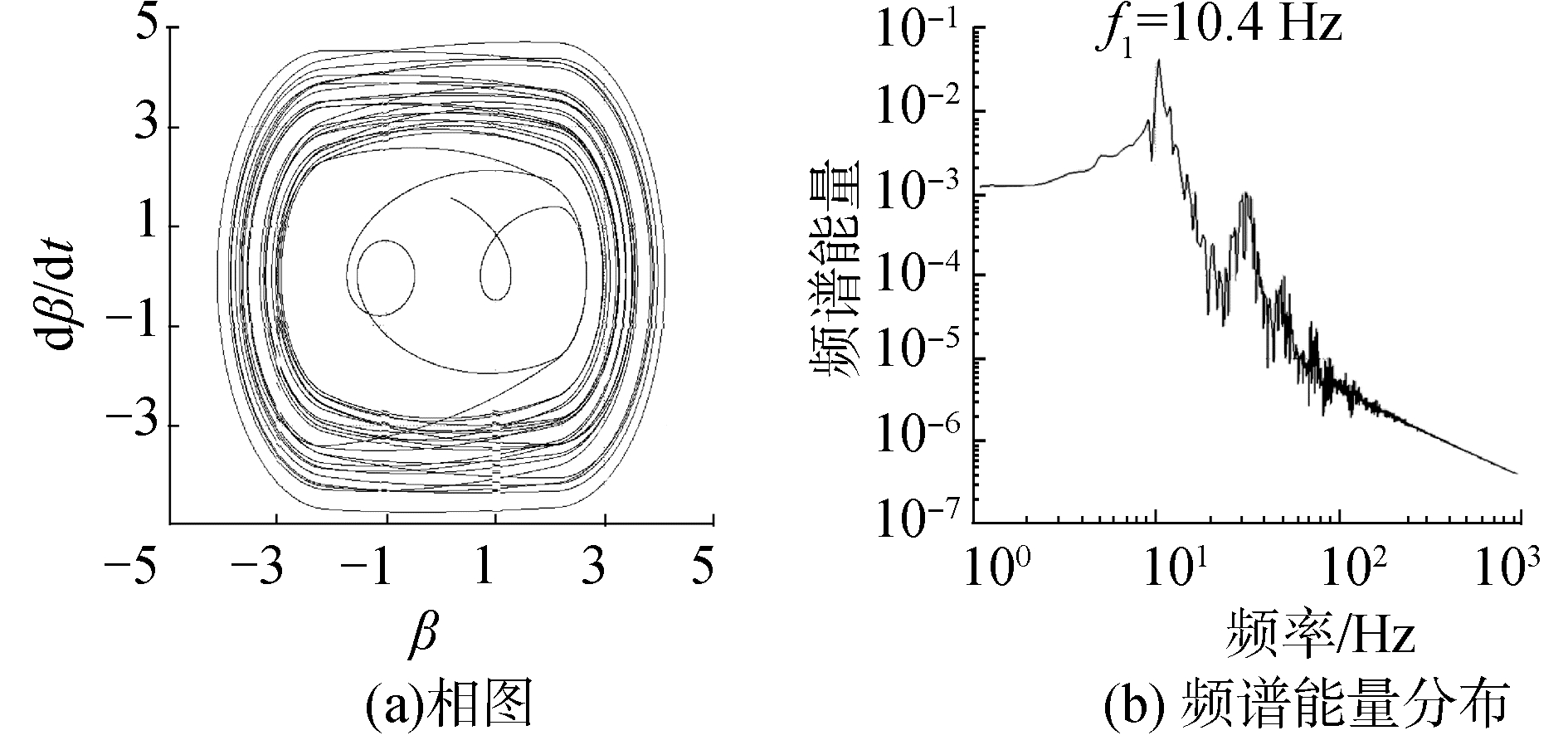
|
Download:
|
| 图 11 来流速度比V/Vf=0.55时后缘操纵面偏角的相图和频谱能量分布 Fig. 11 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.55 | |

|
Download:
|
| 图 12 来流速度比V/Vf=0.60时后缘操纵面偏角的相图和频谱能量分布 Fig. 12 Phase diagram and spectral energy distribution of the skew angle of the trailing edge control surface of velocity at V/Vf=0.60 | |
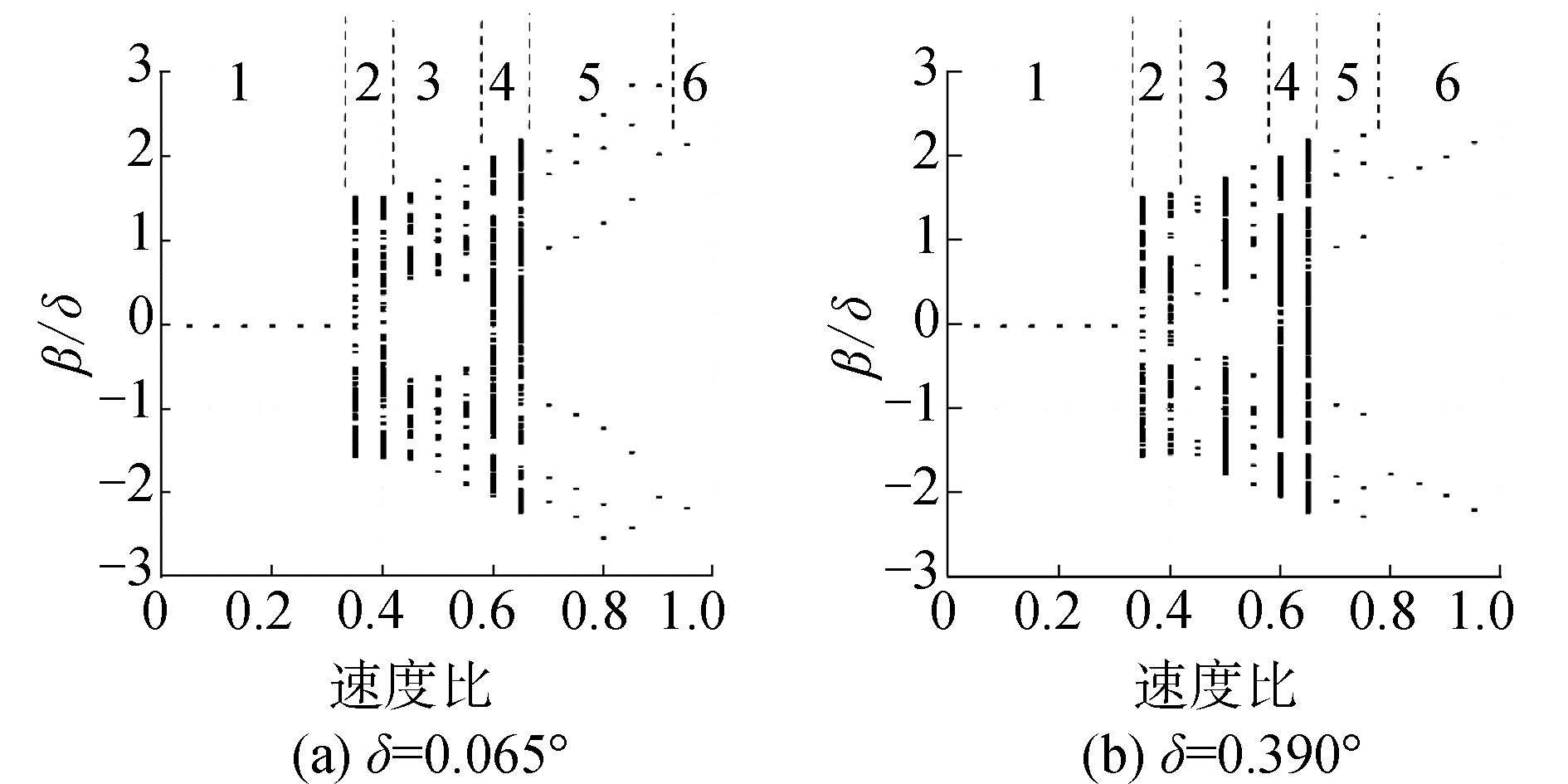
由3.2节计算结果可知,后缘操纵面间隙非线性使得颤振速度大幅下降,系统还出现复杂的LCO和非周期响应。为了研究间隙非线性对颤振特性的影响,以Ma为0.20和0.80为例,初始扰动

|
Download:
|
| 图 13 Ma=0.20时间隙非线性系统的操纵面偏角分岔图 Fig. 13 The bifurcation of the nonlinear system for free-play of control surface at Ma=0.20 注:1.衰减振荡,2.非周期响应,3.LCO | |
|
Download:
|
| 图 14 Ma=0.80时间隙非线性系统的操纵面偏角分岔图 Fig. 14 The bifurcation of the nonlinear system for free-play of control surface at Ma=0.80 注:1.衰减振荡,2.非周期响应,3.复杂LCO,4.非周期响应,5.复杂LCO,6.高频LCO | |
颤振速度下降的主要原因是间隙非线性导致后缘操纵面偏转刚度降低,最极端的情况是当操纵面偏角在±δ范围时,操纵面刚度为0。如果为系统提供一个预加载τ0,此时τβ如下:
| $ {\tau _\beta } = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\tau _0},\\ {\tau _0} + {K_\beta }\left( {\beta - \delta } \right), \end{array}&\begin{array}{l} \left| \beta \right| \le \delta \\ \left| \beta \right| > \delta \end{array} \end{array}} \right. $ | (10) |
预加载τ0可以为后缘操纵面提供了一个张紧力,使β离开±δ范围,仍然假设操纵面偏角是简谐变化:
| $ \beta = {\beta _0} + {\beta _m}\cos \left( {\omega t} \right) $ | (11) |
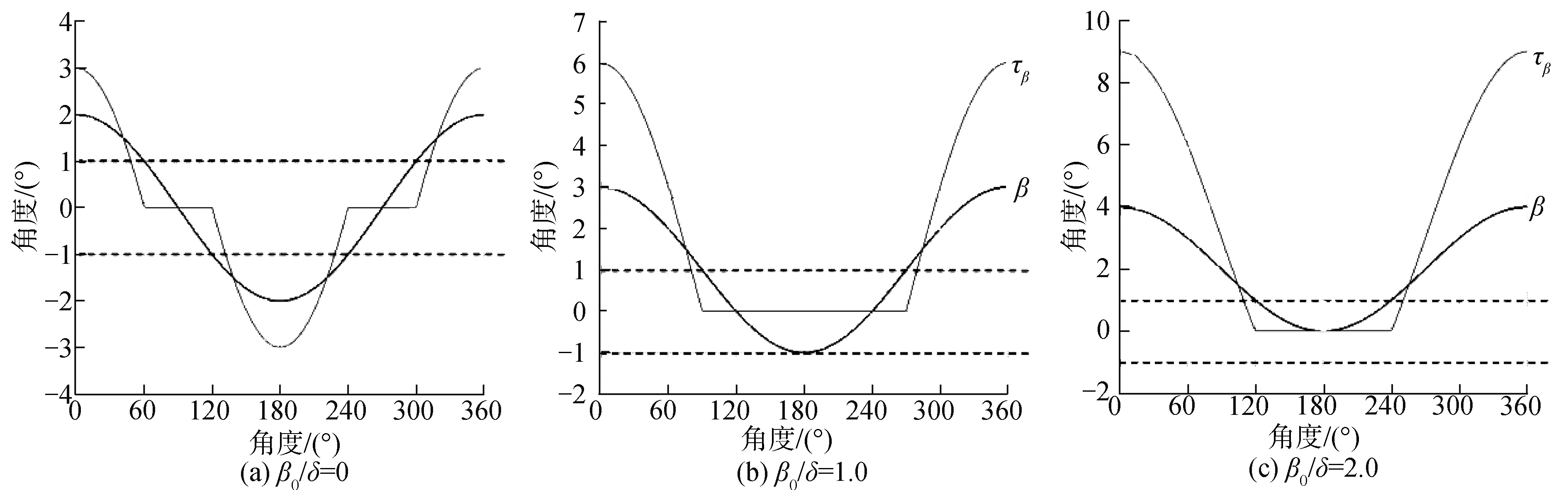
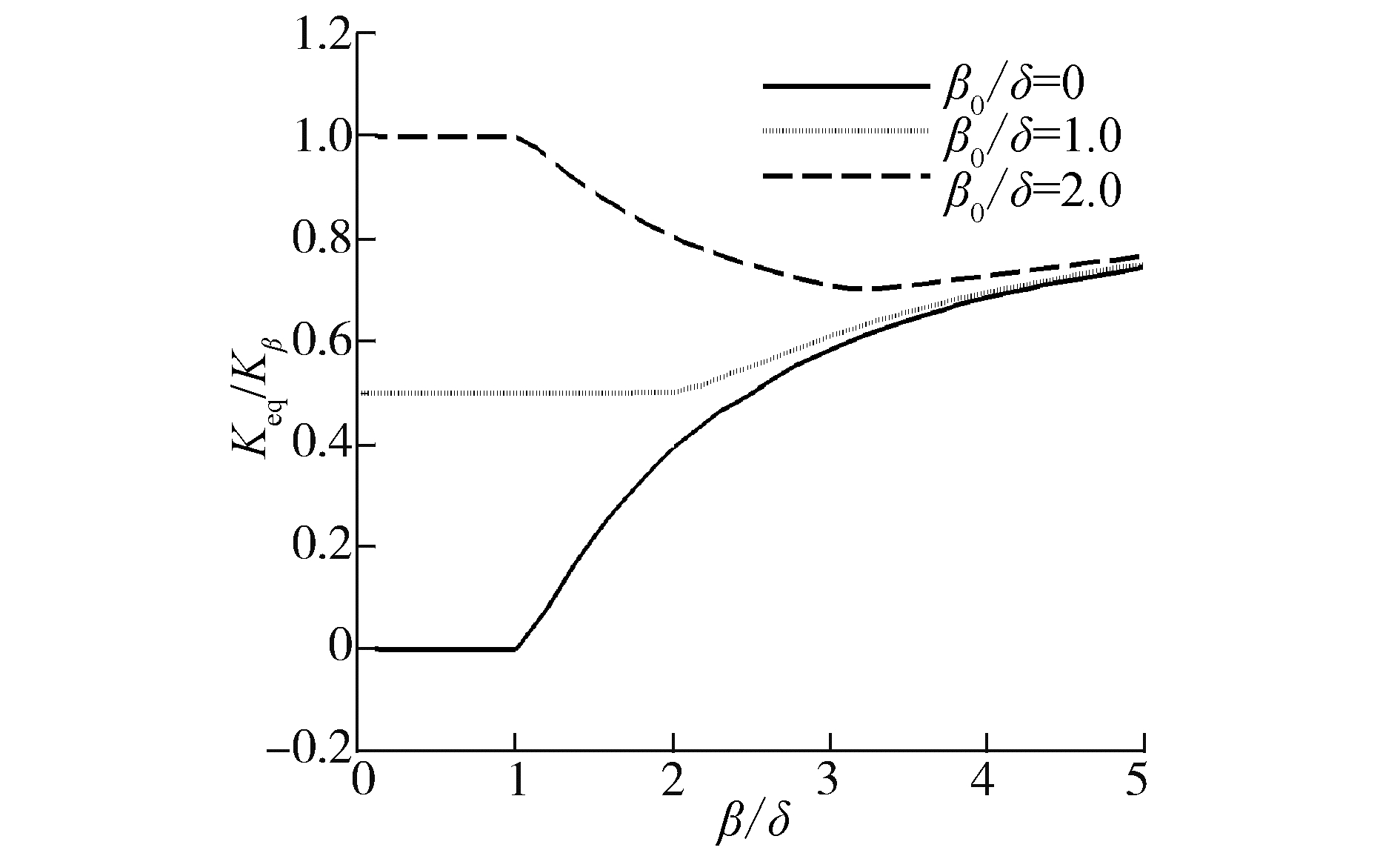
以βm/δ=2.0,Kβ=3.0为例,操纵面偏角和恢复力矩的变化如图 15所示,随着操纵面偏角β离开间隙非线性范围(虚线范围内)的增加,等效刚度显著增加,图 15(a)、(b)和(c)的等效刚度比Keq/Kβ分别为0.391,0.500和0.804。由图 16可见,在偏角振幅βm较小时,τ0可以使后缘操纵面的等效刚度显著增加,从而提高颤振速度。
|
Download:
|
| 图 15 不同初始操纵面偏角β0对应的恢复力矩 Fig. 15 The restoring moments corresponding to the initial control surface deflection angle β0 | |
|
Download:
|
| 图 16 在不同初始偏角β0下等效刚度比Keq/Kβ随着操纵面偏角振幅βm的变化情况 Fig. 16 The equivalent stiffness ratio Keq/Kβ varies with the amplitude of the deflection angle βm of the control surface at different initial skew angles of β0 | |
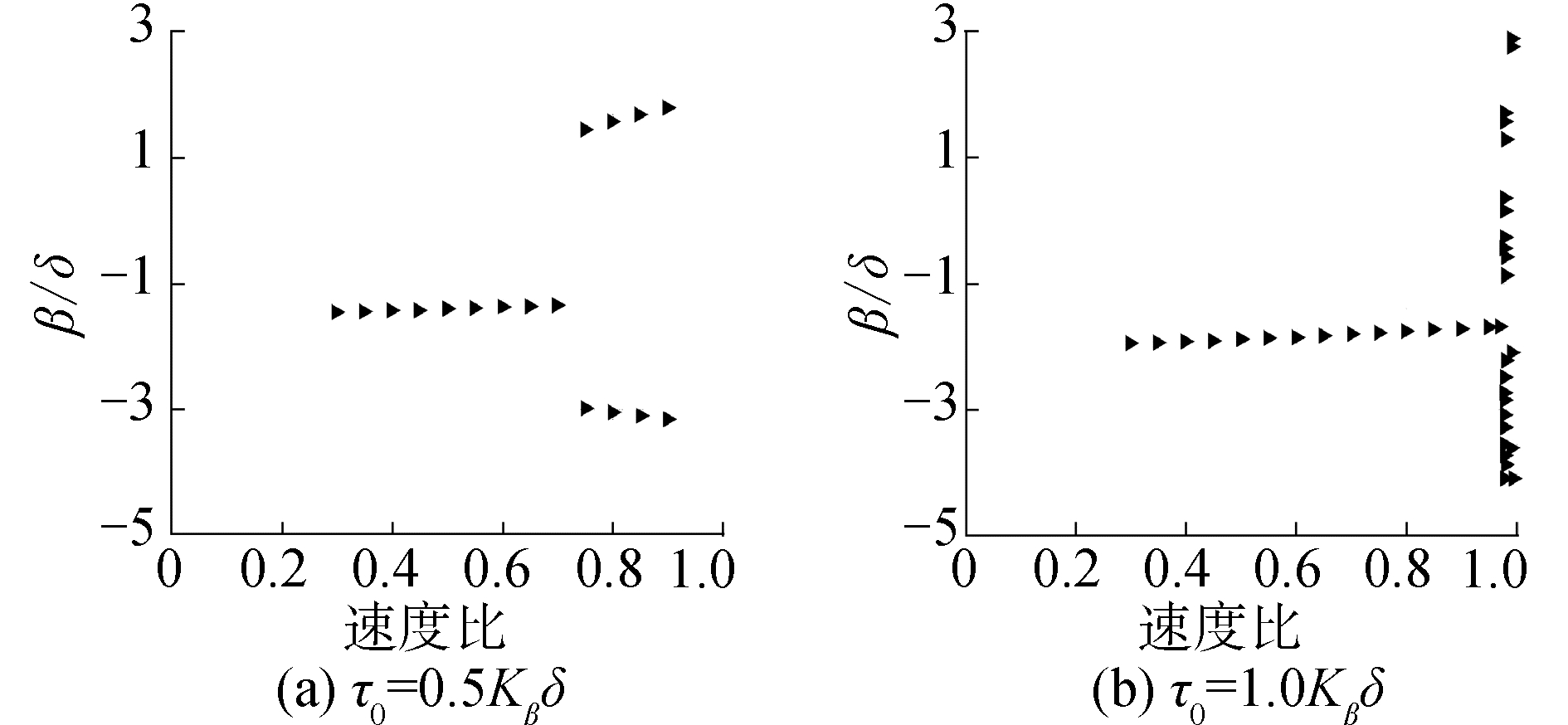
当Ma=0.20、δ=0.39°时,预加载τ0分别为0.5Kβδ和1.0Kβδ的后缘操纵面偏角分岔图如图 17所示。结果表明:预加载τ0可以显著提高颤振速度,分别提升至无间隙非线性系统的75%和98%。
|
Download:
|
| 图 17 Ma=0.20,δ=0.39°时不同预加载的操纵面偏角分岔图 Fig. 17 The bifurcation of different preloaded control surface deflection angle at Ma=0.21, δ=0.39° | |
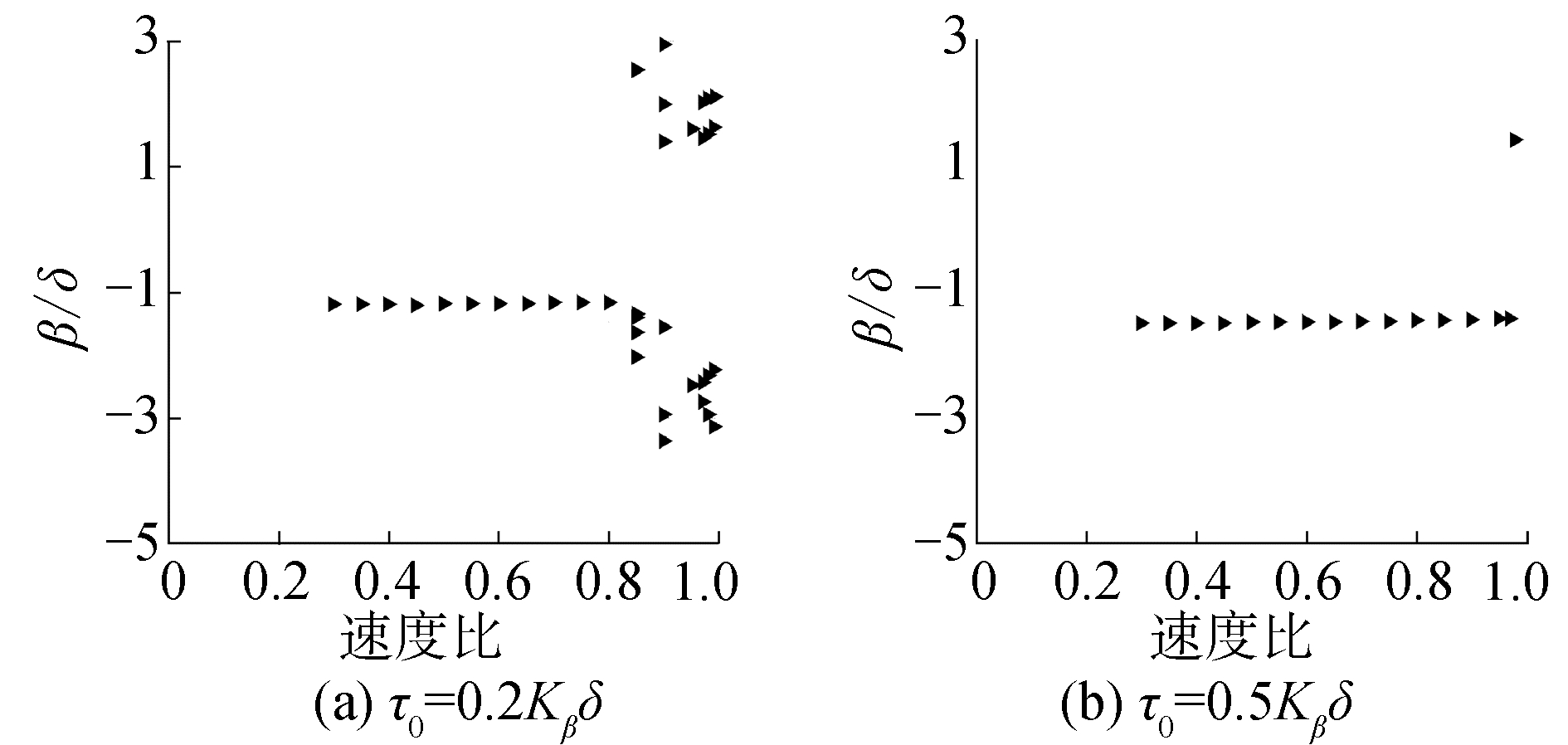
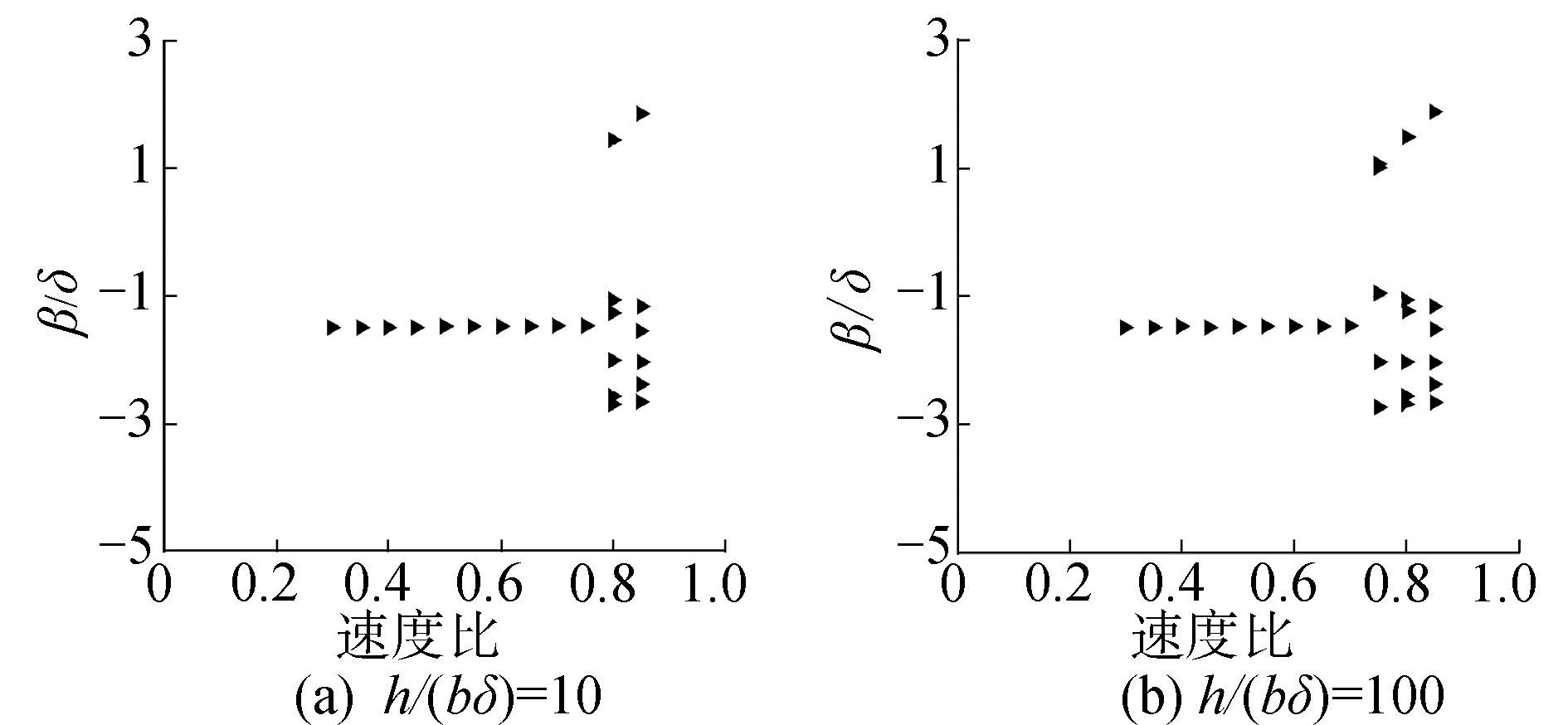
当Ma=0.80、δ=0.39°时,预加载τ0分别为0.2Kβδ和0.5Kβδ的后缘操纵面偏角分岔图如图 18所示,颤振速度分别提升至无间隙非线性系统的80%和98%。此外,初始扰动对预加载系统的颤振速度产生较大影响,如图 19所示,将初始扰动增大10倍和100倍后,系统的颤振速度由0.98Vf下降至0.8和0.75。因此,需要根据实际情况施加预加载来减弱间隙非线性的影响,但是预加载的不足之处在于消耗了最大承载力和响应速度,增加了飞行控制系统设计的复杂性。
|
Download:
|
| 图 18 Ma=0.80,δ=0.39°时不同预加载的操纵面偏角分岔图 Fig. 18 The bifurcation of different preloaded control surface deflection angle at Ma=0.80, δ=0.39° | |
|
Download:
|
| 图 19 Ma=0.80,δ=0.39°,τ0=0.5Kβδ时不同初始扰动的操纵面偏角分岔图 Fig. 19 The bifurcation of different initial disturbance of control surface deflection angle at Ma=0.80, δ=0.39°, τ0=0.5Kβδ | |
1) 分析了低速线性和间隙非线性系统的颤振特性,并与实验结果进行对比,证明了本文颤振时域分析方法的可行性。
2) 通过对不同来流速度下气弹响应的时域计算,得到了间隙非线性影响下产生的5种典型的响应,并通过频谱分析得到了各响应的主要作用频率。
3) 探讨了间隙大小对亚音速和跨声速阶段非线性系统分岔特性的影响,亚音速情况下由于不存在激波的影响,系统主要受到间隙非线性的影响,分岔图基本一致。跨音速阶段由于激波影响,会使得分岔图有明显的变化。
4) 研究了通过预加载措施提高颤振速度可行性,通过预加载可以使得后缘操纵面等效刚度增加,提高系统颤振速度。
| [1] |
DOWELL E H, EDWARDS J, STRGANAC T. Nonlinear aeroelasticity[J]. Journal of aircraft, 2003, 40(5): 857-874. DOI:10.2514/2.6876 (  0) 0)
|
| [2] |
CROFT J. Airbus elevator flutter:annoying or dangerous?[J]. Aviation week and space technology, 2001, 155(9): 41. (  0) 0)
|
| [3] |
CHEN P C, RITZ E, LINDSLEY N. Nonlinear flutter analysis for the scaled F-35 with horizontal-tail free play[J]. Journal of aircraft, 2015, 51(3): 883-889. (  0) 0)
|
| [4] |
ANDERSON W D, MORTARA S. Maximum control surface freeplay, design and flight testing approach on the F-22[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Hawaii, 2007: 1-12.
(  0) 0)
|
| [5] |
TANG Deman, DOWELL E H. Computational/experimental aeroelastic study for a horizontal-tail model with free play[J]. AIAA journal, 2013, 51(2): 341-352. DOI:10.2514/1.J051781 (  0) 0)
|
| [6] |
TANG D, DOWELL E H, VIRGIN L N. Limit cycle behavior of an airfoil with a control surface[J]. Journal of fluids and structures, 1998, 12(7): 839-858. DOI:10.1006/jfls.1998.0174 (  0) 0)
|
| [7] |
EDWARDS J W, BENNETT R M, WHITLOW W, et al. Time-marching transonic flutter solutions including angle-of-attack effects[J]. Journal of aircraft, 1983, 20(11): 899-906. DOI:10.2514/3.48190 (  0) 0)
|
| [8] |
HE Shun, YANG Zhichun, GU Yingsong. Nonlinear dynamics of an aeroelastic airfoil with free-play in transonic flow[J]. Nonlinear dynamics, 2017, 87(4): 2099-2125. DOI:10.1007/s11071-016-3176-4 (  0) 0)
|
| [9] |
胡海岩, 赵永辉, 黄锐. 飞机结构气动弹性分析与控制研究[J]. 力学学报, 2016, 48(1): 1-27. HU Haiyan, ZHAO Yonghui, HUANG Rui. Studies on aeroelastic analysis and control of aircraft structures[J]. Chinese journal of theoretical and applied mechanics, 2016, 48(1): 1-27. DOI:10.3969/j.issn.1006-6616.2016.01.001 (  0) 0)
|
| [10] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 254-258. YAN C. The computational fluid dynamics method and its application[M]. Beijing: Beihang University Press, 2006: 254-258. (  0) 0)
|
| [11] |
张伟伟.基于CFD技术的高效气动弹性分析方法研究[D].西安: 西北工业大学, 2006: 68-69. ZHANG Weiwei. Efficient analysis for aeroelasticity based on computational fluid dynamics[D]. Xi'an: Northwestern Polytechnical University, 2006: 68-69. http://cdmd.cnki.com.cn/article/cdmd-10699-2007214276.htm (  0) 0)
|
| [12] |
方同, 薛璞. 振动理论及应用[M]. 西安: 西北工业大学出版社, 1998: 100-107. FANG Tong, XUE Pu. Vibration theory and application[M]. Xi'an: Northwestern Polytechnical University Press, 1998: 100-107. (  0) 0)
|
| [13] |
DOWELL E H, TANG Deman. Nonlinear aeroelasticity and unsteady aerodynamics[J]. AIAA journal, 2002, 40(9): 1697-1707. DOI:10.2514/2.1853 (  0) 0)
|
| [14] |
CONNER M D, TANG D M, DOWELL E H, et al. Nonlinear behavior of a typical airfoil section with control surface freeplay:a numerical and experimental study[J]. Journal of fluids and structures, 1997, 11(1): 89-109. DOI:10.1006/jfls.1996.0068 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


