孔流与堰流在泄水建筑物中同时存在是一种复杂的水力学现象,这种泄流方式已经广泛出现在水利防洪工程中,例如:大坝的多层泄水,水力自动翻板闸门开启以及新型浮体闸的运行等[1-5]。当上游水体流经泄水建筑物时,水流会在泄水建筑物的影响下出现水体分层,分别经建筑物的上、下通过,出现分流现象[6]。国内外学者对孔、堰同时存在的条件下泄流量研究主要采用2种方式:1)分别采用孔流与堰流公式对2种不同的泄流进行计算,最后通过叠加给出泄流量[7-10];2)采用堰流公式,直接计算泄流量并加以修正系数调整得到孔堰并存时的泄流量[11-14]。上述2种方法,通过叠加孔、堰流泄流公式得到的泄流能力较精确,然而在不同的水利工程中,需分别通过模型实验得到叠加系数,公式通用性不高。仅采用堰流公式则忽略了孔流的影响,作为一个整体,孔口泄流与堰顶泄流存在内部作用,相互影响[15-17],且直接通过修正堰流公式得到泄流量的方法误差较大,在实际工程的应用中难以推广。为解决上述问题,本文将孔堰复合流中孔流与堰流的分界点命名为孔堰复合流的分流点。分流点的竖向位置作为孔流和堰流的临界点是影响2种不同泄流方式的重要指标。在分流点以上,来流水体经泄水建筑上部溢流下泄形成堰流流态;分流点以下,水体以孔口出流的形式进入到下游中形成孔流流态。分流点竖向位置的确定可以明确给出孔流和堰流的临界位置,进而分别得到2种不同泄流方式的泄流量。关于分流点竖向位置的研究国内外学者较少涉及,目前尚无相关的理论计算公式。鉴于此,得到一个可以用于计算孔堰复合流分流点竖向位置的公式是非常有意义的。
本文基于大量室内水槽模型实验,通过水力学基本理论分析,分析孔、堰流同时存在时,分流点竖向位置的分布特性。通过量纲分析,得到影响分流点竖向位置的无量纲参数:上下游水位差与上游水位的比值(ΔH/H),孔口高度与孔堰高度(e/a)、孔堰长度与孔堰高度(L/a)以及雷诺数(Re);基于最小二乘法,采用多元线性回归模型模型,建立了分流点竖向位置与不同参数的数学模型,得到参数对分流点竖向位置的敏感性影响大小;通过统计学指标比较5种模型的精确性,得到计算分流点竖向位置的最优数学模型表达式;同时,对最优模型中各参数的相关性及共线性进行比较,采用显著性检验以及残差分析对表达式进行了检验,验证了函数表达式的正确性。
1 实验装置及方法本实验在明渠有机玻璃水槽中进行,水槽基本尺寸为10.00 m×0.30 m×0.50 m(长×宽×高)。实验装置为一自循环系统,主要由水泵、调节阀门、稳流浮板、有机玻璃水槽、控制尾门、三角薄壁量水堰、回水箱等组成。孔堰结构实验区域设置于水槽中部。图 1为分流点测量实验区,图 2为实验装置示意图。

|
Download:
|
| 图 1 分流点测量实验区 Fig. 1 Experimental section of diversion point | |

|
Download:
|
| 图 2 实验装置示意 Fig. 2 Schematic of the experimental device | |
为探究不同孔堰结构以及水力参数对分流点竖向位置的影响,共进行了178组实验。实验过程中,孔堰结构宽度与水槽宽度相同,保持孔堰结构宽度B(0.30 cm)以及孔堰结构高度a(0.10 cm)不变。设置不同的来流单宽流量q(分别为0.05 m2/s、0.06 m2/s、0.07 m2/s、0.08 m2/s),采用长高比(L/a)分别为1.00、2.00、3.00、4.00的孔堰结构(L为孔堰结构沿水流方向的长度:0.10 m、0.20 m、0.30 m、0.40 m),设置3种不同的孔口高度e(e为孔堰结构距水槽底部的距离:0.02、0.05、0.10 m)以及不同的上下游水位差ΔH(0.01、0.02、0.03、0.04 m;ΔH=H-H′;H为上游水位,H′为下游水位)进行实验。实验工况设计见表 1,水力参数示意图见图 3。图 3中,y为分流点的竖向距离,其为从水槽底部到分流点的垂直距离,cm;V为孔堰结构上游区域的断面垂向平均流速,m/s。
| 表 1 实验工况设计表 Table 1 Experimental design conditions |

|
Download:
|
| 图 3 水力参数示意 Fig. 3 Schematic of hydraulic parameters | |
实验过程中,对分流点位置的测量采用声学多普勒流速仪(ADV),其采用脉冲相干处理技术,测速范围为0.01~250.00 cm/s。通过测量单点的三维流速,得到沿水槽中心纵剖面处,垂直与水流方向流速为0的点即为分流点。待实验工况下的水流达到稳定后测量分流点。由于随着孔口高度以及上游来流条件的变化,分流点的位置会发生变化,在水槽上部安装三维位移系统,将ADV测点置于水槽纵断面中,通过前后以及上下移动流速仪选定分流点位置。由于实际测量中分流的不稳定性,分流点的位置在前后及上下均会有较小波动,采用间隔10 s测量5次最终取均值的方法得到分流点的位置。
2 实验结果分析 2.1 无因次分析关于分流点竖向位置的变化并无系统研究,考虑到水流绕流经过孔堰结构水力特性复杂,实验过程中,对影响分流点的竖向位置y([L])的参数:孔堰段长度L([L])、孔堰高度a([L])、孔口高度e([L])、上游水位H([L])、水位差ΔH([L])、重力加速度g([L/T-2])、水的运动粘滞系数υ(L2/T-1)以及来流平均流速V([LT-1])进行分析。采用雷利法,分流点竖向位置的物理方程式可表示为:
| $ f\left( {y,L,e,a,H,{\rm{d}}H,g,u,V} \right) = 0 $ | (1) |
选取上游水位H[L]和重力加速度g[L/T2]为2个基本物理量,依据π定理得到:π1=y/H,π2=L/H,π3=e/H,π4=a/H,π5=ΔH/H,
| $ Y = f\left( {\Delta H/H,e/a,L/a,\mathit{Re}} \right) $ | (2) |
除少数情况外(如土壤中的渗流),实际工程中的水利工程,如管道、河渠及各种水工建筑物中的液流多属于紊流。实验过程中控制雷诺数的取值5.0 > lg(Re) > 4.5。影响分流点竖向位置比的水力学参数分别为L/a、e/a、ΔH/H以及Re,为探究4种不同的影响因子与Y的关系,分别对4种影响因素进行分析。
图 4为不同孔堰结构L/a与Y在不同ΔH/H下的散点图。从图 5(a)中可以看出,当ΔH/H=0.01较小时,e/a固定不变时,随着L/a的增加,Y的值几乎保持不变;且不同的e/a下,L/a对Y的影响几乎相同:当e/a=0.20时,L/a的增大并未引起Y的增大,Y几乎保持水平,相同的趋势同样出现在e/a=0.50以及1.00。随着ΔH/H的增大,L/a的变化对Y的影响几乎相同。实验过程中,当孔口高度e及水力条件不变时,随着孔堰结构沿水流长度L的增加,分流点的位置并未存在明显的变化,说明孔堰结构沿长度的变化对流经堰上以及孔口的流量配比没有明显的影响。而当孔口高度e变化时,分流点的竖向位置发生很明显的变化,该位置随着孔口高度的增大而向上移动。

|
Download:
|
| 图 4 Y与L/a散点 Fig. 4 Y plotted against different L/a | |
|
Download:
|
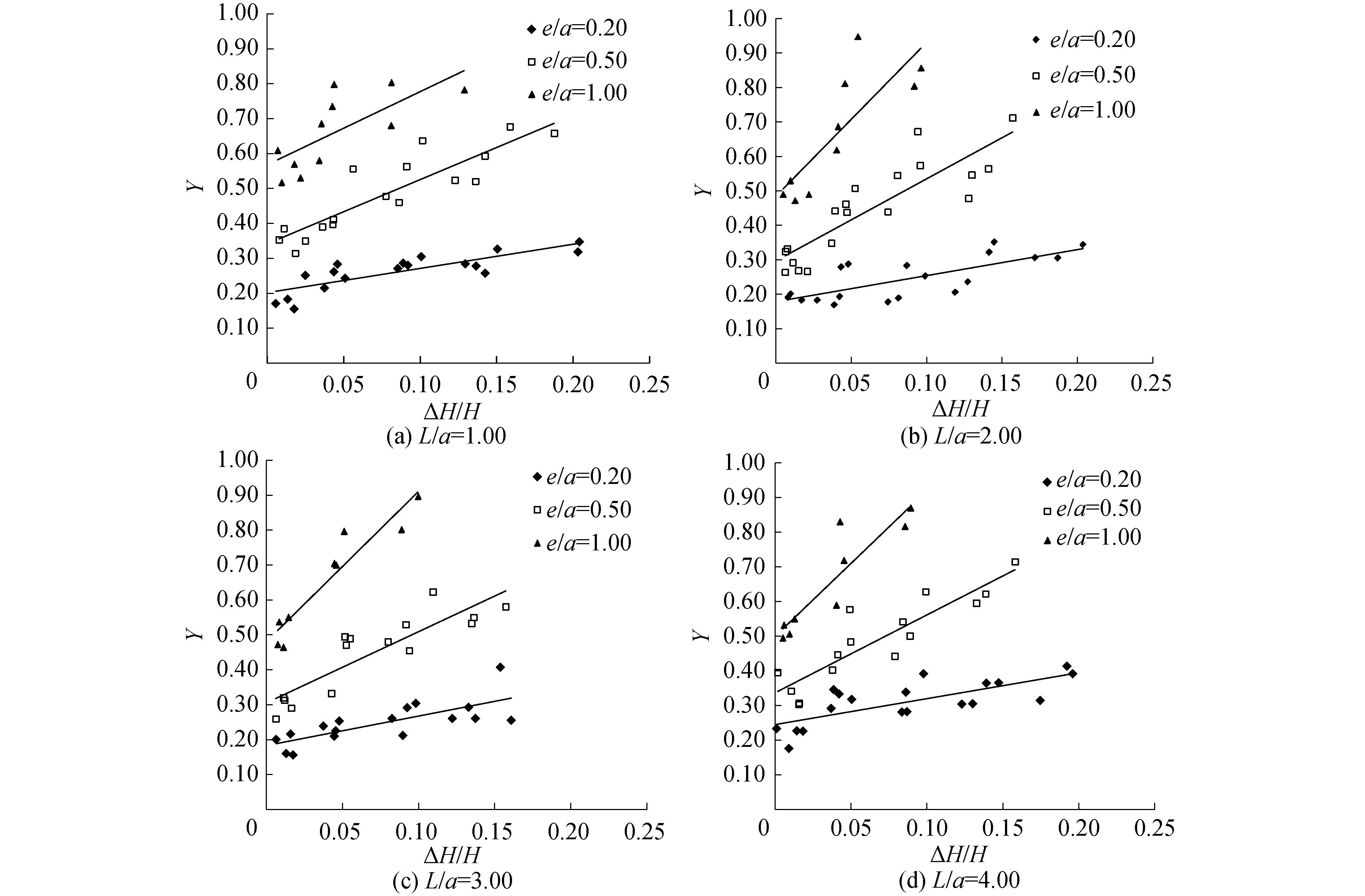
| 图 5 Y与ΔH/H散点 Fig. 5 Y plotted against different ΔH/H | |
图 5给出了Y在不同孔堰结构长度下与ΔH/H的关系图。从图中可以看出,分流点的竖向位置随着上下游水位差ΔH/H的增大而增大。以图 5(a)为例,保持孔堰结构L/a不变,当孔口高度e/a不同时,ΔH/H对Y的影响随着e/a的不同而发生变化,当e/a较大时,ΔH/H对Y的影响较大;在相同的ΔH/H下,Y随着e/a的增大而增大,这与图 4得到相同的结论。增大上下游水位差可以增大分流点竖向位置比。当保持上游水位不变时,水位差的增大,会引起分流点竖向位置的上升,因此,孔口的泄流能力增加。在实际水利工程中,当存在双层泄水建筑物时,减小下游水位,增大上下游水位差,可以增大底孔的泄流能力。实验过程中观察到,在相同的孔口高度以及水位差下,当上游水位H增加时,分流点的位置略微下降,上游水位的增加导致孔堰结构流经堰流区域的流量增大,从而经由孔口下泄的流量所占比例减小,因而Y出现减小的现象。
图 6为Y与lg(Re)散点图。在实验所在的紊流流速范围内(5.0 > lg(Re) > 4.5),可以看出随着lg(Re)的增大,不同孔口高度下的孔堰结构分流点的位置存在不同的趋势。以图 6(a)为例,当孔口高度较小(e/a =0.20, 0.50)时,在实验范围内,随着lg(Re)的增大,Y呈现微弱的减小趋势,而在孔口高度较大时(e/a=1.00),随着lg(Re)的增大,分流点呈现增大的趋势。相同的现象同样出现在图 6(b)~(d)中,且随着浮体结构沿水流长度的增大,这种变化趋势更加明显。

|
Download:
|
| 图 6 Y与lg(Re)散点 Fig. 6 Y plotted against different lg(Re) | |
对实验工况分析可知,分流点的竖向位置比Y与ΔH/H,e/a,L/a,lg(Re)存在相应关系。为得到分流点竖向位置比的计算表达式,采用多元线性拟合模型,分别将4种因子对Y的影响进行拟合。为得到不同因子对Y的影响敏感性,分别建立5种数学模型。
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{a}} \right):\\ \;\;\;\;\;\;\;\;Y = f\left( {\Delta H/H,e/a,L/a,\lg\left( {\mathit{Re}} \right)} \right) \end{array} $ | (3) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{b}} \right):\\ \;\;\;\;\;\;\;\;Y = f\left( {e/a,L/a,\lg\left( {\mathit{Re}} \right)} \right) \end{array} $ | (4) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{c}} \right):\\ \;\;\;\;\;\;\;\;Y = f\left( {\Delta H/H,e/a,\lg\left( {\mathit{Re}} \right)} \right) \end{array} $ | (5) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{d}} \right):\\ \;\;\;\;\;\;\;\;Y = f\left( {\Delta H/H,e/a,L/a} \right) \end{array} $ | (6) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{e}} \right):\\ \;\;\;\;\;\;\;\;Y = f\left( {\Delta H/H,L/a,\lg\left( {\mathit{Re}} \right)} \right) \end{array} $ | (7) |
通过图 4~6分析可知,Y与L/a,lg(Re)呈现线性关系,且这种线性关系(斜率)随着其他因素的变化几乎无明显变化;随着孔堰比e/a的增大,Y呈现明显的增加趋势;而ΔH/H对Y的影响随着e/a的变化呈现不同的变化趋势,随着e/a的增大斜率明显增大,因此将变量
基于最小二乘法的数学统计以及各无量纲因子与分流点竖向位置比的相关关系,得到在淹没出流条件下,不同影响子对Y的影响敏感性,通过多元线性拟合得到5种数学模型的表达式如下:
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{a}} \right):\\ \;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {Y = 1.73 + 0.372\frac{e}{a} + 0.014\frac{L}{a} + }\\ {3.94\frac{e}{a} \cdot \frac{{\Delta H}}{H} - 0.34\lg \left( {\mathit{Re}} \right)} \end{array} \end{array} $ | (8) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{b}} \right):\\ \;\;\;\;\;\;\;\;Y = 1.594 + 0.494\frac{e}{a} + 0.009\frac{L}{a} - 0.298\lg \left( {\mathit{Re}} \right) \end{array} $ | (9) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{c}} \right):\\ \;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {Y = 1.74 + 0.371\frac{e}{a} + 3.899\frac{e}{a} \cdot \frac{{\Delta H}}{H} - }\\ {0.335\lg \left( {\mathit{Re}} \right)} \end{array} \end{array} $ | (10) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{d}} \right):\\ \;\;\;\;\;\;\;\;Y = 0.101 + 0.363\frac{e}{a} + 0.013\frac{L}{a} + 3.903\frac{e}{a} \cdot \frac{{\Delta H}}{H} \end{array} $ | (11) |
| $ \begin{array}{l} {\rm{MOD}}\left( {\rm{e}} \right):\\ \;\;\;\;\;\;\;\;Y = 0.492 + 0.005\frac{L}{a} + 0.505\frac{{\Delta H}}{H} - 0.024\lg \left( {\mathit{Re}} \right) \end{array} $ | (12) |
实验过程中,为保证孔、堰流2种条件的出现,孔堰结构处于淹没状态。依据实验条件,上述关系式需满足以下适用条件,即H > e+a,e > 0.067H;ΔH < 0.25H;5.0 > lg(Re) > 4.5。
比较孔堰结构分流点竖向位置比Y的5种预测模型的拟合优度,采用统计学指标:决定修正系数AMCC(用于调整由于参数个数带来的相关性计算误差)、估计标准误差RMSE以及回归标准偏差ZRE进行比较,从中选取拟合度最好且误差最小的模型。其中,AMCC、RMSE及ZRE的定义为:
| $ {R^2} = \frac{{\sum\nolimits_{k = 1}^K {{{\left( {{Y_{k{\rm{ - pre}}}} - \bar Y} \right)}^2}} }}{{\sum\nolimits_{k = 1}^K {{{\left( {{Y_{k{\rm{ - exp}}}} - \bar Y} \right)}^2}} }} $ | (13) |
| $ {A_{{\rm{MCC}}}} = {R^2} - \frac{{J \times \left( {1 - {R^2}} \right)}}{{K - J - 1}} $ | (14) |
| $ {R_{{\rm{MSE}}}} = \sqrt {\frac{{\sum\limits_{k = 1}^K {{{\left( {{Y_{k{\rm{ - exp}}}} - {Y_{k{\rm{ - pre}}}}} \right)}^2}} }}{{K - J - 1}}} $ | (15) |
| $ {Z_{{\rm{R}}{{\rm{E}}_k}}} = \frac{{{Y_{k{\rm{ - exp}}}} - {Y_{k{\rm{ - pre}}}}}}{{\hat \sigma }} $ | (16) |
式中:K为总的实验工况数;J为无量纲自变量因子的数目;Y为实验的分流点竖向位置比Yexp的平均值;
表 2给出了5种不同模型拟合优度比较,可以看出MOD(a)的拟合效果最好,而模型MOD(e)的拟合效果最差;在模型MOD(c)和MOD(d)中,拟合的效果弱低于MOD(a),这说明孔堰结构在沿水流方向的改变以及水流中雷诺数的变化,对分流点位置的影响相对较弱;而对于MOD(b),其拟合优度较差,说明ΔH/H对Y的影响作用较为显著,是不可忽略因素;对于MOD(e)而言,拟合效果最差,说明变量e/a是影响模型拟合优度的最主要因素。对于模型MOD(b)~MOD(d)得到4种无量纲因子对分流点竖向位置比的影响敏感性大小依次排列为:e/a、ΔH/H、lg(Re)、L/a。
| 表 2 5种模型的AMCC、RMSE和ZRE比较 Table 2 Values of AMCC, RMSE and ZRE for five models |
比较5种模型,最终选用MOD(a)用于分流点竖向位置的表达,此时,公式的拟合度最高。即:
| $ \begin{array}{*{20}{c}} {Y = 1.73 + 0.372\frac{e}{a} + 0.014\frac{L}{a} + }\\ {3.94\frac{e}{a} \cdot \frac{{\Delta H}}{H} - 0.34\lg \left( {Re} \right)} \end{array} $ |
式中:H > e+a,e > 0.067H;ΔH < 0.25H;5.0 > lg(Re) > 4.5。
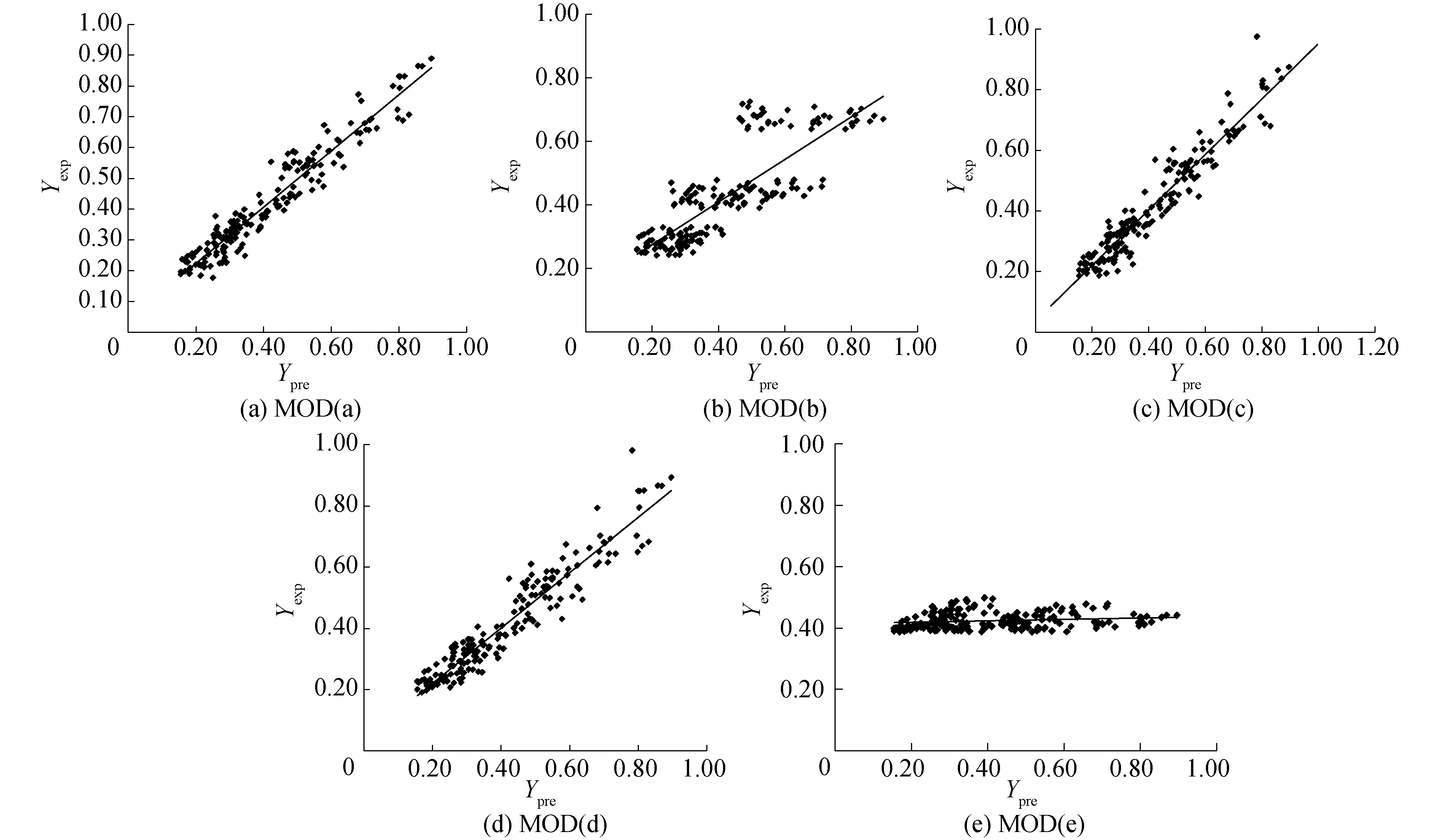
图 7为不同模型对Y的预测值与实验值的对比。其中MOD(a)与实验值的拟合效果最好,MOD(c)和MOD(d)由于分别缺少影响较小的变量L/a以及lg(Re),因此拟合效果仅次于MOD(a); MOD(b)中由于缺少变量ΔH/H,因此e/a对结果影响明显,散点图呈现随e/a变化成不连续性的分布形式;MOD(e)中由于缺少主要变量e/a,因此拟合结果与实验值相差很大。
|
Download:
|
| 图 7 Y的理论值与实验值散点分布 Fig. 7 Comparison between theoretical value and experimental value of the Y | |
通过对比5种模型,得到MOD(a)的拟合优度最高,但要判断回归方程的适用性和拟合效果,需对模型进行进一步检验。对回归方程MOD(a)进行方程的整体显著性F检验,实验过程中,选取95%的置信区间,得到F的值为519.4;对模型的自相关进行判断采用DW检验,DW值为1.96,即模型不存在自相关问题;对模型各变量进行两两相关的皮尔森系数计算,得到各自变量因子之间的相关系数较低,各个自变量序列之间不相关;为排除模型的不稳定性,采用方差膨胀因子法,同时对MOD(a)进行多重共线性诊断,得到VIF值最大仅为1.18,变量之间不存在多重共线性。其中F检验、DW检验以及VIF检验公式为:
| $ F = \frac{{\sum\limits_{k = 1}^K {{{\left( {{Y_{k{\rm{ - pre}}}} - \bar Y} \right)}^2}/K} }}{{\sum\limits_{k = 1}^K {{{\left( {{Y_{k{\rm{ - exp}}}} - {Y_{k{\rm{ - pre}}}}} \right)}^2}/\left( {K - J - 1} \right)} }} $ | (17) |
| $ {D_W} = \frac{{\sum\limits_{t = 2}^K {\left( {{e_t} - {e_{t - 1}}} \right)} }}{{\sum\limits_{t = 2}^K {e_t^2} }} $ | (18) |
| $ {V_{IFi}} = {\left( {1 - R_i^2} \right)^{ - 1}} $ | (19) |
式中:Ri2为自变量xi对其余剩余自变量的复判定系数;et为在t时刻的误差项,其余变量含义与上相同。图 8为MOD(a)的残差相应统计量以及残差带有正态概率曲线的直方图,从图中可以看出,关于残差分布服从期望为零的正态分布,且95%的标准化残差分布介于-2~2,证明模型假定是合理的。

|
Download:
|
| 图 8 MOD(a)残差分布直方图(平均值=0,标准差=0.989,N=178) Fig. 8 MOD(a) Residual distribution histogram(mean=0, standard deviation=0.989, N=178) | |
通过上述对模型MOD(a)的检验可知,其用来表述孔堰分流点的竖向位置是合理以及精确的。
4 结论1) 分流点的竖向位置与上下游水位差与上游水位的比值(ΔH/H),孔口高度与孔堰高度(e/a)、孔堰结构体型(L/a)以及雷诺数(Re)有关,并随着4种无因参数的不同,呈现不同的规律:分流点受结构体型长度的变化影响不大;随着孔口开度以及水位差的变化影响较明显,并呈现正相关关系;雷诺数对分流点位置的影响随着孔口高度的变化发生变化。
2) 通过5种不同的参数模型,分别对4种无量纲因子对分流点竖向位置影响的敏感性进行了分析,得到影响分流点位置的因子敏感性大小排列为e/a、ΔH/H、lg(Re)以及L/a。
3) 通过5种模型统计指标的比较,得到预测分流点位置的最优模型MOD(a)(AMCC=0.921,RMSE=0.051和ZRE=0.989),并进一步验证了模型的正确性以及合理性,该公式拟合度高、结构简单、通用性强,可对分流点的竖向位置进行描述。
| [1] |
CUI Zhen, FU Zongfu, DAI Wenhong, et al. Submerged fixed floating structure under the action of surface current[J]. Water, 2018, 10(2): 102. DOI:10.3390/w10020102 (  0) 0)
|
| [2] |
SAADATNEJADGHARAHASSANLOU H, GHAREHBAGHI A, MEHDIZADEH S, et al. Experimental investigation of discharge coefficient over novel kind of sharp-crested Ⅴ-notch weir[J]. Flow measurement and instrumentation, 2017, 54: 236-242. DOI:10.1016/j.flowmeasinst.2017.02.008 (  0) 0)
|
| [3] |
SAAD N Y, FATTOUH E M. Hydraulic characteristics of flow over weirs with circular openings[J]. Ain shams engineering journal, 2017, 8(4): 515-522. DOI:10.1016/j.asej.2016.05.007 (  0) 0)
|
| [4] |
AL-SAADI A K I. Study coefficient of discharge for a combined free flow over weirand under Gate for Multi Cases[J]. Euphrates journal of agriculture science, 2013, 5(4): 26-35. (  0) 0)
|
| [5] |
SEVERI A, MASOUDIAN M, KORDI E, et al. Discharge coefficient of combined-free over-under flow on a cylindrical weir-gate[J]. ISH journal of hydraulic engineering, 2015, 21(1): 42-52. DOI:10.1080/09715010.2014.939503 (  0) 0)
|
| [6] |
PARSAIE A, AZAMATHULLA H M, HAGHIABI A H. Prediction of discharge coefficient of cylindrical weir-gate using GMDH-PSO[J]. ISH journal of hydraulic engineering, 2018, 24(2): 116-123. DOI:10.1080/09715010.2017.1372226 (  0) 0)
|
| [7] |
SAMANI J M, MAZAHERI M. Combined flow over weir and under gate[J]. Journal of hydraulic engineering, 2009, 135(3): 224-227. DOI:10.1061/(ASCE)0733-9429(2009)135:3(224) (  0) 0)
|
| [8] |
徐岗, 王月华. 水力自控翻板闸门泄流量计算探讨[J]. 浙江水利科技, 2014, 42(2): 62-65. XU Gang, WANG Yuehua. Discussion on discharge calculation of hydraulic automatic flap gate[J]. Zhejiang hydrotechnics, 2014, 42(2): 62-65. (  0) 0)
|
| [9] |
潘攀, 魏振磊, 尚岳全, 等. 斜倾盖板水石分流池的分流能力分析[J]. 浙江大学学报:工学版, 2016, 50(8): 1456-1462. PAN Pan, WEI Zhenlei, SHANG Yuequan, et al. Analysis on separation ability of inclined plate water-stone shunt pool[J]. Journal of Zhejiang University:engineering edition, 2016, 50(8): 1456-1462. (  0) 0)
|
| [10] |
FU Zongfu, CUI Zhen, DAI Wenhong, et al. , Discharge coefficient of combined orifice-weir flow[J]. Water-SUI, 2018, 10(6): 699. DOI:10.3390/w10060699 (  0) 0)
|
| [11] |
叶镇国. 水力自控翻转闸门过流特性[J]. 湖南大学学报, 1984, 11(3): 58-75. YE Zhenguo. Discharge characteristics of automatic gates controlled by hydraulic pressure[J]. Journal of Hunan University, 1984, 11(3): 58-75. (  0) 0)
|
| [12] |
叶镇国. 水力自控翻板闸门泄流水力关联理论[J]. 湖南大学学报, 1994, 21(3): 98-105. YE Zhenguo. Hydraulic correlative discharge theory of automatic turning gate controlled by hydraulic pressure[J]. Journal of Hunan University, 1994, 21(3): 98-105. (  0) 0)
|
| [13] |
潘梦钦, 林宗燊, 谢佩珍. 双层泄水建筑物泄流能力试验研究[J]. 福州大学学报, 1984(3): 67-77. PAN Mengqin, LIN Zongxin, XIE Peizhen. A Study on discharge capacity of water passing both the weir (or Spillway) and the conduit[J]. Journal of Fuzhou University, 1984(3): 67-77. (  0) 0)
|
| [14] |
华子平. 对淹没宽顶堰泄流能力计算公式的探讨[J]. 河海大学学报, 1998, 26(3): 97-101. HUA Ziping. A calculating formula for spillway capacity of drowned wide crest weirs[J]. Journal of Hohai University, 1998, 26(3): 97-101. DOI:10.3321/j.issn:1000-1980.1998.03.020 (  0) 0)
|
| [15] |
李国斌, 高亚军, 陈月华, 等. 韩国Janghang海堤工程防洪闸泄流能力试验研究[J]. 水利水运工程学报, 2006(2): 13-17. LI Guobin, GAO Yajun, CHEN Yuehua, et al. Experimental study on floodgate of Janghang seawall project in South Korea[J]. Hydro-science and engineering, 2006(2): 13-17. DOI:10.3969/j.issn.1009-640X.2006.02.003 (  0) 0)
|
| [16] |
李乃稳, 许唯临, 周茂林, 等. 高拱坝坝身表孔和深孔水流无碰撞泄洪消能试验研究[J]. 水利学报, 2008, 39(8): 927-933. LI Naiwen, XU Weilin, ZHOU Maolin, et al. Experimental study on energy dissipation of flood discharge in high arch dams without impact of jets in air[J]. Journal of hydraulic engineering, 2008, 39(8): 927-933. DOI:10.3321/j.issn:0559-9350.2008.08.006 (  0) 0)
|
| [17] |
李国栋, 李珊珊, 牛争鸣. 表孔、底孔联合泄洪流场数值模拟与冲刷趋势分析[J]. 四川大学学报:工程科学版, 2016, 48(3): 26-34. LI Guodong, LI Shanshan, NIU Zhengming. Numerical simulation of surface outlet and bottom outlet joint flood discharge energy dissipationand scour trend analysis[J]. Journal of Sichuan University:engineering science edition, 2016, 48(3): 26-34. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


