2. 北京控制工程研究所, 北京 100190
2. Beijing Institute of Control Engineering, Beijing 100190, China
现代空间技术的发展使得航天器结构的设计逐渐趋于小型化、灵巧化。不仅要保证体积小、质量轻、在发射阶段收拢性好,待航天器入轨后,还应能够在足够大的空间范围内展开,航天器机动过程中能保持结构稳定,大柔性结构在这些方面具有一定优势。同时,为了打破长期飞行任务对星上能源的限制,利用空间场力进行推进的方式也逐渐被采纳[1-3]。
由数十或数百根带电导线组成的虚拟太阳风电动帆就是一种典型的空间系绳,其质量超轻、收拢性好、展开后覆盖范围极广的优良性能使其成为颇具前景的无工质推进方式。电动帆的概念是由Janhune等[4]提出,主要依靠作用在通电导线上的太阳风动压提供动力。NASA在欧洲团队的研究基础上,设计了电子枪装置,在实验室条件下验证了等离子体推进的方式,并初步分析了不同装配形式的绳索展开运动的过程[5]。发射阶段导线缠绕于一圆柱轮毂上,入轨后中心轮毂开始转动,导线末端带有一质量块,依靠质量块产生的离心力拉动导线从中心轮轴逐渐伸出,完成展开后的导线束形成虚拟帆面。通电导线是极细长的绳索,这种结构固然具有一定优势,却也给帆面保持、导线运动状态预测以及姿态控制等造成困难。电帆自旋过程中如无能量耗散则系统动量守恒,绳索质量很小但长度很长,系统质量惯量主要集中在位于绳末端的质量块上。离心力作用下的绳索与末端质量动量交换过程中,绳上各点的位置、速度极易受到影响而发生改变,进而影响虚拟帆面形状。
爱沙尼亚于2013年5月发射ESTCube-1科学实验微小卫星[6],星上携带有单根长10 m的导线,目的是在近地轨道验证通电线缆能够在与空间粒子的相互作用下产生推力。然而由于展开机构异常,使得导线未能成功展开,使得推力验证实验未能完成[7]。该星上的导线开始收拢于一封闭轮毂中,中心体起旋后末端质量拉动线缆沿缠绕方向转动,采用了送线展开的方式,这种方式极易使得导线因摩擦等因素而展开失败。本文研究电帆柔索通过离心力甩动展开的方式,这种方式下柔索更容易展开,但由于极大的长细比,放线过程中柔索产生的大变形与大转动影响了展开的稳定性,需要对自旋展开过程中影响动力学特性的因素加以分析,其核心在于建立适合描述大变形与大转动的柔索动力学模型。
柔索连续体一般采用物理离散化方法进行建模,Kamman等[8]基于集中质量方法将长度可变的海底拖曳线缆分解成一段质量聚集在两端的无质量绳段,绳段之间在端点处通过球铰约束副连接,内部不产生变形,仅由相对转动模拟弯曲变形;Buckham等[9]利用改进的集中质量方法建立考虑轴向伸长的线缆模型,节点之间不再依靠位置约束连接,而是通过弹簧阻尼力连接。集中质量方法虽然简单,但仅保留了绳索的质量特性而完全忽略了惯量特性,不能准确描述梁段的转动运动,一定程度上造成了模型的不准确。Wang等[10]研究了柔性多体系统中的有限段离散方法,并给出了单元连接处弹性集中参数的选取原则,并将有限段的使用对象由均匀梁扩展至非均匀、形状不规则梁。孔宪仁等[11]运用Hamilton原理建立了空间绳系展开动力学模型,研究绳系展开过程中绕线盘出线、系绳振动以及末端质量的运动规律;Fulton等[12]分别针对绳索统一缠绕在中心轮毂和独立缠绕2种形式的电帆展开机构,采用刚性细杆简化模型建立了展开动力学模型并初步分析了展开运动过程。
本文采用有限段方法建立电帆柔索的动力学模型,针对中心轮毂缠绕方式,仿真分析不同转速与末端质量情况下,分析柔索的自旋展开动力学特性。
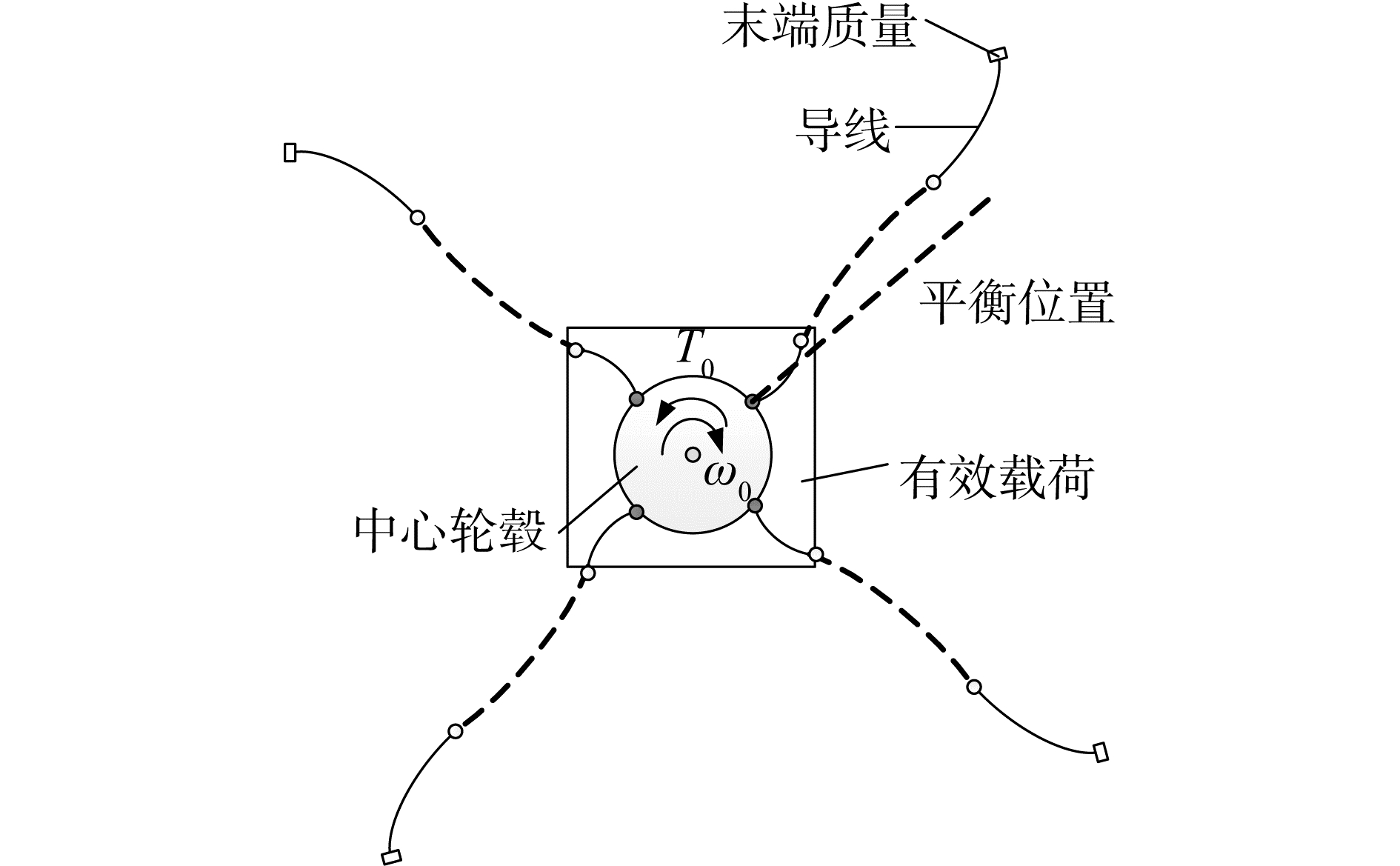
1 基于有限段方法的电帆柔索模型电帆原理示意图如图 1所示。典型电帆结构由有效载荷、中心轮毂、细长导线和末端质量组成。多条导线在发射阶段缠绕在中心轮毂上,通过自旋方式进行展开,结构如图 2所示。电帆柔索具有挠性,以承受轴向拉力为主,抗弯能力较弱,基于有限段的离散方法能够较好地反映出这一特性,绳段之间通过六维弹簧阻尼器连接,在多体动力学软件中以bushing单元力的形式出现,可建立3个方向的受力变形关系。另外,绳段初始状态下紧密缠绕于电帆的中心轮毂上,通过建立接触碰撞力等效两者之间的相互作用力,保持转动过程中柔索时刻张紧。

|
Download:
|
| 图 1 电帆工作示意 Fig. 1 Principle diagram of electric sail | |
|
Download:
|
| 图 2 电帆结构示意 Fig. 2 Diagram of E-sail structure | |
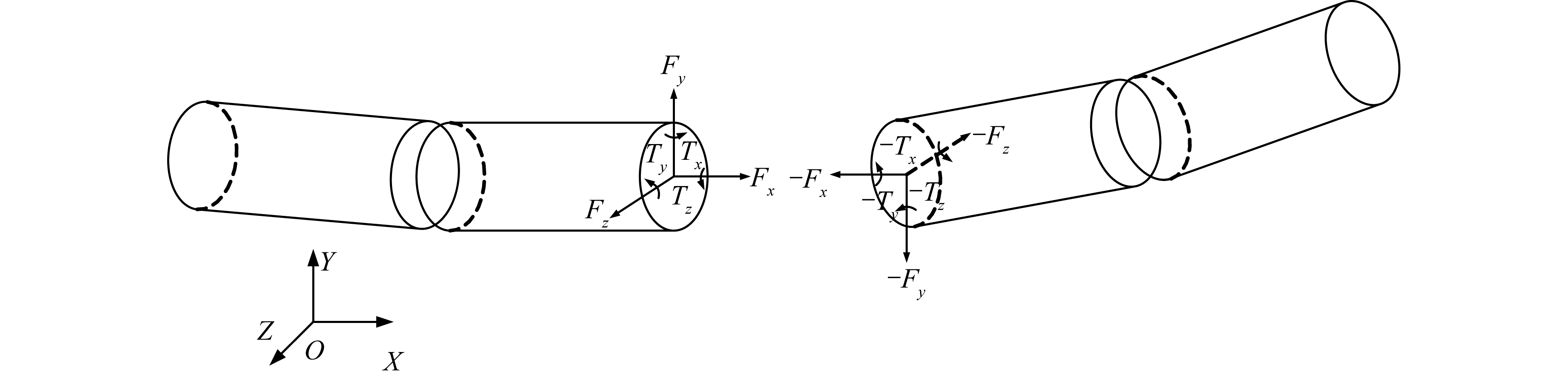
有限段方法是将索梁离散成自身不产生变形的刚性小段,与依靠弹簧阻尼连接的集中质量方法不同,后者绳段内处处可变形,而有限段方法仅在两端点处通过柔性连接体现索梁的连续变形,即相对平移和转角,正确选择弹簧阻尼系数是准确描述柔索大变形的关键[13]。
如图 3所示,相邻两绳段在连接点处分别建立局部坐标系Oi-XiYiZi与Oj-XjYjZj,定义X为轴向,YOZ平面为径向平面,对于三轴平移、转动方向上变形彼此独立的线性绳段,粘弹性力、力矩刚度、阻尼系数矩阵非对角线上均为零元素。
| $ \begin{array}{l} \left[ \begin{array}{l} {F_x}\\ {F_y}\\ {F_z}\\ {T_x}\\ {T_y}\\ {T_z} \end{array} \right] = \left[ {\begin{array}{*{20}{l}} {{k_{11}}}&{}&{}&{}&{}&{}\\ {}&{{k_{22}}}&{}&{}&{\bf{0}}&{}\\ {}&{}&{{k_{33}}}&{}&{}&{}\\ {}&{}&{}&{{k_{44}}}&{}&{}\\ {}&{{\mathit{\boldsymbol{k}}_{{\rm{sym}}}}}&{}&{}&{{k_{55}}}&{}\\ {}&{}&{}&{}&{}&{{k_{66}}} \end{array}} \right]\left[ \begin{array}{l} \Delta {r_x}\\ \Delta {r_y}\\ \Delta {r_z}\\ \Delta {\theta _x}\\ \Delta {\theta _y}\\ \Delta {\theta _z} \end{array} \right] - \\ \left[ {\begin{array}{*{20}{l}} {{c_{11}}}&{}&{}&{}&{}&{}\\ {}&{{c_{22}}}&{}&{}&{\bf{0}}&{}\\ {}&{}&{{c_{33}}}&{}&{}&{}\\ {}&{}&{}&{{c_{44}}}&{}&{}\\ {}&{{\mathit{\boldsymbol{k}}_{{\rm{sym}}}}}&{}&{}&{{c_{55}}}&{}\\ {}&{}&{}&{}&{}&{{c_{66}}} \end{array}} \right]\left[ \begin{array}{l} \Delta {v_x}\\ \Delta {v_y}\\ \Delta {v_z}\\ \Delta {\omega _x}\\ \Delta {\omega _y}\\ \Delta {\omega _z} \end{array} \right] + \left[ \begin{array}{l} {F_{{x_0}}}\\ {F_{{y_0}}}\\ {F_{{z_0}}}\\ {T_{{x_0}}}\\ {T_{{y_0}}}\\ {T_{{z_0}}} \end{array} \right] \end{array} $ | (1) |
|
Download:
|
| 图 3 有限段柔索模型 Fig. 3 Model of finite segment of flexible tether | |
式中:Δri、Δθi, i=x, y, z为连接两节点处的相对位移与相对转角;Δvi、Δωi为相对平移、转动速度;Fi0、Ti0为初始力和力矩。对于圆形截面的绳段,刚度系数分别为:
| $ \left\{ \begin{array}{l} {k_{11}} = \frac{{EA}}{L}\\ {k_{22}} = {k_{33}} = \frac{{GA}}{L}\\ {k_{44}} = \frac{{G{\rm{ \mathsf{ π} }}{d^4}}}{{32L}}\\ {k_{55}} = {k_{66}} = \frac{{EI}}{L} = \frac{{E{\rm{ \mathsf{ π} }}{d^4}}}{{64L}} \end{array} \right. $ | (2) |
式中:k11为拉伸刚度系数;k22、k33为剪切刚度系数;k44为扭转刚度系数;k22、k33为弯曲刚度系数;E、G为弹性模量和刚性模量;A、d、L分别为绳段横截面积、直径以及段长;I为截面惯性矩。
粘性阻尼系数按以下关系给出[14]:
| $\left\{ \begin{array}{l} {c_{ii}} = 2\xi \sqrt {{k_{ii}}m} , \;\;\;\;\;i = 1, 2, 3{\rm{ }}\\ {c_{jj}} = 2\xi \sqrt {{k_{jj}}{I_{jj}}} , \;\;j = 4, 5, 6 \end{array} \right. $ | (3) |
式中ξ为阻尼因子。
1.2 柔索-中心轮毂接触作用自旋展开运动过程中,电帆柔索依靠与中心轮毂之间的接触作用力保持缠绕及张紧的状态,因此接触碰撞力对系统运动特性的影响不可忽略,需在圆柱绳段与中心轮毂之间不断地进行碰撞检测。使用Herz模型建立柔索-中心轮毂之间的非线性接触力,假设接触碰撞产生纯弹性变形,定义接触碰撞力为:
| $ {F_{{\rm{imp}}}} = K{\delta ^n} $ | (4) |
式中:δ为弹性变形量;n为力指数;K为等效接触刚度系数,与构成接触碰撞对两体的几何、材料特性有关,是接触碰撞力模型的主要影响参数。取值过低会使柔索与中心轮毂几何体之间互相切入,与物理实际不符;过高会产生较大接触碰撞力使柔索在与轮毂接触过程中产生剧烈振动,不利于保持展开相位变化稳定。接触刚度系数与材料、几何参数之间满足[15]:
| $ K = \frac{4}{{3({\sigma _1} + {\sigma _1})}}{R^{1/2}} $ | (5) |
式中:σ1、σ2为材料参数,与弹性模量E和泊松比υ相关;R与两物体在接触点处的曲率半径有关:
| $\left\{ \begin{array}{l} {\sigma _i} = (1 - \upsilon _i^2)/{E_i}, \;\;\;\;\;\;i = 1, 2\\ 1/R = 1/{R_1} + 1/{R_2} \end{array} \right. $ | (6) |
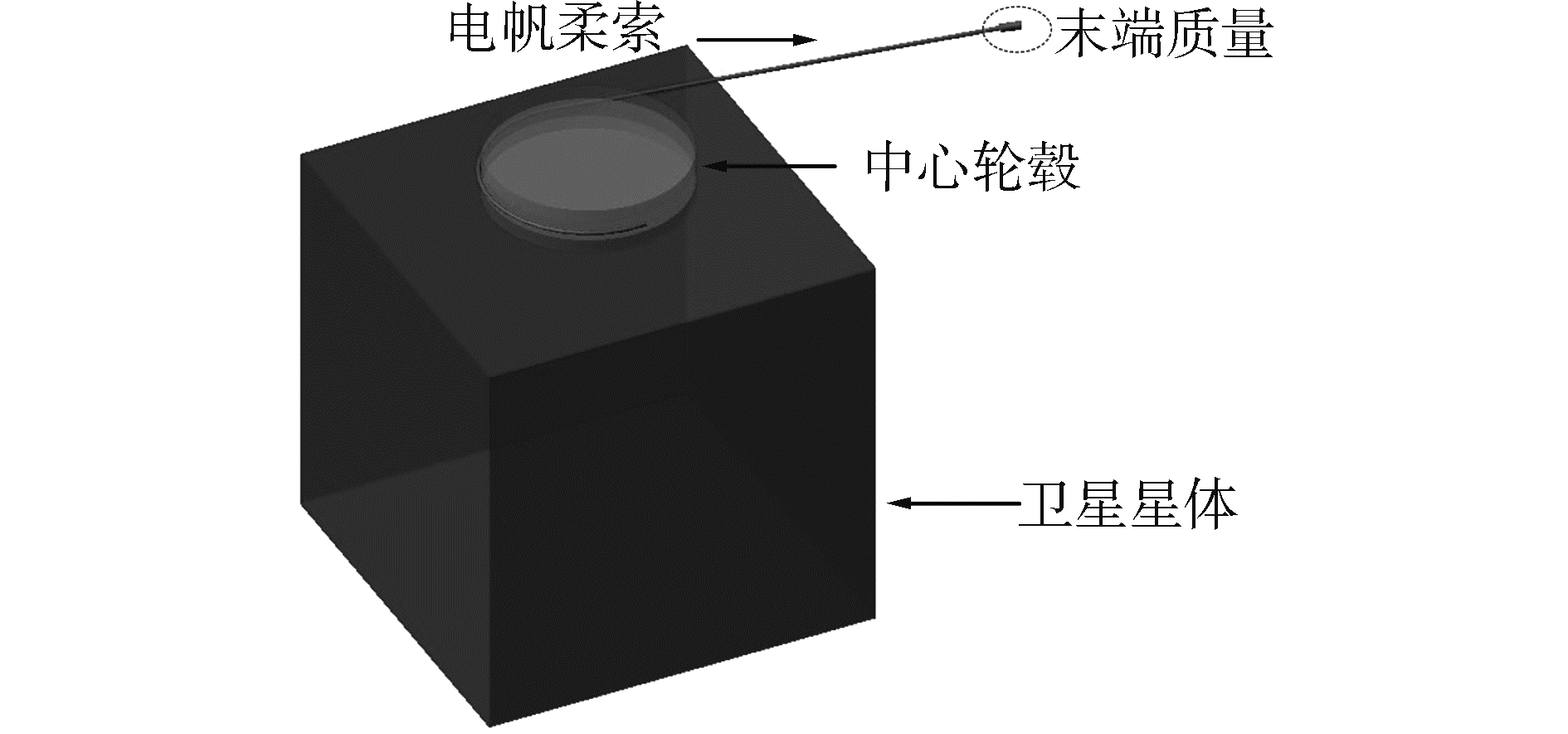
电帆多体动力系统的组成如图 4所示,细长柔索缠绕于中心轮毂上,一端与轮毂固定,另一端携带一圆柱形质量块,整体安装在卫星星体上与之通过转动约束副连接在一起,转动轴与安装面垂直。系统模型参数的选取如表 1所示。
|
Download:
|
| 图 4 卫星星体+电帆结构组成 Fig. 4 Satellite astral body + E-sail structures | |
| 表 1 电帆多体系统模型参数表 Table 1 Model parameters of multi-body system of E-sail |
动力学仿真模拟电帆真空中的运动过程,重力加速度取为0 kg·m/s2,卫星星体在空间中自由漂浮并以一定角速度绕轮毂安装轴做自旋转动,中心轮毂开始转动后受到星体施加的作用力矩以消除相对角速度差,转速逐步增加至与星体同步,使得柔索在星体作用力矩下由轮毂带动展开,作用力矩为:
| $ \mathit{\boldsymbol{M}} = {k_p}({\mathit{\boldsymbol{\theta }}_b} - {\mathit{\boldsymbol{\theta }}_h}) + {k_d}({\mathit{\boldsymbol{\dot \theta }}_b} - {\mathit{\boldsymbol{\dot \theta }}_h}) $ | (7) |
式中:kp、kd分别为角度与角速度力矩系数;θb、θh为星体与轮毂的转动角度;
柔索的离散化模型参数见表 2。
| 表 2 柔索有限段模型参数表 Table 2 Model parameters of Finite segment of flexible tether |
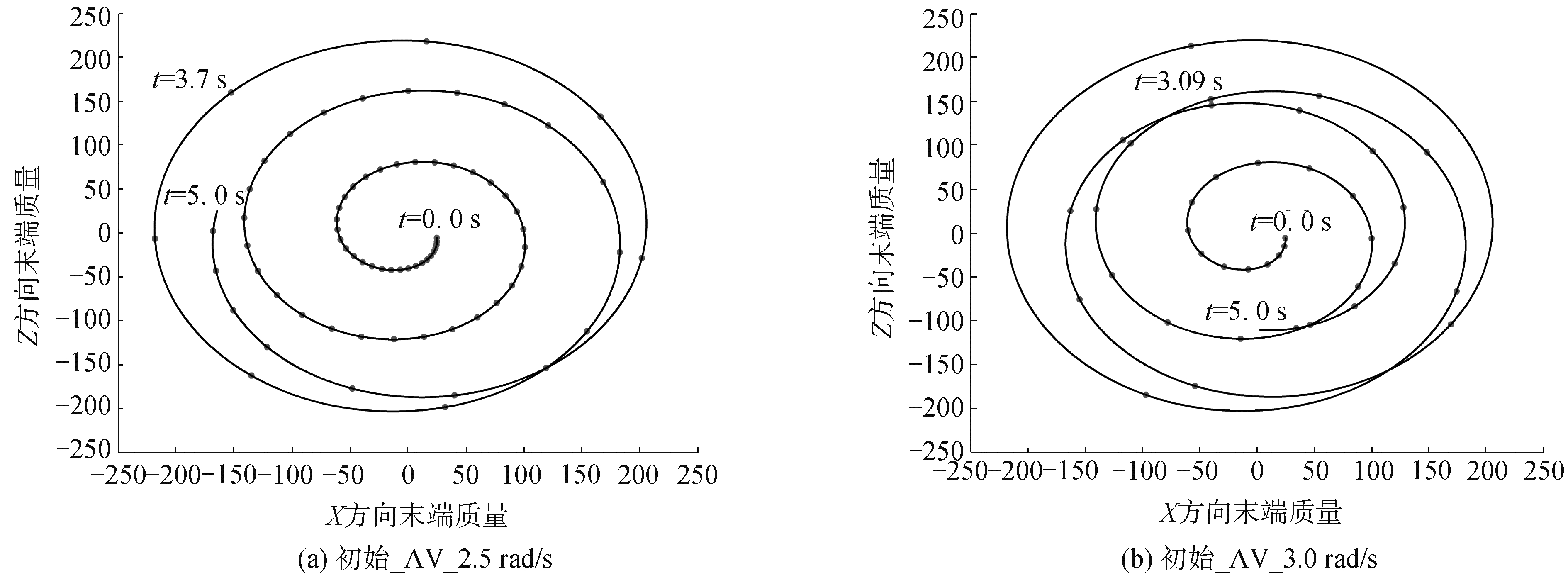
仿真初始时刻,卫星星体与中心轮毂之间具有相对角速度差,力矩控制参数取kp=10, kd=5,相对转动角速度分别取2.5 rad/s与3 rad/s,研究角速度对柔索自旋展开动力学特性的影响,设初始状态下安装轴为Y轴,展开平面为XZ平面,展开时间共计5 s。
输出不同相对初始角速度下,电帆末端质量的位置运动分布,如图 5(a)、(b)所示,转速越大,平均相位变化的周期越短。展开开始阶段,末端质量逐渐远离转动中心,运动至某一时刻后,末端质量的相位半径开始逐渐减小,柔索经加速后的角速度大于星体的驱动角速度,待柔索完全展开后开始反向缠绕。角速度为2.5 rad/s时,反向缠绕发生于3.7 s,增至3 rad/s后,柔索于3.09 s开始反缠,驱动转速越大,柔索越提前加速至超越轮毂转动角速,完全展开后柔索沿轴向的转动速度差越大。
|
Download:
|
| 图 5 末端质量运动位置分布 Fig. 5 Movement positional distribution of end mass | |
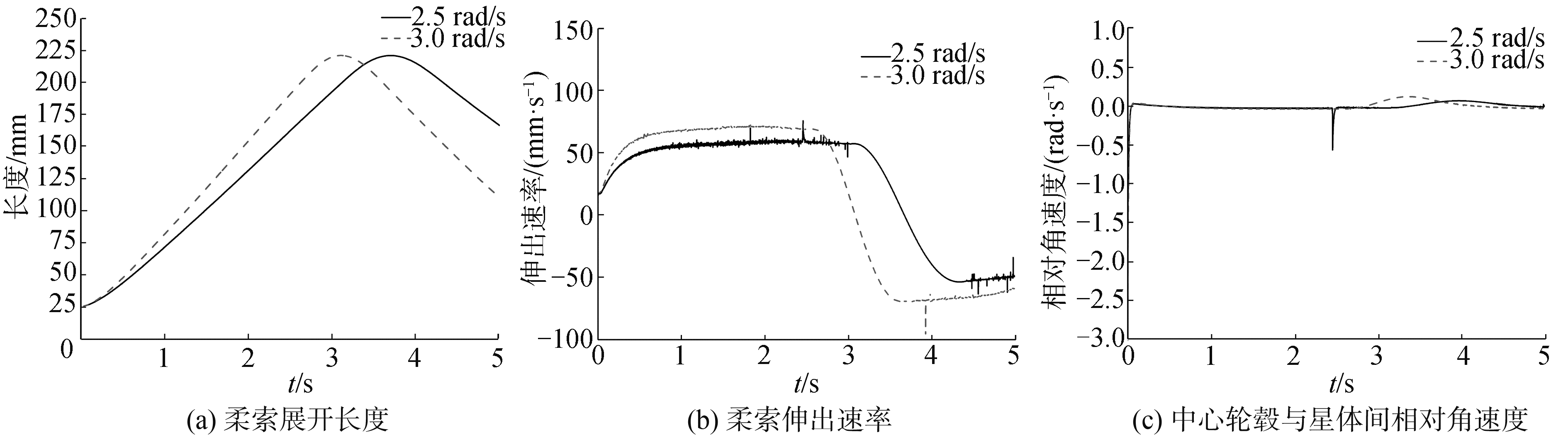
图 6(a)为柔索末端质量至转动中心距离的变化曲线,可以更加直观地反映出图 5中相位半径的变化趋势。
|
Download:
|
| 图 6 不同展开速度下自旋展开运动特性曲线 Fig. 6 The motion characteristics of spin expansion with different driven angular velocity | |
图 6(b)为柔索伸长速率的曲线,柔索展开伸出过程前0.5 s内,展开速率逐渐递增,0.5 s后的一段时间内保持在一常值附近,展开末段开始递减,减小至零后柔索开始反向缠绕。
结合图 6(c)中星体与轮毂之间的相对转动角速度进行分析可知,驱动速度较大时的柔索对轮毂的反作用越明显,尤其在即将完全展开时刻前后,柔索伸出速率降低得更快,导致星体与轮毂之间的速度差出现明显波动变化。
柔索末端质量处的拉力变化如图 7(a)所示,除柔索完全展开前后绳内拉力变化较平稳、趋于平滑曲线外,其他时刻内由于柔索与轮毂之间接触力的变化使得内部张力出现密集波动,由开始展开到完全展开的阶段,总体变化趋势经历了先增大后减小的过程。

|
Download:
|
| 图 7 末端质量对绳段运动特性的影响曲线 Fig. 7 The graph of tether′s kinetic characteristic with endmass | |
不考虑电帆携带末端质量的情况,仅研究绳索在中心轮毂带动下的展开过程,取初始相对角速度3 rad/s,展开时间共计5 s进行仿真。
图 7(b)中柔索末端在运动相位曲线的最外层t=3.18 s时开始反缠收缩,与图 5(b)中末端带有4.3 g质量块时相比,完全展开的时间略有滞后,位置距离转动中心比带质量块时更远,说明没有质量块的作用导致展开变慢,但柔索更容易从较大的弯曲变形状态中恢复至自然伸长。
对比图 7(c)中的伸出速率曲线不难看出,由于不带质量块的电帆柔索整体惯性较小,其展开的运动状态更容易随星体的驱动而改变,初始阶段伸出速率比带末端质量时增加得更快。图 7(d)显示出无质量时的张力很小,变化很微弱,由于惯性的原因,伸出速率曲线上出现突变,变化不平滑。
5 结论1) 通过有限段物理离散化方法建立的刚柔耦合动力学模型,准确描述了自旋展开过程中柔索的运动状态。
2) 驱动角速度影响展开速率以及柔索运动相位的变化,角速度越大展开越快,末端随半径的增加产生的离心力也越大,会使柔索更早出现反向缠绕的现象。
3) 末端质量影响系统的惯性特性,质量越大,运动状态越不易改变,进而导致柔索弯曲变形不易恢复,但随之产生的绳内张紧力能加快展开的进程,并保持展开的稳定变化。尤其对更大长细比的柔索,适当增加末端质量能保证展开的顺利进行。
总体而言,驱动速度与末端质量共同影响了系统动量,速度较大或末端带有质量时,动量交换过程中的柔索与中心轮毂之间产生的相互作用力增加,影响了帆面的保持。
| [1] |
JANHUNEN P, TOIVANEN P, ENVALL J, et al. Overview of electric solar wind sail applications[J]. Proceedings of the Estonian academy of sciences, 2014, 63(2S): 267-278. DOI:10.3176/proc.2014.2S.08 (  0) 0)
|
| [2] |
COSMO M L, LORENZINI E C. Tethers in space handbook[M]. 3rd ed.[s.l.], National Aeronautics and Space Administration, 1997.
(  0) 0)
|
| [3] |
FUNASE R, KAWAGUCHI J, MORI O, et al. IKAROS, a solar sail demonstrator and its application to trojan asteroid exploration[C]//Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Honolulu, Hawaii, 2012.
(  0) 0)
|
| [4] |
JANHUNEN P. Electric sail for spacecraft propulsion[J]. Journal of propulsion and power, 2004, 20(4): 763-764. DOI:10.2514/1.8580 (  0) 0)
|
| [5] |
WIEGMANN B, VAUGHN J, SCHNEIDER T, et al. Findings from NASA's 2015-2017 Electric Sail Investigations[EB/OL]. (2017-06-11). https://ntrs.nasa.gov/search.jsp?R=201700124392018-10-30T07:57:53+00:00Z.
(  0) 0)
|
| [6] |
ENVALL J, JANHUNEN P, TOIVANEN P, et al. E-sail test payload of ESTCube-1 nanosatellite[J]. arXiv preprint arXiv: 1404.6961, 2014.
(  0) 0)
|
| [7] |
SLAVINSKIS A, PAJUSALU M, KUUSTE H, et al. ESTCube-1 in-orbit experience and lessons learned[J]. IEEE aerospace and electronic systems magazine, 2015, 30(8): 12-22. DOI:10.1109/MAES.2015.150034 (  0) 0)
|
| [8] |
KAMMAN J W, HUSTON R L. Modeling of variable length towed and tethered cable systems[J]. Journal of guidance, control, and dynamics, 1999, 22(4): 602-608. (  0) 0)
|
| [9] |
BUCKHAM B, NAHON M, SETO M, et al. Dynamics and control of a towed underwater vehicle system, part Ⅰ:model development[J]. Ocean engineering, 2003, 30(4): 453-470. DOI:10.1016/S0029-8018(02)00029-X (  0) 0)
|
| [10] |
WANG Y, HUSTON R L. A lumped parameter method in the nonlinear analysis of flexible multibody systems[J]. Computers & structures, 1994, 50(3): 421-432. (  0) 0)
|
| [11] |
孔宪仁, 徐大富, 杨正贤, 等. 空间绳系系统自由展开建模与仿真[J]. 振动与冲击, 2011, 30(5): 37-42. KONG Xianren, XU Dafu, YANG Zhengxian, et al. Modeling and simulation for free deployment of a space tether system[J]. Journal of vibration and shock, 2011, 30(5): 37-42. DOI:10.3969/j.issn.1000-3835.2011.05.008 (  0) 0)
|
| [12] |
FULTON J, SCHAUB H. Sensitivity analysis of the electric sail deployment dynamics parameters[C]//Proceedings of the 5th International Conference on Tethers in Space. Ann Arbor, Michigan, 2016.
(  0) 0)
|
| [13] |
WITTBRODT E, ADAMIEC-WÓJCIK I, WOJCIECH S. Dynamics of flexible multibody systems:rigid finite element method[M]. Berlin: Springer, 2006.
(  0) 0)
|
| [14] |
HAMPER M B, RECUERO A M, ESCALONA J L, et al. Use of finite element and finite segment methods in modeling rail flexibility:a comparative study[J]. Journal of computational and nonlinear dynamics, 2012, 7(4): 041007. DOI:10.1115/1.4006728 (  0) 0)
|
| [15] |
FLORES P, AMBRÓSIO J, CLARO J C P, et al. Influence of the contact-impact force model on the dynamic response of multi-body systems[J]. Proceedings of the institution of mechanical engineers, part K:journal of multi-body dynamics, 2006, 220(1): 21-34. DOI:10.1243/146441906X77722 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


