近年来,欠驱动船的运动控制问题备受关注,大多数海上航行船舶的独立控制输入量少于其自由度,属于典型的欠驱动系统。因为一般非完整系统的研究结论不能直接应用于欠驱动船,使得欠驱动船的跟踪控制器设计相对因难。此外欠驱动船在复杂环境下进行航行与作业时,实际控制系统受到各种不确定性的影响,因此,对参数不确定性和外部干扰具有良好鲁棒性的滑模控制方法得到广泛关注和应用[1-3]。控制元件的物理限制通常会导致执行器存在非线性特征(如饱和、死区、继电特性等), 这就使所设计控制策略难以取得期望的实际效果,同时也增加了控制器设计的难度。因此,关于控制输入受限情况下控制系统的分析与综合问题逐渐受到学者的关注,并取得了一些研究成果[4-6]。
常规滑模控制(sliding mode control, SMC)通常要求不确定项为已知有界约束,然而实际工程中不确定项的界通常无法确知;为了保证对不确定项和干扰的鲁棒性,通常选取较大的切换增益,将增大系统抖振。目前,有2种方法可放宽SMC算法对不确定项先验知识的要求即扰动观测器技术[7-8]和自适应滑模控制技术[9-12],但基于扰动观测器的SMC算法一般假设干扰由一个线性的外源系统产生[13],干扰的复杂性和未知性导致这一假设在实际中难以满足。而参数自适应滑模控制器通过时变的边界层宽度和控制增益,有效抑制输入抖振的同时提高跟踪精度。张元涛等[9]针对不确定非线性系统的跟踪控制提出一种基于切换增益和sigmoid函数边界层厚度的参数自适应滑模方法;丛炳龙等[10]针对刚体航天器的鲁棒姿态控制问题,提出一种改进的自适应滑模控制,在传统滑模面设计中增加一个衰减函数, 减少由系统初始误差过大而引起的SMC到达段对自适应过程的影响;于靖等[11]针对存在扰动和参数不确定的MIMO非线性系统设计了基于干扰观测器的边界层自适应滑模控制器,通过梯度下降法设计边界层宽度自适应律。但是上述文献均未考虑输入受限的情况。文献[14-17]针对饱和特性分析已做相关研究。王瑞芬等[14]考虑控制输入饱和受限下的不确定系统滑模控制问题,设计了积分型切换面和具有特殊结构的滑模控制律, 可以在参数不确定和控制受限影响下保证系统状态轨迹有限时间内到达指定的切换面;Huang等[15]针对输入饱和下的欠驱动船舶跟踪控制,级联系统下采用饱和状态反馈控制实现系统全局渐进稳定;Zheng等[16]基于径向基神经网络(radial basis fuzzy neural network, RBFNN)和饱和辅助系统扩展反步方法。然而多数文献并未涉及欠驱动水面船相关运动控制问题的研究。
鉴于上述问题,本文以欠驱动水面船为研究对象,在无需确知不确定项并考虑输入饱和的情况下,提出一种基于饱和补偿辅助系统的参数自适应滑模控制方法。
1 数学模型建立及问题描述在本文中,·和
考虑模型非线性阻尼项、外部干扰及输入饱和的影响,涵盖欠驱动水面船从低速到高速的应用,其三自由度的运动学和动力学模型分别为[18-19]:
| $ \left\{ \begin{array}{l} \dot x = u\cos \psi - v\sin \psi \\ \dot y = u\sin \psi + v\cos \psi \\ \dot \psi = r \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} \dot u = \frac{{{m_{22}}}}{{{m_{11}}}}vr - \frac{{{d_{\rm{u}}}}}{{{m_{11}}}}u - \frac{{{d_{{\rm{uu}}}}}}{{{m_{11}}}}\left| u \right|u + \frac{1}{{{m_{11}}}}{\rm{Sa}}{{\rm{t}}_{\rm{u}}}\left( {{\tau _{\rm{u}}}} \right) + \frac{{{\sigma _{\rm{u}}}}}{{{m_{11}}}}\\ \dot v = - \frac{{{m_{11}}}}{{{m_{22}}}}ur - \frac{{{d_{\rm{v}}}}}{{{m_{22}}}}v - \frac{{{d_{{\rm{vv}}}}}}{{{m_{22}}}}\left| v \right|v + \frac{{{\sigma _{\rm{v}}}}}{{{m_{22}}}}\\ \dot r = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}uv - \frac{{{d_{\rm{r}}}}}{{{m_{33}}}}r - \frac{{{d_{{\rm{rr}}}}}}{{{m_{33}}}}\left| r \right|r + \\ \;\;\;\;\frac{1}{{{m_{33}}}}{\rm{Sa}}{{\rm{t}}_{\rm{r}}}\left( {{\tau _{\rm{r}}}} \right) + \frac{{{\sigma _{\rm{r}}}}}{{{m_{33}}}} \end{array} \right. $ | (2) |
式中:x、y、ψ分别表示大地坐标系下USV位置坐标和航向;u、v、r表示船体坐标系下纵向、横向和艏摇角速度;τu和τr表示纵向力和偏航力矩;σj(j=u, v, r)表示外部干扰; mii(i=1, 2, 3)表示船的惯性矩阵,为已知项;du、dv、dr和duu、dvv、drr表示线性和非线性水动力阻尼项;饱和函数定义如下:
| $ {\rm{Sa}}{{\rm{t}}_ * }\left( {{\tau _ * }} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\tau _{ * \max }},\\ {\tau _ * },\\ {\tau _{ * \min }}, \end{array}&\begin{array}{l} {\tau _ * } \ge {\tau _{ * \max }}\\ {\tau _{ * \min }} \le {\tau _ * } < {\tau _{ * \max }}\\ {\tau _ * } < {\tau _{ * \min }} \end{array} \end{array}} \right. $ | (3) |
式中:τ*为不考虑输入饱和的控制律;*分别代表u和r;τ*min、τ*max为饱和限制最小值与最大值。
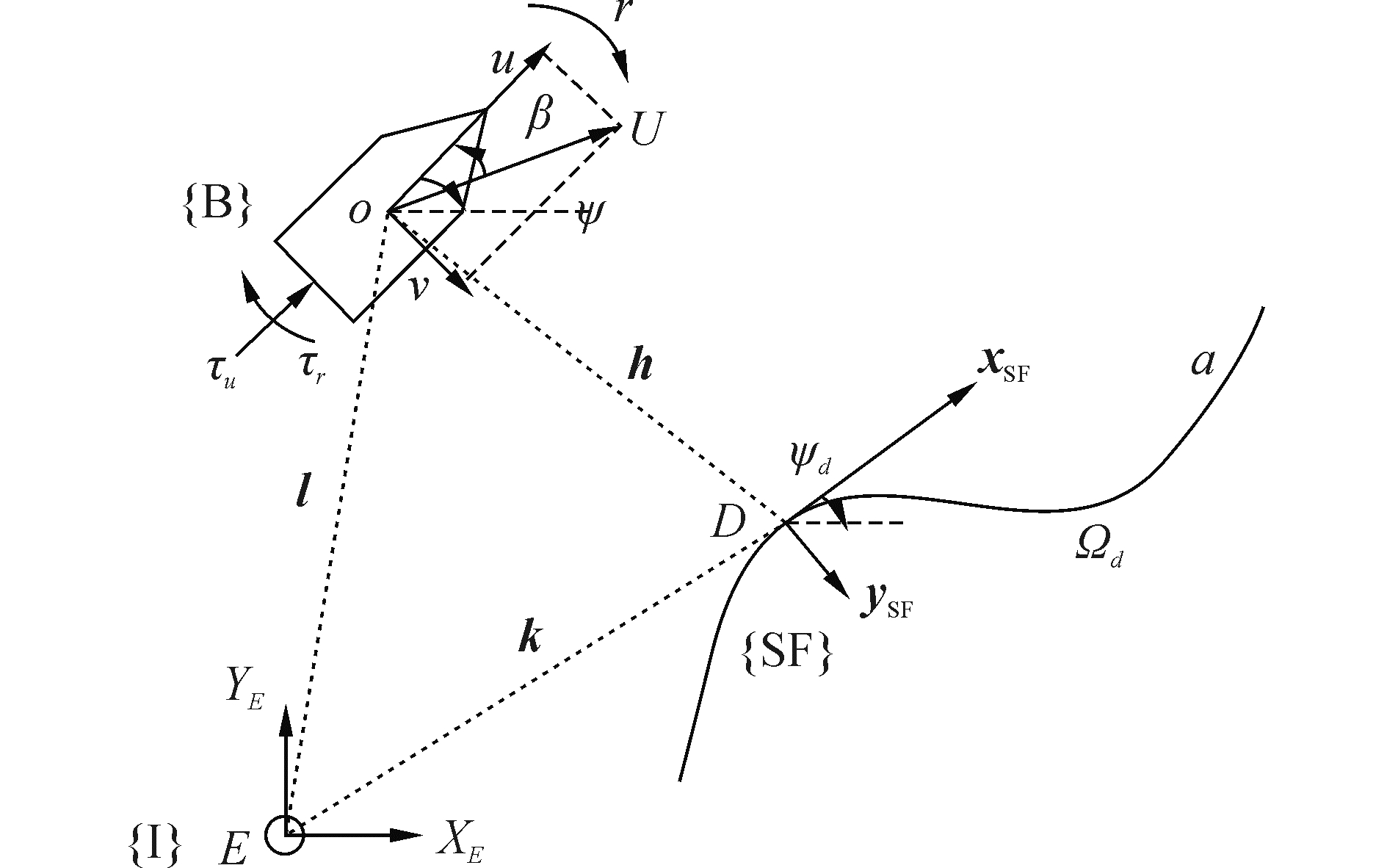
欠驱动水面船在SF坐标系下的路径跟踪原理图如图 1所示。{SF}表示Serrete-Frenet坐标系,{I}表示大地坐标系,{B}表示船体坐标系。Ωd为预先设定的参考路径,O为USV质心,D为O在Ωd上的正交投影点,E为大地坐标系原点,xSF、ySF分别是D点的单位切向量、单位法向向量。为了方便控制器设计和稳定性分析,给出如下假设:
|
Download:
|
| 图 1 欠驱动水面船路径跟踪原理 Fig. 1 Path following schematic for the USV | |
1) 外部扰动σj(j=u, v, r)有界且为慢变过程,满足
综上所述,欠驱动水面船路径跟踪问题的控制目标为:针对非线性系统式(1)和(2),结合饱和补偿辅助系统设计参数自适应滑模控制律T=(τu,
|
Download:
|
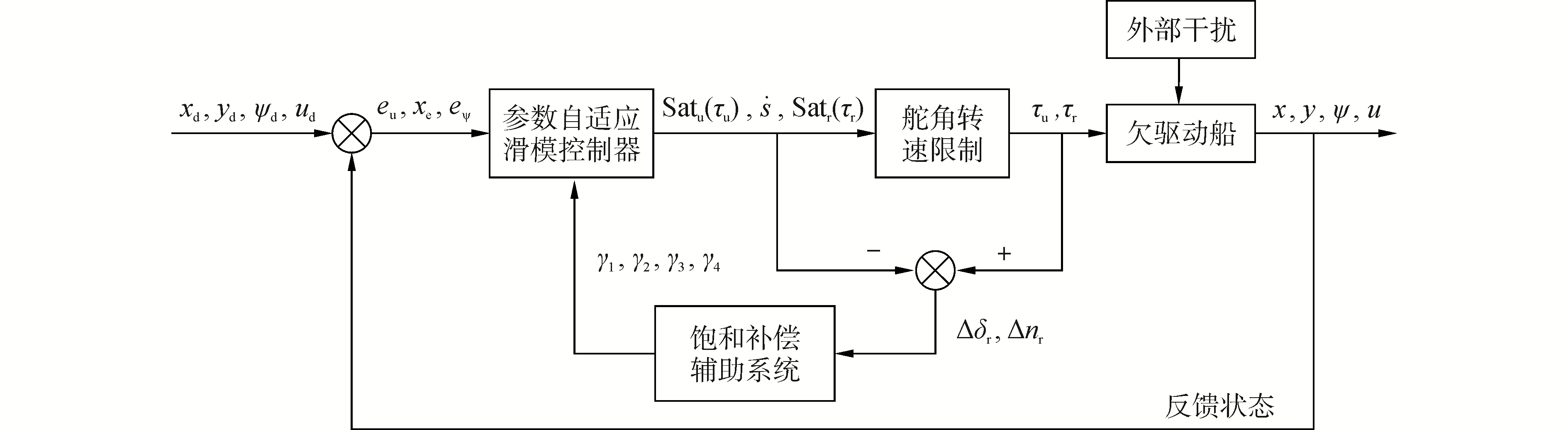
| 图 2 路径跟踪的结构框图 Fig. 2 Blockdiagram for path following | |
结合Serrete-Frenet移动坐标系,将切向速度作为虚拟控制输入
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_{\rm{e}}} = \mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{d}}}\\ {\mathit{\boldsymbol{y}}_{\rm{e}}} = \mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{y}}_{\rm{d}}}\\ {\psi _{\rm{e}}} = \psi + \beta - {\psi _{\rm{d}}} \end{array} \right. $ | (4) |
式中:ψd=arctan(
选取参考路径上的切向速度作为期望速度ud:
| $ \left\{ \begin{array}{l} {u_{\rm{d}}} = \dot s\\ {r_{\rm{d}}} = {k_{\rm{s}}}\dot s \end{array} \right. $ | (5) |
式中:rd表示期望艏向角角速度;
如图 1所示,向量l, k, h可以建立如下关系:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}^{\rm{T}}}{{\left( {\frac{{{\rm{d}}\mathit{\boldsymbol{l}}}}{{{\rm{d}}t}}} \right)}_{\left\{ {\rm{I}} \right\}}} = {{\left( {\frac{{{\rm{d}}\mathit{\boldsymbol{k}}}}{{{\rm{d}}t}}} \right)}_{\left\{ {{\rm{SF}}} \right\}}} + {{\left( {\frac{{{\rm{d}}\mathit{\boldsymbol{h}}}}{{{\rm{d}}t}}} \right)}_{\left\{ {{\rm{SF}}} \right\}}} + }\\ {{\mathit{\boldsymbol{r}}_d} \times \mathit{\boldsymbol{h}}}\\ {{\mathit{\boldsymbol{R}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}}\\ {\mathit{\boldsymbol{\dot y}}}\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{u_{\rm{d}}}}\\ 0\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot x}}}_{\rm{e}}}}\\ {{{\mathit{\boldsymbol{\dot y}}}_{\rm{e}}}}\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {r_{\rm{d}}}{\mathit{\boldsymbol{y}}_{\rm{e}}}}\\ {{r_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{e}}}}\\ 0 \end{array}} \right]} \end{array} $ | (6) |
式中:旋转变换矩阵
由向量间关系和式(4)~(6)可得路径跟踪的误差方程:
| $ \left\{ \begin{array}{l} {{\dot x}_e} = - \dot s + {k_s}\dot s{y_e} + U\cos {\psi _e}\\ {{\dot y}_e} = - {k_s}\dot s{x_e} + U\sin {\psi _e}\\ {{\dot \psi }_e} = r + \dot \beta - {r_d} \end{array} \right. $ | (7) |
式中合速度
利用式(7)设计参数自适应滑模控制律T=(τu,
1) 设计航速、位置和艏向角跟踪子系统的滑模控制律,航速跟踪滑模面函数为:
| $ {s_1} = {e_{\rm{u}}} = u - {u_{\rm{d}}} $ | (8) |
两端求导并选取指数趋近律:
| $ {{\dot s}_i} = - {k_i}{\mathop{\rm sgn}} \left( {{s_i}} \right) - {\varepsilon _i}{s_i} $ | (9) |
式中:ki、εi(i=1, 2, 3)分别表示切换增益和指数趋近项系数。
根据式(2)、(9),航速滑模控制律为:
| $ \begin{array}{*{20}{c}} {{\rm{Sa}}{{\rm{t}}_{\rm{u}}}\left( {{\tau _{\rm{u}}}} \right) = - {m_{11}}\left[ {{k_1}{\mathop{\rm sgn}} \left( {{s_1}} \right) + {\varepsilon _1}{s_1}} \right] - {m_{22}}ur + }\\ {{d_{\rm{u}}}u + {d_{{\rm{uu}}}}\left| u \right|u - {{\hat \sigma }_{\rm{u}}}} \end{array} $ | (10) |
位置跟踪滑模面函数为:
| $ {s_2} = {x_{\rm{e}}} $ | (11) |
同样选取指数趋近律,为了避免奇异值,位置跟踪控制器设计:
| $ \dot s = u\cos {\psi _e} + {\varepsilon _2}{s_2} + {k_2}{\mathop{\rm sgn}} \left( {{s_2}} \right) $ | (12) |
艏向角跟踪的终端滑模面函数为
| $ {s_3} = {e_\psi } + c{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|^{\left( {p/q} \right)}} $ | (13) |
式中:艏向角跟踪误差eψ=ψe-ω,趋近角ω=-arctan(uye);c、p、q为待设计参数,c>0,p、q都是奇数且大于0。
对(13)式两端求导,可得:
| $ {{\dot s}_3} = {{\dot e}_{\rm{ \mathsf{ ψ} }}} + c\frac{p}{q}{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|^{\left( {p/q - 1} \right)}}\left( {\dot r + \ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega } \right) $ | (14) |
同样选取指数趋近律,艏向角跟踪控制器子系统的滑模控制律表示为:
| $ \begin{array}{l} {\rm{Sa}}{{\rm{t}}_r}\left( {{\tau _{\rm{r}}}} \right) = - \frac{{{m_{33}}q}}{{cp}}{\left| {{{\dot e}_\psi }} \right|^{\left( {1 - p/q} \right)}}\left[ {{{\dot e}_\psi } + {\varepsilon _3}{s_3} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{k_3}{\mathop{\rm sgn}} \left( {{s_3}} \right)} \right] - {m_{33}}\left( {\ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\left( {{m_{11}} - {m_{22}}} \right)uv + {d_{\rm{r}}}r + {d_{{\rm{rr}}}}\left| r \right|r - {{\hat \sigma }_{\rm{r}}} \end{array} $ | (15) |
2) 设计参数自适应滑模控制律,首先通过Lyapunov稳定性理论及控制输入与输出设计切换增益和边界层的自适应律,将如下sigmoid函数引入滑模控制律替换符号函数:
| $ \mathit{\Phi }\left( {{\lambda _i},{s_i}} \right) = \frac{{1 - \exp \left( { - {\lambda _i}{s_i}} \right)}}{{1 + \exp \left( { - {\lambda _i}{s_i}} \right)}} $ | (16) |
式中:λi(i=1, 2, 3)表示边界层厚度参数。
选取Lyapunov函数如下:
| $ {{\tilde V}_i} = \frac{1}{2}e_i^2 $ | (17) |
式中:e1=eu, e2=xe, e3=eψ。记系统控制输出pi,系统控制输入Ui,其中p1=u, p2=xe, p3=ψe,U1=Satu(τu), U2=
| $ \begin{array}{l} {{\dot V}_{1i}} = \frac{{\partial {{\tilde V}_i}}}{{\partial {e_i}}}\frac{{\partial {e_i}}}{{\partial {p_i}}}\frac{{\partial {p_i}}}{{\partial {U_i}}}\frac{{\partial {U_i}}}{{\partial {k_i}}}\frac{{\partial {k_i}}}{{\partial t}} = \\ \;\;\;\;\;\;\; - {e_i}\frac{{\partial {p_i}}}{{\partial {U_i}}}\frac{1}{{g\left( {{p_i}} \right)}}\frac{{1 - \exp \left( { - {\lambda _i}{s_i}} \right)}}{{1 + \exp \left( { - {\lambda _i}{s_i}} \right)}}{{\dot k}_i} \end{array} $ | (18) |
| $ \begin{array}{l} {{\dot V}_{2i}} = \frac{{\partial {{\tilde V}_i}}}{{\partial {e_i}}}\frac{{\partial {e_i}}}{{\partial {p_i}}}\frac{{\partial {p_i}}}{{\partial {U_i}}}\frac{{\partial {U_i}}}{{\partial {\lambda _i}}}\frac{{\partial {\lambda _i}}}{{\partial t}} = \\ \;\;\;\;\;\;\; - {e_i}\frac{{\partial {p_i}}}{{\partial {U_i}}}\frac{{{k_i}}}{{g\left( {{p_i}} \right)}}\frac{{2{s_i}\exp \left( { - {\lambda _i}{s_i}} \right)}}{{{{\left( {1 + \exp \left( { - {\lambda _i}{s_i}} \right)} \right)}^2}}}{{\dot \lambda }_i} \end{array} $ | (19) |
其中:
切换增益和边界层厚度的参数自适应律设计如下:
| $ \left\{ \begin{array}{l} {{\dot {\hat k}}_i} = {\eta _i}g\left( {{p_i}} \right){e_i}{\mathop{\rm sgn}} \left( {\frac{{\partial {p_i}}}{{\partial {U_i}}}} \right)\left( {\frac{{1 - \exp \left( { - {\lambda _i}{s_i}} \right)}}{{1 + \exp \left( { - {\lambda _i}{s_i}} \right)}}} \right)\\ {{\dot {\hat \lambda} }_i} = {\mu _i}g\left( {{p_i}} \right){e_i}{\mathop{\rm sgn}} \left( {\frac{{\partial {p_i}}}{{\partial {U_i}}}} \right){s_i} \end{array} \right. $ | (20) |
式中:ηi、μi>0是设计参数。
将sigmoid函数和式(20)代入滑模控制律中,可得参数自适应滑模控制律:
| $ \left\{ \begin{array}{l} {\rm{Sa}}{{\rm{t}}_{\rm{u}}}\left( {{\tau _{\rm{u}}}} \right) = - {m_{11}}\left[ {{{\hat k}_1}\mathit{\Phi }\left( {{{\hat \lambda }_1},{s_1}} \right) + {\varepsilon _1}{s_1}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{m_{22}}vr + {d_u}u + {d_{\rm{uu}}}\left| u \right|u - {{\hat \sigma }_{\rm{u}}}\\ \dot s = u\cos {\psi _{\rm{e}}} + {\varepsilon _2}{s_2} + {{\hat k}_2}\mathit{\Phi }\left( {{{\hat \lambda }_2},{s_2}} \right)\\ {\rm{Sa}}{{\rm{t}}_{\rm{r}}}\left( {{\tau _{\rm{r}}}} \right) = - \frac{{{m_{33}}q}}{{cp}}{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|^{\left( {1 - p/q} \right)}}\left[ {{{\dot e}_{\rm{ \mathsf{ ψ} }}} + {\varepsilon _3}{s_3} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\hat k}_3}\mathit{\Phi }\left( {{{\hat \lambda }_3},{s_3}} \right)} \right] - {m_{33}}\left( {\ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{m_{11}} - {m_{33}}} \right)uv + {d_{\rm{r}}}r + {d_{{\rm{rr}}}}\left| r \right|r - {{\hat \sigma }_{\rm{r}}} \end{array} \right. $ | (21) |
3) 结合饱和补偿辅助系统的参数自适应滑模控制律设计,选用饱和函数形式限制控制输入舵角δr,限制条件下的艏向角控制输入δra:
| $ {\delta _{ra}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\delta _{{\rm{r}},\max }},\\ {\delta _{\rm{r}}},\\ - {\delta _{{\rm{r}},\max }}, \end{array}&\begin{array}{l} {\delta _{{r}}} > {\delta _{{\rm{r}},\max }}\\ \left| {{\delta _{\rm{r}}}} \right| \le {\delta _{{\rm{r}},\max }}\\ {\delta _{\rm{r}}} < - {\delta _{{\rm{r,max}}}} \end{array} \end{array}} \right. $ | (22) |
式中:-35°≤δr<35°,饱和误差Δδr=δra-δr。
艏向角饱和补偿辅助系统为:
| $ \left\{ \begin{array}{l} {{\dot \gamma }_1} = - {c_1}{\gamma _1} + {\gamma _2}\\ {{\dot \gamma }_2} = - {c_2}{\gamma _2} + \frac{1}{{{m_{33}}}}\Delta {\delta _{\rm{r}}}\\ {e_{\rm{ \mathsf{ ψ} }}} = \psi + \beta - {\psi _{\rm{d}}} - {\gamma _1} \end{array} \right. $ | (23) |
式中:ci>0(i=1, 2, 3, 4)。
则带有饱和补偿系统的转艏力矩为:
| $ \begin{array}{l} {\tau _{\rm{r}}} = - \frac{{{m_{33}}q}}{{cp}}{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|^{\left( {1 - p/q} \right)}}\left[ {{{\dot e}_{\rm{ \mathsf{ ψ} }}} + {\varepsilon _3}{s_3} + {{\hat k}_3}\mathit{\Phi }\left( {{{\hat \lambda }_3},{s_3}} \right)} \right] - \\ \;\;\;\;\;\;{m_{33}}\left( {\ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega + {c_1}\left( { - {c_1}{\gamma _1} + {\gamma _2}} \right) + {c_2}{\gamma _2}} \right) + \\ \;\;\;\;\;\;\Delta {\delta _{\rm{r}}} - \left( {{m_{11}} - {m_{22}}} \right)uv + {d_{\rm{r}}}r + {d_{{\rm{rr}}}}\left| r \right|r - {{\hat \sigma }_{\rm{r}}} \end{array} $ | (24) |
被限制的转速nra为:
| $ {n_{{\rm{ra}}}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {n_{{\rm{r,max}}}},\\ {n_{\rm{r}}}, \end{array}&\begin{array}{l} {n_r} > {n_{{\rm{r,max}}}}\\ 0 < {n_r} \le {n_{{\rm{r,max}}}} \end{array} \end{array}} \right. $ | (25) |
式中:nr,max=2 000 rad/min,Δnr=nra-nr。
被限制转速饱和补偿系统可以表示为:
| $ \left\{ \begin{array}{l} {{\dot \gamma }_3} = - {c_3}{\gamma _3} + {\gamma _4}\\ {{\dot \gamma }_4} = - {c_4}{\gamma _4} + \frac{1}{{{m_{22}}}}\Delta {n_{\rm{r}}} \end{array} \right. $ | (26) |
则带有饱和补偿系统的纵向推力为:
| $ \begin{array}{l} {\tau _{\rm{u}}} = - {m_{11}}\left[ {{{\hat k}_1}\mathit{\Phi }\left( {{{\hat \lambda }_1},{s_1}} \right) + {\varepsilon _1}{s_1} - \left( { - {c_3}{\gamma _3} + {\gamma _4}} \right)} \right] - \\ \;\;\;\;\;\;{m_{22}}vr + {d_{\rm{u}}}u + {d_{{\rm{uu}}}}\left| u \right|u - {{\hat \sigma }_{\rm{u}}} \end{array} $ | (27) |
定理:满足假设1~4的欠驱动水面船闭环系统式(1)、(2),在参数自适应滑模控制律式(20)、(21)和带饱和补偿系统的滑模控制律式(24)和(27)的控制下。对于任意初始条件,通过调整设计参数使跟踪误差渐进收敛到零值小的领域内,保证系统是全局稳定的。
证明:选取Lyapunov函数:
| $ \left\{ \begin{array}{l} V = {V_1} + {V_2} + {V_3}\\ {V_1} = 1/2e_{\rm{u}}^2 + 1/\left( {2\kappa } \right)\tilde \sigma _{\rm{u}}^2\\ {V_2} = 1/2x_{\rm{e}}^2 + 1/2y_{\rm{e}}^2\\ {V_3} = 1/2s_3^2 + 1/\left( {2\kappa } \right)\tilde \sigma _{\rm{r}}^2 \end{array} \right. $ | (28) |
对V1两端求导,并将式(2)代入得,
| $ \begin{array}{l} {{\dot V}_1} = {e_{\rm{u}}}\left( {\frac{{{m_{22}}}}{{{m_{11}}}}vr - \frac{{{d_{\rm{u}}} + {d_{{\rm{uu}}}}\left| u \right|}}{{{m_{11}}}}u + \frac{1}{{{m_{11}}}}{\rm{Sa}}{{\rm{t}}_{\rm{u}}}\left( {{\tau _{\rm{u}}}} \right) + } \right.\\ \;\;\;\;\;\;\left. {\frac{{{\sigma _u}}}{{{m_{11}}}}} \right) - \frac{1}{\kappa }{{\tilde \sigma }_{\rm{u}}}{{\dot {\hat \sigma} }_{\rm{u}}} = {e_{\rm{u}}}\left( { - {{\hat k}_1}\mathit{\Phi }\left( {{{\hat \lambda }_1},{s_1}} \right) - } \right.\\ \;\;\;\;\;\;\left. {{\varepsilon _1}{s_1} + \left( { - {c_3}{\gamma _3} + {\gamma _4}} \right)} \right) - \frac{1}{\kappa }{{\tilde \sigma }_{\rm{u}}}\left( {{{\dot {\hat \sigma} }_{\rm{u}}} - \frac{\kappa }{{{m_{11}}}}{e_{\rm{u}}}} \right) \end{array} $ | (29) |
选取
| $ \begin{array}{*{20}{c}} {{{\dot V}_1} = - {\varepsilon _1}e_{\rm{u}}^2 - \left( {{{\hat k}_1}\mathit{\Phi }\left( {{{\hat \lambda }_{\rm{1}}},{e_{\rm{u}}}} \right) + {c_3}{\gamma _3} - {\gamma _4}} \right){e_{\rm{u}}} \le }\\ { - {\varepsilon _1}e_{\rm{u}}^2 \le 0} \end{array} $ | (30) |
对V2两端求导,并将(7)和(21)式代入得:
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} = {x_{\rm{e}}}\left( { - \dot s + {k_{\rm{s}}}\dot s{y_{\rm{e}}} + U\cos {\psi _{\rm{e}}}} \right) + }\\ {{y_{\rm{e}}}\left( { - {k_{\rm{s}}}\dot s{x_{\rm{e}}} + U\sin {\psi _{\rm{e}}}} \right)}\\ { = {x_{\rm{e}}}\left( { - {\varepsilon _2}{s_2} - {{\hat k}_2}\mathit{\Phi }\left( {{{\hat \lambda }_2},{s_2}} \right)} \right) + {y_{\rm{e}}}u\sin {\psi _{\rm{e}}} \le }\\ { - {\varepsilon _2}x_{\rm{e}}^2 - {{\hat k}_2}\mathit{\Phi }\left( {{{\hat \lambda }_2},{x_{\rm{e}}}} \right){x_{\rm{e}}} \le 0} \end{array} $ | (31) |
对V3两端求导,并将式(2)和(24)代入得:
| $ \begin{array}{l} {{\dot V}_3} = {s_3}\left( {{{\dot e}_{\rm{ \mathsf{ ψ} }}} + c\frac{p}{q}{{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|}^{\left( {p/q - 1} \right)}}\left( {\dot r + \ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega } \right)} \right) - \\ \;\;\;\;\;\;\;\frac{1}{\kappa }{{\tilde \sigma }_{\rm{r}}}{{\dot {\hat \sigma} }_{\rm{r}}} = {s_3}\left[ {c\frac{p}{q}{{\left| {{{\dot e}_{\rm{ \mathsf{ ψ} }}}} \right|}^{\left( {p/q - 1} \right)}} \cdot } \right.\\ \;\;\;\;\;\;\;\left( {\frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}uv - \frac{{{d_{\rm{r}}}}}{{{m_{33}}}}r - \frac{{{d_{{\rm{rr}}}}}}{{{m_{33}}}}\left| r \right|r + } \right.\\ \;\;\;\;\;\;\;\left. {\left. {\frac{1}{{{m_{33}}}}{\rm{Sa}}{{\rm{t}}_{\rm{r}}}\left( {{\tau _{\rm{r}}}} \right) + \frac{{{\sigma _{\rm{r}}}}}{{{m_{33}}}} + \ddot \beta - {{\dot r}_{\rm{d}}} - \ddot \omega } \right)} \right] + \\ \;\;\;\;\;\;\;{{\dot e}_{\rm{ \mathsf{ ψ} }}} - \frac{1}{\kappa }{{\tilde \sigma }_{\rm{r}}}{{\dot {\hat \sigma} }_{\rm{r}}} = - {s_3}\left( {{\varepsilon _3}{s_3} + {{\hat k}_3}\mathit{\Phi }\left( {{{\hat \lambda }_3},{s_3}} \right)} \right) - \\ \;\;\;\;\;\;\;{s_3}\rho \left( {{c_1}\left( { - {c_1}{\gamma _1} + {\gamma _2}} \right) + {c_2}{\gamma _2}} \right) + \frac{{{s_3}\rho }}{{{m_{33}}}}\Delta {\delta _{\rm{r}}} - \\ \;\;\;\;\;\;\;\frac{1}{\kappa }{{\tilde \sigma }_{\rm{r}}}\left( {{{\dot {\hat \sigma} }_{\rm{r}}} - \frac{{{s_3}\rho }}{{{m_{33}}}}\kappa } \right) \end{array} $ | (32) |
选取
| $ {{\dot V}_3} \le - {\varepsilon _3}s_3^2 - {{\hat k}_3}\mathit{\Phi }\left( {{{\hat \lambda }_3},{s_3}} \right){s_3} \le 0 $ | (33) |
综上所述,
以文献[20]中的CyberShipⅡ数学模型(1:70)进行仿真研究,针对具有外部干扰和输入饱和的欠驱动水面船路径跟踪控制问题,利用基于饱和补偿辅助系统的参数自适应滑模控制器(adaptive sliding mode control, ASMC)和常规滑模控制器(sliding mode control, SMC)进行仿真对比实验,以下仿真图中的ASMC指基于饱和补偿辅助系统的参数自适应滑模控制器。其中船长1.255 m,质量23.8 kg,m11=25.8, m22=33.8, m33=2.76, du=0.722 53, dr=1.9, dv=0.889 65, duu=1.327 42, dvv=36.472 8, drr=0.75,参考路径为:xd=10sin(θ/15), yd=θ。
USV初始状态为[x(0), y(0), ψ(0), u(0), v(0), r(0)]=[-5, 3, 0.785, 0.25, 0, 0]。期望速度ud=3 m/s。切换增益和边界厚度的自适应律初始值为
|
Download:
|
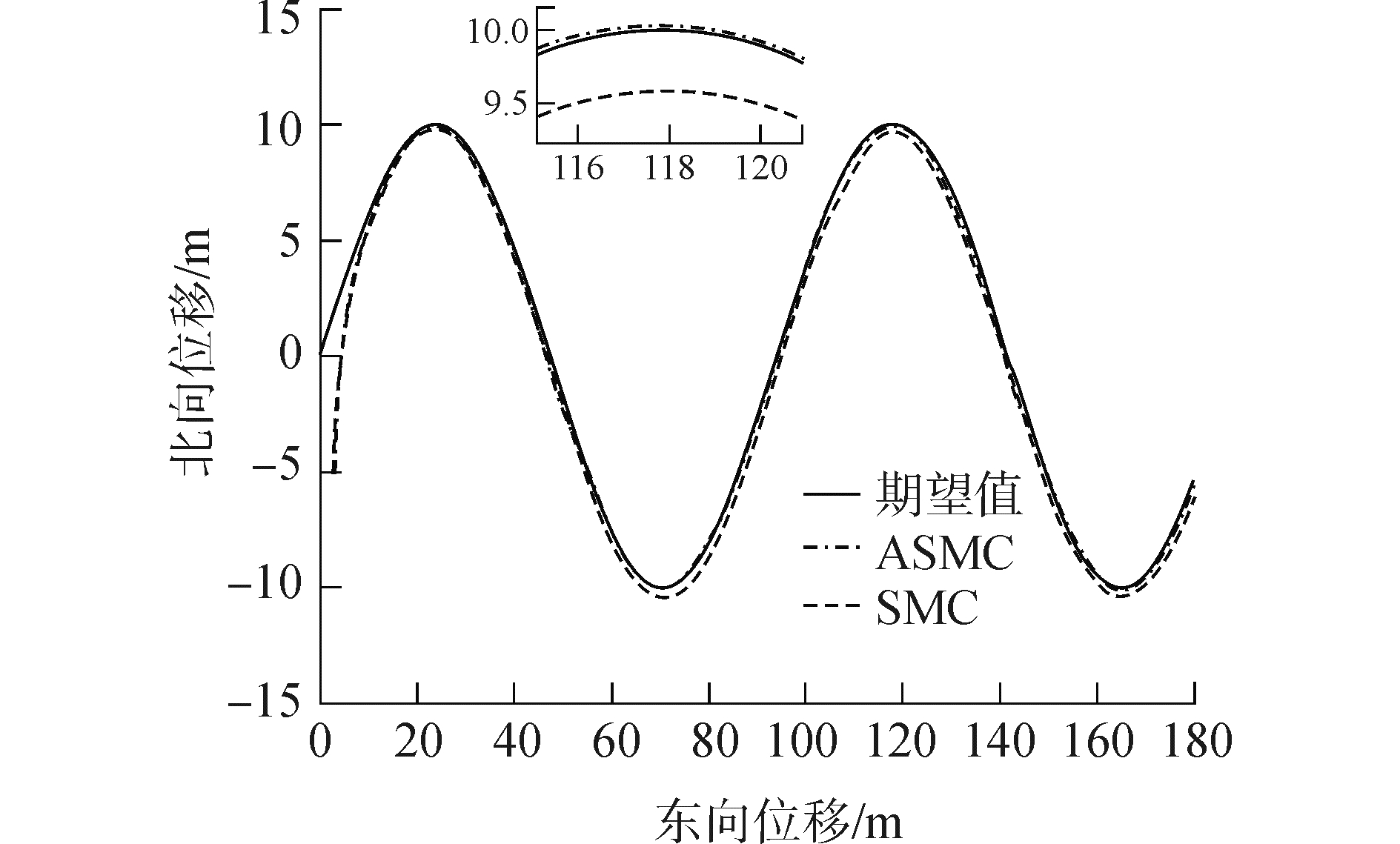
| 图 3 欠驱动水面船路径跟踪的位置 Fig. 3 Position of path following for USV | |

|
Download:
|
| 图 4 切换增益变化 Fig. 4 The switching gain | |

|
Download:
|
| 图 5 边界层厚度变化 Fig. 5 The boundary layer thickness | |
|
Download:
|
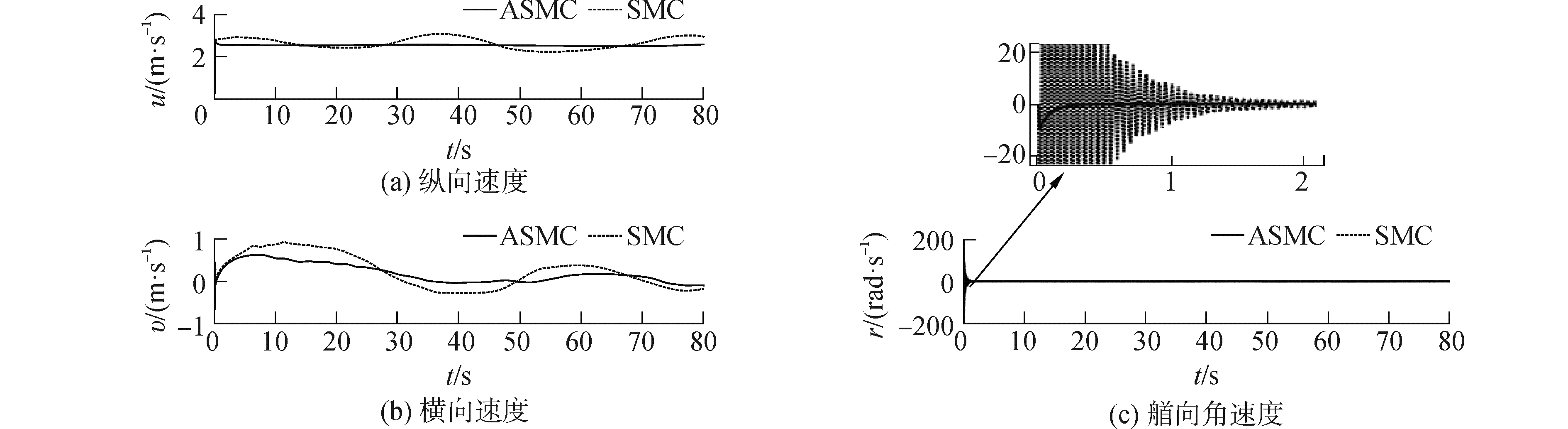
| 图 6 欠驱动水面船路径跟踪的速度量 Fig. 6 Velocity of path following for underactuated unmanned surface vehicle | |
|
Download:
|
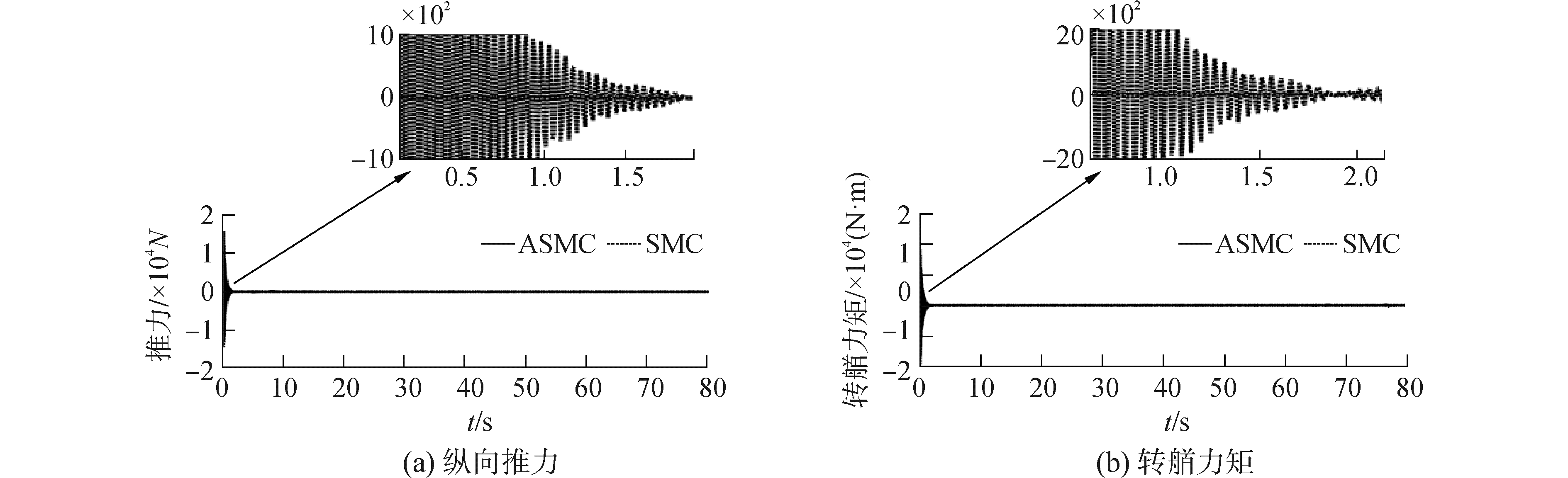
| 图 7 欠驱动水面船路径跟踪控制输入曲线 Fig. 7 Contral input of path following for underctuated unmanmed surface vehicle | |
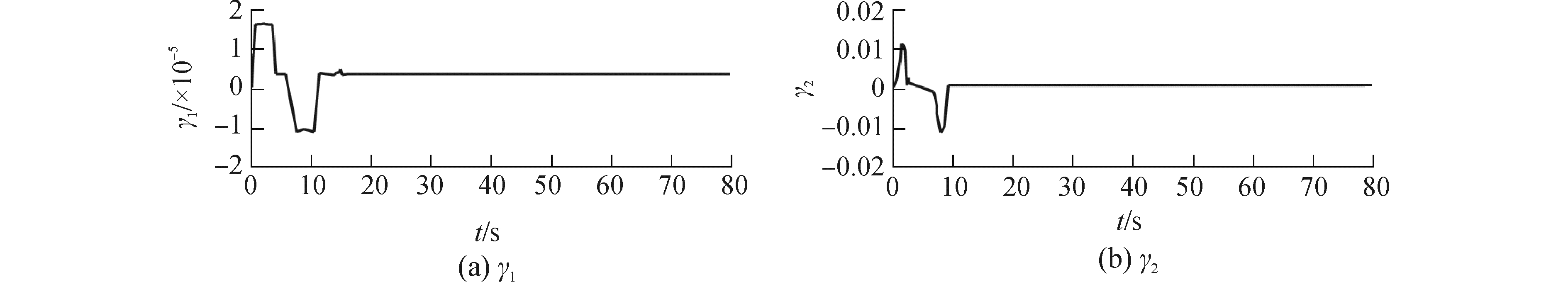
|
Download:
|
| 图 8 饱和补偿量γ1, γ2的变化 Fig. 8 Variation of saturation compensation γ1, γ2 | |
从切换增益变化图(图 4)和边界层厚度变化图(图 5)的情况可以看出,所提出的自适应律使得切换增益和边界层厚度不再是恒定的数值;进而通过欠驱动水面船路径跟踪位置效果对比图(图 3)和欠驱动水面船路径跟踪速度量的比较结果(图 6)可以看出基于饱和补偿系统的参数自适应滑模控制的控制效果更好,可以看出ASMC方法相比SMC方法稳态误差和抖振有明显减少,跟踪精度有明显提高;因此本文所提方法可以有效减弱系统抖振和提高跟踪精度。
从图 6(b)可以看出,欠驱动船水平运动的横向速度有限,这也从数值仿真的角度佐证了假设2的合理性;从纵向推力和转艏力矩仿真图(图 7)可以看出,相比于SMC方法,控制输入的饱和程度在使用基于饱和补偿系统的ASMC方法后也得到明显降低;同时结合艏向角饱和补偿量的变化(图 8)可以看出,在误差从初始值收敛的阶段,有效的补偿了由于误差过大引起的控制输入饱和问题。
4 结论1) 与传统SMC方法相比,基于饱和补偿辅助系统的ASMC方法可以有效减弱抖振,提高跟踪精度,改善控制效果。
2) 所提方法通过Serrete-Frenet移动坐标系将切向速度作为虚拟控制输入解决USV的欠驱动特性。
3) 所提方法无需确知不确定项的界,同时补偿输入饱和误差,有效解决外部干扰和输入饱和下的欠驱动水面船路径跟踪问题。
实际情况下执行器提供的力和力矩会延时作用于各个自由度上,短时间中对于各自由度高度耦合的欠驱动水面船的影响更为明显,因此时滞问题是后续研究的重点。
| [1] |
朱齐丹, 于瑞亭, 夏桂华, 等. 风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J]. 控制理论与应用, 2012, 29(7): 959-964. ZHU Qidan, YU Ruiting, XIA Guihua, et al. Sliding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances[J]. Control theory & applications, 2012, 29(7): 959-964. (  0) 0)
|
| [2] |
李湘平, 吴汉松, 阮苗锋. Serret-Frenet框架下的神经滑模船舶路径跟踪控制[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(1): 180-184. LI Xiangping, WU Hansong, RUAN Miaofeng. Neural sliding mode control for tracking of ships under serret-renet frame[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2015, 39(1): 180-184. DOI:10.3963/j.issn.2095-3844.2015.01.041 (  0) 0)
|
| [3] |
焦鑫, 江驹. 非线性系统自适应鲁棒控制器设计[J]. 哈尔滨工程大学学报, 2016, 37(3): 402-407. JIAO Xin, JIANG Ju. Design of an adaptive robust controller for nonlinear system[J]. Journal of Harbin Engineering University, 2016, 37(3): 402-407. (  0) 0)
|
| [4] |
CHWA D. Global tracking control of underactuated ships with input and velocity constraints using dynamic surface control method[J]. IEEE transactions on control systems technology, 2011, 19(6): 1357-1370. DOI:10.1109/TCST.2010.2090526 (  0) 0)
|
| [5] |
HARMOUCHE M, LAGHROUCHE S, CHITOUR Y. Global tracking for underactuated ships with bounded feedback controllers[J]. International journal of control, 2014, 87(10): 2035-2043. (  0) 0)
|
| [6] |
CHEN Mou, ZHOU Yanlong, GUO W W. Robust tracking control for uncertain MIMO nonlinear systems with input saturation using RWNNDO[J]. Neurocomputing, 2014, 144: 436-447. DOI:10.1016/j.neucom.2014.04.032 (  0) 0)
|
| [7] |
CHEN Mou, CHEN Wenhua. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer[J]. International journal of adaptive control and signal processing, 2010, 24(1): 51-64. (  0) 0)
|
| [8] |
CHEN Wenhua. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME transactions on mechatronics, 2004, 9(4): 706-710. DOI:10.1109/TMECH.2004.839034 (  0) 0)
|
| [9] |
张元涛, 石为人, 邱明伯. 一类不确定非线性系统的参数自适应滑模控制[J]. 华中科技大学学报(自然科学版), 2011, 39(5): 79-82. ZHANG Yuantao, SHI Weiren, QIU Mingbai. Parameter adaptive sliding mode control for a class of uncertain nonlinear systems[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2011, 39(5): 79-82. (  0) 0)
|
| [10] |
丛炳龙, 刘向东, 陈振. 一种改进的自适应滑模控制及其在航天器姿态控制中的应用[J]. 控制与决策, 2012, 27(10): 1471-1476. CONG Binglong, LIU Xiangdong, CHEN Zhen. An improved adaptive sliding mode control for spacecraft attitude control[J]. Control and decision, 2012, 27(10): 1471-1476. (  0) 0)
|
| [11] |
于靖, 陈谋, 姜长生. 基于干扰观测器的非线性不确定系统自适应滑模控制[J]. 控制理论与应用, 2014, 31(8): 993-999. YU Jing, CHEN Mou, JIANG Changsheng. Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer[J]. Control theory & applications, 2014, 31(8): 993-999. (  0) 0)
|
| [12] |
齐辉, 张泽, 许江涛, 等. 基于Nussbaum增益滑模自适应控制的导弹制导控制一体化设计[J]. 控制与决策, 2017, 32(1): 93-99. QI Hui, ZHANG Ze, XU Jiangtao, et al. Integrated guidance and control of missile based on Nussbaum gain adaptive sliding mode control method[J]. Control and decision, 2017, 32(1): 93-99. (  0) 0)
|
| [13] |
HUANG Y J, KUO T C, CHANG S H. Adaptive sliding-mode control for nonlinear systems with uncertain parameters[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2008, 38(2): 534-539. DOI:10.1109/TSMCB.2007.910740 (  0) 0)
|
| [14] |
王瑞芬, 贾廷纲, 牛玉刚. 一类控制输入饱和受限的不确定系统滑模控制[J]. 控制理论与应用, 2011, 28(9): 1154-1158. WANG Ruifen, JIA Tinggang, NIU Yugang. Sliding-mode control for uncertain systems with input saturation[J]. Control theory & applications, 2011, 28(9): 1154-1158. (  0) 0)
|
| [15] |
HUANG Jiangshuai, WEN Changyun, WANG Wei, et al. Global stable tracking control of underactuated ships with input saturation[J]. Systems & control letters, 2015, 85: 1-7. (  0) 0)
|
| [16] |
ZHENG Zewei, SUN Liang. Path following control for marine surface vessel with uncertainties and input saturation[J]. Neurocomputing, 2016(177): 158-167. (  0) 0)
|
| [17] |
司文杰, 董训德, 王聪. 输入饱和的一类切换系统神经网络跟踪控制[J]. 自动化学报, 2017, 43(8): 1383-1392. SI Wenjie, DONG Xunde, WANG Cong. Adaptive neural tracking control design for a class of uncertain switched nonlinear systems with input saturation[J]. Acta automatica sinica, 2017, 43(8): 1383-1392. (  0) 0)
|
| [18] |
LIAO Yulei, ZHANG Mingjun, WAN Lei, et al. Trajectory tracking control for underactuated unmanned surface vehicles with dynamic uncertainties[J]. Journal of Central South University, 2016, 23(2): 370-378. DOI:10.1007/s11771-016-3082-4 (  0) 0)
|
| [19] |
XIANG Xianbo, LIU Chao, LAPIERRE L, et al. Synchronized path following control of multiple homogenous underactuated AUVs[J]. Journal of systems science and complexity, 2012, 25(1): 71-89. DOI:10.1007/s11424-012-0109-2 (  0) 0)
|
| [20] |
SKJETNE R, SMOGELI Ø N, FOSSEN T I. A nonlinear ship manoeuvering model:identification and adaptive control with experiments for a model ship[J]. Modeling, identin & control, 2004, 25(1): 3-27. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


