2. 中船第九设计研究院工程有限公司, 上海 200063
2. China Shipbuilding NDRI Engineering Co., Ltd., Shanghai 200063, China
波浪、潮汐等往复流作用下的泥沙运动不但是影响河口海岸地区地形地貌以及环境演化的一项重要因素,也是影响海底管道等建筑物安全的重要因子。对于沙质海岸,由于推移质对水流条件的响应远远快于悬移质,往复流作用下的推移质输沙强度预测在现实工程中尤为重要。因此,推移质输沙强度计算是港口海岸与近海工程重点关注的对象。
现有的研究大部分基于准恒定流的假定,将输沙问题划分至每一个微小的时间段进行分析,将单向流推移质输沙模型应用其中,结合实验数据推导或拟合出适用于往复流输沙的推移质输沙强度计算公式[1-5],可总结为推移质输沙强度是希尔兹数幅值和临界值的函数。这类公式虽然对实验数据有较好的拟合效果,但没有客观反映输沙规律与水流条件相互作用的内在机制,因此对往复流输沙规律的描述上仍然存在缺陷,这种分析方法最重要的不足在于忽略了惯性力作用对泥沙运动的影响,认为泥沙颗粒运动对流场变化的响应是瞬时的。然而,泥沙运动对于变化的水流条件需要响应时间,在许多研究的实验观测中都曾指出泥沙浓度、泥沙颗粒运动速度、瞬时输沙强度等物理量相对于水质点速度存在相位差的现象[6-9],即“相位滞后效应”。
目前,国内研究极少关注到相位滞后这一问题[10-12],国外考虑相位滞后效应的推移质输沙强度计算模型也较少,只有文献[13-18]进行过类似的研究。其总体思路认为相位滞后效应的产生导致底床泥沙浓度峰值与泥沙运动速度峰值错开,实际情况的推移质输沙强度幅值将相对于准恒定流模型的理论值有所减小,因此相位滞后的效应可以概括至一个小于1的系数中,以此对准恒定流模型进行适当修正。
本文将从泥沙颗粒的受力情况出发,以求得泥沙颗粒的运动速度,同时根据能量守恒准则对单位面积内运动的泥沙颗粒数量进行推导,结合两者,得到一个考虑相位滞后效应的瞬时推移质输沙强度表达式,再利用实验数据,拟合得到一个用于计算半周期平均输沙强度的半理论半经验公式。
1 推移质输沙强度计算式的推导 1.1 相位滞后效应与KC数的关系比较现有的代表性模型中描述相位滞后效应的无量纲参数[13-18],它们都反映惯性力作用与重力作用之比。最初这一参数定义为颗粒沉降时间与往复流周期之比:
| $ \frac{1}{2}\frac{{{U^2}}}{{\left( {s-1} \right)g{W_s}T}}\;\;\;或\;\;\;\frac{{2\pi \Delta }}{{{W_s}T}} $ |
式中:U为水质点运动速度幅值;s为泥沙比重;g为重力加速度;W为泥沙沉速;T为往复流周期;Δ为泥沙跃起高度。
后来,有学者加入切应力项和波流项对原有表达式进行修正:
| $ \frac{{{\upsilon ^{0.25}}{U^{0.5}}}}{{{W_s}{T^{0.75}}}}\exp \left[{-{{\left( {\frac{{{U_{w.{\text{cesf}}}}}}{U}} \right)}^2}} \right]\;\;\;或\;\;\;\frac{\Delta }{{{W_s}T}}\left( {1 -\frac{{\xi {u_w}}}{{{c_w}}}} \right) $ |
式中:υ为水的运动粘滞系数;Uw, crsf为表征推移质运动状态的特征速度;ξ为波流作用系数;cw为水流速度。
从上述表达式的形式可以看出,相位滞后效应参数的值实际上都由水质点速度、泥沙粒径、往复流周期这3个变量决定,并反映了颗粒沉降时间与往复流周期的比值,以此描述惯性力作用与重力作用影响大小。然而,这3个参数在实际计算当中都存在些许问题,如泥沙沉速的不确定性、泥沙跃起高度的不确定性、Uw, crsf如何定义和计算。因此,本文引入Keulegan-Carpenter数(KC)用于描述相位滞后效应对输沙强度的影响,KC的通常被定义为[19]KC=UT/D。
但值得注意的是,泥沙在起动条件满足之后会随着往复水流发生较大位移的运动,所以,反映泥沙运动的KC数定义为:
| $ {\text{KC' = }}\frac{{\left( {u-{u_p}} \right)T}}{D} $ | (1) |
式中u、up分别为水质点和泥沙颗粒的瞬时速度。
进一步对KC表达式进行分析得:
| $ {\text{KC' = }}\frac{{{{\left( {u-{u_p}} \right)}^2}/D}}{{\left| {u-{u_p}} \right|/T}} \sim \frac{{{{\left( {u-{u_p}} \right)}^2}}}{{D\left| {\frac{{{\text{d}}u}}{{{\text{d}}t}} - \frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right|}} $ |
由此可见,KC数表征了泥沙在运动过程中所受的拖曳力与惯性力之比,KC数的大小间接反映了相位滞后效应在推移质输沙过程中的重要程度。
1.2 推移质输沙强度计算公式如图 1所示,运动的泥沙颗粒受到拖曳力Fd、水平压力P和惯性力Fi、摩擦阻力Ff、有效重力G′和上举力Fl的共同作用。对运动的散粒体泥沙颗粒,其受力平衡表达式可以表达为

|
Download:
|
| 图 1 散粒体泥沙颗粒受力情况 Fig. 1 Force analysis for sediment granular particles | |
| $ \begin{gathered} {\rho _s}V\frac{{{\text{d}}{u_p}}}{{{\text{d}}t}} = \rho V\frac{{{\text{d}}u}}{{{\text{d}}t}} + \rho {C_a}V\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}-\frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right) + \hfill \\ \;\;\;\;\;\;\frac{1}{2}\rho {C_d}A{\left( {u-{u_p}} \right)^2}\frac{{u-{u_p}}}{{\left| {u - {u_p}} \right|}} - \hfill \\ \;\;\;\beta \left( {\left( {{\rho _s} - \rho } \right)Vg - \frac{1}{2}\rho {C_l}A{{\left( {u - {u_p}} \right)}^2}} \right) \hfill \\ \end{gathered} $ | (2) |
式中:ρs为泥沙干密度,ρ为水密度;V、A为泥沙颗粒体积和垂直于受力方向的截面积,此处假设泥沙颗粒均为球形;Ca、Cd、Cl、β分别为附加质量力系数、拖曳力系数、上举力系数和阻力系数;等号右边依次为水平压力项、惯性力项、拖曳力项和阻力项,这里的阻力项包括了摩擦阻力和遮蔽阻力的考虑。
式(2)两边同时除于
| $ \begin{gathered} 4\left( {s-1} \right)D\frac{{{\text{d}}u}}{{{\text{d}}t}}/\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}-\frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right) = 4D\left( {s + {C_a}} \right) + \hfill \\ 3D\left( {{C_d}\frac{{u-{u_p}}}{{\left| {u - {u_p}} \right|}} + \beta {C_l}} \right){\left( {u - {u_p}} \right)^2}/\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}} - \frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right) - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;4D\beta \left( {s - 1} \right)g/\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}} - \frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right) \hfill \\ \end{gathered} $ | (3) |
将
| $ \begin{gathered} \left( {4\left( {s-1} \right)D\frac{{{\text{d}}u}}{{{\text{d}}t}} + 4D\beta \left( {s-1} \right)g} \right)/\left( {\frac{{{\text{d}}u}}{{{\text{d}}t}}-\frac{{{\text{d}}{u_p}}}{{{\text{d}}t}}} \right) = \hfill \\ 4D\left( {s + {C_a}} \right) + 3D\left( {{C_d}\frac{{u - {u_p}}}{{\left| {u - {u_p}} \right|}} + \beta {C_l}} \right)f\left( {{\text{KC'}}} \right) \hfill \\ \end{gathered} $ | (4) |
求得运动过程中,颗粒运动的加速度为:
| $ \frac{{{\text{d}}{u_p}}}{{{\text{d}}t}} = \left( {1-\frac{{4\left( {s-1} \right)}}{m}} \right)\frac{{{\text{d}}u}}{{{\text{d}}t}}-\frac{{4\beta \left( {s - 1} \right)g}}{m} $ | (5) |
式中:
| $ m = 4\left( {s + {C_a}} \right) + 3\left( {{C_d}\frac{{u-{u_p}}}{{\left| {u-{u_p}} \right|}} + \beta {C_l}} \right)f\left( {{\text{KC'}}} \right) $ |
两边积分并结合分部积分公式可得到泥沙起动后颗粒运动速度的表达式为:
| $ \begin{gathered} {u_p}\left( t \right) = \left( {1-\frac{{4\left( {s-1} \right)}}{m}} \right)\left( {u\left( t \right)-{u_{cr}}} \right) - \hfill \\ \;\;2\beta \left( {s - 1} \right)g\int_{{t_{cr}}}^t {\frac{1}{m}{\text{d}}t - 12\left( {s - 1} \right)} \cdot \hfill \\ \left( {{C_d}\frac{{u - {u_p}}}{{\left| {u - {u_p}} \right|}} + \beta {C_l}} \right)\int_{{t_{cr}}}^t {\frac{u}{{{m^2}}}f'\left( {{\text{KC'}}} \right){\text{d}}t} \hfill \\ \end{gathered} $ | (6) |
对于泥沙颗粒运动数目的计算,假设面积dA内的推移质泥沙运动距离为dx,这部分泥沙从水流中获取的能量完全由床面切应力提供:
| $ {E_{in}} = \tau {\text{d}}A{\text{d}}x $ | (7) |
根据泥沙起动条件,这部分泥沙维持运动状态需要耗散一定的能量,与泥沙起动切应力密切相关:
| $ {E_k} = {\tau _{cr}}{\text{d}}A{\text{d}}x $ | (8) |
设单位面积运动的泥沙颗粒数目为N,则这部分泥沙在运动过程中因床面摩擦力而引起的能量耗散为:
| $ {E_f} = N{\text{d}}A \cdot \frac{\pi }{6}\beta \left( {{\rho _s}-\rho } \right){D^3}g{\text{d}}x $ | (9) |
根据能量能量守恒Ein=Ek+Ef,可以得到:
| $ N = \frac{6}{{\beta \pi }}\left( {\theta-{\theta _{cr}}} \right)\frac{1}{{{D^2}}} $ | (10) |
式中:θ为希尔兹数;
瞬时推移质输沙强度则表示为:
| $ \varphi \left( t \right) = \frac{{\pi {D^3}N{u_p}}}{{6\sqrt {\left( {s-1} \right)g{D^3}} }} $ | (11) |
将(10)式代入式(11)可得:
| $ \varphi \left( t \right) = \sqrt {\frac{2}{{{f_w}}}} \frac{{\theta-{\theta _{cr}}}}{\beta }\sqrt \theta \frac{{{u_p}}}{{\left| u \right|}}, \;\;\;\;\theta > {\theta _{cr}} $ | (12) |
式中fw为波浪摩擦系数。
考察式(6),在各项系数不变的情况下,up/|u|的值主要和KC′有关,所以up/|u|可以用一个以KC为变量的函数表示。将式(12)在半周期内取平均,半周期平均输沙强度有:
| $ {\phi _{1/2}} = \frac{r}{{\beta \sqrt {{f_w}} }}\left( {{\theta _m}-{\theta _{cr}}} \right)\sqrt {{\theta _m}} \left( {1-F\left( {{\text{KC''}}} \right)} \right) $ | (13) |
式中:r为待定常系数;F(KC″)为与KC″的函数,KC″=(U-ucr)T/D。式(13)可以分为不考虑惯性力影响的准恒定项“
本实验在上海交通大学港口航道与水利工程研究所实验室的U型往复流水槽内进行。实验布置如图 2所示,水槽使用1 cm厚的有机玻璃板制作,其主体长1 000 cm,宽10 cm,高25 cm,两端设置有两对直径为8 cm的圆筒开口,动力装置为曲柄连杆结构的往复电机,电机连有变频器,可以根据需要调节电机的转速,电机行程可以通过更换不同长度的曲柄调节。实验中,曲柄推动活塞推板,通过推动两圆筒内的水体使水槽内产生往复流。水槽左端开口与活塞推板相接,右端开口直接与大气相通。水槽主体距离两端开口10 cm处分别设置一块整流板,以保证实验段流场的稳定。实验段长度为300 cm,位于水槽中心区域,底部铺满5 cm厚的泥沙样本,测量段为实验段中心100 cm长的区域。
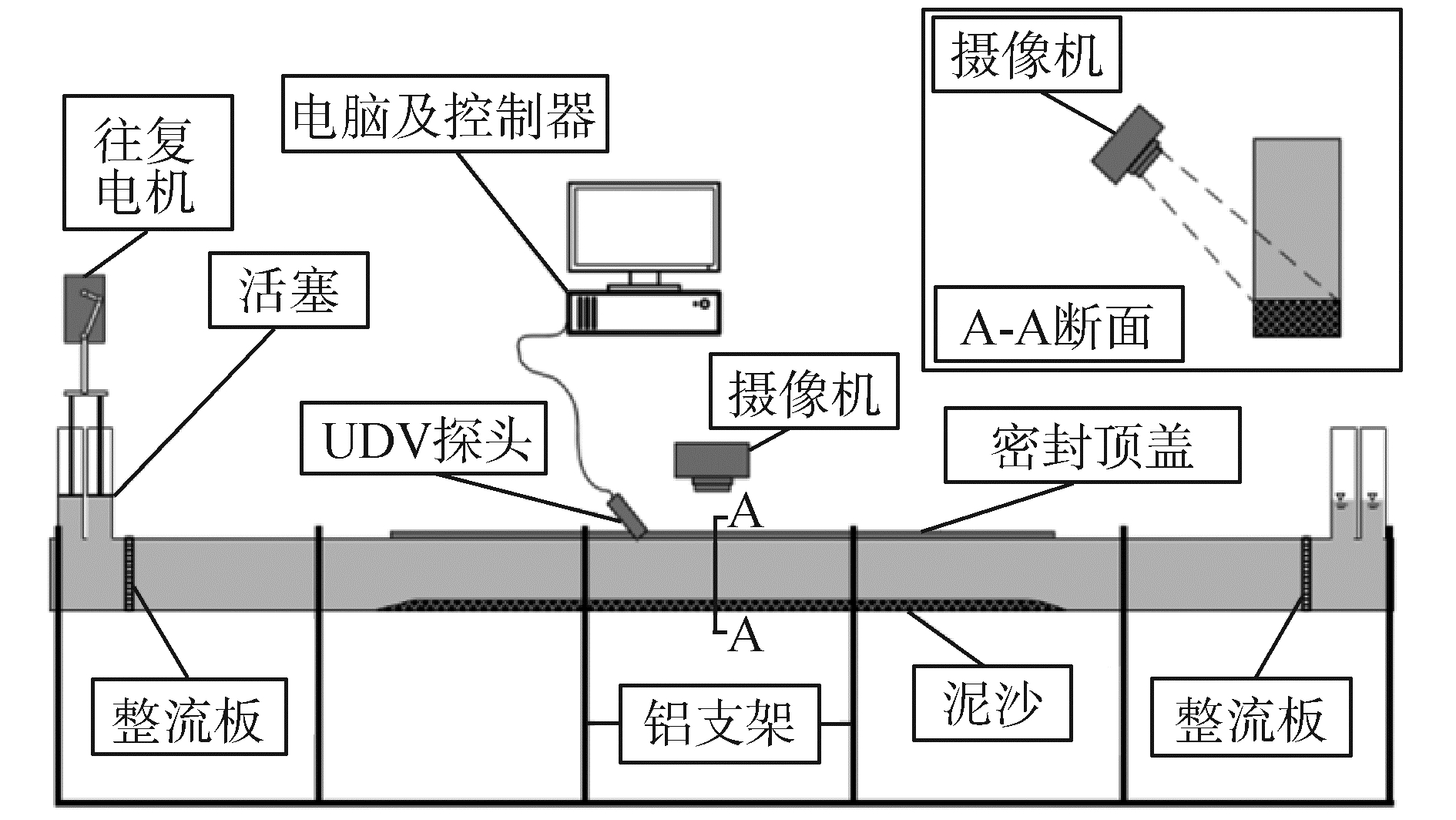
|
Download:
|
| 图 2 实验布置图 Fig. 2 Sketch of the experimental apparatus | |
本研究对3种不同颗粒大小的泥沙进行了总计18组水槽实验,分别为砾石颗粒为主和卵石颗粒的天然非均匀沙与一种尼龙轻质均匀沙,3种实验样品的特征参数如表 1所示,两种非均匀沙的粒径级配曲线见图 3。
| 表 1 3种实验泥沙样本的颗粒特征 Table 1 Characteristics of the three sands |

|
Download:
|
| 图 3 两种非均匀沙的颗粒特征 Fig. 3 Grain size distributions of the two non-uniform sands | |
| 表 2 实验各工况参数 Table 2 Experimental design and results |
通过以上3种泥沙样本的选择,可以在实验中获得尽可能大的KC数范围、希尔兹数范围及输沙强度的范围。实验工况具体设定如表3所示。
实验中,边界层外水质点运动速度采用DOP3000型超声多普勒流速仪进行测量,其采样频率为40 Hz;泥沙颗粒的运动速度和输沙量采用EKEN H8 Plus广角相机进行摄像分析,其图像分辨率为(1 280×720) pixel,摄像频率为240 f/s。为提高实验数据的可靠性,每组实验对35个往复流周期的水质点速度、单位面积泥沙运动颗粒数与泥沙颗粒运动速度进行记录,并取平均值。另外,由于从电机开启至水流呈现较稳定的周期变化需要一段时间的调整,所以在分析数据时忽略前5个周期的数据。
2.2 实验结果以工况Q2为例,测量所得的水质点运动速度、单位面积内泥沙运动颗粒数和泥沙颗粒运动速度在一个周期内随时间变化的规律如图 4所示。
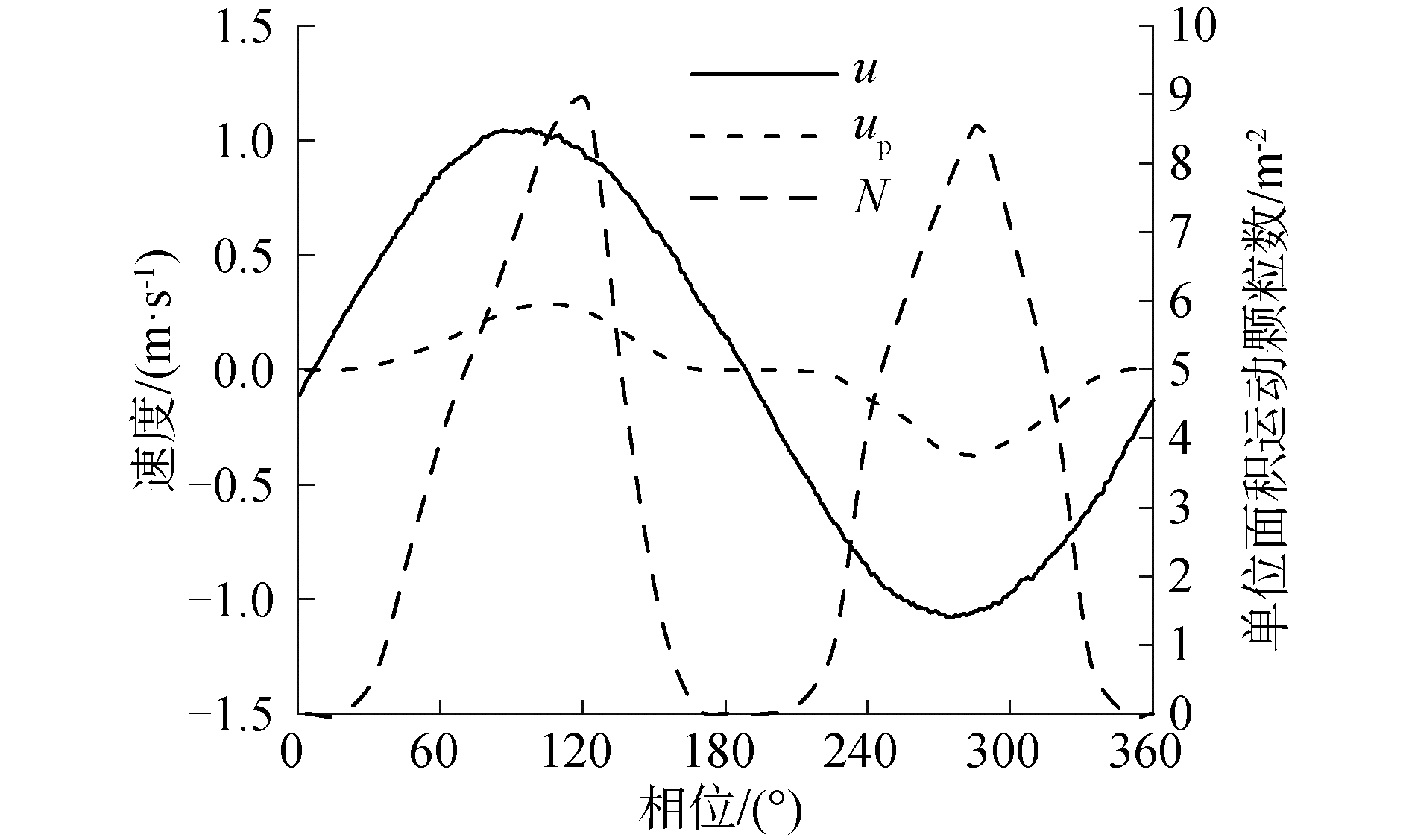
|
Download:
|
| 图 4 u、up、N在一个周期内的变化(工况Q2) Fig. 4 Variation of u, up, N versus time in a period(test Q2) | |
从图 4中可看出,边界层外水质点运动速度非常近似于正弦变化,故可以用u=Usin(ωt)进行描述;单位面积泥沙运动颗粒数与泥沙颗粒运动速度也呈现出周期变化的趋势,但两者的峰值(或谷值)都落后于水质点运动速度峰值若干个相位,即出现了先前所提到的相位滞后现象。
本实验希尔兹数幅值与半周期平均输沙强度的关系如图 5所示。
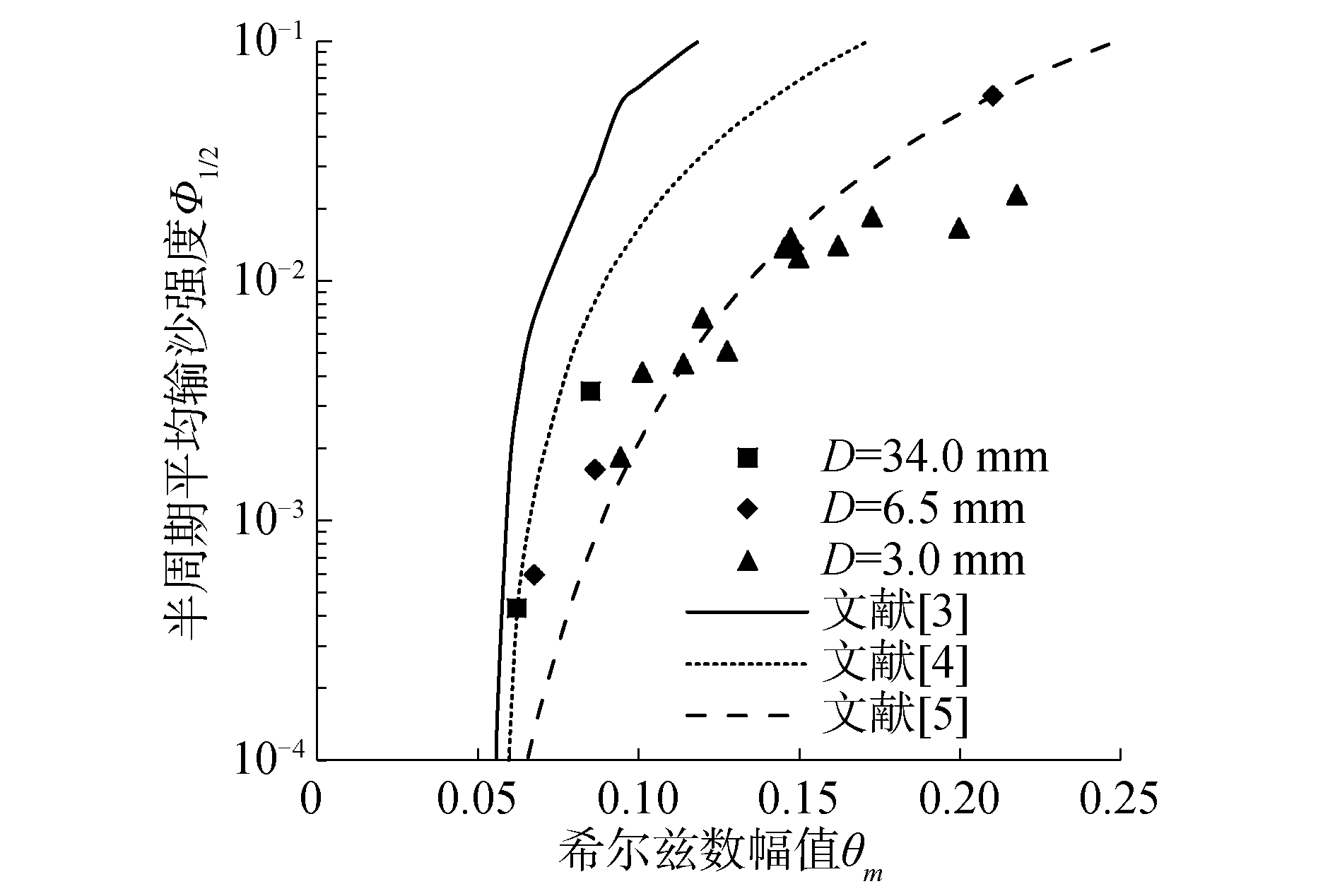
|
Download:
|
| 图 5 希尔兹数幅值与半周期平均输沙强度的关系 Fig. 5 Measured half-cycle averaged bedload transport intensity vs. maximum Shields number | |
从图 5可以观察出,半周期平均输沙强度的值随着希尔兹数幅值增加而增加,但是对于希尔兹数幅值接近的工况,Φ1/2的值仍然呈现出一定的离散特征,说明Φ1/2的值不仅仅取决于θm,还和其他参数(如KC)有关。另外,图 5还描述了3个经典准恒定模型对本实验的模拟情况,发现Soulsby模型和Ribberink模型对Φ1/2的估计均偏大,而Camenen模型对Φ1/2的估计较为合适,但模型对Φ1/2的变化趋势预测效果不佳,而且计算值与实测值有较大偏差。这一现象与之前分析结果一致,即准恒定模型忽略了惯性力作用的影响,导致模型的计算值普遍大于实测值。
3 半理论半经验公式将本文实验数据和以往研究的数据[21-26]汇总。如图 6所示,从数据趋势上看,半周期平均输沙强度与希尔兹数幅值极有可能是幂函数的关系,但数据点离散较大。使用Pearson相关系数分析考察Φ1/2与式(13)中各参数关系,得到Pearson(Φ1/2, θm)=0.865,Pearson(Φ1/2, KC″)=0.765,即半周期平均输沙强度与希尔兹数幅值、KC数有较强的相关程度,这验证了式(13)结构的合理性。
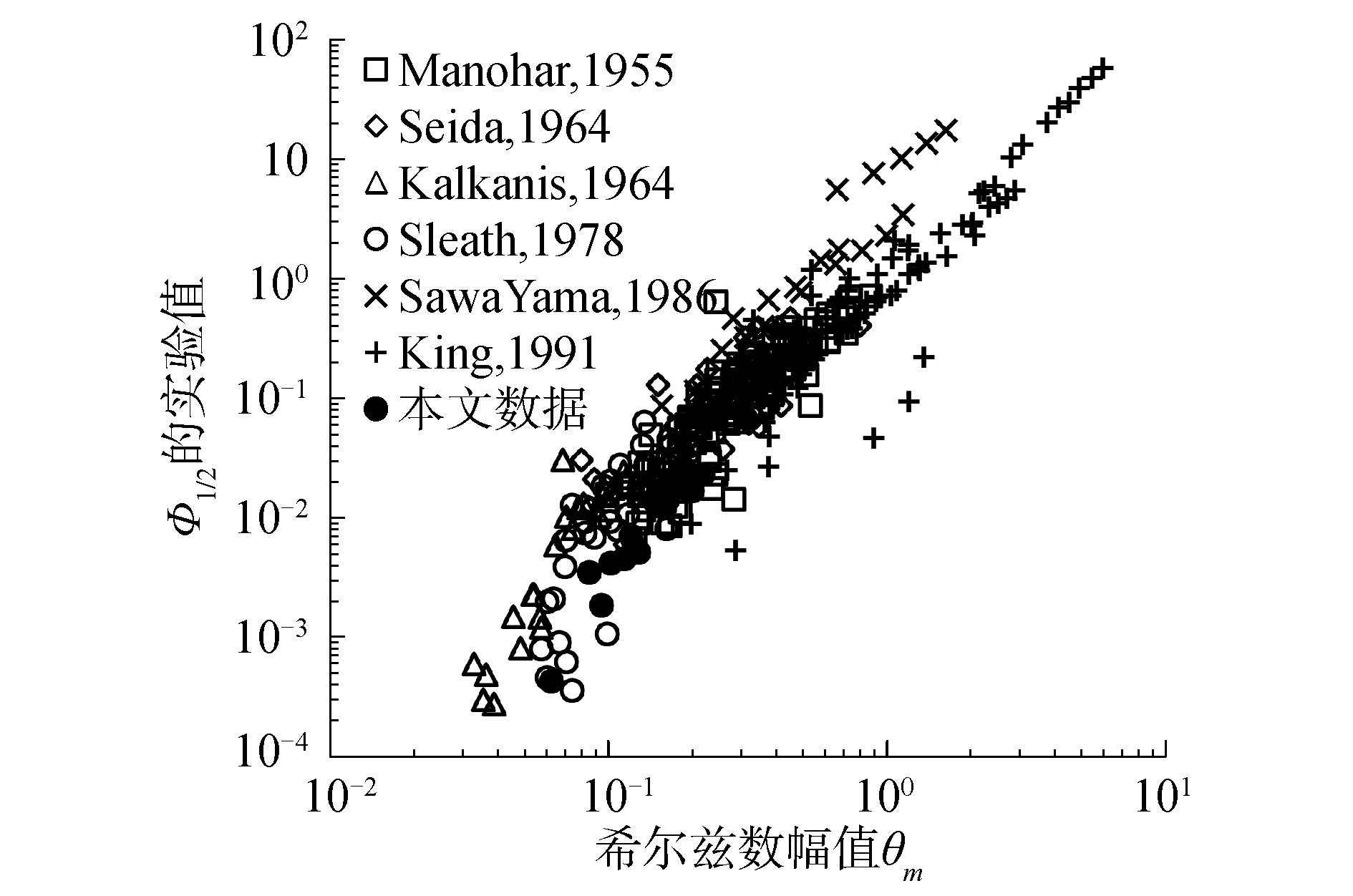
|
Download:
|
| 图 6 实测半周期平均输沙强度与希尔兹数幅值的关系 Fig. 6 Observed half-cycle averaged bedload transport intensity vs. maximum Shields number | |
若不考虑修正项“1-F(KC″)”,式(13)变为:
| $ {\varPhi _{1/2}} = \frac{r}{{\beta \sqrt {{f_w}} }}\left( {{\theta _m}-{\theta _{cr}}} \right)\sqrt {{\theta _m}} $ | (14) |
利用图 6中的实验数据对式(14)进行拟合得到

|
Download:
|
| 图 7 Φ1/2实验值与式(14)计算值的比较 Fig. 7 Measured half-cycle averaged bedload transport intensity vs. calculated results with Eq. (14) | |
从图 7中可以看出,在KC″值较小的情况下,例如KC″ < 500时,式(14)的计算值偏离实验测量值的程度较大,且公式估计值普遍大于实测值;另外,当Φ1/2实验值越小(θm相对值小)时,KC项的影响也越大。这印证了文献[8-10, 14]的观点,即未考虑相位滞后效应会导致对推移质输沙强度产生过高估计。为确定相位滞后修正系数中F(KC″)的表达式,考察其物理意义,当KC″数越大的时候,惯性力影响越小,且输沙强度不可能是负值,所以F(KC″)是值大于0而小于1的减函数。
从最简单的初等函数着手,设F(KC″)=B/ln(KC″),根据已有实验数据对式(13)进行拟合,得到:
| $ {\varPhi _{1/2}} = \frac{r}{{\beta \sqrt {{f_w}} }}\left( {{\theta _m}-{\theta _{cr}}} \right)\sqrt {{\theta _m}} \left( {1-\frac{{2.17}}{{\ln \left( {{\text{KC''}}} \right)}}} \right) $ | (15) |
式(15)中修正项的值随KC″值的变化趋势如图 8所示。从图中可以看出,修正项的值随着KC″的增长而增加的,最后无限趋近于1,其对应的物理意义是惯性力作用的地位越来越小,最后可忽略不计,推移质输沙模型变为准恒定流模型。不过需要注意,当KC″ < 8.76时,修正项就失去了物理意义,修正项的值会出现小于0和大于1的情况,式(15)因此而不适用。

|
Download:
|
| 图 8 修正项与KC″的关系 Fig. 8 Modification term vs. KC″ | |
式(15)的计算值与对应实验值的比较如图 9所示。从图 9中可以发现,分别有88.8%、62.7%的数据落在相对误差为±100%和±50%的范围内,说明式(15)相比于准恒定流模型,较大提高了对实验值的预测精度,特别是改善了对KC″值较小时的模拟效果。然而,式(15)存在一定的使用范围,当KC″值非常大时,推移质输沙强度的预测值偏低。例如,当KC″>10 000,图 9中数据点呈现离散的态势,公式的预测值相对与实验值有较大偏移。该现象可能和实验中出现大量悬移质有关,因为KC″大于10 000对应的实验条件可能是水质点运动速度幅值非常大或者泥沙颗粒的粒径十分小,此时由于水流紊动强度较大、泥沙的重力作用较小,往复流中会有大量泥沙悬浮,这一方面对于实验中推移质输沙量的统计具有很强的干扰作用,另一方面使得式(10)对单位面积床面运动泥沙颗粒数的预测值偏小,因而导致了式(15)对半周期平均输沙强度预测值偏低。
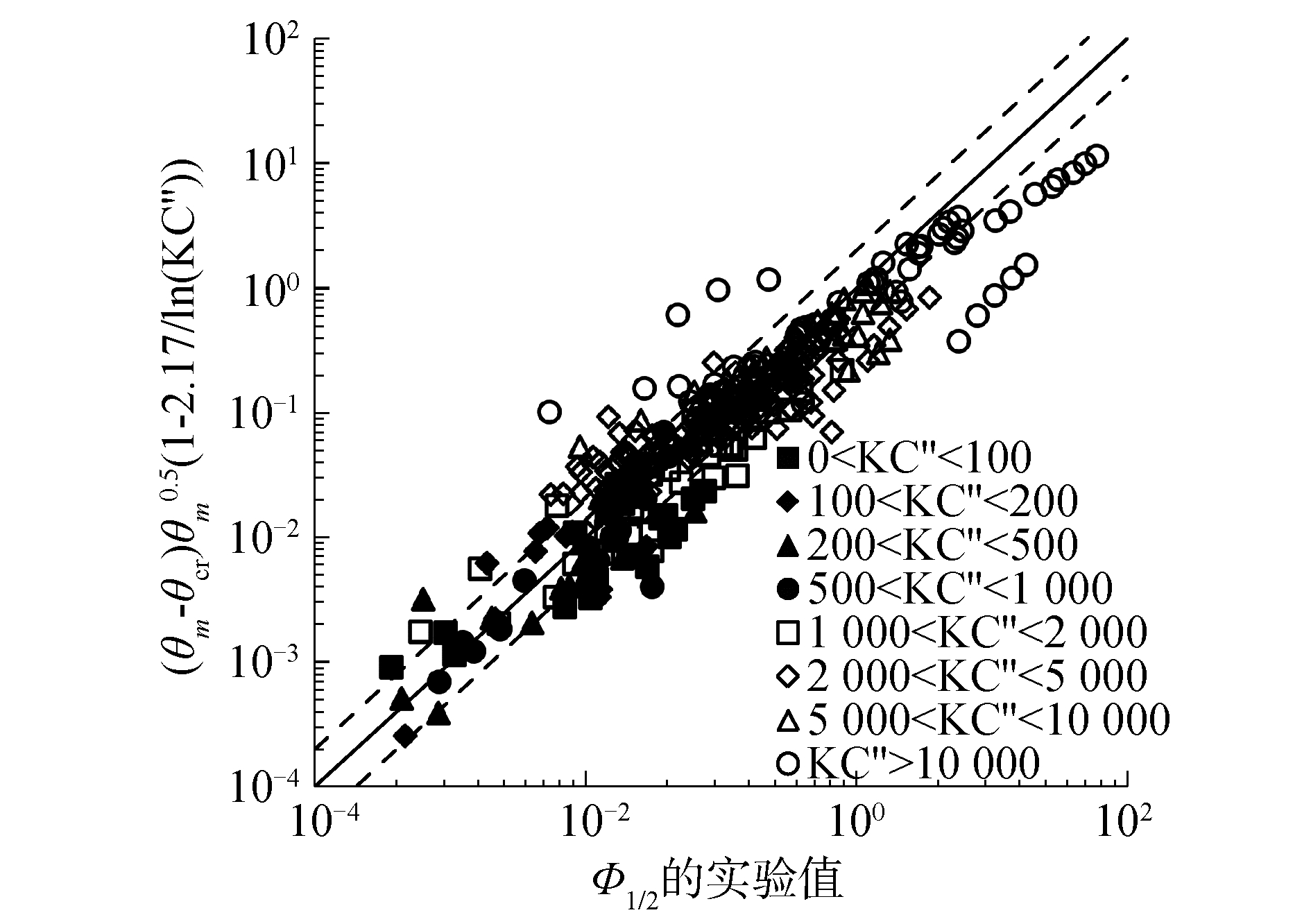
|
Download:
|
| 图 9 Φ1/2实验值与式(15)计算值的比较 Fig. 9 Measured half-cycle averaged bedload transport intensity vs. calculated results with Eq. (15) | |
式(15)与3个经典准恒定流模型[3-5]的比较如图 10所示,主要对KC″值较小,即惯性力作用不可忽略的情况进行分析。从图 10可以看出,当KC″值较小时,3个准恒定流模型对实验结果的预测均偏大,而式(15)改善了这一情况,预测效果相比于前者有较大改善。

|
Download:
|
| 图 10 KC″较小时各公式对实验数据的预测情况比较 Fig. 10 Comparison of the performances of Eq. (15) and three quasi-steady models when KC″ is small | |
1) KC数是影响往复流输沙的一个重要指标。当KC数较小,即泥沙颗粒尺寸相比于水质点运动幅度不可忽略时,惯性力对泥沙运动的影响不可忽略,相位滞后效应导致的输沙强度减弱现象明显。
2) 本文提出的半理论半经验输沙强度计算公式由准恒定流项和KC数修正项两部分组成,前者描述了水动力条件的强弱,后者描述了相位滞后相应对输沙强度的削减作用。公式对半周期平均输沙强度的预测效果相比准恒定流模型有很大提高。
3) 当KC″<8.76时,修正项不具有物理意义;在KC″>10 000的情况下,修正公式的计算值偏低,这说明该公式有一定的适用范围。
| [1] |
MADSEN O S, GRANT W D. Quantitative description of sediment transport by waves[C]//Proceedings of the 15th International Conference on Coastal Engineering. Honolulu, Hawaii, United States, 1976: 1093-1112.
(  0) 0)
|
| [2] |
SLEATH J F A. Measurements of bed load in oscillatory flow[J]. Journal of the waterway, port, coastal and ocean division, 1978, 104(3): 291-307. (  0) 0)
|
| [3] |
SOULSBY R L. The dynamics of marine sands:a manual for practical applications[M]. London: Thomas Thelford, 1997: 163-166.
(  0) 0)
|
| [4] |
RIBBERINK J S. Bed-load transport for steady flows and unsteady oscillatory flows[J]. Coastal engineering, 1998, 34(1/2): 59-82. (  0) 0)
|
| [5] |
CAMENEN B, LARSON M. A general formula for non-cohesive bed load sediment transport[J]. Estuarine, Coastal and Shelf Science, 2005, 63(1/2): 249-260. (  0) 0)
|
| [6] |
HORIKAWA K, WATANABE A, KATORI S. Sediment transport under sheet flow condition[C]//Proceedings of the 18th Conference on Coastal Engineering. Cape Town, South Africa, 1982: 1335-1352.
(  0) 0)
|
| [7] |
AHILAN R V, SLEATH J F A. Sediment transport in oscillatory flow over flat beds[J]. Journal of hydraulic engineering, 1987, 113(3): 308-321. DOI:10.1061/(ASCE)0733-9429(1987)113:3(308) (  0) 0)
|
| [8] |
Van DER A D A, O'DONOGHUE T, RIBBERINK J S. Measurements of sheet flow transport in acceleration-skewed oscillatory flow and comparison with practical formulations[J]. Coastal engineering, 2010, 57(3): 331-342. (  0) 0)
|
| [9] |
O'DONOGHUE T, Van DER A D A. Laboratory experiments for wave-driven sand transport prediction[C]//Proceedings of the NCK-days 2012: Crossing Borders in Coastal Research. Enschede, the Netherlands, 2012: 61-67.
(  0) 0)
|
| [10] |
陈杰, 刘静, 蒋昌波, 等. 波浪作用下泥沙运动研究综述[J]. 泥沙研究, 2014(4): 74-80. CHEN Jie, LIU Jin, JIANG Changbo, et al. Review of sediment transport under waves[J]. Journal of sediment research, 2014(4): 74-80. (  0) 0)
|
| [11] |
马爱兴, 陆永军, 陆彦, 等. 非恒定流作用下砾石推移质输移特性试验研究[J]. 水利学报, 2013, 44(7): 800-809. MA Aixing, LU Yongjun, LU Yan, et al. Experimental study on gravel bed-load transport in unsteady flow[J]. Journal of hydraulic engineering, 2013, 44(7): 800-809. (  0) 0)
|
| [12] |
戚晓明.振荡流作用下的推移质输沙规律研究[D].天津: 天津大学, 2009. QI Xiaoming. Research on bed-load transport under oscillatory flow[D]. Tianjin: Tianjin University, 2009. (  0) 0)
|
| [13] |
SILVA P A, TEMPERVILLE A. Non-steady effects in sand transport[J]. Journal of coastal research, 2006, 39(3): 1479-1483. (  0) 0)
|
| [14] |
DOHMEN-JANSSEN C M, KROEKENSTOEL D F, HASSAN W N, et al. Phase lags in oscillatory sheet flow:experiments and bed load modelling[J]. Coastal engineering, 2002, 46(1): 61-87. (  0) 0)
|
| [15] |
CAMENEN B, LARSON M. Phase-lag effects in sheet flow transport[J]. Coastal engineering, 2006, 53(5/6): 531-542. (  0) 0)
|
| [16] |
DEAN R G, DALRYMPLE R A. Water wave mechanics for engineers and scientists[M]. Englewood Cliffs, NJ: Prentice-Hall, 1984: 232-232.
(  0) 0)
|
| [17] |
KRANENBURG W M, RIBBERINK J S, SCHRETLEN J J L M, et al. Sand transport beneath waves:the role of progressive wave streaming and other free surface effects[J]. Journal of geophysical research:earth surface, 2013, 118(1): 122-139. DOI:10.1029/2012JF002427 (  0) 0)
|
| [18] |
Van DER A D A, RIBBERINK J S, Van DER WERF J J, et al. Practical sand transport formula for non-breaking waves and currents[J]. Coastal engineering, 2013, 76: 26-42. DOI:10.1016/j.coastaleng.2013.01.007 (  0) 0)
|
| [19] |
DIBAJNIA M, WATANABE A. Sheet flow under nonlinear waves and currents[C]//Proceedings of the 23rd International Conference on Coastal Engineering. Venice, Italy, 1992: 226-235.
(  0) 0)
|
| [20] |
NIELSEN P. Coastal bottom boundary layers and sediment transport[M]. Singapore, River Edge, NJ: World Scientific, 1992: 12-13.
(  0) 0)
|
| [21] |
MANOHAR M. Mechanics of bottom sediment movement due to wave action[R]. Washington, DC, USA: U.S. Army Corps of Engineers, 1955.
(  0) 0)
|
| [22] |
KALKANIS G. Transportation of bed material due to wave action[R]. Washington D C, USA: U.S. Army Corps of Engineers, 1964.
(  0) 0)
|
| [23] |
ABOU-SEIDA M M. Bed load function due to wave action[R]. California, USA: University of California, 1965.
(  0) 0)
|
| [24] |
SAWAMOTO M, YAMASHITA T. Sediment transport rate due to wave action[J]. Journal of hydroscience and hydraulic engineering, 1986, 4(1): 1-15. (  0) 0)
|
| [25] |
KING JR D B. Studies in oscillatory flow bedload sediment transport[D]. San Diego, USA: University of California, 1991: 152-173.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


