在某一特定的波频率下,海上多浮体之间会发生复杂的波浪干涉现象,对结构物的安全性和稳定性产生危害[1-2]。姜胜超等[3]基于高阶边界元方法研究了四柱结构的干涉现象,计算结果表明:干涉现象发生时,浮体的波漂移力明显变大,并且浮体周围的波面显著抬升。过大的波漂移力会增加浮式建筑物系泊系统的负载,过大的波面爬升则会导致甲板砰击和上浪现象的发生。为了防止浮体间有害干涉现象的发生,Duclos等[4]研究了随机改变浮体间距这一方式来防止浮体间复杂干涉的发生,但是该方法不利于实际工程应用。Chen等[5]探究了改变浮体间距对改善多个透孔圆柱间有害干涉的可能性,得到了与Duclos等[4]类似的结论。
近年来,通过优化浮体的尺寸参数和布置方式来提高海上建筑物的安全性成为了研究热点。Newman[6]利用WAMIT和多参数优化求解器PRAXIS对环形布置的多个圆柱的尺寸参数进行优化来减小某一特定入射波数下建筑物的散射波能量,即cloaking现象。基于Newman的研究成果,何广华等[7]验证了cloaking现象对浮体波漂移力的低减作用,并发现浮体结构的对称性是浮体群波漂移力减小的重要原因。Iida等[8]基于Tasrief等[9]开发的二进制编码遗传算法,直接对环形布置多浮体的波漂移力进行了优化。随后,Zhang等[10-11]发现了周期性的准cloaking现象,即通过合理改变环形布置多浮体的同心圆半径可以有效减小其波漂移力,并具有一定的周期性。
目前,尚没有关于四柱结构波漂移力的优化研究。本文建立了基于实数编码的遗传算法多参数优化模型。利用该优化模型,选择浮体间距离、浮体吃水和浮体迎浪角作为优化参数对特定波频率下的四柱结构的总波漂移力进行了优化,并分析了优化模型的收敛性。
1 数学模型及数值方法 1.1 四柱结构模型四柱结构的布置情况如图 1所示,由4个相同的截断圆柱构成。4个圆柱浮体等间距分布。图 1(a)中对每个圆柱浮体进行了编号,波浪从x轴负方向入射时,浮体1与入射波方向间的角度为迎浪角β(顺时针为正)。图 1(b)为四柱结构的立体图。本文的尺寸参数以圆柱半径r为标准进行无量纲化。

|
Download:
|
| 图 1 四柱结构的计算模型 Fig. 1 The notations of the four-column structure | |
多浮体水动力计算数值模型以拉普拉斯方程为基本控制方程。速度势满足线性边界条件。
根据线性叠加定理,速度势可以表示为:
| $ \varPhi \left( {x, y, z;t} \right) = \operatorname{Re} \left[{\frac{{g{\zeta _0}}}{{{\text{i}}\omega }}\phi \left( {x, y, z} \right)\exp \left( {{\text{i}}\omega t} \right)} \right] $ | (1) |
式中ζ0和ω表示入射波波幅和圆频率。
为了计算第n个浮体的速度势,在第n个浮体上引入局部柱坐标系。基于Kagemoto等[12]的波浪交互理论。本数值模型充分考虑了浮体间的波浪交互作用;即第n个浮体的入射势由入射势和其他浮体产生的扰动势两大部分组成,其总速度势可表示为:
| $ \begin{gathered} {\phi ^n}\left( p \right) = \psi _I^n\left( p \right) + {\psi ^n}\left( p \right) = \hfill \\ \left( {\phi _I^n\left( p \right) + \sum\limits_{k = 1, k \ne n}^4 {{\psi ^{kn}}\left( p \right)} } \right) + {\psi ^n}\left( p \right) = \hfill \\ \sum\limits_{m =- \infty }^\infty {\left[{\left( {\alpha _m^n + \sum\limits_{k = 1, k \ne n}^4 {A_m^{kn}} } \right){{\text{J}}_m}\left( {{k_0}{r_n}} \right) + {\text{A}}_m^n{\text{H}}_m^{\left( 2 \right)}\left( {{k_0}{r_n}} \right)} \right]} \cdot \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{Z_0}\left( z \right)\exp \left( { -{\text{i}}m{\theta _n}} \right) \hfill \\ \end{gathered} $ | (2) |
式中:Jm(k0rn)表示m阶的第一类贝塞尔函数; Hm(2)表示m阶的第二类汉克尔函数; Amn为第n个浮体散射波的复数波幅,由高阶边界元方法[12]计算可得:
| $ A_m^{kn} = \sum\limits_{l =-\infty }^\infty {A_l^k{\text{H}}_{l-m}^{\left( 2 \right)}\left( {{k_0}{L_{kn}}} \right){\alpha _{no}}\exp \left( {-{\text{i}}\left( {l - m} \right)} \right)} $ | (3) |
| $ \alpha _m^n = {\alpha _m}\exp \left( {-{\text{i}}{k_0}\left( {{x_{on}}\cos \beta + {y_{on}}\sin \beta } \right)} \right) $ | (4) |
Kashiwagi等[13]采用朗斯基矩阵推导出了波漂移力的表达式。本文采用同样的方法,利用式(2)可以计算得到四柱结构中第n个浮体的波漂移力:
| $ \begin{gathered} \frac{{F_x^n - {\text{i}}F_y^n}}{{\rho g\zeta _0^2r}} = \hfill \\ \frac{{\text{i}}}{{2{C_0}Kr}}\sum\limits_{m = - \infty }^\infty {\left[ {2A_m^nA_{m + 1}^{n*} + \left( {\alpha _{m + 1}^{n*} + \sum\limits_{k = 1,k \ne n}^4 {A_{m + 1}^{kn*}} } \right)A_m^n + } \right.} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {\alpha _m^n + \sum\limits_{k = 1,k \ne n}^4 {A_m^{kn}} } \right)A_{m + 1}^{n*}} \right] \hfill \\ \end{gathered} $ | (5) |
| $ {C_0} = \frac{{{k_0}}}{{K + \left( {k_0^2-{K^2}} \right)h}} $ | (6) |
遗传算法是一种模仿基因染色体优胜劣汰进化过程的优化算法。遗传算法每一代种群中的N个个体代表着N种优化参数的组合方式。算法中的种群模拟染色体,而N个个体模拟N个基因。算法通过遗传算子的操作实现种群中个体的进化,即优胜劣汰过程。算法中的遗传算子包括选择、交叉、变异、精英保留等。本文采用了实数编码的遗传算法。遗传算法的流程图如图 2所示。

|
Download:
|
| 图 2 遗传算法流程 Fig. 2 The Flow process of the genetic algorithm | |
本文设定种群中的个体数量为N=100。选择算子采用轮盘赌选择算子。种群中第i个个体的选择概率可计算公式为:
| $ P\left( i \right) = \frac{{F_{\max }^2-{F^2}\left( i \right)}}{{N \cdot F_{\max }^2-\sum\limits_{i = 1}^N {{F^2}\left( i \right)} }} $ | (7) |
式中Fmax2指的是N个个体中对应的F2(i)的最大值。
交叉算子采用实值交叉,本文中交叉概率Pc设定为0.6。变异算子是对满足变异概率的已有个体进行一个随机的变化,产生新的个体增加了种群的多样性,为得到潜在最优解提供了可能。本文的变异概率Pm设定为0.05。
精英保留可以将直至当前代的最优解保留下来,避免最优解被交叉算子和变异算子破坏。本文设定了两个算法终止条件:1)精英值经过G1代的进化而没有发生变化;2)总的进化代数ng超过设定的终止代数G2。算法满足两个终止条件中的任意一个即停止计算。
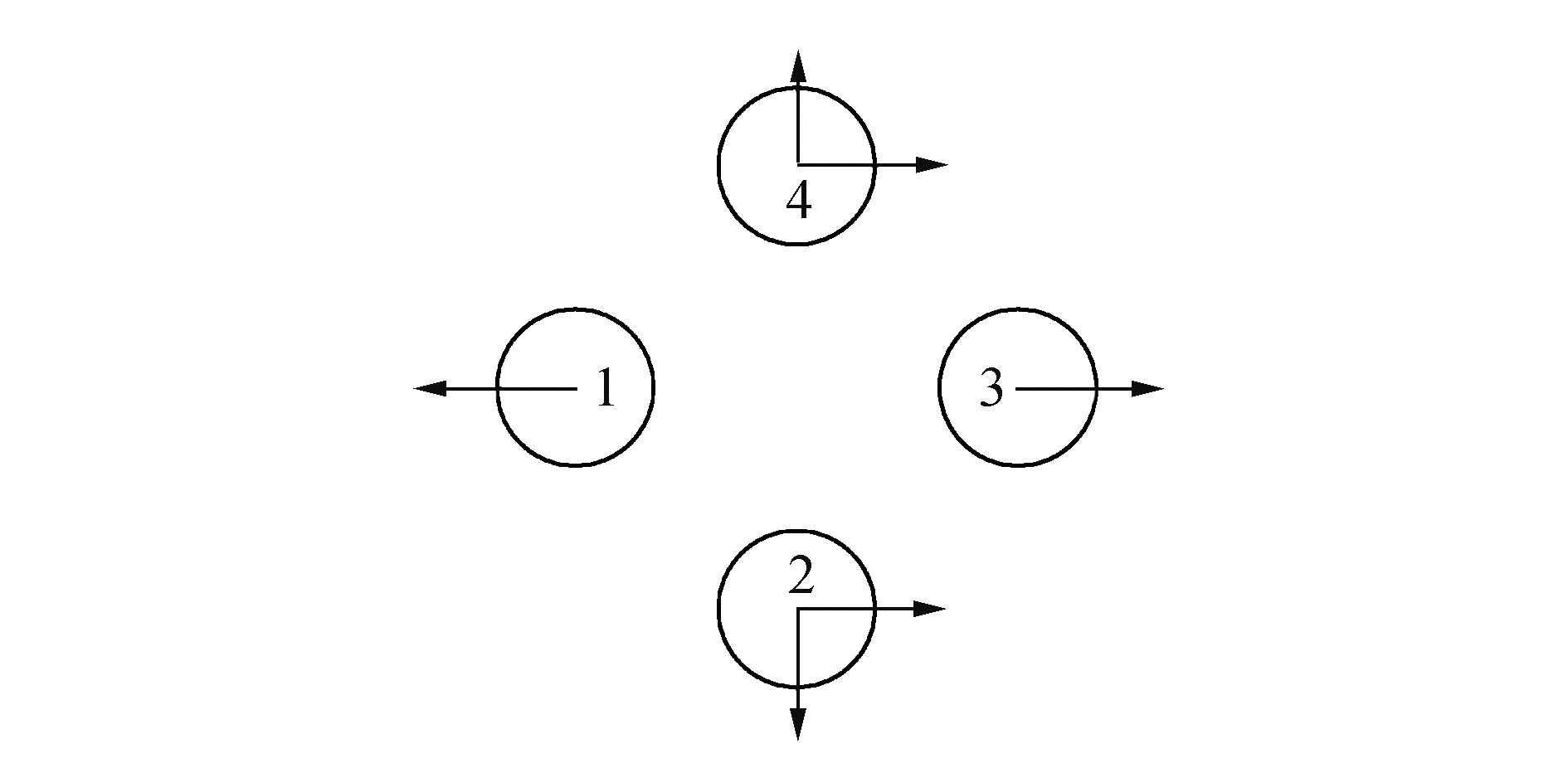
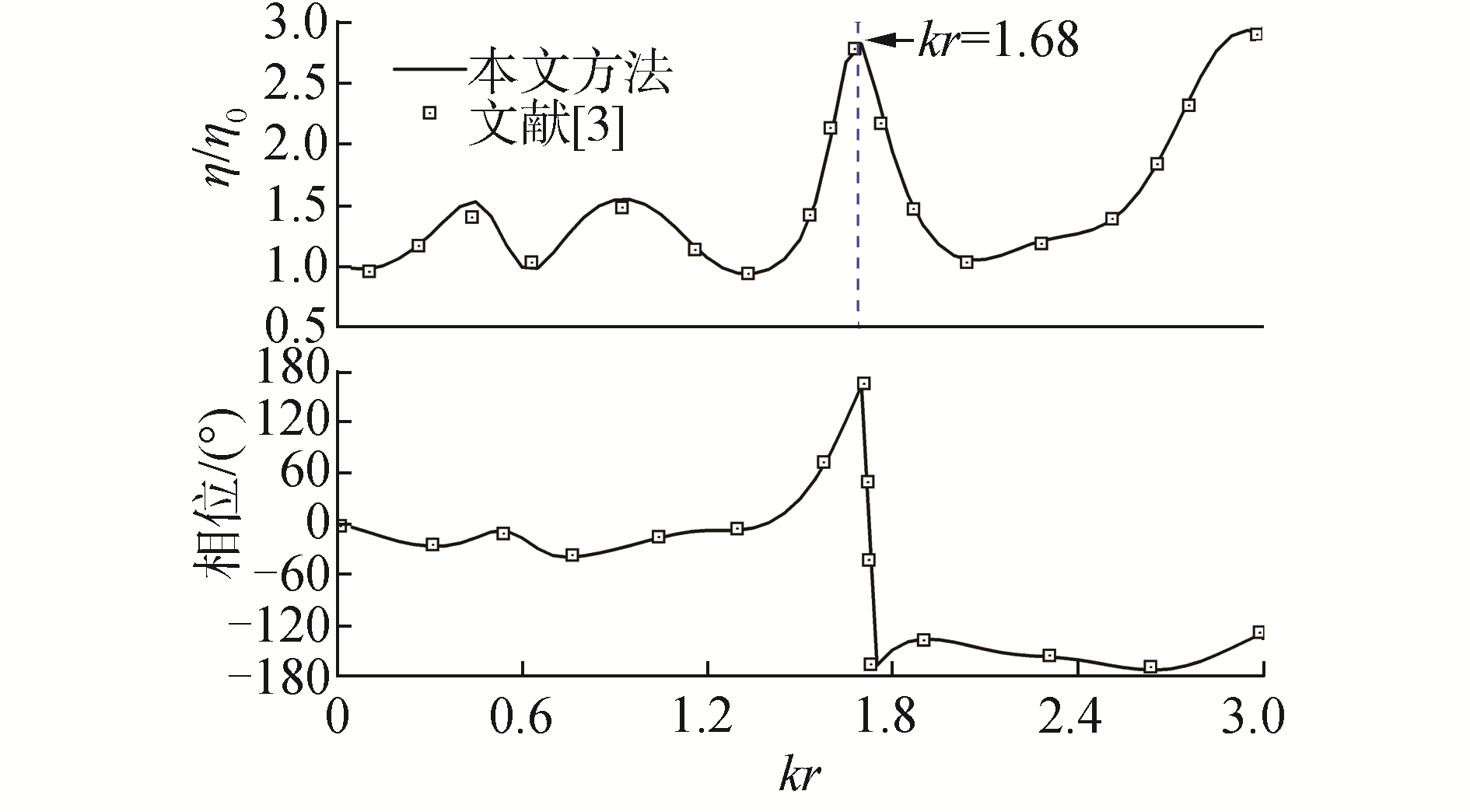
2 数值模拟结果与分析 2.1 数值模型的验证首先,基于本文建立的数值模型,计算了四柱结构在特定尺寸参数和布置情况下的波漂移力和浮体周围的波高,并与已有的数值结果[3]进行了对比。表 1给出了四柱结构的尺寸参数和迎浪角。图 3为不同入射波数下1号圆柱的波漂移力,可以看出本文的数值结果与文献中的计算结果吻合较好。同时可以发现在kr=1.68时,圆柱的波漂移力达到最大值,此时的波浪干涉对结构的安全性危害最大。图 4给出了kr=1.68时每个圆柱所受波漂移力的受力方向。可以发现每个圆柱浮体都有向外运动的趋势。比较有趣的是,由于浮体间的复杂干涉作用,1号圆柱波漂移力的方向与入射波方向相反。
| 表 1 四柱结构参数设置 Table 1 The parameters of the four-column structure |

|
Download:
|
| 图 3 1号圆柱浮体的波漂移力 Fig. 3 The wave drift forces acting on cylinder 1 | |
|
Download:
|
| 图 4 每个圆柱浮体的波漂移力方向 Fig. 4 The direction of the wave drift forces acting on each cylinder | |
图 5给出了图 1中点A(-1.728, 0)在不同入射波数下的波高和相位变化情况,并与已有的数值结果进行了对比。从图中可以看出,本数值方法可以准确地模拟结构附近的波高和相位。同时可以从图 5中发现,结构内部点A处的波高在kr=1.86时显著增大;更具体的结构周围波高分情况会在后面详细讨论。
|
Download:
|
| 图 5 点A处的波高与相位 Fig. 5 The wave height and phase at point A | |
随后,计算了不同入射波数下四柱结构的总波漂移力

|
Download:
|
| 图 6 四柱结构总的波漂移力 Fig. 6 The wave drift force acting on the whole structure | |
考虑到实际情况中浮体一旦建造完毕,其半径不易改变;因此首先浮体的吃水d和浮体到结构中心的距离L作为优化参数对四柱结构的总波漂移力F进行优化。选取kr=1.68作为优化目标波数。遗传算法的终止条件参数取G1=30,G2=100,2个参数的优化范围分别为2.5≤L≤3.5,2.0≤d≤3.5。
经过迭代优化,最终的优化参数和最终的波漂移力如表 2所示。从表 2可以看出,优化参数下四柱结构的总波漂移力减小到优化前的78.97%。
| 表 2 两参优化结果 Table 2 The results of two-parameters optimization |
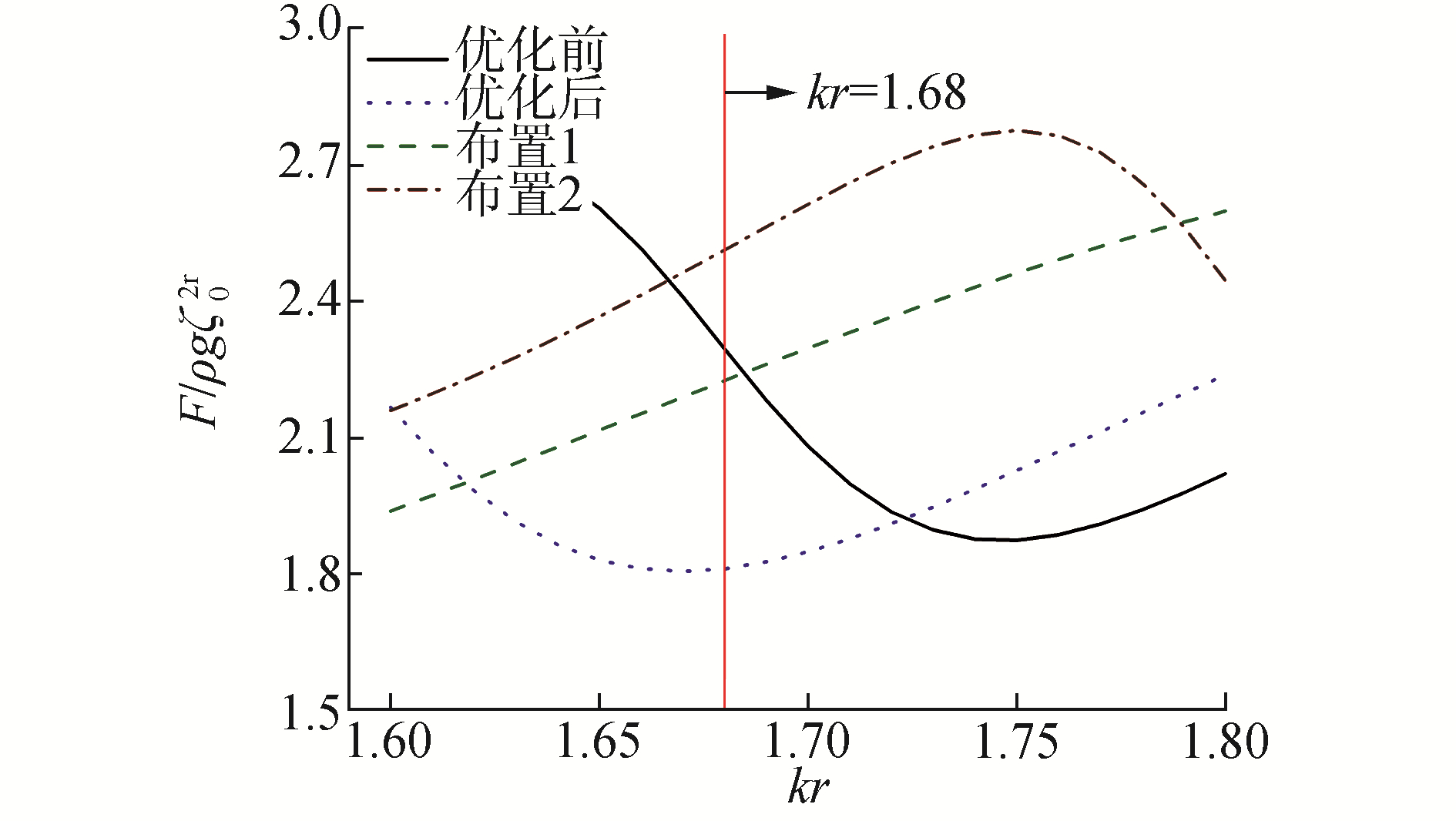
图 7给出了优化前后不同入射波数下四柱结构的总波漂移力,优化参数下的波漂移力相比于优化前在kr=1.68附近都明显地减小。为了校验遗传算法的正确性,选取了优化过程中任意2种L和d的组合加入图 7的对比,2组参数分别取L1=3.2,d1=2.0(布置1)和L2=2.7,d2=2.1(布置2)。从图 7中可以看出,任意给出的2组参数组合下的总波漂移力在kr=1.68都要大于优化参数下的总波漂移力,也验证了优化参数的正确性。
|
Download:
|
| 图 7 两参数优化前后四柱结构总的波漂移力 Fig. 7 The wave drift force acting on the original structure and on the optimized structure with two-parameters optimization | |
为了进一步优化四柱结构的总波漂移力,除了浮体的吃水d、浮体到结构中心的距离L之外,选取迎浪角β作为优化参数对四柱结构的总波漂移力F进行优化。β的优化范围为0°≤β≤45°
经过迭代优化,最终的优化参数和对应的四柱结构的波漂移力如表 3示。从表 3中可以看出,优化参数下四柱结构的总波漂移力减小到优化前的47.71%。图 8给出了优化前后不同入射波数下四柱结构的总波漂移力;可以发现,优化参数下的波漂移力相比优化前不止在kr=1.68显著减小,在kr>1.68的范围内也明显地减小。需要指出的是,在kr<1.3的范围内优化参数下的波漂移力比优化前有一定的增大,因此针对某一入射波数得到的优化参数有一定的适用范围。
| 表 3 优化结果 Table 3 The optimized results |

|
Download:
|
| 图 8 优化前后四柱结构总的波漂移力 Fig. 8 The wave drift force acting on the original structure and on the optimized structure | |
图 9中给出了优化前后每个圆柱的波漂移力F。从图中可以看出,优化参数下的每个圆柱的波漂移力在kr=1.68时的显著增大现象消失,并且在其他波数也没有出现显著增大的现象。这说明该组优化参数可以适用于较大的波频率范围。

|
Download:
|
| 图 9 优化前后每个圆柱浮体的波漂移力 Fig. 9 The wave drift forces acting on each cylinders with the optimized parameters | |
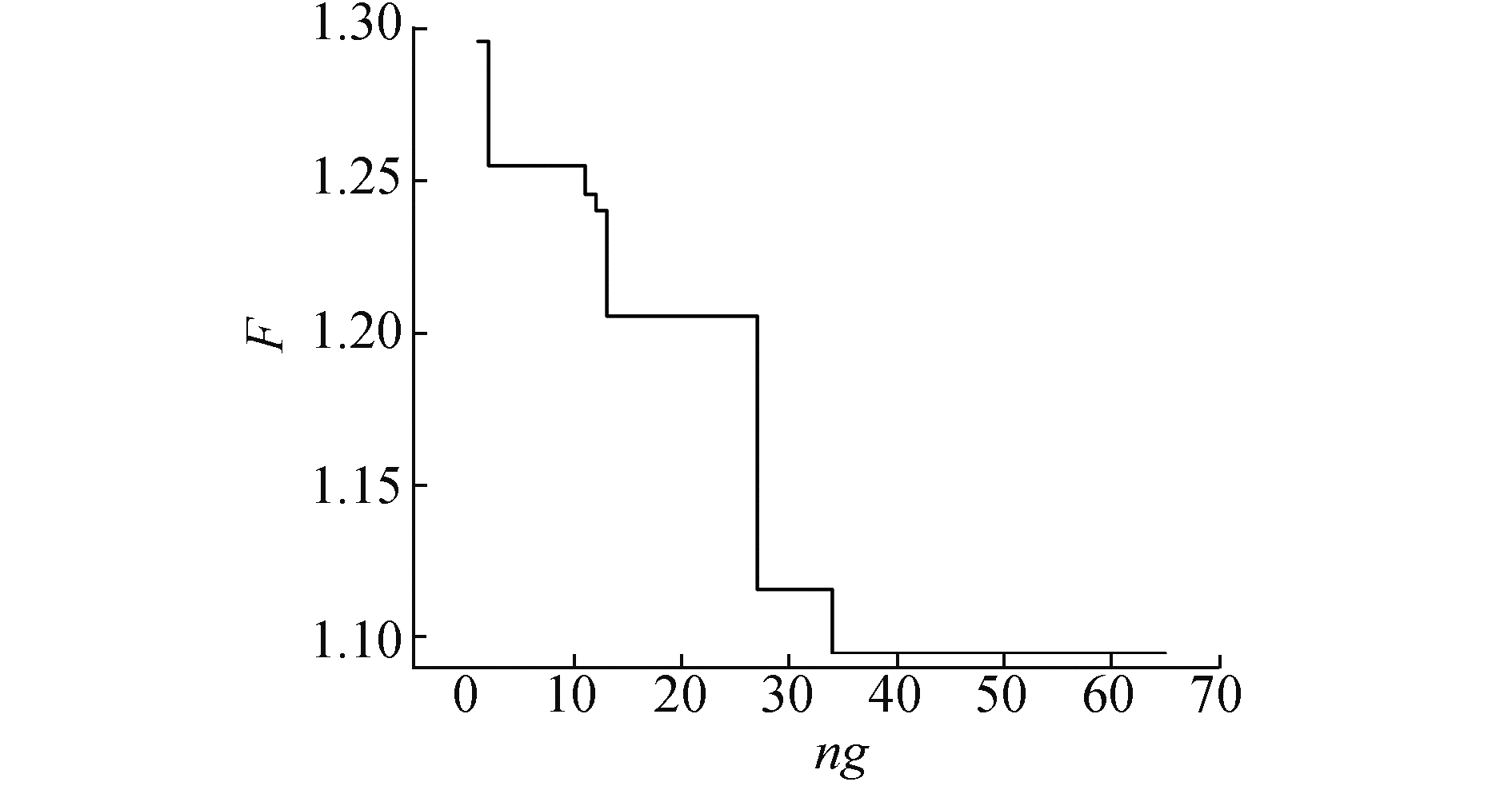
为了分析优化算法的高效性和可靠性,对算法的优化过程进行了分析。图 10给出了优化目标F的精英值的迭代过程,从图 10中可以发现优化目标F的最优值在ng=35时得到,在ng=65时遗传算法因满足终止条件而终止。
|
Download:
|
| 图 10 优化过程中的目标函数精英值 Fig. 10 The elite of optimized objective F in the optimization process | |
图 11展示了优化过程中的3个具有代表性的代数(ng=1, 35, 65)下种群中的个体情况。图中每一个圆球代表一个个体,球心的坐标由个体所包含的3个参数的大小决定,圆球的大小由55/F2决定,圆球的颜色由1/F2决定。很显然,圆球越大,颜色越深时,代表个体更有竞争力。图 11(a)为第一代的种群,即初始种群中的个体情况。通过圆球在3个坐标平面中的投影可以看出初始种群中个体在空间分布的随机性,保证了初始种群个体的多样性。图 11(b)给出了进化过程里种群中个体的情况,可以看出种群中的个体逐渐向一定的区域收敛,缺乏竞争力的个体逐渐被淘汰。图 11(c)为终止代种群中的个体情况,可以看出种群中个体更加集中。图 11(c)与图 11(b)相比有很多个体的位置是不同的,这是由于交叉算子和变异算子产生了新的个体。通过上述分析验证了遗传算法中遗传算子的有效性。需要指出的是种群中的个体相对于参数L和β收敛性更好,而对于参数d则收敛不明显,这说明参数d对优化目标F的影响较小。

|
Download:
|
| 图 11 优化过程中3个典型种群中的个体 Fig. 11 The individuals in three typical generations | |
为了找到浮体波漂移力减小的原因,对浮体周围的波浪场进行了分析。
首先,探究优化前四柱结构中每个圆柱周围的波面与其波漂移力的关系。由图 3可知,在kr=1.68时每个圆柱的波漂移力都显著增大。因此,图 12给出了kr=1.68时每个圆柱附近的波剖面图。为了更好地对比,图 12(a)给出了孤立圆柱沿入射波方向的波剖面图。图 12(b)给出了四柱结构中1号柱和3号柱的沿入射波方向的波剖面,可以看出1号柱两侧的波高虽然相差不是特别大,但是其相位却相差很大,而3号柱两侧的波高相差很大。图 12(c)给出了2号柱和4号柱垂直于入射波方向的波剖面图;图 12(d)给出了4号柱沿入射波方向的波剖面图,可以发现与图 12(b)类似的规律。

|
Download:
|
| 图 12 优化前每个圆柱浮体两侧的波剖面 Fig. 12 The wave profile in the two sides of the original cylinders | |
因此,可以得出结论:每个圆柱浮体的波漂移力在kr=1.68时的显著增加是由其两侧波高差和相位差共同导致的。并且,在kr=1.68时,圆柱浮体附近急剧增加的波高可能会产生甲板砰击和上浪等现象,对海上建筑物的安全性产生危害。
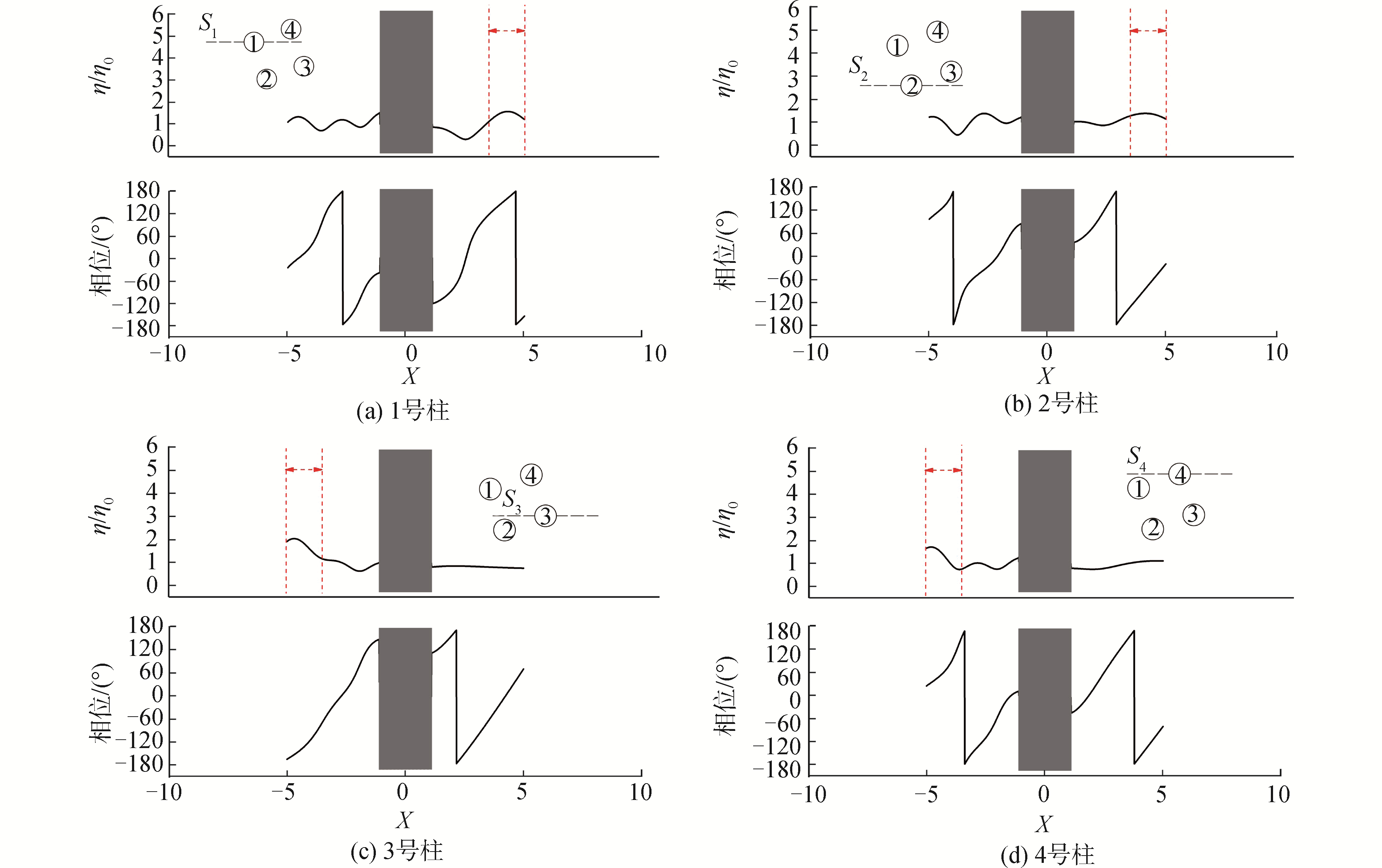
同样,对优化后的四柱结构中每个圆柱附近的波面展开分析。图 13给出了在kr=1.68时优化后的每个圆柱沿入射波方向的波剖面。从图 13中可以明显看出,优化后的每个圆柱两侧的波高差相对于优化前明显减小,相位差也很小。这与图 8中优化后的每个圆柱浮体在kr=1.68的波漂移力相对应。因此,验证了每个圆柱波漂移力及其两侧波浪场的关系。需要指出的是,在图 13中对应每个圆柱附近有一区域的波高较大,这是因为该区域比较靠近其他圆柱浮体的表面而引起的波面抬升。
|
Download:
|
| 图 13 优化后每个圆柱浮体两侧的波剖面 Fig. 13 The wave profile in the two sides of the optimized cylinders | |
1) 本文建立的数值模型可以准确地模拟海上多浮体间的波浪干涉现象。
2) 本文建立的基于实数编码的遗传算法优化模型可以有效地实现多浮体波漂移力的优化。
3) 优化后,不仅实现了四柱结构的总波漂移力的有效减小,而且每个浮体的波漂移力及其周围的波浪场也得到了明显改善。
4) 浮体波漂移力的减小与其迎浪侧和背浪侧波高差和相位差的改善密切相关。
| [1] |
MANIAR H D, NEWMAN J N. Wave diffraction by a long array of cylinders[J]. Journal of fluid mechanics, 1997, 339: 309-330. DOI:10.1017/S0022112097005296 (  0) 0)
|
| [2] |
EVANS D V, PORTER R. Near-trapping of waves by circular arrays of vertical cylinders[J]. Applied ocean research, 1997, 19(2): 83-99. DOI:10.1016/S0141-1187(97)00015-1 (  0) 0)
|
| [3] |
姜胜超, 吕林, 滕斌, 等. 四柱结构在波浪作用下的近场干涉[J]. 哈尔滨工程大学学报, 2011, 32(5): 546-554. JIANG Shengchao, LYU Lin, TENG Bin, et al. Hydrodynamic analyses for near-trapping of a four-cylinder structure under water waves[J]. Journal of Harbin Engineering University, 2011, 32(5): 546-554. DOI:10.3969/j.issn.1006-7043.2011.05.002 (  0) 0)
|
| [4] |
DUCLOS G, CLÉMENT A H. Wave propagation through arrays of unevenly spaced vertical piles[J]. Ocean engineering, 2004, 31(13): 1655-1668. DOI:10.1016/j.oceaneng.2004.03.006 (  0) 0)
|
| [5] |
CHEN J T, LIN Y J, LEE Y T, et al. Water wave interaction with surface-piercing porous cylinders using the null-field integral equations[J]. Ocean engineering, 2011, 38(2/3): 409-418. (  0) 0)
|
| [6] |
NEWMAN J N. Cloaking a circular cylinder in water waves[J]. European journal of mechanics-B/fluids, 2014, 47: 145-150. DOI:10.1016/j.euromechflu.2013.11.005 (  0) 0)
|
| [7] |
何广华, 张志刚, 张子豪, 等. 群遮效应对海上结构物波漂移力的低减作用[J]. 哈尔滨工程大学学报, 2017, 38(11): 1676-1681. HE Guanghua, ZHANG Zhigang, ZHANG Zihao, et al. Reduction in wave drift force on marine structures by cloaking phenomenon[J]. Journal of Harbin Engineering University, 2017, 38(11): 1676-1681. (  0) 0)
|
| [8] |
ⅡDA T, KASHIWAGI M, HE Guanghua. Numerical confirmation of cloaking phenomenon on an array of floating bodies and reduction of wave drift force[J]. International journal of offshore and polar engineering, 2014, 24(4): 241-246. (  0) 0)
|
| [9] |
TASRIEF M, KASHIWAGI M. Improvement of ship geometry by optimizing the sectional area curve with binary-coded genetic algorithms (BCGAs)[C]//Proceedings of the 23th International Offshore and Polar Engineering Conference. Anchorage, USA, 2013: 869-875.
(  0) 0)
|
| [10] |
ZHANG Zhigang, HE Guanghua, JU Xiaoqun, et al. Study on influence of geometrical dimensions of floating bodies on cloaking phenomenon[C]//Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea, 2016: 1-8.
(  0) 0)
|
| [11] |
ZHANG Zhigang, HE Guanghua, KASHIWAGI M, et al. A quasi-cloaking phenomenon to reduce the wave drift force on an array of adjacent floating bodies[J]. Applied ocean research, 2018, 71: 1-10. DOI:10.1016/j.apor.2017.11.011 (  0) 0)
|
| [12] |
KAGEMOTO H, YUE D K P. Interactions among multiple three-dimensional bodies in water waves:an exact algebraic method[J]. Journal of fluid mechanics, 1986, 166: 189-209. DOI:10.1017/S0022112086000101 (  0) 0)
|
| [13] |
KASHIWAGI M, YOSHIDA S. Wave drift force and moment on a VLFS supported by a great number of floating columns[J]. International journal of offshore and polar engineering, 2001, 11: 176-183. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


