目前,风力发电机主要分为水平轴风机和垂直轴风机,而Savonius风机就是一种较为常见的阻力型垂直轴风机。传统的Savonius风机具有结构简单、自启动性能好、噪声小和造价低等优点,使得其在小型风机发电领域具有广阔的应用前景[1]。
Savonius风机与其他水平轴风机和升力型垂直轴风力机相比,其气动性能较差、风能转化率低,普通Savonius风机的最高发电效率仅为25%。因此,国内外学者通过实验方法和数值模拟方法从风机基本结构参数、叶轮几何参数和风机辅助结构等各方面来研究改善Savonius风机的气动性能,从而提高其风能转化率[2]。文献[3]通过风洞实验得出高径比为5的风机的风能利用率为0.25。文献[4]通过实验得出两叶片的Savonius风机性能高于三叶片和四叶片的Savonius风机。文献[5]利用风洞实验得出风机孔隙比在0.2左右时,风能转化率最高。文献[6]利用CFD方法对非定常流中的Savonius风机进行数值模拟,研究表明:在CFD中,2D/k-ω模型可以获得较好的仿真效果。文献[7]通过风洞实验发现通过叠加风机的数量(风机在垂直方向上进行安装叠加,旋转轴相同)也可以提高风机输出功率。
此外,也有学者通过改善风机辅助机构来提高Savonius风机的发电功率。文献[8]通过在风机周围安装集风箱来改善流场特性。文献[9]在风机上安装类似于水轮机的吸气装置,从而提高风机的自启动特性。文献[10]研究了导流板对Banki风机气动性能的影响。文献[11]研究了单个集风板对风机的静力矩影响。此类方法通过改变流场特性,使得来流风集中作用于风机的正力矩区域,从而提高风能转化率。
也有些学者从叶轮几何参数优化角度进行研究。文献[12]将传统半圆型叶轮改为扭转型叶轮;文献[13]利用4种翼型叶轮代替传统半圆型叶轮;文献[14]对样条曲线叶轮进行了研究。研究结果表明,此类方法可以降低负力矩和提高正力矩,从而提高Savonius风机的发电效率。
本文提出通过优化叶轮双侧外形来提高Savonius风机的发电效率,相较于通过添加附加结构和优化风机的基本结构参数来提高风机的发电效率,本文更注重于对叶轮本身形状进行优化,因此在其他改善方法的基础上,同样可以叠加使用本文提出的方案。对Savonius风机进行二维非定常流体动力数值计算,研究相同尖速比条件下,叶轮的转矩和功率特性;并利用Kriging代理模型和粒子群优化算法寻找最优的叶轮形状;最后,对叶轮双侧外形对叶轮发电效率影响的原因进行论述。
1 Savonius风机叶轮两叶片Savonius风机叶轮的二维示意图如图 1所示,图中U为来流速度,ω为叶轮旋转角速度。该型叶轮的主要几何参数包括:叶片外侧椭圆的短轴长2R1、叶片内侧椭圆的弦长R2、叶片的长轴长2R,叶轮直径D,两片叶片之间的间隙比为0.05。叶轮的初始位置如下图 1所示,θ=0°。

|
Download:
|
| 图 1 叶轮的二维平面示意 Fig. 1 2-D schematic of the turbine | |
为了能够准确的描述叶轮形状,本文对叶轮做出如下定义:
| $ {\delta _1} = \frac{{{R_1}}}{R} $ | (1) |
| $ {\delta _2} = \frac{{{R_2}}}{R} $ | (2) |
则叶轮的形状可以用一个数组δ=(δ1, δ2)准确描述出来。对于常规半圆型的Savonius风力机叶轮,则有δ=(δ1, δ2)=(1, 1)。为了方便对比,叶轮形状和实验叶轮相同[15]。
为了研究风机叶轮形状对风机发电效率的影响,通过改变δ1的大小(分别为1.36、1.24、1.12、1、0.88、0.76和0.64,共7组)和δ2的大小。对应于δ1,仿真工况共分成7组,每组叶轮固定δ1的大小,改变δ2,例如对于δ1=1.36,δ2从1.36开始递减,每隔0.12仿真一次,共仿真6次(如表 1所示为其中一组仿真几何参数设置)。遵循上述仿真设置规律,仿真工况总数为42。
| 表 1 仿真几何参数设置 Table 1 Geometry parameter setting of simulation |
为便于分析,定义如下无量纲化系数:
尖速比
| $ \lambda = \frac{{\omega D}}{{2U}} $ | (3) |
力矩系数
| $ {C_m} = \frac{M}{{0.25\rho S{U^2}D}} $ | (4) |
发电功率系数
| $ {C_p} = \frac{P}{{0.5\rho S{U^3}}} = \lambda {C_m} $ | (5) |
式中: D为叶轮直径, m;ω为叶轮旋转角速度,rad/s;U为风速,m/s;M为叶轮所受力矩,N·m;ρ为流体密度(取气体密度ρ=1.225 kg/m3);S为叶轮的迎风面积(S=DH,H为叶轮的纵向高度);P为功率,W。
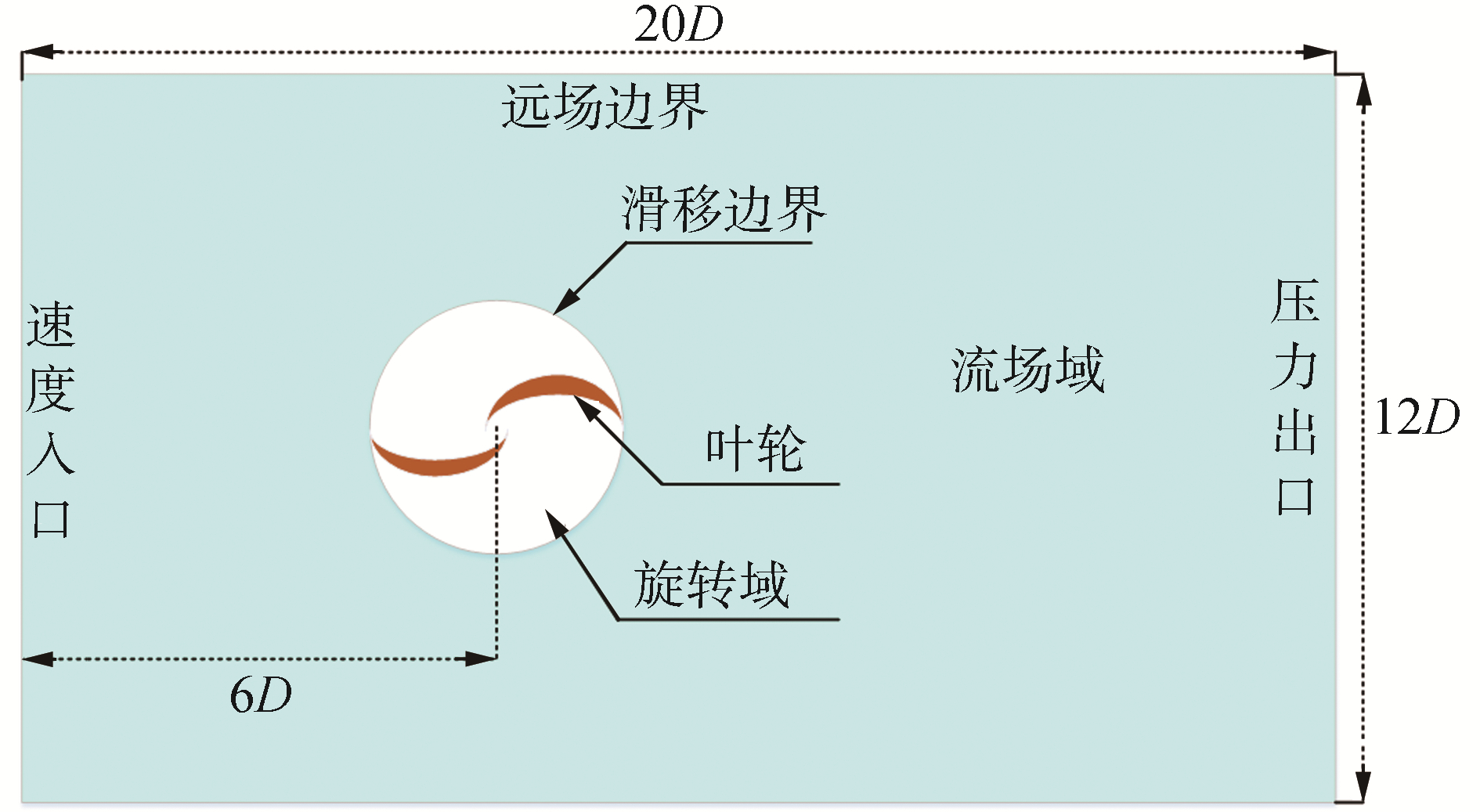
2 计算数学模型 2.1 数值模型设置为了提高计算效率,且采用的叶轮为直叶轮,因此理论上可以将叶轮从三维模型简化成二维模型,默认叶轮的纵向高度为H=1 m,忽略风力机其他的附加机构。在实际流体数值计算中,要避免计算域过窄,计算域过窄使得有限边界对计算结果产生负面影响(过大会增加不必要的计算量)。本文将计算域设为一个矩形区域,其长度为20D,宽度为12D。风力机叶轮位于水平对称轴且距流场入口为6D,如图 2所示为计算域设置。
|
Download:
|
| 图 2 计算域示意图 Fig. 2 Sketch map of computational domain | |
采用滑移网格技术,计算域包括流场域和叶轮旋转域,叶轮旋转域包裹有叶轮。入场边界为速度入口;出场边界为压力出口;流场域与叶轮旋转域的交界边界为滑移边界;叶轮为为无滑移壁面;上下远场边界为光滑壁面。
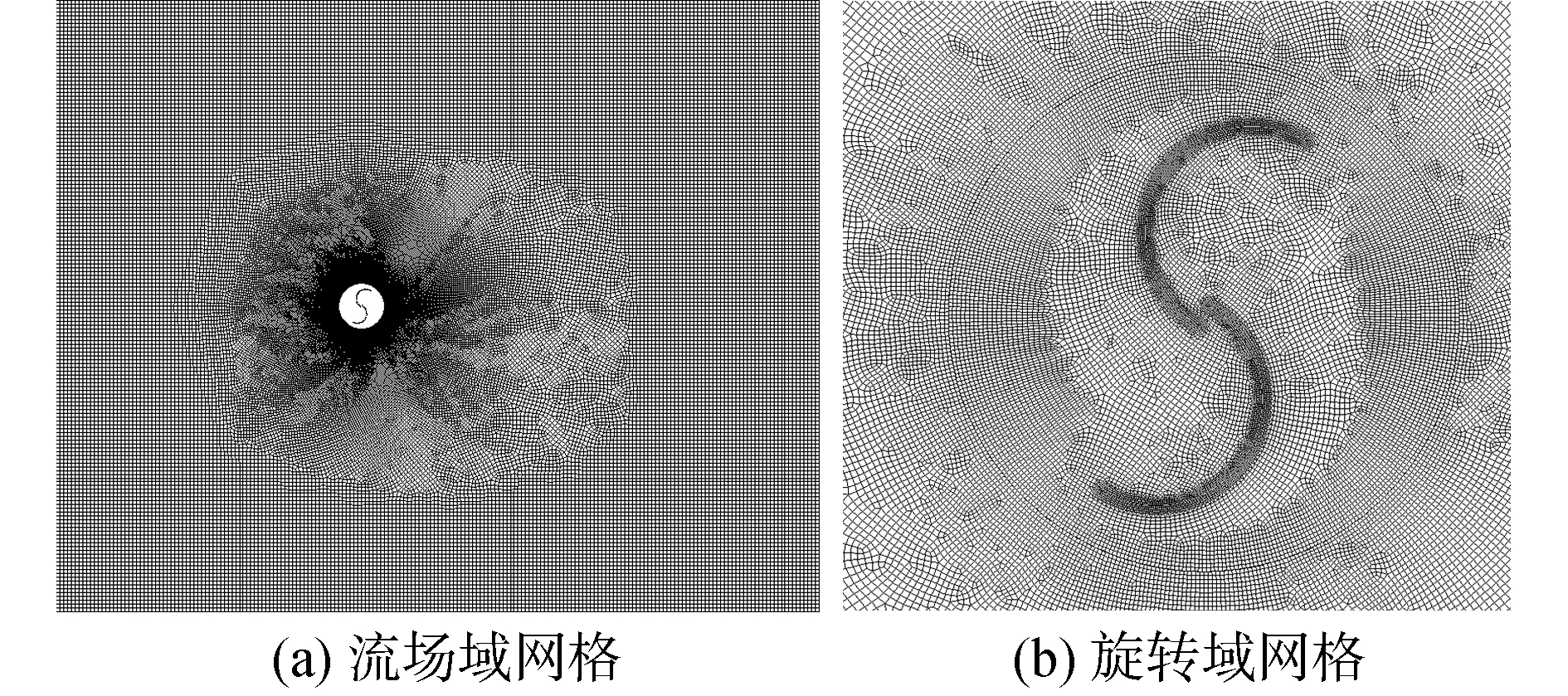
利用ANASYS 15.0中的mesh对模型进行网格划分,采用四边形网格(如图 3(a)所示)。对旋转域和叶轮处的网格进行加密处理,可提高叶轮力矩计算的精确度,网格处理如图 3(b)所示。
|
Download:
|
| 图 3 网格划分 Fig. 3 Mesh generation | |
本文计算采用SST k-ω模型[6],其能够很好的处理近壁处低雷诺数的数值计算。控制方程的离散格式采用Standard方法;压力-速度耦合采用SIMPLEC算法;模拟的求解格式均采用二阶迎风格式。每个工况计算10个旋转周期,每个旋转周期设定180个时间步,即每个时间步旋转域转动2°,残差收敛标准均设为1×10-5。
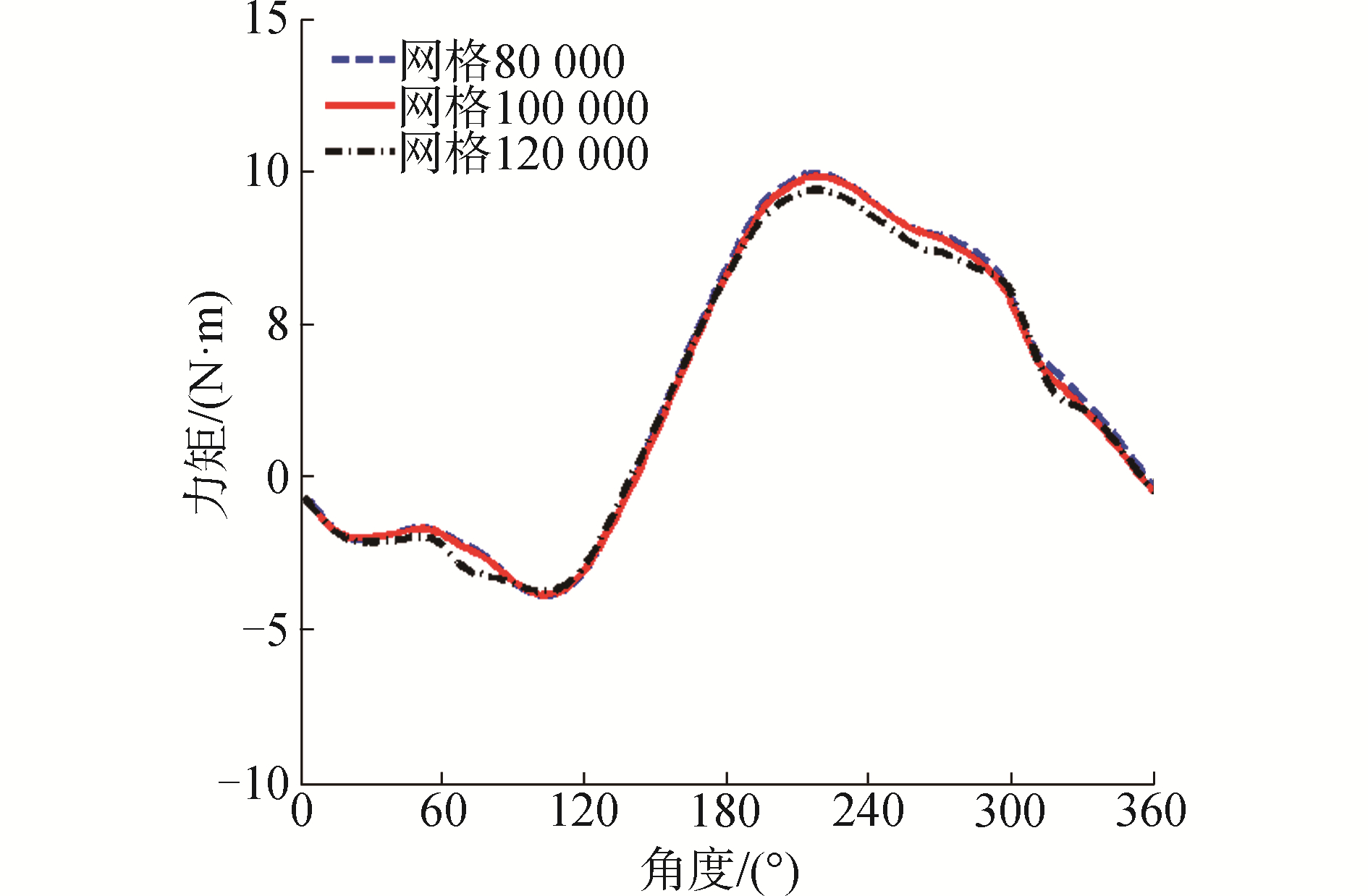
2.2 网格无关性验证计算模型需进行网格无关性验证。通过加密叶片附近网格的节点分布,使网格总数分别约为80 000、100 000和120 000。如图 4所示为不同网格数的叶轮力矩系数变化曲线(λ=0.5,在一个旋转周期内)。
|
Download:
|
| 图 4 网格无关性验证 Fig. 4 Results of the grid verification | |
从图 4可以看到,网格数约为100 000和120 000的计算结果差别不超过0.5%。可以认为当网格数大于120 000时,计算结果基本不受网格数的影响,将总体网格数设为约120 000(静止域网格数约40 000,旋转域网格数约80 000)。
2.3 数值模型实验验证数值模型建立后,为保证其仿真结果的准确性,需要进行实验对比验证。对叶轮δ=(1, 1)进行不同尖速比条件下的实验验证,数值仿真的结果同美国Sandia实验室的实验结果进行比对[15]。由图 5可知,SST k-ω湍流模型仿真的结果基本吻合实验结果。当λ≤0.8时,数值仿真结果略高于实验结果,但误差不差过10%;当λ>0.8时,数值仿真结果基本与实验结果重合。因此,数值计算模型可以较好地对叶轮的力矩特性进行描述。

|
Download:
|
| 图 5 数值模型验证 Fig. 5 The validation of numerical models | |
Kriging模型是一种方差最小无偏估计模型。利用叶轮形状参数(δ1和δ2)来建立Kriging代理模型,该模型可以描述优化目标Cp和叶轮形状参数之间的关系。设欲近似的的函数为y(x),并假设Kriging模型的响应值和自变量之间的关系为:
| $ y\left( x \right) = \beta + Z\left( x \right) $ |
式中:β为待定参数;Z(x)具有以下性质:
| $ \left\{ \begin{gathered} {\text{E}}\left[{Z\left( x \right)} \right] = 0 \hfill \\ {\text{Var}}\left[{\left( {Z\left( x \right)} \right.} \right] = {\sigma ^2} \hfill \\ {\text{F}}\left[{Z\left( x \right)Z\left( {{x_i}} \right)} \right] = {\sigma ^2}R\left( {x, {x_i}} \right) \hfill \\ \end{gathered} \right. $ |
式中:σ2是协方差;R(x, xi)为两个数据点之间的变异函数,R(x, xi)被定义为:
| $ R\left( {x, {x_i}} \right) = \exp \left[{-\sum\limits_{i = 1}^n {{\theta _k}{{\left( {{x_{ki}}-{x_k}} \right)}^2}} } \right] $ |
式中θk为变异函数参数。
利用实验数据点(42个仿真工况)及其相对应的响应值(Cp),形成一个相关矩阵为:
| $ \mathit{\boldsymbol{R}} = \left[{\begin{array}{*{20}{c}} {R\left( {{x_1}, {x_1}} \right)}& \cdots &{R\left( {{x_1}, {x_N}} \right)} \\ \vdots&\vdots&\vdots \\ {R\left( {{x_N}, {x_1}} \right)}& \cdots &{R\left( {{x_N}, {x_N}} \right)} \end{array}} \right] $ |
预测点与实验数据之间的相关矩阵为:
| $ \mathit{\boldsymbol{r}} = \left[{\begin{array}{*{20}{c}} {R\left( {x, {x_1}} \right)} \\ \vdots \\ {R\left( {x, {x_N}} \right)} \end{array}} \right] $ |
得到Kriging代理模型的响应值函数为:
| $ \hat y\left( x \right) = \hat \beta + {\mathit{\boldsymbol{r}}^{\text{T}}}\left( x \right){\mathit{\boldsymbol{R}}^{-1}}\left( {\mathit{\boldsymbol{Y}}-\mathit{\boldsymbol{X}}\hat \beta } \right) $ |
式中:X为实验数据自变量值矩阵;Y为响应值向量;
| $ \hat \beta = {\left( {{\mathit{\boldsymbol{X}}^{\text{T}}}{\mathit{\boldsymbol{R}}^{-1}}\mathit{\boldsymbol{X}}} \right)^{-1}}{\mathit{\boldsymbol{X}}^{\text{T}}}{\mathit{\boldsymbol{R}}^{-1}}\mathit{\boldsymbol{Y}} $ |
模型建成后,需要通过检验函数来检验,一般误差检验函数值越小越好[16],常用的检验函数为方均根误差。
粒子群算法是一种并行算法,其所讨论的问题是在众多可行方案中寻找最优方案,它的思想源于人工生命和演化计算理论。PSO算法具有概念简单、全局优化性能好、控制参数少等优点。PSO算法流程如下:
1) 初始化粒子(初始化速度和位置);
2) 计算适应度函数值;
3) 如果当前粒子适应度函数值大于历史最优值,那么历史最优值将被当前值替代;
4) 计算粒子群的最优解。如果粒子群的历史最优比全局最优要好,那么粒子群的全局最优被历史最优替代;
5) 对每个粒子的速度和位置进行更新;
6) 进化代数增加1,没有达到终止条件,转至2);否则,结束算法并输出最优值。
PSO算法流程图如图 6所示。
|
Download:
|
| 图 6 PSO算法流程图 Fig. 6 Flow chart of PSO algorithm | |
PSO算法可通过MATLAB编程语言来实现,将Kriging代理模型中的响应值函数作为PSO优化算法的目标函数,最终建立Kriging-PSO优化模型。
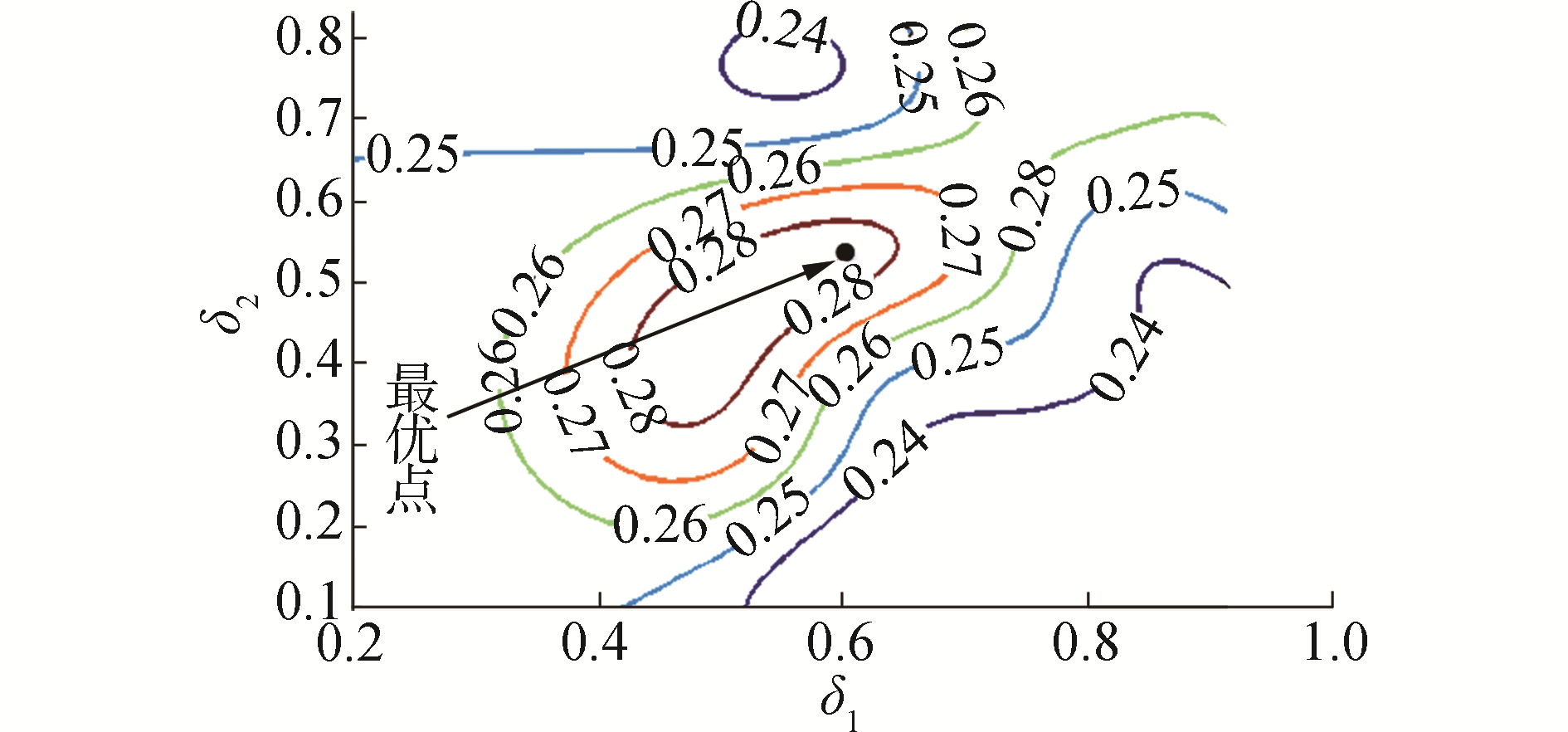
3 计算结果分析 3.1 优化结果Kriging-PSO优化模型对Savonius风力机叶轮双侧外形优化的结果为:双侧最优形状为(0.626 8, 0.541 3),对应的最优发电功率系数为0.284。Kriging模型的响应面如图 7所示,寻得最优点如图 8所示。

|
Download:
|
| 图 7 Kriging模型的响应面 Fig. 7 The response surface of Kriging model | |
|
Download:
|
| 图 8 最优点 Fig. 8 The best point | |
对Kriging模型进行验证,发现样本点与响应值之间的误差非常小,其数量级为10-4,且均方差根误差趋近于零,验证了Kriging模型的准确性[17]。
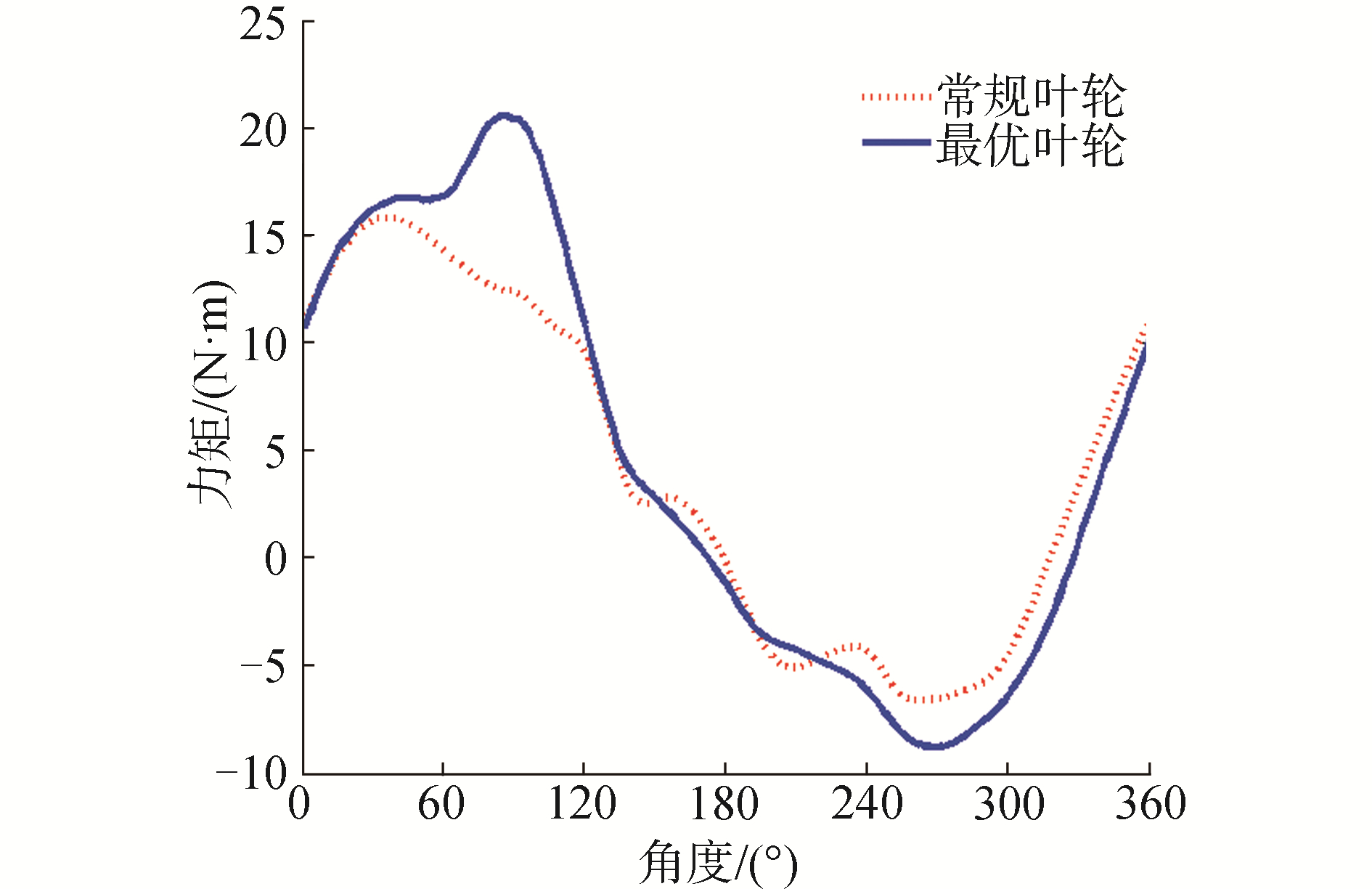
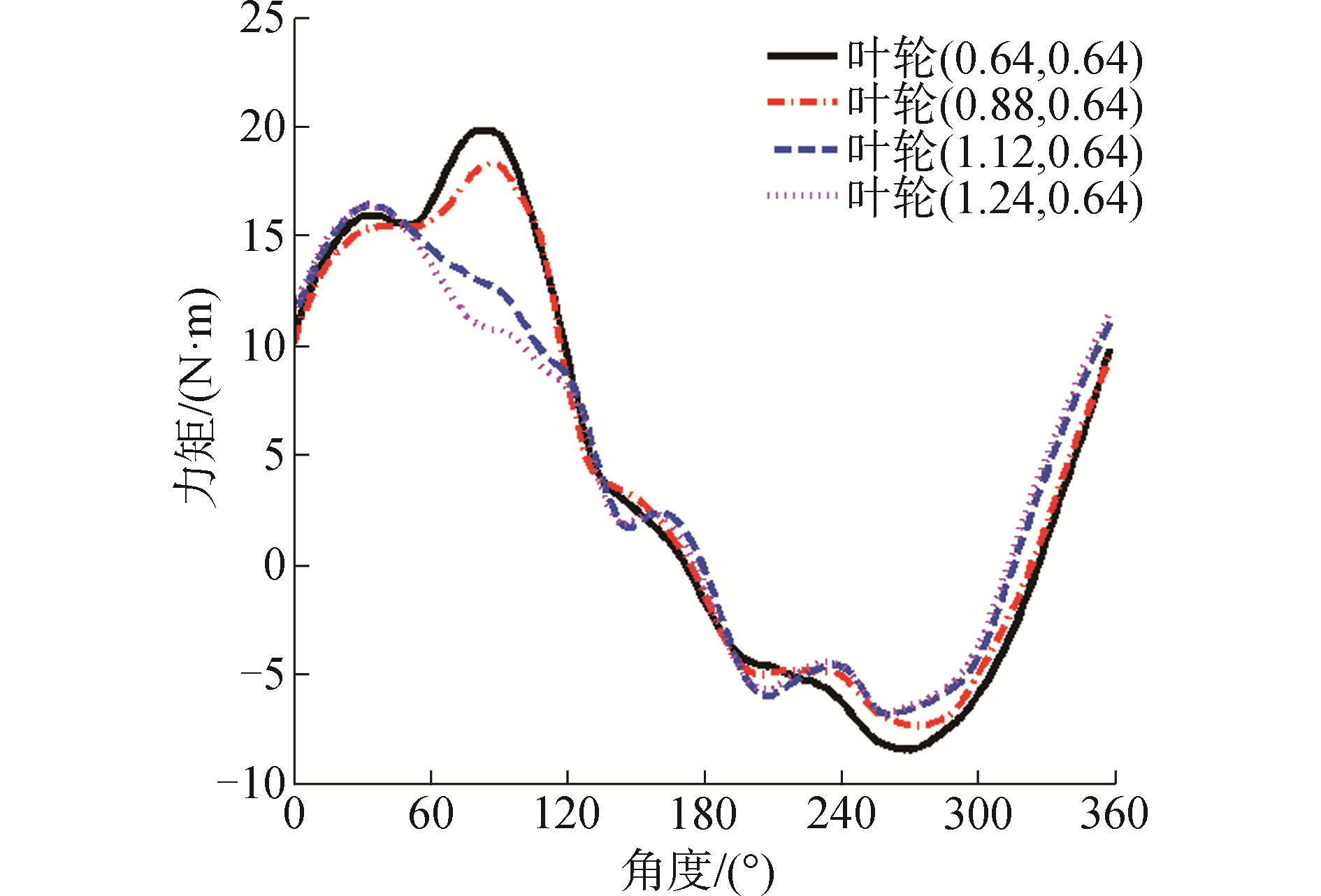
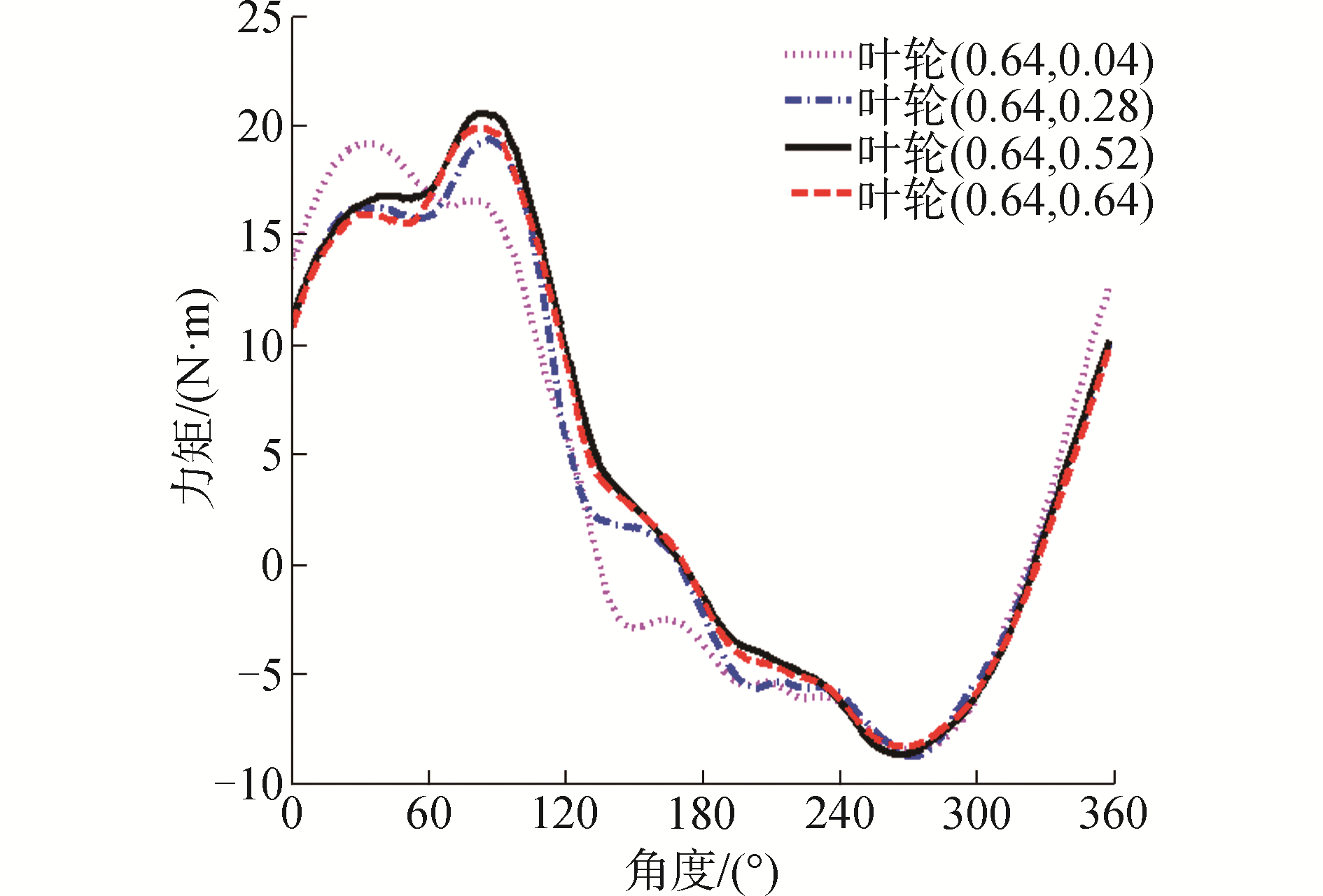
3.2 叶轮力矩特性分析对比优化叶轮δ=(0.626 8, 0.541 3)和常规叶轮δ=(1, 1),可以分析双侧外形参数对叶轮特性的影响。如图 9所示为一个周期内,最优叶轮和常规叶轮单个叶片的力矩系数变化曲线。从图中可以看出:1)一个周期内,叶片力矩系数呈正负变化,叶片力矩系数大约在-30° < θ < 160°为正力矩;2)优化叶轮相较于常规叶轮,力矩系数的峰值点位置发生变化,最大力矩值提高。通过对比可以得到以下规律:1)优化叶轮的正力矩平均值提高;2)优化叶轮的负力矩平均值的绝对值也是提高的。上述规律1有利于提高叶轮的功率系数,而规律2不利于提高叶轮的功率系数。如图 10所示, 当δ2=0.64时,δ1分别为0.64、0.88、1.12和1.24时一个周期内的力矩系数变化曲线;如图 11所示, δ1=0.64时,δ2分别为0.04、0.28、0.52和0.64时一个周期内的力矩系数变化曲线。由图 10和图 11可知,双侧参数δ1和δ2都对叶轮的力矩特性产生影响。但由于上述两个规律的相互制约,因此存在一最优的双侧外形参数使得功率系数最大化,最优叶轮为δ=(0.626 8, 0.541 3)。
|
Download:
|
| 图 9 优化前后叶轮力矩系数的变化曲线(λ=1.0) Fig. 9 Moment coefficients curves before and after optimization(λ=1.0) | |
|
Download:
|
| 图 10 δ1变化时的力矩系数曲线(λ=1.0) Fig. 10 Moment coefficient curves when δ1 changes(λ=1.0) | |
|
Download:
|
| 图 11 δ2变化时的力矩系数曲线(λ=1.0) Fig. 11 Moment coefficient curves when δ2 changes(λ=1.0) | |
图 12分别是常规叶轮和优化叶轮位于正力矩区域(θ=72°)的压力分布云图,由压力云图可知:相较于常规叶轮,优化叶轮叶片迎风方向凹面上压力增大,背风方向凸面以及凹面上的压力变化不大,叶片变钝,正力矩增加,叶轮的功率特性得到改善。

|
Download:
|
| 图 12 叶轮优化前后的压力云图(正力矩区域,λ=1.0) Fig. 12 Pressure nephogram before and after impeller optimization(positive torque region, λ=1.0) | |
图 13分别是常规叶轮和优化叶轮位于负力矩区域(θ=288°)的压力云图分布,由压力云图可知:相较于常规叶轮,优化叶轮叶片背风方向凸面上压力明显减小;迎风方向凸面以及凹面上的压力变化不大,叶片变钝,使得叶片负阻力的绝对值增加,负阻力矩的绝对值变大,即减小了叶轮的负阻力矩。

|
Download:
|
| 图 13 叶轮优化前后的压力云图(负力矩区域,λ=1.0) Fig. 13 Pressure nephogram before and after impeller optimization(negative torque region, λ=1.0) | |
1) 优化叶轮相比于常规叶轮,最大力矩系数提高,最小力矩系数减小;
2) 叶片力矩系数在一个旋转周期内,呈现一次正负交替的变化;
3) 基于Kriging-PSO优化模型找到最优形状的Savonius风机叶轮, 叶轮最优形状为(0.626 8,0.541 3),最优发电效率系数为0.284,相比于常规叶轮(0.265)提高了7.17%。
本文研究可为Savonius风机叶轮外形优化提供一种可供参考的数值模拟方法和优化方法。
| [1] |
王睿哲. Savonius风力机叶片主要参数优化设计研究[D].呼和浩特: 内蒙古工业大学, 2015. WANG Ruizhe. Study on optimal design of main parameters for blades of Savonius wind turbine[D]. Hohhot: Inner Mongolia University of Technology, 2015. http://www.bigengculture.com/kejilunwen/dianlilw/723875.html (  0) 0)
|
| [2] |
李志强. Savonius风机气动增效的曲-直集风流动控制[D].哈尔滨: 哈尔滨工业大学, 2016. LI Zhiqiang. Flow control of aerodynamic performance improvement of Savonius wind rotor via a arc-straight shaped curtain[D]. Harbin: Harbin Institute of Technology, 2016. (  0) 0)
|
| [3] |
ALEXANDER A J, HOLOWNIA B P. Wind tunnel tests on a Savonius rotor[J]. Journal of wind engineering and industrial aerodynamics, 1978, 3(4): 343-351. DOI:10.1016/0167-6105(78)90037-5 (  0) 0)
|
| [4] |
MAHMOUD N H, EL-HAROUN A A, WAHBA E, et al. An experimental study on improvement of Savonius rotor performance[J]. Alexandria engineering journal, 2012, 51(1): 19-25. DOI:10.1016/j.aej.2012.07.003 (  0) 0)
|
| [5] |
BISWAS A, GUPTA R, SHARMA K K. Experimental investigation of overlap and blockage effects on three-bucket Savonius rotors[J]. Wind engineering, 2007, 31(5): 363-368. DOI:10.1260/030952407783418702 (  0) 0)
|
| [6] |
DOBREV I, MASSOUH F. CFD and PIV investigation of unsteady flow through Savonius wind turbine[J]. Energy procedia, 2011, 6: 711-720. DOI:10.1016/j.egypro.2011.05.081 (  0) 0)
|
| [7] |
RAJKUMAR M J, SAHA U K, MAITY D. Simulation of flow around and behind a Savonius rotor[J]. International energy journal, 2005, 6(2): 83-90. (  0) 0)
|
| [8] |
IRABU K, ROY J N. Characteristics of wind power on Savonius rotor using a guide-box tunnel[J]. Experimental thermal and fluid science, 2007, 32(2): 580-586. (  0) 0)
|
| [9] |
TIAN Wenlong, MAO Zhaoyong, ZHANG Baoshou, et al. Shape optimization of a Savonius wind rotor with different convex and concave sides[J]. Renewable energy, 2018, 117: 287-299. (  0) 0)
|
| [10] |
毛昭勇, 卫超, 黄伟超, 等. 导流板对Banki式风机性能的影响分析[J]. 兵工学报, 2014, 35(8): 1324-1328. MAO Zhaoyong, WEI Chao, HUANG Weichao, et al. Influence of deflector baffle on performance of Banki wind turbine[J]. Acta armamentarii, 2014, 35(8): 1324-1328. DOI:10.3969/j.issn.1000-1093.2014.08.029 (  0) 0)
|
| [11] |
李鹿野, 张维竞. 某小型风机提高风能利用率的研究[J]. 节能技术, 2015, 33(4): 295-298, 315. LI Luye, ZHANG Weijing. Improvement of a small wind turbine with curtaining[J]. Energy conservation technology, 2015, 33(4): 295-298, 315. DOI:10.3969/j.issn.1002-6339.2015.04.002 (  0) 0)
|
| [12] |
ALDOS T K. Savonius rotor using swinging blades as an augmentation system[J]. Wind engineering, 1984, 8(4): 214-220. (  0) 0)
|
| [13] |
TABASSUM S A, PROBERT S D. Vertical-axis wind turbine:a modified design[J]. Applied energy, 1987, 28(1): 59-67. (  0) 0)
|
| [14] |
KAMOJI M A, KEDARE S B, PRABHU S V. Experimental investigations on single stage, two stage and three stage conventional Savonius rotor[J]. International journal of energy research, 2008, 32(10): 877-895. DOI:10.1002/er.v32:10 (  0) 0)
|
| [15] |
BLACKWELL B F, SHELDAHL R E, FELTZ L V. Wind tunnel performance data for two-and three-bucket Savonius rotors, SAND76-0131[R]. New Mexico: US Sandia Laboratories, 1977.
(  0) 0)
|
| [16] |
谢延敏, 徐笑梅, 罗征志. 基于Kriging模型的翻边成形参数优化[J]. 塑性工程学报, 2010, 17(5): 4-9. XIE Yanmin, XU Xiaomei, LUO Zhengzhi. Research on parameter optimization in flanging process based on Kriging metamodel[J]. Journal of plasticity engineering, 2010, 17(5): 4-9. (  0) 0)
|
| [17] |
冯吉路, 孙志礼, 李皓川, 等. 基于Kriging模型的轴承结构参数优化设计方法[J]. 航空动力学报, 2017, 32(3): 723-729. FENG Jilu, SUN Zhili, LI Haochuan, et al. Optimization design method of bearing structure parameters based on Kriging model[J]. Journal of aerospace power, 2017, 32(3): 723-729. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


