在福岛事故发生后,新一代先进反应堆设计对固有安全性提出了更高的要求。非能动系统依靠自然循环、重力等自然法则作为驱动力,减少了对外部电源与人员干预的依赖,仅依靠堆的固有安全性就能使反应堆趋于相对安全的状态。因此,非能动设计是新一代核电站设计的特点与趋势[1],其可靠性分析研究也成为了人们关注的焦点。
由于实现系统功能的机理不同,非能动系统可靠性分析的方法也与能动方法有所区别[2]。作为驱动的自然力与阻力数量级上接近,由参数不确定性所引入的物理失效过程是非能动系统可靠性分析的关键与难点[3]。正是由于物理失效过程的存在,使得非能动系统即使硬件全部可靠,也存在着系统偏离运行状态而无法实现其功能的可能,Burgazzi将这种失效称为功能失效[4-5]。
近年来,国内外针对非能动系统可靠性分析做了大量工作。Marques等[6-7]分别研究了非能动系统可靠性评估方法RMPS和REPAS。谢国锋等[8]利用响应面与蒙特卡洛法等针对清华10 MW高温气冷堆的非能动系统进行计算。王冬青等[10-11]
采用基于重要取样的子集模拟法与优化的线性取样法对AP1000[9]非能动余热排出系统功能失效进行计算,在保证计算精度的前提下,具有较高的计算效率。玉宇等[12]利用相关性分析减少神经网络响应面法的输入参数,极大提高了计算效率。目前,国内、外的研究对象主要是分散式布置的反应堆,国内的研究者大多针对AP1000的非能动系统进行分析,对一体化压水堆非能动系统的可靠性研究工作尚有不足。由于一体化压水堆主要设备的结构布置与分散式布置压水堆有所区别,在非能动系统投入后,反应堆内的自然循环特性也并不相同,因此,在关键参数的选取以及热工水力模型的建立上都会存在差异,具有研究分析的意义。此外,目前的非能动可靠性分析方法集中于分析物理过程的失效,如何将其整合到概率安全分析(PSA)中,将物理失效与硬件失效合理的结合考虑仍是一个难题[13-15]。
针对现有研究存在的不足[16],本文以一体化压水堆IPWR200[17]为研究对象,分析其非能动余热排出系统的可靠性。考虑到一体化堆与分散式布置压水堆在结构与运行特性上的区别,影响系统功能的关键参数于系统在发生事故后的响应也必然有所差异。通过层次分析法选定影响系统功能的关键参数,并通过拉丁超立方抽样选取样本作为输入,通过最佳估算程序RELAP5建立热工水力模型后传递不确定性计算得到响应值,合理设计神经网络结构并运用神经网络响应面法作为替代模型,定量计算系统的物理过程失效概率。本文将计算得到的物理失效概率作为底事件整合到PSA故障树模型中,合理地考虑物理失效与设备失效对系统功能的综合影响,定量计算了非能动余热排出系统的失效概率。
1 非能动可靠性非能动安全系统的作用机理是自然循环、重力驱动等自然法则,相对于能动系统,其驱动力的数量级要小很多,导致非能动系统的运行状态对参数不确定性的影响更加敏感[18]。由于安装、制造等工程误差以及核电厂运行状态的波动,使系统的结构参数与运行参数X(x1, x2,…, xn)存在一定范围的波动,这种不确定性的存在可能导致系统功能的失效。
| $ g\left( \mathit{\boldsymbol{X}} \right) = Y\left( \mathit{\boldsymbol{X}} \right)-A\left\{ {\begin{array}{*{20}{l}} < &{{\rm{成功状态}}}\\ { = 0}&{{\rm{极限状态}}}\\ { > 0}&{{\rm{失效状态}}} \end{array}} \right. $ | (1) |
式中:Y(X)为用来传递不确定性的复杂热工水力程序,通常是隐式的函数;A是根据系统功能所确立的失效准则,通过判断g(X)的值确定系统状态。系统的物理失效概率可由式(2)进行计算:
| $ P\left( F \right)=\iint{\cdots \int{{{I}_{F}}\left( {{x}_{1}}, {{x}_{2}}, \cdots, {{x}_{n}} \right)\text{d}{{\mathit{x}}_{1}}\text{d}{{\mathit{x}}_{2}}\cdots \text{d}{{\mathit{x}}_{n}}}} $ | (2) |
式中:IF(X)为指示函数,当g(X)>0时,其值为1;否则为0。
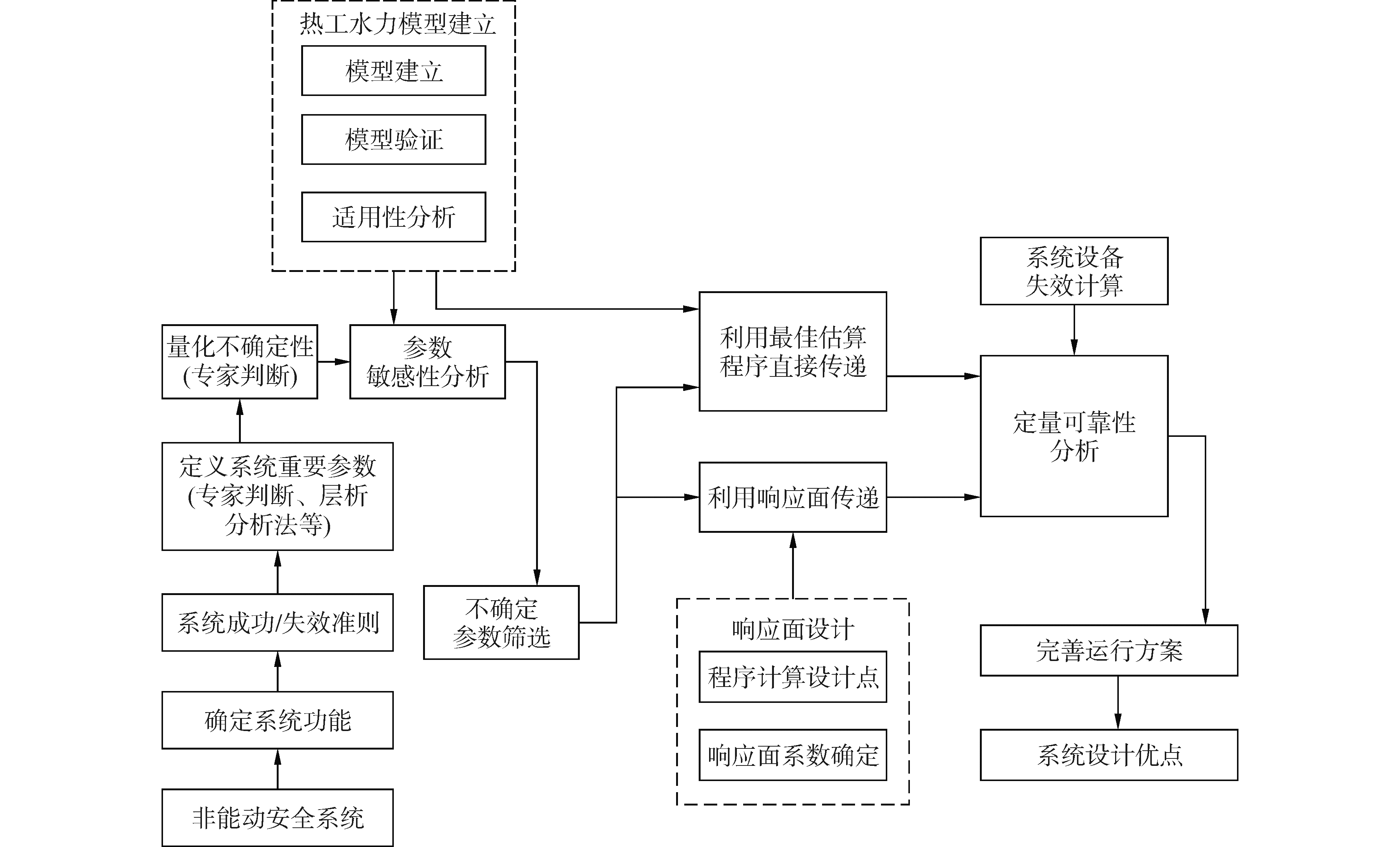
由于g(X)是由复杂热工水力程序得到的响应值,其指示函数不具有明确的表达式,因此式(2)的积分值需要采用数值的方法求解。非能动安全系统可靠性分析可以采用直接蒙特卡洛、减少方差的抽样技术、响应面法等。由于直接蒙特卡洛方法的计算所需的样本个数与系统失效概率成反比,加之每次运行RELAP5等系统分析程序都需要数小时的时间,对于失效概率较小的非能动系统来说,计算量显然是难以承受的。通过响应面法替代复杂的热工水力程序极大地提高计算效率[19],利用拉丁超立方抽样方法对参数进行抽样提高了样本的填充性,较少样本就可以形成满足精度要求的响应面。本文的分析框架如图 1所示。
|
Download:
|
| 图 1 可靠性分析框架 Fig. 1 Flow chart of reliability assessment method | |
IPWR200是热功率为200 MW的多用途一体化压水堆,目前已经完成了热工水力及堆芯物理设计(主要应用于浮动核电站、船用核动力装置的相关研究,其主要特点是采用板状燃料元件以及套管式直流式蒸汽发生器)。12台蒸汽发生器与4台主泵分四组环绕堆芯布置,IPWR200采用二次侧余热排出系统,其结构图如图 2所示。正常运行状态下,PRHRS管道中装满冷却水,PRHRS进口管线隔离阀处于常开状态,出口处设有并联的气动隔离阀并处于常关状态。当发生全厂断电事故时,给水中断,主给水隔离阀与主蒸汽隔离阀关闭,PRHRS出口管道上的气动隔离阀在失去电力或触发控制信号时自动打开,管道中的冷却水迅速进入OTSG带走一回路热量汽化后进入PRHRS热交换器,将热量传递给冷却水箱。水箱作为最终热阱可以长期有效地带走反应堆衰变热,确保反应堆的安全性。

|
Download:
|
| 图 2 非能动余热排出系统结构图 Fig. 2 Schematic diagram of the PRHRS | |
非能动余热排出系统的功能是当发生事故时通过自然循环带走反应堆衰变热,防止堆芯冷却剂出现汽化,确保堆芯包壳的完整性。
确保堆芯出口具有一定的过冷度,建立稳定的冷却剂自然循环是顺利带走衰变热的关键,本文选择冷却剂堆芯出口温度作为判别系统状态的依据,认为当冷却剂堆芯出口温度高于局部沸腾的临界时,开始出现局部沸腾,导致燃料棒与冷却剂之间的传热恶化,非能动系统丧失设计时的换热能力,堆芯衰变热无法顺利导出,偏离安全运行状态。
根据所确定的失效准则,选择影响系统功能的关键参数。由于非能动余热排出系统涉及复杂的热工水力过程,其功能的实现受到很多参数的影响。考虑过多的不确定性参数会大幅度增加热工水力程序的计算量,而一些参数对系统功能的影响较小,将这些影响较小的参数采用设计值对可靠性计算结果并不会造成明显的影响的同时,可以大幅度地减少输入参数维度,进而减少生成响应面时所需的样本数量,是合理有效的方法[20]。
本文采用层次分析法(analytic hierarchy process, AHP)进行重要参数的筛选。AHP是一种模拟人类面对复杂问题时的选择问题而提出的方法,该方法简洁、实用,将复杂问题的结构形式化,广泛应用于各领域的决策问题。AHP方法主要包括三个步骤:
1) 建立决策目标层的结构,对所有对目标层有影响的元素进行分解,较低一层的元素对上一层中元素有直接影响;
2) 两两比较同一层各元素对上一层某元素的相对重要度,构造判断矩阵;
3) 计算各底层元素对决策目标层影响的相对权重,并作一致性检验。
构建层次分析结构如图 3所示,根据专家的工程经验,通过两两比较各参数得出相对权重。反应堆功率直接影响到衰变热的大小。上升段高度影响到冷、热源位差,冷却水箱的初始水温关系到冷源的温度,这两个参数都直接影响到自然循环能力。PHRHS进口阻力系数及管径对自然循环流动有较大影响,系统换热受到PRHR管壁厚以及换热器管径等参数的影响。经过分析与判断矩阵计算后,筛选得到影响系统功能的关键参数有:反应堆初始功率、PRHRS进口阻力系数、PRHR HX换热面积、冷却水箱初始水温、二次侧压力、PRHR HX管径、PRHRS上升段管径、PRHR管壁厚、上升段高度。

|
Download:
|
| 图 3 层次分析模型 Fig. 3 Analytic hierarchy process model | |
非能动系统的作用机理是基于自然循环等物理法则,系统功能的实现依赖于热工水力现象。因此,运行环境的变化、制造安装及测量的误差、系统运行状态的波动等都会造成系统参数具有不确定性[21]。本文只关注参数不确定性对系统可靠性带来的影响,不考虑模型不确定性。
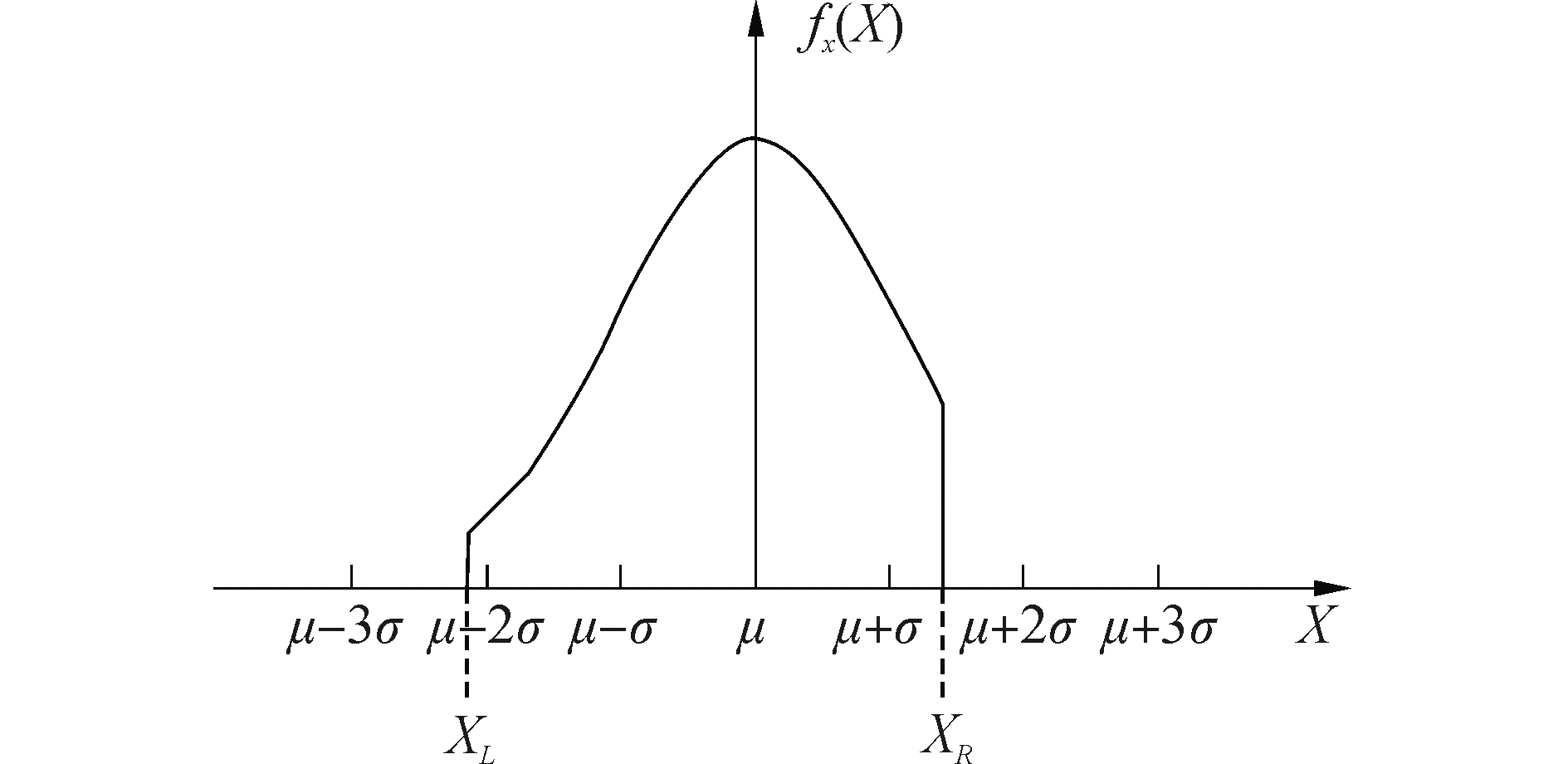
通过AHP确定9个影响系统功能的重要参数,根据工程上的3σ原则,服从正态分布的结构参数的波动范围限制在正负3倍标准差以内。由于实际情况下部分参数如换热面积的分布区间并不是完全对称,这里部分参数采用截断正态分布,不仅可以考虑非对称的样本区间,而且可以在更合理的样本范围内抽样,截断正态分布示意如图 4所示。
|
Download:
|
| 图 4 截断正态分布 Fig. 4 Truncated normal distribution | |
服从截断正态分布的概率密度函数fx(x)为
| $ {f_x}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {0, }&{- \infty \le x < {X_L}}\\ {f\left( x \right)/\left[{F\left( {{X_R}} \right)-F\left( {{X_L}} \right)} \right], }&{{X_L} \le x < {X_R}}\\ {0, }&{{X_R} \le x < + \infty } \end{array}} \right. $ | (3) |
式中:F(x)为截断前正态分布的累积概率分布,XL、XR分别为截断的左、右边界。根据文献[22-23]调研结果以及工程经验确定各个参数的不确定性范围,如表 1所示。
| 表 1 不确定参数分布范围 Table 1 Uncertainty parameter distribution range |
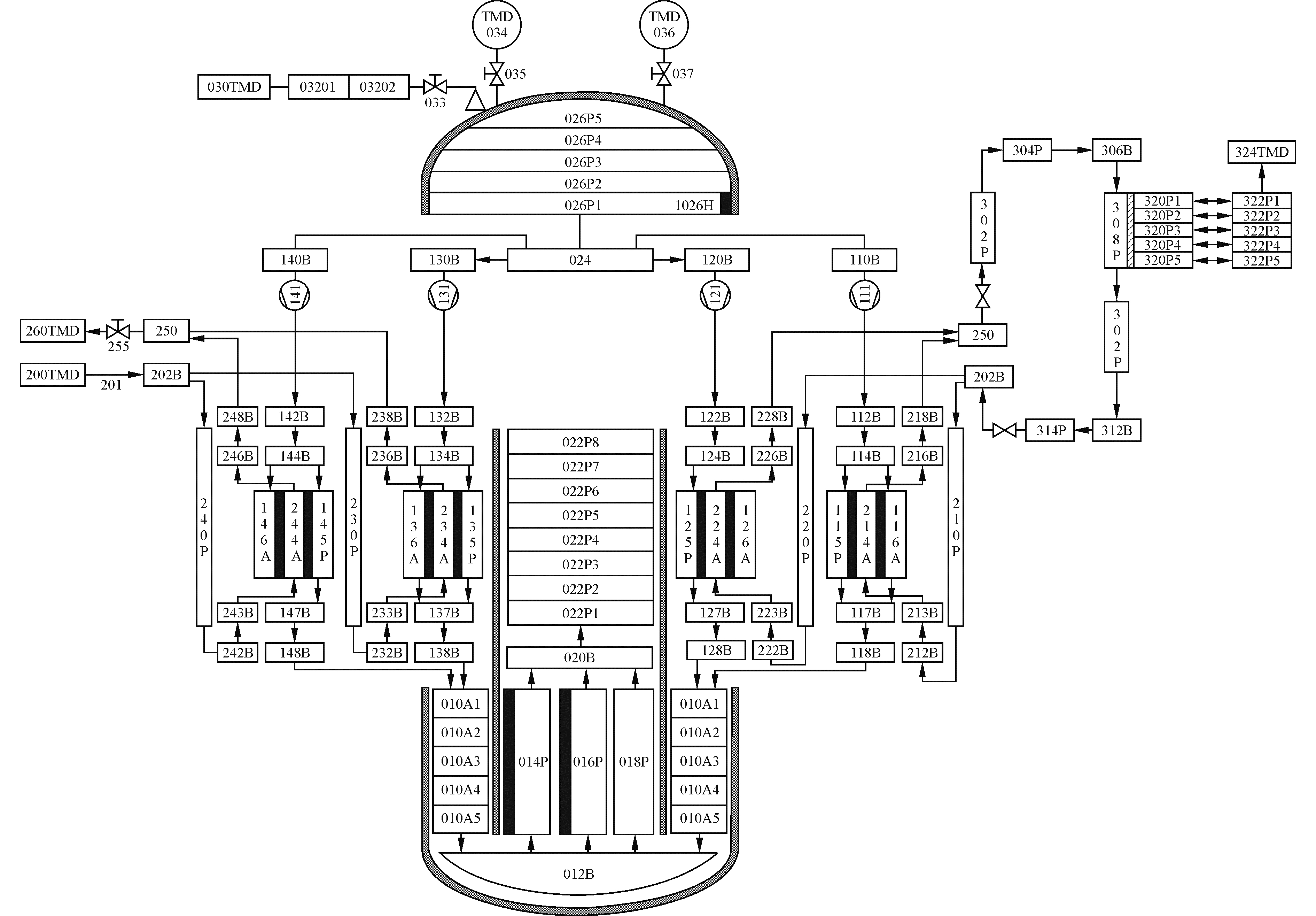
利用拉丁超立方抽样[24](Latin hypercube sampling)代替蒙特卡洛方法的对参数进行抽样。拉丁超立方抽样是改进的蒙卡方法,将参数以相等概率地分到n个不重叠的区间中,并在每个区间内随机抽样,可以提高所抽样本的填充性,较少样本即可反映出参数的概率分布特性,拉丁超立方抽样在输入参数均值、方差等预估效果已得到了广泛的认可,由于拉丁超立方抽样所需的样本数量较少,很大程度上提高了计算效率。采用最佳估算程序RELAP5进行不确定性传递。RELAP5是一款比较成熟的商用轻水堆瞬态分析程序,已广泛应用于事故缓解评价、审评计算等多个方面。夏庚磊等[25]已使用RELAP5对IP200非能动安全系统热工水力特性进行了大量研究,并确定RELAP5具有预测一体化压水堆发生全厂断电事故后瞬态特性的能力。本文利用RELAP5建立主冷却剂系统、非能动余热排出系统等,所构建节点图如图 5所示。
|
Download:
|
| 图 5 非能动余热排出系统RELAP5节点图 Fig. 5 The RELAP5 nodalization of PRHRS | |
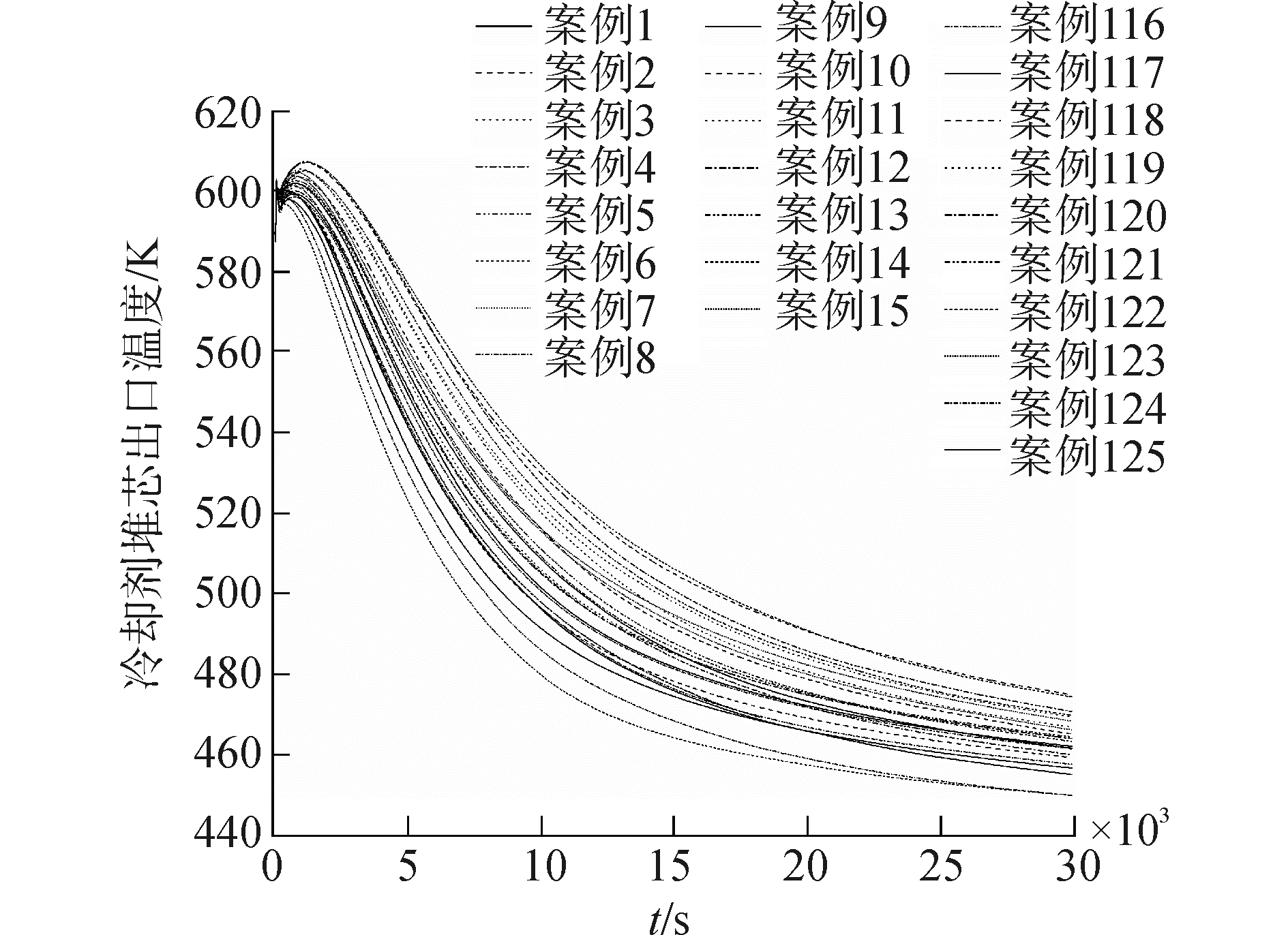
利用拉丁超立方抽样所抽取的样本参数值作为RELAP5稳态运行参数值,建立稳定运行状态作为初始工况。采用保守的事故序列:即在300 s时发生全厂断电事故,主冷却剂泵立刻停转,SG给水在断电后逐渐减少,在5 s内完全关闭,在断电后10 s紧急停堆并隔离主蒸汽管线,非能动余热排出系统在发生事故后15 s投入。进行瞬态计算分析,通过输出参数最高堆芯冷却剂出口温度值y用于训练人工神经网络。图 6列出了部分样本的计算结果,可以看出在不同的结构参数与运行状态下,堆芯冷却剂出口温度具有不同的响应特性。
|
Download:
|
| 图 6 RELAP5部分计算结果 Fig. 6 Part of RELAP5 calculation results | |
本文采用神经网络响应面法[26]进行可靠性计算。基于神经元发挥作用的方式,经过训练与反馈,使得方法具有很好的非线性拟合能力。采用RELAP5计算的结果中的110组{x1, x2, x3, x4, x5, x6, x7, x8, x9, y}作为训练集,15组作为测试集。本文中采用的隐含层为1,隐含层节点数为10。经过分析比较得知,以上结构的神经网络适合于分析本文中的问题。在训练神经网络时,由于初始迭代点的不同,每次训练结果的均方差MSE不同。训练样本100次,取MSE最小的神经网络用于热工水力程序的替代模型。根据选定的最优神经网络,以及输入参数分布范围,分别利用蒙特卡洛抽样抽取1 000、10 000、100 000、500 000、1 000 000组数据。将抽取样本数据输入到训练好的神经网络响应面中,得到输出值即冷却剂堆芯出口温度。图 7中为样本数量1 000、10 000个时神经网络的训练结果。

|
Download:
|
| 图 7 神经网络训练结果 Fig. 7 Artificial neural network training results | |
为了避免单次计算结果存在的误差,取10次计算结果的平均值作为该样本数量下可靠性的最终结果。非能动余热排出系统的物理失效概率如表 2所示。由计算结果可知,当计算次数大于100 000次时,失效概率已收敛。神经网络计算得到的非能动余热排出系统物理失效概率约为0.003 44。
| 表 2 系统物理失效概率 Table 2 System physical process failure probability |
将3.3节计算得到的物理失效概率作为底事件整合到故障树分析模型中[27]。本文中涉及的设备和部件失效概率主要来源于NUREG/CR-6928通用数据库。以非能动余热排出系统失效作为顶事件建立故障树,故障树如图 8所示。为方便分析本文做出以下假设:除PRHRS外的硬件设备失效不予考虑,且认为系统物理失效与硬件失效独立,不考虑由设备故障引入的物理现象失效概率。

|
Download:
|
| 图 8 PRHRS故障树模型 Fig. 8 Fault tree model of PRHRS | |
对非能动余热排出系统故障树定量计算,顶事件失效概率Q=4.708×10-3,最小割集及重要度如表 3所示(截取对顶事件失效重要度大于1%的割集)。由故障树计算结果可知:非能动系统物理过程失效对系统失效影响最大;PRHR止回阀失效、PRHR换热器堵塞、换热器管侧泄漏等部件失效对系统失效具有较大贡献度。可以提高对以上部件的检测与维修频率,减少关键部位的失效概率,提高系统的可靠性。
| 表 3 最小割集及重要度 Table 3 Minimal cutset and importance |
1) 利用神经网络响应面法可以很好地描述输入参数与响应值之间的非线性关系,解决了二阶多项式响应面对于复杂模型精度不够的问题,且避免了直接蒙特卡洛方法计算量过大的问题;
2) 利用故障树计算IPWR非能动余热排出系统失效概率,其中物理过程失效是导致系统失效的主要原因,重要度为73%;
3) 利用神经网络方法进行拟合计算时,失效点较少,对于失效区域的拟合精度仍有提升空间,可以考虑优化抽样方法,提高失效样本点的数目。
| [1] |
谢国锋, 何旭洪, 童节娟, 等. 响应面方法计算HTR-10余热排出系统物理过程的失效概率[J]. 物理学报, 2007, 56(6): 3192-3197. XIE Guofeng, HE Xuhong, TONG Jiejuan, et al. Calculating physical failure probability of HTR-10's residual heat removal system by response surface method[J]. Acta physica sinica, 2007, 56(6): 3192-3197. DOI:10.3321/j.issn:1000-3290.2007.06.027 (  0) 0)
|
| [2] |
MARQUÈS M, PIGNATEL J F, SAIGNES P, et al. Methodology for the reliability evaluation of a passive system and its integration into a probabilistic safety assessment[J]. Nuclear engineering and design, 2005, 235(24): 2612-2631. DOI:10.1016/j.nucengdes.2005.06.008 (  0) 0)
|
| [3] |
BURGAZZI L. Evaluation of uncertainties related to passive systems performance[J]. Nuclear engineering and design, 2004, 230(1/2/3): 93-106. (  0) 0)
|
| [4] |
BURGAZZI L. Reliability study of a special decay heat removal system of a gas-cooled fast reactor demonstrator[J]. Nuclear engineering and design, 2014, 280: 473-480. DOI:10.1016/j.nucengdes.2014.09.032 (  0) 0)
|
| [5] |
BURGAZZI L. Addressing the challenges posed by advanced reactor passive safety system performance assessment[J]. Nuclear engineering and design, 2011, 241(5): 1834-1841. DOI:10.1016/j.nucengdes.2011.02.002 (  0) 0)
|
| [6] |
MARQUÈS M, PIGNATEL J F, D'AURIA F, et al. Reliability methods for passive systems[C]//Proceedings of 2004 International Congress on Advances in Nuclear Power Plants. Pittsburgh, PA, 2004: 13-17.
(  0) 0)
|
| [7] |
NAYAK A K, JAIN V, GARTIA M R, et al. Reliability assessment of passive containment isolation system using APSRA methodology[J]. Annals of nuclear energy, 2008, 35(12): 2270-2279. DOI:10.1016/j.anucene.2008.08.011 (  0) 0)
|
| [8] |
谢国锋, 童节娟, 何旭洪, 等. 用Monte Carlo方法计算HTR-10余热排出系统物理过程的失效概率[J]. 核动力工程, 2008, 29(2): 85-87. XIE Guofeng, TONG Jiejuan, HE Xuhong, et al. Calculation of physical failure probability of HTR-10 residual heat removal system by Monte Carlo method[J]. Nuclear power engineering, 2008, 29(2): 85-87. (  0) 0)
|
| [9] |
SCHULZ T L. Westinghouse AP1000 advanced passive plant[J]. Nuclear engineering and design, 2006, 236(14/15/16): 1547-1557. (  0) 0)
|
| [10] |
WANG Baosheng, WANG Dongqing, JIANG Jin, et al. Efficient estimation of the functional reliability of a passive system by means of an improved Line Sampling method[J]. Annals of nuclear energy, 2013, 55: 9-17. DOI:10.1016/j.anucene.2012.12.015 (  0) 0)
|
| [11] |
WANG Baosheng, WANG Dongqing, JIANG Jin, et al. Efficient functional reliability estimation for a passive residual heat removal system with subset simulation based on importance sampling[J]. Progress in nuclear energy, 2015, 78: 36-46. DOI:10.1016/j.pnucene.2014.07.043 (  0) 0)
|
| [12] |
YU Yu, MA Guohang, HAO Zulong, et al. Correlation analysis for screening key parameters for passive system reliability analysis[J]. Annals of nuclear energy, 2015, 77: 23-29. DOI:10.1016/j.anucene.2014.10.035 (  0) 0)
|
| [13] |
ZIO E, PEDRONI N. Building confidence in the reliability assessment of thermal-hydraulic passive systems[J]. Reliability engineering & system safety, 2009, 94(2): 268-281. (  0) 0)
|
| [14] |
ZIO E, PEDRONI N. How to effectively compute the reliability of a thermal-hydraulic nuclear passive system[J]. Nuclear engineering and design, 2011, 241(1): 310-327. DOI:10.1016/j.nucengdes.2010.10.029 (  0) 0)
|
| [15] |
MATHEWS T S, ARUL A J, PARTHASARATHY U, et al. Integration of functional reliability analysis with hardware reliability:an application to safety grade decay heat removal system of Indian 500 MWe PFBR[J]. Annals of nuclear energy, 2009, 36(4): 481-492. (  0) 0)
|
| [16] |
RAMAKRISHNAN M. Integration of functional reliability analysis and system hardware reliability through Monte Carlo simulation[J]. Annals of nuclear energy, 2016, 95: 54-63. DOI:10.1016/j.anucene.2016.04.032 (  0) 0)
|
| [17] |
刘建阁, 彭敏俊, 蒋立国. 多用途一体化轻水堆初步设计方案和安全分析[J]. 原子能科学技术, 2009, 43(增刊1): 210-214. LIU Jian'ge, PENG Minjun, JIANG Liguo. Primary design and safety analysis of multi-application integrated light water reactor[J]. Atomic energy science and technology, 2009, 43(Suppl.1): 210-214. (  0) 0)
|
| [18] |
蒋立志, 蔡琦, 张永发. 核动力装置非能动系统可靠性及参数敏感性分析[J]. 核动力工程, 2017, 38(5): 91-95. JIANG Lizhi, CAI Qi, ZHANG Yongfa. Reliability and parameter sensitivity analysis of passive system in nuclear power plants[J]. Nuclear power engineering, 2017, 38(5): 91-95. (  0) 0)
|
| [19] |
潘晓磊, 王家群, 胡丽琴, 等. 基于响应面拟合方法中国铅基研究实验堆非能动余热排出系统可靠性分析[J]. 核技术, 2016, 39(5): 050602. PAN Xiaolei, WANG Jiaqun, HU Liqin, et al. Response-surface-fitting method based reliability analysis for passive decay heat removal system of China lead-based research reactor[J]. Nuclear techniques, 2016, 39(5): 050602. (  0) 0)
|
| [20] |
MA Guohang, YU Yu, HUANG Xiong, et al. Screening key parameters related to passive system performance based on analytic hierarchy process[J]. Annals of nuclear energy, 2015, 85: 1141-1151. DOI:10.1016/j.anucene.2015.07.032 (  0) 0)
|
| [21] |
KIRCHSTEIGER C. A new approach to quantitative assessment of reliability of passive systems[J]. Safety science, 2005, 43(10): 771-777. DOI:10.1016/j.ssci.2005.08.016 (  0) 0)
|
| [22] |
夏少雄, 王家群, 潘晓磊, 等. 中国铅基研究堆非能动余热排出系统可靠性分析[J]. 核技术, 2015, 38(2): 020605. XIA Shaoxiong, WANG Jiaqun, PAN Xiaolei, et al. Reliability analysis of passive decay heat removal system of China lead-based research reactor[J]. Nuclear techniques, 2015, 38(2): 020605. (  0) 0)
|
| [23] |
BUCKNOR M, GRABASKAS D, BRUNETT A J, et al. Advanced reactor passive system reliability demonstration analysis for an external event[J]. Nuclear engineering and technology, 2017, 49(2): 360-372. DOI:10.1016/j.net.2017.01.005 (  0) 0)
|
| [24] |
HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability engineering & system safety, 2003, 81(1): 23-69. (  0) 0)
|
| [25] |
XIA Genglei, PENG Minjun, DU Xue. Calculation analysis on the natural circulation of a passive residual heat removal system for IPWR[J]. Annals of nuclear energy, 2014, 72: 189-197. DOI:10.1016/j.anucene.2014.02.018 (  0) 0)
|
| [26] |
张矾, 崔震华, LEE J C. 用人工神经网络方法进行非能动安全壳冷却系统可靠性分析[J]. 核科学与工程, 2004, 24(1): 44-48, 23. ZHANG Fan, CUI Zhenhua, LEE J C. Reliability quantification of PCCS through artificial neural network algorithm[J]. Chinese journal of nuclear science and engineering, 2004, 24(1): 44-48, 23. DOI:10.3321/j.issn:0258-0918.2004.01.009 (  0) 0)
|
| [27] |
郭海宽, 赵新文, 蔡琦, 等. AP1000非能动余热排出系统可靠性与概率安全评价模型的融合[J]. 核动力工程, 2017, 38(6): 9-13. GUO Haikuan, ZHAO Xinwen, CAI Qi, et al. Integrating reliability of passive residual heat removal system for AP1000 into probabilistic safety assessment[J]. Nuclear power engineering, 2017, 38(6): 9-13. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


