2. 中国电力科学研究院, 北京 100055
2. China Electric Power Research Institute, Beijing 100055, China
在海流作用下,海洋立管、海上浮式装置的系泊缆等圆柱结构通常在横流向(cross-flow, CF)和顺流向(in-line, IL)发生涡激振动(vortex-induced vibration, VIV)。VIV与海洋工程中圆柱结构的疲劳损伤密切相关,长期以来,其发生机理及振动特性已得到广泛研究[1-4]。
由于涡激振动横流向振幅更大,圆柱VIV的大多数研究中,主要关注CF振动[5]。Jauvtis和Williamson[6]表明质量比m* < 6.0时(m*=4 ms/ρπD2, 结构质量与排开流体质量之比),圆柱IL振动不可忽略。谷家扬等[7]研究了刚性圆柱VIV特性,亦表明圆柱IL振动的影响十分显著。海洋工程中的圆柱结构质量比较小[8],结构IL振动不可忽略,应引起广泛关注。徐万海等[9]研究了考虑管土作用的海底悬跨管道纯顺流向VIV特性。Chaplin等[10]开展柔性圆柱VIV实验,IL控制模态和响应频率一般为CF的2倍。Trim等[11]研究了柔性圆柱VIV疲劳特性,虽然IL振动位移较小,但其频率较高,造成的疲劳损伤与横流向位于同一数量级。
目前,圆柱VIV预报主要依靠经验模型,合理选取流体力系数是涡激振动预报成功与否的关键。研究发现几乎所有模型预报结果均与实验结果存在差异,IL振动的差异更为显著[12]。研究圆柱顺流向VIV流体力特性,对提高IL响应预报精度具有重要意义。Aronsen[13]测量了刚性圆柱纯顺流向振动的流体力,并绘制了流体力系数云图。Yin等[14]通过刚性圆柱VIV实验表明,结构CF和IL同时振动时,IL流体力系数显著增大。Sanaati等[15]测量了柔性圆柱VIV流体力系数,研究了脉动阻力系数与轴向力之间的关系。唐国强[16]采用有限元法识别了柔性圆柱VIV流体力系数,表明:IL流体力系数的大小与力和位移之间的相位差有关。Song等[17]逆向求解柔性圆柱VIV的流体力,脉动阻力系数与IL位移和频率密切相关,与刚性圆柱差异显著,附加质量系数沿圆柱轴向分布不均匀,位移节点处出现突变现象。
为深入了解圆柱顺流向VIV特性并准确预报VIV响应,关于IL流体力的识别及流固耦合机理研究有待进一步开展。本文实验观测圆柱VIV响应特性,根据模态分析法将IL应变信息转化为位移信息,并将位移作为输入参数,建立有限元模型逆向求解IL流体力,通过最小二乘法获得脉动阻力系数和附加质量系数。结合计算结果,研究圆柱顺流向VIV的流固耦合机理,通过振动特性、流体力特性分析,阐述顺流向VIV及流体力的特有规律。
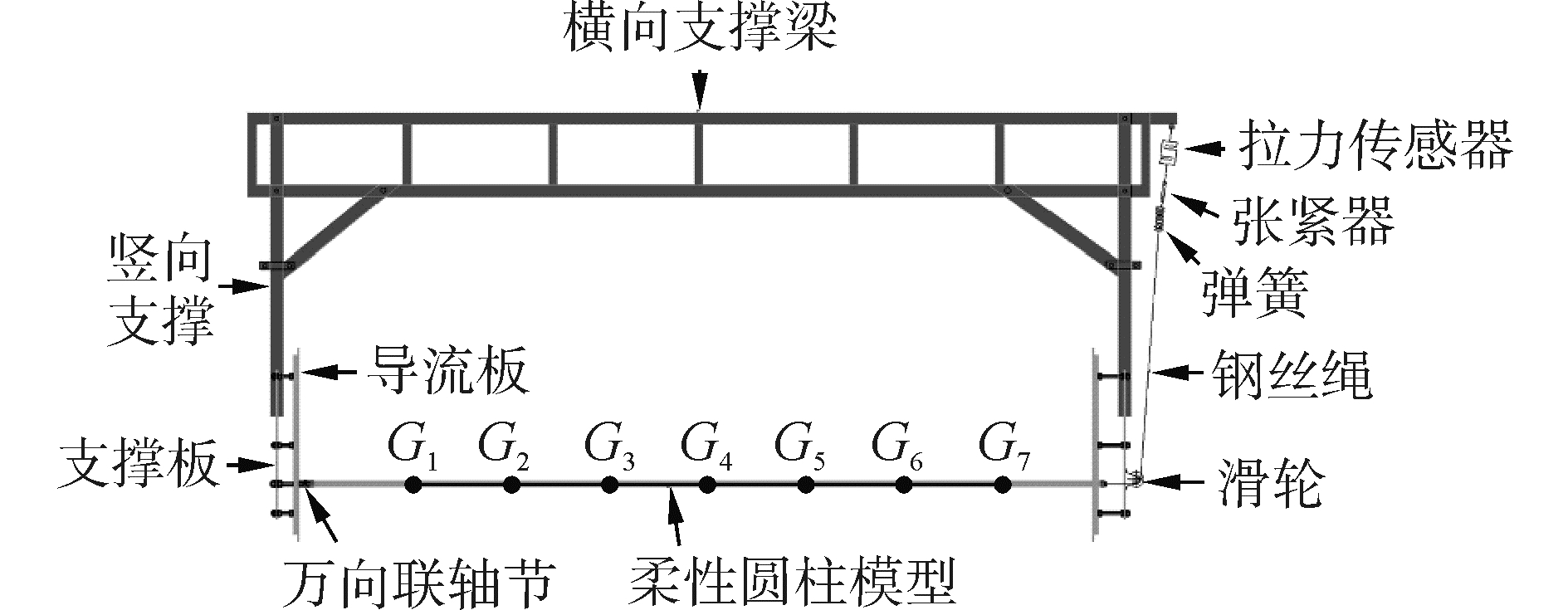
1 实验设计为了研究圆柱顺流向涡激振动响应及流体力特性,设计了室内模型实验。实验在天津大学水利工程仿真与安全国家重点实验室的拖曳水池(长137.0 m,宽7.0 m,深3.3 m)中开展。主要实验装置如图 1所示。
|
Download:
|
| 图 1 实验装置示意图 Fig. 1 The schematic diagram of the experimental equipment | |
柔性圆柱模型内芯为铜管,等间距布置7个测点,从左至右依次记为G1~G7,每个测点沿来流方向布置一组应变片,采用半桥接法测量IL振动的应变信息,并用薄硅胶膜进行水密和绝缘防护。铜管外部附有硅胶管,保护测量导线和应变片,确保模型外部光滑。模型一端通过万向联轴节固定于支撑板,另一端通过钢丝绳连接弹簧、张紧器和拉力传感器,调节并测量模型轴向力。横向支撑梁可固定于拖车底部,使圆柱模型完全浸没在距水池自由表面1.0 m深处。
拖车匀速拖动圆柱模型模拟均匀来流条件,速度范围为0.05~1.00 m/s,间隔0.05 m/s。拖车速度稳定后开始采样,采样频率为100 Hz,采样时间为50 s。拖曳实验开始前,分别在空气和静水中开展自由衰减实验,测量得到圆柱结构的固有频率和阻尼比。实验中的圆柱模型主要参数如表 1所示。
| 表 1 圆柱模型主要参数 Table 1 The principal parameters of the cylinder model |
为了确保实验数据稳定可靠,本文去除了采样区间中前10 s和后10 s的数据,最终得到完全稳定的区间为30 s长的数据。对该部分数据进行滤波处理,以消除噪声干扰。采用快速傅里叶变换(FFT),对实验数据带通滤波,滤波带宽为1.0~40.0 Hz,即滤除低于1.0 Hz的拖车等机械装置的低频干扰和高于40.0 Hz的高频电测干扰。自由衰减实验中测得的结构前七阶静水固有频率位于2.0~25.0 Hz,1.0~40.0 Hz的滤波带宽不会造成有效振动信息丢失。
柔性圆柱在来流作用下受到拖曳力,产生一定的挠曲变形,如图 2所示。顺流向位移xIL可以表示为平均位移x和VIV位移x之和:
| $ {x_{{\rm{IL}}}} = x + \bar x $ | (1) |

|
Download:
|
| 图 2 柔性圆柱均匀来流作用下顺流向位移示意图 Fig. 2 IL displacement of the flexible cylinder in uniform flow | |
同理,IL应变εIL也可以表示为平均位移产生的应变ε和VIV位移产生的应变ε之和:
| $ {\varepsilon _{{\rm{IL}}}} = \varepsilon + \bar \varepsilon $ | (2) |
平均位移不随时间变化,因此只关注VIV位移。从应变εIL中去除平均位移产生的应变ε,只对VIV位移产生的应变ε进行分析。
模态分析法是柔性圆柱涡激振动实验数据处理的常用方法,通过模态分解可根据结构不同离散测点的应变信息,重构任一点的振动位移[16, 18]。圆柱顺流向VIV位移可表示为
| $ x\left( {z,t} \right) = \sum\limits_{n = 1}^S {{w_n}\left( t \right){\varphi _n}\left( z \right)} $ | (3) |
式中:wn(t)为权重系数,n为圆柱结构的模态阶次,S为确定结构位移所需的最高模态数目。在此次实验中,根据结构的固有频率和最高来流速度可大致判断出结构振动最高激发6阶模态。因此,参与计算的最高模态数S应大于6。但实验中布置了7个测点,为保证求解,S不能大于测点数。所以,S取为7。
| $ {\varphi _n}\left( z \right) = \sin \frac{{n{\rm{ \mathsf{ π} }}z}}{L} $ | (4) |
根据圆柱曲率计算公式:
| $ \frac{1}{\kappa } = \frac{{x''}}{{{{\left( {1 + {{\left( {x'} \right)}^2}} \right)}^{3/2}}}} $ | (5) |
其中κ=R/ε (z, t),R为结构半径,ε (z, t)为结构应变,x′和x″分别表示x对z求一阶和二阶偏导数。由于式(5)中含有x′的项为小量,可忽略不计,得到如下公式:
| $ \frac{\varepsilon }{R} = x''\left( {z,t} \right) = - \sum\limits_{n = 1}^S {{{\left( {\frac{{n{\rm{ \mathsf{ π} }}}}{L}} \right)}^2}{w_n}\left( t \right)\sin \frac{{n{\rm{ \mathsf{ π} }}z}}{L}} $ | (6) |
由式(6)计算得到权重系数后,根据式(3)即可获得结构IL位移。采用模态法重构振动位移时,不用考虑模态之间的竞争,只需确保参与计算的最高模态数S大于结构所能激发的最高模态阶次。结构的模态竞争能通过计算出的权重系数反映出来[10]。
3 流体力计算柔性圆柱顺流向VIV的控制方程采用欧拉-伯努力梁模型:
| $ {\rm{EI}}\frac{{{\partial ^4}x}}{{\partial {z^4}}} - T\frac{{{\partial ^2}x}}{{\partial {z^2}}} + c\frac{{\partial x}}{{\partial t}} + m\frac{{{\partial ^2}x}}{{\partial {t^2}}} = {f_x} $ | (7) |
式中:EI为结构的弯曲刚度,T为圆柱模型端部轴向力,c为结构阻尼,m为结构单位长度质量,t表示时间,IL为流体力fx中不包含平均拖曳力[16-17]。
将结构离散为若干单元的组合,结合边界条件,式(7)可转化为有限元形式:
| $ \mathit{\boldsymbol{M\ddot X}} + \mathit{\boldsymbol{C\dot X}} + \mathit{\boldsymbol{KX}} = {\mathit{\boldsymbol{F}}_x} $ | (8) |
式中:M为质量矩阵,C为结构阻尼矩阵。K是刚度矩阵,为弯曲刚度矩阵KE和由轴向力产生的刚度矩阵KP之和。Fx顺流向流体载荷矩阵,X为顺流向振动响应矩阵,
| $ \mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}} $ | (9) |
式中α和β为常系数:
| $ \left\{ \begin{array}{l} \alpha = \frac{{2{\omega _j}{\omega _k}\left( {{\xi _j}{\omega _k} - {\xi _k}{\omega _j}} \right)}}{{{\omega _k}^2 - {\omega _j}^2}}\\ \beta = \frac{{2\left( {{\xi _k}{\omega _k} - {\xi _j}{\omega _j}} \right)}}{{{\omega _k}^2 - {\omega _j}^2}} \end{array} \right. $ | (10) |
式中:ωk和ωj分别为第k阶和第j阶模态的圆频率,ξk和ξj分别为第k阶和第j阶模态的阻尼比,通过空气中的自由衰减实验获得。根据式(8)可得IL流体载荷矩阵Fx,进而求出IL流体力fx。
顺流向流体力fx可分解为与速度同相位的脉动阻力和与加速度同相位的附加质量力[13],即
| $ {f_x} = \frac{{\rho Dl}}{{2\sqrt 2 {{\dot x}_{rms}}}}{U^2}{C_D}\dot x - \frac{1}{4}\rho {\rm{ \mathsf{ π} }}{D^2}l{C_a}\ddot x $ | (11) |
式中:CD脉动阻力系数,Ca附加质量系数,ρ流体力密度,D圆柱外径,l结构单元长度,U来流速度,
| $ {C_D} = \frac{{2\sqrt 2 {{\dot x}_{rms}}}}{{\rho Dl{U^2}}}\frac{{\left( {{Q_2}{Q_5} - {Q_3}{Q_4}} \right)}}{{\left( {{Q_2}^2 - {Q_1}{Q_4}} \right)}} $ | (12) |
| $ {C_a} = \frac{4}{{{\rm{ \mathsf{ π} }}\rho {D^2}l}}\frac{{\left( {{Q_1}{Q_5} - {Q_2}{Q_3}} \right)}}{{\left( {{Q_2}^2 - {Q_1}{Q_4}} \right)}} $ | (13) |
式中:
式中N为采样点的个数。
IL位移与流体力之间的相位差ψ为
| $ \psi = \arctan \left( {\frac{{\rho Dl{U^2}{C_D}\dot x/2\sqrt 2 {{\dot x}_{rms}}}}{{ - \rho {\rm{ \mathsf{ π} }}{D^2}l{C_a}\ddot x/4}}} \right) $ | (14) |
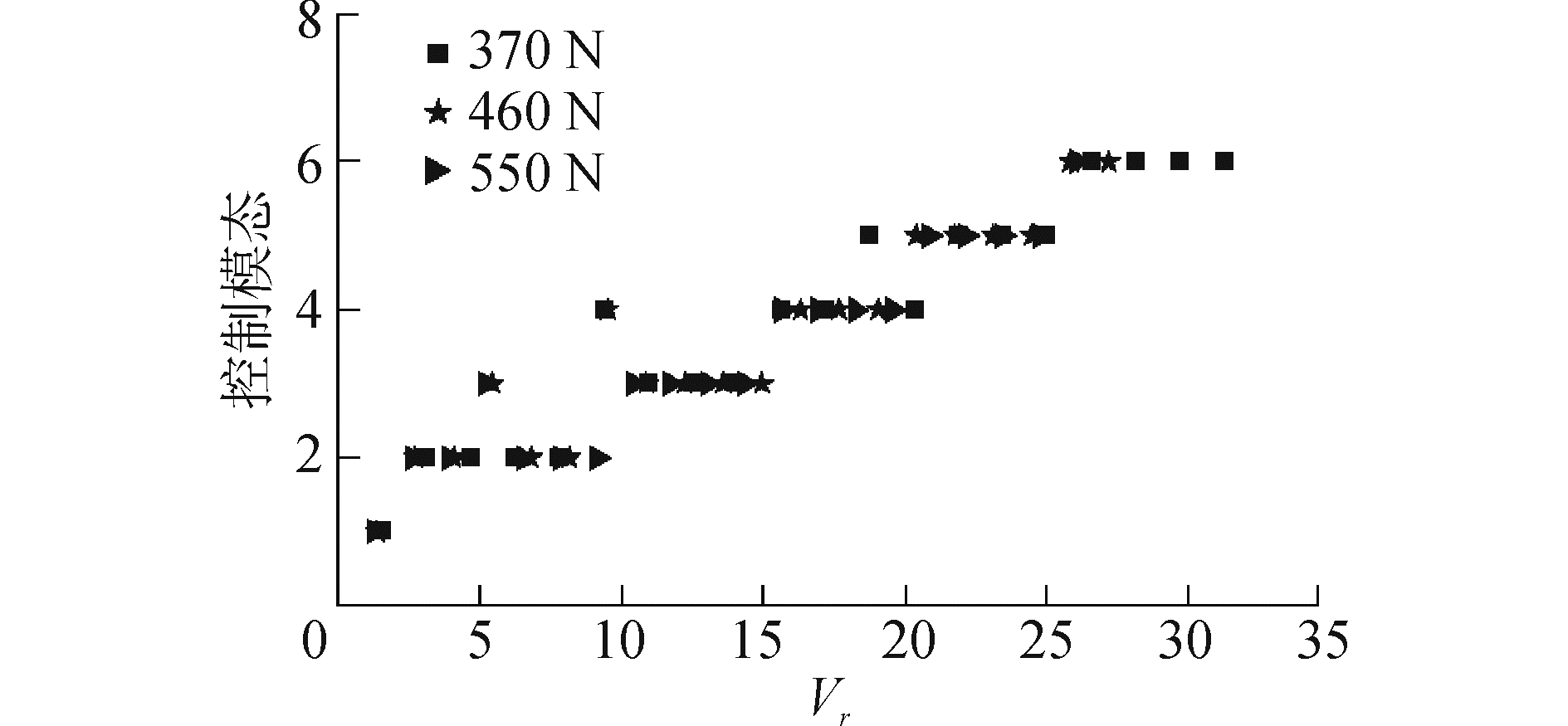
顺流向VIV的控制模态如图 3所示。横轴为约化速度Vr (Vr=U/f1D, f1为结构静水中的1阶固有频率),随Vr增大,IL控制模态呈阶梯状上升,最高可达6阶。Vr≈5.0时,轴向力T为460、550 N的工况控制模态由2阶跳跃至3阶;Vr≈9.0时,轴向力T分别为370、460 N的工况控制模态由2阶跳跃至4阶;Vr≈18.0时,轴向力T=370 N的工况控制模态由4阶跳跃至5阶。上述控制模态跳跃现象表明顺流向VIV存在激烈的模态竞争。涡激振动通常是多模态共同参与,在跳跃点附近,模态竞争较弱,而跳跃点处模态竞争过于激烈,导致上述的跳跃现象发生。
|
Download:
|
| 图 3 顺流向控制模态 Fig. 3 The dominated mode in IL direction | |
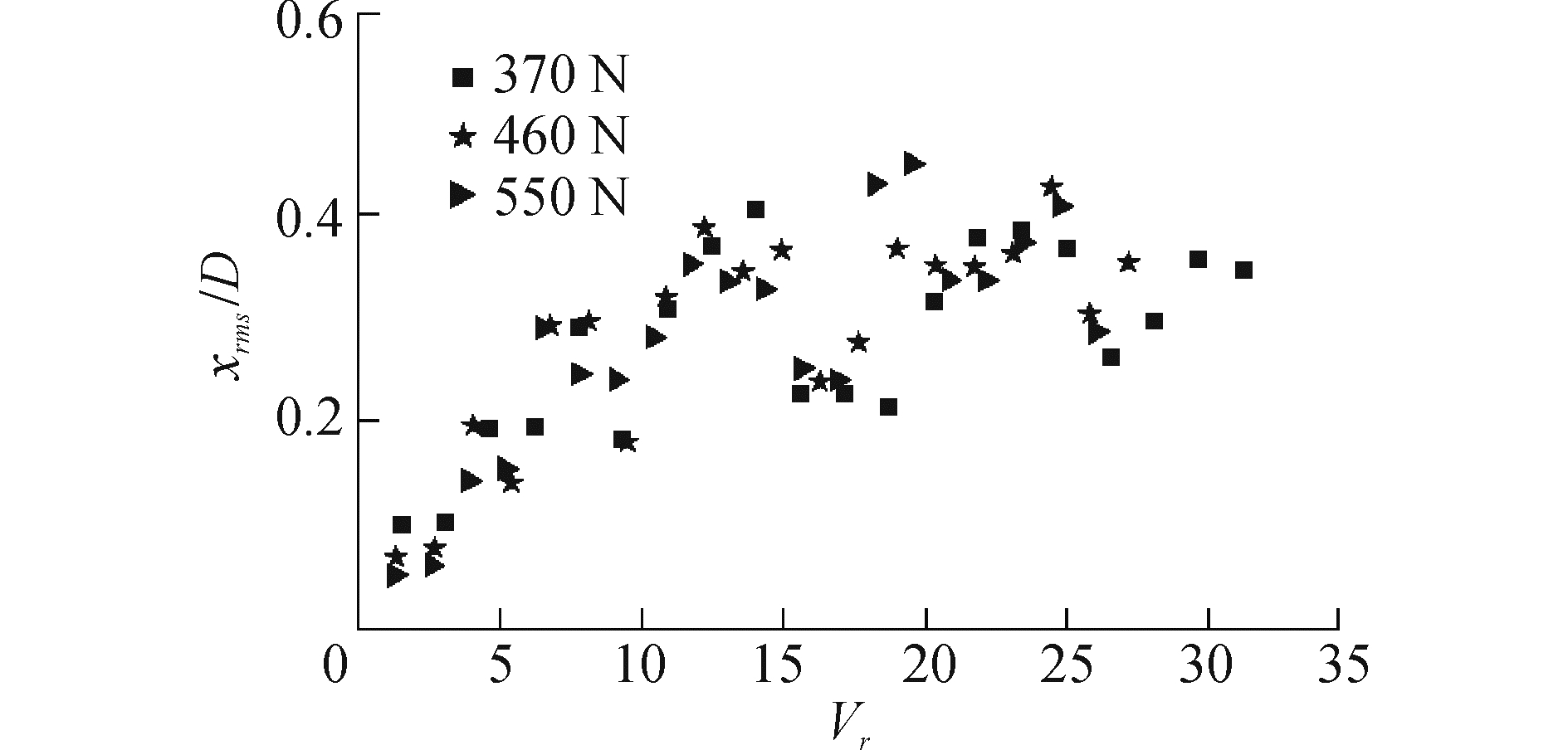
图 4为IL最大位移均方根随Vr变化情况。IL最大位移均方根的最大值为0.45D,一般CF振动位移的最大值约为1.50D,IL位移远小于CF位移。IL振动同样产生“锁定”现象,在模态控制区,IL位移显著增大,出现极值点,如图 4中Vr≈8.0、14.0、25.0时。在不同控制模态转换区域,IL位移急剧降低,如Vr≈9.0、15.0、26.0时。随着模态逐渐升高,IL位移的极值逐渐增大。2阶模态IL位移极值为0.30,进入3阶模态,极值为0.40,大于2阶模态的极值。当控制模态继续增大,5阶模态极值为0.43,极值点的大小趋于平稳。
|
Download:
|
| 图 4 顺流向位移最大均方根 Fig. 4 Max RMS of IL displacement | |
测点处位移时间历程曲线(不包含平均位移)和频谱如图 5所示,选取的工况为T=460 N,Vr=12.2,控制模态为3阶。IL振动呈稳定状态,不同测点处的振幅差别较大。由于此工况下控制模态为3阶,所以G3和G5测点处的位移较小。由频谱图可知,控制频率为9.1 Hz,同时IL振动出现幅值较小的低阶和高阶频率成份,分别为5.4和14.5 Hz,表明顺流向VIV具有多模态共同参与的特性。

|
Download:
|
| 图 5 测点处顺流向位移时间历程曲线和频谱图(T=460 N Vr=12.2) Fig. 5 The history and spectra of the IL displacement at measurement points (T=460 N Vr=12.2) | |
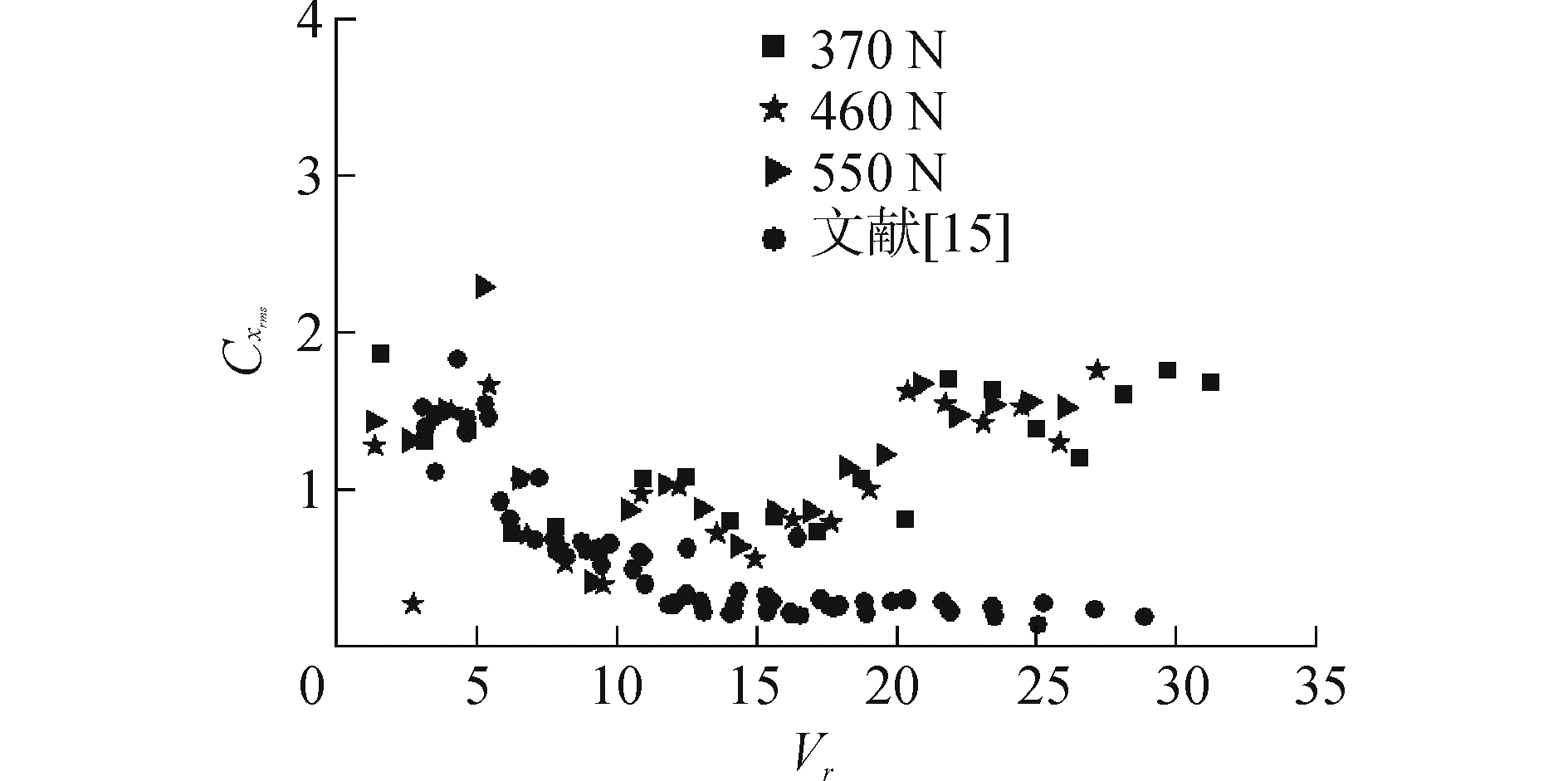
顺流向流体力合力系数Cx(=2fx/ρDU2)均方根如图 6所示。Sanaati等[15]实验测量了顺流向流体力合力,其选用了质量比为1.0,长径比为200的圆柱模型,模型的刚度主要通过轴向拉力提供,雷诺数范围为1 000~16 000。Sanaati等[15]并未给出IL响应位移的结果,仅给出了IL响应频率和流体力合力系数的结果,相应的合力系数均方根绘制于图 6中。控制模态较低时(Vr < 10.0),IL合力系数与文献[15]的结果基本吻合,Vr>10.0时其结果远小于本实验的结果,原因可能是因为文献[15]的模型刚度主要由轴向力控制。对比图 4和图 6可知,IL合力系数在模态控制区亦出现极值,而且早于IL位移极值出现,例如:3阶模态,合力系数的极值出现于Vr≈12.0时,位移的极值出现于Vr≈14.0时;5阶模态,合力系数的极值出现于Vr≈22.0时,位移的极值出现于Vr≈26.0时。不同控制模态转换间歇,合力系数与位移同时降低。由此可知,在模态控制区,IL位移随Vr的变化与合力系数相比具有一定的迟滞效应。
|
Download:
|
| 图 6 顺流向流体力合力系数均方根 Fig. 6 RMS of IL total fluid force coefficients | |
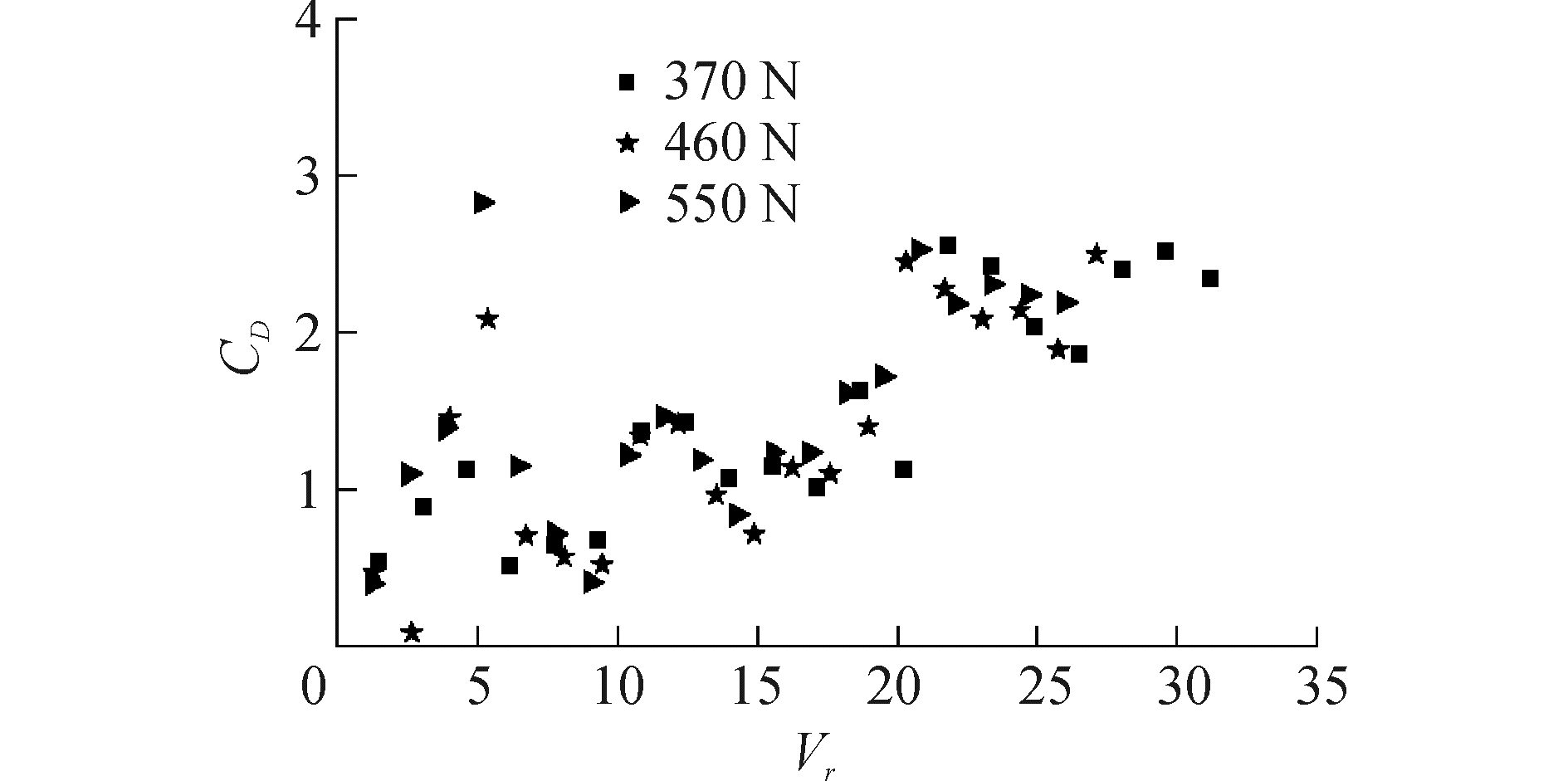
脉动阻力系数如图 7所示。脉动阻力系数表示结构与流体之间的能量传递,正值表明结构从流体吸收能量。由图 7可知,柔性圆柱结构IL振动需要一直从流体摄入能量,在模态控制区吸收的能量较多,不同模态转换间歇吸收的能量较少。上述现象产生的原因在于模态控制区,圆柱振幅增大;而在模态转换间隙,振幅迅速减小。5阶模态的脉动阻力系数大于3阶模态的结果,但由图 4可知3阶和5阶模态下的极值大小基本相同。由此可知,脉动阻力系数除与位移相关,还受响应频率的影响,高阶模态响应频率升高,圆柱振动需吸收较多能量,脉动阻力系数显著增大。图 7中,T分别为460、550 N工况下Vr≈5.0时脉动阻力系数显著增大,原因在于此约化速度IL振动出现模态跳跃现象,如图 3所示,控制频率急剧增大,从而导致脉动阻力系数升高。
|
Download:
|
| 图 7 脉动阻力系数随约化速度变化规律 Fig. 7 Vary drag coefficients versus reduced velocity | |
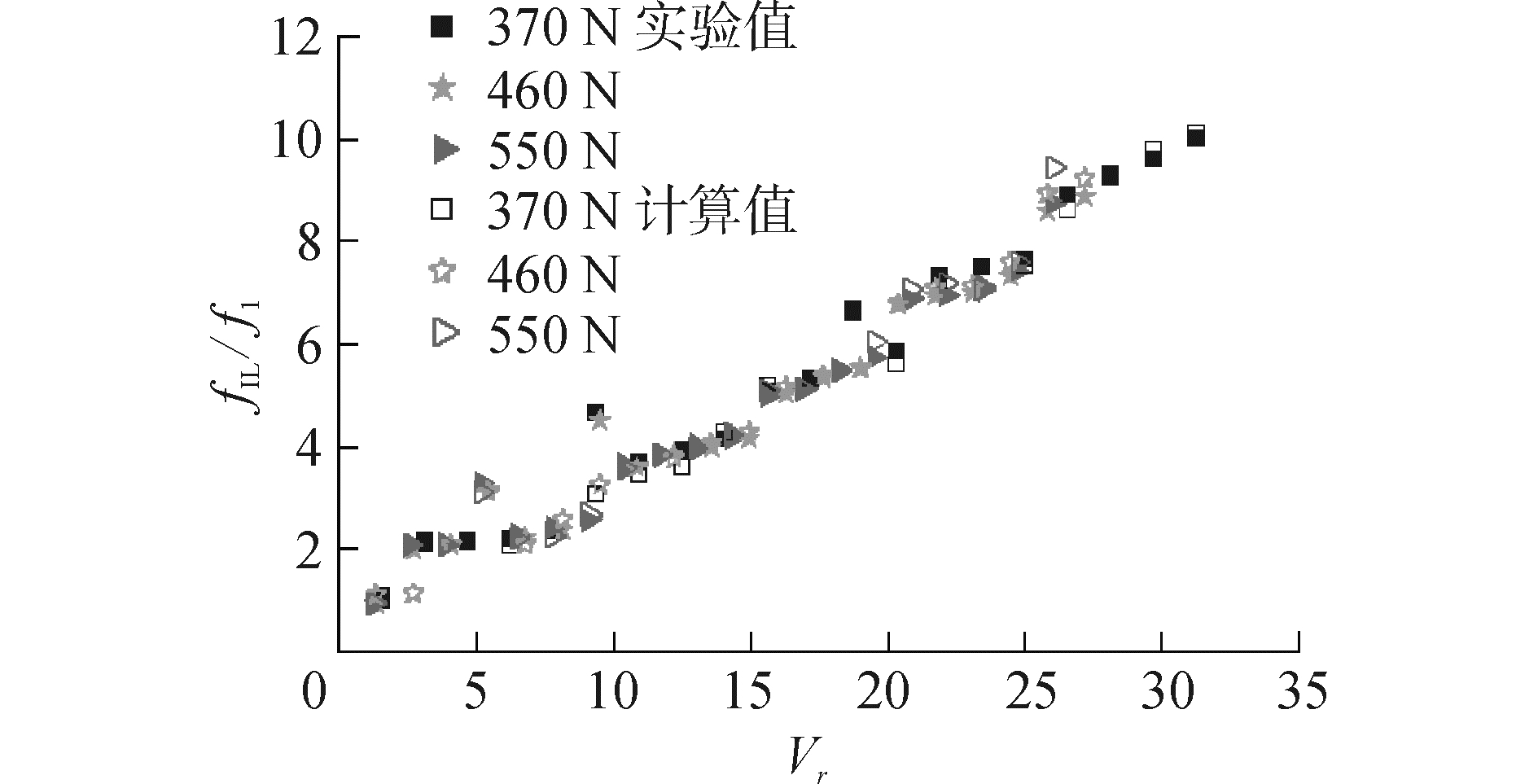
图 8和图 9分别给出了附加质量系数和无量纲控制频率。附加质量系数与控制频率关系密切。模态控制区,控制频率随Vr平缓增大,附加质量系数则呈相反变化,随Vr逐渐减小至0左右。不同模态转换间歇,控制频率阶梯上升,而附加质量系数亦突然增大。进入下一阶模态又重复上述变化。随着控制模态逐渐升高,附加系数在模态转换间歇的增长幅度降低,在模态控制区的变化趋势缓和。根据附加质量系数:
| $ {f_n} = \frac{n}{{2L}}\sqrt {\frac{T}{{{m_s} + {m_a}}} + {{\left( {\frac{{n\pi }}{L}} \right)}^2}\frac{{EI}}{{{m_s} + {m_a}}}} $ | (15) |

|
Download:
|
| 图 8 附加质量系数随约化速度变化规律 Fig. 8 The added mass coefficients versus reduced velocity | |
|
Download:
|
| 图 9 无量纲控制频率 Fig. 9 Dimensionless dominate frequency | |
计算了柔性圆柱VIV过程中的固有频率。n为模态阶次,ma(=CaρπD2/4)为附加质量,可由附加质量系数计算。由图 9可知,计算得到的结构固有频率在模态控制区与控制频率吻合较好,表明“锁定”现象出现时,泄涡频率锁定在结构固有频率附近。
对比图 4和图 7可知,在模态控制区,响应位移逐渐增大至极值,而脉动阻力系数则迅速达到极值后逐渐降低。模态控制区,IL振动启动时脉动阻力系数达到极值,表明结构从流体吸收较多的能量。随着Vr增大,IL位移逐渐增大,脉动阻力系数逐渐减小,表明结构获取的能量减少,从而限制位移持续增大。脉动阻力系数降低至极小值,此时IL位移急剧降低,IL振动转入下一阶模态。上述过程表明顺流向VIV具有自限制特性,随着振幅逐渐增大,圆柱IL振动使脉动阻力减小,从而抑制振幅持续上升。
4.3 顺流向流固耦合机制图 8和图 9表明,在模态控制区,响应频率逐渐升高,附加质量系数逐渐降低。虽然随着Vr增大,漩涡脱落频率(大致与IL振动响应频率相等)逐步升高,但结构振动使周围附加水体质量减小,导致结构固有频率升高,使其接近响应频率。结构IL振动使响应频率持续“锁定”在自身固有频率附近,造成振幅显著增大,表明顺流向VIV具有自激励特性。
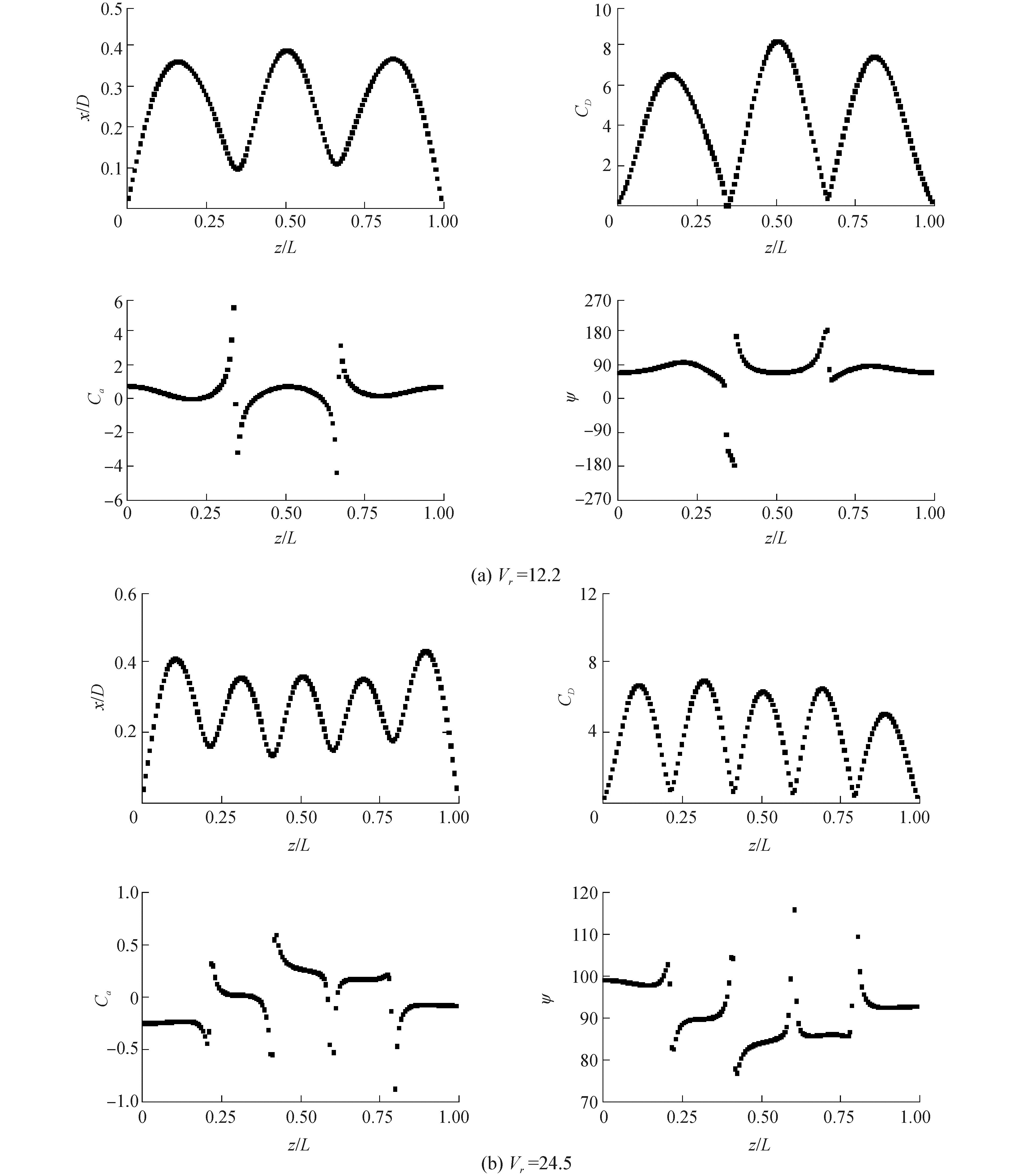
为深入分析顺流向流固耦合特性,绘制了IL位移均方根、流体力系数以及位移与流体力间相位差的轴向分布图,如图 10所示。图 10(a)中的实验工况为轴向力T=460 N,约化速度Vr=12.2,控制模态为3阶。IL位移均方根出现3个极大值点和2个极小值点,脉动阻力系数的轴向分布与位移具有高度的一致性,位移取得极小值时,脉动阻力系数接近于零。附加质量系数在位移节点处突变,随位移的变化而变化。脉动阻力系数和附加质量系数的大小与流体力和位移之间的相位差密切相关。相位差轴向分布不均匀,除位移节点处,整体位于45°~90°,此时附加质量系数均为正值,并随相位差的变化而变化。位移节点处,相位差突变为-180°或180°,此时附加质量系数产生突变,脉动阻力系数基本为零。
|
Download:
|
| 图 10 顺流向位移均方根、流体力系数及相位差的轴向分布 Fig. 10 The axial distribution of IL displacement RMS, fluid force coefficients and phases (T=460 N) | |
图 10(b)中实验工况的轴向力T=460 N,约化速度Vr=24.5,控制模态为5阶。位移均方根出现5个极大值点和4个极小值点。与图 10类似,脉动阻力系数与位移的轴向分布基本相同。附加质量系数在位移节点处产生突变,局部区域附加质量系数保持平稳,不随位移发生变化。相位差位于70°~120°,整体保持平稳,仅在位移节点处突变。相位差等于90°时,附加质量系数接近于零,小于90°时,附加质量系数为正值,反之为负值。由于位移节点处的相位差不等于-180°或180°,所以脉动阻力系数并不为零。脉动阻力系数和附加质量系数均受流体力与位移间相位差的影响,柔性圆柱顺流向VIV问题仍需关注此相位差。
5 结论1) 模态控制区,IL位移逐渐增大,脉动阻力系数逐步减小,顺流向VIV具有自限制特性。高阶控制模态,响应频率较高,脉动阻力系数显著增大。附加质量系数在模态控制区逐渐减小,结构固有频率增大,使响应频率“锁定”在固有频率附近,体现了顺流向VIV的自激励特性。
2) 脉动阻力系数的轴向分布与IL位移均方根具有高度一致性,取得极值点的位置基本相同。附加质量系数在位移节点处突变,响应频率较高时,附加质量系数在局部区域保持平稳。IL位移与流体力间的相位差与脉动阻力系数和附加质量系数密切相关,是顺流向VIV流固耦合作用中重要参数。
本文的研究工作弥补了圆柱顺流向VIV研究方面的不足,相关研究成果可为海洋工程中圆柱结构的设计提供必要的理论支持。然而,本文仅重点研究了IL振动控制频率下的流体力特性,柔性圆柱VIV存在多模态共存现象,除控制频率外,IL振动还包括其他频率成分,多频成分下的流体力对IL振动的影响仍有待进一步研究。
| [1] |
SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(4): 389-447. DOI:10.1016/j.jfluidstructs.2004.02.005 (  0) 0)
|
| [2] |
WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations[J]. Journal of wind engineering and industrial aerodynamics, 2008, 96(6/7): 713-735. (  0) 0)
|
| [3] |
徐万海, 马烨璇, 罗浩, 等. 小倾角倾斜柔性圆柱涡激振动实验研究[J]. 哈尔滨工程大学学报, 2017, 38(2): 195-200. XU Wanhai, MA Yexuan, LUO Hao, et al. Vortex-induced vibration of an inclined flexible cylinder with a small yaw angle[J]. Journal of Harbin Engineering University, 2017, 38(2): 195-200. (  0) 0)
|
| [4] |
及春宁, 邢国源, 张力, 等. 倾斜流作用下柔性立管涡激振动的数值模拟[J]. 哈尔滨工程大学学报, 2018, 39(2): 324-331. JI Chunning, XING Guoyuan, ZHANG Li, et al. Numerical simulations of vortex-induced vibration of flexible riser subjected to inclined flow[J]. Journal of Harbin Engineering University, 2018, 39(2): 324-331. (  0) 0)
|
| [5] |
KHALAK A, WILLIAMSON C H K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of fluids and structures, 1999, 13(7/8): 813-851. (  0) 0)
|
| [6] |
JAUVTIS N, WILLIAMSON C H K. Vortex-induced vibration of a cylinder with two degrees of freedom[J]. Journal of fluids and structures, 2003, 17(7): 1035-1042. DOI:10.1016/S0889-9746(03)00051-3 (  0) 0)
|
| [7] |
谷家扬, 杨琛, 朱新耀, 等. 质量比对圆柱涡激特性的影响研究[J]. 振动与冲击, 2016, 35(4): 134-140. GU Jiayang, YANG Chen, ZHU Xinyao, et al. Influences of mass ratio on vortex induced vibration characteristics of a circular cylinder[J]. Journal of vibration and shock, 2016, 35(4): 134-140. (  0) 0)
|
| [8] |
HUERA-HUARTE F J, BANGASH Z A, GONZALEZ L M. Towing tank experiments on the vortex-induced vibrations of low mass ratio long flexible cylinders[J]. Journal of fluids and structures, 2014, 48: 81-92. DOI:10.1016/j.jfluidstructs.2014.02.006 (  0) 0)
|
| [9] |
徐万海, 谢武德, 彭碧瑶, 等. 考虑管土作用悬跨管道纯顺流向涡激振动研究[J]. 哈尔滨工程大学学报, 2016, 37(9): 1184-1189. XU Wanhai, XIE Wude, PENG Biyao, et al. Study on pure in-line vortex-induced vibrations of free-spanning pipeline considering pipe-soil interaction at shoulders[J]. Journal of Harbin Engineering University, 2016, 37(9): 1184-1189. (  0) 0)
|
| [10] |
CHAPLIN J R, BEARMAN P W, HUARTE F J H, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current[J]. Journal of fluids and structures, 2005, 21(1): 3-24. DOI:10.1016/j.jfluidstructs.2005.04.010 (  0) 0)
|
| [11] |
TRIM A D, BRAATEN H, LIE H, et al. Experimental investigation of vortex-induced vibration of long marine risers[J]. Journal of fluids and structures, 2005, 21(3): 335-361. DOI:10.1016/j.jfluidstructs.2005.07.014 (  0) 0)
|
| [12] |
CHAPLIN J R, BEARMAN P W, CHENG Y, et al. Blind predictions of laboratory measurements of vortex-induced vibrations of a tension riser[J]. Journal of fluids and structures, 2005, 21(1): 25-40. DOI:10.1016/j.jfluidstructs.2005.05.016 (  0) 0)
|
| [13] |
ARONSEN K H. An experimental investigation of in-line and combined in-line and cross-flow vortex induced vibrations[D]. Trondheim: Norwegian University of Science and Technology, 2007: 39-114.
(  0) 0)
|
| [14] |
YIN Decao, LARSEN C M. On determination of VIV coefficients under shear flow condition[C]//Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, 2010: 547-556.
(  0) 0)
|
| [15] |
SANAATI B, KATO N. Vortex-induced vibration (VIV) dynamics of a tensioned flexible cylinder subjected to uniform cross-flow[J]. Journal of marine science and technology, 2013, 18(2): 247-261. DOI:10.1007/s00773-012-0204-z (  0) 0)
|
| [16] |
唐国强.立管涡激振动数值模拟方法及物理模型实验[D].大连: 大连理工大学, 2011: 125-141. TANG Guoqiang. A study on numerical and experimetal investigation into vortex-induced vibration of marine risers[D]. Dalian: Dalian University of Technology, 2011: 125-141. (  0) 0)
|
| [17] |
SONG Leijian, FU Shixiao, CAO Jing, et al. An investigation into the hydrodynamics of a flexible riser undergoing vortex-induced vibration[J]. Journal of fluids and structures, 2016, 63: 325-350. DOI:10.1016/j.jfluidstructs.2016.03.006 (  0) 0)
|
| [18] |
LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J]. Journal of fluids and structures, 2006, 22(4): 557-575. DOI:10.1016/j.jfluidstructs.2006.01.002 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


