2. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001;
3. 北京系统工程研究院 水声对抗技术重点实验室, 北京 100000
2. Science and Technology on Underwater Acoustic Laboratory, Harbin Engineering University, Harbin 150001, China;
3. Key Laboratory of Underwater Acoustic Antagonizing, Beijing Institute of Systems Engineering, Beijing, 100000, China
近年来水声通信成为了无线通信中一个比较热门的研究方向。而海洋信道是一个多途效应严重、可利用带宽有限、海洋环境噪声大、不均匀介质折射、衰落严重、快速时变和多普勒效应严重的复杂信道,可以说是无线信道中最为复杂的一种信道[1]。要实现远程、高速、稳健的水声通信仍具有巨大的挑战性。
水声信道的多途效应导致水声通信中产生严重的码间干扰,严重时甚至导致通信链的中断。判决反馈均衡器(decision feedback equalization, DFE)相比于线性均衡器,其增加了判决反馈回路,能根据已经检测判决出来的符号信息估计出过去时刻信息对当前时刻信息的干扰并通过反馈回路反馈到均衡器中消除掉,有效地抑制信道多途效应导致的码间干扰。这在时不变信道中能够取得较好的均衡效果。但是由于受海面波浪、洋流等不确定因素的影响,水声信道是随时间随机变化的随机时变信道,这严重影响了判决反馈均衡器的均衡性能。针对信道的随机时变特性,自适应算法的研究就显得十分重要。引入自适应算法的自适应均衡器能够随时间追踪信道变化,从而降低信道的随机变化对均衡系统的影响[2-5],提高均衡系统的均衡性能。还有利用海豚进行仿生通信[6]、进行矢量多载波通信[7]和单矢量的不同通信方式[8-9]从而获取更低的均衡误码率。
为了进一步改善均衡系统性能,降低误码率,文献[10]中研究了自适应误差反馈DFE均衡器(self-adaption decision-feedback equalizer using error feedback, EFB-ADFE)。在无线数字通信系统中,当信噪比较高时,EFB-ADFE比DFE的均衡后的误码率更低、均衡性能更好。因为误差反馈滤波器的引入可以有效的降低DFE中误差信号间的相关性,从而降低均衡后的误码率。但是在低信噪比条件下,EFB-ADFE的均衡性能不但没有改善,反而增大了系统的计算复杂度。而海洋信道的环境噪声大、信道结构复杂、时延扩展严重,在水声通信中接收信噪比通常较低、码间干扰严重,故EFB-ADFE直接应用到水声通信中很难在性能上有所提升。
针对此问题,本文分别建立了基于单矢量水听器的自适应多通道误差反馈的判决反馈均衡器(self-adaption multichannel decision-feedback equalizer using error feedback, EFB-AMDFE)和基于单矢量水听器的矢量时反自适应多通道误差反馈DFE均衡系统(self-adaption multichannel decision-feedback equalizer using error feedback with Time-Reversal in vector, EFB-AMDFE-TR),并分别从算法的理论分析、模型建立和外场实验数据处理分析三方面进行充分的推演、验证。
1 基于单矢量的时反自适应多通道误差反馈DFE均衡系统 1.1 自适应误差反馈DFE均衡器如图 1所示为EFB-ADFE的结构框图,其中前馈滤波器(feed-forward filter, FFF)为L+1阶,反馈滤波器(feed-back filter, FBF)为M阶,误差反馈滤波器(error feedback filter, EBF)为N阶,d(n)为n时刻均衡器判决后的输出信号[10]。

|
Download:
|
| 图 1 自适应误差反馈DFE均衡器框图 Fig. 1 Block diagram of adaptive EFB-ADFE | |
EFB-ADFE的FFF在n时刻的输入信号和其滤波器权系数向量分别为
| $ \mathit{\boldsymbol{X}}\left( N \right) = \left[ {\begin{array}{*{20}{c}} {x\left( n \right)}&{x\left( {n - 1} \right)}& \cdots &{x\left( {n - L} \right)} \end{array}} \right] $ | (1) |
| $ \mathit{\boldsymbol{W}}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {{w_f}\left( 0 \right)}&{{w_f}\left( 1 \right)}& \cdots &{{w_f}\left( {n - L} \right)} \end{array}} \right] $ | (2) |
EFB-ADFE的FBF在n时刻的输入信号和FBF的权系数向量分别为
| $ \mathit{\boldsymbol{D}}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {d\left( {n - 1} \right)}&{d\left( {n - 2} \right)}& \cdots &{d\left( {n - M} \right)} \end{array}} \right] $ | (3) |
| $ {\mathit{\boldsymbol{W}}_b}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {{w_b}\left( 1 \right)}&{{w_b}\left( 2 \right)}& \cdots &{{w_b}\left( {n - M} \right)} \end{array}} \right] $ | (4) |
EFB在n时刻的输入信号和EBF的权系数向量分别为
| $ \mathit{\boldsymbol{E}}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {e\left( {n - 1} \right)}&{e\left( {n - 2} \right)}& \cdots &{e\left( {n - N} \right)} \end{array}} \right] $ | (5) |
| $ {\mathit{\boldsymbol{W}}_e}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {{w_e}\left( 1 \right)}&{{w_e}\left( 2 \right)}& \cdots &{{w_e}\left( {n - N} \right)} \end{array}} \right] $ | (6) |
EFB-ADFE的FFF、FBF与EBF的输入信号向量和滤波器权系数向量分别用Xine(n)、Wine(n)表示如下:
| $ {\mathit{\boldsymbol{X}}_{{\rm{ine}}}}\left( n \right) = {\left( {\mathit{\boldsymbol{X}}\left( n \right),\mathit{\boldsymbol{D}}\left( n \right),\mathit{\boldsymbol{E}}\left( n \right)} \right)^{\rm{T}}} $ | (7) |
| $ {\mathit{\boldsymbol{W}}_{{\rm{ine}}}}\left( n \right) = {\left( {{\mathit{\boldsymbol{W}}_f}\left( n \right),{\mathit{\boldsymbol{W}}_b}\left( n \right),{\mathit{\boldsymbol{W}}_e}\left( n \right)} \right)^{\rm{T}}} $ | (8) |
为了推理更加简洁方便,选用1阶EFB,即E(n)=[e(n-1)]。在实际应用中,选用越高阶的EFB其均衡性能越好,但通常不大于FBF的阶数。
EFB-ADFE判决检测前的信号为
| $ y\left( n \right) = \mathit{\boldsymbol{X}}_{{\rm{ine}}}^{\rm{T}}\left( n \right){\mathit{\boldsymbol{W}}_{{\rm{ine}}}}\left( n \right) = \mathit{\boldsymbol{W}}_{{\rm{ine}}}^{\rm{T}}\left( n \right){\mathit{\boldsymbol{X}}_{{\rm{ine}}}}\left( n \right) $ | (9) |
EFB-ADFE在n时刻的残差为
| $ e\left( n \right) = d\left( n \right) - y\left( n \right) $ | (10) |
均衡系统是基于最小均方误差准则的,自适应算法是根据残差大小对滤波器权系数向量Wine(n)进行自适应调整,直到得到最优权向量。将最优权向量代入代价函数即可得到最小代价函数。
自适应判决反馈均衡器(self-adaption decision-feedback equalizer, ADFE)的最小代价函数为
| $ {J_{\min }} = {\rm{E}}\left[ {{\mathit{\boldsymbol{d}}^2}\left( n \right)} \right] - {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{P}} $ | (11) |
其中:P =E[d(n)XdT(n)],R=E[Xd(n)XdT(n)],Xd(n)=[X(n) D(n)]。
为了与ADFE的最小代价函数做比较,EFB-ADFE的最小代价函数用分块矩阵的逆矩阵公式进行简化运算后,可得到
| $ \begin{array}{*{20}{c}} {{J_{e,\min }} = {\rm{E}}\left[ {{\mathit{\boldsymbol{d}}^2}\left( n \right)} \right] - {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{P}} - }\\ {{{\left( {\delta _{\rm{e}}^2} \right)}^{ - 1}}{{\left( {{\rm{E}}\left[ {d\left( n \right)e\left( {n - 1} \right)} \right]} \right)}^2}} \end{array} $ | (12) |
当e(n)平稳时,δe2=E[e2(n)]=E[e2(n-1)]。
对比式(11)和(12)可知,因为(δe2)-1(E[d(n)e(n-1)])2非负项,所以EFB-ADFE的最小代价函数比ADFE的最小代价函数小(δe2)-1(E[d(n)e(n-1)])2。因为EFB-ADFE将过去时刻的误差反馈到均衡器中,降低了误差间的相关性,在高信噪比条件下取得较ADFE更低的均衡后误码率。但是在低信噪比条件下,EFB-ADFE的均衡性能就会受到严重限制,所以EFB-ADFE在环境噪声复杂、信道多途效应严重的水声通信中很难取得良好的均衡效果。
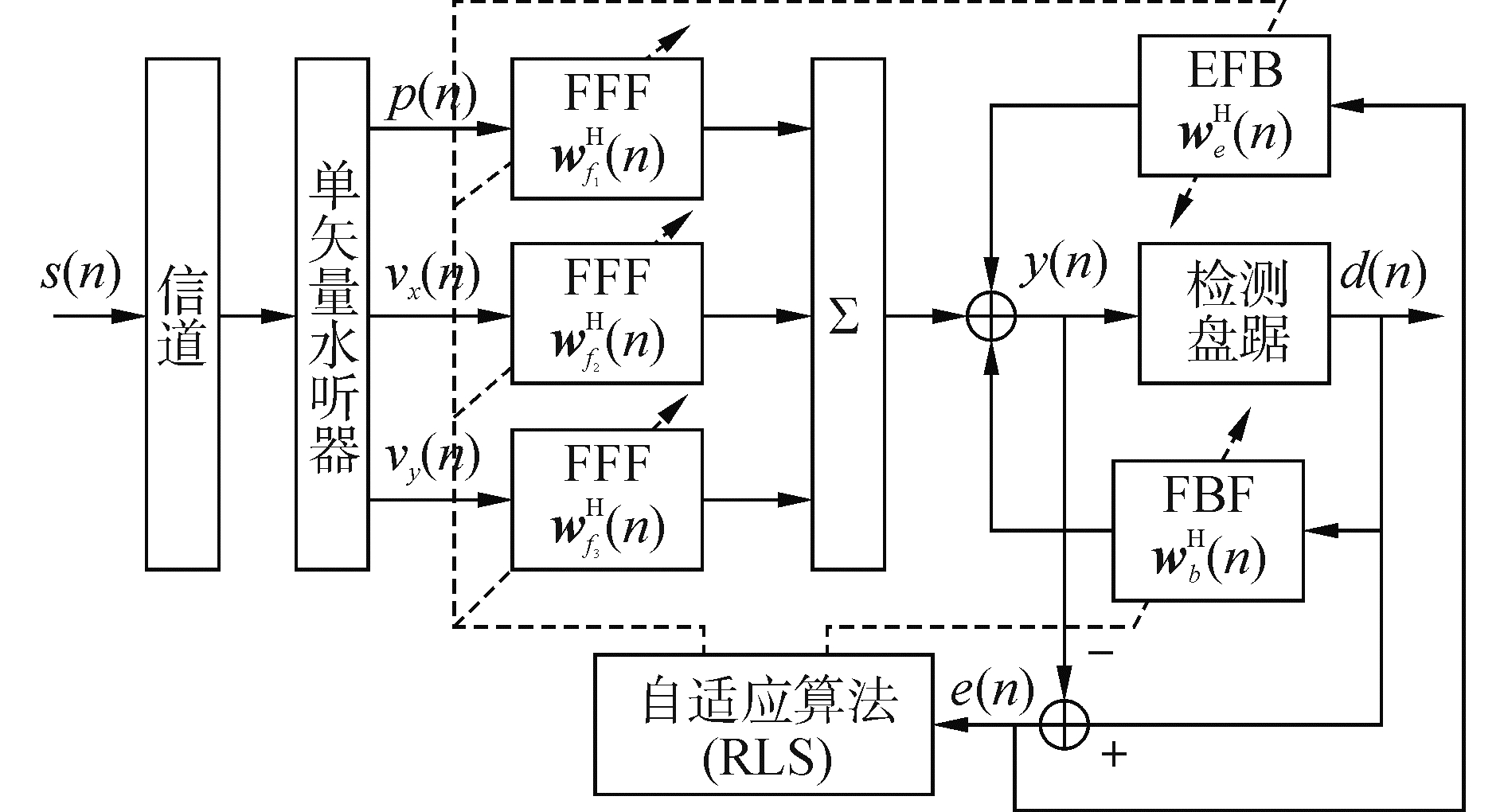
1.2 单矢量自适应多通道误差反馈DFE均衡系统针对复杂的海洋环境噪声,利用矢量水听器能同步共点的测出矢量场中的声压与振速、振速通道具有偶极子指向性的物理特性和矢量场中信号的声压与振速是相干的、环境噪声的声压与振速是非相干的矢量场特性,建立了基于单矢量的EFB-AMDFE进行抗噪声,其原理框图如图 2所示。
|
Download:
|
| 图 2 单矢量自适应多通道DFE均衡器原理框图 Fig. 2 Block diagram of adaptive EFB-AMDFE based on single vector hydrophone | |
矢量水听器是由声压水听器和质点振速传感器组合而成的,其可以同步共点地输出声场中的声压与振速,能更全面的反应声场特性。若声压信号为p(t)=x(t),则由声学欧姆定律得v(t)=1/ρc·x(t),二维矢量水听器(下文所述的矢量水听器均指二维的)的声压与振速信号可表示为
| $ \begin{array}{l} p\left( t \right) = x\left( t \right)\\ {v_x}\left( t \right) = \left( {1/\rho c} \right) \cdot x\left( t \right)\cos \theta \\ {v_y}\left( t \right) = \left( {1/\rho c} \right) \cdot x\left( t \right)\sin \theta \end{array} $ | (13) |
式中:ρc为声阻抗,θ为声源相对矢量水听器的水平方位角。
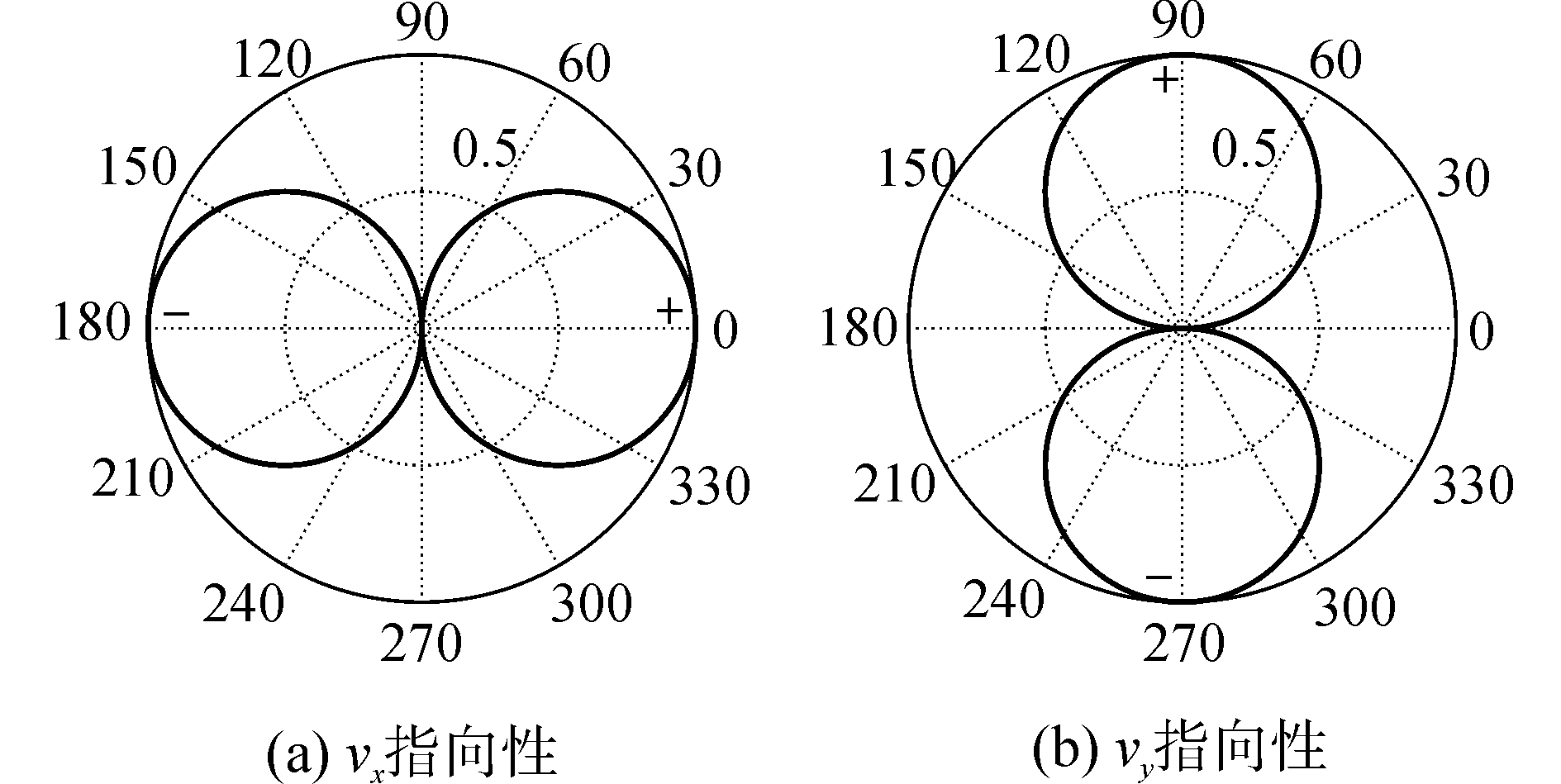
矢量水听器的水平振速vx(t)、vy(t)具有相互垂直的偶极子指向性,如图 3所示。振速通道只接收指向性方向上传来的信号,这可以有效地抑制环境噪声接收。且在各向同性环境噪声中声压与振速的噪声功率满足δp2=1/2·δvx2=1/2·δvy2关系。
|
Download:
|
| 图 3 二维矢量水听器的振速偶极子指向性 Fig. 3 The vibrational dipole directivity of the two-dimensional vector hydrophone | |
由式(13)可以看出,在声矢量场中,声压p与水平振速vx、vy是相干的。但在海洋环境噪声场中却不是这样的,假设np(t)为不同入射角的j个互不相关各态历经随机噪声声压,且
| $ \begin{array}{l} {n_p}\left( t \right) = \sum\limits_j {{n_j}\left( t \right)} \\ {n_{vx}}\left( t \right) = \sum\limits_j {{n_u}\left( t \right)\cos {\theta _j}} \\ {n_{vy}}\left( t \right) = \sum\limits_j {{n_j}\left( t \right)\sin {\theta _j}} \end{array} $ | (14) |
式中θj为[0, 2π]内均匀分布的随机变量。
则声压通道与水平振速通道v的噪声互相关系数为
| $ \begin{array}{l} {\rho _{{\rm{pvx}}}} = \frac{{{\rm{E}}\left[ {{n_p}\left( t \right)n_{vx}^ * \left( t \right)} \right]}}{{\sqrt {{\rm{E}}\left[ {{{\left| {{n_p}\left( t \right)} \right|}^2}} \right]{\rm{E}}\left[ {{{\left| {{n_{vx}}\left( t \right)} \right|}^2}} \right]} }} = \\ \;\;\;\;\;\frac{{\sum\limits_j {\overline {n_j^2\left( t \right)} \cdot \overline {\cos {\theta _j}} } }}{{\sqrt {{\rm{E}}\left[ {{{\left| {{n_p}\left( t \right)} \right|}^2}} \right]{\rm{E}}\left[ {{{\left| {{n_{vx}}\left( t \right)} \right|}^2}} \right]} }} \end{array} $ | (15) |
式中是对x的时间平均。因为θj为[0, 2π]内均匀分布的随机变量,所以
综上所述可得,利用矢量水听器的振速偶极子指向性可以有效抑制环境噪声的接收;利用矢量场中声压与振速信号是相干的,但声压与振速的噪声是非相干的矢量场特性进行多通道的均衡处理可以有效地抑制接收信号中的噪声干扰。所以单矢量EFB-AMDFE均衡系统的抗噪声能力更强。
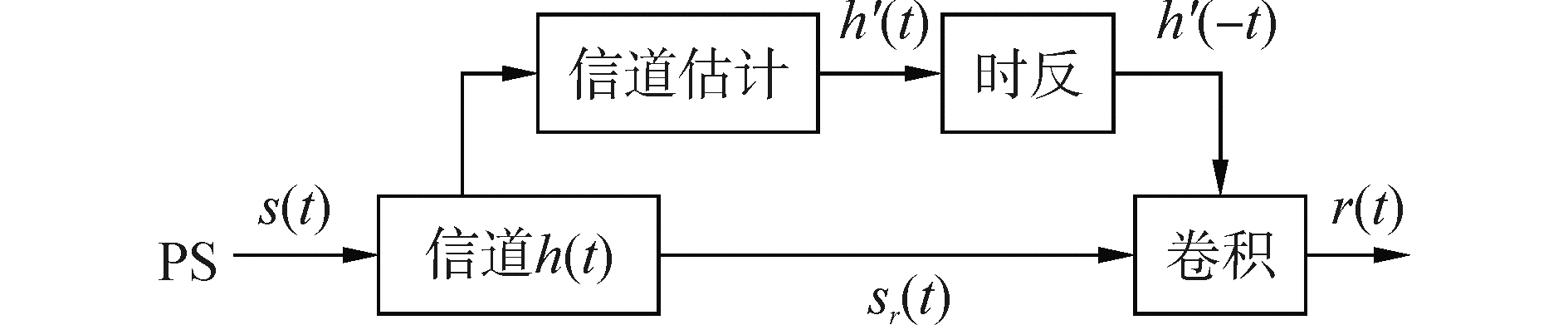
1.3 被动时间反转技术针对水声信道中严重的信道多途效应,利用时间反转镜可以重组多途信号的空时聚焦特性来抑制信道多途干扰,增强均衡系统的抗信道多途干扰能力。被动时间反转镜的原理框图如图 4所示。
|
Download:
|
| 图 4 被动时反原理框图 Fig. 4 Block diagram of passive Time-Reversal | |
接收机的接收信号可表示为
| $ {s_r}\left( t \right) = s\left( t \right) \otimes h\left( t \right) + n\left( t \right) $ | (16) |
则被动时反的输出信号可表示为
| $ \begin{array}{*{20}{c}} {r\left( t \right) = {s_r}\left( t \right) \otimes h'\left( { - t} \right) = }\\ {\left[ {s\left( t \right) \otimes h\left( t \right)} \right] \otimes h'\left( { - t} \right) + n\left( t \right) \otimes h'\left( { - t} \right) = }\\ {s\left( t \right) \otimes q\left( t \right) + n\left( t \right) \otimes h'\left( { - t} \right)} \end{array} $ | (17) |
式中:s(t)为发射信号,h(t)为信道冲激响应函数,n(t)为环境噪声,sr(t)为接收信号,h′(-t)为信道估计结果,q(t)=h(t)
当信道估计足够精确,则q(t)相当于是信道冲击响应函数h(t)的自相关函数,可以近似为δ函数, 有效地抑制了信道的多途干扰,此时被动时反的输出信号r(t)就近似为发射信号s(t)。且信道多途结构越复杂,时反效果越好。水声信道的多途结构是十分复杂的,特别是在浅海的远距离通信中。故在浅海水下通信中,被动时间反转镜技术得到广泛应用。
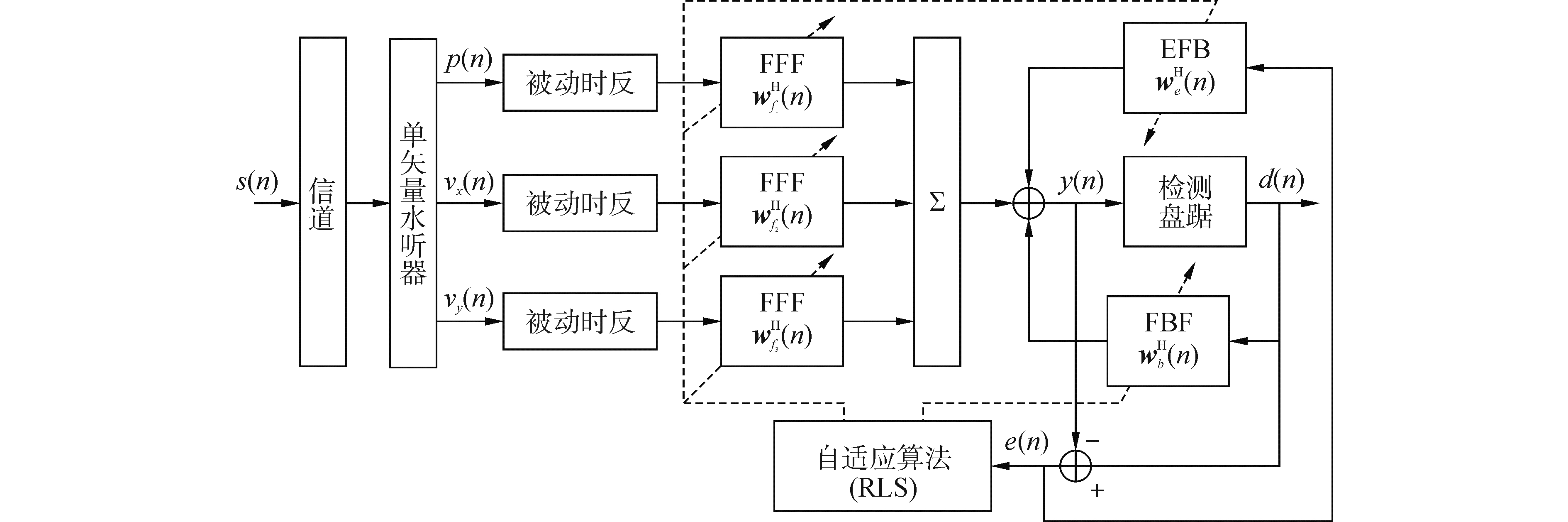
1.4 矢量EFB-AMDFE-TR均衡系统为了在环境噪声复杂、信道多途干扰严重的水声通信中取得更好的均衡性能,建立了基于单矢量水听器的EFB-AMDFE-TR均衡系统,其原理框图如图 5所示。
|
Download:
|
| 图 5 矢量时反自适应多通道误差反馈DFE原理框图 Fig. 5 Block diagram of EFB-AMDFE-TR based on single vector hydrophone | |
EFB-AMDFE-TR不仅保留了EFB-ADFE在信道结构简单、高信噪比条件下能取得良好均衡性能的优点,而且该系统利用了矢量场中声压与振速的信号是相干的、环境噪声是非相干的矢量场特性和矢量水听器振速通道的偶极子指向性进行有效的抑制环境噪声干扰;且利用时间反转镜可以重组多途信号的空时聚焦特性进行抗信道多途干扰。这极大地增强了系统的抗噪声能力和抗信道多途干扰能力,使得该系统在水声通信中能取得良好的均衡效果。
2 系统仿真实验结果利用基于射线理论的声传播模型模拟了海深为100 m,发射深度为20 m、接收深度为30 m、收发间距为1 000 m的水声信道。仿真实验的信道冲激响应和信道的频率响应如图 6所示。

|
Download:
|
| 图 6 仿真信道的信道冲激响应和频率响应 Fig. 6 The channel impulse response and frequency response of simulation channel | |
从图 6中可以看到,收发间距为1 000 m的水信道的时延扩展约为50 ms,且信道结构十分复杂,这导致水声通信存在严重的码间干扰。从图 6(b)的信道频率响应可以看出,水声信道的频率响应呈“梳状滤波器”结构,即水声信道衰落具有严重的频率选择特性,导致信号波形在传输过程中会发生畸变。
2.1 自适应误差反馈DFE的均衡结果信号调制方式为QPSK,采样频率为48 kHz,通信速率为2 kbit/s,FFF为35阶,FBF为25阶,EFB为25阶。
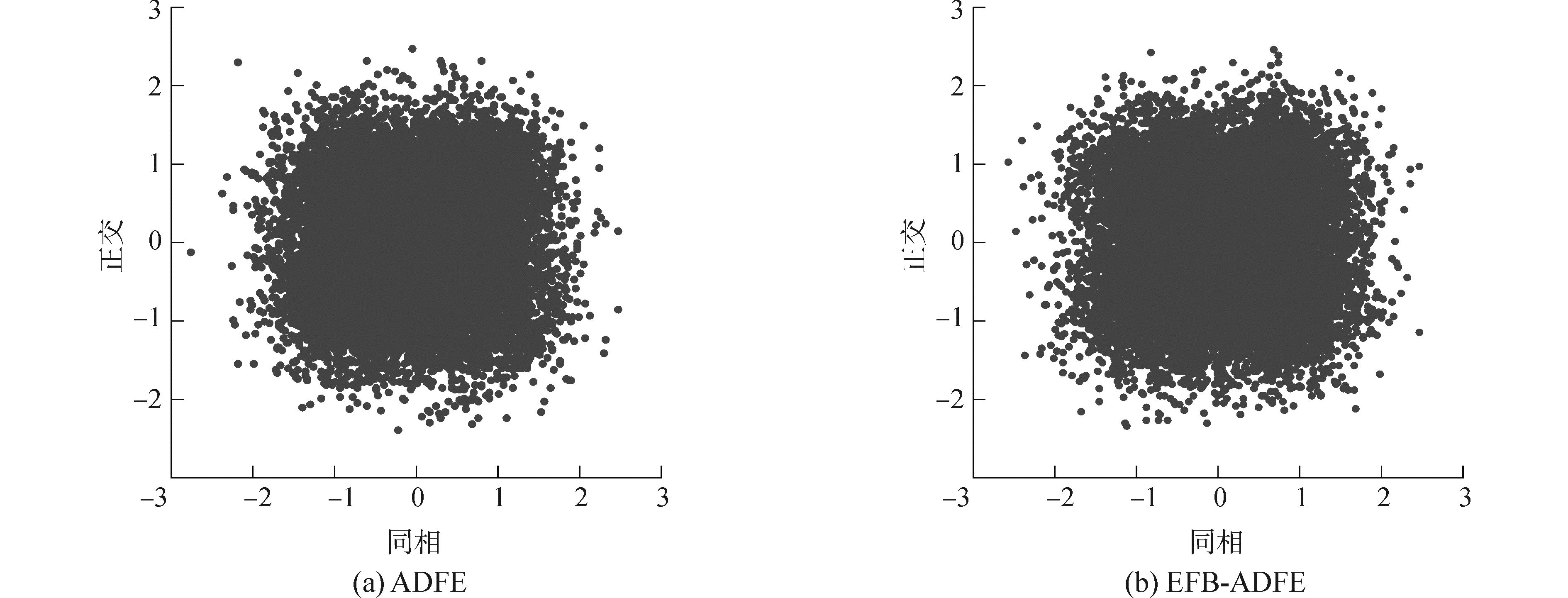
图 7是窄带信噪比为0 dB(本文所有的信噪比均指窄带信噪比)条件下的ADFE和EFB-ADFE的均衡后星座图。
|
Download:
|
| 图 7 SNR=0 dB时ADFE和EFB-ADFE均衡后的星座图 Fig. 7 The balanced constellation of the ADFE and EFB-ADFE with SNR=0 dB | |
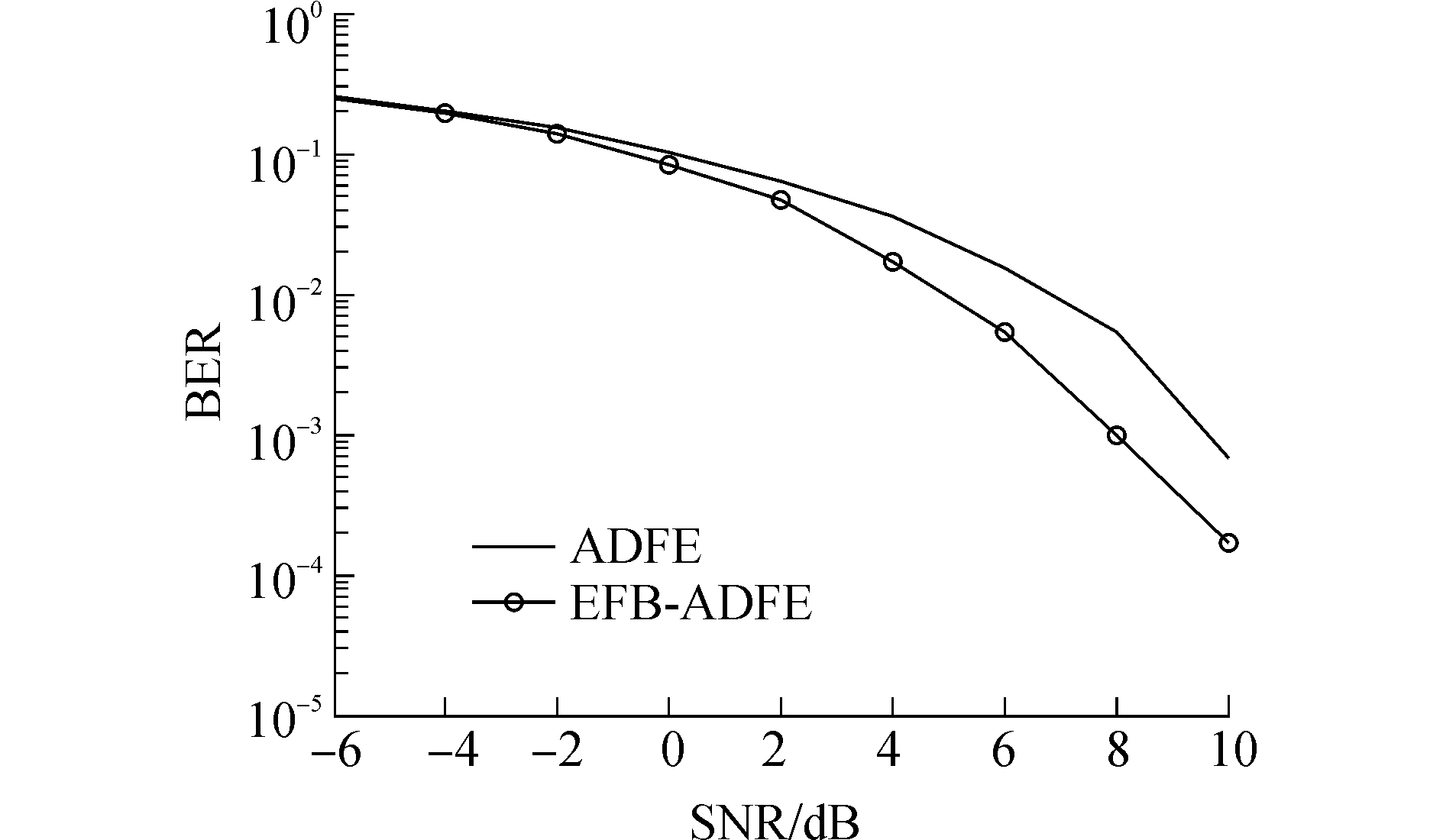
从图 8中两者均衡后的误码率曲线比较图中可知,在SNR大于2 dB条件下,EFB-ADFE的误码率比ADFE的误码率低;但是在SNR小于0 dB时,ADFE与EFB-ADFE的误码率曲线是重叠在一起的;同时从图 7中两者在SNR=0 dB时的均衡后的星座图来看很难区分谁的均衡性能更好。即相比于ADFE,在高信噪比条件下,EFB-ADFE取得更好的均衡性能,但是在低信噪比条件下,EFB-ADFE的均衡性能并没有获得提升。即EFB-ADFE在环境噪声复杂、信道多途干扰严重的水声通信中很难取得良好的均衡效果。
|
Download:
|
| 图 8 ADFE和EFB-ADFE均衡后的误码率曲线 Fig. 8 The balanced error rate curve of the ADFE and EFB-ADFE | |
信号调制方式为QPSK,采样频率为48 kHz,通信速率为2 kbit/s,FFF为35阶,FBF为25阶,EFB为25阶。
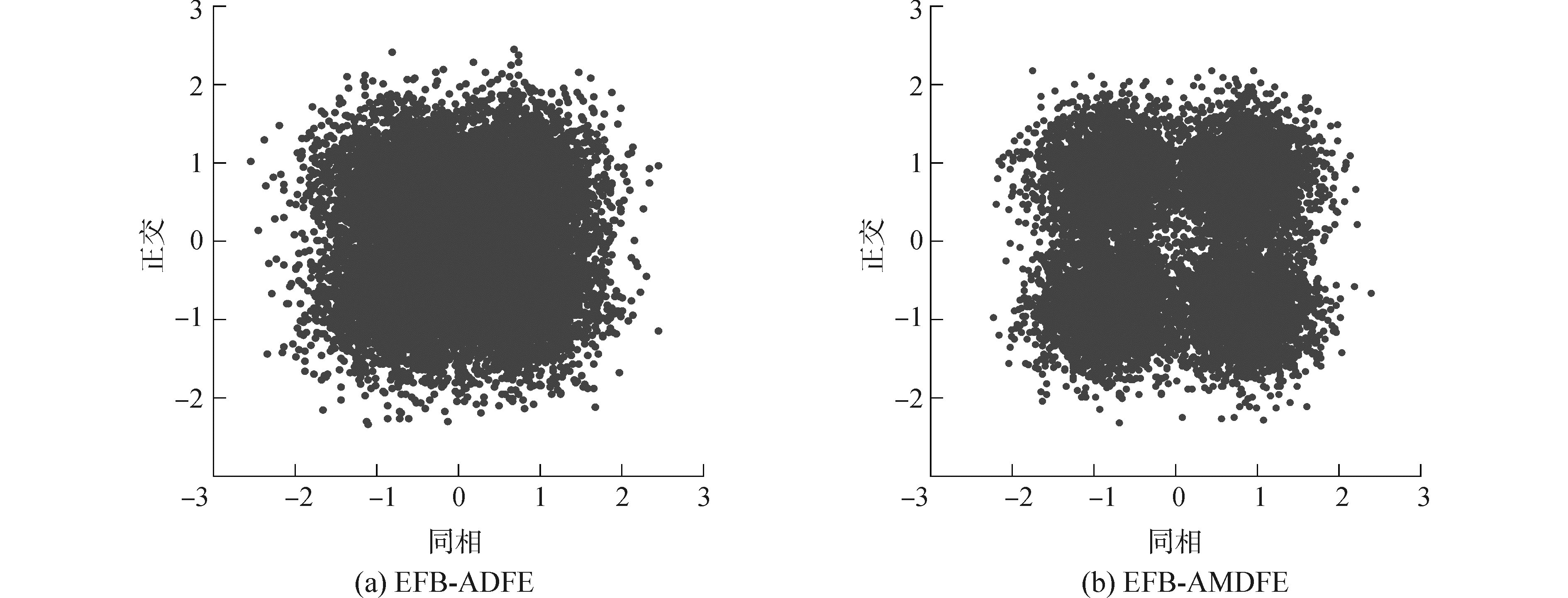
图 9为SNR=0 dB条件下EFB-ADFE和EFB-AMDFE均衡后的星座图。
|
Download:
|
| 图 9 SNR=0 dB EFB-ADFE和EFB-AMDFE均衡后的星座图 Fig. 9 The balanced constellation of the AMDFE and EFB-AMDFE with SNR=0 dB | |
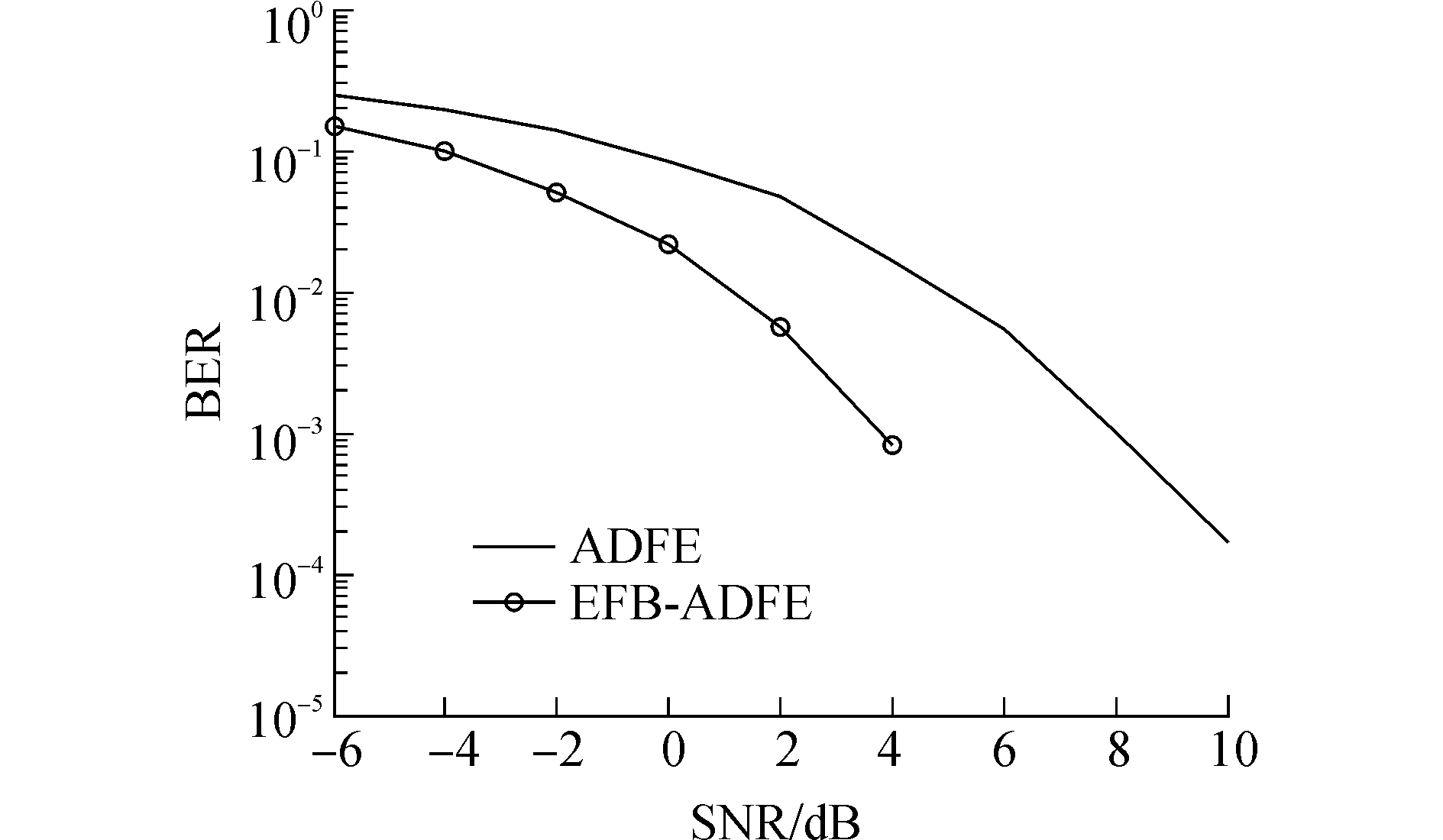
从图 9中EFB-ADFE和EFB-AMDFE均衡后的星座图对比可知,EFB-AMDFE均衡后的星座图明显比EFB-ADFE均衡后的星座图的更加收敛, EFB-AMDFE的输出增益比EFB-ADFE的输出增益高2.5 dB;且对比图 10两者的误码率曲线可知,EFB-AMDFE在SNR大于4 dB时就已经实现了零误码解码,即使在SNR小于0 dB条件下,EFB-AMDFE的误码率也明显比EFB-ADFE的均衡后的误码率低。说明相比于EFB-ADFE,EFB-AMDFE的均衡性能得到明显的提升。但是这还不满足水声通信正确解码的需求,故而在此基础上引入了被动时间反转镜技术。
|
Download:
|
| 图 10 EFB-ADFE和EFB-AMDFE均衡后的误码率曲线 Fig. 10 The balanced error rate curve of the EFB-ADFE and EFB-AMDFE | |
信号调制方式为QPSK,采样频率为48 kHz,通信速率为2 kbit/s,FFF为35阶,FBF为25阶,EFB为25阶。
图 11为SNR=0 dB条件下的EFB-ADFE、EFB- AMDFE和EFB-AMDFE-TR均衡后星座图以及三者的误码率曲线。

|
Download:
|
| 图 11 SNR=0 dB时,EFB-ADFE、EFB-AMDFE和EFB-AMDFE-TR均衡后星座图和误码率比较曲线 Fig. 11 The balanced constellation of the EFB-ADFE, EFB-AMDFE and EFB-AMDFE-TR with SNR=0 dB and error rate comparison curves | |
对比图 11的均衡结果可知,在SNR=0 dB时,EFB-ADFE、EFB-AMDFE和EFB-AMDFE-TR三者均衡后的星座图中,EFB-AMDFE-TR均衡后的星座图最收敛、EFB-AMDFE的次之,EFB-ADFE均衡后的星座图最为发散;且从表 1可知,EFB-AMDFE-TR均衡后的输出增益比EFB-AMDFE的输出增益高1.22 dB,比EFB-ADFE的输出增益高3.73 dB;说明在SNR=0 dB时,EFB-AMDFE-TR的均衡效果最佳,EFB-AMDFE次之,EFB-ADFE的均衡效果最差。由图 11(d)中三者均衡后的误码率曲线的比较可知,当SNR大于4 dB时,EFB-AMDFE-TR和EFB-AMDFE都实现了零误码均衡,但EFB-ADFE的误码率还较大;即使在SNR小于4 dB时,EFB-AMDFE均衡后的误码率明显比EFB-ADFE均衡后的误码率要低,而EFB-AMDFE-TR均衡后的误码率则比EFB-AMDFE均衡后的误码率更低,说明三者中EFB-AMDFE-TR均衡系统的均衡性能最好。
| 表 1 SNR=0 dB时不同均衡结构的均衡输出增益表 Table 1 A balanced output gain table for different equilibrium structures with SNR=0 dB |
综合上述的对比分析结果可得,利用矢量场中信号的声压与振速是相干的、噪声是非相干的矢量场特性和矢量水听器振速的偶极子指向性进行抗环境噪声,利用时间反转镜的空时聚焦特性重组多途信号的特性进行抗信道多途干扰的单矢量EFB-AMDFE-TR均衡系统具有较强的抗噪声能力和抗信道多途干扰的能力,在水声通信中能取得良好的均衡效果。
3 实验数据处理结果2015年12月松花江水下实验,水深5.7 m,发射换能器深度为3 m,接收阵元水深为1.5 m,通信距离1 km。通信速率为2 kbit/s,中心频率为6 kHz,带宽为4 kHz,采样频率为48 kHz,信号长度为12.5 s。
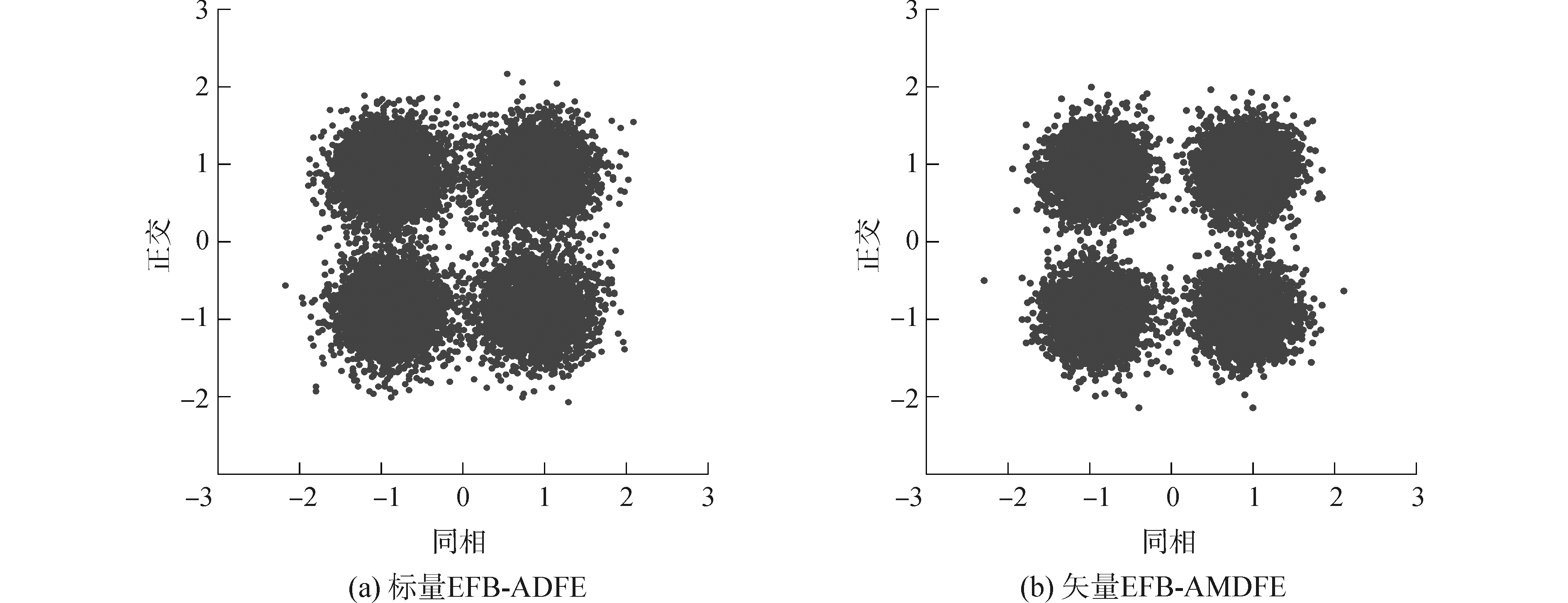
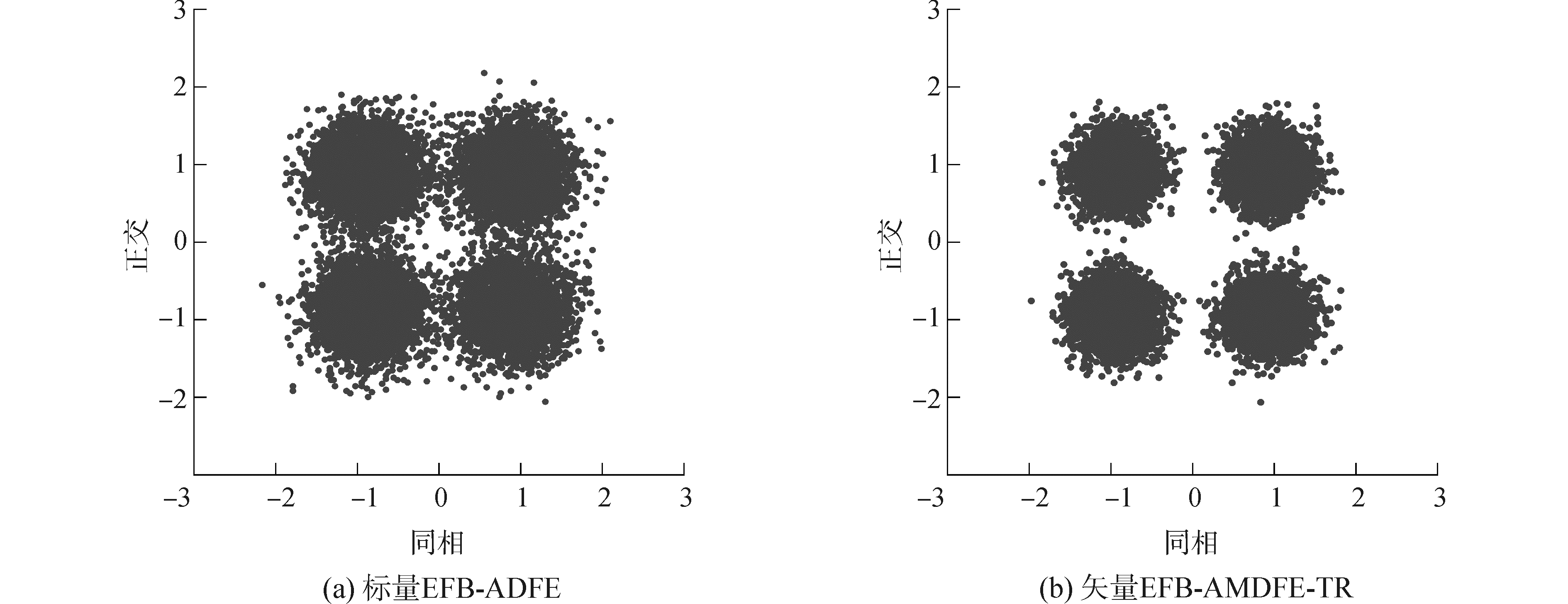
由表 2和图 12可知,EFB-AMDFE比EFB-ADFE的输出增益高1.42 dB,且EFB-AMDFE比EFB-ADFE的均衡后误码率低0.31%;说明EFB-AMDFE在实际的水声通信中的抗噪声能力比EFB-ADFE的更强,均衡后的效果更好。由图 13和表 2可知,EFB-AMDFE-TR比EFB-AMDFE的输出增益高1.31 dB,EFB-AMDFE-TR比EFB-ADFE的输出增益高2.73 dB,且EFB-AMDFE-TR实现了零误码解码。综上所述可得,相比于EFB-ADFE, 基于单矢量的EFB-AMDFE-TR均衡后的误码率更低、输出增益更高;说明本文所提算法不仅能保留EFB-ADFE的优点,且该系统的抗噪声能力和抗信道多途效应干扰能力都更强,在水声通信中能取得更好的均衡效果。
| 表 2 不同均衡结构的实验数据处理结果表 Table 2 Experimental data processing results table of different equilibrium structures |
|
Download:
|
| 图 12 EFB-ADFE和EFB-AMDFE的实验数据处理结果 Fig. 12 Experimental data processing results of EFB-ADFE and EFB-AMDFE | |
|
Download:
|
| 图 13 EFB-ADFE和EFB-AMDFE-TR的实验数据处理结果 Fig. 13 Experimental data processing results of EFB-ADFE and EFB-AMDFE-TR | |
1) EFB-AMDFE均衡后的输出增益比EFB-ADFE的均衡输出增益高,说明基于单矢量的EFB-AMDFE均衡系统的抗噪声能力比基于单标量的EFB-ADFE均衡系统的更强;
2) EFB-AMDFE-TR的均衡输出增益比EFB-AMDFE的均衡输出增益高,说明时间反转技术能进一步有效地提高接收信号信噪比和降低多途信道对信号的码间干扰。这对实现远程、高速、稳健的水下信息传输有着重要意义。
| [1] |
贾宁, 黄建纯. 水声通信技术综述[J]. 物理, 2014, 43(10): 650-657. JIA Ning, HUANG Jianchun. An overview of underwater acoustic communications[J]. Physics, 2014, 43(10): 650-657. DOI:10.7693/wl20141002 (  0) 0)
|
| [2] |
刘云涛, 杨莘元. 内嵌数字锁相环的自适应空时联合均衡器在水下高速数字通信中的应用研究[J]. 哈尔滨工程大学学报, 2005, 26(5): 658-662. LIU Yuntao, YANG Shenyuan. Research of adaptive spatio-temporal DFE with embedded DPLL in high-speed underwater digital communication[J]. Journal of Harbin Engineering University, 2005, 26(5): 658-662. DOI:10.3969/j.issn.1006-7043.2005.05.021 (  0) 0)
|
| [3] |
冯驰, 赵春晖, 张哲. 一种自适应判决反馈盲均衡器[J]. 哈尔滨工程大学学报, 2004, 25(3): 367-371. FENG Chi, ZHAO Chunhui, ZHANG Zhe. A blind adaptive decision feedback equalizer[J]. Journal of Harbin Engineering University, 2004, 25(3): 367-371. DOI:10.3969/j.issn.1006-7043.2004.03.024 (  0) 0)
|
| [4] |
LUO Yasong, LIU Zhong, HU Shengliang, et al. Self-adjusting decision feedback equalizer for variational underwater acoustic channel environments[J]. Journal of systems engineering and electronics, 2014, 25(1): 26-33. DOI:10.1109/JSEE.2014.00004 (  0) 0)
|
| [5] |
SONG H C, HODGKISS W S, KUPERMAN W A, et al. Improvement of time-reversal communications using adaptive channel equalizers[J]. IEEE journal of oceanic engineering, 2006, 31(2): 487-496. DOI:10.1109/JOE.2006.876139 (  0) 0)
|
| [6] |
QIAO Gang, ZHAO Yunjiang, LIU Songzuo, et al. Dolphin sounds-inspired covert underwater acoustic communication and micro-modem[J]. Sensors, 2017, 17(11): E2447. DOI:10.3390/s17112447 (  0) 0)
|
| [7] |
ADEBISI B, RABIE K M, IKPEHAI A, et al. Vector OFDM transmission over non-Gaussian power line communication channels[J]. IEEE systems journal, 2017. DOI:10.1109/JSYST.2017.2669086 (  0) 0)
|
| [8] |
FAUZIYA F, LALL B, AGRAWAL M. Vector sensor based channel equalizer for underwater communication systems[C]//Proceedings of the 7th Annual Computing and Communication Workshop and Conference. Las Vegas, NV, USA, 2017: 1-5.
(  0) 0)
|
| [9] |
FAUZIYA F, LALL B, AGRAWAL M. Vector transducer based MISO communications system: capacity analysis[C]//Proceedings of Oceans. Aberdeen, UK, 2017: 1-5.
(  0) 0)
|
| [10] |
KIM D W, HAN S H, EUN M S, et al. An adaptive decision feedback equalizer using error feedback[J]. IEEE transactions on consumer electronics, 1996, 42(3): 468-477. DOI:10.1109/30.536144 (  0) 0)
|
| [11] |
刘凇佐, 周锋, 孙宗鑫, 等. 单矢量水听器OFDM水声通信技术实验[J]. 哈尔滨工程大学学报, 2012, 33(8): 941-947. LIU Shongzo, ZHOU Feng, SUN Zongxin, et al. Experimental study of OFDM underwater acoustic communication using a vector hydrophone[J]. Journal of Harbin Engineering University, 2012, 33(8): 941-947. DOI:10.3969/j.issn.1006-7043.201111055 (  0) 0)
|
| [12] |
殷敬伟, 张晓, 赵安邦, 等. 时间反转镜在水声通信网上行通信中的应用[J]. 哈尔滨工程大学学报, 2011, 32(1): 1-5. YIN Jingwei, ZHANG Xiao, ZHAO Anbang, et al. The application of a virtual time reversal mirror to upstream communication of underwater acoustic networks[J]. Journal of Harbin Engineering University, 2011, 32(1): 1-5. DOI:10.3969/j.issn.1006-7043.2011.01.001 (  0) 0)
|
| [13] |
孙琳, 李若, 周天. 基于被动时反的时分复用下行通信研究[J]. 哈尔滨工程大学学报, 2013, 34(10): 1254-1260. SUN Lin, LI Ruo, ZHOU Tian. A research of time division multiplexed downlink communications using passive time reversal[J]. Journal of Harbin Engineering University, 2013, 34(10): 1254-1260. (  0) 0)
|
| [14] |
宫改云, 姚文斌, 潘翔. 被动时反与自适应均衡相联合的水声通信研究[J]. 声学技术, 2010, 29(2): 129-134. GONG Gaiyun, YAO Wenbin, PAN Xiang. A study of underwater acoustic communication based on the joint processing of passive time reversal and adaptive equalization[J]. Technical acoustics, 2010, 29(2): 129-134. DOI:10.3969/j.issn.1000-3630.2010.02.003 (  0) 0)
|
| [15] |
梁国龙, 马巍, 范展, 等. 矢量声纳高速运动目标稳健高分辨方位估计[J]. 物理学报, 2013, 62(14): 144302. LIANG Guolong, MA Wei, FAN Zhan, et al. A high resolution robust localization approach of high speed target based on vector sonar[J]. Acta physica sinica, 2013, 62(14): 144302. DOI:10.7498/aps.62.144302 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


