柔索驱动并联机构是一种由柔索代替传统并联机构的连杆而构成的新型并联机构。柔索驱动并联机构主要由静平台、驱动单元、牵引轮、柔索、铰链、末端执行器等组成,是一种将驱动元件的力和运动通过柔索传递给末端执行器的并联机构形式[1-3]。因为柔索物理特性可以在牵引轮上大量缠绕,所以机构具有比刚性并联机构更大的工作空间、更高的负载/质量比、轻便灵活等优点,实际被广泛应用于物料搬运、工业加工、虚拟现实等领域[4-5]。与刚性并联机构相比,因为柔索只能承受拉力而不能承受压力,要求末端执行器在工作空间内运动过程中每根柔索拉力必须都大于零[6]。机构的工作空间是机构末端执行器的工作区域,是末端执行器所能达到空间点的集合。工作空间的大小是设计机构之初最先考虑的问题,也是衡量一个机构性能的重要指标,能够用于衡量机构的技术性能。柔索并联机构工作空间的定义、性质与传统刚性并联机构不同。柔索并联机构工作空间的大小通常取决于柔索的根数、柔索与静平台的连接位置和柔索与末端执行器的连接位置。柔索与静平台和末端执行器的连接位置即为柔索的布局。由于柔索的单向受力特性,对柔索并联机构设计布局时必须同时考虑运动和受力两个方面的约束条件[7]。研究人员根据柔索的数目m和机构自由度数n之间的关系对柔索并联机构进行了划分,当m≤n时为欠约束机构,m=n+1为完全约束机构,m>n+1为冗余约束机构[8-9]。
对于完全约束机构和冗余约束机构,郑亚青等[9]对其力螺旋封闭工作空间和力螺旋可行工作空间分别给出了定义,力封闭工作空间只与并联机构的布局有关,对于机构末端执行器受到任何外力,柔索拉力都有可行解的空间点的集合,外力不能对其产生影响;力螺旋可行工作空间与并联机构的布局和作用在末端执行器上的外力变化范围有关,是对于机构末端执行器受到一定范围的外力柔索都具有可行解的空间点的集合。
目前,大部分关于柔索并联机构工作空间的研究主要是采用数值法和解析法。Cong B P等[10]提出递归维数缩减法对给定区域内的点进行逐点判断,然而实现的程序复杂、计算量大。GOUTTEFARDE等[11]研究了柔索的根数变化对机构结构矩阵的影响,推导出了机构力螺旋封闭工作空间的边界表达式,但是该方法仅用于柔索数目大于3的3自由度平面柔索并联机构。DIAO等[12]提出一种采用矩阵逆运算就可判断力封闭条件的快速求解算法。刘欣等[13]提出一种根据力螺旋封闭定理和结构矩阵线性关系性质求解6自由度完全约束和冗余约束柔索并联机构力螺旋封闭工作空间边界解析表达式的算法。FERRARESI等[14]提出了一种基于结构矩阵零空间来判断力螺旋封闭工作空间条件的算法,该算法用于9跟柔索驱动的6自由度并联机构。欧阳波等[15]以文献[14]的力螺旋封闭工作空间算法为基础,提出了一种通用的力螺旋封闭工作空间算法。
关于力螺旋可行工作空间及柔索布局对工作空间影响的研究相对较少。HAY等[16]研究了柔索布局确定,采用动态优化算法使并联机构灵巧工作空间最大化,但该算法仅适用于3自由度的平面并联机构。张耀军等[17]对平面4柔索3自由度并联机构的力螺旋可行工作空间算法和柔索布局进行了研究。本文以文献[14-15]求解柔索并联机构力螺旋封闭工作空间的算法为基础,结合文献[18]给出的平面机构力螺旋可行工作空间算法,给出一种用于求解空间柔索并联机构力螺旋可行工作空间的算法。用此算法对典型布局的空间8柔索并联机构力螺旋可行工作空间进行求解,对比分析验证了本文提出的力螺旋可行工作空间算法的正确性。本文提出一种柔索布局方案,对其力螺旋封闭工作空间及力螺旋可行工作空间求解,并与典型布局方案的力螺旋封闭工作空间及力螺旋可行工作空间对比分析说明本文柔索布局方案的优势。
1 柔索并联机构模型由m根柔索牵引的n自由度并联机构,模型简图及构型参数如图 1所示,O-xyz坐标系和O1-xyz坐标系分别代表机构的全局坐标系和末端执行器质心的局部坐标系。

|
Download:
|
| 图 1 柔索驱动并联机构简图及构型参数 Fig. 1 Structural diagram and configuration parameters of cable driven parallel mechanism | |
滑轮与柔索连接点的位置Ai在全局坐标系O内的矢量表示为ai,移动坐标系原点O1在全局坐标系O内的矢量表示为b,末端执行器与柔索的铰接点位置Bi在局部坐标系内的位置矢量表示为ri,末端执行器在全局坐标系内对应z-y-x的位姿角表示为(α, β, γ)。
| $ {\mathit{\boldsymbol{l}}_i} = {\mathit{\boldsymbol{a}}_i} - \left( {\mathit{\boldsymbol{b}} + {}^O{\mathit{\boldsymbol{R}}_{{O_1}}}{\mathit{\boldsymbol{r}}_i}} \right)\;\;\;i = 1,2, \cdots ,m $ | (1) |
式中:
| $ {}^O{\mathit{\boldsymbol{R}}_{{O_1}}} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma }&{\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma }\\ {\sin \alpha \cos \beta }&{\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma }\\ { - \sin \beta }&{\cos \beta \sin \gamma }&{\cos \beta \cos \gamma } \end{array}} \right] $ |
是表示局部坐标系到全局坐标系的旋转矩阵。
柔索的单位矢量为
| $ {\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{l}}_i}/\left\| {{\mathit{\boldsymbol{l}}_i}} \right\|\;\;\;i = 1,2, \cdots ,m $ | (2) |
通常当柔索并联机构末端执行器受到外力旋量为(F, M)时,由m根柔索驱动的n自由度末端执行器会产生大小相等方向相反的力旋量来平衡外力旋量和末端执行器的重力G。满足力和力矩平衡条件,柔索驱动并联机构静力学模型如下:
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^m {{\mathit{\boldsymbol{t}}_i}} = - \mathit{\boldsymbol{F}} - \mathit{\boldsymbol{G}}\\ \sum\limits_{i = 1}^m {{\mathit{\boldsymbol{r}}_i} \times {\mathit{\boldsymbol{t}}_i}} = - \mathit{\boldsymbol{M}} \end{array} \right. $ | (3) |
式中: ti=tiui(i=1, 2, …, m),ti是第i根柔索拉力,把ti=tiui, w1=-F-G, w2=-M, w=[w1; w2]代入式(3)得
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^m {{t_i}{\mathit{\boldsymbol{u}}_i}} = {\mathit{\boldsymbol{w}}_1}\\ \sum\limits_{i = 1}^m {{\mathit{\boldsymbol{r}}_i} \times {t_i}{\mathit{\boldsymbol{u}}_i}} = {\mathit{\boldsymbol{w}}_2} \end{array} \right. $ |
整理可得表达形式:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_1}}&{{\mathit{\boldsymbol{u}}_2}}& \cdots &{{\mathit{\boldsymbol{u}}_m}}\\ {{\mathit{\boldsymbol{r}}_1} \times {\mathit{\boldsymbol{u}}_1}}&{{\mathit{\boldsymbol{r}}_2} \times {\mathit{\boldsymbol{u}}_2}}& \cdots &{{\mathit{\boldsymbol{r}}_m} \times {\mathit{\boldsymbol{u}}_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{t_1}}\\ {{t_2}}\\ \vdots \\ {{t_m}} \end{array}} \right] = \mathit{\boldsymbol{w}} $ | (4) |
定义P为柔索的结构矩阵,t为各柔索的拉力幅值,式(4)可以表示为
| $ \mathit{\boldsymbol{Pt}} = \mathit{\boldsymbol{w}} $ | (5) |
根据力螺旋封闭工作空间条件,末端执行在工作空间内的任意一点受到外力螺旋(F, M)时,每一根柔索的拉力t均为正值:
| $ \mathit{\boldsymbol{t}} > \mathit{\boldsymbol{0}} $ | (6) |
因为柔索的单向受力特性,所以通常6自由度柔索并联机构的柔索都是冗余布局,致使结构矩阵P并不是一个方阵,所以对于式(5)求解柔索拉力时采用结构矩阵P的广义逆矩阵:
| $ {\mathit{\boldsymbol{t}}_{\min }} = {\mathit{\boldsymbol{P}}^ + } \cdot \mathit{\boldsymbol{w}} $ | (7) |
式中P+为结构矩阵P的广义逆矩阵。
式(5)的一般解为
| $ \mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_{\min }} + {\mathit{\boldsymbol{t}}^ * } $ | (8) |
式中t*一定属于结构矩阵P的零空间:
| $ \mathit{\boldsymbol{P}} \cdot {\mathit{\boldsymbol{t}}^ * } = \mathit{\boldsymbol{0}} $ | (9) |
可以判断出求解柔索力t的式具有无穷多个解。t*需要同时满足式(6)及式(9)两个条件,显然t*的倍数也可以满足式(10),所以一定存在一个适当的实数c∈R+满足式(5),即
| $ \mathit{\boldsymbol{P}}\left( {{\mathit{\boldsymbol{t}}_{\min }} + c \cdot {\mathit{\boldsymbol{t}}^ * }} \right) = \mathit{\boldsymbol{w}} $ | (10) |
式中:c·t*∈null(P);tmin+c·t*> 0。
3 力螺旋可行工作空间求解算法定理[18]:三维空间位姿X属于6自由度柔索并联机构的力螺旋封闭工作空间,只有满足条件rank(P)=6∩
满足秩为6的条件同时需要满足矩阵零空间内的列矢量线性相关且以下不等式成立:
| $ \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}& \cdots &{{k_{1\left( {m - n} \right)}}}\\ {{k_{21}}}&{{k_{22}}}& \cdots &{{k_{2\left( {m - n} \right)}}}\\ {{k_{31}}}&{{k_{32}}}& \cdots &{{k_{3\left( {m - n} \right)}}}\\ \vdots&\vdots&\vdots&\vdots \\ {{k_{m1}}}&{{k_{m2}}}& \cdots &{{k_{m\left( {m - n} \right)}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ \vdots \\ {{x_{m - n}}} \end{array}} \right] > 0 $ | (11) |
式中:kij属于结构矩阵P的零空间产生的元素,xj为未知数。
根据结构矩阵零空间内列矢量间的线性相关性,满足力螺旋封闭时,不等式组(11)需要满足下列不等式:
| $ \left\{ \begin{array}{l} \frac{{ - {k_{q2}}}}{{{k_{q1}}}}{x_2} + \cdots + \frac{{ - {k_{q\left( {m - n} \right)}}}}{{{k_{q1}}}}{x_{m - n}} > 0\;\;\;q = 1,2, \cdots ,{N_{kn}}\\ \frac{{ - {k_{z2}}}}{{{k_{z1}}}}{x_2} + \cdots + \frac{{ - {k_{z\left( {m - n} \right)}}}}{{{k_{z1}}}}{x_{m - n}} > 0\;\;\;z = 1,2, \cdots ,{N_{kz}}\\ \left( {\frac{{{k_{p2}}}}{{{k_{p1}}}} - \frac{{{k_{q2}}}}{{{k_{q1}}}}} \right){x_2} + \cdots + \left( {\frac{{{k_{p\left( {m - n} \right)}}}}{{{k_{p1}}}} - \frac{{{k_{q\left( {m - n} \right)}}}}{{{k_{q1}}}}} \right){x_{m - n}} > 0\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p = 1,2, \cdots ,{N_{kp}} \end{array} \right. $ | (12) |
式中:Nkn为ki1 < 0的个数,Nkp为ki1>0的个数,Nkz为ki1=0的个数,推导过程见文献[14-15]。
力螺旋可行工作空间需要满足柔索力螺旋封闭条件外还需要一个最小正值从而保证末端执行器在运动过程中柔索不松弛,此外柔索的最大拉力不能无限大,应该更切合实际,最大值应小于驱动电机驱动柔索达到的最大拉力值或是柔索极限拉力值。力螺旋可行工作空间内柔索拉力可以描述为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Pt}} = \mathit{\boldsymbol{w}}}&{\left( {0 < {t_{\min }} \le {t_i} \le {t_{\max }}\;\;i = 1,2, \cdots ,m} \right)} \end{array} $ | (13) |
式中tmin与tmax分别为柔索拉力的最小值和最大值。
为了保证末端执行器在力螺旋可行工作空间内的移动路径连续时柔索拉力不发生跳变,采用拉力的1-范数为优化目标[19],优化柔索拉力为
| $ \begin{array}{*{20}{c}} {\min t = \sum\limits_{i = 1}^m {{t_i}} }\\ {{\rm{s}}.\;{\rm{t}}.\;\;\left\{ \begin{array}{l} \mathit{\boldsymbol{Pt}} = \mathit{\boldsymbol{w}}\\ 0 < {t_{\min }} \le {t_i} \le {t_{\max }} \end{array} \right.} \end{array} $ | (14) |
满足力螺旋封闭条件式(11)的同时满足柔索实际拉力范围的末端执行器工作空间为力螺旋可行工作空间。对于完全约束和冗余约束柔索并联机构力螺旋可行工作空间的求解算法步骤如图 2所示。

|
Download:
|
| 图 2 力螺旋可行工作空间算法流程 Fig. 2 Flow of the wrench feasible workspace algorithm | |
6自由度柔索并联机构如图 3所示,8个电机安装在静平台上,由柔索传递力和运动给位于静平台内的末端执行器,电机位置和柔索与静平台铰接点位置可以根据实际要求改动。

|
Download:
|
| 图 3 柔索并联机构示意图 Fig. 3 Schematic diagram of cable parallel mechanism | |
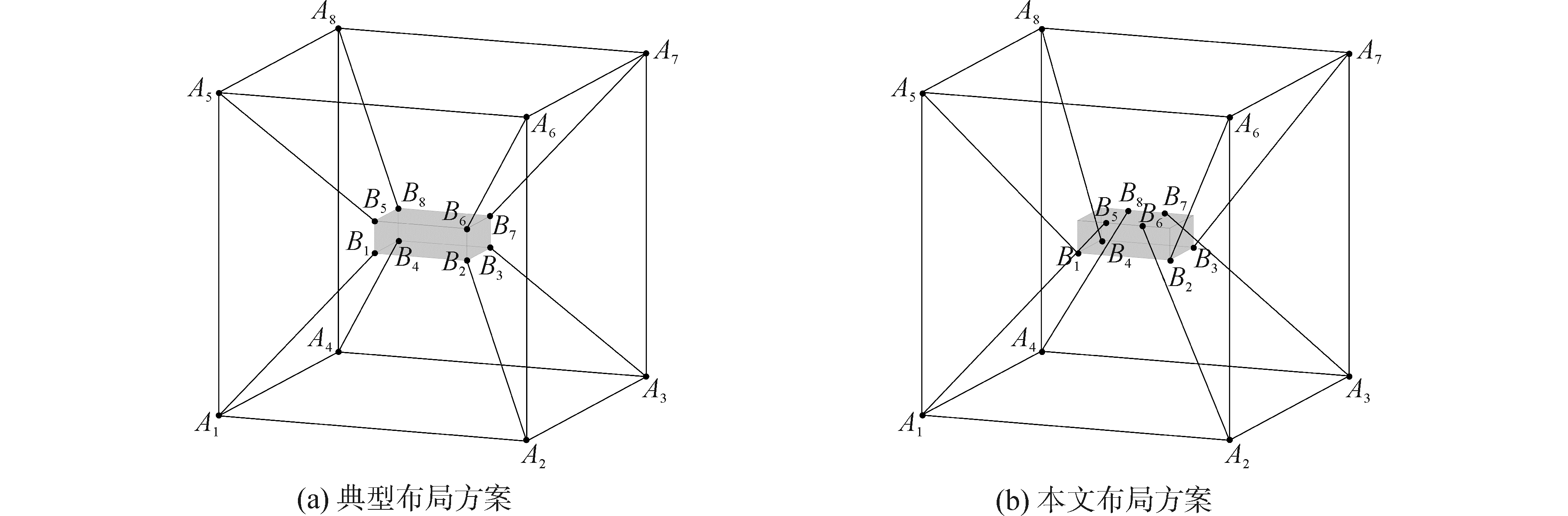
柔索并联机构工作空间的大小除了受柔索拉力变化范围、外载荷、末端执行器的位姿角影响外,还与柔索布局及柔索与末端执行器的铰接位置有关。对比在静平台和末端执行器尺寸确定时两种柔索布局方案的力螺旋可行工作空间的大小。图 4所示为两种柔索布局方案的6自由度柔索驱动并联机构简图。
|
Download:
|
| 图 4 6自由度柔索驱动并联机构简图 Fig. 4 Schematic diagram of 6 degree of freedom cable driven parallel mechanism | |
采用第3节提出的工作空间算法计算图 4典型布局方案(a)及本文布局方案(b)的力螺旋可行工作空间。图 4中6自由度柔索驱动并联机构简图,并联机构有8个驱动电机安装在边长为1 000 mm的立方体8个顶点上,顶点由Ai (i=1, 2, …, 8)表示。末端执行器是一个长、宽、高分别为300 mm、200 mm、100 mm的长方体,长方体与柔索的铰接点记为Bi(i=1, 2, …, 8)。本文布局方案(b)柔索与末端执行器的铰接点B5、B6距左端面100 mm,B7、B8距右端面100 mm。静平台上建立全局坐标系,原点O位于点A1,A1A2方向为x轴方向,A1A4方向为y轴方向,A1A5方向为z轴方向。在末端执行器质心点建立局部坐标系,局部坐标系原点O1位于末端执行器质心点,B1B2方向为x轴方向,B1B4方向为y轴方向,B1所在的第3条棱边所对应的方向为z轴方向。
采用Matlab环境对两种布局进行仿真分析,设定搜索步长为0.04 m,末端执行器的质量为5 kg。仿真实验过程主要对比两种柔索布局方案在末端执行器不同位姿角(α, β, γ)时设定区域的力螺旋封闭工作空间及不同柔索拉力范围限制时力螺旋可行工作空间的大小。
图 5为典型布局方案的末端执行器在不同位姿角(α, β, γ)时对应的力螺旋封闭工作空间及柔索拉力范围为5 N < t < 200 N时的力螺旋可行工作空间。图 5的阴影形状为机构的力螺旋封闭工作空间,可以看出力螺旋封闭工作空间是连续的、封闭的,并且位于静平台尺寸内部,与文献[11]数值方法算出的力螺旋封闭工作空间一致,从而验证算法的有效性。图 5的蓝色点集形成的空间为力螺旋可行工作空间,其在三个坐标面内的投影为红色点集所示,可以看出力螺旋可行工作空间位于力螺旋封闭工作空间内部,这与实际情况一致,进一步验证算法的正确性及所求力螺旋可行工作空间的准确性。

|
Download:
|
| 图 5 典型布局方案的末端执行器位姿角 Fig. 5 The end effector attitude angle of typical layout scheme | |
采用同一算法及搜索步长对本文布局方案(b)的末端执行器在不同位姿角时进行仿真分析,其仿真结果如图 6所示。

|
Download:
|
| 图 6 新布局方案的末端执行器位姿角 Fig. 6 The end effector attitude angle of new layout scheme | |
图 6为本文布局方案末端执行器在不同位姿角(α, β, γ)时力螺旋封闭工作空间及柔索拉力范围为5 N < t < 200 N时的力螺旋可行工作空间。图 6 (a)的阴影部分体积明显小于图 5 (a)的阴影部分体积,说明在末端执行器位姿角(0°, 0°, 0°)时,典型布局方案的力螺旋封闭工作空间更大。然而,图 6 (a)的蓝色点集表示的力螺旋可行工作空间明显大于图 5 (a)的蓝色点集表示的力螺旋可行工作空间,说明新布局方案的力螺旋可行工作空间更大。图 6 (b)~(c)阴影部分体积及蓝色点集体积明显大于图 5 (b)~(c),表明本文布局方案在末端执行器具有相同位姿角(3°, 0°, 0°)和(-3°, 0°, 3°)时具有更大的力螺旋封闭工作空间及力螺旋可行工作空间,从而说明新布局方案末端执行器位姿角变化范围更大。
为了进一步说明本文柔索布局方案的优势,对比末端执行器在不同位姿角及柔索拉力范围时两种方案所具有的力螺旋封闭工作空间点数及力螺旋可行工作空间点数。对比结果如表 1~3所示。
| 表 1 末端执行器的位姿角为(0°, 0°, 0°) Table 1 End effector attitude angle(0°, 0°, 0°) |
| 表 2 末端执行器的位姿角为(3°, 0°, 0°) Table 2 End effector attitude angle (3°, 0°, 0°) |
| 表 3 末端执行器的位姿角为(-3°, 0°, 3°) Table 3 End effector attitude angle (-3°, 0°, 3°) |
从表 1~3的工作空间数据点可以看出,除末端执行位姿为(0°, 0°, 0°)时,其他位姿角时本文方案比典型方案具有更大的力螺旋封闭工作空间和力螺旋可行工作空间;相同柔索拉力范围,本文方案具有的力螺旋可行工作空间更大;当柔索拉力范围减小时典型方案的力螺旋可行工作空间点数减少的更快,新方案相对减少较慢,说明典型方案力螺旋可行工作空间受外力螺旋影响较大,抵抗外力的能力相对较差,而本文方案力螺旋可行工作空间受到外力时具有更大的工作空间,可以抵抗更大的外力旋量。
从表 1~3可以看出当末端执行器在同一位姿角下,柔索拉力范围变小时典型方案和本文方案的力螺旋封闭工作空间点没有任何变化,这与力螺旋封闭工作空间只与末端执行器位姿角有关这一结论相吻合。然而,力螺旋可行工作空间随着柔索拉力范围的减小而减小,随着末端执行器位姿角复杂而减小,这与实际情况相符。本文方案比典型方案的力螺旋可行工作空间点数提升约19%。
综上所述,总结分析可以得出柔索并联机构的力螺旋可行工作空间相比于力螺旋封闭工作空间对于机构的性能分析时更具指导意义,不仅与静平台结构有关,还与柔索的布局及柔索拉力范围有关。
4.2 柔索与末端执行器铰接点位置优化从4.1节柔索布局典型方案与本文方案对比分析可知,本文柔索布局方案具有更大的力螺旋可行工作空间。本节对本文方案的柔索与末端执行器的铰接位置进行优化分析,确定最优位置。当末端执行器的同一棱边上具有交叉布置的柔索时,柔索将会限制机构的一个转动自由度,所以同一棱边上不应产生交叉布置的柔索。为保证柔索并联机构具有一定的稳定性及刚度,同一棱边上的柔索需要保持一定距离,因此同一棱边上的柔索具有最适合布局。
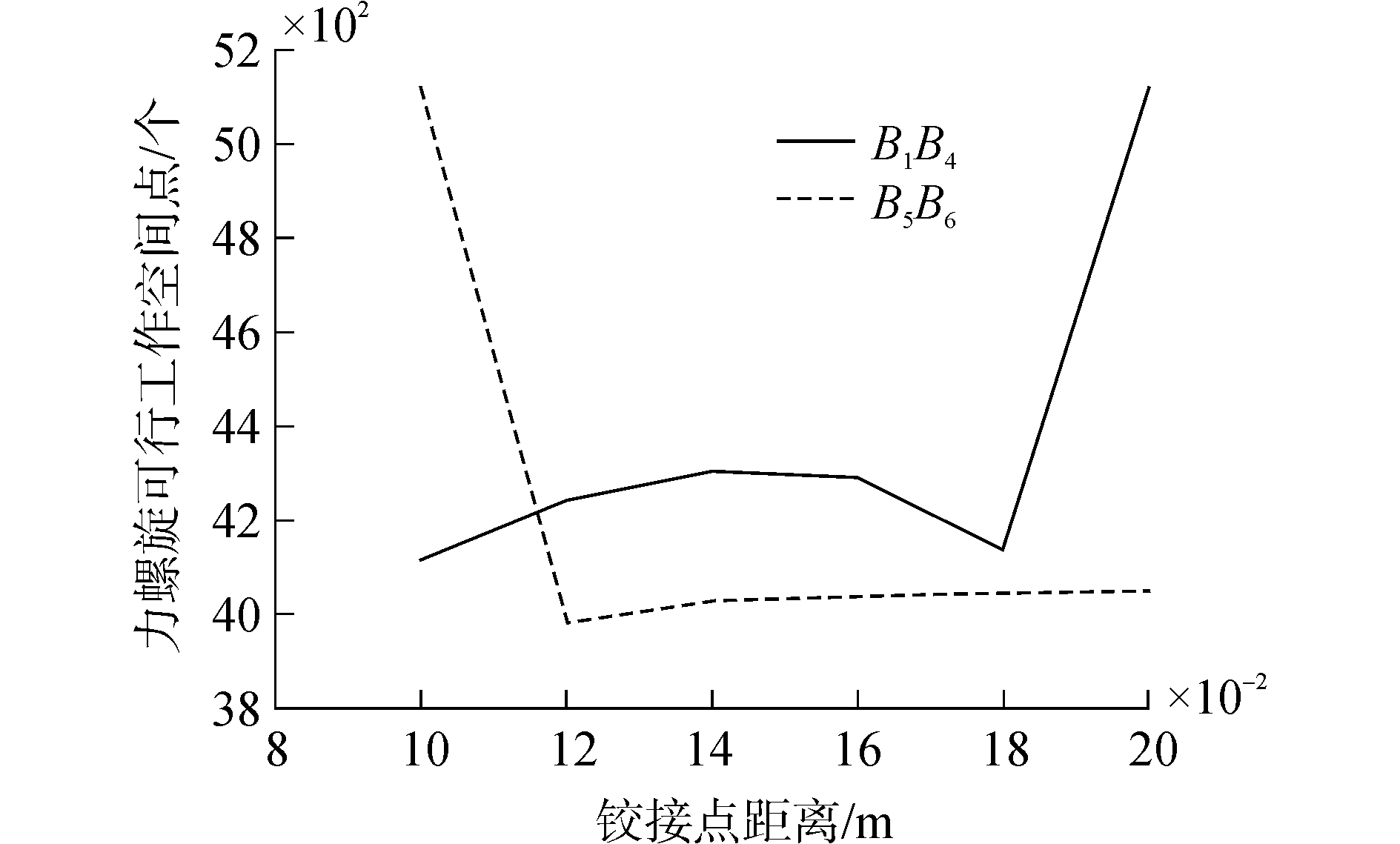
为了确定柔索与末端执行器的最佳铰接点位置,对末端执行器棱边铰接点采用对称变化及等距离变化观察力螺旋可行工作空间点数。对图 4本文方案棱边铰接点B1与B4和铰接点B2与B3对称且同时以距离10 mm减小,铰接点B5与B6和铰接点B7与B8对称且同时以10 mm增大。图 7为末端执行器棱边铰接点距离变化时对力螺旋可行工作空间的影响图。
|
Download:
|
| 图 7 距离对空间点数的影响 Fig. 7 The influence of distance on spatial points | |
从图 7可以看出,柔索与末端执行器铰接点B1和B4距离为0.2 m,B2和B3距离为0.2 m柔索并联机构的力螺旋可行工作空间点个数达到最大值;铰接点B5和B6距离为0.1 m,B7和B8距离为0.1 m柔索并联机构的力螺旋可行工作空间点个数达到最大值。力螺旋可行工作空间点个数越多说明末端执行器在给定的静平台区域限制范围内能够遍历的区域空间组成的体积越大,从而可以确定柔索与末端执行器铰接点最优位置。
5 结论1) 将仿真实例的力螺旋封闭工作空间与文献的数值方法形成的工作空间对比可知,采用解析方法的正确性及力螺旋可行工作空间的有效性。
2) 通过对柔索并联机构理论推导和仿真实验分析,确定力螺旋封闭工作空间和力螺旋可行工作空间的判断条件;通过对8柔索6自由度柔索并联机构仿真分析,确定柔索拉力范围对力螺旋可行工作空间的影响以及表明采用力螺旋可行工作空间评价机构性能的相对准确性。
3) 与典型布局8柔索6自由度并联机构工作空间相对比,证明本文新布局方案增加了力螺旋可行工作空间点数,并对本文布局方案柔索与末端执行器的铰接点进行优化,确定了最佳铰接点位置。
因为对于本文布局优化方法采用的是固定一个方向铰接点坐标,只改变一个方向坐标的优化方法,所以在后续研究工作应该采用一种同时改变两个坐标的优化算法对机构进行优化。
| [1] |
TANG Xiaoqiang. An overview of the development for cable-driven parallel manipulator[J]. Advances in mechanical engineering, 2014, 6. DOI:10.1155/2014/823028 (  0) 0)
|
| [2] |
张志刚, 张锦绣. 基于高斯伪谱法的系绳式InSAR系统展开滑模控制[J]. 哈尔滨工程大学学报, 2017, 38(2): 293-299. ZHANG Zhigang, ZHANG Jinxiu. Sliding mode control of a tethered InSAR system deployment on the basis of the Gauss pseudospectral method[J]. Journal of Harbin Engineering University, 2017, 38(2): 293-299. (  0) 0)
|
| [3] |
GOUTTEFARDE M, COLLARD J F, RIEHL N, et al. Geometry selection of a redundantly actuated cable-suspended parallel robot[J]. IEEE transactions on robotics, 2015, 31(2): 501-510. DOI:10.1109/TRO.2015.2400253 (  0) 0)
|
| [4] |
杨恒, 薛开. 六自由度并联机构变搜索原点迭代正解方法[J]. 应用科技, 2016, 43(2): 54-58. YANG Heng, XUE Kai. Iterative method for forward kinematics of the stewart platform with dynamic search origin[J]. Applied science and technology, 2016, 43(2): 54-58. (  0) 0)
|
| [5] |
NING Kejun, ZHAO Mingyang, LIU Jie. A new wire-driven three degree-of-freedom parallel manipulator[J]. Journal of manufacturing science and engineering, 2006, 128(3): 816-819. DOI:10.1115/1.2194061 (  0) 0)
|
| [6] |
于亮亮, 仇原鹰, 苏宇. 高速柔索牵引摄像机器人动力工作空间研究[J]. 工程力学, 2013, 30(11): 245-250. YU Liangliang, QIU Yuanying, SU Yu. Dynamic workspace of a high-speed cable-driven camera robot[J]. Engineering mechanics, 2013, 30(11): 245-250. (  0) 0)
|
| [7] |
LAU D, EDEN J, TAN Ying, et al. CASPR: a comprehensive cable-robot analysis and simulation platform for the research of cable-driven parallel robots[C]//Proceeding of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems. Daejeon, South Korea, 2016: 3004-3011.
(  0) 0)
|
| [8] |
ABBASNEJAD G, CARRICATO M. Direct geometrico-static problem of underconstrained cable-driven parallel robots with n cables[J]. IEEE transactions on robotics, 2015, 31(2): 468-478. DOI:10.1109/TRO.2015.2393173 (  0) 0)
|
| [9] |
郑亚青, 刘雄伟, 林麒. 绳牵引并联机构奇异性分析及无奇异机构设计[J]. 机械工程学报, 2006, 42(2): 52-62. ZHENG Yaqing, LIU Xiongwei, LIN Qi. Singularity analysis of wire-driven parallel manipulators and design of singuarliry-free manipulators[J]. Chinese journal of mechanical engineering, 2006, 42(2): 52-62. (  0) 0)
|
| [10] |
PHAM C B, YEO S H, YANG Guilin, et al. Force-closure workspace analysis of cable-driven parallel mechanisms[J]. Mechanism and machine theory, 2006, 41(1): 53-69. DOI:10.1016/j.mechmachtheory.2005.04.003 (  0) 0)
|
| [11] |
GOUTTEFARDE M, GOSSELIN C M. Analysis of the wrench-closure workspace of planar parallel cable-driven mechanisms[J]. IEEE transactions on robotics, 2006, 22(3): 434-445. DOI:10.1109/TRO.2006.870638 (  0) 0)
|
| [12] |
DIAO Xiumin, MA Ou. A method of verifying force-closure condition for general cable manipulators with seven cables[J]. Mechanism and machine theory, 2007, 42(12): 1563-1576. DOI:10.1016/j.mechmachtheory.2007.06.008 (  0) 0)
|
| [13] |
刘欣, 仇原鹰, 盛英. 绳牵引并联机器人工作空间的判定条件与解析表达[J]. 机械工程学报, 2011, 47(3): 28-35. LIU Xin, QIU Yuanying, SHENG Ying. Criteria conditions and analytic expression of workspace of wire-driven parallel manipulators[J]. Journal of mechanical engineering, 2011, 47(3): 28-35. (  0) 0)
|
| [14] |
FERRARESI C, PAOLONI M, PESCARMONA F. A new methodology for the determination of the workspace of six-DOF redundant parallel structures actuated by nine wires[J]. Robotica, 2007, 25(1): 113-120. (  0) 0)
|
| [15] |
欧阳波, 尚伟伟. 6自由度绳索驱动并联机器人力封闭工作空间的快速求解方法[J]. 机械工程学报, 2013, 49(15): 34-41. OUYANG Bo, SHANG Weiwei. Efficient computation method of force-closure workspace for 6-DOF cable-driven parallel manipulators[J]. Journal of mechanical engineering, 2013, 49(15): 34-41. (  0) 0)
|
| [16] |
HAY A M, SNYMAN J A. Optimization of a planar tendon-driven parallel manipulator for a maximal dextrous workspace[J]. Engineering optimization, 2005, 37(3): 217-236. DOI:10.1080/03052150512331328303 (  0) 0)
|
| [17] |
张耀军, 张玉茹, 戴晓伟. 基于工作空间最大化的平面柔索驱动并联机构优化设计[J]. 机械工程学报, 2011, 47(13): 29-34. ZHANG Yaojun, ZHANG Yuru, DAI Xiaowei. Optimal design for planar cable-driven parallel mechanism with respect to maximizing workspace[J]. Journal of mechanical engineering, 2011, 47(13): 29-34. (  0) 0)
|
| [18] |
郑亚青.绳牵引并联机构若干关键理论问题及其在风洞支撑系统中的应用研究[D].泉州: 华侨大学, 2004. ZHENG Yaqing. Research on some key theoretical problems of rope traction parallel mechanism and its application in wind tunnel support system[D]. Quanzhou: Huaqiao University, 2004. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


