2. 高新船舶与深海开发装备协同创新中心, 上海, 200240;
3. 上海海洋大学 工程学院, 上海 201306
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. College of Engineering Science and Technology, Shanghai Ocean University, Shanghai 201306, China
船舶制造是典型的拉式生产方式,分段由钢板焊接而成,是建造船体的基本单位。分段在总组之前需要经过预舾装、涂装、舾装、预装配等操作。
这些操作需要在不同堆场内进行,平板车负责分段在堆场间的运输。为了船舶能按时完成,所有分段的操作都应按照计划表精确执行,平板车需要在预定的时间内在堆场间运输分段。分段运输的延迟可能导致整个生产计划的延迟,因此,平板车的调度是十分重要的。
国内外对此类平板车堆场间调度研究相对较少。Roh等[1]以最小化空载的行驶距离和多平板车路径干涉为优化目标,先用蚁群算法获得初始解,然后用遗传算法搜索更优的解,提出基于两种算法的混合优化算法。Kim等[2]用两种算法,将空载运行时间、拖期时间及延迟时间作为目标函数,设计了GA和SEA算法,并通过实例比较了两种算法的性能指标。张志英等[3]以最小化临时分段移动量和平板车在堆场中的行驶距离为优化目标,运用遗传算法确定了分段在堆场中的最优停放位置和进出场路。陶宁蓉[4]考虑了分段进出堆场的任务顺序对调度方案的影响, 并运用启发式算法和禁忌搜索对结果进行了优化。张志英等[5]以最小化临时分段移动量和平板车在堆场中的行驶距离为优化目标建立优化模型,提出一种最短路径算法对问题进行求解,并比较该算法与Dijkstra算法的求解效果。陈凯等[6]考虑了分段进场的时间窗约束,以最小化分段移动度为目标,提出多链DNA遗传算法对分段的移动顺序、放置位置和运输路径进行优化。陈云云等[7]考虑分段涂装作业中的调度问题,以最小化最大完工时间为优化目标,构造了基于重排策略的启发式算法,得到较优的分段涂装调度计划。
本文考虑平板车与任务分段之间的承重约束、由于任务优先级产生任务之间的前后约束以及任务的时间窗约束,以平板车空载运行时间和任务未满足时间窗始点和终点约束而产生的惩罚时间作为目标函数,设计了遗传算法和两种构造邻域空间策略的禁忌搜索算法构建的混合优化算法对该调度问题进行求解,设计深度优先遍历算法求解考虑转向次数的最优路径。
1 堆场间调度问题描述文中研究的问题可以做以下描述:有m个待执行的分段运输任务和n个运输平板车,每个任务包括任务号、分段重量、任务运输起点和终点、任务时间窗(任务可以开始执行的时间点和任务必须完成的时间点)、任务优先级(优先级高的任务必须先完成)。每个平板车有各自的承重能力。每个任务必须由满足其分段承重需求的一辆平板车从任务运输起点运送至终点[4, 8]。任务在由释放时间和截止时间组成的时间窗内开始执行和完成,任务时间窗约束为松约束。本文要解决的问题:1)运输任务的最优序列。2)运输任务对应哪个平板车执行。3)平板车运行时的最优路径。4)各个任务的开始执行时间和完成时间。
图 1是某船厂的道路路口情况、堆场的位置以及平板车停放位置。下面举例说明平板车执行任务时候的实际流程。假设平板车T1任务序列是任务A和任务B,任务A:将目标分段从平直中心运输到涂装平台;任务B:将目标分段从9号平台运送至曲面车间。那么平板车实际的执行流程是,从平板车停放位置运行到平直中心的堆场,提取分段,负载运行至涂装平台,放下分段。然后空载运行至9号平台,提取目标分段,负载运行至曲面车间。如果平板车执行完任务,则空载运行至停放位置。堆场内分段提取时间,以及堆场内的运行时间不在本文研究范围内。

|
Download:
|
| 图 1 道路及堆场分布图 Fig. 1 Roads and yards distribution | |
考虑到堆场实际情况以及便于堆场间调度问题的研究,假设:1)最重的任务分段的重量不大于最大承重量的平板车的承重量。2)平板车运输分段的过程一旦开始执行,不会被其他因素打断。3)平板车在同一时刻最多只能运输一个分段。4)道路上不存在平板车干涉。5)平板车到达堆场装载分段和卸载分段的时间为常数。
2 堆场间调度模型的建立 2.1 堆场路口矩阵图依据路口以及堆场布局图,文中采用路口表达堆场之间路径的方法。编写程序时,基于16个路口,构建一个16×16的对称矩阵H来表示两个路口之间是否可以通行。H中的元素Hij表示第i个路口与第j个路口之间是否可以通行。Hij=1表示可以通行,Hij=0表示不可以通行。
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{H_{11}}}& \cdots &{{H_{116}}}\\ \vdots & \ddots & \vdots \\ {{H_{161}}}& \cdots &{{H_{1616}}} \end{array}} \right] $ |
评价平板车运行路径优劣的因素主要有:1)路径长度。2)若为负载运行时,还需考虑转向次数[5]。对于90°折线型路径,转向只能有两种情况:1)水平方向转垂直方向。2)垂直方向转水平方向。无论处于哪种转向情况,任意发生转向的3点的坐标,均满足如下公式:
| $ \begin{array}{l} \left| {{x_A} - {x_B}} \right| = 0, \left| {{y_B} - {y_C}} \right| = 0, \\ \left| {{y_A} = {y_B}} \right| = 0, \left| {{x_B} - {x_C}} \right| = 0。\end{array} $ |
式中:xp为路口p的横坐标; yp为路口p的纵坐标;p为路口编号,p=1, 2, …, 16。执行任务i时平板车负载运行的转向次数
| $ \begin{array}{l} {X_j} = \left\{ \begin{array}{l} 1, \left| {{x_j} - {x_{j + 1}}} \right| = 0\;\;\;{\rm{and}}\;\;\;\left| {{y_{j + 1}} - {y_{j + 2}}} \right| = 0\\ 0, {\rm{否则}} \end{array} \right., \\ {Y_j} = \left\{ \begin{array}{l} 1, \left| {{y_j} - {y_{j + 1}}} \right| = 0\;\;\;{\rm{and}}\;\;\;\left| {{x_{j + 1}} - {x_{j + 2}}} \right| = 0\\ 0, {\rm{否则}} \end{array} \right., \end{array} $ |
n为执行任务i时路径中包含的路口个数。
构建评价函数时,若平板车为空载运行,评价函数为空载行驶时间ktih;若为负载运行,评价函数为负载行驶时间加上由于转向所带来的延迟时间:
| $ f{t_i} + T \times {m_i} $ |
式中:ktih为平板车执行完任务i后紧接着执行任务h的任务间空载运行时间;fti为平板车执行任务i的负载运行时间;T为平板车负载运行时转向一次消耗的时间,min/次。
2.3 堆场间调度模型1) 决策变量:
yil表示任务i由平板车l执行与否的决策变量。若执行为1,不执行为0。
zihl表示平板车l执行任务顺序的决策变量。若平板车l执行完任务i后紧接着执行任务h为1,否则为0。
zOil表示平板车是否执行其第一个任务的决策变量。若任务i是平板车l的第一个任务则为1,否则为0。
Oi表示任务i是否满足其时间窗始点约束的决策变量。若si>ri, Oi=0, 若si<ri, Oi=1。
Ei表示任务i是否满足其时间窗终点约束的决策变量。若ci≥di, Ei=1,若ci<di, Ei=0。其中,i、h为运输任务编号,i, h=1, 2, …, n;l为平板车编号,l=1, 2, …, m;si为任务i的实际开始执行时间;ci为任务i的实际完成时间;ri为任务i的释放时间,即可以开始执行的时间;di为任务i的截止时间,即必须完成的时间。
将平板车执行两个任务之间的空载运行时间、不满足任务时间窗始点约束、时间窗终点约束造成的惩罚时间的权重和作为目标函数:
| $ \begin{array}{l} {\rm{Min}}z = \alpha \times \sum\limits_{l = 1}^t {\sum\limits_{h = 1, h \ne i}^n {\sum\limits_{i = 1}^n {{z_{ihl}} \cdot k{t_{ih}}} } } + \\ \beta \times \sum\limits_{i = 1}^n {{O_i} \cdot \left( {{s_i} - {r_i}} \right)} + \gamma \times \sum\limits_{i = 1}^n {{E_i} \cdot \left( {{c_i} - {d_i}} \right)} \end{array} $ |
式中:α为平板车空载运行时间的权重,β为未满足任务时间窗始点约束产生的惩罚时间权重,γ为未满足时间窗终点约束产生的惩罚时间权重。
2) 约束条件:
| $ \sum\limits_{l = 1}^m {{y_{il}} = 1, \;\;\;\;\forall i} $ | (1) |
| $ \left( {{s_i} + f{t_i}} \right) \cdot p{r_{ih}} \le {s_h}, \forall i, h $ | (2) |
| $ {s_i} + f{t_i} + {z_{ihl}} \cdot k{t_{ih}} - {s_h} \le \left( {1 - {z_{ihl}}} \right) \cdot Q, \forall i, h \ne i, l $ | (3) |
| $ C{W_l} \ge {W_i} \cdot {y_{il}}, \forall i, l $ | (4) |
| $ \sum\limits_{i = 1}^n {{z_{Oil}} = 1, \forall l} $ | (5) |
| $ \sum\limits_{j = 1, j \ne i}^n {{z_{jil}} + {z_{Oil}} = {y_{il}}, } \forall i, l $ | (6) |
| $ \sum\limits_{j = 1, j \ne i}^n {{z_{ijl}} \le {y_{il}}, } \forall i, l $ | (7) |
约束(1)限制每一个任务被执行且仅被一辆平板车执行。约束(2)考虑到任务之间存在优先级,即先完成优先级高的任务。此处主要指不同分段之间存在优先级约束,因为同一个分段的不同工序一般时间窗上会有先后顺序。假定任务i比任务h优先级高,则在后任务h需要在先任务i完成之后开始执行。约束(3)表示平板车l执行完任务i后紧接着执行任务h,则任务i和任务h之间存在时间限制。约束(4)限制平板车的运输能力不小于任务分段的重量;约束(5)~(7)表示如果任务被一个平板车执行,那么这个任务在该平板车的运输计划中只能出现一次。
3 堆场间调度模型求解方法 3.1 模型求解方法遗传算法在组合优化问题中具有较好的效果,广泛应用于TSP问题。禁忌搜索算法依靠禁忌表的存在,可能在搜索中跳出局部最优,同时不同的构造邻域的方法也增加了邻域空间的多样性,具有很好的求解效果。除此之外,任务前后约束是十分重要的,而禁忌搜索中的禁忌表恰好可以一定程度上减小任务前后约束被破坏[9];个体染色体修复也可以保护约束条件[10]。因此本文设计在遗传算法求解一个较优解之后,启动禁忌搜索算法继续求解, 混合优化算法设计如下:
1) 初始化。读取任务信息和平板车信息。
2) 产生初始种群。将待调度任务排序,分配给平板车。形成的一个可行解作为一个调度方案(染色体)。
3) 编码。文中的染色体是基于正整数构成的两个一维数组,分别表示任务序列和平板车序列。任务序列中的第N个基因上的数字表示任务号,平板车序列中的第N个基因上的数字表示执行该任务的平板车号。因此,任务序列和平板车序列是一一对应关系,除此之外,每个车上的任务序列还表示执行顺序。图 2表示10个任务4辆平板车产生的染色体。该染色体表示将任务3分配给平板车1,任务1分配给平板车2,任务5分配给平板车3,任务7分配给平板车4,以此类推。平板车1上有任务3和任务8,那么在平板车执行的时候,先执行任务3再执行任务8。其余平板车同理。

|
Download:
|
| 图 2 染色体示例 Fig. 2 Example of the chromosome | |
4) 解码。计算每个染色体的适应度。即依据任务序列和平板车序列的对应关系将各个任务按照在任务序列中的顺序分配给各个平板车,解码后各个平板车上的任务顺序表示任务执行顺序。依据每个平板车上的任务号调用深度优先遍历算法求解负载运行时间和空载运行时间,得到各个任务的开始执行时间和结束时间。计算适应度。数学模型中的目标函数可以用来对个体表现的评价。但本文中目标函数与个体表现成反比,因此,用一个较大的整数M减去目标函数作为本文中算法的适应度函数。
5) 选择。选择操作使用经典轮盘赌。
6) 单点交叉。两条父代染色体中选择其中一条,随机选择一断点,进行交叉操作。断点右侧基因序列继承到子代时的顺序与另外一个父代中相应基因序列的顺序保持一致,如图 3所示。

|
Download:
|
| 图 3 单点交叉图 Fig. 3 One point crossover | |
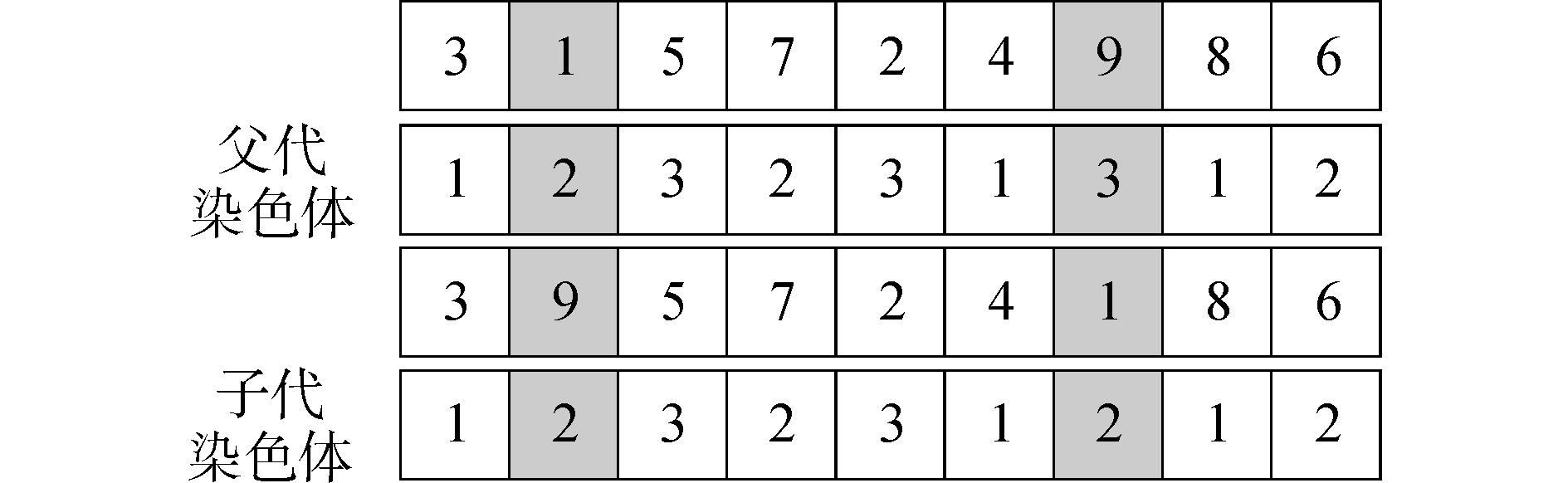
7) 保护约束条件的交换变异。父代染色体中任务之间满足约束条件,因此在进行交换变异中,选择两个点进行交换变异,为了防止因为随机选择破坏任务前后约束关系,设定交换变异的两点选择是在无前后约束的任务中选择。在父代染色体中,假设任务7和任务4是具有前后约束的任务对,那么在随机选择交换变异的任务范围内就不包括任务7和任务4。例如,随机选择结果为任务1和任务9,得到子代的任务序列的过程如图 4所示:在进行交换变异时,需要考虑任务序列变异后的情况是否满足平板车承重能力约束,如果不满足需要随机选择平板车。此时需要判断平板车3和任务1之间是否满足平板车承重与任务重量之间的约束,平板车2和任务9之间同理。如果平板车3和任务1之间不满足约束,则在满足承重要求的平板车里随机产生一个。
|
Download:
|
| 图 4 交换变异 Fig. 4 Exchange mutation | |
8) 再生。在父代染色体中按适应度大小排列,选择一定数量的适应度高的染色体直接保留到下一代中,即保留父代中“精英”染色体。
9) 禁忌搜索初始化。将遗传算法求得最优序列作为禁忌搜索的初始解。将具有前后任务约束的任务对添加到禁忌表中,并设置其禁忌长度为迭代次数。
10) 禁忌搜索邻域结构。此处设计两种构造邻域解的方法:①对任务序列进行局部搜索。交换两个任务序列的基因获得邻域解,如果交换后不满足平板车承重约束,则随机产生平板车序列;若满足,则不变。②对平板车序列进行局部搜索。选择两个任务序列的基因,随机生成满足其承重要求的平板车。基于以上两种构造邻域解的方法,提出两种策略。
策略1:在每一次迭代中,产生每一个邻域解时随机选择①、②。
策略2:在每一次迭代中,产生邻域解时,其中一半的邻域解选择①,另一半的邻域解选择②。
11) 更新禁忌表。禁忌表用于记录邻域变换的操作,进行一次禁忌搜索操作后,更新禁忌长度和禁忌表中的元素。本文采用“任务号-任务号”作为禁忌元素存放在禁忌表中。
12) 特赦准则。当邻域中的所有元素都被禁忌,或者在某次迭代中选择禁忌表中的元素可以得到当前最好的解,则在本次迭代中特赦该禁忌元素。
13) 停止操作。搜索过程中进行两个计数,一个是总迭代步数,另一个是评价函数连续未得到改善的步数。当算法迭代次数达到预先设定的值,将获得的当前个体挑选出来。该个体解码后获得的调度方案即为算法求解的最优方案。
3.2 深度优先遍历算法求解最优路径本文求解最短路径的时候考虑了转向的因素,经典的Dijkstra算法并不合适。本文采用深度优先遍历算法,遍历所有可行路径,方便考虑转向的因素。将距离起始堆场出口最近的路口作为start0,将距离目标堆场的入口最近的路口作为end0。求解start0和end0之间所有负载运行的可行路径。同理,将距离目标堆场的出口最近的路口作为start1,距离下一个任务的起始堆场的入口最近的路口作为end1。求解star1和end1之间所有空载运行的可行路径。在可行路径中搜索评价函数最优的路径作为最优路径。求解最优路径的步骤:
1) 读取路口矩阵,构建路口网络图。
2) 读取任务序列,读取任务序列中相应起始堆场内的路径和目标堆场内的路径。
3) 根据坐标求解距离堆位最近的路口start0, end0;start1, end1。
4) 调用深度优先遍历算法求解负载运行和空载运行star0, end0;start1, end1之间的所有可行路径,分别保存在数组sumPath0和sumPath1中。
5) 依据负载运行还是空载运行选择相应的评价函数,计算路径的评价函数值。
6) 计算数组中的所有可行路径,选择评价函数最优的作为最优路径。
4 实例验证与结果分析 4.1 实例验证为了验证模型及算法的可行性与正确性。以某船厂的实际调度任务为例,利用Visual Studio 2012软件求解。输入参数如下:1)船厂路口矩阵图; 2)任务分段信息; 3)平板车信息; 4)时间窗约束信息。5)算法参数:第一步遗传算法种群个数40,迭代次数100。第二步禁忌搜索的邻域搜索长度40,禁忌长度28,迭代次数100,无改善解代数为60。堆场间任务计划如表 1,得到的调度方案如表 2。
| 表 1 堆场间任务计划 Table 1 Task plan between yards |
| 表 2 调度方案 Table 2 Dispatch plan |
从调度结果可以看出,平板车与执行任务之间满足承重约束;实例中任务2优先级高于任务9,结果满足任务优先级约束,绝大多数任务满足时间窗约束;平板车执行任务时行驶路径满足厂区布局图。实例验证算法的有效性。
4.2 数值试验分析 4.2.1 算法对比分析用不同任务数和不同平板车数的组合来比较遗传算法和两种策略的遗传-禁忌混合优化算法的求解效果。每次试验运行5次取其平均值,结果如表 3所示。将上述数据按任务数量和平板车数量作图,比较不同方法求得最优解,不满足任务时约束的任务数量,以及求解提升程度Ⅰ如图 5所示。无论从任务数量还是平板车数量角度看,策略1、策略2的求解效果都明显优于文中的遗传算法。从任务数角度观察,最优解时的目标函数值、不满足任务时间窗约束的任务数、指数I具有一致性。任务数为20、40时,策略1求得目标函数值、指数I、不满足任务时间窗约束的任务数均优于策略2,而任务数为30时,策略2均优于策略1。从平板车数量角度观察,当平板车数为4和5时,一致性依然成立,且策略1优于策略2,但平板车数为3时,一致性不成立。从问题的求解量角度观察,当任务数量和平板车数量增多的时候,组合情况极具增加,随机选择构建邻域解集合(策略1)可以很好的适应较大规模问题的求解,在任务数为40、平板车数为4和5的时候,策略1求解均优于策略2。而基于策略2的稳定选择构建邻域解集合,在任务数量和平板车数量较小的时候,具有很好的稳定性,在任务数为30、平板车数为3时,策略2求解优于策略1。

|
Download:
|
| 图 5 不同任务数、平板车数求解性能对比 Fig. 5 Contrast about different tasks and flatcars | |
| 表 3 不同任务数、平板车数求解结果 Table 3 Results about different tasks and flat cars |
为了对比明显,在此定义F表示第一阶段遗传算法求得最优解,Z表示对应算法迭代后求得最优解,I=(F-Z)/F表示解的提升,N表示解中不满足时间窗约束的任务数。t表示迭代求解时间其中,B表示任务数量,T表示平板车数量。取B=20, 30, 40;T=3, 4, 5;其中B=20时第一阶段迭代25次,最终求解迭代50次。B=30时,第一阶段迭代50次,最终求解迭代100次。B=40时,第一阶段迭代100次,最终求解迭代300次。
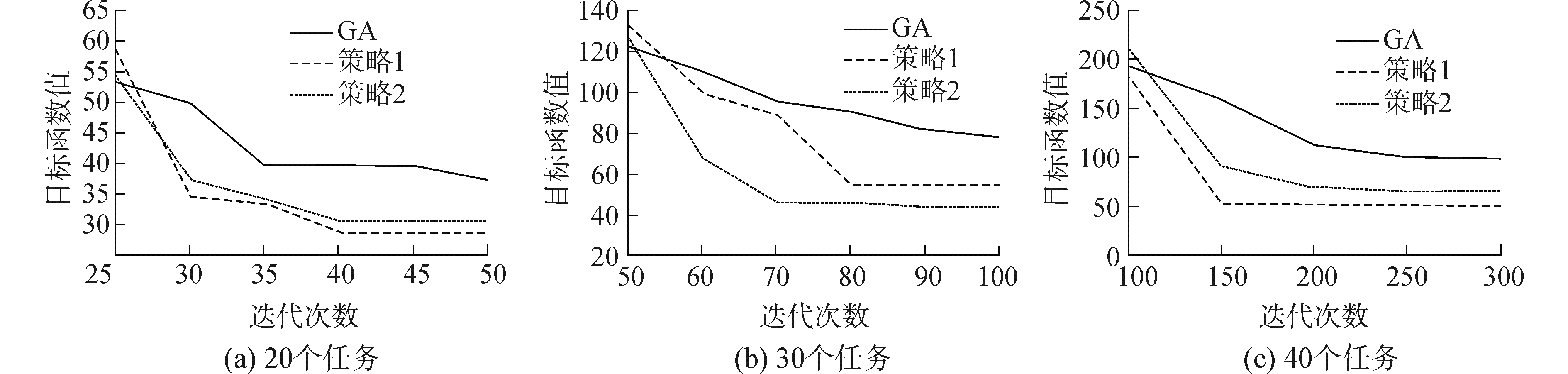
4.2.2 算法收敛性分析为了更深入的比较3种算法的求解质量。本节从算法收敛性的角度出发,比较3种方法的收敛速度。以5辆平板车,20、30、40个任务为例,得到3种方法求解过程中目标函数值与迭代次数的关系,从图 6中可以明显观察到在设定的迭代次数中遗传算法均没有收敛,而策略1在40、80、150代的时候已经收敛;策略2在40、90、200代的时候已经收敛。从收敛性的角度观察发现,任务数量为20时,策略1、策略2收敛速度相当,但在开始的5次迭代里,策略1目标函数值下降最多;任务数为30时,策略1仍然比策略二先收敛;任务数为40时,策略1明显优于策略2。
|
Download:
|
| 图 6 算法收敛性分析 Fig. 6 Convergence analysis | |
1) 数值实验表明文中提出方法的有效性和实用性, 目标函数相比传统按照调度员经验的分配方式有明显优势,能够解决分段任务数量较大的调度状况。
2) 算法性能方面,相对主流方法,从求解效果和收敛速度方面具有优势。
由于研究基于较多的假设,没有考虑多车协同运输,需要进一步研究;如何缩减大任务量下的求解时间,还需要进一步研究。
| [1] |
ROH M I, CHA J H. A block transportation scheduling system considering a minimisation of travel distance without loading of and interference between multiple transporters[J]. International journal of production research, 2011, 49(11): 3231-3250. DOI:10.1080/00207543.2010.484427 (  0) 0)
|
| [2] |
JOO C M, KIM B S. Block transportation scheduling under delivery restriction in shipyard using meta-heuristic algorithms[J]. Expert systems with applications, 2014, 41(6): 2851-2858. DOI:10.1016/j.eswa.2013.10.020 (  0) 0)
|
| [3] |
张志英, 徐建祥, 计峰. 基于遗传算法的船舶分段堆场调度研究[J]. 上海交通大学学报, 2013, 47(7): 1036-1042. ZHANG Zhiying, XU Jianxiang, JI Feng. Shipbuilding yard scheduling approach based on genetic algorithm[J]. Journal of Shanghai jiao Tong University, 2013, 47(7): 1036-1042. (  0) 0)
|
| [4] |
陶宁蓉.船舶分段建造过程中的资源调度优化研究[D].上海: 上海交通大学, 2013. TAO Ningrong. Research on resouce scheduling problems during ship block assembly process[D]. Shanghai: Shanghai Jiao Tong University, 2013. (  0) 0)
|
| [5] |
张志英, 申钢, 刘祥瑞, 等. 基于最短路算法的船舶分段堆场调度[J]. 计算机集成制造系统, 2012, 18(9): 1982-1990. ZHANG Zhiying, SHEN Gang, LIU Xiangrui, et al. Block storage yard scheduling of shipbuilding based on shortest-path algorithm[J]. Computer integrated manufacturing systems, 2012, 18(9): 1982-1990. (  0) 0)
|
| [6] |
陈凯, 蒋祖华, 刘建峰, 等. 带有进场时间窗的船舶分段堆场调度[J]. 上海交通大学学报, 2016, 50(9): 1390-1398. CHEN Kai, JIANG Zuhua, LIU Jianfeng, et al. Shipbuilding yard scheduling with block inbound time window[J]. Journal of Shanghai jiao Tong University, 2016, 50(9): 1390-1398. (  0) 0)
|
| [7] |
陈云云, 张志英. 船舶分段涂装作业重入调度优化算法[J]. 哈尔滨工程大学学报, 2016, 37(8): 1103-1110. CHEN Yunyun, ZHANG Zhiying. Optimization algorithm for reentrant scheduling in block painting operations[J]. Journal of Harbin Engineering University, 2016, 37(8): 1103-1110. (  0) 0)
|
| [8] |
HU Zhihua, WEI Chen. Synchronizing vehicles for multi-vehicle and one-cargo transportation[J]. Computers & industrial engineering, 2018, 119: 36-49. (  0) 0)
|
| [9] |
曾建智, 张志英. 基于智能算法的船舶分段堆场调度计划与优化[J]. 哈尔滨工程大学学报, 2016, 37(1): 41-47. ZENG Jianzhi, ZHANG Zhiying. Block stockyard scheduling and optimizing based on an intelligent algorithm[J]. Journal of Harbin Engineering University, 2016, 37(1): 41-47. (  0) 0)
|
| [10] |
孟令通, 朱洪渊, 蒋祖华, 等. 基于遗传算法的平板车调度优化方法[J]. 哈尔滨工程大学学报, 2018, 39(3): 554-560. MENG Lingtong, ZHU Hongyuan, JIANG Zuhua, et al. Flat-car scheduling opyimization method based on genetic algorithm[J]. Journal of Harbin Engineering University, 2018, 39(3): 554-560. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


