2. 电子科技大学 机器人中心, 四川 成都 611731
2. Center for Robotics, University of Electronic Science and Technology of China, Chengdu 611731, China
并联机构具有刚度大、承载能力强等诸多优点,广泛应用于运动模拟、并联机床和产品的测试中[1-5]。在船舶运动模拟实验中,六自由度并联机构用来模拟船舶在海浪作用下的平移、升降、俯仰和偏航等六自由度运动[6-9]。液压驱动并联机构存在功耗高、易漏油和维护难等缺点。而电动并联机构具有功耗低、可靠性高、易维护的优点,在实际工程中越来越多的取代液压并联机构。然而,电动并联机构也存在驱动能力偏小的弱点,因此如何降低电动并联机构的功耗并提高其驱动能力,使其适应重载船舶运动模拟试验台的要求变得非常重要。辅以冗余驱动单元来平衡负载的重力是弥补电动缸驱动力不足的有效方法之一;对并联机构各参数进行优化设计,也可以提高并联机构的驱动能力。
近些年来,国内外学者在冗余并联机构的优化上取得了不少成果。孙小勇等[11-12]对并联机构速度进行了优化;Fiore E等[13]对应用于风力系统的六自由度并联机构进行了动力学优化,并进行了对比分析;Alessandro C等[14]针对3T1R型并联机构提出了自己的驱动力优化方案。也有不少学者针对冗余并联机构驱动力的优化进行研究:Yao J等[15]优化了五自由度的并联机构的驱动力;邵华等[16]对四自由度冗余并联机床的驱动力进行了优化;董成林等[17]分析并优化了还有一条冗余支链的4-UPS & UP并联机构的运动学性能;杨志东等[18]针对二自由度并联冗余振动台的加载力提出了优化方案。
本文采用3条恒力气动冗余支腿平衡部分重力负载,以降低驱动支腿的载荷。采用免疫遗传算法对有3条冗余支腿的电动六自由度摇摆台进行基于速度、驱动力和功率的多目标优化设计,以获得并联机构的最优结构参数。并将优化后的结构进行仿真对比验证,对结果进行了分析和讨论。
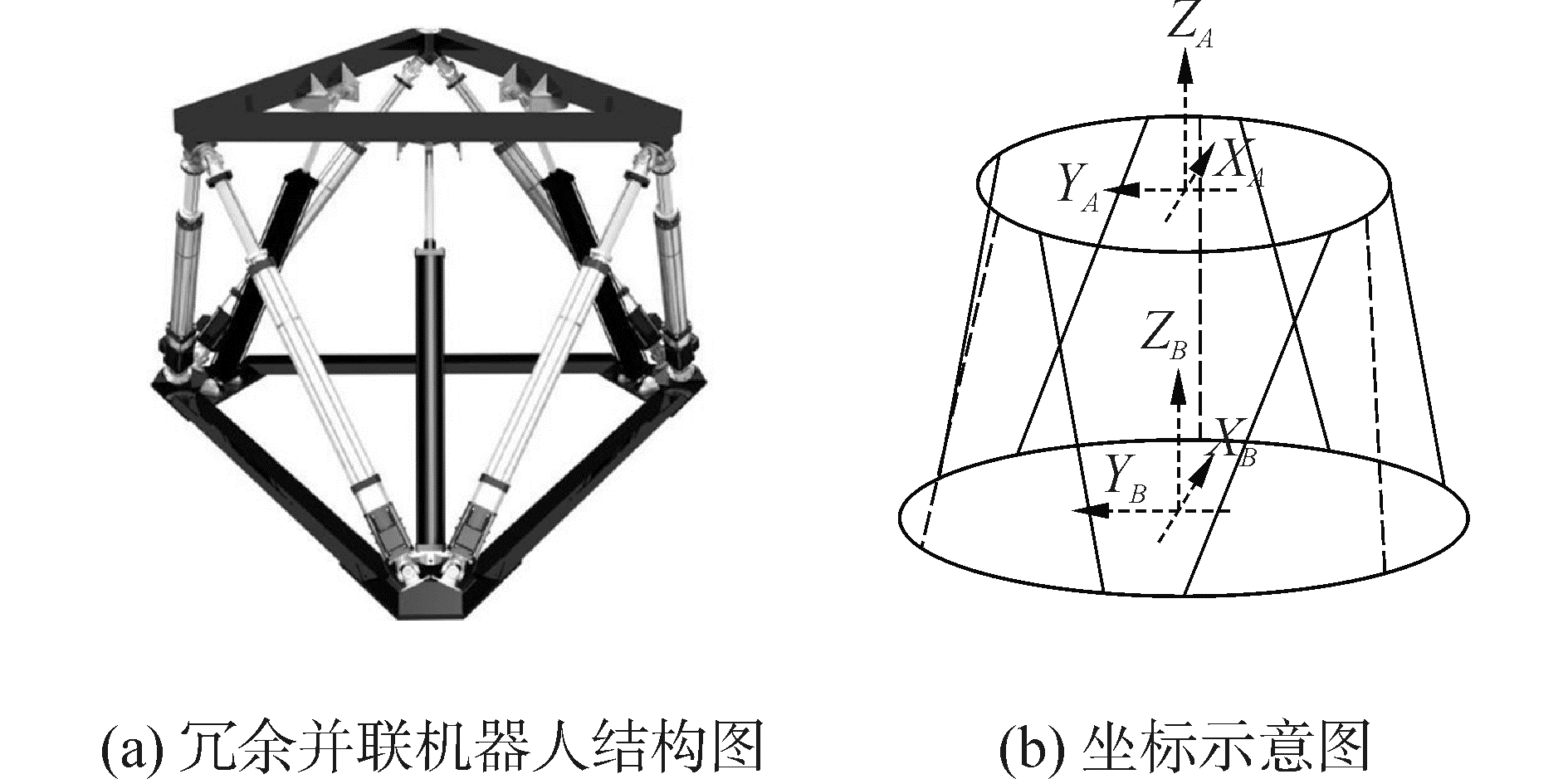
1 数学建模与动力学分析 1.1 冗余并联机构结构六自由度冗余并联机器人是在steward平台的基础上,增加3条冗余气动支腿构成的。如图 1(a)所示。该冗余并联机构由上、下平台、6条电动支腿、3条气动冗余支腿以及连接各支腿和上、下平台的铰链组成。3条冗余支腿位于相邻电动支腿所在平面的法平面上。
|
Download:
|
| 图 1 冗余并联机器人结构图与坐标示意图 Fig. 1 Parallel mechanism structure and coordinatesketch-map | |
重物与冗余机构的上平台相连,总质量为15 000 kg。如果没有冗余支腿,平台自身与负载的重力及运动中的惯性载荷均由电动支腿平衡。当采用三条气动冗余支腿时,冗余驱动力会平衡部分重力。此时,电动支腿的负荷会减少,从而在一定程度上降低了电动支腿的功耗。
1.2 坐标系的建立为方便后续的运动学及动力学研究,在下平台中心处建立右手坐标系,此为静坐标系。然后建立动坐标系,动系的坐标中心与动(上)平台中心重合。初始位置时,两坐标系的坐标轴均平行且正方向相同。如图 1(b)所示。
初始状态时,动、静坐标系原点之间的方向向量为:t0=[0 0 h]T。随着上平台不断运动,t=[q1 q2 q3]T表示动平台的平移运动,θ=[q4 q5 q6]T表示动平台的旋转运动,其中q4、q5、q6分别表示运动平台姿态的横滚(roll)、俯仰(pitch)和偏转(yaw)角度。
因此,由动坐标系到静坐标系的坐标旋转矩阵R为
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{q_5} \cdot {\rm{c}}{q_6}}&{ - {\rm{c}}{q_4} \cdot {\rm{s}}{q_6} + {\rm{s}}{q_4} \cdot {\rm{s}}{q_5} \cdot {\rm{s}}{q_6}}&{{\rm{s}}{q_4} \cdot {\rm{s}}{q_6} + {\rm{c}}{q_4} \cdot {\rm{s}}{q_5} \cdot {\rm{c}}{q_6}}\\ {{\rm{c}}{q_5} \cdot {\rm{s}}{q_6}}&{{\rm{c}}{q_4} \cdot {\rm{c}}{q_6} + {\rm{s}}{q_4} \cdot {\rm{s}}{q_5} \cdot {\rm{s}}{q_6}}&{ - {\rm{s}}{q_4} \cdot {\rm{c}}{q_6} + {\rm{c}}{q_4} \cdot {\rm{s}}{q_5} \cdot {\rm{s}}{q_6}}\\ { - {\rm{s}}{q_5}}&{{\rm{s}}{q_4} \cdot {\rm{c}}{q_5}}&{{\rm{c}}{q_4} \cdot {\rm{c}}{q_5}} \end{array}} \right] $ |
式中:c、s为cos、sin的缩写[19]。
各电动支腿在静坐标系中的向量表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1}}&{{\mathit{\boldsymbol{L}}_2}}&{{\mathit{\boldsymbol{L}}_3}}&{{\mathit{\boldsymbol{L}}_4}}&{{\mathit{\boldsymbol{L}}_5}}&{{\mathit{\boldsymbol{L}}_6}} \end{array}} \right] = }\\ {\mathit{\boldsymbol{R}} \cdot \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{P}}_0} - \mathit{\boldsymbol{B}}} \end{array} $ | (1) |
式中:P=[t … t]3×6,P0=[t0…t0]3×6。A为电动支腿与上平台相连的铰点坐标矩阵,B为电动支腿与下平台相连的铰点坐标矩阵。
同理,各冗余支腿在静坐标系中的向量表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_i} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{e1}}}&{{\mathit{\boldsymbol{L}}_{e2}}}&{{\mathit{\boldsymbol{L}}_{e3}}} \end{array}} \right] = }\\ {\mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{A}}_{ei}} + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{t}} + {\mathit{\boldsymbol{t}}_0}}&{\mathit{\boldsymbol{t}} + {\mathit{\boldsymbol{t}}_0}}&{\mathit{\boldsymbol{t}} + {\mathit{\boldsymbol{t}}_0}} \end{array}} \right] - {\mathit{\boldsymbol{B}}_{ei}},i = 1,2,3} \end{array} $ | (2) |
式中:Aei为冗余支腿与上平台相连的铰点坐标矩阵,Bei为冗余支腿与下平台相连的铰点坐标矩阵。
1.3 运动学、动力学分析为求运动支腿伸长的速度,对等式(1)的两端求导,可得
| $ \mathit{\boldsymbol{\dot L}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot L}}}_1}}&{{\mathit{\boldsymbol{L}}_2} \cdots {{\mathit{\boldsymbol{\dot L}}}_6}} \end{array}} \right] = \mathit{\boldsymbol{\dot P}} + \mathit{\boldsymbol{\hat \omega }} \times \mathit{\boldsymbol{RA}} $ | (3) |
令
| $ \mathit{\boldsymbol{\dot L}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{E}}&{ - \mathit{\boldsymbol{R}}{{\mathit{\boldsymbol{\tilde a}}}_1}{\mathit{\boldsymbol{R}}^{\rm{T}}}}\\ \vdots&\vdots \\ \mathit{\boldsymbol{E}}&{ - \mathit{\boldsymbol{R}}{{\mathit{\boldsymbol{\tilde a}}}_1}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \end{array}} \right]\mathit{\boldsymbol{\dot q}} = \mathit{\boldsymbol{J\dot q}} $ | (4) |
其中
由此可计算各支腿的伸长速度:
| $ {{\mathit{\boldsymbol{\dot D}}}_i} = \frac{1}{{\left| {{{\mathit{\boldsymbol{\dot L}}}_i}} \right|}}\mathit{\boldsymbol{\dot L}}_i^{\rm{T}} \cdot {{\mathit{\boldsymbol{\dot L}}}_i} $ | (5) |
根据上述运动学的分析,利用牛顿-欧拉法建立并联机构的系统动力学方程,牛顿第二定律推导的上平台的力平衡方程:
| $ \sum\limits_{i = 1}^6 {{\mathit{\boldsymbol{e}}_i} \cdot {f_i}} + \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{e}}_{ei}} \cdot {f_e}} - \mathit{\boldsymbol{mg}} = \mathit{\boldsymbol{m\ddot p}} $ | (6) |
由欧拉公式得到的上平台旋转方向力平衡公式:
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^6 {\left( {\mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{a}}_i}} \right) \times \left( {{\mathit{\boldsymbol{e}}_i} \cdot {f_i}} \right)} + \sum\limits_{i = 1}^3 {\left( {\mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{a}}_{ei}}} \right) \times \left( {{\mathit{\boldsymbol{e}}_{ei}} \cdot {f_e}} \right)} = }\\ {\mathit{\boldsymbol{I\dot \omega }} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }}} \end{array} $ | (7) |
式中:fi为第i条电动支腿驱动力的幅值(i=1, 2, …, 6);fe为冗余支腿驱动力的幅值;ei为第i条电动支腿方向的单位向量:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_i} = \frac{1}{{\left| {{L_i}} \right|}}{L_i}}&{i = 1,2, \cdots ,6} \end{array} $ |
eei为第i条冗余支腿方向的单位向量:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_{ei}} = \frac{1}{{\left| {{\mathit{\boldsymbol{L}}_{ei}}} \right|}}{\mathit{\boldsymbol{L}}_{ei}}}&{i = 1,2,3} \end{array} $ |
I为上平台在静坐标系下的惯性矩;
根据上述分析可知,单支电动支腿的功率峰值为
| $ \begin{array}{*{20}{c}} {{W_{\max }} = \max \left( {{f_i} \cdot {{\dot D}_i}} \right)}&{i = 1,2, \cdots ,6} \end{array} $ | (8) |
过大的扭矩会导致电机剧烈升温,影响电机及相关元件的电气和机械性能。超速运转易对系统其他的机械部件(轴承等)造成过度的磨损,影响机械的寿命。因此,只有合理地平衡并联机器人工作时作用力和速度的峰值
根据前文叙述,需要优化的结构参数有:电动支腿上、下铰点所处的外接圆半径ra、rb,相邻铰点间的直线距离la、lb,冗余支腿上、下铰点所处的外接圆半径rae、rbe,冗余支腿对上平台的支持力fe,初始状态时上、下平台的高度差h。故待优化的设计变量为
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{r_a}}&{{r_b}}&{{l_a}}&{{l_b}}&{{r_{ae}}}&{{r_{be}}}&{{f_e}}&h \end{array}} \right] $ |
并联机构工作时需要模拟船舶运动时的摇摆和晃动,为待测试仪器提供测试环境。为此选取了4种典型的运动作为优化时考虑的特征运动:沿固定坐标系Y、Z轴的平移,沿X、Z轴的转动。具体运动参数见表 1。
| 表 1 4种特征运动 Table 1 Four typical movement modes |
本文针对并联机构的设计目的是尽可能地降低运动过程中电动支腿速度、作用力和功率的峰值,这是一个典型的多目标优化问题。通常的处理方法就是多目标加权法[20]。但是由于力和速度在物理意义上完全不同,单位和数量级都不同,所以在此之前需进行两者的正规化处理:
| $ {V_{\max }} = \frac{{\max \left( {{{\dot D}_i}} \right) - {v_{\min }}}}{{{v_{\max }} - {v_{\min }}}} $ | (9) |
| $ {F_{\max }} = \frac{{\max \left( {{f_i}} \right) - {f_{\min }}}}{{{f_{\max }} - {f_{\min }}}} $ | (10) |
| $ {P_{\max }} = \frac{{\max \left( {{P_i}} \right) - {P_{\min }}}}{{{P_{\max }} - {P_{\min }}}} $ | (11) |
式中:vmin、vmax分别表示理论的速度极限值,根据现场工况的实际需求和电机的承受极限分别取0和2.5 m/s;fmin、fmax表示驱动力的理论极值,分别取0、140 kN;Pmin、Pmax表示功率的理论极值,分别取0、120 kW。
由此,可以得出目标函数的表达式:
| $ \min f\left( X \right) = {a_1}\left| {{V_{\mathit{max}}}} \right| + {a_2}\left| {{F_{\max }}} \right| + {a_3}\left| {{P_{\max }}} \right| $ |
式中:a1、a2、a3分别为速度项、驱动力项和功率项的权重系数,可根据实际的工况需求选取不同的权重值,但是三者之间要满足关系:a1+a2+a3=1。结合船舶运动模拟的工况设定,本文选取a1=0.4、a2=0.3、a3=0.3。
2.3 约束条件考虑到运动模拟对机构工作空间的需求、并联机器人现场的工作环境以及支腿在最大伸长时的稳定性,设定设计变量的各个参数取值范围:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = }\\ {\left[ {\begin{array}{*{20}{c}} {{r_a}/m}&{{r_b}/m}&{{l_a}/m}&{{l_b}/m}&{{r_{ae}}/m}&{{r_{be}}/m}&{{f_e}/kN}&{h/m} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {\left[ {1.5,2.5} \right]}&{\left[ {2.0,3.0} \right]}&{\left[ {0.2,0.6} \right]}&{\left[ {0.2,0.6} \right]} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} {\left[ {1.5,2.5} \right]}&{\left[ {2.0,3.0} \right]}&{\left[ {0.4,1.5} \right]}&{\left[ {1.3,3.0} \right]} \end{array}} \right]} \end{array} $ |
经过仿真验证,在上述取值范围内,机构的球绞没有超出最大摆角限制,各支腿在全尺寸运动范围内也没有发生干涉。故该组约束条件可以满足本文机构设计的线性约束条件和非线性约束条件。
综上所述,可以给出本文所设计的冗余机构的优化模型:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{Find}}\;\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{r_a}}&{{r_b}}&{{l_a}}&{{l_b}}&{{r_{ae}}}&{{r_{be}}}&{{f_e}}&h \end{array}} \right]}\\ {\min f\left( \mathit{\boldsymbol{X}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\;\mathit{\boldsymbol{X}} \in {\mathit{\boldsymbol{L}}_X}} \end{array}} \right. $ | (12) |
免疫遗传算法是借鉴生物的免疫系统,与传统的遗传算法相结合的新型优化算法。传统的遗传算法中,初始种群个体根据对环境的适应性,做出淘汰或繁衍后代的选择。随着种群的不断演化,种群中个体对环境的适应性不断提高,最终达到最佳表现[21-23]。
而在生物的免疫过程中,抗原入侵生物本体后,免疫细胞做出反应,产生特异性抗体。随着免疫的不断进行,抗原浓度越来越少,抗体的浓度则不断增加,抗体之间的相互抑制作用增强,抗体的数量逐渐减少,免疫系统在动态变化中保持平衡。同时,免疫细胞分化为记忆细胞,减少了下次相同抗原入侵时的免疫反应时间。
免疫遗传算法中,抗原表示待求解问题的目标函数,问题对应的解为抗体。用抗原和抗体之间的亲和力来描述可行解与最优解的逼近程度。而抗体与抗体之间的亲和力则对应为候选解之间的距离。记忆细胞的分化则表示优良解的保持,使下次相似情况的问题求解更快速。在本文优化求解过程中,抗原为f(X),抗体为X。
可见免疫遗传算法与传统遗传算法之间的区别主要有:种群个体之间的相互作用和抗体群中优良个体的保持。前者能够降低浓度较高的个体的繁殖,从而防止求解陷入局部最优解。而后者能够将优良个体保存在抗体群中,缩短下次搜索的时间。所以,免疫遗传算法在全局搜索能力、局部搜索能力和搜索速度上有着无可比拟的优势[24-30]。
针对本文所述的冗余并联机构优化问题,免疫遗传算法的具体步骤为:首先随机生成一个X的初始种群,其中X中的每一个参数用20位二进制位数表达,每个种群共有20个个体。然后计算种群中的各个个体的目标函数值(抗原和抗体之间的亲和力)和种群中的浓度(抗体与抗体之间的亲和力),根据目标函数值和浓度综合判断哪些个体可以重组产生后代,重组率为0.7。随机选取个体进行变异操作,染色体中的每一个元素变异的概率近似等于0.5。然后,依据临界抗体浓度0.7对比两两抗体之间的相似度。最后得到子代种群并更新抗体群。重复上述步骤,直至满足终止条件。
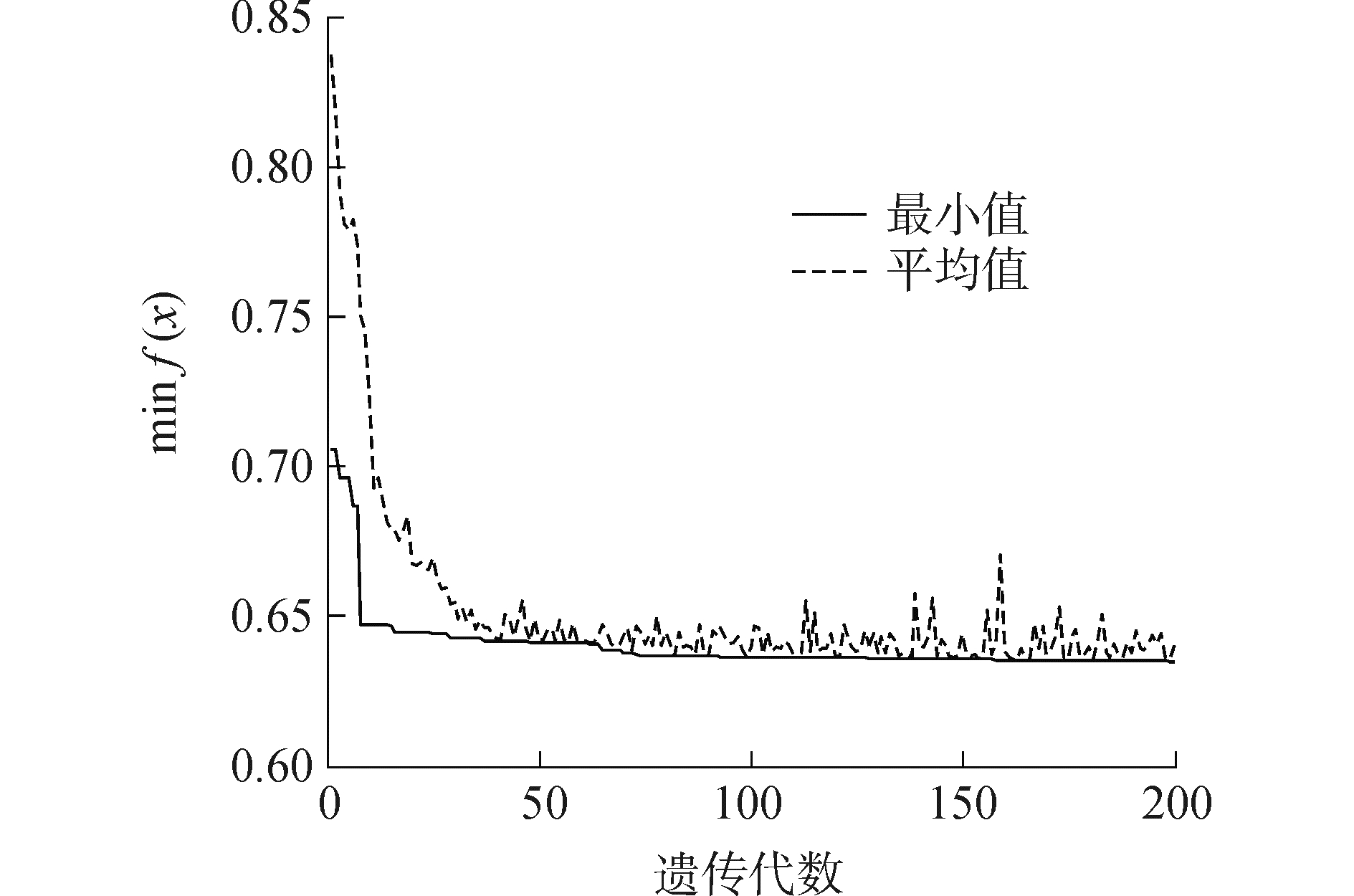
设置迭代次数为200次,可以得出每一代最小值和平均值的变化关系为图 2所示。可以看出,免疫遗传算法在迭代次数内趋于收敛。
|
Download:
|
| 图 2 每代目标函数的最小值和平均值的变化规律 Fig. 2 Variation of max and average value of objective function in each Generation | |
经过优化计算,可以得到一组优化后的结构参数。为验证优化结果的有效性,将优化后的结果与一组典型的参数进行对比仿真验证。这里选择在工业界被广泛应用的力士乐公司的HSE-6-MS-6-C-5/D型六自由度并联机器人作为对比对象。两者的结构参数如表 2所示。优化前后,机构的特征运动速度与作用力对比如图 3、4所示。
|
Download:
|
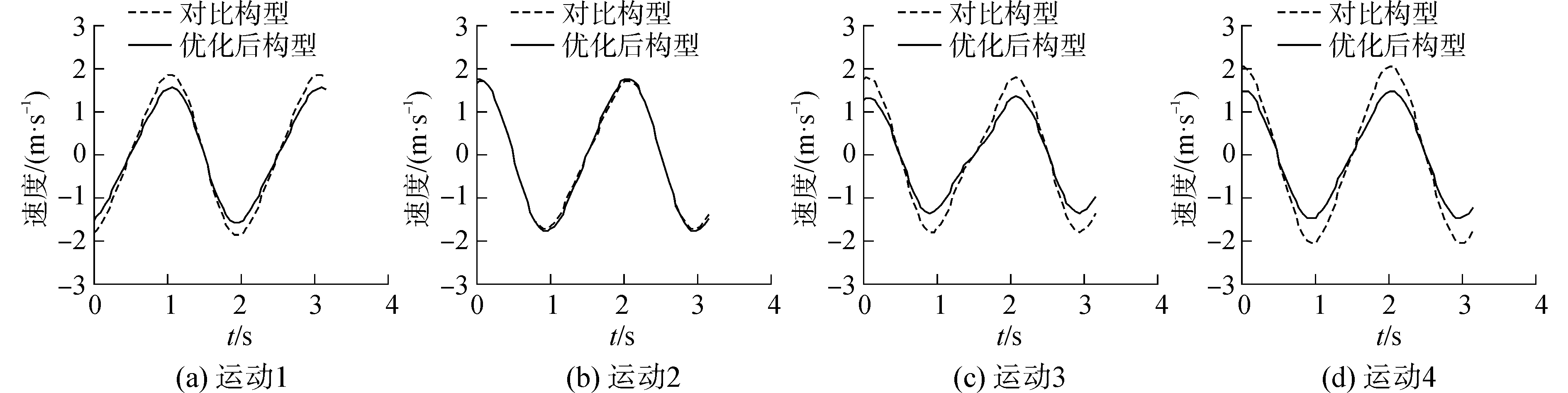
| 图 3 各项特征运动速度峰值对比 Fig. 3 Peak velocity curve of each movement mode | |
|
Download:
|
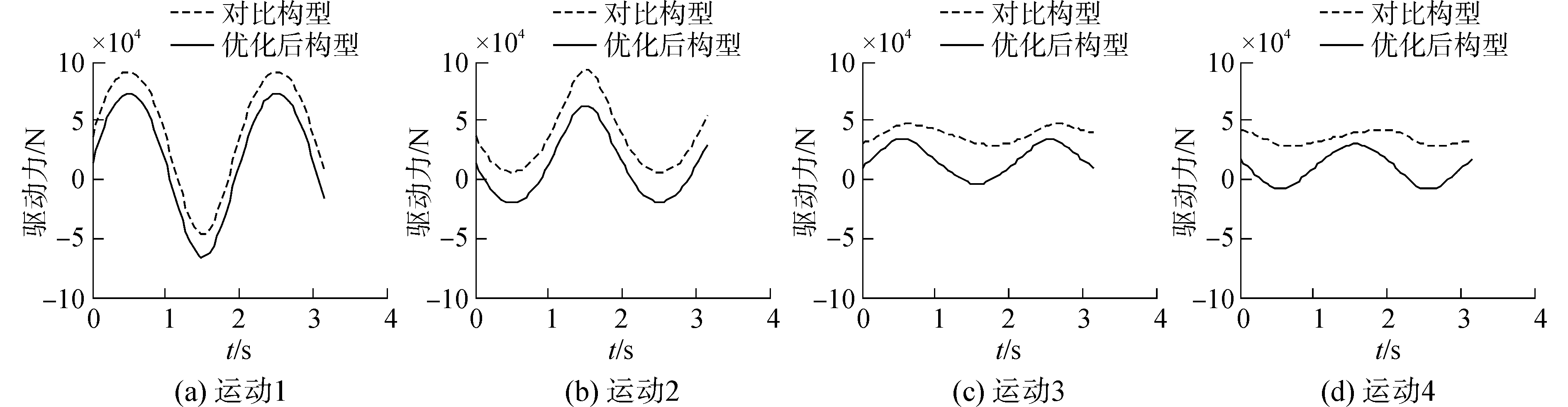
| 图 4 各项特征运动电动支腿驱动力峰值对比 Fig. 4 Driving force curve of each movement mode | |
| 表 2 对比结构参数和优化后的结构参数 Table 2 Structural parameter values of control mechanism and optimized mechanism |
图 3为每项运动中速度峰值所在的支腿的速度曲线。每一张图中的最大值,就是这项特征运动中的速度峰值;四项特征运动中的速度峰值的最大值就是总的速度峰值。
可以看出,特征运动1、3、4中优化后的速度峰值均明显小于对比并联机构;特征运动2中,两者速度曲线基本重合。在全部特征运动中,对比构型的速度峰值出现在特征运动4中,为2.049 3 m/s;优化后速度峰值出现在特征运动2中为1.765 9 m/s,下降了13.83%。因此总的速度峰值也得到显著优化。
图 4为每项运动中作用力峰值所在的支腿的作用力曲线。同理,每一张图中的最大值,就是这项特征运动中电动支腿的驱动力峰值;四项特征运动中的驱动力峰值的最大值就是总的驱动力峰值。
由图 4可知,优化后,每种特征运动的驱动力均得到了不同程度的降低,且优化后的驱动力大致相对于0 N对称分布,符合预期。可以看出,对照构型中驱动力峰值出现在特征运动1中,为96.601 kN;优化后驱动力峰值也同样出现在特征运动1中,为72.931 kN,下降了24.50%,优化效果明显。
优化前后的功率峰值与平均值对比呈现在表 3中,分析表中数据可得,功率峰值出现在B项运动中,对比构型功率峰值为95.398 kW,优化后功率峰值为51.824 kW,下降了45.68%。
| 表 3 4种典型运动的功率峰值 Table 3 Power values of four typical movement modes |
综上所述,本文基于速度峰值、作用力峰值和功率峰值的多目标免疫遗传优化方案,对各项运动参数的优化效果都十分明显。
4 结论1) 冗余支腿能够很好的配合电动支腿的运动,以恒力平衡掉载荷的部分重力,对比工业中常用的典型六自由度并联机构,优化后摇摆台工作时电动支腿的速度、作用力和系统的功耗峰值分别降低了13.83%、24.50%和45.68%。
2) 使用免疫遗传优化算法,保证了种群的个体多样性。在确保优化效果的前提下,能够避免过早地收敛于局部最优解。
3) 采用综合权衡速度、驱动力和功率的多目标优化策略,使其更接近工作环境的实际需求。
| [1] |
周昌春, 方跃法, 叶伟. 6-RRS冗余驱动飞行模拟器运动学与工作空间分析[J]. 北京交通大学学报, 2015, 39(1): 112-117. ZHOU Changchun, FANG Yuefa, YE Wei. Flight simulator with 6-RRS redundant actuation spherical parallel manipulator[J]. Journal of Beijing Jiaotong University, 2015, 39(1): 112-117. (  0) 0)
|
| [2] |
曹毅, 陈海, 秦友蕾, 等. 解耦三转动两平移并联机器人机构型综合[J]. 哈尔滨工程大学学报, 2016, 37(10): 1408-1415. CAO Yi, CHEN Hai, QIN Youlei, et al. Type synthesis of decoupled three-rotational and two-translational parallel robotic manipulators[J]. Journal of Harbin Engineering University, 2016, 37(10): 1408-1415. (  0) 0)
|
| [3] |
常定勇, 方跃法, 叶伟. 双输出3D打印解耦并联机器人的设计与分析[J]. 机械工程学报, 2017, 53(7): 39-46. CHANG Dingyong, FANG Yuefa, YE Wei. Design and analysis of a double output 3D printing decoupling parallel manipulator[J]. Journal of mechanical engineering, 2017, 53(7): 39-46. (  0) 0)
|
| [4] |
赵泽, 仇原鹰, 段学超. 一种构型简单的新型三平动微动并联机器人[J]. 西安电子科技大学学报(自然科学版), 2017, 44(4): 51-55, 131. ZHAO Ze, QIU Yuanying, DUAN Xuechao. Novel 3-DOF micro translational parallel manipulator[J]. Journal of Xidian University(Science and Technology), 2017, 44(4): 51-55, 131. DOI:10.3969/j.issn.1001-2400.2017.04.010 (  0) 0)
|
| [5] |
FU Jianxun, GAO Feng. Optimal design of a 3-leg 6-DOF parallel manipulator for a specific workspace[J]. Chinese journal of mechanical engineering, 2016, 29(4): 659-668. DOI:10.3901/CJME.2016.0121.011 (  0) 0)
|
| [6] |
吴军, 李铁民, 关立文. 飞行模拟器运动平台的计算力矩控制[J]. 清华大学学报(自然科学版), 2006, 46(8): 1405-1408, 1413. WU Jun, LI Tiemin, GUAN Liwen. Computed-torque control for a moving flight simulator platform[J]. Journal of Tsinghua University(Science and Technology), 2006, 46(8): 1405-1408, 1413. DOI:10.3321/j.issn:1000-0054.2006.08.017 (  0) 0)
|
| [7] |
胡佩达, 高钟毓, 张嵘, 等. 基于三轴摇摆台的高精度姿态试验系统[J]. 中国惯性技术学报, 2013, 21(2): 271-274. HU Peida, GAO Zhongyu, ZHANG Rong, et al. High accuracy attitude testing system based on three-axis test table[J]. Journal of Chinese inertial technology, 2013, 21(2): 271-274. DOI:10.3969/j.issn.1005-6734.2013.02.028 (  0) 0)
|
| [8] |
何广华, 陈丽敏, 王佳东. 船舶在波浪中运动的强非线性时域模拟[J]. 哈尔滨工业大学学报, 2017, 49(4): 142-148. HE Guanghua, CHEN Limin, WANG Jiadong. Strongly-nonlinear simulation of ship motions in head waves[J]. Journal of Harbin Institute of Technology, 2017, 49(4): 142-148. (  0) 0)
|
| [9] |
周莎, 张伟, 于天俊, 等. 横摇和纵摇非线性耦合下船舶运动的全局动力学[J]. 振动与冲击, 2017, 36(4): 214-217. ZHOU Sha, ZHANG Wei, YU Tianjun, et al. Global dynamics of ship motions considering the nonlinear coupling between pitch and roll modes[J]. Journal of vibration and shock, 2017, 36(4): 214-217. (  0) 0)
|
| [10] |
马山, 葛文澎, 段文洋, 等. 基于重叠网格的C11集装箱船自由衰减横摇模拟[J]. 华中科技大学学报(自然科学版), 2017, 45(5): 34-39. MA Shan, GE Wenpeng, DUAN Wenyang, et al. Simulation of free decay roll for C11 container ship based on overset gird[J]. Journal of Huazhong University of Science and technology (nature science edition), 2017, 45(5): 34-39. (  0) 0)
|
| [11] |
孙小勇, 郑彬, 鲍捷, 等. 高速6-PSS并联机器人参数优化设计[J]. 农业机械学报, 2015, 46(5): 372-378. SUN Xiaoyong, ZHENG Bin, BAO Jie, et al. Parameter optimization design of high-speed 6-PSS parallel robot[J]. Transactions of the Chinese society for agricultural machinery, 2015, 46(5): 372-378. (  0) 0)
|
| [12] |
曾达幸, 胡志涛, 侯雨雷, 等. 一种新型并联式解耦踝关节康复机构及其优化[J]. 机械工程学报, 2015, 51(9): 1-9. ZENG Daxing, HU Zhitao, HOU Yulei, et al. Novel decoupled parallel mechanism for ankle rehabilitation and its optimization[J]. Journal of mechanical engineering, 2015, 51(9): 1-9. (  0) 0)
|
| [13] |
FIORE E, GIBERTI H. Optimization and comparison between two 6-DoF parallel kinematic machines for HIL simulations in wind tunnel[C]//Proceedings of the 7th International Conference on Mechatronics and Manufacturing. Milano, Italy, 2016: 04012.
(  0) 0)
|
| [14] |
ALESSANDRO C, ROSARIO S. Elastodynamic optimization of a 3T1R parallel manipulator[J]. Mechanism and machine theory, 2014, 73: 184-196. DOI:10.1016/j.mechmachtheory.2013.10.010 (  0) 0)
|
| [15] |
YAO Jiantao, GU Weidong, FENG Zongqiang, et al. Dynamic analysis and driving force optimization of a 5-DOF parallel manipulator with redundant actuation[J]. Robotics and computer-integrated manufacturing, 2017, 48: 51-58. DOI:10.1016/j.rcim.2017.02.006 (  0) 0)
|
| [16] |
邵华, 关立文, 王立平, 等. 冗余并联机床驱动力优化解析[J]. 清华大学学报(自然科学版), 2007, 48(8): 1325-1329. SHAO Hua, GUAN Liwen, WANG Liping, et al. Drive force optimization for a redundant parallel machine[J]. Journal of Tsinghua University(Science and Technology), 2007, 48(8): 1325-1329. (  0) 0)
|
| [17] |
董成林, 刘海涛, 黄田. 含冗余驱动支链4-UPS & UP并联机构的运动学性能分析[J]. 机械工程学报, 2016, 52(5): 124-129. DONG Chenglin, LIU Haitao, HUANG Tian. Kinematic performance analysis of redundantly actuated 4-UPS & UP parallel manipulator[J]. Journal of mechanical engineering, 2016, 52(5): 124-129. (  0) 0)
|
| [18] |
高长虹, 丛大成, 杨志东, 等. 冗余驱动液压振动台内力耦合动态抑制策略[J]. 华南理工大学学报(自然科学版), 2016, 44(1): 93-99. GAO Changhong, CONG Dacheng, YANG Zhidong, et al. Internal force-coupling dynamic suppression strategy for redundantly-actuated hydraulic shaking table[J]. Journal of South China University of Technology (natural science edition), 2016, 44(1): 93-99. (  0) 0)
|
| [19] |
WILSON M, SPONG M W. Robot modeling and control[J]. Industrial robot an international journal, 2006, 17(5): 709-737. (  0) 0)
|
| [20] |
DASGUPTA B, MRUTHYUNJAYA T S. Closed-form dynamic equations of the general stewart platform through the newton-euler approach[J]. Mechanism and machine theory, 1998, 33(7): 993-1012. DOI:10.1016/S0094-114X(97)00087-6 (  0) 0)
|
| [21] |
陈立伟, 黄璐, 齐传斌. 基于遗传算法优化的相关向量机的燃机涡轮叶片故障诊断[J]. 应用科技, 2016, 43(2): 70-74. CHEN Liwei, HUANG Lu, QI Chuanbin. Fault diagnosis for gas turbine blades based on the relevance vector machine optimized by genetic algorithm[J]. Applied science and technology, 2016, 43(2): 70-74. (  0) 0)
|
| [22] |
俞研, 黄皓. 面向入侵检测的基于多目标遗传算法的特征选择[J]. 计算机科学, 2007, 34(3): 197-200. YU Yan, HUANG Hao. Feature selection using multi-objective genetic algorithms for intrusion detection[J]. Computer science, 2007, 34(3): 197-200. DOI:10.3969/j.issn.1002-137X.2007.03.052 (  0) 0)
|
| [23] |
ZHANG Libo, HE Jingjie, WANG Su. Inverse kinematic solutions of dual redundant camera robot based on genetic algorithm[J]. Mathematical problems in engineering, 2017, 2017: 7486178. (  0) 0)
|
| [24] |
MORI K, TSUKIYAMA M, FUKUDA T. Application of an immune algorithm to multi-optimization problems[J]. Electrical engineering in Japan, 1998, 122(2): 30-37. DOI:10.1002/(ISSN)1520-6416 (  0) 0)
|
| [25] |
严心池, 安伟光, 赵维涛, 等. 遗传算法中"免疫算子"的构造与性能[J]. 哈尔滨工程大学学报, 2005, 26(6): 732-735. YAN Xinchi, AN Weiguang, ZHAO Weitao, et al. Conformation and capability of an "immunity operator" in a genetic algorithm[J]. Journal of Harbin Engineering University, 2005, 26(6): 732-735. DOI:10.3969/j.issn.1006-7043.2005.06.008 (  0) 0)
|
| [26] |
LIAO G C, TSAO T P. Application embedded chaos search immune genetic algorithm for short-term unit commitment[J]. Electric power systems research, 2004, 71(2): 135-144. (  0) 0)
|
| [27] |
LUO Wenjian, CAO Xianbin, WANG Xufa. An immune genetic algorithm based on immune regulation[C]//Proceedings of 2002 Congress on Evolutionary Computation. Honolulu, USA, 2002: 801-806.
(  0) 0)
|
| [28] |
HUANG Wei, XU Chunli, ZHANG Jianhua, et al. Study of reactive power optimization based on immune genetic algorithm[C]//Proceedings of 2003 IEEE PES Transmission and Distribution Conference and Exposition. Dallas, TX, USA, 2003: 186-190.
(  0) 0)
|
| [29] |
CHOI B K, YANG B S. Multiobjective optimum design of rotor-bearing systems with dynamic constraints using immune-genetic algorithm[J]. Journal of engineering for gas turbines and power, 2001, 123(1): 78-81. DOI:10.1115/1.1338952 (  0) 0)
|
| [30] |
李晔, 庞永杰, 万磊, 等. 水下机器人S面控制器的免疫遗传算法优化[J]. 哈尔滨工程大学学报, 2006, 27(S1): 324-330. LI Ye, PANG Yongjie, WAN Lei, et al. Immune-genetic optimization of underwater vehicle S surface controller[J]. Journal of Harbin Engineering University, 2006, 27(S1): 324-330. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


