雷达信号调制方式的识别是雷达信号侦察的关键部分,随着雷达信号体制的不断复杂,信号脉冲宽度不断变短,要求信号识别算法具有计算量小、易于实现且能够适应不同体制雷达。国内外学者针对雷达信号调制方式的识别做了大量的研究,其主要方法有:瞬时自相关法[1]、谱相关分析[2]、时频变换法[3]、小波变换法[4]等。信号瞬时自相关法原理简单、可以处理大带宽信号、易于工程实现且实时性较好,但是对非线性信号进行分析效果不好。谱相关分析法适用于雷达信号的检测与分析,不足之处在于计算量过大。时频变换法包括WVD变换及其演进算法,该方法对噪声不敏感,缺点是不适合与多信号分析,因此针对这个缺点,Choi等提出了Choi-Williams分布[5],能够较好地解决交叉项问题,但是降低了时频分辨率。小波变换是一种时间—尺度分析方法,具有多尺度特性,大的尺度对应的是一个对信号的全局的概略描述,而小的尺度则相应地对应于细节性的描述。文献[6]提出了基于分形理论从信号中提取盒维数和信息维数的识别方法,该方法利用各种信号调制方式之间的差异作为分类特征,具有较好的工程应用价值。文献[7]提出了基于复杂度特征的调制信号识别,利用各种信号在信号波形上的差异作为分类的有效特征,给出信号序列重构的新方法来提高信号识别效果。文献[8]根据各种信号的频谱特征不同,利用信号谱峰特性给出了一种雷达信号调制方式的自动识别方法。文献[9]提出了基于频谱和瞬时频率的雷达信号识别方法,该方法利用信号的频谱差异和瞬时频率差异来提取有效特征进行识别。
文献[7]是通过计算信号时域波形的复杂度进行区分,受噪声影响大。因此本文采用文献[7]中的复杂度计算思想,在信号频域上根据雷达信号频谱的几何形状不同,提出一个基于信号频谱复杂度的雷达信号调制识别方法。
1 信号特征分析雷达信号的调制方式差异能够直接反映在信号的时域波形和频域频谱上,由于噪声的影响,通常情况下在时域波形上不能直观的反映调制信号的波形特点。因此,本文根据信号在频谱上的几何形状特征,通过计算信号频谱复杂度来对雷达信号调制方式进行分类识别。本文研究常规雷达信号(NS)、二相编码信号(BPSK)、四相编码信号(QPSK)、线性跳频信号(LFM)、非线性跳频信号(NLFM)和频率编码信号(2FSK)。
1.1 L-Z复杂度特征L-Z复杂度是通过复制和添加两种简单操作来描述一个序列特性的方法。对于雷达调制信号的频谱,从直观上可以看出有明显的几何特征。下面将介绍信号频谱复杂度特征的提取方法。
1.1.1 信号频谱的量化设{s(k)}表示信号的频谱序列,k=1, 2, …, N,对{s(k)}进行量化编码,假设量化级数为L,令a=
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {r\left( k \right) = j,\;\;\;\frac{{a \times j}}{L} < s\left( k \right) \le \frac{{a \times \left( {j + 1} \right)}}{L},}\\ {j = 0,1, \cdots ,L - 1} \end{array}\\ r\left( k \right) = 0,\;\;\;\;\;s\left( k \right) = 0 \end{array} \right. $ | (1) |
式中:{r(k)}表示{s(k)}量化后的具有L个符号的数字序列。
1.1.2 L-Z复杂度的计算过程L-Z复杂度的计算过程如下所述[10]:给定序列为r(1), r(2), …, r(N),初始时向空生成池中添加r(1),不失一般性,设生成池中已有符号串r(1)r(2)…r(l),l<N,并且r(l)是由添加操作完成的,令P=r(1)r(2)…r(l),Q=r(l+1),判断Q是否可以从PQπ中复制,即Q是否为PQπ中的子串(PQπ表示把P、Q拼接在一起,删除最末一个符号得到的符号串),如果能复制,P保持不变,Q续补一个符号,即Q=r(l+1)r(l+2),再回到前面的判断;如果不能,添加Q到生成池,此时的P=r(1)r(2)…r(l)r(l+1),Q=r(l+2),再返回前面的判断。如此反复,直到生成池中包含所有的重构序列,统计添加操作的次数C,记为L-Z复杂度,需要注意的是如果最后一步操作是复制,则C要加1。
1.2 平方频谱特征对于常规雷达信号而言,它在频谱中只有一个离散的单频谱线,即信号频谱复杂度最低。相位编码信号与常规雷达信号的不同之处在于信号的瞬时相位在码元之间会发生跳变。二相编码信号表示跳变180°,四相编码信号表示跳变90°。常规雷达信号相当于它的瞬时相位跳变0°,因此也可以把常规雷达信号看作一种特殊的相位编码信号。常规雷达信号、二相编码信号和四相编码信号有如下关系,以二相编码信号为例:
二相编码信号的数学模型为
| $ x\left( n \right) = A\exp \left\{ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}n/{f_s} + {\rm{ \mathsf{ π} }}c\left( \tau \right) + {\varphi _0}} \right)} \right\} $ | (2) |
式中:A表示信号脉冲幅值,f0表示信号载波频率,fs表示采样频率,c(τ)取值只有0和1,表示编码序列值,φ0是初相。
对二相编码信号进行平方可以得到:
| $ {x^2}\left( n \right) = {A^2}\exp \left\{ {{\rm{j}}\left( {4{\rm{ \mathsf{ π} }}{f_0}n/{f_s} + 2{\rm{ \mathsf{ π} }}c\left( \tau \right) + 2{\varphi _0}} \right)} \right\} $ | (3) |
式(3)进一步化简可以得出:
| $ {x^2}\left( n \right) = {A^2}\exp \left\{ {{\rm{j}}\left( {4{\rm{ \mathsf{ π} }}{f_0}n/{f_s} + 2{\varphi _0}} \right)} \right\} $ | (4) |
从式(4)可以得出一个结论:二相编码信号平方后退化为一个常规雷达信号,不同之处在于信号的载波频率为2f0。因此平方后信号的频谱中也是只有一根离散单频谱线,也就是说二相编码信号的频谱复杂度经过信号平方处理后,频谱复杂度达到最低,和常规雷达信号频谱复杂度一样。
对于四相编码信号来说,对信号进行平方可以得到一个载波频率为2f0的二相编码信号,继续进行信号平方后可以得到一个载波频率为4f0的常规雷达信号。因此根据二相编码信号和四相编码信号的这一特性,可以利用信号平方法提取信号的频谱复杂度特征,用来进行信号分类识别。
1.3 谱峰特征针对频率编码信号,其在频域上有两个明显的谱峰,根据这一特性可以用来区分频率编码信号和其他类型信号,为了避免噪声带来的影响,对信号频谱{s(k)}进行了平滑,得到平滑频谱{S(k)},设平滑步长为step,则有
| $ S\left( k \right) = \frac{1}{{{\rm{step}}}}\sum\limits_{m = k}^{k + {\rm{step}} - 1} {s\left( m \right)} ,k = 1,2, \cdots ,N - {\rm{step}} $ | (5) |
对于平滑后频谱{S(k)}进行谱峰搜索,其步骤如下:
1) 计算平滑频谱{S(k)}的最大值,设定一个阈值threshold=max(S(k))/2。
2) 将平滑频谱{S(k)}的每一个数,减去阈值threshold后,得到一个新的序列{S*(k)}。
3) 从序列{S*(k)}的第一个位置k=1开始,判断当前位置k所在的数值S*(k)是否小于0;如果小于0,则将当前位置k所在的数值S*(k)置0,直至k=N-step截止,这样序列{S*(k)}中的数值得到了更新。
4) 设初始谱峰数p=0,搜索序列{S*(k)},如果当前位置k所在的数值S*(k)大于0,并且位置k-1所在的数值S*(k-1)小于0,则p加1,序列{S*(k)}这样遍历一遍。
5) 判断p值大小,如果p=2,则表示该信号是频率编码信号,否则为未识别。
1.4 最小二乘直线拟合方差特征线性调频信号和非线性调频信号的瞬时频率存在差异,线性调频信号的瞬时频率是一条直线,而非线性调频信号的瞬时频率是一条曲线。利用最小二乘线性拟合原理,可以计算出拟合直线与信号瞬时频率的方差。根据两种信号最小二乘直线拟合方差不同,可以对这两种信号进行区分。
最小二乘直线拟合原理如下:设f(n)表示信号的瞬时频率,
| $ f\left( {\alpha ,\beta } \right) = \sum\limits_{n = 1}^N {\varepsilon _n^2} = \sum\limits_{n = 1}^N {{{\left[ {f\left( n \right) - \alpha n - \beta } \right]}^2}} $ | (6) |
为了使得总偏差
| $ \frac{{\partial f\left( {\alpha ,\beta } \right)}}{{\partial \alpha }} = - 2\sum\limits_{n = 1}^N {n\left[ {f\left( n \right) - \alpha n - \beta } \right]} = 0 $ | (7) |
| $ \frac{{\partial f\left( {\alpha ,\beta } \right)}}{{\partial \beta }} = - 2\sum\limits_{n = 1}^N {\left[ {f\left( n \right) - \alpha n - \beta } \right]} = 0 $ | (8) |
联合式(7)、(8)求解可得到α和β的表达式:
| $ \alpha = \frac{{N\sum\limits_{n = 1}^N {nf\left( n \right)} - \sum\limits_{n = 1}^N {n\sum\limits_{n = 1}^N {f\left( n \right)} } }}{{N\sum\limits_{n = 1}^N {{n^2}} - {{\left( {\sum\limits_{n = 1}^N n } \right)}^2}}} $ | (9) |
| $ \beta = \frac{{\sum\limits_{n = 1}^N {f\left( n \right)} \sum\limits_{n = 1}^N {{n^2} - \sum\limits_{n = 1}^N {nf\left( n \right)\sum\limits_{n = 1}^N n } } }}{{N\sum\limits_{n = 1}^N {{n^2}} - {{\left( {\sum\limits_{n = 1}^N n } \right)}^2}}} $ | (10) |
根据拟合直线的斜率α和β可求出拟合直线
| $ \varphi = \frac{{\sum\limits_{n = 1}^N {{{\left[ {f\left( n \right) - \hat f\left( n \right)} \right]}^2}} }}{N} $ | (11) |
φ的大小反映了拟合直线和信号瞬时频率的重合程度,当它小于某阈值时,可以认为该信号是线性调频信号,否则判断为曲线,即为非线性调频信号。
2 信号识别流程基于上节的信号特征分析,结合各种信号的频谱复杂度特征,设计了基于频谱复杂度的雷达信号识别流程,如图 1所示。

|
Download:
|
| 图 1 基于频谱复杂度的雷达信号调制方式识别流程 Fig. 1 Radar signal modulation recognition process based on spectrum complexity | |
1) 对接收信号进行FFT变换,求得其功率谱,对功率谱进行平滑去噪处理,利用复杂度计算方法,计算平滑功率谱的复杂度C。
2) 根据复杂度C的大小,设定一个阈值将信号分为常规信号和其他信号两类,其他信号包含二相编码信号、四相编码信号、线性调频信号、非线性调频信号和二频编码信号,若判断为其他信号,则进入步骤3)处理。
3) 对平滑后的功率谱进行谱峰搜索,根据谱峰个数p的值,对信号进行判断,由前面特征分析可知,二频编码信号的谱峰数p为2,因而判断为二频编码信号,否则判断为其他信号,进入步骤4)处理。
4) 对原信号进行平方,求出平方信号的功率谱,并进行频域平滑处理,同样根据复杂度计算方法,计算出平方信号平滑功率谱复杂度square_C,由前面的特征分析可知,二相编码信号平方后退化为常规信号,因而根据这一特点,采取与步骤2)相同的判别方法,对信号进行分类,判断信号是不是二相编码信号,否则进入步骤5)处理。
5) 对比复杂度C与square_C的大小,根据四相编码信号平方退化为二相编码信号、线性跳频信号平方后带宽为原来的两倍这一些特征,可以判断出信号是否属于四相编码信号,否则进入步骤6)处理。
6) 经过前面几步处理之后,剩余的信号为线性调频信号和非线性调频信号,根据前面的特征分析可知,线性调频信号的瞬时频率是一条直线,因而采用最小二乘算法,求出瞬时频率的拟合直线,根据拟合直线与瞬时频率的方差φ大小,设定一个阈值ε,判断信号是否属于线性调频信号,否则属于非线性调频信号。
3 仿真结果与分析本文针对常规雷达信号(NS)、二相编码信号(BPSK)、四相编码信号(QPSK)、线性调频信号(LFM)、非线性调频信号(NLFM)和频率编码信号(2FSK)共6种调制类型信号进行识别实验,其基本仿真参数为:采样频率为1 250 MHz,载波频率为360 MHz,二相编码信号采用13位巴克码,四相编码信号采用16位弗兰克码,线性调频信号的调制带宽为40 MHz,频率编码信号的频率差为40 MHz。
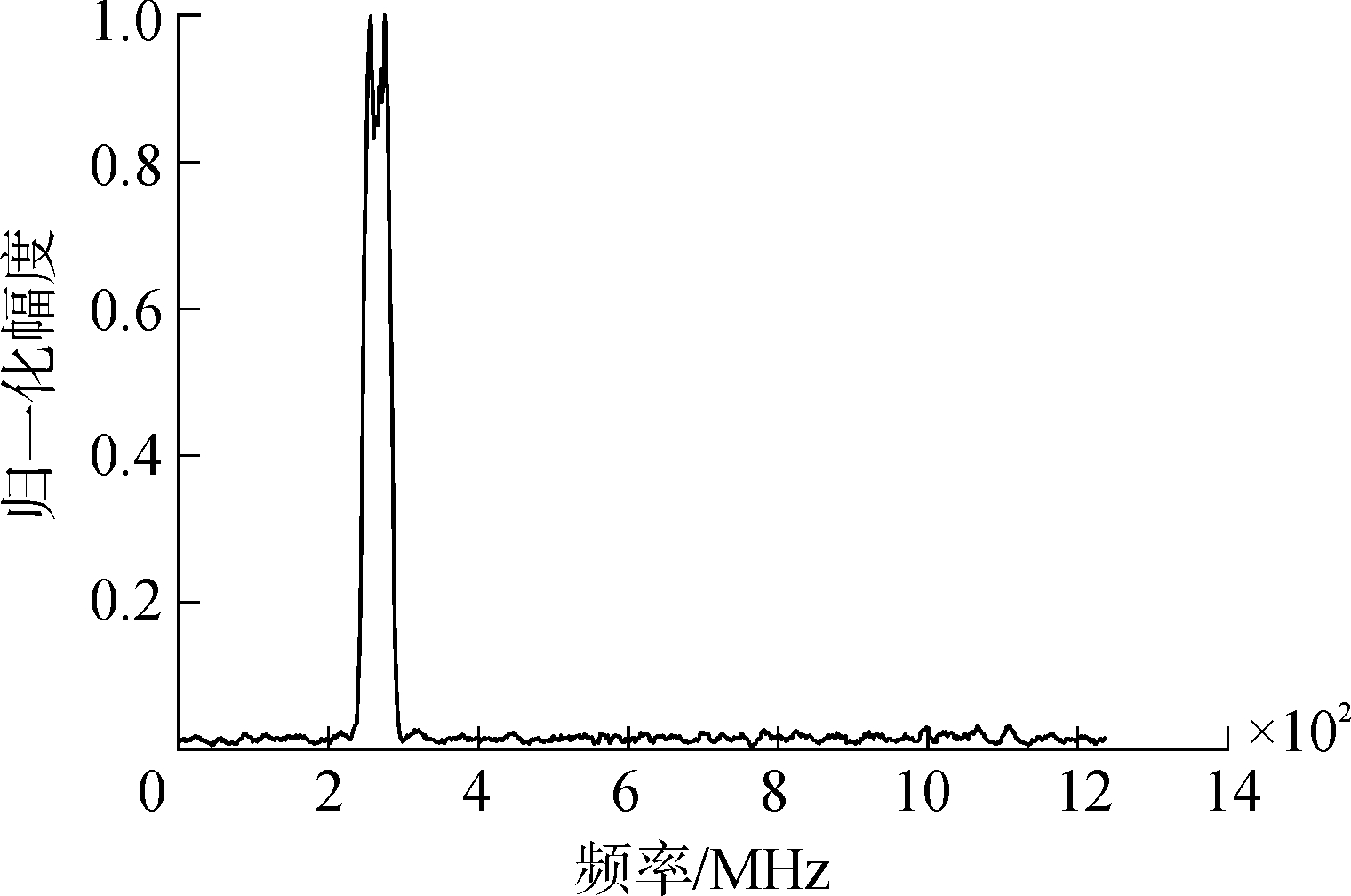
3.1 频谱波形与量化频谱序列对比针对6种雷达信号的幅度频谱,以LFM信号的幅度频谱为例。图 2表示的是在信噪比为6 dB时的LFM信号平滑幅度频谱波形。
|
Download:
|
| 图 2 LFM信号的平滑幅度频谱 Fig. 2 Smooth amplitude spectrum of LFM signal | |
图 3表示的是量化级数为16的LFM信号的量化频谱序列,从图 2、3对比来看,量化频谱序列能够表征频谱波形的特点,因此对量化频谱序列采用复杂度计算方法得出的频谱复杂度C能够表征LFM信号的频谱特征。对其他5种雷达信号采用同样的方法提取出频谱复杂度C,然后可以根据每种信号的频谱复杂度C的差异对信号进行分类。

|
Download:
|
| 图 3 LFM信号的频谱量化序列 Fig. 3 Spectral quantization sequence of LFM signal | |
在采样频率为1 250 MHz,脉宽大小不同的6种雷达信号的复杂度统计如表 1所示。
| 表 1 信号复杂度统计(SNR=6 dB) Tab.1 Signal complexity statistics(SNR=6 dB) |
表 1是在脉冲宽度为1.6 μs(采样点数2 000)、0.4 μs(采样点数500)、0.1 μs(采样点数125)时的6种信号的频谱复杂度统计,从表中可知,常规信号的频谱复杂度最小,其数值稳定在C=4;二相编码信号和四相编码信号的频谱复杂度大小相差不多;线性调频信号和非线性调频信号的频谱复杂度,在脉冲宽度为0.1 μs时频谱复杂度急剧下降,原因在于信号采样频率确定的情况下,采样点数越少,信号频率分辨率越低,因而此时的调频信号在短时间内可以看作是一个常规信号,因而其频谱复杂度和常规信号接近;二频编码信号的频谱复杂度,其数值与相位编码信号的相差不大。根据前面所述的二相编码信号的特征分析可知,二相编码信号平方后计算出的频谱复杂度和常规信号的相同,线性调频信号平方处理后,信号带宽变为原来的2倍,因而信号的频谱复杂度比原来线性调频信号频谱复杂度高。
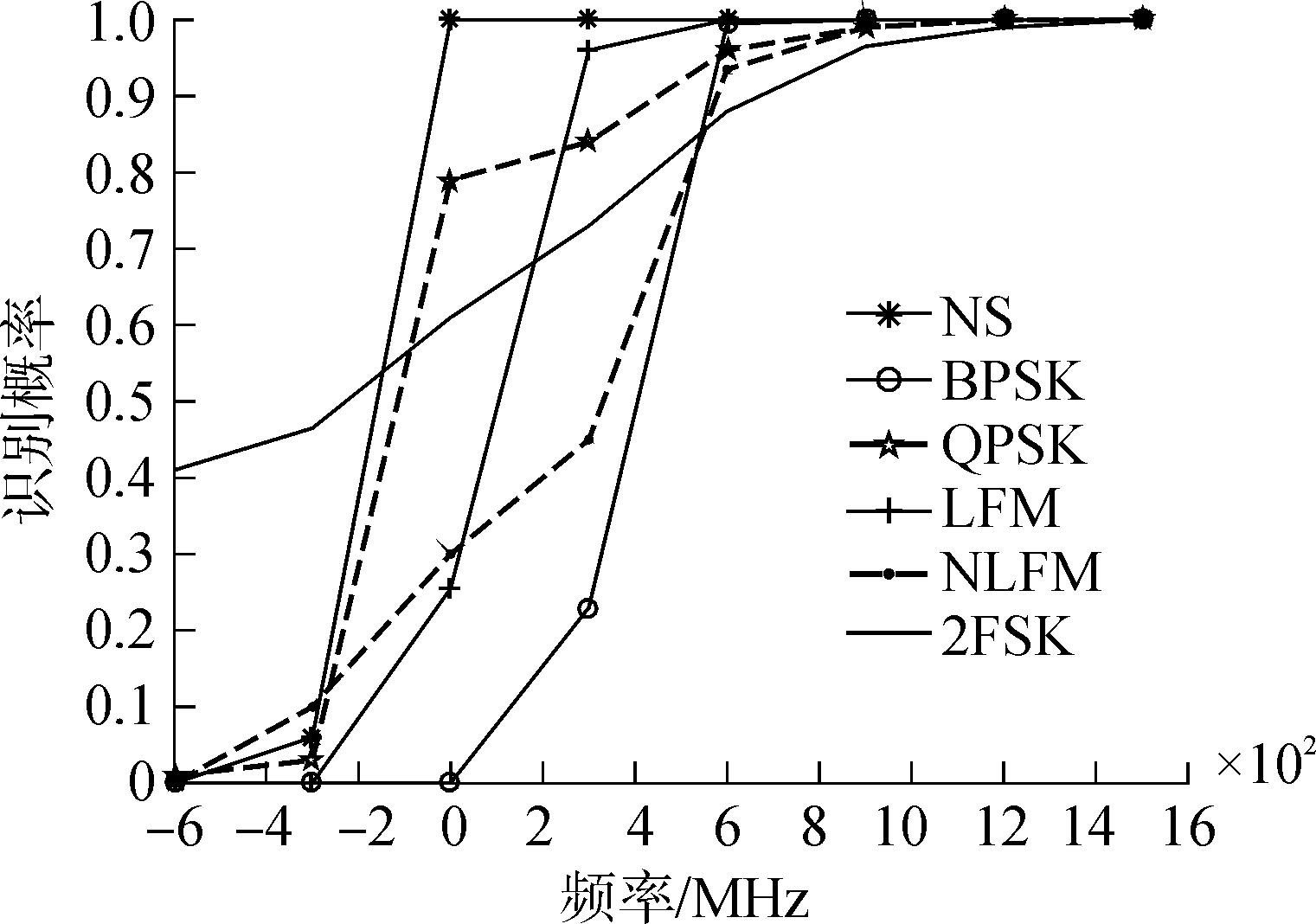
3.3 不同信噪比下的信号识别概率统计在采样点数为500点,即脉冲宽度为0.4 μs的情况,对6种信号做200次蒙特卡洛实验,统计在不同信噪比下的识别概率,其结果如图 4所示。
|
Download:
|
| 图 4 不同信噪比下的信号识别概率统计 Fig. 4 Signal recognition probability statistics under different SNR | |
从图 4中可以得知,常规信号的识别效果最好,在0 dB时就可以达到100%识别,原因在于它的频谱复杂度C数值稳定,受噪声的影响较小;二相编码信号的识别正确概率在信噪比为3 dB时较低,由前面的特征分析可知,二相编码信号平方后,退化为一个常规信号,理想情况下它的平方信号频谱复杂度C和常规信号的频谱复杂度C一样大小,但是由于信号平方后导致信噪比降低,因而它的平方信号频谱复杂度C数值不稳定,误识别为四相编码信号;线性调频信号和非线性调频信号的识别正确概率在信噪比大于6 dB时,能够达到90%以上;二频编码信号的识别正确概率在信噪比为6 dB时也能达到90%以上,说明采用谱峰搜索的方法对其进行识别有比较好的效果。
4 结论1) 根据雷达信号的频谱特点,利用复杂度计算思想从几何形状上描述信号特征,本文根据信号的频谱复杂度特征,设计了一个基于频谱复杂度的雷达信号调制方式识别流程,仿真结果表明,在信号信噪比大于6 dB时,信号正确识别概率总体能够达到90%以上,因此该方法具有较好的识别效果。
2) 本文设计的基于频谱复杂度的雷达信号调制方式识别方法,其依据是信号在频域频谱上能够有明显的几何特征,仿真分析可知,当信号脉冲宽度为0.1 μs时,信号采样点数较少,导致频率分辨率低,因而线性调频信号和非线性调频信号从信号频谱的几何形状上无法区分开来,它们的几何形状和常规雷达信号类似,因而在这种情况下,利用复杂度思想进行识别分类,效果不理想。
3) 总体来说,该方法是基于频谱复杂度的一个识别流程,频率分辨率越高,信号识别效果越好,对于长脉冲信号的识别普遍适用,需要指出的是,对于长脉冲信号而言,每种信号的频谱几何形状都有明显特征,同样采用复杂度思想去识别分类,然而由于数据长度过长会导致识别时间大大增加,但是信号在频域上非零值区间是有限的,因此可以采用信号数据截取的方法,保留频谱上有效几何特征的数据,然后再利用复杂度思想进行分类识别。仿真实验是在信号脉冲点数为500点时的识别统计结果,是在本文仿真条件下所能适用的最小脉冲,具有较好的工程应用价值。
| [1] |
韩立辉, 黄高明, 王鹏. 基于瞬时自相关算法的线性调频雷达信号脉内分析研究[J]. 舰船电子对抗, 2011, 34(3): 1-4, 12. HAN Lihui, HUANG Gaoming, WANG Peng. Research into signals intra-pulse analysis of linear frequency modulation radar based on instantaneous auto-correlation algorithm[J]. Shipboard electronic countermeasure, 2011, 34(3): 1-4, 12. (  0) 0)
|
| [2] |
王茂汶, 李涛, 周涛. 基于瞬时自相关和FRFT的LFM信号检测性能研究[J]. 电子信息对抗技术, 2013, 28(5): 1-5. WANG Maowen, LI Tao, ZHOU Tao. Research on LFM signal detection performance based on instantaneous autocorrelation and FRFT[J]. Electronic information countermeasure technology, 2013, 28(5): 1-5. (  0) 0)
|
| [3] |
GARDNER W. Measurement of spectral correlation[J]. IEEE transactions on acoustics, speech, and signal processing, 1986, 34(5): 1111-1123. DOI:10.1109/TASSP.1986.1164951 (  0) 0)
|
| [4] |
UEUNG G K, GARDNER W A. Search-efficient methods of detection of cyclostationary signals[J]. IEEE trans signal processing, 1996, 44(5): 1214-1223P. DOI:10.1109/78.502333 (  0) 0)
|
| [5] |
VANHOY G, SCHUCKER T, BOSE T. Classification of LPI radar signals using spectral correlation and support vector machines[J]. Analog integrated circuits & signal processing, 2017, 91(2): 305-313. (  0) 0)
|
| [6] |
PACHORI R B, SIRCAR P. Time-frequency analysis using time-order representation and Wigner distribution[C]//Proceedings of 2008 IEEE Region 10 Conference TENCON. Hyderabad, India, 2008: 1-6. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4766782
(  0) 0)
|
| [7] |
ZHANG M, LIU L, DIAO M. LPI radar waveform recognition based on time-frequency distribution[J]. Sensors, 2016, 16(10): 1682. DOI:10.3390/s16101682 (  0) 0)
|
| [8] |
刘歌, 张国毅, 田榛熔. 基于时频图像三维熵特征的雷达信号识别[J]. 火力与指挥控制, 2016, 41(12): 169-173. LIU Ge, ZHANG Guoyi, TIAN Hazen. Radar signal recognition based on time-frequency image 3D entropy features[J]. Fire and command control, 2016, 41(12): 169-173. DOI:10.3969/j.issn.1002-0640.2016.12.039 (  0) 0)
|
| [9] |
冉启文, 谭立英. 小波分析与分数傅里叶变换及应用[M]. 北京: 国防工业出版社, 2002. RAN Qiwen, TAN Liying. Wavelet analysis and fractional Fourier transform and applications[M]. Beijing: National Defense Industry Press, 2002. (  0) 0)
|
| [10] |
陈健, 阔永红, 李建东, 等. 基于小波变换的数字调制信号识别方法的研究[J]. 电子与信息学报, 2006, 28(11): 2026-2029. CHEN Jian, KUO Yonghong, LI Jiandong, et al. Research on digital modulation signal recognition method based on wavelet transform[J]. Journal of electronics and information, 2006, 28(11): 2026-2029. (  0) 0)
|
| [11] |
CHOI H I, WILLIAMS W J. Improved time-frequency representation of multicomponent signals using exponential kernels[J]. IEEE transactions on acoustics, speech, and signal processing, 1989, 37(6): 862-871. DOI:10.1109/ASSP.1989.28057 (  0) 0)
|
| [12] |
吕铁军, 郭双冰, 肖先赐. 调制信号的分形特征研究[J]. 中国科学(E辑), 2001, 44(6): 152-158. LÜ Tiejun, GUO Shuangbing, XIAO Xianci. Study on fractal features of modulation signals[J]. Science in China series:information sciences, 2001, 44(2): 152-158. (  0) 0)
|
| [13] |
吕铁军, 郭双冰, 肖先赐. 基于复杂度特征的调制信号识别[J]. 通信学报, 2002, 23(1): 111-115. LU Tiejun, GUO shuangbing, XIAO Xianci. Modulation signals recognition based on the complexity measure[J]. Journal of China institute of communications, 2002, 23(1): 111-115. (  0) 0)
|
| [14] |
吴振兴, 阮怀林, 何宇. 基于谱特征的雷达信号脉内编码调制样式识别[J]. 电子信息对抗技术, 2015, 30(2): 16-20, 66. WU Zhenxing, RUAN Huailin, HE Yu. Intra-Pulse coding modulated recognition technology of radar signals based on spectrum characteristics[J]. Electronic information warfare technology, 2015, 30(2): 16-20, 66. (  0) 0)
|
| [15] |
马宁, 马亮. 基于频谱和瞬时频率的雷达信号识别方法[J]. 制导与引信, 2014, 35(3): 16-20, 41. MA Ning, MA Liang. A method for radar signal recognition based on the spectrum and instant frequency[J]. Guidance & fuze, 2014, 35(3): 16-20, 41. (  0) 0)
|
| [16] |
LEMPEL A, ZIV J. On the complexity of finite sequences[J]. IEEE transactions on information theory, 1976, 22(1): 75-81. DOI:10.1109/TIT.1976.1055501 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


