2. 火箭军驻211厂军事代表室, 北京 100086;
3. 北京航天发射技术研究所, 北京 100076;
4. 中国科学院微电子研究所, 北京 100029
2. Military Representative Office, Rocket Army in 211 factory, Beijing 100086, China;
3. Beijing Institute of Space Launch of Technology, Beijing 100076, China;
4. Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China
载噪比(carrier to noise ratio,C/N0)是描述接收机性能的一个很重要的输出参数,并且可以衡量跟踪环路的跟踪状态和各个通道的跟踪策略。载噪比不仅是接收机输出给用户的一个测量值,同时也是接收机信号处理中一个重要的控制量,用于定位解算中的加权最小二乘法、设置信号检测门限以抑制互相关干扰,以及利用载噪比来抑制多路径干扰[1]。信号捕获门限与信噪比(signal to noise ratio, SNR)有着直接关系,信号跟踪环路的锁定检测和接收机性能的预估也都与载噪比的测定相关[2]。信噪比是信号功率与噪声功率之比,而载噪比是信噪比的一种归一化表现形式[3]。输出的载噪比估计值可以反映该通道跟踪信号的强度,通常情况下,信号的载噪比越高意味着信号强度越高,则将会得到更精确的伪距和载波相位测量精度以及更好的定位精度。
接收机的载噪比估计依赖于信号功率估计与噪声功率估计,大部分估计算法都是通过I、Q两路累加值估计得到的[4-5]。比较常见的载噪比估计方法有宽窄带功率比值法(narrow to wide power ratio method, NWPRM)[6-8]、方差求和法(variance summing method, VSM)[9-11]、I支路功率方差比方法[12]和平方信噪比方差方法[13]。其中,应用最为广泛的是宽窄带功率比值法,由于其在估计过程中采用了20 ms的相干积分,因此需要先进行比特同步后再估计载噪比值,并且不适用于北斗系统以2 ms调制一个导航电文的GEO卫星;方差求和法在虽然能够应用于GEO卫星,在一些多信号体制接收机中有所应用,但由于其在估计过程中用到了求方差运算,而方差的样本量至少要20 ms以上的数据估计得到的载噪比才具有一定的可信度,因此需要存满20 ms的数据后才能进行运算,这就占用了存储器资源,在实际DSP实现的时候是一种对存储器资源的浪费。
为了解决上述问题,本文提出了一种载噪比估计算法,该方法利用I支路二阶矩和I、Q两支路四阶矩估计的分布特性,推导出了载噪比估计的具体表达式。本文从估计偏差、实现复杂度、适应性和输出时延四个方面对NWPRM、VSM和本文提出的算法进行了分析比较。
1 信号模型当接收机跟踪某个信号时,由该信号通道上I支路和Q支路输出的相干积分值IP(n)和QP(n)的表达式如下[14]
| $ {I_P}\left( n \right) = \frac{A}{2}D\left( n \right)R\left( {{\tau _P}} \right)\sin c\left( {{f_e}T} \right)\cos {\phi _e} + {n_I} $ | (1) |
| $ {Q_P}\left( n \right) = \frac{A}{2}D\left( n \right)R\left( {{\tau _P}} \right)\sin c\left( {{f_e}T} \right)\sin {\phi _e} + {n_Q} $ | (2) |
式中:D(n)是值为±1的数据比特电平值,τP为即时复制C/A码与接收C/A码之间的相位差异,R(·)代表最大值为1的C/A码自相关函数;且信噪比SNR=A2/2σ2, 载噪比C/N0与信噪比SNR的关系为C/N0=SNR/2T; nI和nQ均为均值为零,方差为σ2/2的随机正态噪声。
假设码对齐假设码对齐且码相关过程中卫星电文数据D(t)=1,则上面两式可简化为
| $ {I_P}\left( n \right) = \frac{A}{2}\sin c\left( {{f_e}T} \right)\cos {\phi _e} + {n_I} $ | (3) |
| $ {Q_P}\left( n \right) = \frac{A}{2}\sin c\left( {{f_e}T} \right)\sin {\phi _e} + {n_Q} $ | (4) |
上面两式还可以写成如下一个关于载噪比C/N0的函数:
| $ {I_P}\left( n \right) = \sqrt {\left( {C/{N_0}} \right)\tau /M} \sigma \cos {\phi _e} + {n_I} $ | (5) |
| $ {Q_P}\left( n \right) = \sqrt {\left( {C/{N_0}} \right)\tau /M} \sigma \sin {\phi _e} + {n_Q} $ | (6) |
进一步对以上两式单位化:
| $ {I_P}\left( n \right) = \sqrt {\left( {C/{N_0}} \right)\tau /M} \cos {\phi _e} + {n_I} $ | (7) |
| $ {Q_P}\left( n \right) = \sqrt {\left( {C/{N_0}} \right)\tau /M} \sin {\phi _e} + {n_Q} $ | (8) |
此时,nI和nQ变为均值为零,方差为1/2的随机正态噪声。
另外由式(3)、(4)可知,若φe=0,则有
| $ \left\{ \begin{array}{l} {I_P}\left( n \right) = A/2 + {n_I}\\ {I_Q}\left( n \right) = {n_Q} \end{array} \right. $ | (9) |
式中:nI~N(0, σ2/2),nQ~N(0, σ2/2)。
在推导出I、Q两路每1 ms累加值的概率分布之后,就可以对这些载噪比估计方法进行推导。
2 典型载噪比估计算法 2.1 宽窄带功率比值法宽窄带功率比值法的基本原理是根据信号加噪声的功率在不同噪声带宽上的差异,得到宽带功率和窄带功率并利用二者的比值来计算载噪比C/N0。
带宽为1/T的宽带功率PWB(k)被定义为
| $ {P_{WB}}\left( k \right) = \sum\limits_{n = kM + 1}^{kM + M} {\left( {I_P^2\left( n \right) + Q_P^2\left( n \right)} \right)} $ | (10) |
带宽为1/MT的窄带功率PNB(k)则被定义为
| $ {P_{NB}}\left( k \right) = {\left( {\sum\limits_{n = kM + 1}^{kM + M} {{I_P}\left( n \right)} } \right)^2} + {\left( {\sum\limits_{n = kM + 1}^{kM + M} {{Q_P}\left( n \right)} } \right)^2} $ | (11) |
将窄带功率PNB(k)用相应的宽带功率PWB(k)来进行单位化得到比率值PNW(k)为并对其做平均,得到
| $ {{\bar P}_{NW}}\left( k \right) = \frac{1}{K}\sum\limits_{k = 1}^K {{P_{NW}}\left( k \right)} = \frac{1}{K}\sum\limits_{k = 1}^K {\frac{{{P_{NB}}\left( k \right)}}{{{P_{WB}}\left( k \right)}}} $ | (12) |
由此可求得载噪比C/N0为
| $ C/{N_0} = \frac{1}{T} \cdot \frac{{{{\bar P}_{NW}}\left( k \right) - 1}}{{M - {{\bar P}_{NW}}\left( k \right)}} $ | (13) |
方差求和法的基本原理是通过即时支路输出的I、Q的累加值的期望和方差来分别计算有用信号功率和噪声功率, 从而得到载噪比估计值。
接收信号中信号和噪声总功率为
| $ Z\left( n \right) = I_P^2\left( n \right) + Q_P^2\left( n \right) $ | (14) |
则参量Z的期望Z和方差σZ2分别为
| $ \bar Z = \frac{1}{N}\sum\limits_{n = 1}^N {Z\left( n \right)} $ | (15) |
| $ \sigma _Z^2 = \frac{1}{{N - 1}}\sum\limits_{n = 1}^N {\left( {Z\left( n \right) - \bar Z} \right)} $ | (16) |
因此载噪比估计值C/N0为
| $ C/{N_0} = \frac{1}{{2T}} \cdot \frac{{{P_s}}}{{\sigma _{IQ}^2}} = \frac{1}{T} \cdot \frac{{\sqrt {{Z^2} - \sigma _Z^2} }}{{\bar Z - \sqrt {{Z^2} - \sigma _Z^2} }} $ | (17) |
该方法是基于I路信号累加值的二阶矩和I、Q两路信号累加值的四阶矩估计,具体的推导如下。
定义I路信号累加值的二阶矩:
| $ {M_{I2}} = \frac{1}{N}\sum\limits_{n = 1}^N {I_p^2\left( n \right)} $ | (18) |
由概率论知识可知期望和方差的关系如下[15]
| $ E\left( {{X^2}} \right) = {E^2}\left( X \right) + D\left( X \right) $ | (19) |
由式(9)、(19)可得到MI2的均值为
| $ E\left( {{M_{I2}}} \right) = \frac{{{A^2}}}{4} + \frac{{{\sigma ^2}}}{2} $ | (20) |
定义I、Q两路信号累加值的四阶矩:
| $ {M_4} = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {I_P^2\left( n \right) + Q_P^2\left( n \right)} \right)}^2}} $ | (21) |
将式(9)代入式(21)可得
| $ {M_4} = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {{{\left( {{n_I} + \frac{A}{2}} \right)}^2} + n_Q^2} \right)}^2}} $ | (22) |
进一步展开可得
| $ {M_4} = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {\frac{{{A^2}}}{4} + A{n_I} + n_I^2 + n_Q^2} \right)}^2}} $ | (23) |
令M′=
| $ E\left( {M'} \right) = \frac{{{A^2}}}{4} + {\sigma ^2} $ | (24) |
由概率论知识, 可知若X~N(0, 1)则有
因此,当nI~N(0, σ2/2),令
由χ2分布性质,可知
| $ D\left( {{Y^2}} \right) = 2\;即\;D\left( {\frac{2}{{{\sigma ^2}}}n_I^2} \right) = 2 $ | (25) |
可得到
| $ D\left( {n_I^2} \right) = \frac{{{\sigma ^4}}}{2} $ | (26) |
同理可得
| $ D\left( {n_Q^2} \right) = \frac{{{\sigma ^4}}}{2} $ | (27) |
因此M′的方差为
| $ D\left( {M'} \right) = \frac{{{A^2}}}{2}{\sigma ^2} + {\sigma ^4} $ | (28) |
将式(28)代入式(19)可得
| $ E\left( {{M_4}} \right) = \frac{{{A^4}}}{{16}} + {A^2}{\sigma ^2} + 2{\sigma ^4} $ | (29) |
MI2的均值的平方E(MI4)为
| $ E\left( {{M_{I4}}} \right) = \frac{{{A^4}}}{{16}} + \frac{{{A^2}{\sigma ^2}}}{4} + \frac{{{\sigma ^4}}}{4} $ | (30) |
1) 方案一:
令
| $ M{P_1} = \frac{{{A^4} + 16{A^2}{\sigma ^2} + 32{\sigma ^4}}}{{{A^4} + 4{A^2}{\sigma ^2} + 4{\sigma ^4}}} $ | (31) |
解式(31)得到
| $ \frac{{{A^2}}}{{2\sigma _1^2}} = \frac{{M{P_1} - 4 - \sqrt {M{P_1} + 8} }}{{1 - M{P_1}}} $ | (32) |
| $ \frac{{{A^2}}}{{2\sigma _2^2}} = \frac{{M{P_1} - 4 - \sqrt {M{P_1} + 8} }}{{1 - M{P_1}}} $ | (33) |
式(33)得到的值为一个假值。
因此,可以得到载噪比C/N0:
| $ C/{N_0} = \frac{{{A^2}}}{{2{\sigma ^2}}} \cdot \frac{1}{{2T}} = \frac{1}{{2T}} \cdot \frac{{M{P_1} - 4 - \sqrt {M{P_1} + 8} }}{{1 - M{P_1}}} $ | (34) |
2) 方案二:
令
| $ M{P_2} = \frac{{{A^4} + 4{A^2}{\sigma ^2} + 4{\sigma ^4}}}{{{A^4} + 16{A^2}{\sigma ^2} + 32{\sigma ^4}}} $ | (35) |
解式(35)得到
| $ \frac{{{A^2}}}{{2\sigma _1^2}} = \frac{{4M{P_2} - 1 - \sqrt {8MP_2^2 + M{P_2}} }}{{1 - M{P_2}}} $ | (36) |
| $ \frac{{{A^2}}}{{2\sigma _2^2}} = \frac{{4M{P_2} - 1 + \sqrt {8MP_2^2 + M{P_2}} }}{{1 - M{P_2}}} $ | (37) |
式(36)得到的值为一个假值。
因此,可以得到载噪比C/N0:
| $ \begin{array}{*{20}{c}} {C/{N_0} = \frac{1}{{2T}} \cdot \frac{{{A^2}}}{{2{\sigma ^2}}} = }\\ {\frac{1}{{2T}} \cdot \frac{{4M{P_2} - 1 + \sqrt {8MP_2^2 + M{P_2}} }}{{1 - M{P_2}}}} \end{array} $ | (38) |
方案一和方案二在本质上是一样的,方案二的实质就是方案一中式(31)等式两边分子分母同时调换解出的结果。下面从理论和测试两个方面来验证其一致性。
3.2.1 理论验证将方案一中的
| $ C/{N_0} = \frac{1}{{2T}} \cdot \frac{{{M_4} - 4{M_{I4}} - \sqrt {{M_{I4}}{M_4} + 8M_{I4}^2} }}{{{M_{I4}} - {M_4}}} $ | (39) |
将方案二中的
| $ C/{N_0} = \frac{1}{{2T}} \cdot \frac{{4{M_{I4}} - {M_4} + \sqrt {8M_{I4}^2 + {M_{I4}}{M_4}} }}{{{M_4} - {M_{I4}}}} $ | (40) |
对比式(39)、(40)可以发现两式是相同的。因此,从理论上来讲两种方案结果一致得到验证。
3.2.2 数据测试验证仿真采用真实GPS中频数据,中心频率为1 572.42 MHz,数字基带中频为4.092 MHz,采样频率为16.368 MHz,取1 ms相干积分,对1 000次估计结果取平均。无多普勒频率残差的情况下,对两种方案的载噪比估计进行仿真,得到的仿真结果如表 1。
| 表 1 两种方案实测数据验证 Tab.1 The validation of two schemes |
由表 1可知,两种方案得到的载噪比相同。但是方案一中计算载噪比的表达式更为简单,计算量相对来讲更小。因此在后面的测试比较中采用方案一来与其他几种算法进行测试比较性能。并将新方法命名为I支路矩方法(I branch moment method, IBMM)。
4 性能分析几种算法在载噪比估计偏差、算法实现复杂度、输出时延、适应性等方面存在差异。下面将分别从这四个方面进行仿真分析。
4.1 估计偏差比较 4.1.1 仿真数据测试分析理论仿真采用Matlab生成GPS 19号卫星数据,仿真参数:采样频率为16.368 MHz,系统中频为4.092 MHz。为了更精准的对比分析上述三种算法,本文采用长度相同的数据来进行性能分析,具体仿真方案为:宽窄带法采用20 ms相干积分,对50次估计结果取平均;其他两种算法均是取1 ms相干积分,对1 000次估计结果取平均。无多普勒频率残差的情况下,对信号功率为-138~-120 dB·m的数据三种算法分别进行载噪比估计仿真,得到的载噪比估计偏差如下:
由图 1可知,在弱信号条件下,方差求和法的估计偏差为0.5 dB, IBMM偏差为0.6 dB, NWPRM偏差为0.65 dB, 说明IBMM和NWPRM弱信号应用时性能较差;在强信号条件下,四种算法偏差均在0.5 dB以内,算法性能相当。总的来说,本文提出的算法性能介于宽窄带和方差求和法之间。
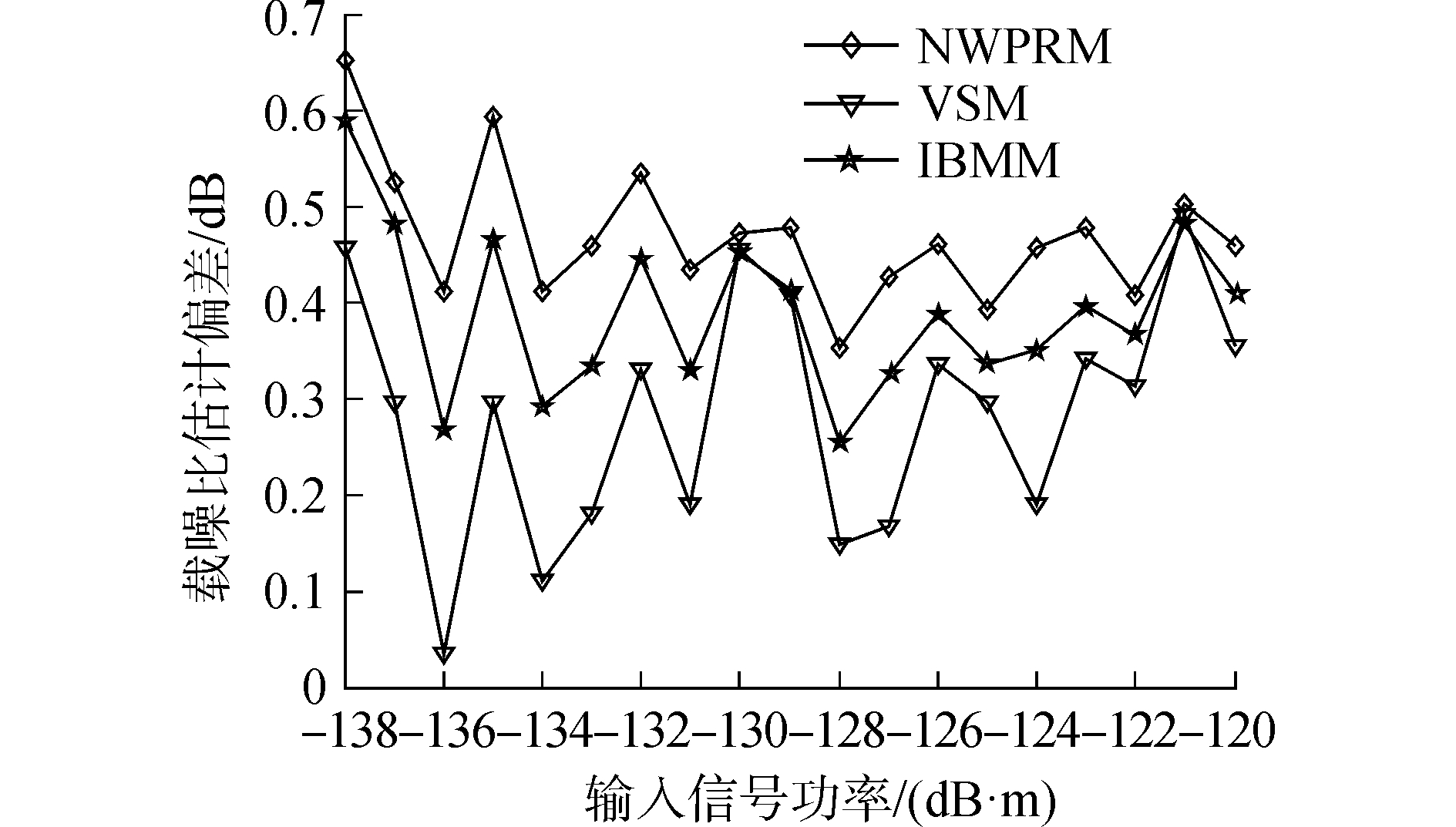
|
Download:
|
| 图 1 仿真数据载噪比估计偏差 Fig. 1 The C/N0 estimation deviation of simulated data | |
仿真采用真实GPS中频数据,中心频率为1 572.42 MHz,数字基带中频为4.092 MHz,采样频率为16.368 MHz,其他参数和理论仿真一致。对各算法所能达到的载噪比估计偏差进行仿真,得到的仿真结果如图 2。

|
Download:
|
| 图 2 实测数据载噪比估计偏差 Fig. 2 The C/N0 estimation deviation of measured data | |
由图 2可知,几种算法的估计偏差相差不大,都在0.5 dB以内。其中,在信号较强的三组数据时,I支路矩估计法的偏差介于宽窄带和矩估计法之间。上述实测结果和理论分析一致,说明本文提出算法的正确性。总的来说,三种算法的估计性能相差不大。
4.2 算法实现复杂度比较 4.2.1 运算量比较对三种算法的运算量进行分析,为了精确的比较三种算法的运算量,采用长度相同的数据来进行性能分析,具体方案为:宽窄带法采用20 ms相干积分,对50次估计结果取平均;其他两种算法均是取1 ms相干积分,对1 000次估计结果取平均。具体结果如表 2。
| 表 2 三种算法运算量比较 Tab.2 The calculation comparison of three algorithm |
由表 2可知,三种算法中,NWPRM和IBMM算法的运算量相当,VSM与IBMM相比不仅多了开方运算而且加法次数接近多了1 000次,因此本文提出的算法运算量较为适中。
4.2.2 占用存储器资源比较在实际应用到DSP中时,由于VSM在求方差时会用到均值,而均值是在存满1 000次结果得到的,因此VSM需要先将1 000个数据存储后再进行运算。其中,存储一组数据需要的存储器大小为1 000×8 byte,这会对存储器资源造成巨大的浪费。但NWPRM和IBMM在DSP中应用时可以做到实时的运算,存储一组数据需要的存储器大小仅为2×8 byte,并不会占用太大的存储器空间。因此,本文提出的算法对存储器资源消耗较少。
4.3 输出时延比较宽窄带法计算载噪比时是每20 ms输出一个结果。方差求和法计算载噪比时含有求方差运算,至少是2 ms输出一个结果。通常情况下,要达到比较准确的估计输出,方差求和法需要20 ms的数据来准确估计样本的方差。而本文提出的方法则使用比较灵活,可以1 ms输出一个结果,也可以设置为任意时间长度输出。
4.4 适应性比较目前GNSS包含了美国的GPS、俄罗斯的GLONASS、欧盟的Galileo、中国的Compass(北斗)。其中北斗的GEO卫星2 ms调制一个导航电文,宽窄带法采用20 ms相干积分,因此它不能直接应用于BD系统。方差求和法虽然能2 ms输出一个结果,但要达到比较准确的载噪比估计值输出时,方差求和法则需要20 ms的数据来准确估计样本的方差。而本文提出的方法可以任意ms输出一个结果,提升了适应性,可广泛用于北斗等GNSS系统。
5 结论1) 仿真数据和实测数据都表明,本文提出的IBMM算法的估计偏差介于NWPRM和VSM之间,三种算法的估计偏差都维持在0.5 dB以内,总的来说,三种算法的估计性能相差不大。
2) 从实现复杂度方面来看,三种算法中,VSM的运算量最大且实现复杂度较高,存储数据过程中会对存储器资源造成极大的浪费;NWPRM和本文提出的IBMM运算量相当,且都能做到实时的运算,不会占用太大的存储器空间。
3) 输出时延和适应性比较结论:NWPRM和VSM存在20 ms的输出时延,而本文提出的算法则可以做到任意毫秒输出一个结果,而NWPRM不能应用于北斗系统,要能够准确估计GEO卫星的载噪比值时,VSM就不适用了,而本文提出的IBMM算法可广泛应用于北斗等GNSS系统,在这方面具有明显的优势。
| [1] |
何文涛, 徐建华, 叶甜春. GPS弱信号的自适应载噪比估计算法[J]. 电子技术应用, 2010, 36(6): 111-114. HE Wentao, XU Jianhua, YE Tianchun. Adaptive C/N estimation method of GPS weak signal[J]. Application of electronic technique, 2010, 36(6): 111-114. (  0) 0)
|
| [2] |
袁建国, 欧松林. GPS接收机并行捕获算法的研究[J]. 重庆邮电大学学报(自然科学版), 2016, 25(4): 470-474. YUAN Jianguo, OU Songlin. Study on parallel acquisition algorithm for GPS receiver[J]. Journal of Chongqing university of posts and telecommunications (natural science edition), 2016, 25(4): 470-474. (  0) 0)
|
| [3] |
SHARAWI M S, AKOS D M, ALOI D N. GPS C/N0 estimation in the presence of interference and limited quantization levels[J]. IEEE transactions on aerospace and electronic systems, 2007, 43(1): 227-238. DOI:10.1109/TAES.2007.357129 (  0) 0)
|
| [4] |
BRAASCH M S, VAN DIERENDONCK A J. GPS receiver architectures and measurements[J]. Proceedings of the IEEE, 1999, 87(1): 48-64. DOI:10.1109/5.736341 (  0) 0)
|
| [5] |
BORIO D, GIOIA C, BALDINI G. Asynchronous pseudolite navigation using C/N0 measurements[J]. Journal of navigation, 2016, 69(3): 639-658. DOI:10.1017/S037346331500082X (  0) 0)
|
| [6] |
傅金琳, 赵子阳, 李醒飞. 一种改进的功率比值法载噪比估算算法[J]. 中国惯性技术学报, 2015, 23(5): 642-647. FU Jinlin, ZHAO Ziyang, LI Xingfei. Improved power ratio method of carrier-to-noise ratio estimation algorithm[J]. Journal of Chinese inertial technology, 2015, 23(5): 642-647. (  0) 0)
|
| [7] |
GROVES P D. GPS signal to noise measurement in weak signal and high interference environments[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation. Long Beach, CA, 2005: 644-645. http://www.researchgate.net/publication/268388942_GPS_Signal-to-Noise_Measurement_in_Weak_Signal_and_High-Interference_Environments
(  0) 0)
|
| [8] |
BHUIYAN M Z H, SÖDERHOLM S, THOMBRE S, et al. Performance evaluation of carrier-to-noise density ratio estimation techniques for BeiDou Bl signal[C]//IEEE Ubiquitous Positioning Indoor Navigation and Location Based Service. Corpus Christ, TX, USA, 2015: 19-25. http://www.researchgate.net/publication/268519598_Performance_Evaluation_of_Carrier-to-Noise_Density_Ratio_Estimation_Techniques_for_BeiDou_B1_Signal
(  0) 0)
|
| [9] |
LI Li, CHEONG J W, WU Jinghui, et al. Improvement to multi-resolution collective detection in GNSS receivers[J]. Journal of navigation, 2014, 67(2): 277-293. DOI:10.1017/S0373463313000635 (  0) 0)
|
| [10] |
PSIAKI M L, AKOS D M, THOR J. A comparison of "Direct RF Sampling" and "Downconvert & sampling" GNSS receiver architectures[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR, 2003: 1942-1952. https://www.ion.org/publications/abstract.cfm?articleID=5380/
(  0) 0)
|
| [11] |
蒋君伟, 段晓辉, 林阳. GPS信号载噪比估计算法的研究[J]. 北京大学学报(自然科学版), 2009, 45(3): 409-414. JIANG Junwei, DUAN Xiaohui, LIN Yang. The research of estimation method for GPS C/N0[J]. Acta scientiarum naturalium universitatis pekinensis, 2009, 45(3): 409-414. (  0) 0)
|
| [12] |
巴晓辉, 刘海洋, 郑睿, 等. 一种有效的GNSS接收机载噪比估计方法[J]. 武汉大学学报(信息科学版), 2011, 36(4): 457-460. BA Xiaohui, LIU Haiyang, ZHENG Rui, et al. An effective carrier-to-noise ratio estimation method for GNSS receiver[J]. Geomatics and information science of Wuhan university, 2011, 36(4): 457-460. (  0) 0)
|
| [13] |
FALLETTI E, PINI M, PRESTI L L. Low complexity carrier-to-noise ratio estimators for GNSS digital receivers[J]. IEEE transactions on aerospace and electronic systems, 2011, 47(1): 420-437. DOI:10.1109/TAES.2011.5705684 (  0) 0)
|
| [14] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2017: 306-364. XIE Gang. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2017: 306-364. (  0) 0)
|
| [15] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2010: 46-103. SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability theory and mathematical statistics[M]. 4th ed. Beijing: Higher Education Press, 2010: 46-103. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


