材料的组织演变是一个复杂的热力学过程,通常需经过大量且复杂的实验才能研究透彻。随着计算技术的发展,可以通过计算机模拟这一过程,这将大大缩短研究周期,节约研究费用。蒙特卡罗法就是众多模拟方法的一种[1-2]。
采用蒙特卡罗方法模拟组织演变的第一个环节就是生成初始组织。目前,大多数学者[3-11]是(以二维为例)将材料的微观结构离散为二维的网格点,每个网格点(代表实际多晶材料的一个体积单元)被随机赋予一个晶体学取向,取向一致的单元组成一个晶粒。不过这种方法存在缺陷,那就是容易产生微晶(晶粒只包含一个单元),这与实际的材料组织形成过程不符。因为不管是结晶过程还是固态相变过程中,微小晶粒都具有很大的表面能,极不稳定,很容易被大晶粒吞并而无法保存下来。因此,采用这种方法生成的初始组织,与实际情况有所偏差,这势必影响后续的模拟过程。本文则根据材料组织的形成特点,采用voronoi图[12-15]生成初始组织,可以避免上述情况的出现。voronoi图是由俄罗斯数学家Voronoi于1908年提出的,这一模型有着实际的物理意义,voronoi图反映了自然界普遍存在的一种现象,用它代表材料组织有一定的合理性。
据此本文用voronoi方法成初始组织。首先根据一定的算法随机生成一定数目的晶核坐标,然后利用Matlab软件生成非限制voronoi图,并对其进行剪裁,使之与实际情况相符,最后采用一定的算法在数据结构层次真正生成了初始组织。
1 voronoi图的生成 1.1 非限制性voronoi图Matlab的MPT工具箱中的voronoi(X, Y)函数有生成voronoi图的功能, 其调用格式为
| $ \left[ {{\rm{Vertex\_X,Vertex\_Y}}} \right] = {\rm{voronoi}}\left( {X,Y} \right) $ | (1) |
式中:X、Y为平面上n个随机点(晶核)的坐标矩阵,可通过一定的随机方法产生;Vertex_X, Vertex_Y是生成的voronoi图中各个边的顶点坐标矩阵。
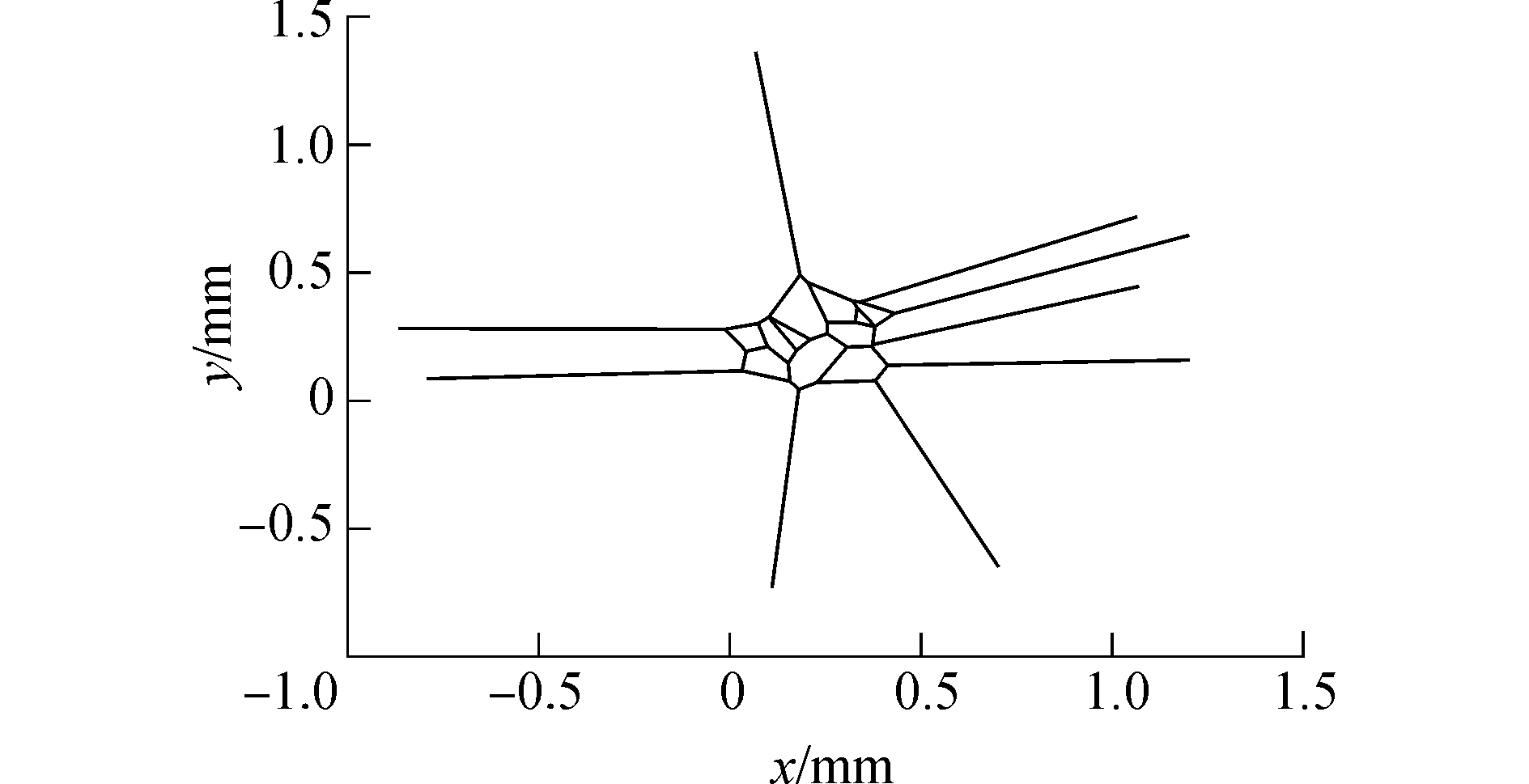
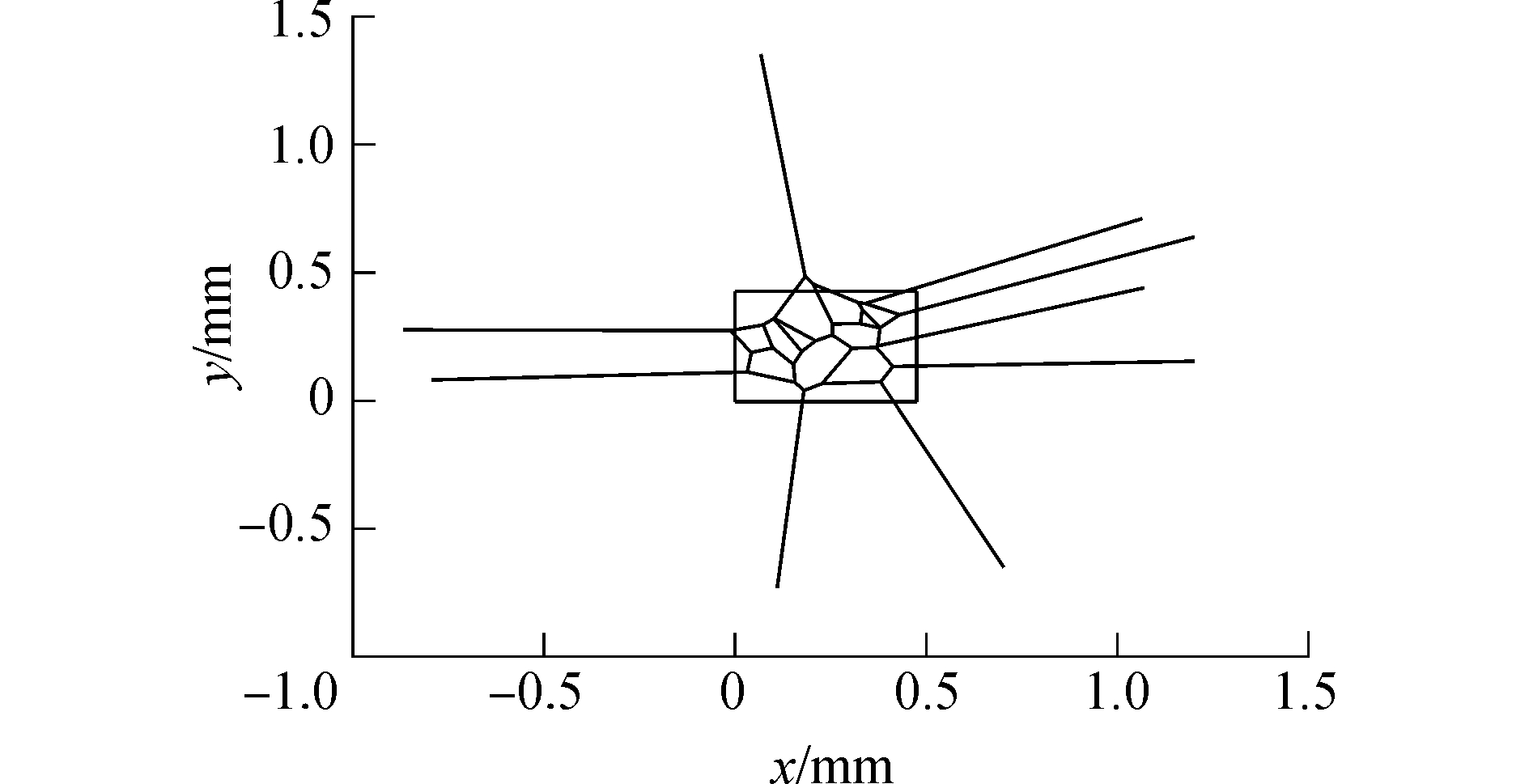
调用voronoi(X, Y)函数后,会生成图 1所示的voronoi图,不过此图是非限制性voronoi图,图形中有的多边形伸长很远,超过了边界,相当于晶粒过度长大,这是不符合实际情况的,金属结晶时,必须受到器壁的限制,故需要将四边形(容器界限)以外的部分裁剪掉,使非限制性voronoi图变为限制性voronoi图,即图 2。
|
Download:
|
| 图 1 非限制性voronoi图 Fig. 1 The unrestricted voronoi diagram | |
|
Download:
|
| 图 2 voronoi图与边界 Fig. 2 The voronoi diagram and its periphery | |
把非限制性voronoi图变为限制性voronoi图,在几何上就是把超出边界的那些线段裁剪掉,通过简单的解析几何方法就能完成。
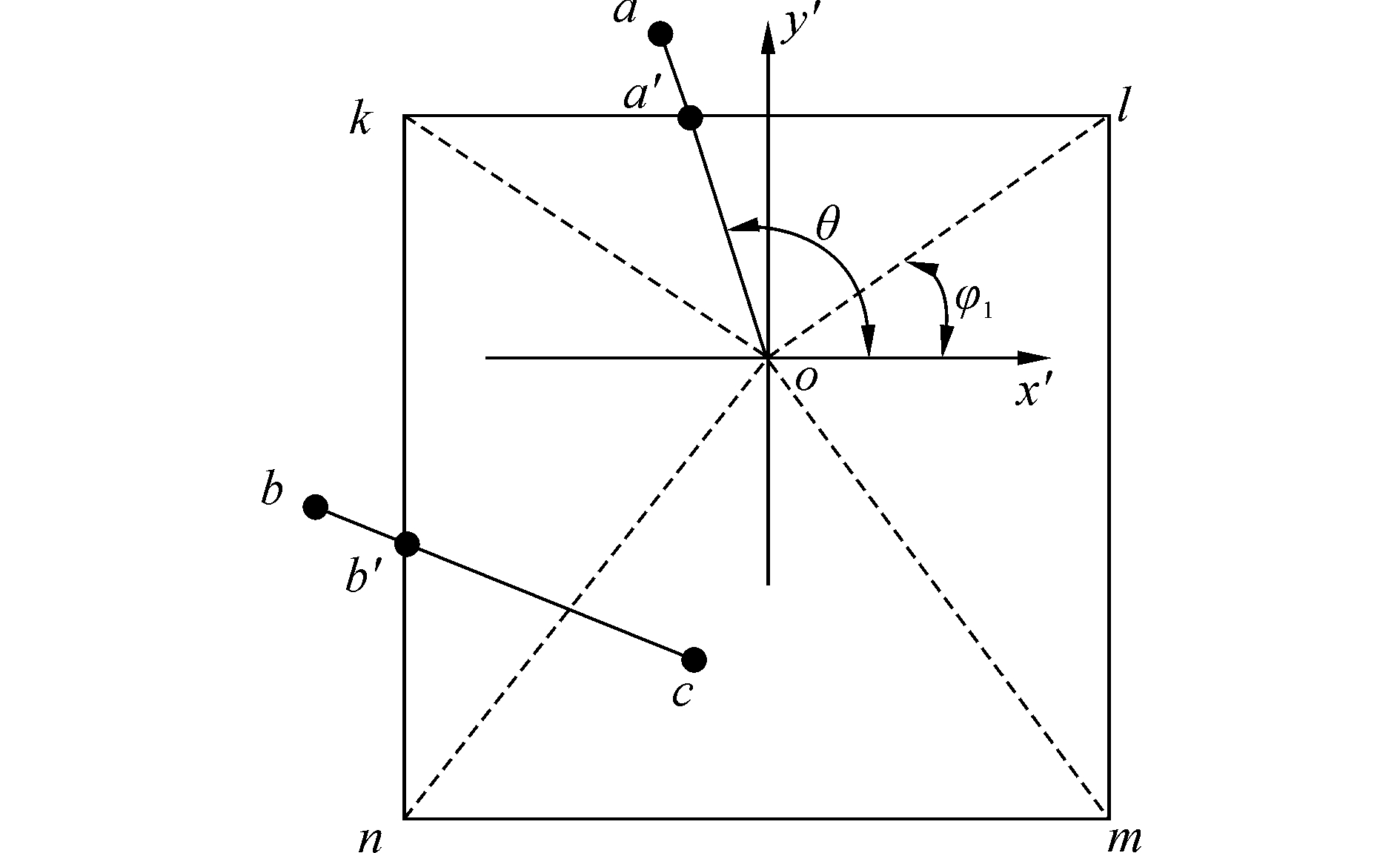
如图 3,假设非限制voronoi图中的某线段oa超出了边界,端点o在界内, 另一端点a在界外,则对其裁剪的算法如下:
|
Download:
|
| 图 3 非限制性voronoi图的剪裁 Fig. 3 The cutting of the unrestricted voronoi diagram | |
设线段oa的序号为i,端点o和a的坐标分别为Vertex_X(1, i), Vertex_Y(1, i)和Vertex_X(2, i),Vertex_Y(2, i)。
在起始点o建立局部坐标系x′oy′, 并计算oa与ox′的夹角θ;然后将o点与边界四个角点k、l、m、n连线并分别计算这些连线与ox′的夹角φk、φl、φm、φn(图中只标出了φl)。
最后将θ与φk、φl、φm、φn相比较,判断线段所在区间,如果φl<θ<φk,,则表明oa与四边形上边界kl相交,可以通过下式求出oa与上边界的交点a′的坐标:
| $ {{x'}_a} = {x_o} + \left( {{y_k} - {y_o}} \right){\rm{c}}\tan \theta $ | (2) |
其中:yk是k点纵坐标,且yk=y′a;ctan θ=
其他线段的处理与此类似,不过需要指出的是,上面的局部坐标系应随所处理线段的不同而不同,比如处理线段cb时,局部坐标系原点应移至c点,并在新的局部坐标系下重新连接k、l、m、n点,再计算θ、φk、φl、φm、φn,求出新的角度后,再按上述方法处理,将bb′裁剪掉。
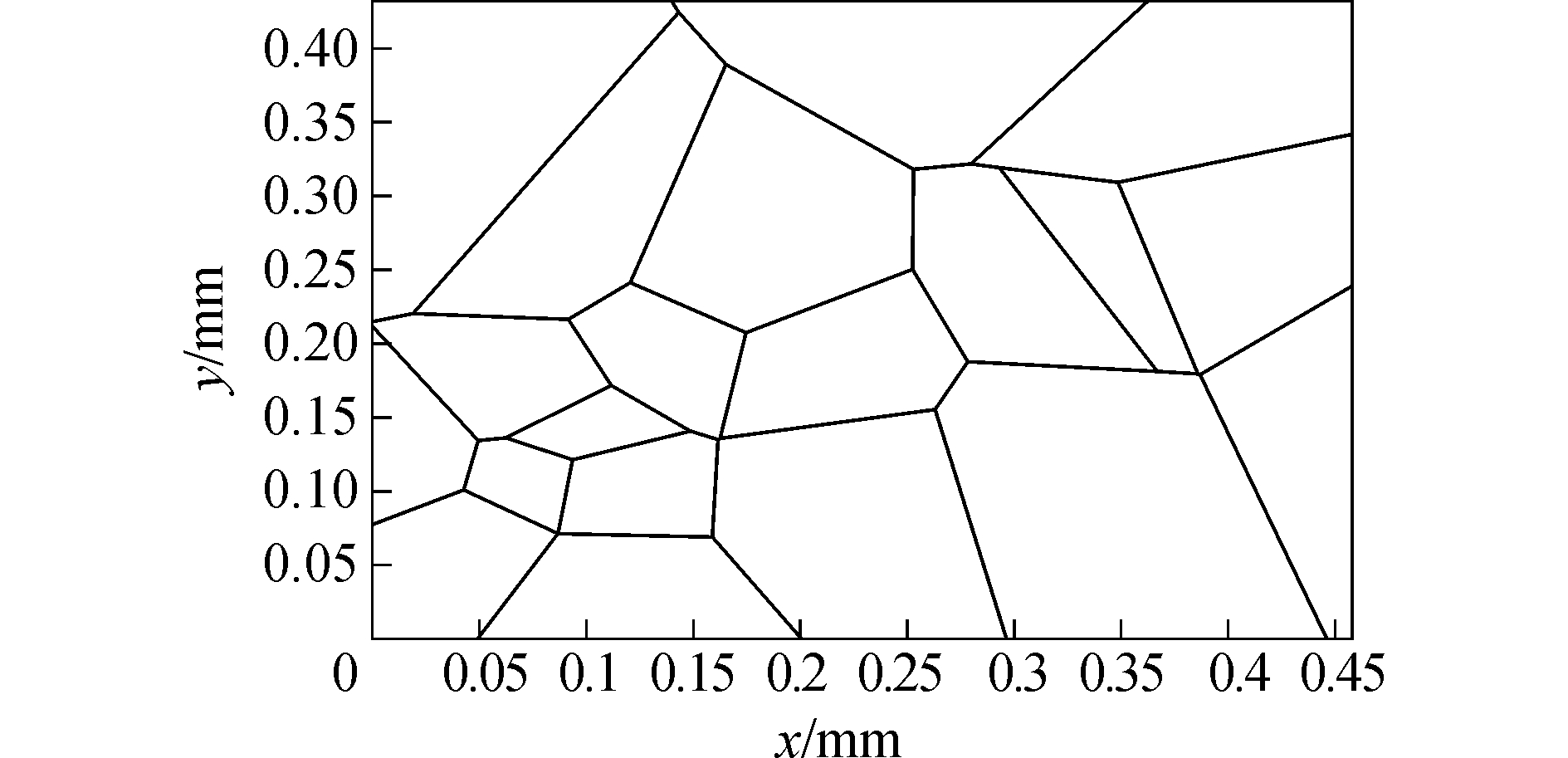
所有线段都作如此处理,最后就得到了改进后的voronoi图,如图 4。本文所说的所有线段是指一个端点在界内,另一端点在界外的那些线段,而两个端点均位于界内的线段则不需处理。
|
Download:
|
| 图 4 限制性voronoi图 Fig. 4 The restricted voronoi diagram | |
voronoi图被直线分割成很多区域,直观上,每个区域似乎代表一个晶粒,但这只是表面现象。程序生成voronoi图时,并没有把属于同一多边形(晶粒)的直线归在一起,因此在数据结构层次上,这些线段之间没有逻辑联系,为此还要做另一项重要工作,就是把每个晶粒(多边形)所包含的晶界(线段)找到,并存储在一起。
为此首先设计了两个数据结构poly和poly_find。poly用于存储某一多边形的所有边线顶点坐标,poly_find用于存储已经搜索到的多边形。
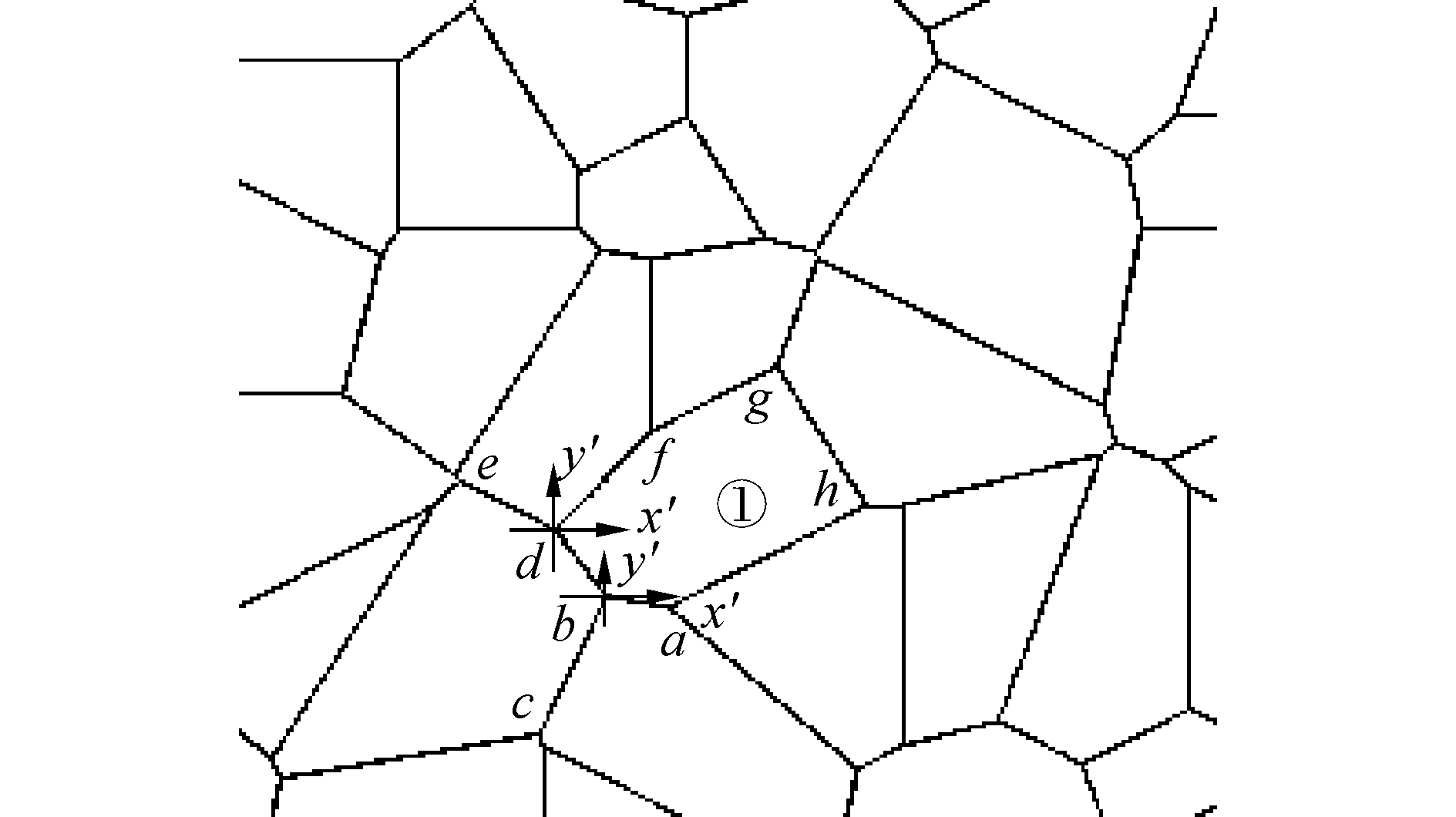
以图 5中的多边形①为例,说明具体方法。该多边形包括a、b、d、f、g、h六个顶点和ab、bd、df、fg、gh、ha六条边。下面的工作就是将这些边搜索出来并存储到数据结构poly中。
|
Download:
|
| 图 5 晶粒的生成 Fig. 5 The generation of a crystal grain | |
1) 首先选择任一条边,(如ab)作为开始,先将这条边的始点a和终点b的坐标添加到poly中:
| $ {\rm{poly}}.\;{\rm{coor}}\left( {1,{\rm{count}}} \right) = {x_a} $ |
| $ {\rm{poly}}.\;{\rm{coor}}\left( {2,{\rm{count}}} \right) = {y_a} $ |
| $ {\rm{poly}}.\;{\rm{coor}}\left( {1,{\rm{count}} + {\rm{1}}} \right) = {x_b} $ |
| $ {\rm{poly}}.\;{\rm{coor}}\left( {2,{\rm{count}} + {\rm{2}}} \right) = {y_b} $ |
其中:count为该多边形第count个顶点,此时count=1。
2) 接下来在b点选择下一条属于多边形①的边。因为从b点有两条出发线段的bd和bc,必须选择线段bd而舍弃bc。为了能做到这一点,需在b点建立一个如图 5所示的局部坐标系y′bx′,然后计算bd、bc与bx′轴正方向所成的夹角θd、θc(图中未标出,可参考图 3中的θ的定义),然后按顺时针方向进行搜索,也就是说沿着多边形①的边界行走时,多边形始终在行走方向的右侧。
由于θd<θc,满足顺时针搜索要求,因此bd被选择,其坐标被存储到poly:
| $ {\rm{poly}}.\;{\rm{coor}}\left( {1,{\rm{count}} + {\rm{2}}} \right) = {x_d} $ |
| $ {\rm{poly}}.\;{\rm{coor}}\left( {2,{\rm{count}} + {\rm{2}}} \right) = {y_d} $ |
如果连接b点的线段不止两条,其处理过程仍一样,仍选择θ最小的那条线段,这就保证了在b点处所选的线段一定属于多边形①。
3) 接下来,把bd边当成ab边,重复上述过程,就会搜索到f点, 将f点信息记录到poly结构中:
| $ {\rm{poly}}.\;{\rm{coor}}\left( {1,{\rm{count}} + {\rm{3}}} \right) = {x_f} $ |
| $ {\rm{poly}}.\;{\rm{coor}}\left( {2,{\rm{count}} + {\rm{3}}} \right) = {y_f} $ |
4) 在上述搜索过程中,每搜索到新的线段,都需要将新线段的终点(如df线段的f点)的坐标与最初起始点的坐标(即xa、ya)相比较,如果xf=xa且yf=ya,则说明线段首尾相接,形成闭合多边形,至此搜索结束,否则继续搜索。当搜索到一个完整的多边形后,就可以把poly添加到结构poly_find中:poly_find (n)=poly,n为多边形(晶粒)序号。
再选择其他线段(尚不属于任何多边形的线段),重复1)~4),直到所有的多边形及其所包含的边都找到。
3 计算实例为了验证上述方法的合理性,利用Matlab开发了软件,并利用该软件生成了初始组织,如图 6所示。在生成初始组织时,首先要确定模拟区域大小和晶核数目,本文中该模拟区域的大小为0.5 mm×0.43 mm,而晶核数目则根据以下方法进行估算。

|
Download:
|
| 图 6 初始组织 Fig. 6 The initial materials microstructure | |
本文假定模拟区域是某一结晶完毕的钢铁材料的一个局部。液态钢铁材料结晶时,晶核数目可根据均匀形核理论进行估算:
| $ I = {I_0}\exp \left( { - \frac{{16{\rm{ \mathsf{ π} }}{\sigma ^3}}}{{3\Delta G_v^2KT}}} \right) \cdot \exp \left( { - \frac{Q}{{KT}}} \right) $ | (3) |
式中: I0为形核率系数,1041 m-3·s-1[16]; K为波尔兹曼常数,1.38×10-23 J·K-1; Q为单个原子扩散激活能,J; Gv为液、固单位体积自由能之差,即相变驱动力,J·m-3; σ为表面张力,0.254 J·m-2[16]; T为实际凝固温度,K; ΔT为过冷度,K;
金属铁液、固两相摩尔自由能之差为
| $ {G_m} = \frac{{\Delta {H_m}}}{{{T_m}}}\Delta T $ | (4) |
式中:ΔHm为金属液、固两相摩尔焓变,15.2 kJ·mol-3[16]; Tm为铁熔点,1 809 K[16]; 利用式(4)计算了Gm然后将之换算为单位体积自由能之差GV,换算方法如下:
| $ {G_V} = \frac{{{G_m}}}{{{V_m}}} $ | (5) |
Vm为液态铁的摩尔体积, 可由下式得到:
| $ {V_m} = \frac{{{M_{F{\rm{e}}}}}}{{{\rho _L}}} $ | (6) |
式中:MFe为铁的摩尔质量,0.056 kg·mol-1; ρL为液态铁的密度,取7 138 kg·m-3
另外,式(3)的Q为单个原子的扩散激活能,根据文献[17]可知液态金属铁的摩尔扩散激活能Qm为46 054 J·mol-1, 因此Q=Qm/N,N为阿佛伽德罗常数。
根据文献[18]可知,50 t钢锭(体积为5.13 m3),凝固时间约为35 400 s,以此为参考,当液态金属铁凝固过冷度达到50 K时,总体积内形核数目大约为
| $ {\rm{core}}\_{\rm{vol}} = I \times 5.13 \times 35400 $ | (7) |
本文的研究区域大小为0.5 mm× 0.43 mm,可看作体积为0.5 mm×0.43 mm×1 mm的三维区域,因此包含的晶核数目约为
| $ {\rm{core}}\_{\rm{zone}} = 0.5 \times 0.43 \times 1 \times {10^{ - 9}}/{\rm{core}}\_{\rm{vol}} \approx 220\left( {个} \right) $ |
故在过冷度为50 K条件下,模拟区域内的晶核数目约为220个,据此生成的初始组织如图 6。
3.2 初始组织可信度评价文献[19]采用IPP软件对纯铁组织的晶粒个数和尺寸分布进行了统计,如图 7(b)所示,图 8则是本文所生成的初始组织的统计结果。文献[29]中统计的晶粒个数为201个,而本文为220个,比较接近,晶粒所在空间区域比本文略小,因此有一定的可比性。

|
Download:
|
| 图 7 晶粒尺寸 Fig. 7 Grain size | |
|
Download:
|
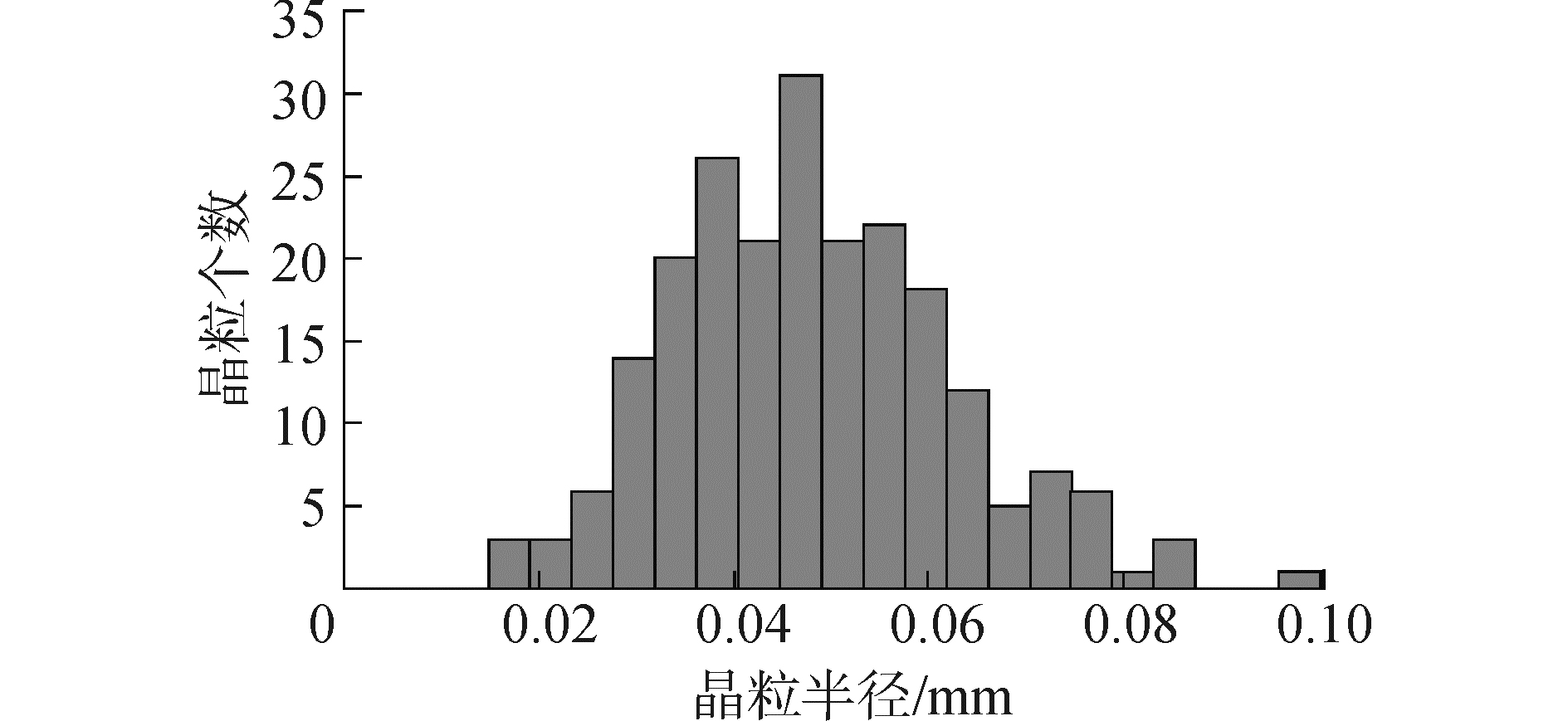
| 图 8 晶粒尺寸分布 Fig. 8 The distribution of grain size in this study | |
对比可见,晶粒尺寸分布都接近正态分布,晶粒的平均尺寸分别为30 μm和50 μm左右,差别不大。这说明用本文提出的算法计算得到的初始组织有一定的可信度,可以用来进行后续的组织演变模拟。
4 结论1) 采用本文提出的算法所生成的初始组织,避免了传统方法所产生的微晶现象,比较符合实际情况。
2) 从统计学角度将生成的组织与实际晶粒组织进行了对比,结果非常接近,表明此方法具有一定的可信度。
| [1] |
ANDERSON M P, SROLOVITZ D J, GREST G S, et al. Computer simulation of grain growth(Ⅰ)-kinetics[J]. Acta metallurgica, 1984, 32(5): 783-791. DOI:10.1016/0001-6160(84)90151-2 (  0) 0)
|
| [2] |
RADHAKRISHNAN B, ZACHARIA T. Simulation of curvature-driven grain growth by using a modified Monte Carlo algorithm[J]. Metallurgical and materials transactions A, 1995, 26(1): 167-180. DOI:10.1007/BF02669802 (  0) 0)
|
| [3] |
MAHIN K W, HANSON K, MORRIS JR W J. Computer simulation of homogeneous nucleation and growth processes[C]//Computer Simulation of Homogeneous Nucleation and Growth Processes. Gaithersburg, MD, USA, 1976: 39-50. https://www.researchgate.net/publication/236365441_Computer_simulation_of_homogeneous_nucleation_and_growth_processes
(  0) 0)
|
| [4] |
张继祥, 关小军, 孙胜. 新改进Monte Carlo法模拟钢板退火过程的晶粒长大[J]. 特殊钢, 2004, 25(1): 21-23. ZHANG Jixiang, GUAN Xiaojun, SUN Sheng. A new modified Monte Carlo algorithm for simulation of grain growth of steel plate during annealing[J]. Special steel, 2004, 25(1): 21-23. (  0) 0)
|
| [5] |
莫春立, 李殿中, 钱百年, 等. 铁素体不锈钢焊接热影响区晶粒长大过程模拟[J]. 金属学报, 2001, 37(3): 307-310. MO Chunli, LI Dianzhong, QIAN Bainian, et al. Simulation of grain growth in welding HAZ of ferrite stainless steel[J]. Acta metallurgica sinica, 2001, 37(3): 307-310. (  0) 0)
|
| [6] |
窦晓峰, 鹿守理, 赵辉. 钢静态再结晶的蒙特卡洛模拟[J]. 钢铁研究, 1997(5): 18-21, 26. DOU Xiaofeng, LU Shouli, ZHAO Hui. Monte carol simulation on static recrystallization of steel[J]. Research on iron & steel, 1997(5): 18-21, 26. (  0) 0)
|
| [7] |
方斌, 黄传真, 崇学文, 等. 用改进的Monte Carlo算法模拟晶粒生长[J]. 材料导报, 2008, 22(5): 126-129. FANG Bin, HUANG Chuanzhen, CHONG Xuewen, et al. Simulation of grain Growth with improved Monte Carlo algorithm[J]. Materials review, 2008, 22(5): 126-129. (  0) 0)
|
| [8] |
林清夫. 二相粒子影响静态再结晶过程的数值模拟研究[J]. 材料热处理技术, 2012, 41(14): 86-88. LIN Qingfu. Numerical simulation on effect of second phase particle on static recrystallization[J]. Material & heat treatment, 2012, 41(14): 86-88. (  0) 0)
|
| [9] |
HUMPHREYS F J. A Network model for recovery and recrystallisation[J]. Scripta metallurgica et materialia, 1992, 27(11): 1557-1562. DOI:10.1016/0956-716X(92)90144-4 (  0) 0)
|
| [10] |
DAVIES C H J. The effect of neighbourhood on the kinetics of a cellular automaton recrystallisation model[J]. Scripta metallurgica et materialia, 1995, 33(7): 1139-1143. DOI:10.1016/0956-716X(95)00335-S (  0) 0)
|
| [11] |
MARX V, GOTTSTEIN G. Simulation of the texture evolution of aluminium alloys during primary static recrystallization using a cellular automaton approach[J]. Materials research society symposium proceedings, 1998: 529. DOI:10.1557/PROC-529-107 (  0) 0)
|
| [12] |
刘金义, 刘爽. Voronoi图应用综述[J]. 工程图学学报, 2004(2): 125-132. LIU Jinyi, LIU Shuang. A survey on applications of Voronoi diagrams[J]. Journal of engineering graphics, 2004(2): 125-132. (  0) 0)
|
| [13] |
刘宇雁, 包喜荣, 李振亮, 等. 采用改进的Monte Carlo方法实现晶粒生长的拓扑变化[J]. 安徽工业大学学报, 2005, 22(4): 319-321, 333. LIU Yuyan, BAO Xirong, LI Zhenliang, et al. Using improved Monte Carlo method to realizating the topology change of grain growth[J]. Journal of Anhui University of Technology, 2005, 22(4): 319-321, 333. (  0) 0)
|
| [14] |
钟晓征, 陈伟元, 王豪才, 等. 多晶材料晶粒生长的Monte Carlo计算机模拟方法Ⅰ模拟正常晶粒生长[J]. 功能材料, 1999, 30(3): 232-235. ZHONG Xiaozheng, CHEN Weiyuan, WANG Haocai, et al. Monte Carlo computer methods for simulating grain growth of polycrystalline material Ⅰ Simulating normal grain growth[J]. Functional materials, 1999, 30(3): 232-235. (  0) 0)
|
| [15] |
沈满德, 余圣甫, 王宁. 蒙特卡罗法模拟晶粒生长过程中的Voronoi模型[J]. 机械工程材料, 2006, 30(3): 11-13. SHEN Mande, YU Shengfu, WANG Ning. Voronoi model in Monte Carlo simulation of grain growth[J]. Materials for mechanical engineering, 2006, 30(3): 11-13. (  0) 0)
|
| [16] |
黄诚, 宋波, 毛红, 等. 铁液洁净度对凝固热力学参数的影响[J]. 钢铁研究学报, 2003, 15(4): 9-11, 17. HUANG Cheng, SONG Bo, MAO Hong, et al. Dependence of thermodynamic parameters of solidification on liquid iron cleanness[J]. Journal of iron and steel research, 2003, 15(4): 9-11, 17. (  0) 0)
|
| [17] |
王增辉, 倪明玖. 液态纯铁自扩散系数研究[J]. 工程热物理学报, 2011, 32(8): 1403-1405. WANG Zenghui, NI Mingjiu. Research on self-diffusion coefficient of liquid pure iron[J]. Journal of engineering thermophysics, 2011, 32(8): 1403-1405. (  0) 0)
|
| [18] |
赵亚楠, 郭建政, 李绍敏, 等. 大型钢锭凝固模拟计算中空间与时间步长选取[J]. 铸造, 2013, 62(9): 861-864. ZHAO Yanan, GUO Jianzheng, LI Shaomin, et al. Selection of mesh size and time step in solidification simulation of large ingot[J]. Foundry, 2013, 62(9): 861-864. (  0) 0)
|
| [19] |
朱家明. 基于图像分析软件的晶粒尺寸分布统计[J]. 压电与声光, 2013, 35(4): 585-587. ZHU Jiaming. The measurement of grain size distribution through image analysis software[J]. Piezoelectrics & acoustooptics, 2013, 35(4): 585-587. DOI:10.11977/j.issn.1004-2474.2013.04.030 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


