2. 哈尔滨工业大学 复合材料与结构研究所, 黑龙江 哈尔滨 150001
2. Center for Composite Materials and Structures, Harbin Institute of Technology, Harbin 150001, China
轻质纳米复合材料由于具有优异的热传导性能,因此具有广泛的应用范围[1-4]。其中,纳米复合材料中纳米填料广泛采用碳纳米材料。碳纳米管(carbon nanotubes,CNTs)由于具备准一维特性及超拓扑结构,因此CNTs的优异的电学、热学、化学、力学性能得到了极大关注[1]。室温环境下测量单壁碳纳米管(single-walled carbon nanotubes, SWCNTs)的轴向导热率高达6 600 W/(m-1·k)[2]。SWCNTs可以应用于高性能结构及功能性纳米复合材料中的增强项及功能项。很多研究者使用SWCNTs制备高导热纳米材料[3-8]。
然而,由于CNTs的纳米尺寸效应及巨大的比表面积,CNTs在聚合物基体中分散不均匀、CNTs与聚合物基体之间缺乏足够的粘结性及CNTs的非定向分布等缺点阻碍了复合材料性能的显著提高[9]。此外,CNTs的物理性质对CNTs的数量、直径、缺陷及所处环境等因素敏感[10],并且对影响单独CNTs物理性质的内在和外在因素的控制比较困难[11]。巴基纸(Buckypaper,BP)(又称纳米纸)是相互纠缠的CNTs构成的自支撑、含有孔隙的薄片状、可以和聚合物相结合的复合材料,巴基纸中CNTs分散均匀、纳米结构可控、CNTs含量可以高达60%,巴基纸解决了纳米填料在聚合物基体中的均匀分散问题[12-13]。巴基纸复合材料具有优异的力学、热学及电学性质,可以应用于电子、航天、航空工业等领域。由于碳纳米管巴基纸具有巨大的比表面积及可协调的网络结构,因此和纳米填料相比,巴基纸极大地提高了复合材料的导电性,因而巴基纸在制备导电性的巴基纸基复合材料方面显现出较高的优越性[14]。研究表明,碳纳米管巴基纸不仅在平面方向、更重要的是在垂直于巴基纸方向及厚度方向具有更好的导热性能。由于巴基纸及巴基纸基复合材料中CNTs形成网络结构,因此可以获得较高的导热率,在大功率电子设备散热方面具有广泛的应用前景[15-16]。
具有优异导热性能的巴基纸/聚合物复合材料可以用于解决先进电子设备、散热器、连接器、印刷电路板的散热问题。然而,目前国内外学者对于巴基纸/聚合物复合材料的热学性能的研究相对较少[17-20],尤其是对于巴基纸/聚合物复合材料的热传导分析及优化设计方面研究更为少见。因此,本文采用有限元软件FLUENT分别模拟研究了不同工况条件下矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料的热传导性能,分析了加热功率及聚合物基体导热系数等因素对加热过程中巴基纸/聚合物复合材料达到稳态所需时间及温度分布的影响规律。
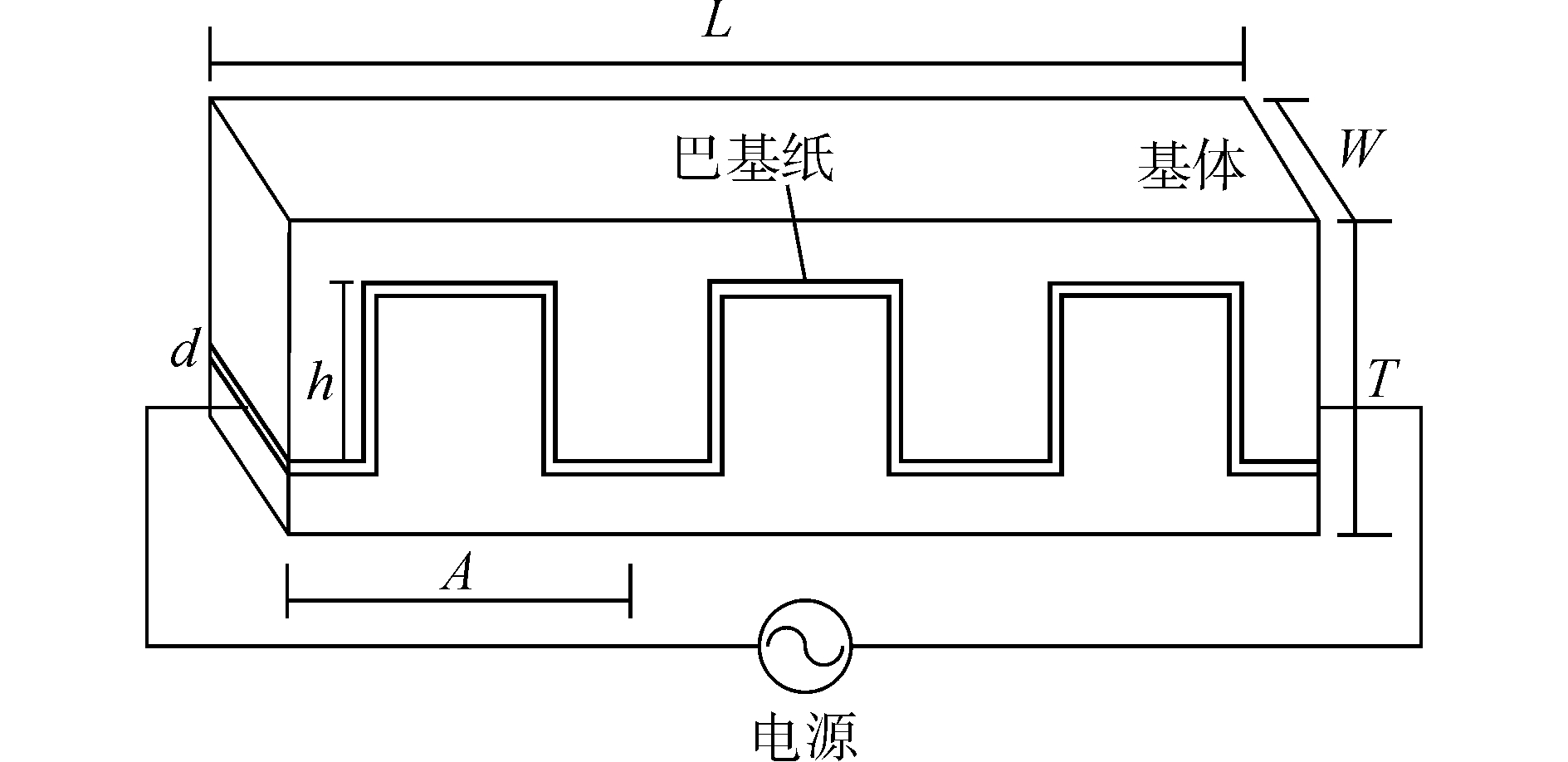
1 有限元模拟方案图 1为矩形弯曲巴基纸增强聚合物基复合材料的加热装置示意图,由于巴基纸具有导电性,接通电源后巴基纸产生的热量传递至聚合物基体,一定时间后整个加热装置逐渐达到热稳定状态。如图 1所示,加热模型总高度T为100 mm,总宽度W为50 mm,总长度L为600 mm,巴基纸加热片厚度d为10 mm。
|
Download:
|
| 图 1 加热试验装置示意图 Fig. 1 Images of heating experimental device | |
图 2所示为通过PROE 5.0软件分别建立的矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料几何模型,模型总高度T为100 mm,总宽度W为50 mm,总长度L为600 mm。图 2(a)及2(b)中矩形弯曲及正弦形巴基纸加热片均为5个弯曲周期A(A为120 mm),矩形弯曲巴基纸加热片的弯曲高度h为60 mm,图 2(c)中正弦形巴基纸加热片的振幅为30 mm。

|
Download:
|
| 图 2 不同形状巴基纸基复合材料几何模型 Fig. 2 Geometric models of nanocomposite with different shape buckypapers | |
采用ICEM对模型进行网格划分后,使用有限元软件FLUENT对矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料不同加热工况进行数值模拟,分析加热功率和聚合物基体导热系数对巴基纸/聚合物基复合材料加热过程中温度场分布及不同时刻的温度分布规律:
1) 加热功率:5、15、25、50 W。
2) 导热系数:巴基纸导热系数为1 W/(m·K),聚合物基体导热系数分别为0.02、0.05、0.1和0.2 W/(m·K)。
采用有限元软件FLUENT模拟巴基纸加热片对聚合物基体加热过程的计算时,所用边界条件及其初始值如下。外边界设置为第三类边界条件,自然对流换热系数设为10 W/(m2·K),环境温度设为300 K;巴基纸厚度设为10 mm;加热功率设为25 W。巴基纸及聚合物基体的比热容分别为1 000 J/(kg·K)和1 300 J/(kg·K)。巴基纸及聚合物基体的密度分别为500 kg/m3和1 000 kg/m3。
模拟计算时,由于聚合物基体不释放热量,所以设定聚合物基体的单位体积内热源qv=0;假设巴基纸加热片将电加热功率全部转化为内能,因此巴基纸加热片的单位体积内热源qv=加热功率/VBP。
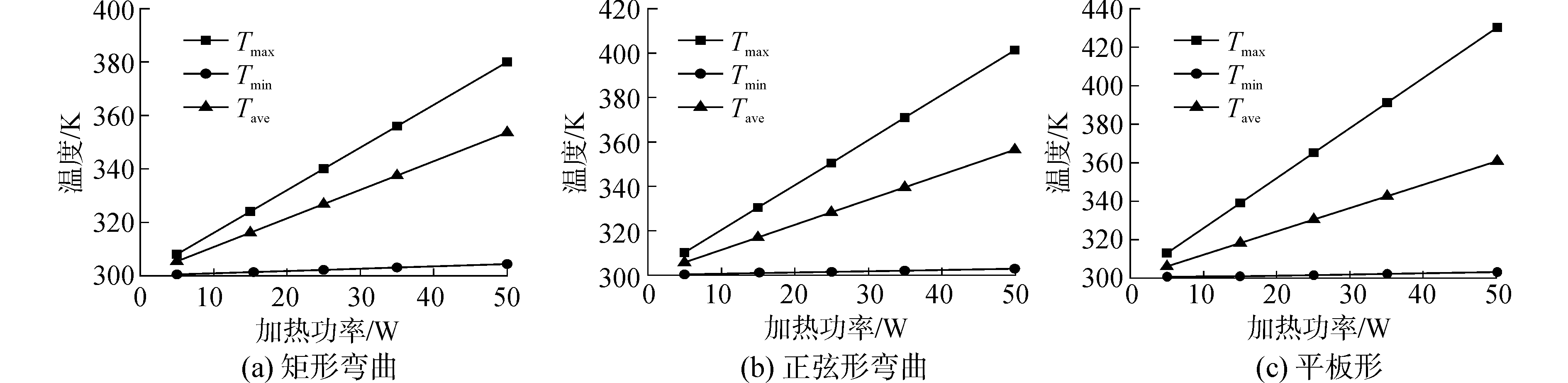
2 结果与讨论 2.1 加热功率的影响图 3为巴基纸加热片的形状、厚度、弯曲数量等条件相同情况下,加热功率分别为5、15、25、50 W时,矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料加热达到稳态时在z=0中心截面上的典型温度(最高温度、最低温度和平均温度)随加热功率的变化曲线。
|
Download:
|
| 图 3 不同形状巴基纸基复合材料沿z=0截面典型温度变化曲线 Fig. 3 Typical temperature curves of composite reinforced with different shapes along the section z=0 | |
从图 3可以看出,无论巴基纸加热片是平板形还是进行矩形弯曲或正弦形弯曲,复合材料加热达到稳态后,典型温度(最高温度、最低温度和平均温度)都随加热功率成线性变化。与矩形弯曲及正弦形巴基纸相比,平板形巴基纸体积最小,当采用相同的功率进行加热时,平板形巴基纸的单位体积内热源最大,从而导致平板形巴基纸增强聚合物基复合材料的平均温度最高,正弦形巴基纸增强聚合物基复合材料的平均温度次之,矩形弯曲巴基纸增强聚合物基复合材料的平均温度最低。因此,可根据实际工况中温度需要选择巴基纸加热片形状。
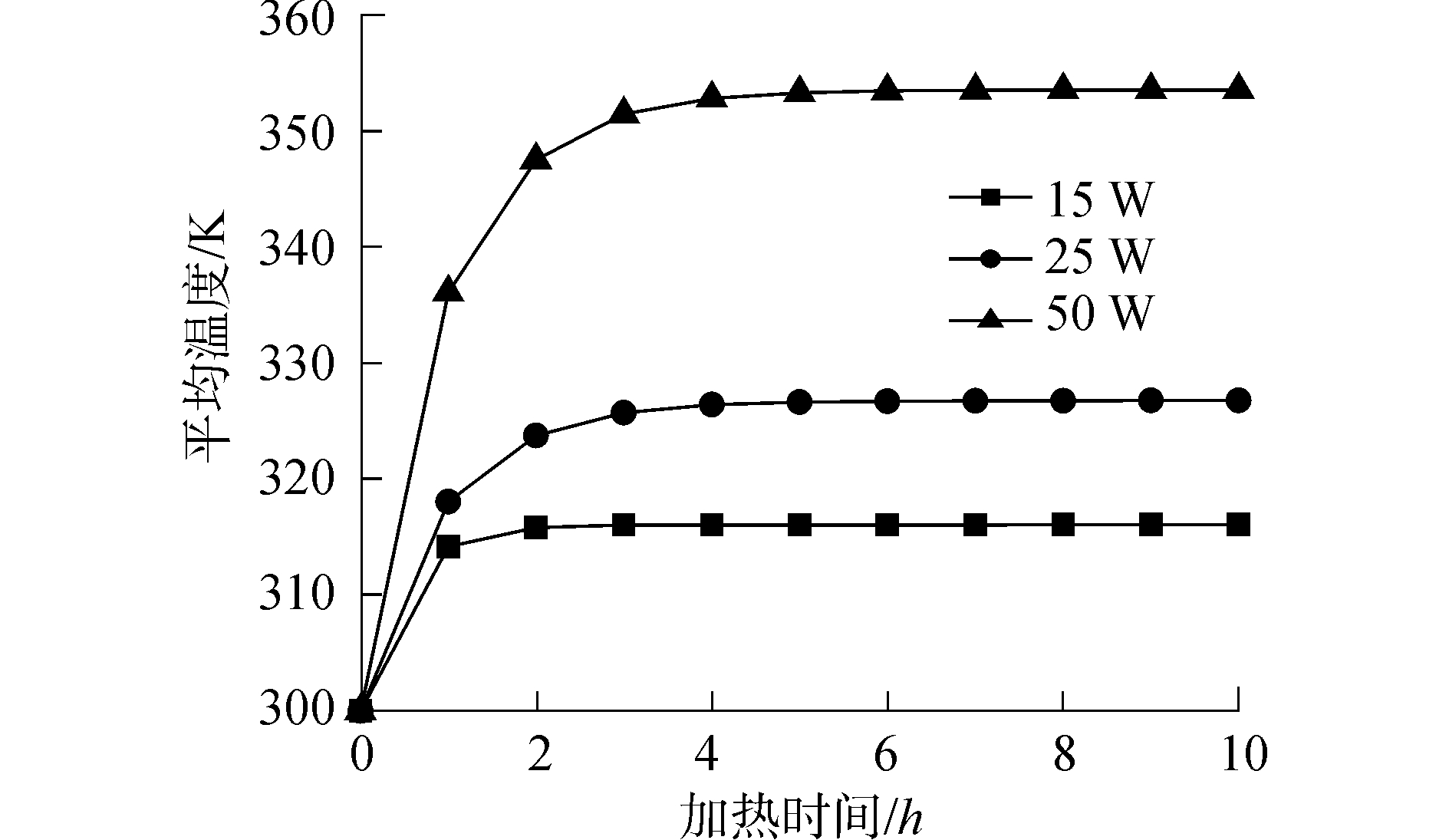
图 4为以矩形弯曲巴基纸增强聚合物基复合材料为例,在巴基纸加热片厚度、形状等条件相同的情况下,采用FLUENT软件分析了加热功率分别为15、25和50 W时,矩形弯曲巴基纸增强聚合物基复合材料加热达到稳态过程中在z=0截面上平均温度随加热时间的变化曲线。
|
Download:
|
| 图 4 不同加热功率作用下矩形弯曲巴基纸基复合材料在z=0截面平均温度随时间的变化曲线 Fig. 4 Average temperature curves of composite reinforced by pulse bending buckypaper with different heating power versus time along the section z=0 | |
由图 4可知,随着加热功率由15 W增至50 W,矩形弯曲巴基纸增强聚合物基复合材料平均温度水平也增高,并且随着加热的持续进行,复合材料的升温速率也逐渐减缓。这是由于加热功率增大导致巴基纸加热片的单位体积内热源增大,因而巴基纸加热片所能达到的温度水平越高;并且由于对流散热速率低于产热量的增大速率使复合材料达到稳态所需要的时间也增长。
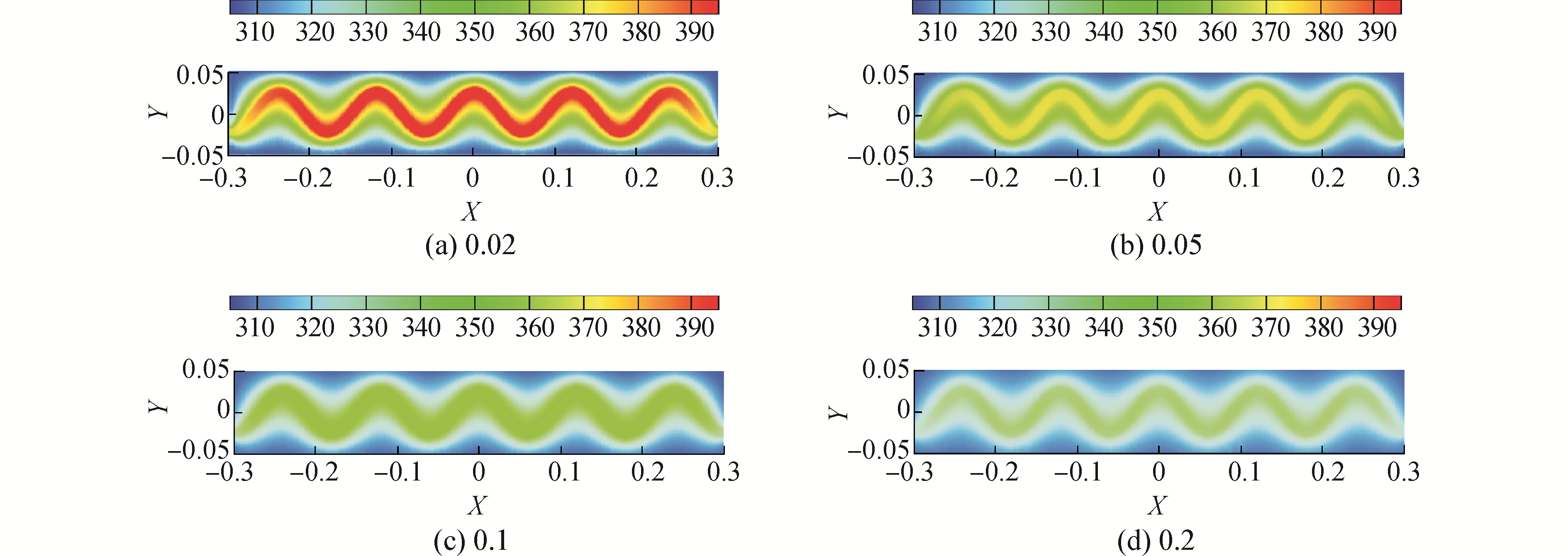
2.2 聚合物基体导热系数的影响图 5~7为巴基纸加热片形状、厚度、弯曲数量、加热功率等条件相同情况下,巴基纸导热系数为1 W/(m·K),聚合物基体导热系数分别为0.02、0.05、0.1和0.2 W/(m·K)时,矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料加热达到稳态时在z=0截面上的温度分布云图。

|
Download:
|
| 图 5 不同导热系数条件下矩形弯曲巴基纸基复合材料在z=0截面的温度分布 Fig. 5 Temperature distribution of composite reinforced by pulse bending buckypaper with different thermal conductivity along the section z=0 | |
|
Download:
|
| 图 6 不同导热系数条件下正弦形巴基纸基复合材料在z=0截面的温度分布 Fig. 6 Temperature distribution of composite reinforced by sinusoidal buckypaper with different thermal conductivity along the section z=0 | |

|
Download:
|
| 图 7 不同导热系数条件下平板形巴基纸基复合材料在z=0截面的温度分布 Fig. 7 Temperature distribution of composite reinforced by flatbuckypaper with different thermal conductivity along the section z=0 | |
由图 5~7可知,矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料加热达到稳态时,最高温度均随聚合物基体材料导热系数的增大而降低,而最低温度均随聚合物基体材料导热系数的增大而升高。由图 5~7的温度分布云图可以看出,随着聚合物基体导热系数由0.02 W/(m·K)增大至0.2 W/(m·K),矩形弯曲、正弦形及平板形巴基纸增强聚合物基复合材料加热达到稳态时在z=0截面上的温度分布越来越均匀。分析认为,随着聚合物基体材料导热系数增大,由巴基纸加热片产生的热量更容易通过聚合物基体材料传导至外界面散出,热量不易在聚合物基体材料内部积累,并且热量分布更加均匀,因此最高温度和平均温度呈降低趋势,最低温度则呈升高趋势。
图 8为以矩形弯曲巴基纸增强聚合物基复合材料为例,在巴基纸加热片厚度、加热功率等条件相同的情况下,采用FLUENT分析了聚合物基体导热系数发生变化时,矩形弯曲巴基纸增强聚合物基复合材料加热达到稳态过程中平均温度的变化规律。

|
Download:
|
| 图 8 不同导热系数条件下矩形弯曲巴基纸基复合材料在z=0截面平均温度随时间的变化曲线 Fig. 8 Average temperature curves of composite reinforced by pulse bending buckypaper with different thermal conductivity versus time along the section z=0 | |
由图 8可知,聚合物基体导热系数越大,复合材料达到稳态所需时间越小,这是由于随着聚合物基体导热系数λ的增大,热扩散系数α越大(α=λ/ρc,ρ和c分别为材料密度和热容)。由于表征导热速率的热扩散系数α增大,使得聚合物基体导热速率增大,进而导致巴基纸增强聚合物基复合材料达到稳态所需要的时间越小。
3 结论1) 当采用相同的功率加热时,平板形巴基纸增强聚合物基复合材料的平均温度最高,正弦形巴基纸增强聚合物基复合材料的平均温度次之,矩形弯曲巴基纸增强聚合物基复合材料的平均温度最低。
2) 随着加热功率的增大,巴基纸增强聚合物基复合材料加热达到稳态后整体温度水平呈线性增长,且达到稳态时所需要的时间也延长。这是由于对流散热速率小于产热量的增大速率,导致巴基纸增强聚合物基复合材料达到稳态所需时间增长。并且随着加热的持续进行,复合材料的升温速率也逐渐减缓。
3) 随着聚合物基体材料导热系数的增大,巴基纸增强聚合物基复合材料达到稳态所需要的时间越短,温度分布更加均匀。这是由于随着聚合物基体材料导热能力的增强,巴基纸加热片的热量更容易散出,热量不易在聚合物基体内部积累。
| [1] |
VALCÁRCEL M, CÁRDENAS S, SIMONET B M. Role of carbon nanotubes in analytical science[J]. Analytical chemistry, 2007, 79(13): 4788-4797. DOI:10.1021/ac070196m (  0) 0)
|
| [2] |
BERBER S, KWON Y K, TOMANEK D. Unusually high thermal conductivity of carbon nanotubes[J]. Physical review letters, 2000, 84(20): 4613-4616. DOI:10.1103/PhysRevLett.84.4613 (  0) 0)
|
| [3] |
POP E, MANN D, WANG Qian, et al. Thermal conductance of an individual single-wall carbon nanotube above room temperature[J]. Nano letter, 2006, 6(1): 96-100. DOI:10.1021/nl052145f (  0) 0)
|
| [4] |
HONE J, WHITNEY M, ZETTL A. Thermal conductivity of single-walled carbon nanotubes[J]. Physical review B:condensed matter, 1999, 59(4): R2514-R2516. DOI:10.1103/PhysRevB.59.R2514 (  0) 0)
|
| [5] |
谢璠, 齐暑华, 李珺鹏, 等. 聚合物基导热复合材料的研究进展[J]. 中国胶粘剂, 2011, 20(9): 59-64. XIE Fan, QI Shuhua, LI Junpeng, et al. Research progress of polymer-based composites with thermal conductivity[J]. China adhesives, 2011, 20(9): 59-64. (  0) 0)
|
| [6] |
闫盼盼, 熊伟, 张保丰, 等. CF/CNTs多尺度混杂填充PA6复合材料性能研究[J]. 塑料科技, 2018, 46(1): 37-41. YAN Panpan, XIONG Wei, ZHANG Baofeng, et al. Study on properties of CF/CNTs multiscale hybrid filled PA6 composites[J]. Plastics science and technology, 2018, 46(1): 37-41. (  0) 0)
|
| [7] |
刘珍红, 孙晓刚, 陈珑, 等. 碳纳米管纸/纳米硅复合电极的锂离子电池性能[J]. 材料工程, 2018, 46(1): 99-105. LIU Zhenhong, SUN Xiaogang, CHEN Long, et al. Performance of lithium ion batteries with carbon nanotube paper/Nano silicon composite electrode[J]. Journal of materials engineering, 2018, 46(1): 99-105. DOI:10.11868/j.issn.1001-4381.2016.000175 (  0) 0)
|
| [8] |
王俊, 朱振华, 张明华, 等. CB/MWCNTs/PP导电复合材料的制备与性能表征[J]. 塑料工业, 2017, 46(11): 107-112. WANG Jun, ZHU Zhenhua, ZHANG Minghua, et al. Preparation and characterization of CB/MWCNTs/PP conductive composites[J]. China plastics industry, 2017, 46(11): 107-112. DOI:10.3969/j.issn.1005-5770.2017.11.025 (  0) 0)
|
| [9] |
CHANG C Y, PHILLIPS E M, LIANG R, et al. Alignment and properties of carbon nanotube buckypaper/liquid crystalline polymer composites[J]. Journal of applied polymer science, 2013, 128(3): 1360-1368. (  0) 0)
|
| [10] |
ROMERO H E, BOLTON K, ROSÉN A, et al. Atom collision-induced resistivity of carbon nanotubes[J]. Science, 2005, 307(5706): 89-93. DOI:10.1126/science.1102004 (  0) 0)
|
| [11] |
WANG Chuan, ZHANG Jialu, RYU K, et al. Wafer-scale fabrication of separated carbon nanotube thin-film transistors for display applications[J]. Nano letter, 2009, 9(12): 4285-4291. DOI:10.1021/nl902522f (  0) 0)
|
| [12] |
LAHIFF E, LEAHY R, COLEMAN J N, et al. Physical properties of novel free-standing polymer-nanotube thin films[J]. Carbon, 2006, 44(8): 1525-1529. DOI:10.1016/j.carbon.2005.12.018 (  0) 0)
|
| [13] |
CHENG Qunfeng, BAO Jianwen, PARK J, et al. High mechanical performance composite conductor:multi-walled carbon nanotube sheet/bismaleimide nanocomposites[J]. Advanced functional materials, 2009, 19(20): 3219-3225. DOI:10.1002/adfm.v19:20 (  0) 0)
|
| [14] |
LU Haibao, LIANG Fei, GOU Jihua, et al. Synergistic effect of self-assembled carbon nanopaper and multi-layered interface on shape memory nanocomposite for high speed electrical actuation[J]. Journal of applied physics, 2014, 115(6): 064907. DOI:10.1063/1.4865326 (  0) 0)
|
| [15] |
CHEN Hongyuan, CHEN Minghai, DI Jiangtao, et al. Architecting three-dimensional networks in carbon nanotube buckypapers for thermal interface materials[J]. The journal of physical chemistry C, 2012, 116(6): 3903-3909. DOI:10.1021/jp2086158 (  0) 0)
|
| [16] |
DÍEZ-PASCUAL A M, GUAN Jingwen, SIMARD B, et al. Poly(phenylene sulphide) and poly(ether ether ketone) composites reinforced with single-walled carbon nanotube buckypaper:Ⅱ-Mechanical properties, electrical and thermal conductivity[J]. Composites part A:applied science and manufacturing, 2012, 43(6): 1007-1015. DOI:10.1016/j.compositesa.2011.11.003 (  0) 0)
|
| [17] |
吕海宝. 电驱动与溶液驱动形状记忆聚合物混合体系及其本构方程[D]. 哈尔滨: 哈尔滨工业大学, 2010. LYU Haibao. Electro-and solution-active shape memory polymer blends and their thermodynamic constitutive equation[D]. Harbin: Harbin Institute of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10213-2011012955.htm (  0) 0)
|
| [18] |
刘金世, 薛庆忠. 碳纳米管复合材料的有效热导率[J]. 石油大学学报(自然科学版), 2004, 28(5): 142-144. LIU Jinshi, XUE Qingzhong. Effective thermal conductivity of carbon nanotube composites[J]. Journal of the University of Petroleum, China(nature science), 2004, 28(5): 142-144. (  0) 0)
|
| [19] |
YANG K, HE J, PUNEET P, et al. Tuning electrical and thermal connectivity in multiwalled carbon nanotubebuckypaper[J]. Journal of Physics Condensed Matter an institute of physics, 2010, 22(33): 334215-334220. DOI:10.1088/0953-8984/22/33/334215 (  0) 0)
|
| [20] |
MEMON M O, HAILLOT S, LAFDI K. Carbon nanofiber based buckypaper used as a thermal interface material[J]. Carbon, 2011, 49(12): 3820-3828. DOI:10.1016/j.carbon.2011.05.015 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


